当前位置：首页 > news >正文

从零开始学习Slam--数学概念

news 来源：原创 2025/8/27 0:34:06

正交矩阵

矩阵的转置等于它的逆矩阵，这样的矩阵称之为正交矩阵
即： $Q^T Q = I$ ，
这样的矩阵列向量都是单位向量且两两正交。

旋转矩阵属于特殊的正交群，即SO(n)，这里n通常是3，所以SO(3)就是三维旋转矩阵的群。
行列式为1的正交矩阵构成SO(n)，而行列式为-1的正交矩阵则可能包含反射变换 $^2$ 。旋转不应该改变物体的手性，所以行列式必须是1。而 正交性保证了旋转时向量的长度和夹角不变 $^1$ ，所以旋转矩阵必须是正交的，行列式1。

注释1：首先，正交性为什么能保证不拉伸或压缩物体呢？可能是因为正交矩阵作用于向量时，保持向量的长度不变。比如，如果有一个向量v，经过正交矩阵Q变换后的长度应该是v的原始长度。
数学上： $(Qv)^T (Qv) = v^T Q^T Q v = v^T v = ||v||²$ 。所以长度确实不变。那夹角呢？
两个向量v和w的夹角由内积决定：

变换后的内积 $Qv)·(Qw) = v^T Q^T Q w = v^T w$ ，所以内积不变，夹角也不变。所以正交性确实保证了旋转操作不会改变长度和夹角，也就是不拉伸或压缩。

注释2 ：之前在介绍旋转矩阵时讲过一个方法：“绕谁谁不变”，所以向量 $a,b]^T$ 绕x轴旋转之后变为 $a,-b]^T$ ,所以反射矩阵为 $\begin{bmatrix} 1&0 \\ 0&-1 \end{bmatrix}$ ,行列式的值为-1

行列式

计算方法

在这里插入图片描述

性质

矩阵是否可逆
若det(A) ≠ 0，则矩阵 A 可逆（非奇异矩阵）。
若det(A) = 0，则矩阵 A 不可逆（奇异矩阵）。
线性变换的几何意义
行列式的绝对值表示矩阵对应线性变换对空间的体积缩放比例：
二维矩阵：行列式是面积缩放因子。
三维矩阵：行列式是体积缩放因子。例如，若 det(A) = 2, 则线性变换将原空间的体积放大2倍。
方向是否改变
行列式的符号反映线性变换是否改变空间的方向：
det(A) > 0 : 保持空间方向（如纯旋转）。
det(A) < 0 : 反转空间方向（如镜像反射）。
矩阵的正交性与旋转
正交矩阵（列向量为单位正交向量）的行列式值为 ±1.
det(A) = 1: 对应旋转变换（如 SO(n) 群）。
det(A) = -1: ：包含反射变换（改变手性）。
特征值的乘积
行列式等于矩阵所有特征值的乘积：
det(A) = ${\lambda }_{1}*{\lambda }_{2}*{\lambda }_{3}*{\lambda }_{4}*{\lambda }_{5}...$

李群与李代数

李群

李群是同时具有光滑流形结构和群结构的数学对象，群操作（乘法与取逆）是光滑的。例如：
SO(3)：三维旋转矩阵群，元素是3×3正交矩阵，行列式为1。四元数是旋转的一种表示方式（属于 SO(3)）
SE(3)：三维刚体变换群（旋转+平移），元素是4×4齐次变换矩阵。

光滑流形结构（Smooth Manifold Structure）：流形是可以局部看作点组成的空间。而“光滑”意味着这个空间是处处平滑的，没有尖角或断点。也就是说，在流形上的每一点周围都可以找到一个局部，使得这部分在数学上可以和一个欧氏空间（例如平面在二维，或者三维空间）完全一致，而且这些局部映射是光滑的（平滑无突变）。简单来说，光滑流形就是一个处处可以进行微分运算的空间。

群结构（Group Structure）：群是集合上定义了一种满足特定条件的二元运算（通常称为“乘法”，但不是字面意义上的乘法）的代数结构。这些条件包括：

封闭性：对于任意的群内元素 a 和 b，它们的运算结果 a * b 也必定属于这个群。
结合律：对于任意的群内元素 a, b, 和 c，恒有 $(a * b) * c = a * (b * c)$ 。
运算封闭性下，群总包含一个单位元e，使得对于群内任意元素 a，恒有 $a * e = e * a = a$ 。
对于群内任意元素 a，都存在一个逆元 $a^{-1}$ ，使得 $a * a^{-1} = a^{-1} * a = e$ 。简单来说，群结构是以一个集合和满足特定性质的运算为基础的代数结构。

群操作（Group Operation）：在上面群结构的定义中，我们使用了“运算”这个词，指的是群内元素之间可以进行的某种操作。这种操作一般被称为群操作，它必须满足上面定义的群结构所要求的那几个条件（封闭性、结合律、包含单位元和逆元）。最直观的理解就是，给定群中的任意两个元素，它们经过群操作后得到的结果仍然是这个群的一个合法元素，而且这个操作需满足一系列的代数性质。

李代数（Lie Algebra）

李代数是与李群对应的向量空间，附加一个李括号运算（非交换的二元运算）。它描述了李群在单位元处的切空间，可以看作李群的局部线性近似。例如：
so(3)：对应SO(3)的李代数，由3×3反对称矩阵组成（形式为 ${\omega }_{×}$ ，其中 ${ω∈\mathbb{R}}^{3}$ )
se(3)：对应SE(3)的李代数，包含平移和旋转分量，形式为 $[ρ,ω]^⊤∈\mathbb{R}^6$
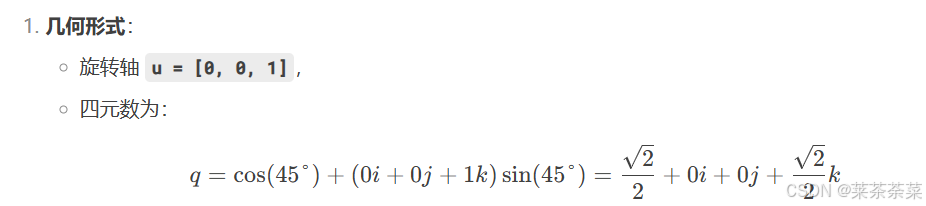
在这里插入图片描述

李括号运算：
李括号运算（Lie bracket operation）是定义在李代数上的一个特定类型的二元运算，它反映了李代数与相关的李群之间的微分结构。具体来说，李括号运算是一个从李代数的两个元素到李代数的映射，记作 ([X, Y])，其中 (X) 和 (Y) 是李代数中的元素。
李括号运算有以下几个重要性质：

双线性：对任意的元素 (X, Y, Z) 和标量 (a, b) （来自相关的标量域），有 [ [aX + bY, Z] = a[X, Z] + b[Y, Z] ] 和 [ [X, aY + bZ] = a[X, Y] + b[X, Z]. ]
交错(反对称)性：对于任意的 (X)，有 [ [X, X] = 0. ] 进一步推论出 ([X, Y] = -[Y, X])。
雅可比恒等式：对于任意的 (X, Y, Z), 有 [ [[X, Y], Z] + [[Y, Z], X] + [[Z, X], Y] = 0 ]

李括号运算并不总是可交换的，也就是说，通常情况下 $\neq [Y,X])$ 。具体到李代数与李群之间的关系，李代数可以被看作李群在单位元（即李群的恒等元素）的切空间，李括号反映了李群上流形局部的非交换性，即群操作在局部上的非交换性质。将李群上的局部微分结构（通过切空间）转化为代数结构上的运算，李括号就是非常关键的形式化工具。

例如，在一般的线性李代数 $(\mathfrak{gl}(n))$ 中，李括号运算是由矩阵的换位子定义的，即对于两个 ${[n \ n]}$ 矩阵 (A) 和 (B)，定义李括号为： $[A, B] = A B - B A$ 其中 (AB)被理解为矩阵乘法。这个交换子运算满足上述李括号的所有性质，并且可以明确表示两个算子在操作上的非交换性。

李群与李代数的相互转换

李群与李代数通过**指数映射（Exponential Map）和对数映射（Logarithmic Map）**相互转换：

指数映射：李代数 → 李群
在这里插入图片描述

${a}_{×}$ 是旋转轴单位向量 a 的反对称矩阵，θ 是旋转角度

上面的推导使用了反对称矩阵的性质：

向量三重积公式：a × (b × c) = (a·c)b - (a·b)c

在这里插入图片描述

对比一下之前多维矩阵旋转的罗德里格斯公式：
在这里插入图片描述
我们发现：矩阵形式的罗德里格斯公式在系数上进行了归一化处理，以适应矩阵指数的形式

在这里插入图片描述

优化中的应用

无约束优化：在李代数空间中，旋转表示为3维向量 ${ω∈\mathbb{R}}^{3}$ ，无需正交性或行列式约束，可直接用梯度下降等算法优化。

更新步骤：每次优化迭代后，通过指数映射将李代数增量转换为李群（旋转矩阵），确保结果始终满足约束。
在这里插入图片描述

/**\* \brief SE3 Vertex parameterized internally with a transformation matrixand externally with its exponential map*/class G2O_TYPES_SBA_API VertexSE3Expmap : public BaseVertex<6, SE3Quat>{
public:EIGEN_MAKE_ALIGNED_OPERATOR_NEWVertexSE3Expmap();bool read(std::istream& is);bool write(std::ostream& os) const;virtual void setToOriginImpl() {_estimate = SE3Quat();}virtual void oplusImpl(const number_t* update_)  {Eigen::Map<const Vector6> update(update_);setEstimate(SE3Quat::exp(update)*estimate());        //更新方式}
};

正交矩阵

行列式

计算方法

性质

李群与李代数

李群

李代数（Lie Algebra）

李群与李代数的相互转换

优化中的应用

相关文章：