当前位置：首页 > news >正文

数据结构--树二叉树顺序结构存储的二叉树（堆）

news 来源：原创 2025/5/15 4:42:38

前言

前面我们学习了顺序表、链表、栈和队列，这些都是线性的数据结构。今天我们要来学习一种非线性的数据结构——树。

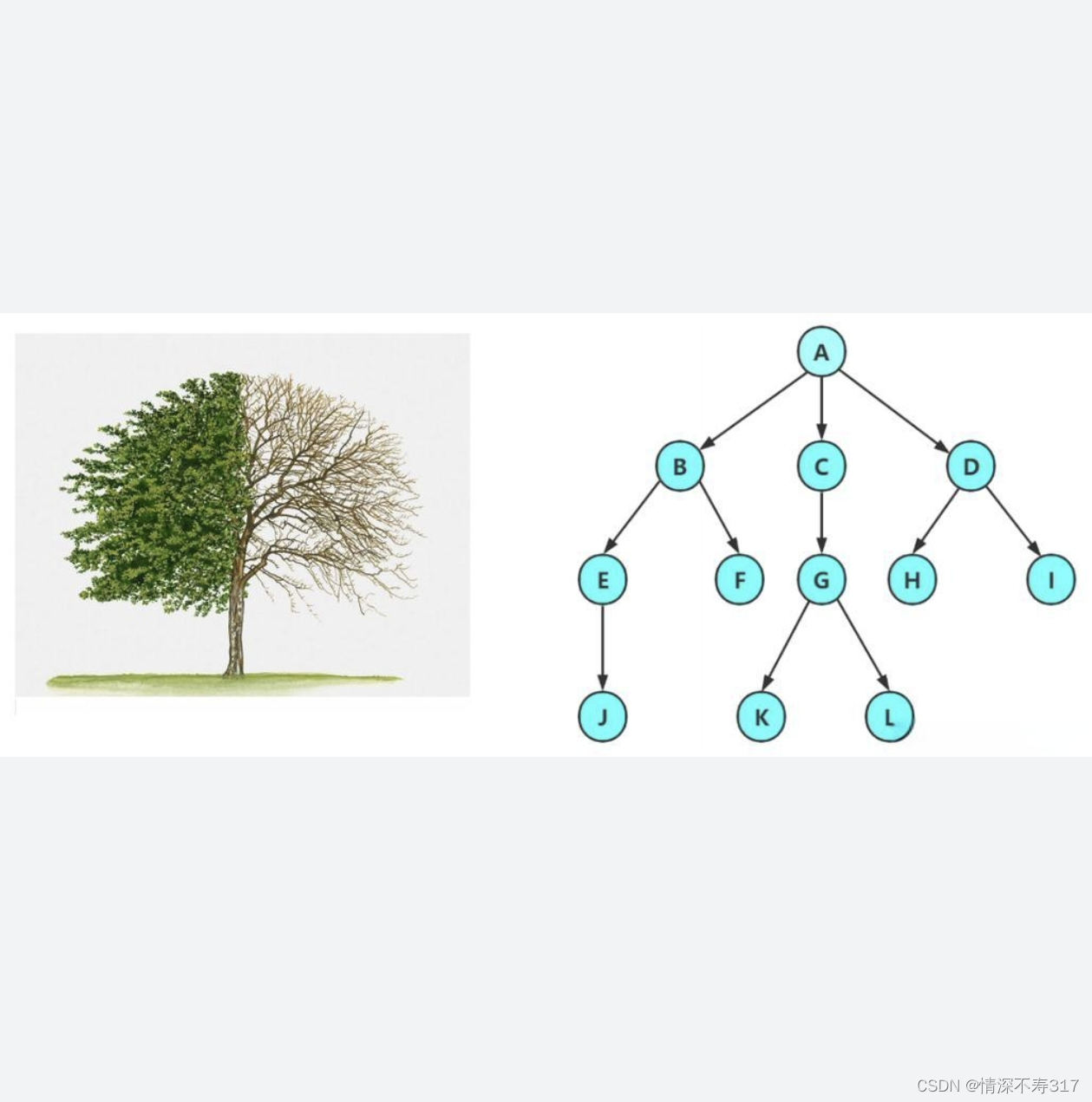
树的概念及结构

树的概念

树是一种非线性的数据结构，是由n（n≥0）个有效结点组成的一个具有层次关系的集合。

树有一个特殊的结点——根结点 根结点没有前驱结点。
除根结点外，其余结点被分成M（M＞0）个互不相交的集合T1、T2、……、Tm，其中每一个集合Ti(1≤i≤m)又是一颗结构与树类似的子树。每棵子树的根结点有且只有一个前驱，但可以有0个或多个后继。
因此，树是递归定义的。

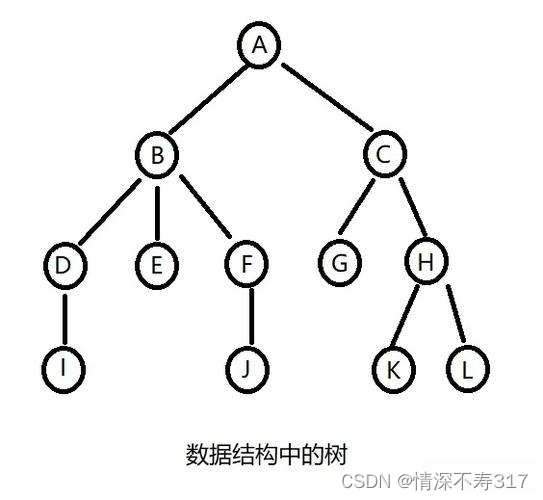
注意：树形结构中，子树之间不能有交集，否则就不是树形结构。

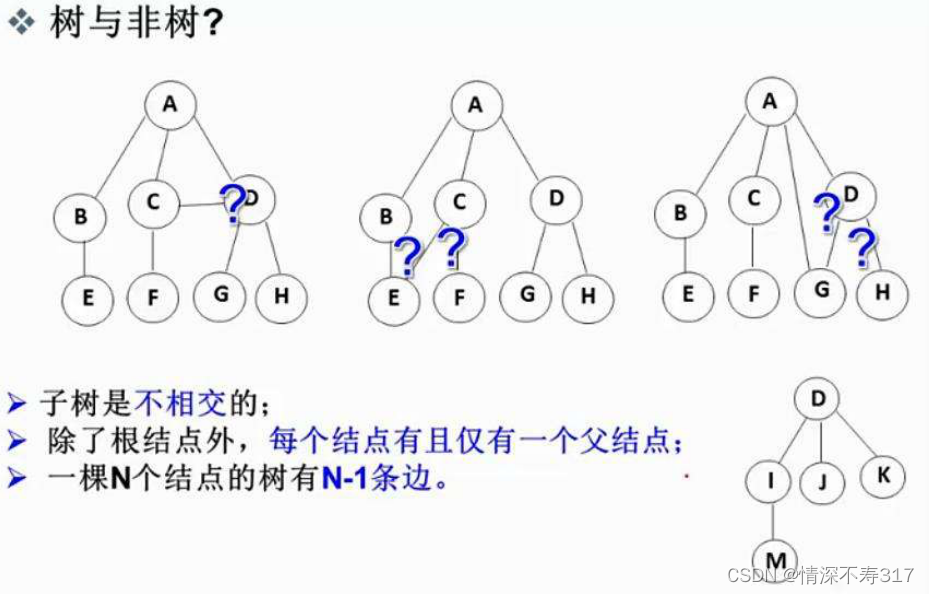
与树相关的概念

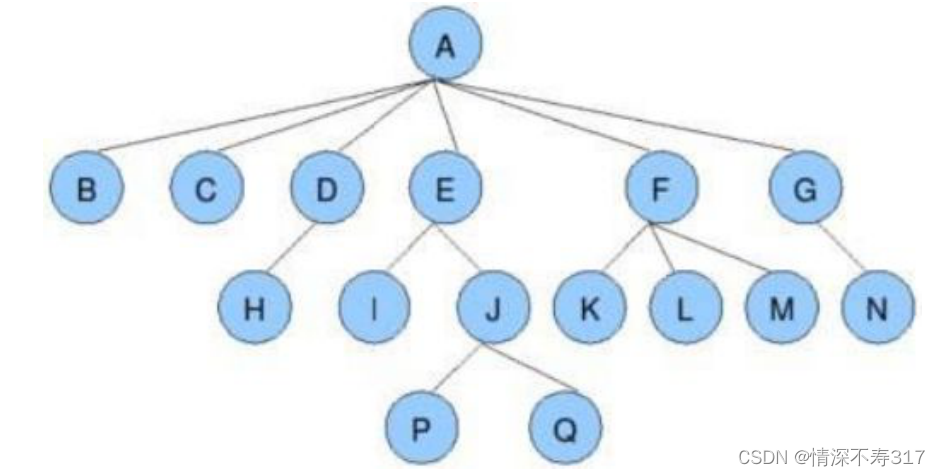
节点的度：一个节点含有的子树的个数称为该节点的度。（如上图中节点A的度为6）

树的度：一棵树中，最大的节点的度称为树的度。（如上图中树的度为6）

叶子节点或终端节点：度为0的节点为叶子节点。（如上图中B、C、H、I、P、Q、K、L、M、N都为叶子节点）

非终端节点或分支节点：度不为0的结点。（如上图中D、E、J、F、G节点为分支节点）

双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点。（例如，A是B的父节点）

孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点。（例如，B是A的孩子节点）

兄弟节点：具有相同父节点的节点互称为兄弟节点。（例如，B和C互为兄弟节点）

堂兄弟节点：双亲在同一层的节点互为堂兄弟。（例如，H和I互为堂兄弟节点）

节点的祖先：从根节点到该节点所经过分支上的所有节点。（上图中A是所有节点的祖先）

子孙：以某节点为根的子树中任意一个节点都称为该节点的子孙。（如上图中，所有节点都是A的子孙）

树的高度或深度：树中节点的最大层次。（上图中，树的高度为4）

森林：由m（m＞0）棵互不相交的树的集合称为森林。

树的表示

树的结构相对线性表就比较复杂了，要存储表示起来就比较麻烦了。既要保存值域，又要保存结点和结点之间的关系，实际中树有很多种表示方式，如：双亲表示法、孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。在这里，我们简单了解比较常用的孩子兄弟表示法：

左孩子右兄弟

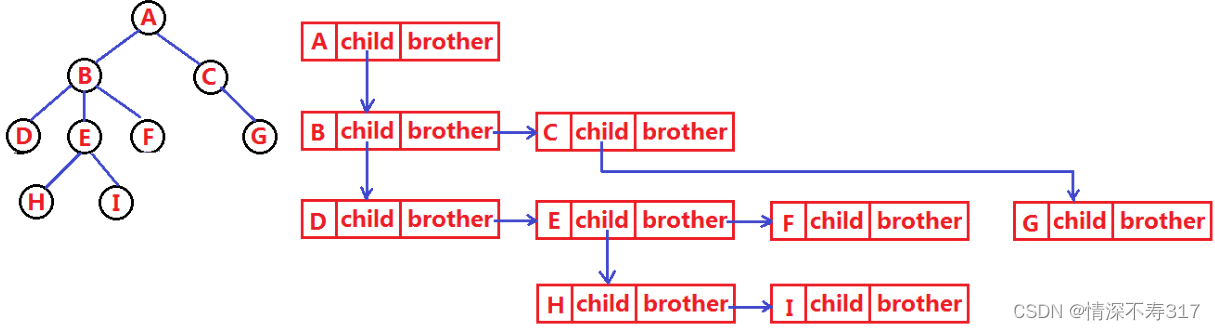
树在实际中的运用

树在实际中的运用：表示文件系统的目录结构。

我们一起来看一下树在Linux树状目录结构和Windows文件系统层次结构中的应用。

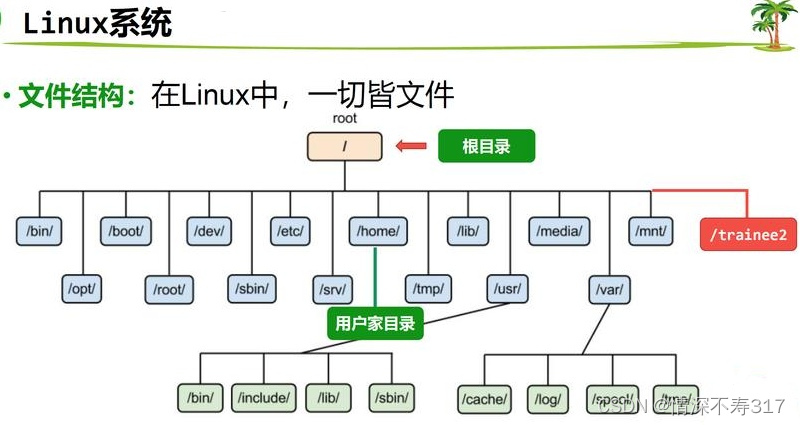
Windows文件系统层次结构

这里的C盘、E盘和D盘就是根，每个根下面可以有多个文件或者目录，空目录的话就是当前结构中的叶子节点（不考虑未来可能添加内容的情况下）。

二叉树的概念及结构

概念

二叉树是指树中节点的度不大于2的有序树，它是一种最简单且最重要的树形结构。每个节点最多只能有两棵子树，且有左右之分。

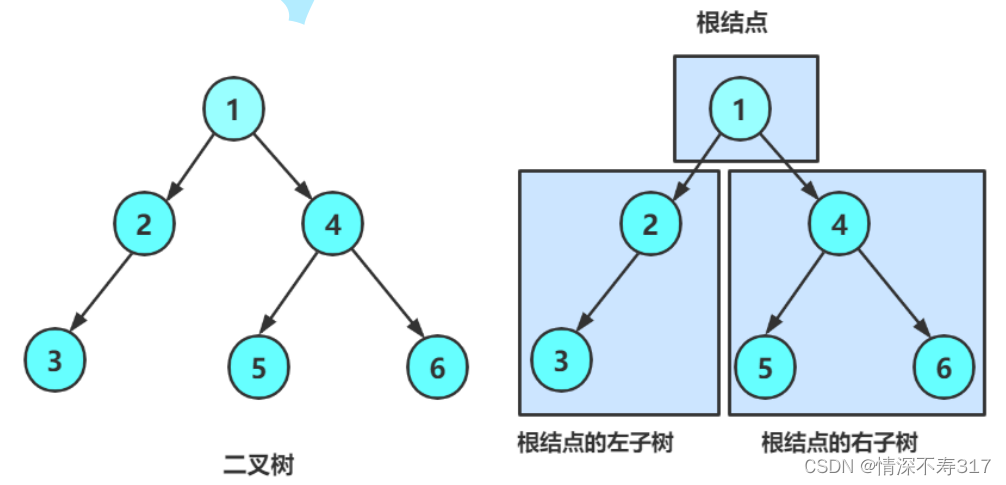
特殊的二叉树

满二叉树

如果一个二叉树的每一层的结点树都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为k，且结点总数是2ᵏ-1，那它就是满二叉树。

完全二叉树

完全二叉树是效率很高的数据结构，它是由满二叉树引来的。对于深度为k的且有n个结点的二叉树，当且仅当它每一个结点都与深度为k的满二叉树中的编号从1到n的结点一一对应时，则称之为完全二叉树。满二叉树是一种特殊的完全二叉树。（如一个完全二叉树有h层，那它前h-1层是满二叉树，最后一层要求从左到右都是连续的。）

我们通过一张图片能更好地理解满二叉树和完全二叉树的结构：

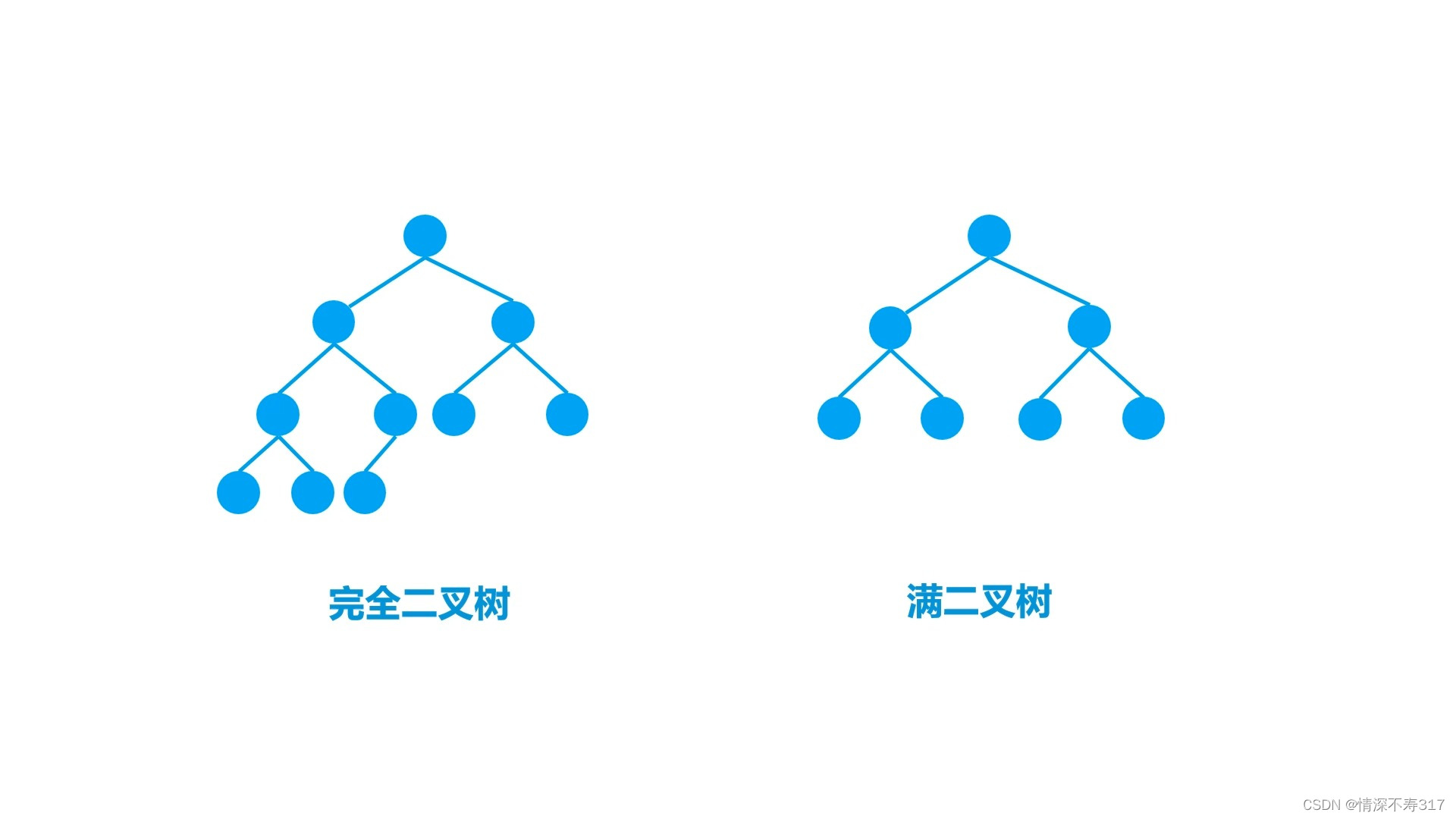
二叉树的性质

我们令一棵二叉树里叶子结点的数量为n0，度为2的分支结点的数量为n2，高度为h，一共有n个结点。

n0=n2+1
如果该二叉树为满二叉树，那么它一共有2ʰ-1个结点
如果该二叉树为完全二叉树，那么它的节点数量的范围为[2ʰ⁻¹，2ʰ-1]
非空二叉树的第i层最多有2ⁱ⁻¹个节点
如果该二叉树为满二叉树，那么它的深度h=log₂（n+1）
父节点与孩子结点在数组中的下标关系（具体见二叉树的顺序结构部分的讲解）。

二叉树的存储结构

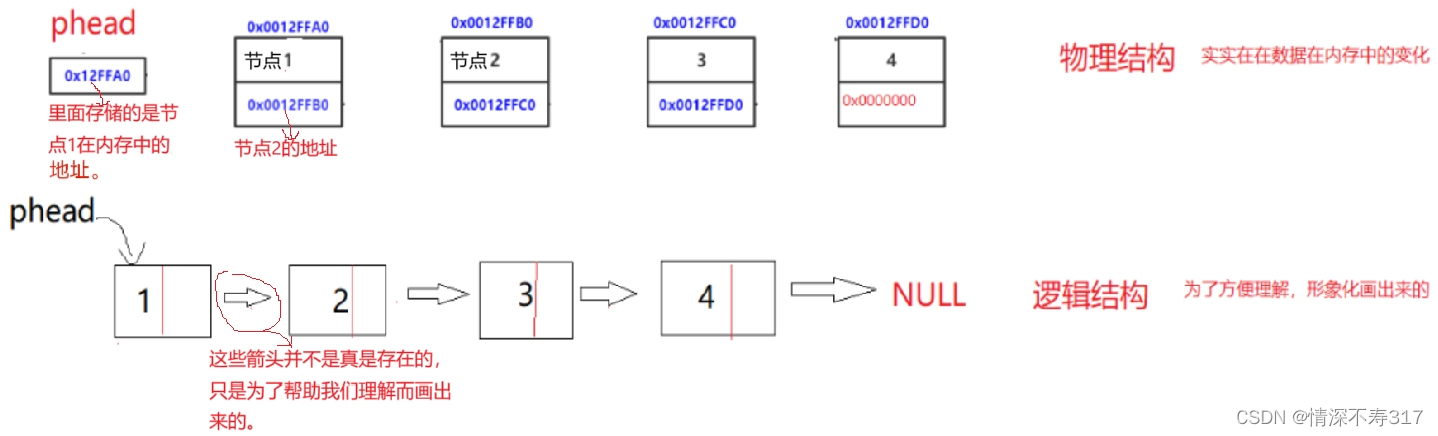
在讲二叉树的存储结构之前，我们要先弄懂逻辑结构和物理结构的概念。

逻辑结构描述了数据元素之间的逻辑关系，而物理结构则描述了数据元素在计算机中的存储方式。

我们以链表为例进行讲解，帮助我们更好地理解这两个概念：

二叉树一般可以使用两种存储结构：顺序结构和链式结构。

二叉树的顺序结构

普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储。

（ps：需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事，一个是数据结构，一个是操作系统中管理内存的一块区域分段。）

父节点与孩子结点在数组中的下标关系

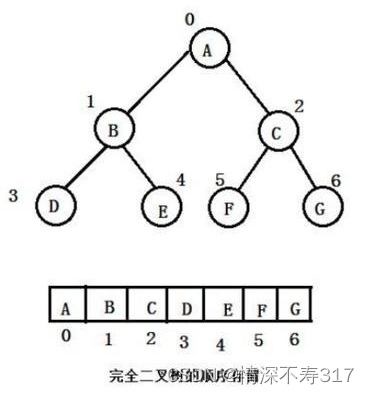
如果该二叉树为完全二叉树，按照从上到下、从左到右的数组顺序对所有节点从0开始编号，则对于序号为i的结点有：

i＞0时，i位置节点的双亲序号为（i-1）/2；i=0时，i为根节点编号，无双亲节点。
2i+1＜n时，左孩子序号为2i+1（2i+1≥n，否则无左孩子）。
2i+1＜n时，右孩子序号为2i+2（2i+2≥n，否则无右孩子）。

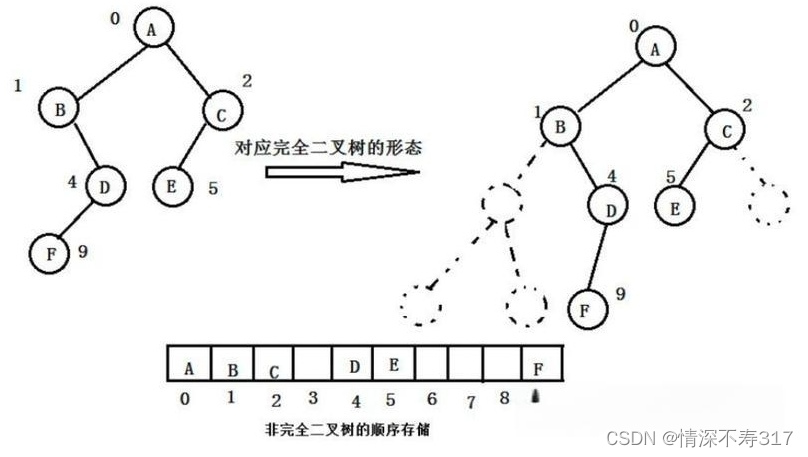
这种存储方式更适合存储满完全二叉树；如果存储其他二叉树，由于结构的特点会出现浪费空间的情况。我们通过一张非完全二叉树的顺序存储图片来理解为什么会出现浪费的情况：

什么是堆？

堆是一种特殊的完全二叉树，通常分为最大堆（大根堆）和最小堆（小根堆）：

最大堆：每个节点的值都大于或等于其子节点的值。这意味着根节点的值是整棵树中的最大值。
最小堆：每个节点的值都小于或等于其子节点的值。这意味着根节点的值是整棵树中的最小值。

后续二叉树顺序结构的实现我们主要来实现堆。

二叉树的实现（堆的实现）

堆的数据结构

#define INIT_CAPACITY 4 //初始化堆可容纳的数据个数typedef int dataType;
typedef struct Heap
{dataType* a;//指向堆中实际存储数据的数组int size;//堆中当前存储的元素个数int capacity;//堆的容量，即堆最多可以存储多少个元素
}heap;

初始化堆

void initHeap(heap* pheap)
{assert(pheap);pheap->a = (dataType*)malloc(sizeof(dataType) * INIT_CAPACITY);if (pheap->a == NULL) {perror("malloc fail");return;}pheap->capacity = INIT_CAPACITY;pheap->size = 0;printf("The heap has been initialized.\n");
}

因为这里的堆是基于数组来实现的，所以它的初始化初始化跟前面顺序表的初始化很相似。

堆的插入

向上调整法

堆的插入需要用到向上调整法，以大顶堆为例，现在我们有一个数组模拟出来的大顶堆：

接下来我们要往堆中插入数据80：

① ② ③ ④

我们先看图①，在这个大顶堆中，新插入的80比当前堆顶元素数据70大，所以要让80成为这个大顶堆的堆顶元素。从前面我们知道，通过父子结点之间的下标关系，我们很容易调整父子结点之间的位置。所以我们让80（下标为7）作为孩子节点，让它与它的父节点10（下标为3）比较大小，发现孩子节点比父节点大，所以我们交换两个节点的位置就达到了图②的效果。

图②中的80与10交换位置后，新插入节点的下标得到了更新：80节点的下标变为3，10节点的下标变为7，所以父子的关系也会改变。此时80节点的成为了10节点的父节点，80节点的父节点是下标为1的60节点。准备继续比较新插入节点与它更新下标后父节点的大小：由于80与它的父节点里的数据60比较后还是80大，所以还要进行调整，60节点与80节点交换位置，就达到了图③的效果。

以此类推，80与70交换位置，最终80成了堆顶元素。

向上调整法的时间复杂度是多少呢？我们预估最坏的情况，就是新插入的元素比当前堆中所有元素的数据都大，那他就要调整的次数就是h-1次（难以理解就配合上面例子中的图片去理解）h-1=log₂（n+1），所以它的时间复杂度就是log₂n。

代码

void swap(dataType* x, dataType* y)
{dataType tmp = *x;*x = *y;*y = tmp;
}
void adjustUp(dataType* a, int child)
{assert(a);int parent = (child - 1) / 2;//求新插入节点的父节点下标while (child > 0) //关于这个退出条件，后面会讲解{if (a[child] > a[parent]) {//新插入的节点数据大于父节点数据的情况：swap(&a[parent], &a[child]);//交换父子结点的位置//更新新插入节点的下标，准备继续比较它与更新下标后父节点的大小child = parent;parent = (child - 1) / 2;}else {//新插入节点的数据小于或等于父节点的数据，符合大顶堆，直接退出循环break;}}
}
void pushHeap(heap* pheap, dataType x)
{assert(pheap);if (pheap->size == pheap->capacity) {//容量满了，要插入数据就得扩容dataType* tmp = (dataType*)realloc(pheap->a,sizeof(dataType) * pheap->capacity * 2);if (tmp == NULL) {perror("realloc fail");return;}pheap->a = tmp;pheap->capacity *= 2;}pheap->a[pheap->size] = x;//插入新数据adjustUp(pheap->a, pheap->size);//向上调整法++pheap->size;
}

为什么在adjustUp里面的循环退出条件是child<=0的时候呢？我们知道这里的while循环和里面的内容的主要作用是确保新插入堆中的元素能够“上浮”（也就是向上调整法）到其正确的位置，从而维护堆的性质。而这里的child就是新插入元素在刚插入的时候和以及不断更新位置后下标的位置。有两种情况：第一种情况，如果堆中有节点，且新插入的元素比堆中的任意一个节点的数据都大，那它的的下标位置在“上浮”过程中会更新到0，也就说明已经到了堆顶位置，不用再“上浮”了；第二种情况，如果堆本来就为空，那么新插入元素的下标就是0，也不需要“上浮”来调整位置。

总结

1.检查并扩容（如需）：若堆满，则扩容。
2.末尾插入：将新元素添加到堆数组的末尾。
3.向上调整：
从新元素开始，与其父节点比较。
若新元素大，则交换位置，并继续向上比较直至不需交换或到达根节点。
4.更新大小：堆大小加1。

堆的删除

在堆的数据结构中，特别是二叉堆（包括大顶堆和小顶堆），堆顶元素总是具有特定的性质：在大顶堆中，堆顶是最大的元素；在小顶堆中，堆顶是最小的元素。因此，删除堆顶元素是堆操作中的一个核心功能，这一操作在很多堆的应用中都至关重要，所以我们主要讲解堆顶元素的删除。

向下调整法

堆的删除需要用到向下调整法，还是以大顶堆为例：

我们要删除堆顶元素80：

① ② ③ ④

我们看图①，我们先把要删除的堆顶元素80和堆中最后一个元素10交换位置，交换位置后，后面再调整过程中我们就不用在管这个末尾元素80了（这个末尾元素也就相当于被删除了）。

交换位置后，原来的大顶堆达到了图②的效果。我们发现此刚刚交换上来的元素10所在的位置不符合大顶堆的性质，元素10小于它的两个孩子节点70和30。我们需要把交换上来的元素10与孩子节点中最大的一个交换位置，而最大的孩子节点的数据是70。

交换位置后，达到了图③的效果。此时元素10的下标位置和原来在堆中对应的父子关系也发生了变化——元素10的孩子节点的数据为56和10。我们还是让元素10与孩子节点中最大的那个进行交换。

最终达到了图④的效果。

我们通过前面对向上调整法的时间复杂度的推断，很容易推断出这里的时间复杂度也是log₂n。

代码

int getMax(dataType* a, int x, int y)
{if (a[x] > a[y]){return x;}else {return y;}
}
void adjustDown(dataType* a, int parent, int size)
{assert(a);while (parent < size)//parent就是原来交换上面的最后一个元素。后续向下调整的过程中，它的下标不能超出当前堆中的最后一个元素的下标{int lChild = 2 * parent + 1, rChild = 2 * parent + 2;//更新parent的孩子节点的下标int swapChild;//用来记录parent最大的孩子节点的下标if (rChild < size) {//如果parent有两个孩子节点，求出最大的孩子节点的下标swapChild = getMax(a, lChild, rChild);}else {//如果此时parent只有一个孩子，那肯定是左孩子，swapChild直接保存左孩子的下标swapChild = lChild;}if (swapChild < size && a[parent] < a[swapChild]) {//如果父节点小于其最大的孩子，则交换它们，并将parent更新为交换后的孩子下标，以便继续向下调整。swap(&a[parent], &a[swapChild]);parent = swapChild;}else {//如果父节点不小于其孩子，或者已经到达堆的底部，则停止调整。break;}}
}
void popHeap(heap* pheap)
{assert(pheap);if (pheap->size == 0) {//堆中无元素，就不能再删除元素了printf("The heap has been already emtied!\n");return;}swap(&pheap->a[0], &pheap->a[pheap->size - 1]);//先把要删除的堆顶元素和堆中最后一个元素交换位置--pheap->size;//交换位置后，删除此时最后一个元素adjustDown(pheap->a, 0, pheap->size);//向下调整法，使得交换位置后的堆符合大顶堆的性质}

总结

1.检查非空：若堆为空，则直接返回。
2.交换并减小：将堆顶与末尾元素交换，然后减小堆大小。
3.向下调整：从新的堆顶开始，与其孩子比较并交换（如需），直至堆性质恢复或到达堆底。

判断堆是否为空

bool isEmpty(heap* pheap)
{assert(pheap);if (pheap->size == 0) {return true;}else {return false;}
}

获取堆顶元素

dataType topHeap(heap* pheap)
{assert(pheap);assert(!isEmpty(pheap));return pheap->a[0];
}

获取堆里的元素个数

int sizeHeap(heap* pheap)
{assert(pheap);return pheap->size;
}

测试案例

void test() {heap hp;initHeap(&hp);pushHeap(&hp, 80);pushHeap(&hp, 10);pushHeap(&hp, 56);pushHeap(&hp, 30);pushHeap(&hp, 60);pushHeap(&hp, 70);pushHeap(&hp, 25);pushHeap(&hp, 15);for (int i = 0; i < sizeHeap(&hp); i++) {printf("%d ", hp.a[i]);}printf("\n");while (!isEmpty(&hp)) {popHeap(&hp);}if (isEmpty(&hp)) {printf("The heap has been emptied!\n");}destroyedHeap(&hp);
}

前言