当前位置：首页 > news >正文

2024 ICPC香港站 L.Flipping Paths的一种解法

news 来源：原创 2025/9/16 1:16:55

太变态了，场上被硬控了两个小时，最后20分钟思路熬出来了但是没写对~，糖完了。怎么说呢，香港站这样的轻量级赛站，这次强队也很少，导致很多题目的难度升级了，这道L题是一道银牌题，不少队伍面临过L与否决定着打铁或者拿银的境况，然后这题作为第三题是一个纯思维的银牌题，那么第四题开始的每道题都是大于等于银牌的上位难度了，我还打算写一下浙大的经典麻将题H的题解。

记住题目中这个最多跑400次的这个点，要考~，然后是接下来这个输出格式，也要考hhh。

OK，反正这么多英文想必也不爱看，我直接口一下题：就是给你一个黑白格子的n*m的表格，你每次可以从(1,1)走到(n,m)，这条路径只能向下或者向右，每次经过的格子颜色发生反转（即黑色变成白色，白色变成黑色），然后你需要构造最多不超过400条路径使得所有格子变成黑色或者白色。

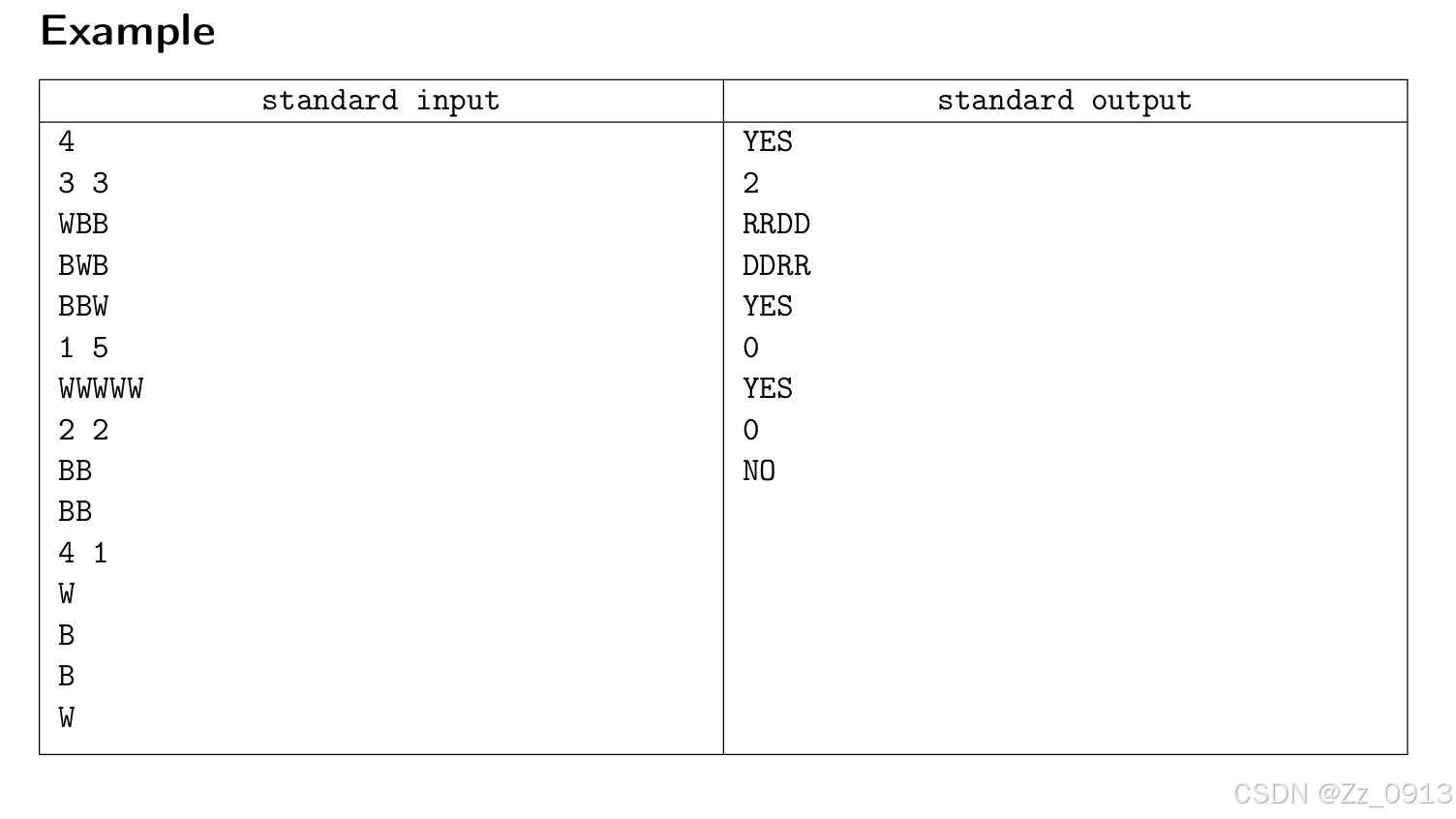
给大家举个例子叭，这里我用红色格子表示黑色，绿色格子表示白色：

初始：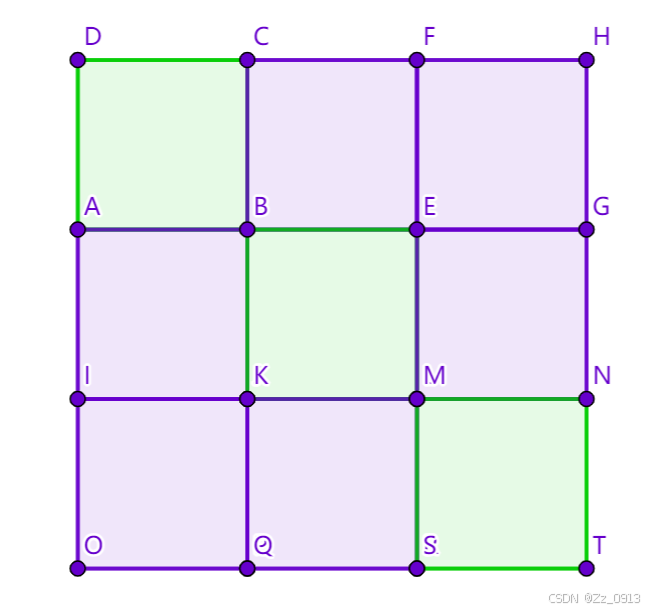

RRDD：

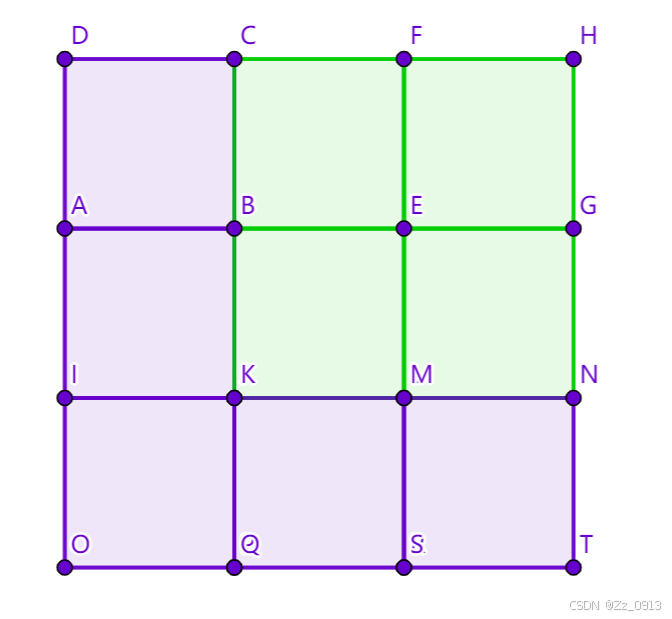
DDRR:

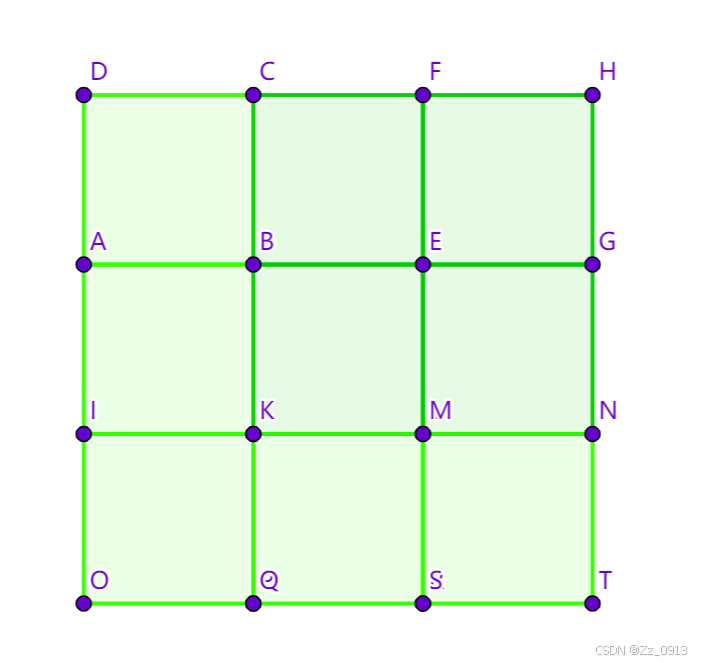
因此看起来好像没什么非常直白的解法，那就想办法去构造一种走法：

考虑每次从左上往右下行走的时候，如果在一行中存在反颜色的格子，那就向右，直到走到最远的反向颜色的格子后然后再向下，一直到最后一行走到(n,m)，每行都是如此行走。

然后对于目标颜色需要都枚举，白色的跑一次，黑色的跑一次。

然后题目中这个400次的过程没有很详细的含义，其实是代表着上述算法跑了超过400次可以证明这张图是无解的，而400这个数字其实是出题团队在出题的时候推出来的，神奇吧？

那么我们只需要一直走，在400以内如果出现了目标情况那就退出正反馈，否则超过400次就直接退出返回非法。

那么代码就很简单了，真的就是纯思维题🤣：

#include<bits/stdc++.h>
#define Alex std::ios::sync_with_stdio(false),std::cin.tie(0),std::cout.tie(0);
//#define int long long
#define double long double
const int QAQ = 0;
const int mod = 1e9 + 7;
const int P = 998244353;
const double eps = 1e-10;
const double pi = std::acos(-1.0);
using namespace std;inline void Fre() { int liujiahui = 142857; }int n,m;
char F[555][555];
int a[555][555];int L[555];char ans[555][555];inline bool check(char c)
{int cnt;for(int i = 1;i <= n;i++)for(int j = 1;j <= m;j++)if(F[i][j] == c) a[i][j] = 1;else a[i][j] = 0;for(int k = 1;k <= 401;k++){bool o = true;for(int i = 1;i <= n;i++)for(int j = 1;j <= m;j++)if(a[i][j] != 0) o = false;if(o){cnt = k - 1;break;	}if(k > 400) return false;L[k] = 0;int y = 1;for(int i = 1;i <= n;i++){a[i][y] = a[i][y] ^ 1;int t = 1;for(int j = m;j;j--){if(a[i][j] == 1){t = j;break;}}while(y < t){y++;a[i][y] = a[i][y] ^ 1;L[k]++;ans[k][L[k]] = 'R';}if(i < n) {L[k]++;ans[k][L[k]] = 'D';}else{while(y < m){y++;a[n][y] = a[n][y] ^ 1;L[k]++;ans[k][L[k]] = 'R';}}}ans[k][L[k] + 1] = 0;}std::cout<<"YES"<<'\n';std::cout<<cnt<<'\n';for(int i = 1;i <= cnt;i++) std::cout<<ans[i] + 1<<'\n';return true;
}signed main()
{Fre();ios::sync_with_stdio(false),cin.tie(0);Alex;int _;_ = 1;std::cin>>_;while(_--){std::cin>>n>>m;for(int i = 1;i <= n;i++)for(int j = 1;j <= m;j++) std::cin>>F[i][j];if(check('W') == false && check('B') == false) {std::cout<<"NO"<<'\n';continue;}}return QAQ;
}

初始：

RRDD：

DDRR:

相关文章：