人工智能数学基础学习PPT
学习视频:人工智能 -数学基础
文章目录
- 1.简介
- 1.函数
- 2.极限
- 3.无穷小与无穷大
- 4.连续性与导数
- 5.偏导数
- 6.方向导数
- 7.梯度
- 2.微积分
- 1.微积分基本想法
- 2.微积分的解释
- 3.定积分
- 4.定积分性质
- 5.牛顿-莱布尼茨公式
- 3.泰勒公式与拉格朗日
- 1.泰勒公式
- 2.一点一世界
- 3.阶数的作用
- 4.阶乘的作用
- 5.拉格朗日乘子法
- 4.线性代数基础
- 1.行列式概述
- 2.矩阵与数据的关系
- 3.矩阵基本操作
- 4.矩阵的几种变换
- 5.矩阵的秩
- 6.内积与正交
- 5.特征值与矩阵分解
- 1.特征值与特征向量
- 2.特征空间与应用
- 3.SVD要解决的问题
- 4.特征值分解
- 5.SVD矩阵分解
- 6.随机变量
- 1.离散型随机变量
- 2.连续型随机变量
- 3.简单随机抽样
- 4.似然函数
- 5.极大似然估计
- 7.概率论基础
- 1.概率与频率
- 2.古典概型
- 3.条件概率
- 4.条件概率小例子独立性
- 5.独立性
- 6.二维离散型随机变量
- 7.二维连续型随机变量
- 8.边缘分布
- 9.期望
- 10.期望求解
- 11.马尔科夫不等式
- 12.切比雪夫不等式
- 13.后验概率估计
- 14.贝叶斯拼写纠错实例
- 15.垃圾邮件过滤实例
- 8.数据科学你得知道的几种分布
- 1.正态分布
- 2.二项式分布
- 3.泊松分布
- 4.均匀分布
- 5.卡方分布
- 6.beta分布
- 9.核函数变换
- 1.核函数的目的
- 2.线性核函数
- 3.多项式核函数
- 4.核函数实例
- 5.高斯核函数
- 6.参数的影响
- 10.熵与激活函数
- 1.熵的概念
- 2.熵的大小意味着什么
- 3.激活函数
- 4.激活函数的问题
- 11.回归分析
- 1.回归分析概述
- 2.回归方程定义
- 3.误差项的定义
- 4.最小二乘法推导与求解
- 5.回归方程求解小例子
- 6.回归直线拟合优度
- 7.多元与曲线回归问题
- 8.Python工具包介绍
- 9.statsmodels回归分析
- 10.高阶与分类变量实例
- 11.案例:汽车价格预测任务概述
- 12.案例:缺失值填充
- 13.案例:特征相关性
- 14.案例:预处理问题
- 15.案例:回归求解
- 12. 假设检验
- 1.假设检验基本思想
- 2.左右侧检验与双侧检验
- 3.Z检验基本原理
- 4.Z检验实例
- 5.T检验基本原理
- 6.T检验实例
- 7.T检验应用条件
- 8.卡方检验
- 9.假设检验中的两类错误
- 10.Python假设检验实例
- 11.Python卡方检验实例
- 13.相关分析
- 1.相关分析概述
- 2.皮尔森相关系数
- 3.计算与检验
- 4.斯皮尔曼等级相关
- 5.肯德尔系数
- 6.质量相关分析
- 7.偏相关与复相关
- 14.方差分析
- 1.方差分析概述
- 2.方差的比较
- 3.方差分析计算方法
- 4.方差分析中的多重比较
- 5.多因素方差分析
- 6.Python方差分析实例
- 15.聚类分析
- 1.层次聚类概述
- 2.层次聚类流程
- 3.层次聚类实例
- 4.Kmeans聚类算法
- 1.KMEANS算法概述
- 2.KMEANS工作流程
- 3.KMEANS迭代可视化展示
- 5.DBSCAN聚类算法
- 1.DBSCAN聚类算法
- 2.DBSCAN工作流程
- 3.DBSCAN可视化展示
- 6.聚类算法实践
- 1.多种聚类算法概述
- 2.聚类案例实战
- 16.贝叶斯分析
- 1.贝叶斯分析概述
- 2.概率的解释
- 3.贝叶斯学派与经典统计学派的争论
- 4.贝叶斯算法概述
- 5.贝叶斯推导实例
- 6.贝叶斯拼写纠错实例
- 7.贝叶斯解释
- 8.垃圾邮件过滤实例
- 8.经典求解思路
- 9.MCMC概述
- 10.PYMC3概述
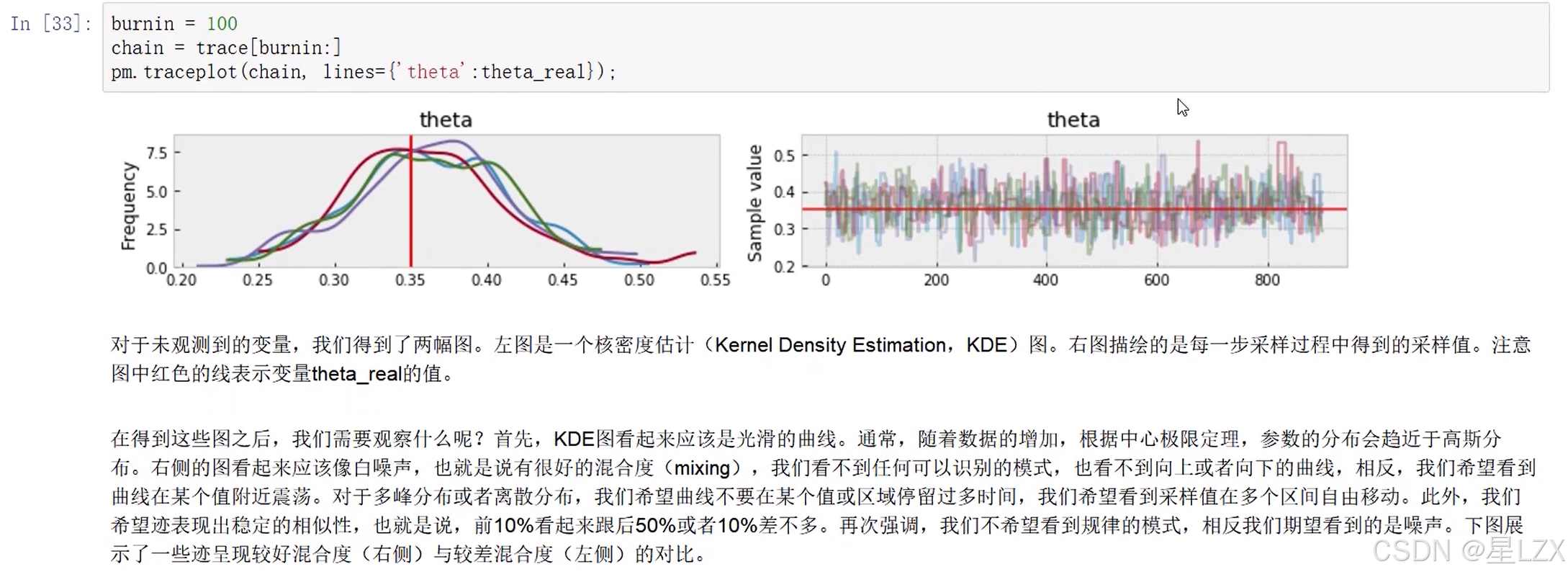
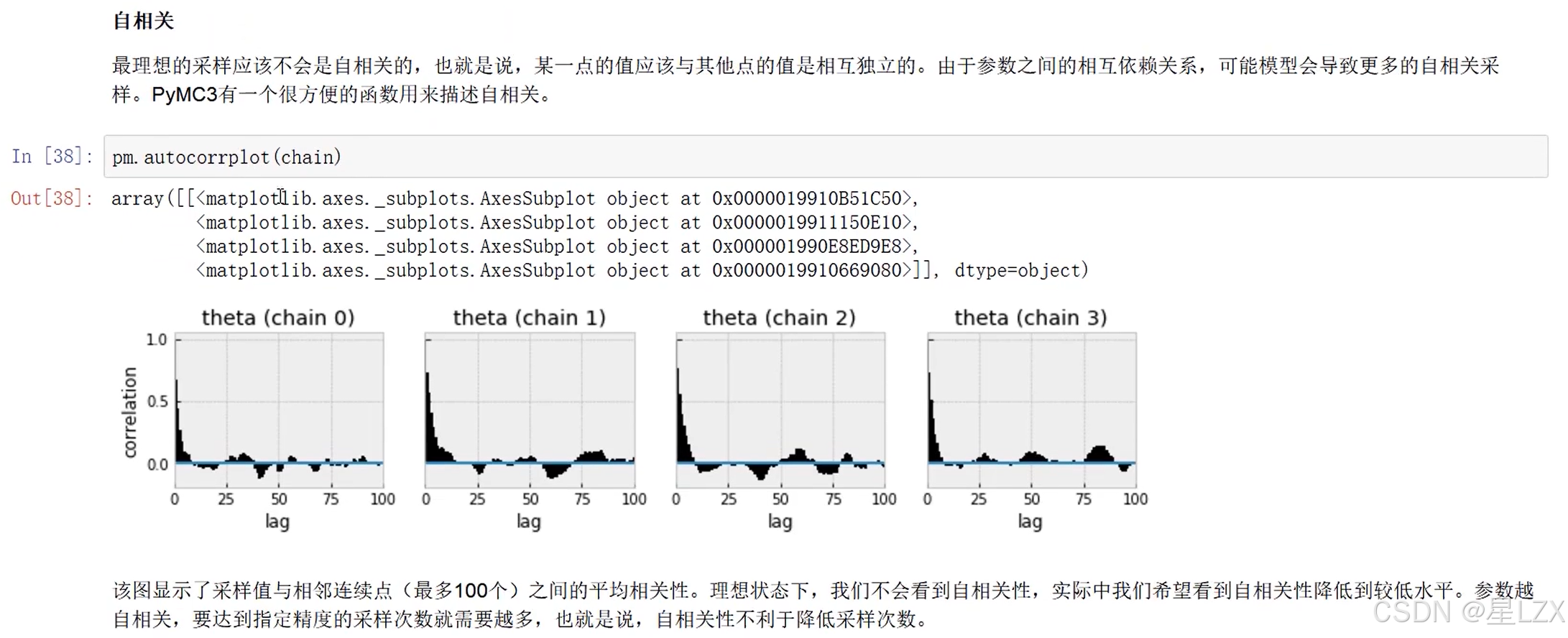
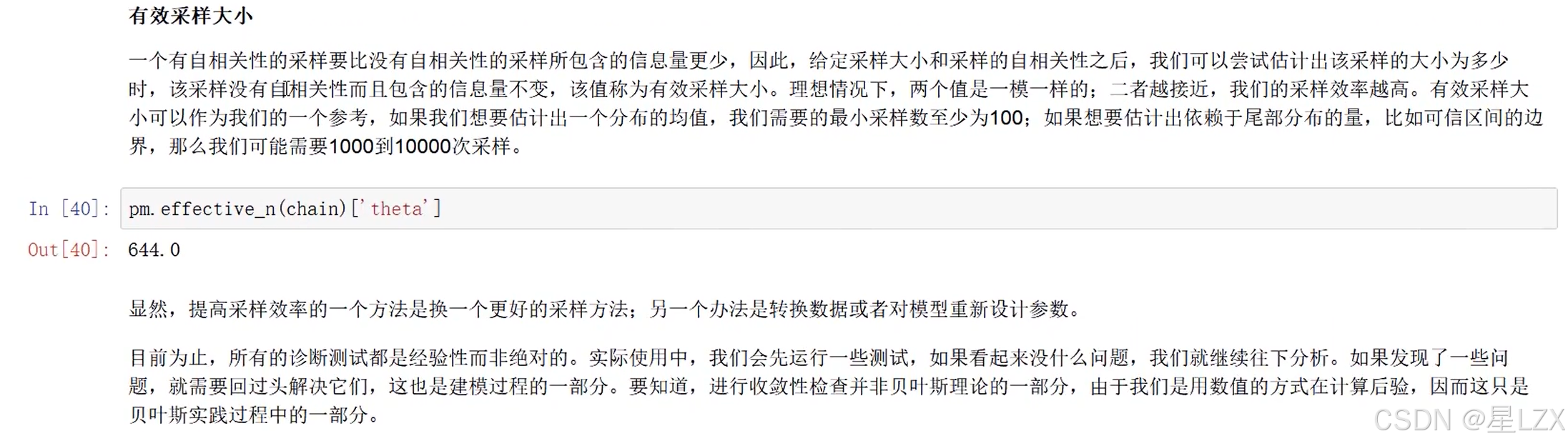
- 11.模型诊断
- 12.模型决策
1.简介
1.函数



2.极限





3.无穷小与无穷大




4.连续性与导数


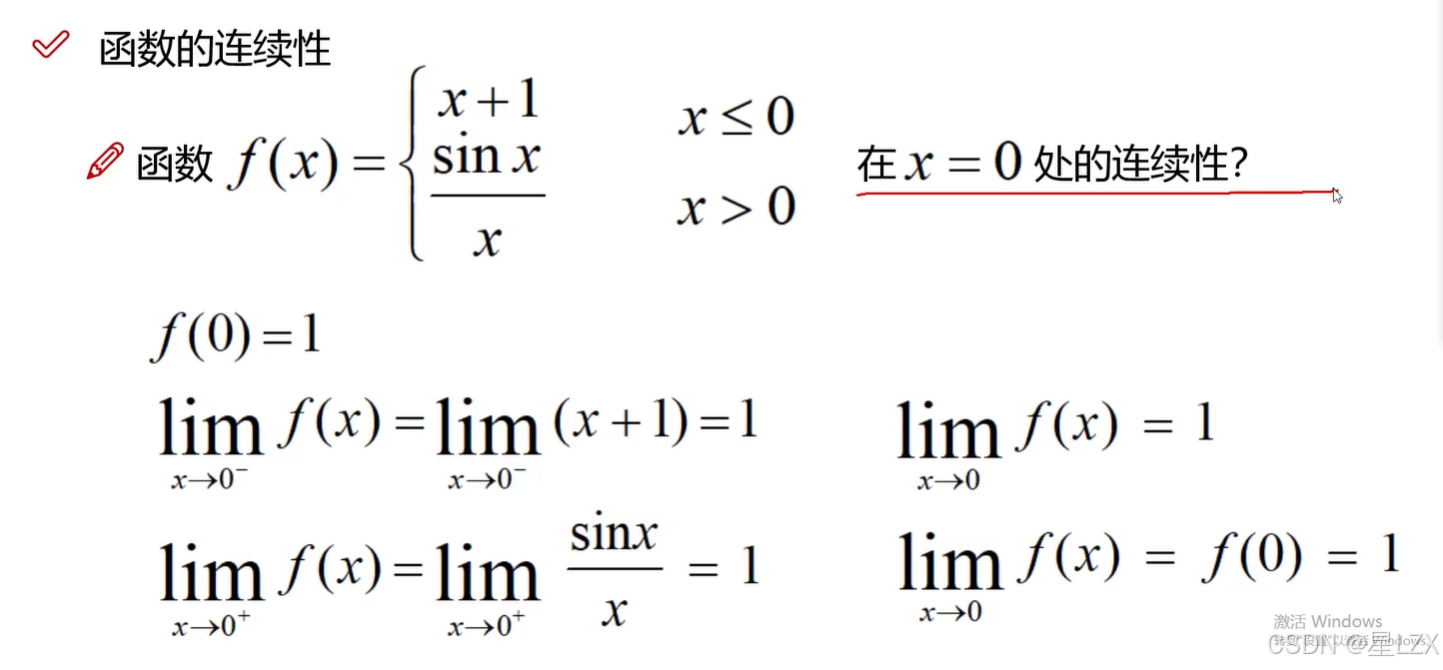







5.偏导数




6.方向导数




7.梯度



2.微积分
1.微积分基本想法


2.微积分的解释




3.定积分




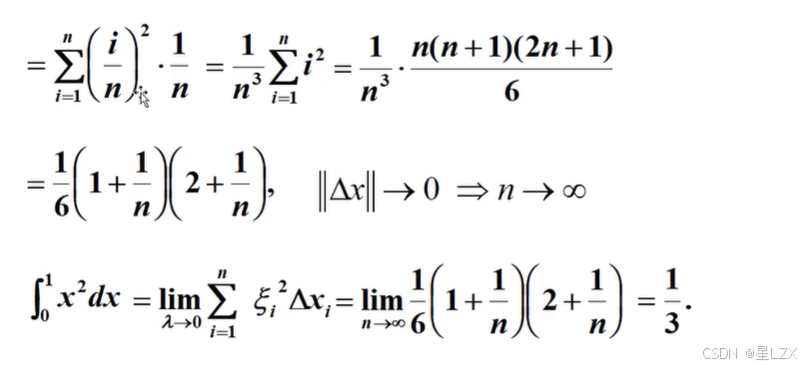
4.定积分性质



5.牛顿-莱布尼茨公式





3.泰勒公式与拉格朗日
1.泰勒公式


2.一点一世界





3.阶数的作用




4.阶乘的作用





5.拉格朗日乘子法









4.线性代数基础
1.行列式概述




2.矩阵与数据的关系





3.矩阵基本操作

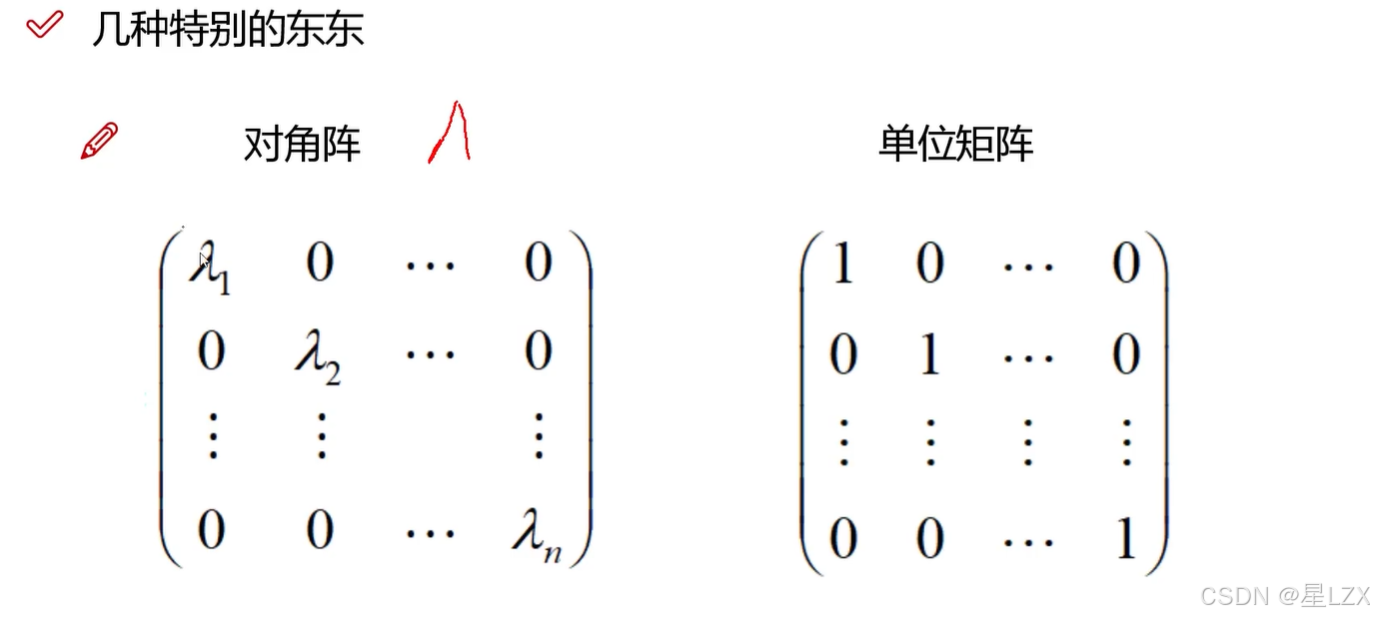





4.矩阵的几种变换




5.矩阵的秩






6.内积与正交







5.特征值与矩阵分解
1.特征值与特征向量



2.特征空间与应用


3.SVD要解决的问题
4.特征值分解



5.SVD矩阵分解






6.随机变量
1.离散型随机变量




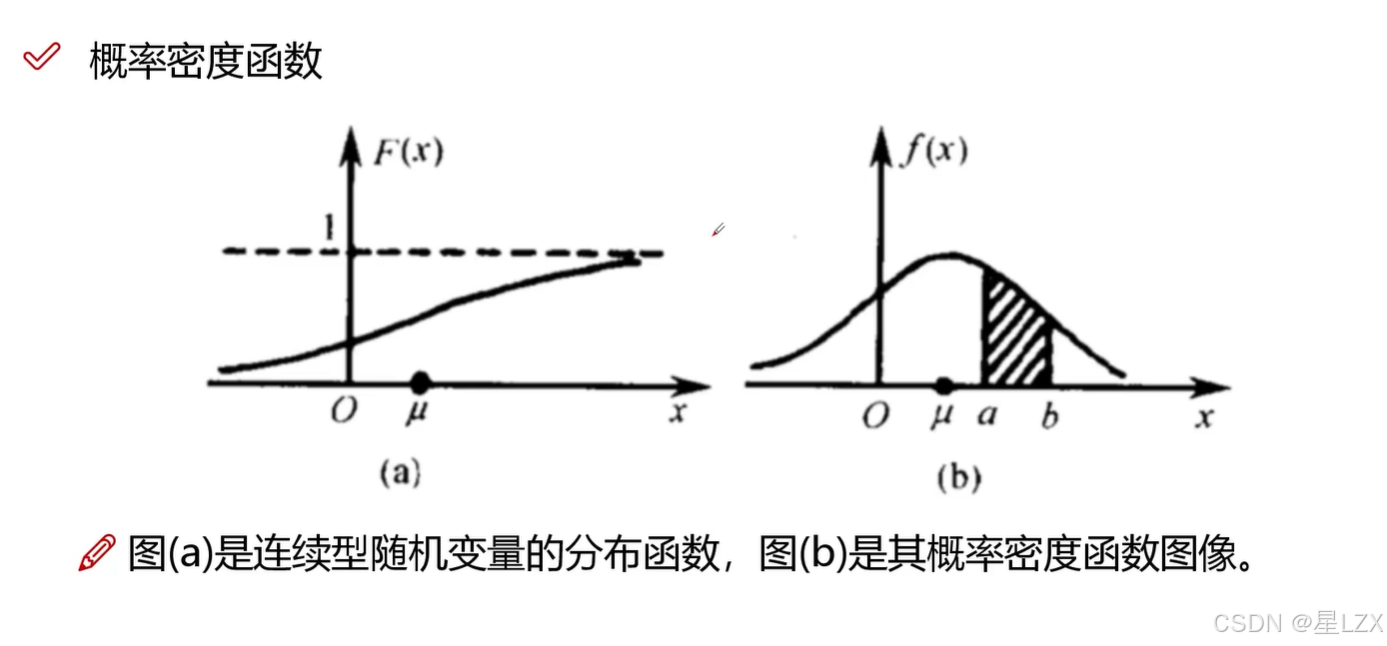
2.连续型随机变量





3.简单随机抽样

4.似然函数



5.极大似然估计





7.概率论基础
1.概率与频率




2.古典概型


3.条件概率





4.条件概率小例子独立性


5.独立性





6.二维离散型随机变量






7.二维连续型随机变量


8.边缘分布






9.期望


10.期望求解





11.马尔科夫不等式



12.切比雪夫不等式




13.后验概率估计






14.贝叶斯拼写纠错实例





15.垃圾邮件过滤实例






8.数据科学你得知道的几种分布
1.正态分布

import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
import matplotlib.style as style
from IPython.core.display import HTML#PLOTTING CONFIG
%matplotlib inline
style.use('fivethirtyeight')
plt.rcParams["figure.figsize"]=(14,7)
plt.figure(dpi=100)#PDF
plt.plot(np.linspace(-4,4,100),stats.norm.pdf(np.linspace(-4,4,100))/ np.max(stats.norm.pdf(np.linspace(-3, 3, 100))),)
plt.fill_between(np.linspace(-4,4,100),stats.norm.pdf(np.linspace(-4,4,100))/np.max(stats.norm. pdf(np.linspace(-3, 3, 100))),alpha=.15,)# CDF
plt.plot(np.linspace(-4,4,100),stats.norm.cdf(np.linspace(-4,4,100)),)# LEGEND
plt. text(x=-1.5, y=.7, s="pdf (normed)", rotation=65, alpha=.75, weight="bold", color="#008fd5")
plt.text(x=-.4,y=.5,s="cdf",rotation=55,alpha=.75,weight="bold", color="#fc4f30")# TICKS
plt.tick_params(axis = 'both',which= 'major', labelsize = 18)
plt.axhline(y=0,color='black',linewidth=1.3, alpha =.7)
# TITLE
plt.text(x=-5,y=1.25,s="Normal Distribution - Overview",fontsize=26,weight='bold',alpha=.75)
plt.text(x=-5,y=1.1,s="Depicted below are the normed probability density function (pdf) and the cumulative density\nfunction (cdf) of a normally distributed random variable y~ (μ, o), given μ = 0 and o = 1.",fontsize=19,alpha=.85)

均值
plt.figure(dpi=100)
#PDFMU=0
plt.plot(np.linspace(-4,4,100),stats.norm.pdf(np.linspace(-4,4,100)),)
plt.fill_between(np.linspace(-4,4,100),stats.norm.pdf(np.linspace(-4,4,100)),alpha=.15,)#PDFMU=2
plt.plot(np.linspace(-4,4,100),stats.norm.pdf(np.linspace(-4,4,100),loc=2),)
plt.fill_between(np.linspace(-4,4, 100),stats.norm.pdf(np.linspace(-4,4,100),loc=2),alpha=.15,)#PDFM=-2
plt.plot(np.linspace(-4,4,100),stats.norm.pdf(np.linspace(-4,4,100),loc=-2),)
plt.fill_between(np.linspace(-4,4,100),stats.norm.pdf(np.linspace(-4,4,100),loc=-2),alpha=.15,)# LEGEND
plt.text(x=-1,y=.35, s="$ \mu= 0$", rotation=65, alpha=.75, weight="bold", color="#008fd5")
plt.text(x=1, y=.35,s="$ \mu = 2$", rotation=65, alpha=.75, weight="bold", color="#fc4f30")
plt.text(x=-3,y=.35,s="$ \mu = -2$", rotation=65, alpha=.75, weight="bold", color="#e5ae38")# TICKS
plt.tick_params(axis='both',which ='major', labelsize = 18)
plt.axhline(y=0,color='black',linewidth=1.3, alpha =.7)# TITLE,
plt.text(x=-5,y=0.51,s="Normal Distribution - $ \mu $",fontsize=26,weight='bold',alpha=.75)
plt.text(x=-5,y= 0.45,s="Depicted below are three normally distributed random variables with varying $ \mu $. As one can easily\nsee the parameter $\mu$ shifts the distribution along the x-axis.",fontsize=19,alpha=.85)

标准差
plt.figure(dpi=100)#PDF SIGMA =1
plt.plot(np.linspace(-4,4,100),stats.norm.pdf(np.linspace(-4,4,100),scale=1),)
plt.fill_between(np.linspace(-4,4,100),stats.norm.pdf(np.linspace(-4,4,100),scale=1),alpha=.15,)#PDF SIGMA =2
plt.plot(np.linspace(-4,4,100),stats.norm.pdf(np.linspace(-4,4,100),scale=2),)
plt.fill_between(np.linspace(-4,4,100),stats.norm.pdf(np.linspace(-4,4,100),scale=2),alpha=.15,)#PDF SIGMA =0.5
plt.plot(np.linspace(-4,4,100),stats.norm.pdf(np.linspace(-4,4,100),scale=0.5),)
plt.fill_between(np.linspace(-4,4,100),stats.norm.pdf(np.linspace(-4,4,100),scale=0.5),alpha=.15,)# LEGEND
plt.text(x=-1.25, y=.3,s="$ \sigma = 1$", rotation=51, alpha=.75, weight="bold", color="#008fd5")
plt.text(x=-2.5,y=.13,s="$ \sigma = 2$", rotation=11, alpha=.75, weight="bold", color="#fc4f30")
plt. text(x=-0.75,y=.55, s="$ \sigma = 0.5$", rotation=75, alpha=.75, weight="bold", color="#e5ae38")# TICKS
plt.tick_params(axis='both',which='major', labelsize = 18)
plt.axhline(y=0,color='black',linewidth=1.3,alpha =.7)# TITLE, SUBTITLE & FOOTER
plt.text(x=-5,y=0.98,s="Normal Distribution - $ \sigma $",fontsize=26,weight='bold',alpha=.75)
plt.text(x=-5,y= 0.87,s="Depicted below are three normally distributed random variables with varying $\sigma $. As one can easily\nsee the parameter $\sigma$ “sharpens” the distribution (the smaller $ \sigma $ the sharper the function).",fontsize=19,alpha=.85)


from scipy.stats import norm#draw a single sample
print(norm.rvs(),end="\n\n")#draw l0 samples
print(norm.rvs(size=10),end="\n\n")#adjust mean (loc’)and standard deviation (scale’)
print(norm.rvs(loc=10,scale=0.1),end="\n\n")


from scipy.stats import norm
#additional imports for plotting purpose
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams["figure.figsize"] = (14, 7)#relative likelihood of x and y
x = -1
y = 2
print("pdf(x) = {} \npdf(y)= {}".format(norm.pdf(x), norm.pdf(y)))#continuous pdf for the plot
x_s=np.linspace(-3,3,50)
y_s = norm.pdf(x_s)
plt.scatter(x_s, y_s);


from scipy.stats import norm#probability ofxless or equal 0.3
print("P(X <0.3)={}".format(norm.cdf(0.3)))#probabilityofxin [-0.2,+0.2]
print("P(-0.2<X<0.2)={}".format(norm.cdf(0.2) - norm.cdf(-0.2)))


plt.figure(dpi=100)
##### COMPUTATION #####
#DECLARING THE "TRUE"PARAMETERS UNDERLYING THE SAMPLE
mu_real=10
sigma_real=2# DRAW A SAMPLE OF N=100O
np.random.seed(42)
sample = stats.norm.rvs(loc=mu_real, scale=sigma_real, size=1000)#ESTIMATE MU AND SIGMA
mu_est = np.mean(sample)
sigma_est = np.std(sample)
print("Estimated MU: {}\nEstimated SIGMA: {}".format(mu_est, sigma_est))#### PLOTTING ####
# SAMPLE DISTRIBUTION
plt.hist(sample, bins=50,density=True, alpha=.25)# TRUE CURVE
plt.plot (np.linspace(2, 18, 1000), norm.pdf(np.linspace(2, 18, 1000), loc=mu_real, scale=sigma_real))# ESTIMATED CURVE
plt.plot (np.linspace(2, 18, 1000), norm.pdf(np.linspace(2, 18, 1000), loc=np.mean(sample), scale=np.std(sample)))# LEGEND
plt.text(x=9.5,y=.1,s="sample", alpha=.75, weight="bold", color="#008fd5")
plt.text(x=7, y=.2, s="true distrubtion", rotation=55, alpha=.75, weight="bold", color="#fc4f30")
plt.text(x=5, y=.12, s="estimated distribution", rotation=55, alpha=.75, weight="bold", color="#e5ae38")# TICKS
plt.tick_params(axis ='both',which='major',labelsize= 18)
plt.axhline(y=0,color='black',linewidth= 1.3,alpha =.7)# TITLE
plt.text(x=0,y=0.3,s="Normal Distribution",fontsize=26,weight='bold',alpha=.75)

2.二项式分布


import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
import matplotlib.style as style
from IPython.core.display import HTML# PLOTTING CONFIG
%matplotlib inline
style.use('fivethirtyeight')
plt.rcParams["figure.figsize"] = (14, 7)
plt.figure(dpi=100)# PDF (Probability Mass Function)
x_values = np.arange(21) # X-axis values from 0 to 20
plt.bar(x=x_values, height=stats.binom.pmf(x_values, p=0.5, n=20), width=0.75, alpha=0.75)# CDF (Cumulative Distribution Function)
plt.plot(x_values, stats.binom.cdf(x_values, p=0.5, n=20), color="#fc4f30")# LEGEND
plt.text(x=4.5, y=0.7, s="pmf (normed)", alpha=0.75, weight="bold", color="#008fd5")
plt.text(x=14.5, y=0.9, s="cdf", alpha=0.75, weight="bold", color="#fc4f30")# TICKS
plt.xticks(np.arange(21)) # Ensure the X-axis has ticks from 0 to 20
plt.tick_params(axis='both', which='major', labelsize=18)# Set X and Y limits to ensure the graph fits within 0-20 on X-axis
plt.xlim(0, 20)
plt.axhline(y=0.005, color='black', linewidth=1.3, alpha=0.7)# TITLE, SUBTITLE & FOOTER
plt.text(x=-2.5, y=1.25, s="Binomial Distribution - Overview", fontsize=26, weight='bold', alpha=0.75)
plt.text(x=-2.5, y=1.1,s="Depicted below are the normed probability mass function (pmf) and the cumulative density\n""function (cdf) of a Binomial distributed random variable $y \sim Binom(N, p) $, given $ N= 20$ and $p=0.5 $.",fontsize=19, alpha=0.85)


plt.figure(dpi=100)
# PUF P = .2
plt.scatter(np.arange(21),(stats.binom.pmf(np.arange(21),p=.2,n=20)),alpha=0.75,s=100)
plt.plot(np.arange(21),(stats.binom.pmf(np.arange(21),p=.2,n=20)),alpha=0.75,)
#PDFP = .5
plt.scatter(np.arange(21),(stats.binom.pmf(np.arange(21),p=.5,n=20)),alpha=0.75,s=100)
plt.plot(np.arange(21),(stats.binom.pmf(np.arange(21),p=.5,n=20)),alpha=0.75,)
#PDFP = .9
plt.scatter(np.arange(21),(stats.binom.pmf(np.arange(21),p=.9,n=20)),alpha=0.75,s=100)
plt.plot(np.arange(21),(stats.binom.pmf(np.arange(21),p=.9,n=20)),alpha=0.75,)# LEGEND
plt.text(x=3.5, y=0.075, s="$p = 0.2$", alpha=0.75, weight="bold", color="#008fd5")
plt.text(x=9.5, y=0.075, s="$p = 0.5$", alpha=0.75, weight="bold", color="#fc4f30")
plt.text(x=17.5, y=0.075, s="$p = 0.9$", alpha=0.75, weight="bold", color="#e5ae38")# TICKS
plt.xticks(range(21)[::2])
plt.tick_params(axis='both', which='major', labelsize=18)
plt.axhline(y=0,color='black',linewidth=1.3, alpha =0.7)# TITLE, SUBTITLE & FOOTER
plt.text(x=-2.5, y=0.37, s="Binomial Distribution - $p$", fontsize=26, weight='bold', alpha=0.75)
plt.text(x=-2.5, y=0.32,s="Depicted below are three Binomial distributed random variables with varying $p $. As one can see\nthe parameter $p$ shifts and skews the distribution",fontsize=19, alpha=0.85)


plt.figure(dpi=100)
# PUF N = 10
plt.scatter(np.arange(11),(stats.binom.pmf(np.arange(11),p=.5,n=10)),alpha=0.75,s=100)
plt.plot(np.arange(11),(stats.binom.pmf(np.arange(11),p=.5,n=10)),alpha=0.75,)
#PUF N = 15
plt.scatter(np.arange(16),(stats.binom.pmf(np.arange(16),p=.5,n=15)),alpha=0.75,s=100)
plt.plot(np.arange(16),(stats.binom.pmf(np.arange(16),p=.5,n=15)),alpha=0.75,)
#PUF N = 20
plt.scatter(np.arange(21),(stats.binom.pmf(np.arange(21),p=.5,n=20)),alpha=0.75,s=100)
plt.plot(np.arange(21),(stats.binom.pmf(np.arange(21),p=.5,n=20)),alpha=0.75,)# LEGEND
plt.text(x=6, y=0.225, s="$N = 10$", alpha=0.75, weight="bold", color="#008fd5")
plt.text(x=8.5, y=0.2, s="$N = 15$", alpha=0.75, weight="bold", color="#fc4f30")
plt.text(x=11, y=0.175, s="$N = 20$", alpha=0.75, weight="bold", color="#e5ae38")# TICKS
plt.xticks(range(21)[::2])
plt.tick_params(axis='both', which='major', labelsize=18)
plt.axhline(y=0,color='black',linewidth=1.3, alpha =0.7)# TITLE, SUBTITLE & FOOTER
plt.text(x=-2.5, y=0.31, s="Binomial Distribution - $N$", fontsize=26, weight='bold', alpha=0.75)
plt.text(x=-2.5, y=0.27,s="Depicted below are three Binomial distributed random variables with varying $N$. As one can see\nthe parameter $N$ streches the distribution (the larger $N$ the flatter the distribution)",fontsize=19, alpha=0.85)


import numpy as np
from scipy.stats import binom#draw a single sample
np.random.seed(42)
print(binom.rvs(p=0.3, n=10),end="\n\n")#draw l0 samples
print(binom.rvs(p=0.3,n=10,size=10),end="\n\n")


from scipy.stats import binom#additional imports for plotting purpose
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams["figure.figsize"]=(14,7)#likelihood of x and y
x = 1
y = 7
print("pmf(X=1) = {}\npmf(X=7) = {}".format(binom.pmf(k=x,p=0.3, n=10), binom.pmf(k=y, p=0.3, n=10)))
#continuous pdf for the plot
x_s= np.arange(11)
y_s=binom.pmf(k=x_s,p=0.3, n=10)
plt.scatter(x_s,y_s, s=100)


from scipy.stats import binom#probability of x less or equal 0.3
print("P(X<3)={}".format(binom.cdf(k=3, p=0.3, n=10)))#probability of x in [-0.2,+0.2]
print("P(2<X<=8)= {}".format(binom.cdf(k=8, p=0.3, n=10) - binom.cdf(k=2, p=0.3, n=10)))

3.泊松分布





import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
import matplotlib.style as style
from IPython.core.display import HTML# PLOTTING CONFIG
%matplotlib inline
style.use('fivethirtyeight')
plt.rcParams["figure.figsize"] = (14, 7)
plt.figure(dpi=100)# PDF (Probability Mass Function) for Poisson Distribution
mu = 5 # Rate (lambda) for Poisson distribution
x_values = np.arange(20) # X-axis values from 0 to 19 (since Poisson PMF is defined for non-negative integers)
plt.bar(x=x_values, height=stats.poisson.pmf(x_values, mu), width=0.75, alpha=0.75)# CDF (Cumulative Distribution Function) for Poisson Distribution
plt.plot(x_values, stats.poisson.cdf(x_values, mu), color="#fc4f30")# LEGEND
plt.text(x=8, y=0.45, s="pmf (normed)", alpha=0.75, weight="bold", color="#008fd5")
plt.text(x=8.5, y=0.9, s="cdf", alpha=0.75, weight="bold", color="#fc4f30")# TICKS
plt.xticks(np.arange(21)) # X-axis ticks from 0 to 20
plt.tick_params(axis='both', which='major', labelsize=18)
plt.axhline(y=0.005, color='black', linewidth=1.3, alpha=0.7)# TITLE, SUBTITLE & FOOTER
plt.text(x=-2.5, y=1.25, s="Poisson Distribution - Overview", fontsize=26, weight='bold', alpha=0.75)
plt.text(x=-2.5, y=1.1,s="Depicted below are the normed probability mass function (pmf) and the cumulative density\n""function (cdf) of a Poisson distributed random variable $ y \sim Poi(\lambda) $, given $ \lambda=5 $.",fontsize=19, alpha=0.85)

plt.figure(dpi=100)# PUF LAM = 1
plt.scatter(np.arange(20),(stats.poisson.pmf(np.arange(20),mu=1)),alpha=0.75,s=100)
plt.plot(np.arange(20),(stats.poisson.pmf(np.arange(20),mu=1)),alpha=0.75,)
#PUF LAM = 5
plt.scatter(np.arange(20),(stats.poisson.pmf(np.arange(20),mu=5)),alpha=0.75,s=100)
plt.plot(np.arange(20),(stats.poisson.pmf(np.arange(20),mu=5)),alpha=0.75,)
#PUF N = 10
plt.scatter(np.arange(20),(stats.poisson.pmf(np.arange(20),mu=10)),alpha=0.75,s=100)
plt.plot(np.arange(20),(stats.poisson.pmf(np.arange(20),mu=10)),alpha=0.75,)# LEGEND
plt.text(x=3, y=0.1, s="$\lambda = 1$", alpha=0.75,rotation=-65, weight="bold", color="#008fd5")
plt.text(x=8.25, y=0.075, s="$\lambda = 5$", alpha=0.75,rotation=-35, weight="bold", color="#fc4f30")
plt.text(x=14.5, y=0.06, s="$\lambda = 10$", alpha=0.75,rotation=-20, weight="bold", color="#e5ae38")# TICKS
plt.xticks(range(21)[::2])
plt.tick_params(axis='both', which='major', labelsize=18)
plt.axhline(y=0,color='black',linewidth=1.3, alpha =0.7)# TITLE, SUBTITLE & FOOTER
plt.text(x=-2.5, y=0.475, s="Poisson Distribution - $\lambda$", fontsize=26, weight='bold', alpha=0.75)
plt.text(x=-2.5, y=0.425,s="Depicted below are three Poisson cistributed random variables with $\lambda $. As one can easily\nsee the parameter $\lambda$ shifts and flattens the distribution (the smaller $\lambda $ the sharper the function)",fontsize=19, alpha=0.85)

import numpy as np
from scipy.stats import poisson#draw a single sample
np.random.seed(42)
print(poisson.rvs(mu=10),end="\n\n")#draw 10 samples
print(poisson.rvs(mu=10,size=10),end="\n\n")


from scipy.stats import poisson
#additional imports for plotting pupose
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams["figure.figsize"]=(14,7)#continuous pdf for the plot
x_s= np.arange(15)
y_s=poisson.pmf(k=x_s,mu=5)
plt.scatter(x_s,y_s,s=100)


from scipy.stats import poisson#probabilityofxless or equal 0.3
print("P(X<=3) = {}".format(poisson.cdf(k=3,mu=5)))#probability ofxin [-0.2, +0.2]
print("P(2<X<=8) = {}".format(poisson.cdf(k=8,mu=5) - poisson.cdf(k=2,mu=5)))


from collections import Counterplt.figure(dpi=100)##:COMPLTATION
# DECLARING THE"TRUE"PARAVETERS LNDERLTING THE SAMPLE
lambda_real = 7# DRAT A SANPLE OF NEIOOO
np.random.seed(42)
sample=poisson.rvs(mu=lambda_real,size=1000)#ESTIMATE MU AND SIGMA
lambda_est = np.mean(sample)
print("Estimated LAMBDA: {}".format(lambda_est))## PLOTTTNG #
# SAMPLE DISTRIBUTION
cnt = Counter(sample)
_,values =zip(*sorted(cnt.items()))
plt.bar(range(len(values)),values/np.sum(values),alpha=0.25)plt.plot(range(18),poisson.pmf(k=range(18), mu=lambda_real), color="#fc4f30")plt.plot(range(18),poisson.pmf(k=range(18), mu=lambda_est), color="#e5ae38")#N LEGED
plt.text(x=6,y=.06,s="sample", alpha=.75, weight="bold", color="#008fd5")
plt.text(x=3.5,y=.14,s="true distrubtion", rotation=60, alpha=.75, weight="bold", color="#fc4f30")
plt. text (x=1, y=.08, s= "estimated distribution", rotation=60, alpha=.75, weight="bold", color="#e5ae38")# TICKS
plt.xticks(range(17)[::2])
plt.tick_params(axis='both',which='major', labelsize = 18)
plt.axhline(y=0.0009,color='black', linewidth = 1.3,alpha=.7)# TITLE, SUBTITLE & FOOTER
plt.text(x=-2.5, y=0.19, s="Poisson Distribution - Parameter Estimation", fontsize=26, weight='bold', alpha=0.75)
plt.text(x=-2.5, y=0.17,s="Depicted below is the distribution of a sample (blue) drawn from a Poisson distribution with $\lambda = 7$. \nAlso the estimated distrubution with $\lambda \sim 6.923$ is shown (yellow).",fontsize=19, alpha=0.85)

4.均匀分布


import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
import matplotlib.style as style
from IPython.core.display import HTML
from setuptools.command.rotate import rotate
from sympy import rotations# PLOTTING CONFIG
%matplotlib inline
style.use('fivethirtyeight')
plt.rcParams["figure.figsize"] = (14, 7)
plt.figure(dpi=100)# PDF
plt.plot(np.linspace(-4,4,100),stats.uniform.pdf(np.linspace(-4,4,100)))
plt.fill_between(np.linspace(-4,4,100),stats.uniform.pdf(np.linspace(-4,4,100)),alpha=.15)# CDF
plt.plot(np.linspace(-4,4,100), stats.uniform.cdf(np.linspace(-4,4,100)), )# LEGEND
plt.text(x=1.5, y=0.7, s="pdf (normed)",rotation=65, alpha=0.75, weight="bold", color="#008fd5")
plt.text(x=0.4, y=0.5, s="cdf", rotation=55,alpha=0.75, weight="bold", color="#fc4f30")# TICKS
plt.tick_params(axis='both', which='major', labelsize=18)
plt.axhline(y=0, color='black', linewidth=1.3, alpha=0.7)# TITLE, SUBTITLE & FOOTER
plt.text(x=-5, y=1.25, s="Nniform Distribution - Overview", fontsize=26, weight='bold', alpha=0.75)

plt.figure(dpi=100)# PDF loc=0,scale=1
plt.plot(np.linspace(-8,8,100),stats.uniform.pdf(np.linspace(-8,8,100),loc=0,scale=1),)
plt.fill_between(np.linspace(-8,8,100),stats.uniform.pdf(np.linspace(-8,8,100),loc=0,scale=1),alpha=.15)# PDF loc=0,scale=2
plt.plot(np.linspace(-8,8,100),stats.uniform.pdf(np.linspace(-8,8,100),loc=0,scale=2),)
plt.fill_between(np.linspace(-8,8,100),stats.uniform.pdf(np.linspace(-8,8,100),loc=0,scale=2),alpha=.15)# PDF loc=-3,scale=3
plt.plot(np.linspace(-8,8,100),stats.uniform.pdf(np.linspace(-4,4,100),loc=-3,scale=3),)
plt.fill_between(np.linspace(-8,8,100),stats.uniform.pdf(np.linspace(-4,4,100),loc=-3,scale=3),alpha=.15)# LEGEND
plt.text(x=-1, y=0.65, s="loc=0,scale=1",rotation=65, alpha=0.75, weight="bold", color="#008fd5")
plt.text(x=1, y=0.65, s="loc=0,scale=2", rotation=65,alpha=0.75, weight="bold", color="#fc4f30")
plt.text(x=-3, y=0.65, s="loc=-3,scale=3", rotation=65,alpha=0.75, weight="bold", color="#e5ae38")# TICKS
plt.tick_params(axis='both', which='major', labelsize=18)
plt.axhline(y=0, color='black', linewidth=1.3, alpha=0.7)# TITLE, SUBTITLE & FOOTER
plt.text(x=-5, y=1.1, s="Nniform Distribution - loc nad scale", fontsize=26, weight='bold', alpha=0.75)

5.卡方分布


import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
import matplotlib.style as style
from IPython.core.display import HTML# PLOTTING CONFIG
%matplotlib inline
style.use('fivethirtyeight')
plt.rcParams["figure.figsize"] = (14, 7)
plt.figure(dpi=100)# PDF
plt.plot(np.linspace(0,20,100),stats.chi2.pdf(np.linspace(0,20,100),df=4),)
plt.fill_between(np.linspace(0,20,100),stats.chi2.pdf(np.linspace(0,20,100),df=4),alpha=.15)# CDF
plt.plot(np.linspace(0,20,100),stats.chi2.cdf(np.linspace(0,20,100),df=4),)# LEGEND
plt.xticks(np.arange(0,21,2))
plt.text(x=11, y=0.25, s="pdf (normed)",alpha=0.75, weight="bold", color="#008fd5")
plt.text(x=11, y=0.85, s="cdf",alpha=0.75, weight="bold", color="#fc4f30")# TICKS
plt.xticks(np.arange(0,21,2))
plt.tick_params(axis='both', which='major', labelsize=18)
plt.axhline(y=0, color='black', linewidth=1.3, alpha=0.7)# TITLE, SUBTITLE & FOOTER
plt.text(x=-2, y=1.25, s=r"Chi-Squared $(\chi^{2})$ Distribution - Overview", fontsize=26, weight='bold', alpha=0.75)
plt.text(x=-2, y=1.1,s="Depicted below are the normed probability density function (pdf) and the cumulative density\nfunction (cdf) of a Chi-Squared distributed random variable $ y \sim \chi^{2}(k) $, given $k$=4.",fontsize=19, alpha=0.85)

plt.figure(dpi=100)# PDF k=1
plt.plot(np.linspace(0,15,500),stats.chi2.pdf(np.linspace(0,15,500),df=1),)
plt.fill_between(np.linspace(0,15,500),stats.chi2.pdf(np.linspace(0,15,500),df=1),alpha=.15)# PDF k=3
plt.plot(np.linspace(0,15,100),stats.chi2.pdf(np.linspace(0,15,100),df=3),)
plt.fill_between(np.linspace(0,15,100),stats.chi2.pdf(np.linspace(0,15,100),df=3),alpha=.15)# PDF k=6
plt.plot(np.linspace(0,15,100),stats.chi2.pdf(np.linspace(0,15,100),df=6),)
plt.fill_between(np.linspace(0,15,100),stats.chi2.pdf(np.linspace(0,15,100),df=6),alpha=.15)plt.text(x=0.5, y=0.7, s="$ k = 1$",rotation=-65,alpha=0.75, weight="bold", color="#008fd5")
plt.text(x=1.5, y=0.35, s="$ k = 3$",alpha=0.75, weight="bold", color="#fc4f30")
plt.text(x=5, y=0.2, s="$ k = 6$",alpha=0.75, weight="bold", color="#e5ae38")# TICKS
plt.tick_params(axis='both', which='major', labelsize=18)
plt.axhline(y=0, color='black', linewidth=1.3, alpha=0.7)# TITLE, SUBTITLE & FOOTER
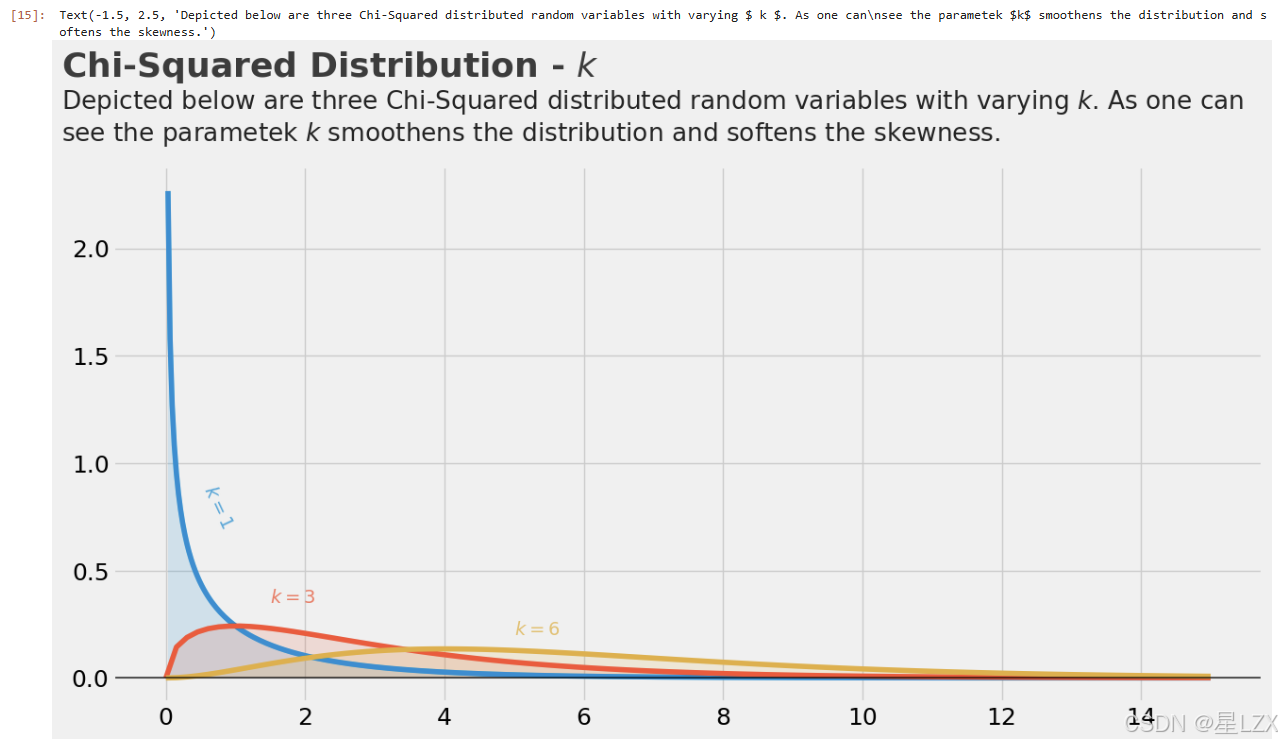
plt.text(x=-1.5, y=2.8, s="Chi-Squared Distribution - $ k $", fontsize=26, weight='bold', alpha=0.75)
plt.text(x=-1.5, y=2.5,s="Depicted below are three Chi-Squared distributed random variables with varying $ k $. As one can\nsee the parametek $k$ smoothens the distribution and softens the skewness.",fontsize=19, alpha=0.85)
import numpy as np
from scipy.stats import chi2#draw a single sample
np.random.seed(42)
print(chi2.rvs(df=4),end="\n\n")
#draw 10 samples
print(chi2.rvs(df=4,size=10),end="\n\n")

from scipy.stats import chi2# additional imports for plotting purpose
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams["figure.figsize"]=(14,7)# continuous pdf for the plot
x_s= np.arange(15)
y_s= chi2.pdf(x=x_s,df=4)
plt.scatter(x_s,y_s, s=100);


from scipy.stats import chi2# probability ofx less or equal 0.3
print("P(X<=3) = {}".format(chi2.cdf(x=3, df=4)))#probability ofxin [-0.2, +0.2]
print("P(2<X<=8) = {}".format(chi2.cdf(x=8, df=4)- chi2.cdf(x=2, df=4)))

6.beta分布



import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
import matplotlib.style as style
from IPython.core.display import HTML# PLOTTING CONFIG
%matplotlib inline
style.use('fivethirtyeight')
plt.rcParams["figure.figsize"] = (14, 7)plt.figure(dpi=100)# PDF
plt.plot(np.linspace(0,1,100),stats.beta.pdf(np.linspace(0,1,100),a=2,b=2),)
print(stats.beta.pdf(np.linspace(0,1,100),a=2,b=2))
plt.fill_between(np.linspace(0,1,100),stats.beta.pdf(np.linspace(0,1,100),a=2,b=2),alpha=.15)# CDF
plt.plot(np.linspace(0,1,100),stats.beta.cdf(np.linspace(0,1,100),a=2,b=2),)plt.text(x=.1, y=0.7, s="pdf (normed)",rotation=-52,alpha=0.75, weight="bold", color="#008fd5")
plt.text(x=0.45, y=0.5, s="cdf",rotation=-40,alpha=0.75, weight="bold", color="#fc4f30")# TICKS
plt.tick_params(axis='both', which='major', labelsize=18)
plt.axhline(y=0, color='black', linewidth=1.3, alpha=0.7)# TITLE, SUBTITLE & FOOTER
plt.text(x=-0.125, y=1.85, s=r"Beta Distribution-Overview", fontsize=26, weight='bold', alpha=0.75)
plt.text(x=-0.125, y=1.6,s="Depicted below are the normed probability density function (pdf) and the cumulative density\nfunction (cdf) of a beta distributed random variable $ y \sim Beta(\\alpha, \\beta)$, given $ \\alpha = 2 $ and $ \\beta = 2$.",fontsize=19, alpha=0.85)



plt.figure(dpi=100)# A=B=1
plt.plot(np.linspace(0,1,200),stats.beta.pdf(np.linspace(0,1,200),a=1,b=1),)
plt.fill_between(np.linspace(0,1,200),stats.beta.pdf(np.linspace(0,1,200),a=1,b=1),alpha=.15)# A=B=10
plt.plot(np.linspace(0,1,200),stats.beta.pdf(np.linspace(0,1,200),a=10,b=10),)
plt.fill_between(np.linspace(0,1,200),stats.beta.pdf(np.linspace(0,1,200),a=10,b=10),alpha=.15)# A=B=100
plt.plot(np.linspace(0,1,200),stats.beta.pdf(np.linspace(0,1,200),a=100,b=100),)
plt.fill_between(np.linspace(0,1,200),stats.beta.pdf(np.linspace(0,1,200),a=100,b=100),alpha=.15)plt.text(x=.1, y=1.45, s=r"$ \alpha=1,\beta=1 $",alpha=0.75, weight="bold", color="#008fd5")
plt.text(x=0.325, y=3.5, s=r"$ \alpha=10,\beta=10 $",rotation=35,alpha=0.75, weight="bold", color="#fc4f30")
plt.text(x=0.4125, y=8, s=r"$ \alpha=100,\beta=100 $",rotation=80,alpha=0.75, weight="bold", color="#e5ae38")# TICKS
plt.tick_params(axis='both', which='major', labelsize=18)
plt.axhline(y=0, color='black', linewidth=1.3, alpha=0.7)# TITLE, SUBTITLE & FOOTER
plt.text(x=-0.1, y=13.75, s=r"Beta Distribution -constant $\frac{\alpha} {\beta}$, varying $\alpha + \beta$", fontsize=26, weight='bold', alpha=0.75)
plt.text(x=-0.1, y=12,s='Depicted below are three beta distributed random variables with' + r'equal $\frac{\alpha} {\beta} $ and varying $\alpha+\beta$.' + '\n' +r'As one can see the sum of $\alpha + \beta$ (mainly) sharpens the distribution (the bigger the sharper).',fontsize=19, alpha=0.85)

plt.figure(dpi=100)# A/B=1/3
plt.plot(np.linspace(0,1,200),stats.beta.pdf(np.linspace(0,1,200),a=25,b=75),)
plt.fill_between(np.linspace(0,1,200),stats.beta.pdf(np.linspace(0,1,200),a=25,b=75),alpha=.15)# A/B=1
plt.plot(np.linspace(0,1,200),stats.beta.pdf(np.linspace(0,1,200),a=50,b=50),)
plt.fill_between(np.linspace(0,1,200),stats.beta.pdf(np.linspace(0,1,200),a=50,b=50),alpha=.15)# A/B=3
plt.plot(np.linspace(0,1,200),stats.beta.pdf(np.linspace(0,1,200),a=75,b=25),)
plt.fill_between(np.linspace(0,1,200),stats.beta.pdf(np.linspace(0,1,200),a=75,b=25),alpha=.15)plt.text(x=0.15, y=5, s=r"$ \alpha=25,\beta=75 $",rotation=80,alpha=0.75, weight="bold", color="#008fd5")
plt.text(x=0.39, y=5, s=r"$ \alpha=50,\beta=50 $",rotation=80,alpha=0.75, weight="bold", color="#fc4f30")
plt.text(x=0.65, y=5, s=r"$ \alpha=75,\beta=25 $",rotation=80,alpha=0.75, weight="bold", color="#e5ae38")# TICKS
plt.tick_params(axis='both', which='major', labelsize=18)
plt.axhline(y=0, color='black', linewidth=1.3, alpha=0.7)# TITLE, SUBTITLE & FOOTER
plt.text(x=-0.1, y=11.75, s=r"Beta Distribution -constant $\alpha + \beta$, varying $\frac{\alpha} {\beta}$", fontsize=26, weight='bold', alpha=0.75)
plt.text(x=-0.1, y=10,s='Depicted below are three beta distributed random variables with' + r'equal $\alpha + \beta$ and varying $\frac{\alpha} {\beta} $.'+'\n'+r'As one can see the fraction of $\frac{\alpha} {\beta} $ (mainly) shifts the distribution($\alpha$ towards 1, $\beta$ towards 0).',fontsize=19, alpha=0.85)

from scipy.stats import beta
# draw a single sample
print(beta.rvs(a=2,b=2),end="\n\n")
# draw 10 samples
print(beta.rvs(a=2,b=2,size=10))

from scipy.stats import beta
# additional import for plotting
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams["figure.figsize"]=(14,7)# continuous pdf for the plot
x_s=np.linspace(0,1,100)
y_s=beta.pdf(a=2,b=2,x=x_s)
plt.scatter(x_s, y_s)


from scipy.stats import beta#probability of x less or equal 0. 3
print("P<0.3)={:.3}".format(beta.cdf(a=2,b=2, x=0.3)))#probability of xin [-0.2, +0.2]
print("P(-0.2 <X< 0.2)= {:.3}".format(beta. cdf(a=2, b=2, x=0.2)- beta.cdf(a=2, b=2, x=-0.2)))

9.核函数变换
1.核函数的目的


2.线性核函数

3.多项式核函数

4.核函数实例

5.高斯核函数
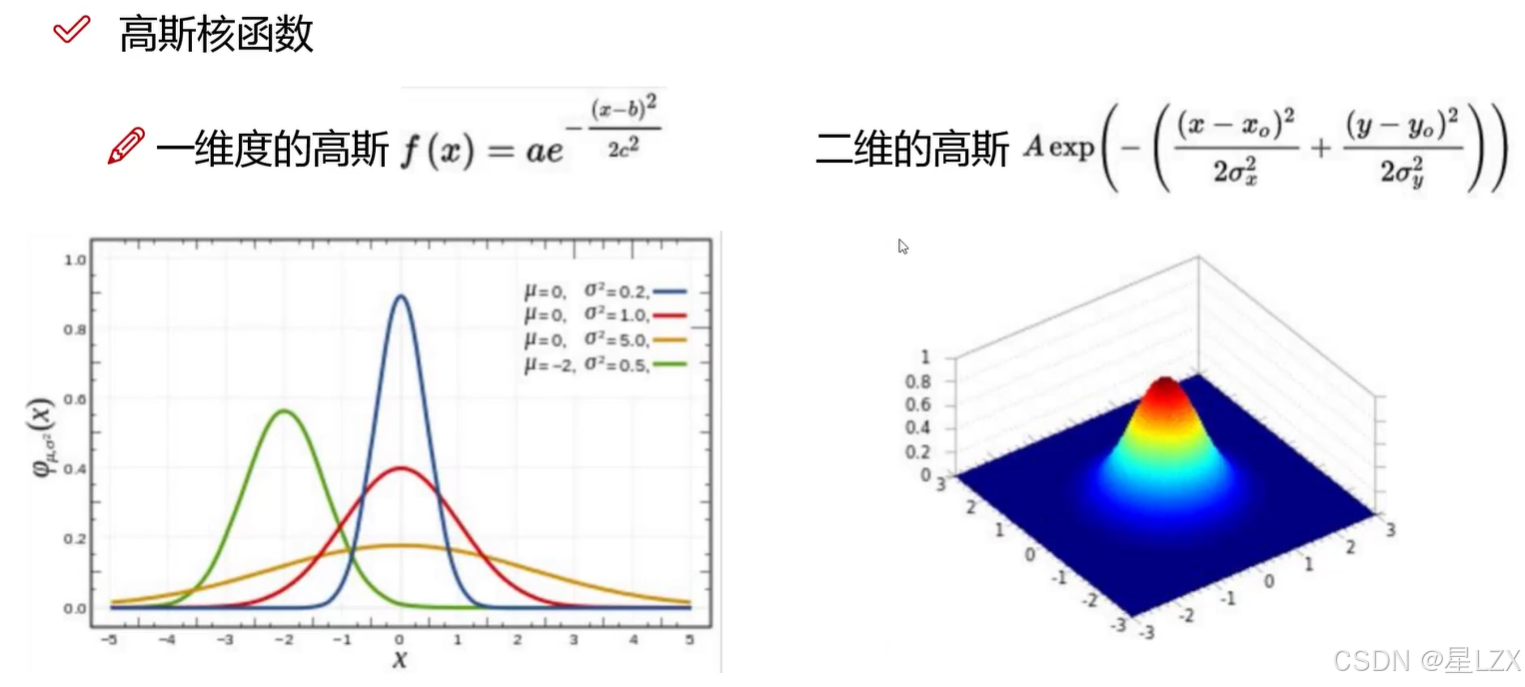


6.参数的影响


10.熵与激活函数
1.熵的概念

2.熵的大小意味着什么


3.激活函数

4.激活函数的问题




11.回归分析
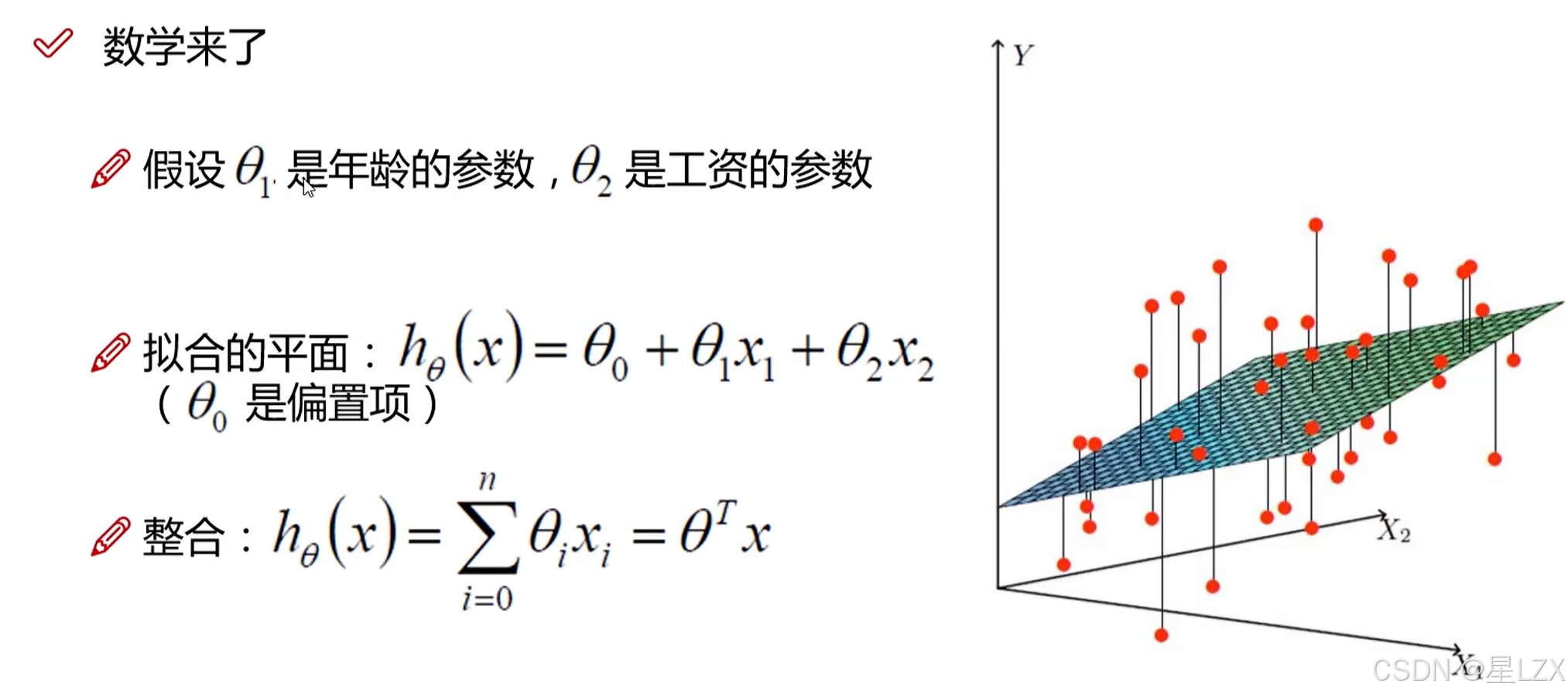
1.回归分析概述



2.回归方程定义


3.误差项的定义


4.最小二乘法推导与求解





5.回归方程求解小例子






6.回归直线拟合优度






7.多元与曲线回归问题






8.Python工具包介绍



9.statsmodels回归分析
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as smnsample =20
x = np.linspace(0, 10,nsample)
x


X = sm.add_constant(x)
X

#β0,β1分别设置成2,5
beta = np.array([2,5])
beta

#误差项
e = np.random.normal(size=nsample)
e

#实际值y
y= np.dot(X, beta)+ e
y

#最小二乘法
model = sm.OLS(y,X)#拟合数据
res = model.fit()#回归系数
res.params

#全部结果
res.summary()

#拟合的估计值
y_= res.fittedvalues
y_

fig, ax=plt.subplots(figsize=(8,6))
ax.plot(x, y,'o',label='data')#原始数据
ax.plot(x, y_,'r--.',label='test')#拟合数据
ax.legend(loc='best')
plt.show()

10.高阶与分类变量实例
#Y=5+2*X+3*X^2
nsample=50
x= np.linspace(0,10,nsample)
X= np.column_stack((x,x**2))
X= sm.add_constant(X)beta = np.array([5,2,3])
e = np.random.normal(size=nsample)
y = np.dot(X, beta)+e
model = sm.OLS(y,X)
results = model.fit()
results.params

results.summary()

y_fitted =results.fittedvalues
fig, ax= plt.subplots(figsize=(8,6))
ax.plot(x,y,'o',label='data')
ax.plot(x, y_fitted,'r--.',label='OLS')
ax.legend(loc='best')
plt.show()


nsample=50
groups = np.zeros(nsample,int)
groups

import pandas as pd
import patsygroups[20:40]=1
groups[40:]=2# 创建一个 pandas Series
group_series = pd.Series(groups)# 使用 patsy.dmatrices 生成设计矩阵
# 公式 'group ~ 0 + C(group)' 表示 group 是因变量,C(group)表示将 group 作为分类变量,'0'表示不包含常数项
dummy = patsy.dmatrix('C(group) - 1', data={'group': group_series})
print(dummy)

x=np.linspace(0,20,nsample)
X=np.column_stack((x,dummy))
X= sm.add_constant(X)
beta =[5,2,3,6,9]
e= np.random.normal(size=nsample)
y=np.dot(X,beta)+e
result=sm.OLS(y,X).fit()
result.summary()

fig,ax=plt.subplots(figsize=(8,6))
ax.plot(x,y,'o',label="data")
ax.plot(x,result.fittedvalues,'r--.',label="OLS")
ax.legend(loc= 'best')
plt.show()







11.案例:汽车价格预测任务概述

#loading packages
import numpy as np
import pandas as pd
from pandas import datetime#data visualization and missing values
import matplotlib.pyplot as plt
import seaborn as sns # advanced yizs
import missingno as msno # missing values
%matplotlib inline
# stats
from statsmodels.distributions.empirical_distribution import ECDF
from sklearn.metrics import mean_squared_error, r2_score# machine learning
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import Lasso, LassoCV
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.ensemble import RandomForestRegressor
seed = 123#importing data(?=missing values)
data = pd.read_csv("Auto-Data.csv", na_values = '?')
data.columns

data.dtypes

# first glance at the data itself
print("In total:",data.shape)
data. head(5)


12.案例:缺失值填充



sns.set(style="ticks")
plt.figure(figsize=(12,5))
c ='#366DE8'#ECDF
plt.subplot(121)
cdf = ECDF(data['normalized-losses'])
plt.plot(cdf.x,cdf.y,label="statmodels",color = c)
plt.xlabel('normalized losses')
plt.ylabel('ECDF');# overall distribution
plt.subplot(122)
plt.hist(data['normalized-losses'].dropna(),bins = int(np.sqrt(len(data['normalized-losses']))),color =c)
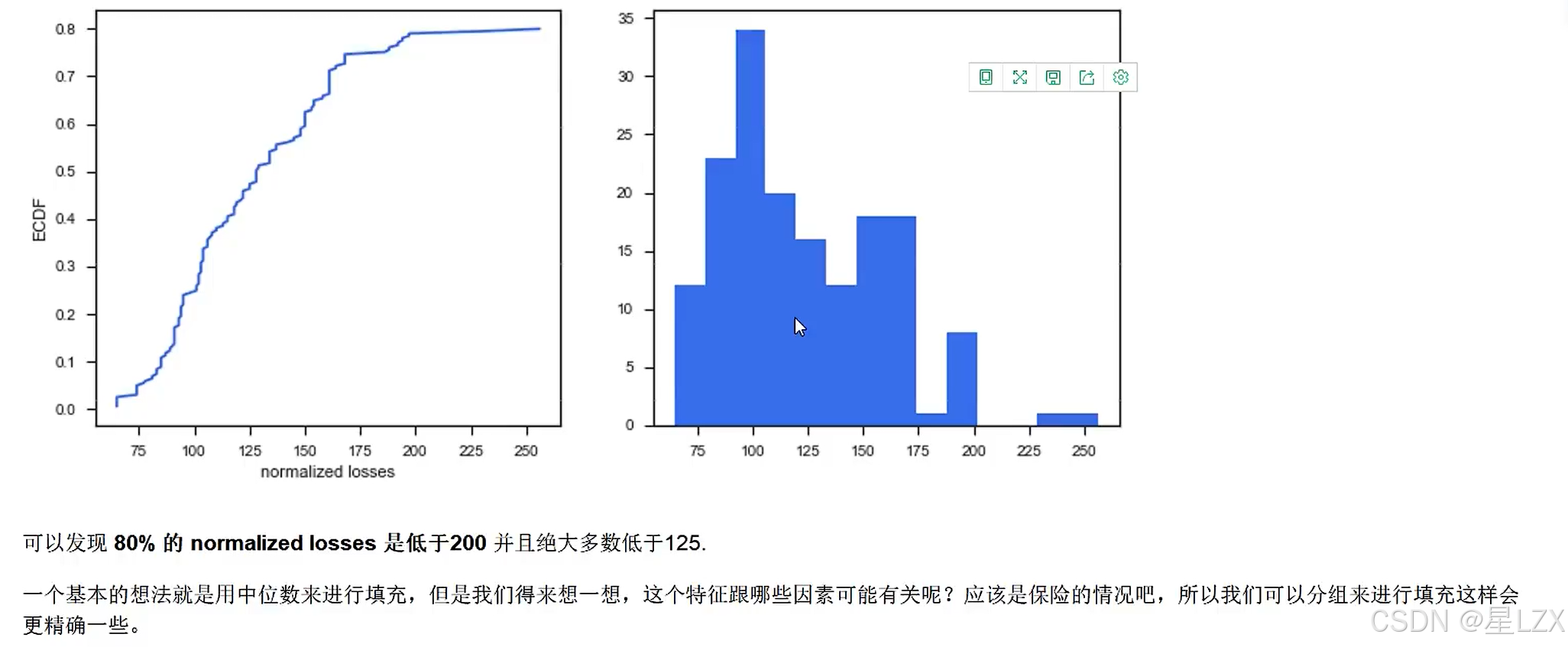


13.案例:特征相关性










14.案例:预处理问题





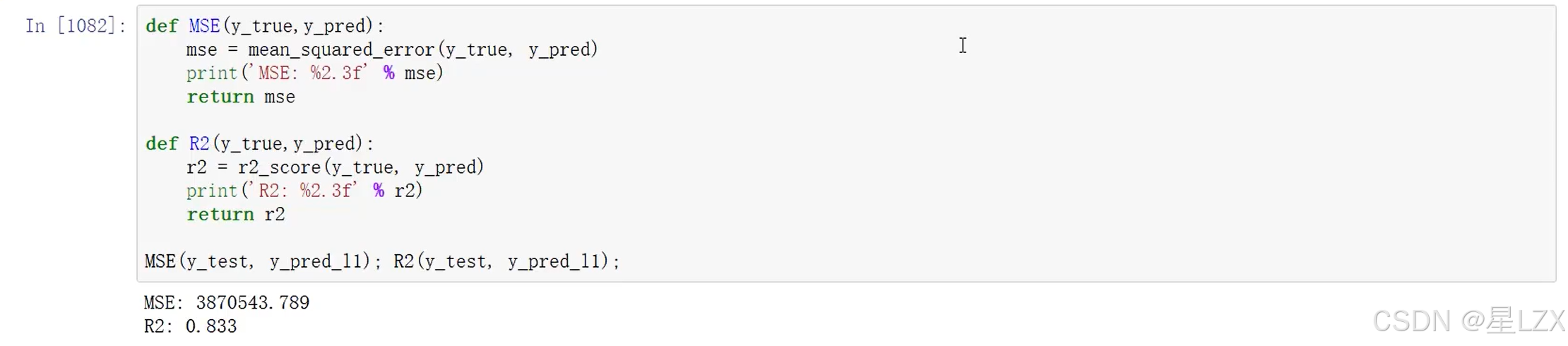
15.案例:回归求解









12. 假设检验
1.假设检验基本思想



2.左右侧检验与双侧检验




3.Z检验基本原理



4.Z检验实例



5.T检验基本原理



6.T检验实例







7.T检验应用条件





8.卡方检验






9.假设检验中的两类错误





10.Python假设检验实例












11.Python卡方检验实例





13.相关分析
1.相关分析概述


2.皮尔森相关系数



3.计算与检验






4.斯皮尔曼等级相关






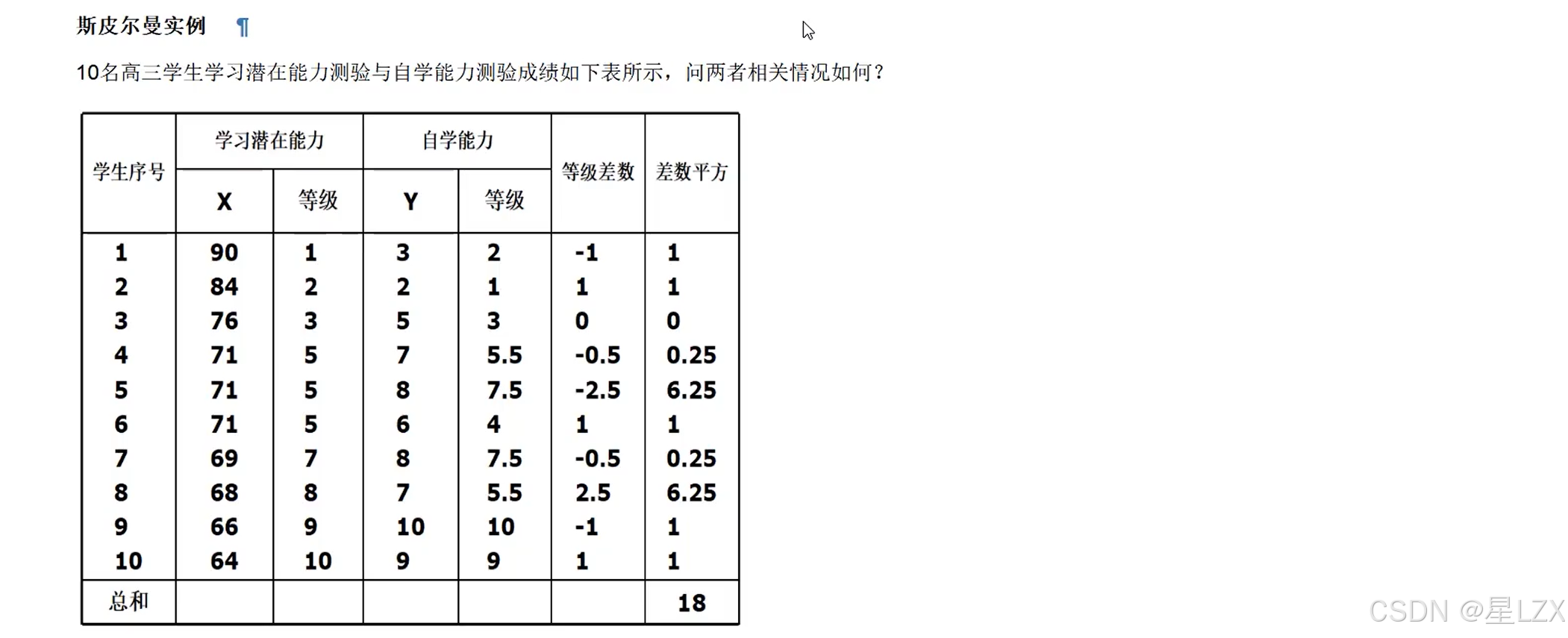

5.肯德尔系数








6.质量相关分析







7.偏相关与复相关








14.方差分析
1.方差分析概述



2.方差的比较





3.方差分析计算方法












4.方差分析中的多重比较





5.多因素方差分析






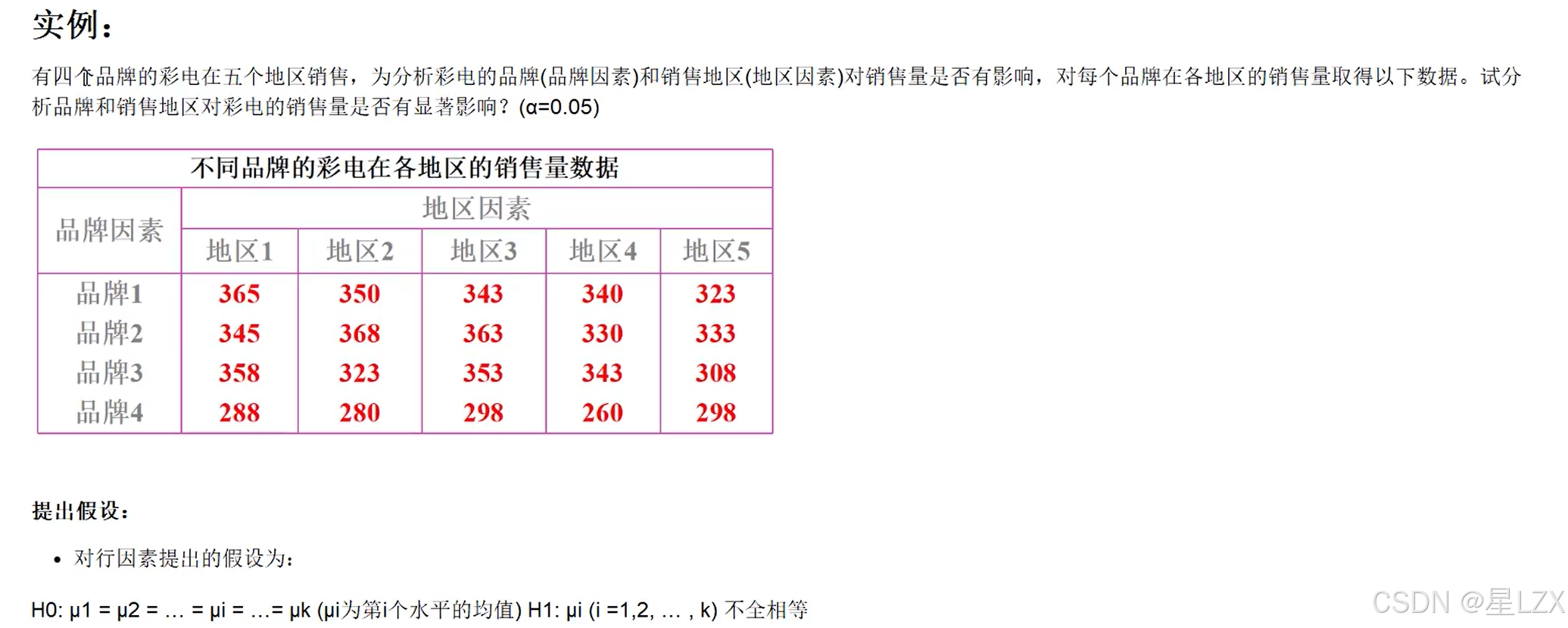



6.Python方差分析实例




15.聚类分析
1.层次聚类概述


2.层次聚类流程



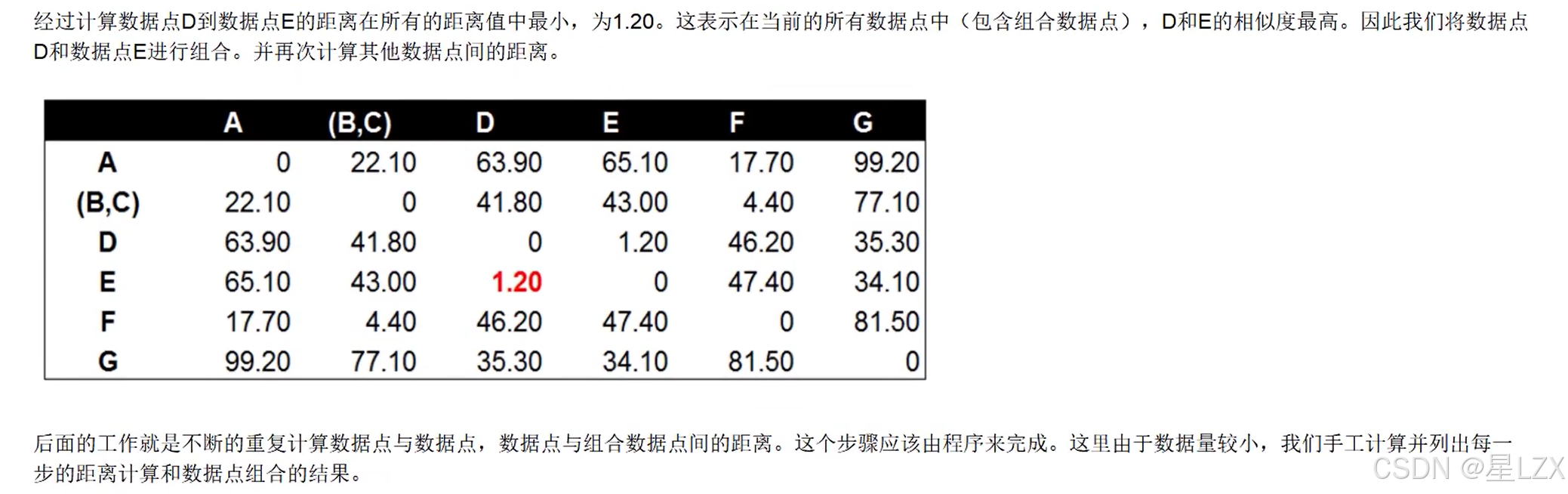


3.层次聚类实例











4.Kmeans聚类算法
1.KMEANS算法概述


2.KMEANS工作流程


3.KMEANS迭代可视化展示
可视化 DBSCAN 聚类
5.DBSCAN聚类算法
1.DBSCAN聚类算法



2.DBSCAN工作流程



3.DBSCAN可视化展示
可视化 DBSCAN 聚类
6.聚类算法实践
1.多种聚类算法概述

2.聚类案例实战














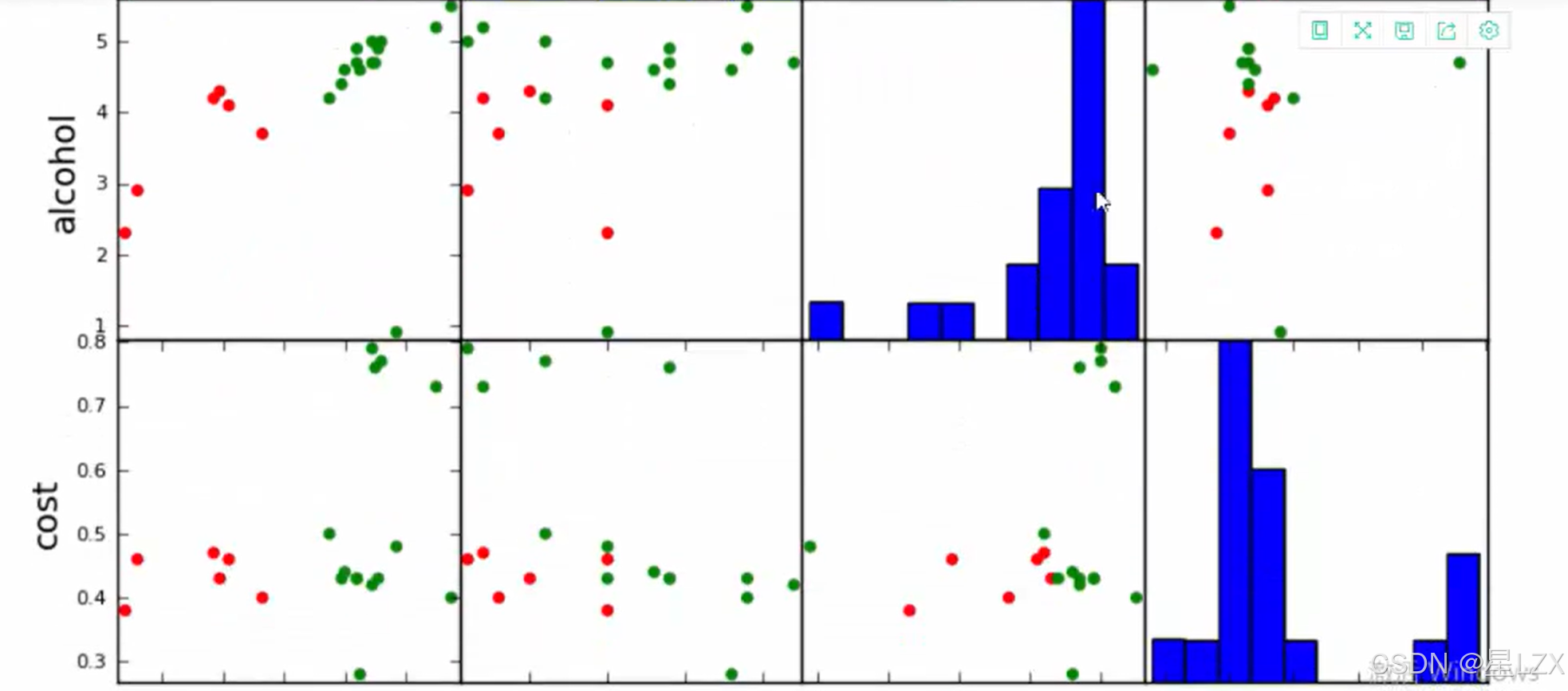



















16.贝叶斯分析
1.贝叶斯分析概述

2.概率的解释




3.贝叶斯学派与经典统计学派的争论


4.贝叶斯算法概述



5.贝叶斯推导实例






6.贝叶斯拼写纠错实例




7.贝叶斯解释






8.垃圾邮件过滤实例





8.经典求解思路











9.MCMC概述






10.PYMC3概述





11.模型诊断





12.模型决策





相关文章:

人工智能数学基础学习PPT
学习视频:人工智能 -数学基础 文章目录 1.简介1.函数2.极限3.无穷小与无穷大4.连续性与导数5.偏导数6.方向导数7.梯度 2.微积分1.微积分基本想法2.微积分的解释3.定积分4.定积分性质5.牛顿-莱布尼茨公式 3.泰勒公式与拉格朗日1.泰勒公式2.一点一世界3.阶数的作用4.…...

企业文件防泄密软件哪个好?
在企业文件防泄密软件领域,天锐绿盾和中科数安都是备受认可的品牌,它们各自具有独特的特点和优势。 以下是对这两款软件的详细比较: 天锐绿盾 功能特点 集成性强:集成了文件加密、数据泄露防护DLP、终端安全管理、行为审计等数据安…...

美丽 百褶裙提示词 + MD
MD 参考教程:Marvelous Designer零基础教学,MD布料制作-百褶裙建模制作,次世代教学_哔哩哔哩_bilibili 【MD新手教程】30分钟教会你制作百褶裙,Marvelous Designer超简单入门案例教程_哔哩哔哩_bilibili 【c4d技术解析】MD百褶裙…...

解释和对比“application/octet-stream“与“application/x-protobuf“
介绍 在现代 Web 和分布式系统的开发中,数据的传输和交换格式扮演着关键角色。为了确保数据在不同系统之间的传输过程中保持一致性,MIME 类型(Multipurpose Internet Mail Extensions)被广泛应用于描述数据的格式和内容类型。在 …...

基于YALMIP和cplex工具箱的微电网最优调度算法matlab仿真
目录 1.课题概述 2.系统仿真结果 3.核心程序与模型 4.系统原理简介 4.1 系统建模 4.2 YALMIP工具箱 4.3 CPLEX工具箱 5.完整工程文件 1.课题概述 基于YALMIP和cplex工具箱的微电网最优调度算法matlab仿真。通过YALMIP和cplex这两个工具箱,完成微电网的最优调…...

AI前端开发技能提升与ScriptEcho:拥抱AI时代的前端开发新范式
随着人工智能技术的飞速发展,AI前端开发岗位对技能的要求也水涨船高。越来越多的企业需要具备AI相关知识和高级前端开发能力的工程师,这使得传统的前端开发模式面临着巨大的挑战。如何提升开发效率,降低人力成本,成为了摆在所有前…...

LeetCode题解:2690. 无穷方法对象,Proxy
Problem: 2690. 无穷方法对象 思路 这个问题的核心在于创建一个对象,该对象能够响应对其任何方法的调用,并返回调用的方法名称。为了实现这一点,我们可以利用 JavaScript 中的 Proxy 对象。Proxy 对象允许我们自定义对象的基本操作ÿ…...

Python中的HTTP客户端库:httpx与request | python小知识
Python中的HTTP客户端库:httpx与request | python小知识 在Python中,发送HTTP请求和处理响应是网络编程的基础。requests和httpx是两个常用的HTTP库,它们都提供了简洁易用的API来发送HTTP请求。然而,httpx作为新一代的HTTP客户端…...

RabbitMQ使用guest登录提示:User can only log in via localhost
guest用户默认是无法使用远程访问的,生产环境建议直接在对应服务器登录使用。 1、通过创建新增用户并赋予权限实现远程登录 添加新用户 rabbitmqctl add_user zjp zjp 设置管理员 rabbitmqctl set_user_tags zjp administrator 设置新用户的权限 rabbitmqctl…...

#渗透测试#批量漏洞挖掘#Crocus系统—Download 文件读取
免责声明 本教程仅为合法的教学目的而准备,严禁用于任何形式的违法犯罪活动及其他商业行为,在使用本教程前,您应确保该行为符合当地的法律法规,继续阅读即表示您需自行承担所有操作的后果,如有异议,请立即停…...
)
基于Matlab实现六自由度机械臂正逆运动仿真(源码)
在机器人技术领域,六自由度机械臂是一种广泛应用的设备,它可以实现空间中的位置和姿态控制。本项目聚焦于六自由度机械臂的正逆运动学仿真,利用MATLAB2016b作为开发工具,旨在深入理解并掌握机械臂的工作原理和运动控制。 正运动学…...

亚信安全正式接入DeepSeek
亚信安全致力于“数据驱动、AI原生”战略,早在2024年5月,推出了“信立方”安全大模型、安全MaaS平台和一系列安全智能体,为网络安全运营、网络安全检测提供AI技术能力。自2024年12月DeepSeek-V3发布以来,亚信安全人工智能实验室利…...

Django 创建第一个项目
Django 创建第一个项目 引言 Django 是一个高级的 Python Web 框架,它鼓励快速开发和干净、实用的设计。本指南将带您从头开始创建一个简单的 Django 项目,以便您能够熟悉 Django 的基本结构和概念。 准备工作 在开始之前,请确保您已经安装了 Python 和 Django。以下是安…...

RL基础概念
RL意味着模型从真实世界中获取反馈,根据策略调整参数,以达到最大化反馈的优化算法; 强化学习的核心在于:1.试错(因为仅凭reward无法得到明确的优化方向,所以需要不断多尝试);2.延迟奖…...

像取快递一样取文件?
看到一个很有意思的项目,像我们做软件分享的感觉会有用,就是现在服务器费用太贵了,如果自建的话感觉不是很值得。 FileCodeBox FileCodeBox 是一个轻量级的文件分享系统,它基于匿名口令分享文本和文件,无需注册登录&…...

Jenkins 新建配置Pipeline任务 三
Jenkins 新建配置Pipeline任务 三 一. 登录 Jenkins 网页输入 http://localhost:8080 输入账号、密码登录 一个没有创建任务的空 Jenkins 二. 创建 任务 图 NewItem 界面左上角 New Item 图NewItemSelect 1.Enter an item name:输入任务名 2.Select an ite…...

React 前端框架搭建与解析
React 前端框架搭建与解析 一、 概述 React 是 Facebook 开源的用于构建用户界面的 JavaScript 库,以其组件化、声明式编程范式以及高效的虚拟 DOM 渲染机制,成为当今最流行的前端框架之一。本文将带领你从零开始搭建一个 React 开发环境,并深入解析其核心概念。 二、 环…...

像指针操作、像函数操作的类
像指针一样的类。把一个类设计成像一个指针。什么操作符运用到指针上? 使用标准库的时候,里面有个很重要的东西叫容器。容器本身一定带着迭代器。迭代器作为另外一种智能指针。迭代器指向容器里的一个元素。迭代器用来遍历容器。 _list_iterator是链表迭…...

15.Python网络编程:进程池、进程间通信、多线程、进程和线程区别、网络通信、端口、IP地址、socket、UDP、TCP、http
1. 进程池(Process Pool) 进程池是通过将多个进程放入池中管理来避免频繁地创建和销毁进程,提高效率。Python 提供了 multiprocessing.Pool 类来实现进程池,它可以用于并行计算任务。 示例:使用进程池 from multipr…...

Ubuntu启动geteck/jetlinks实战:Docker启动
参考: JetLinks 物联网基础平台 安装Docker Ubuntu下载安装Docker-Desktop-CSDN博客 sudo apt install -y docker-compose 下载源码 git clone https://github.com/jetlinks/jetlinks-community.git cd jetlinks-community 启动 cd docker/…...

Newton 差商插值多项式
Newton 差商插值多项式 根据差商定义,把 x x x 看成[ a , b ] a,b] a,b]上一点,可得 f ( x ) f ( x 0 ) f [ x , x 0 ] ( x − x 0 ) f(x)f(x_0)f[x,x_0](x-x_0) f(x)f(x0)f[x,x0](x−x0) f [ x , x 0 ] f [ x 0 , x 1 ] f [ x , x 0 , x 1…...

ubuntu下ollama/vllm两种方式在本地部署Deepseek-R1
1.前言 今年过年,deepseek一下子爆火,导致我前段时间好好用的官网直接挤爆了,一直转圈圈到没心思过了,天天挂热搜,直接导致我的科研工作受阻(dog),好吧,话不多说,看看怎么在本地部署deepseek丝滑享受以及白嫖一下api体验>_<! 部署环境: 系统:ubuntu22.04 显…...

如何使用ps批量去除固定位置水印
使用 Photoshop 批量去除固定位置的水印,有几种方法可以实现自动化,具体取决于水印的复杂程度和你对 Photoshop 的熟悉程度: 1. 动作(Actions) 批处理(Batch): 这是最常用的方法&…...

基于 STM32 的病房监控系统
标题:基于 STM32 的病房监控系统 内容:1.摘要 基于 STM32 的病房监控系统摘要:本系统采用 STM32 微控制器作为核心,通过传感器实时监测病房内的环境参数,如温度、湿度、光照等,并将数据上传至云端服务器。医护人员可以通过手机或…...

Windows部署deepseek-r1
安装Ollama 访问Ollama下载页,选择对应的操作系统进行下载 运行OllamaSetup,进行安装 任务栏出现Ollama图标,运行正常 cmd查看Ollama版本 C:\Users\PC>ollama -v ollama version is 0.5.7 部署模型 deepseek 可访问deepseek模型页,切…...
)
CCFCSP第34次认证第一题——矩阵重塑(其一)
第34次认证第一题——矩阵重塑(其一) 官网链接 时间限制: 1.0 秒 空间限制: 512 MiB 相关文件: 题目目录(样例文件) 题目背景 矩阵(二维)的重塑(reshap…...

webpack打包优化策略
1. 减少打包体积 减少打包文件的大小是为了提高加载速度,降低网络带宽消耗,提升用户体验。常见的减少打包体积的优化策略包括: 代码分割(Code Splitting):将代码拆分成多个小文件,让浏览器按需…...

八股文-2025-02-12
BFC BFC属于普通流。BFC全称是Block Formatting Context,意思就是块级格式化上下文。你可以把BFC看做元素的一个属性,当元素拥有BFC属性,这个元素就可以看作是隔离了的独立容器,容器里边的元素不会影响到容器外部的元素.https://b…...
)
部门管理(体验,最原始方法来做,Django+mysql)
本人初学,写完代码在此记录和复盘 在创建和注册完APP之后(我的命名是employees),编写models.py文件创建表 手动插入了几条数据 1.部门查询 urls.py和views.py在编写之前,都要注意导入对应的库 urls.py:…...

联想拯救者Y9000银河麒麟系统安装Nvidia 4060显卡驱动
查了好多资料, 发现银河麒麟的资料较少, 只能自己试验了, 如有帮助, 点个赞吧~~ 前提: 本人笔记本是联想拯救者Y9000, 独立显卡 Nvidia4060, 主机系统是银河麒麟V10 (2403), 笔记本处于联网状态ÿ…...

深入解析 STM32 GPIO:结构、配置与应用实践
理解 GPIO 的工作原理和配置方法是掌握 STM32 开发的基础,后续的外设(如定时器、ADC、通信接口)都依赖于 GPIO 的正确配置。 目录 一、GPIO 的基本概念 二、GPIO 的主要功能 三、GPIO 的内部结构 四、GPIO 的工作模式 1. 输入模式 2. 输…...

突破数据壁垒,动态住宅代理IP在数据采集中的高效应用
在当今数字化时代,数据已经成为企业和个人决策的重要依据。无论是市场调研、竞争分析,还是价格监控、SEO优化,数据采集都扮演着至关重要的角色。然而,随着技术发展与网络安全措施的日益严格,传统的数据采集方式面临着前…...

Spring 项目接入 DeepSeek,分享两种超简单的方式!
⭐自荐一个非常不错的开源 Java 面试指南:JavaGuide (Github 收获148k Star)。这是我在大三开始准备秋招面试的时候创建的,目前已经持续维护 6 年多了,累计提交了 5600 commit ,共有 550 多位贡献者共同参与…...

SSE与Websocket详解,SSE实现对话框流式输出
SSE详解 SSE(Server-Sent Events)是一种在Web应用中实现单向实时通信的技术,它允许服务器主动向客户端发送更新,而无需客户端不断发起请求。SSE基于HTTP协议,利用HTTP的长连接特性,通过浏览器向服务器发送一个HTTP请求,建立一条持久化的连接,然后服务器可以通过这条连…...

Shell脚本笔记
Linux其他命令 Shell脚本笔记...

Hydra主配置文件和模块化配置管理
在 Hydra 中,我们可以使用 defaults 关键字 在主配置文件 config.yaml 中加载多个子配置文件,从而实现 模块化配置管理。这在深度学习、超参数优化、数据预处理等场景下非常有用。 1️⃣ 配置文件目录结构 假设我们有一个深度学习训练项目,…...

oracle dbms_sqltune 使用
创建测试表 CREATE TABLE test_table (id NUMBER PRIMARY KEY,event_date DATE,value NUMBER );插入测试数据 DECLAREi NUMBER; BEGINFOR i IN 1..1000000 LOOPINSERT INTO test_table (id, event_date, value)VALUES (i, SYSDATE - MOD(i, 365), DBMS_RANDOM.VALUE(1, 1000)…...

Mediamtx+Python读取webrtc流
一、功能思路: 1、我采用ffmpeg -re -stream_loop -1 -i xcc.mp4 -c:v libx264 -profile:v baseline -x264opts "bframes0:repeat_headers1" -b:v 1500k -preset fast -f flv rtmp://127.0.0.1:1835/stream/111推流到mediamtx的rtmp上 2、通过mediamtx自…...
)
Makefile和算法(20250213)
1. Makefile 1.1 功能 管理工程代码的编译和链接,可以一键化实现代码工程的编译和管理。 时间戳:根据时间戳,可以只编译发生修改后的文件 1.2 Makefile 基本语法和相关操作 1.2.1 创建一个Makefile文件 Makefile/makefile(首…...
—— 磁盘管理器 SMGR)
postgresql源码学习(59)—— 磁盘管理器 SMGR
一、 定义及作用 PostgreSQL 的磁盘管理器(Storage Manager,简称 SMGR)是数据库系统中负责管理底层存储的核心模块。磁盘管理器并非直接操作磁盘上的文件,而是通过VFD(虚拟文件描述符,将在后续学习…...

亚冬会绽放“云端”,联通云如何点亮冰城“科技之光”?
科技云报到原创。 35年前,中国第一次承办亚运会,宣传曲《亚洲雄风》红遍大江南北,其中有一句“我们亚洲,云也手握手”。如今回看,这句话仿佛有了更深的寓意:一朵朵科技铸就的“云”,把人和人连…...

寻找最优的路测路线
寻找最优的路测路线 真题目录: 点击去查看 E 卷 200分题型 题目描述 评估一个网络的信号质量,其中一个做法是将网络划分为栅格,然后对每个栅格的信号质量计算。 路测的时候,希望选择一条信号最好的路线(彼此相连的栅格集合)进行演示。 现给出 R 行 C 列的整数数组 Cov…...

某虚拟页式存储管理系统中有一个程序占8个页面,运行时访问页面的顺序是1,2,3,4,5,3,4,1,6,7,8,7,8,5。假设刚开始内存没有预装入任何页面。
某虚拟页式存储管理系统中有一个程序占8个页面,运行时访问页面的顺序是1,2,3,4,5,3,4,1,6,7,8,7,8,5。假设刚开始内存没有预装入任何页面。 (1) 如果采用LRU调度算法,该程序在得到4块内存空间时,会产生多少次缺页中断?请给出详细…...

介绍下SpringBoot如何处理大数据量业务
Spring Boot 处理大数据量业务时,通常会面临性能、内存、数据库负载等挑战。为了高效处理大数据量,Spring Boot 提供了多种解决方案和优化策略。以下是一些常见的处理方式: 1. 分页查询 问题:一次性查询大量数据会导致内存溢出和…...

推荐系统召回算法
推荐系统召回算法 召回算法UserCFItemCFSwing矩阵分解 召回算法 基于协同过滤的召回算法主要是应用在推荐环节的早期阶段,大致可以分为基于用户、基于物品的。两者各有优劣,优点是具有较好的可解释性,缺点是对于稀疏的交互矩阵,效…...
深度分析DeepSeek-R1开源的6种蒸馏模型之间的逻辑处理和编写代码能力区别以及配置要求,并与ChatGPT进行对比(附本地部署教程))
(2025)深度分析DeepSeek-R1开源的6种蒸馏模型之间的逻辑处理和编写代码能力区别以及配置要求,并与ChatGPT进行对比(附本地部署教程)
(2025)通过Ollama光速部署本地DeepSeek-R1模型(支持Windows10/11)_deepseek猫娘咒语-CSDN博客文章浏览阅读1k次,点赞19次,收藏9次。通过Ollama光速部署本地DeepSeek-R1(支持Windows10/11)_deepseek猫娘咒语https://blog.csdn.net/m0_70478643/article/de…...

性格测评小程序03搭建用户管理
目录 1 创建数据源2 搭建后台3 开通权限4 搭建启用禁用功能最终效果总结 性格测评小程序我们期望是用户先进行注册,注册之后使用测评功能。这样方便留存用户的联系信息,日后还可以推送对应的相关活动促进应用的活跃。实现这个功能我们要先创建数据源&…...

Qt接入deepseekv3 API 提供openssl 1.1.1g安装包
1.获取api (有免费10元额度) DeepSeek 记得复制api,避免丢失频繁创建。 2.qt调用https请求 配置网络模块 QT core gui widgets network 直接上代码 拿到代码替换api,和修正qt组件输入和输出即可。 #ifndef DEEPSEEKCLIENT…...

zookeeper分布式锁
1.第一种方式通过创建相同节点,谁能创建成功谁获取到锁,解锁删除节点,没获取到的线程进行自旋操作,直到获取到锁,这种方式跟redis一样,比较耗费cup 2.创建临时序列化节点,判断自己是否是节点下…...

系统漏洞扫描服务:安全风险识别与防护指南
系统安全的关键在于漏洞扫描服务,此服务能迅速发现潜在的安全风险。借助专业的扫描工具和技术,它确保系统稳定运作。以下将简要介绍这一服务的主要特点。 扫描原理 系统漏洞扫描服务依赖两种主要手段:一是通过漏洞数据库进行匹配࿰…...
