当前位置：首页 > news >正文

数据结构与算法：动态规划dp：背包问题：理论基础（状态压缩/滚动数组）和相关力扣题（416. 分割等和子集、1049.最后一块石头的重量Ⅱ、494.目标和）

news 来源：原创 2025/5/18 1:58:22

背包问题

01背包理论基础

对于01背包问题，物品下标为0到i，对应的重量为weight[0]到weight[i]，价值为value[0]到value[i]，每个物品只可以取或不取，背包最大容量为j的场景。

常见的状态转移方程如下：
dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i])

其中，dp[i][j]的含义是：对于下标0到i的物品，任意取放，满足背包剩余最大容量为j的情况下能获得的最大价值。

那么dp[i][j]可以划分为两种情况

取了下标为i的物品，其获得的最大价值为dp[i-1][j-weight[i]]+value[i]
没有取下标为i的物品，其获得的最大价值为dp[i-1][j]

对于该数组的初始化，需要初始化i或j分别为0的边界情况：

i=0 的情况：如果 j >= weight[0]，则我们可以取物品0，此时dp[0][j] = value[0]。否则，我们无法放入物品0，此时dp[0][j] = 0。
j=0的情况：都为0，因为背包容量为0时，无法装入任何物品。

而对于i和j都非零时的情况，我们可以初始化成一个随意的值，因为根据状态转移方程来看，它的数组与它本身没有关系，所以在dp数组赋值时都会被覆盖掉。

接着我们思考它的遍历顺序。
对于这种dp数组为二维数组的情况，两层for循环是可以颠倒位置的。因为无论是先遍历背包，还是先遍历物品，都能保障遍历dp[i][j]时，已经给dp[i-1][j]以及dp[i-1][j-weight[i]赋值了正确的数值了。

注意，对于所有01背包问题，都可以使用回溯算法来解决，对于每个物品取或不取，一共n个物品，那么算法的复杂度就是2的n次方。所以一般回溯会超时。

状态压缩（滚动数组）

而关于刚刚的场景，实际上我们还可以用一维数组来做，也就是常说的状态压缩，或者说滚动数组。

此时状态转移方程为dp[j]=max(dp[j],dp[j-weight[i]]+value[i])。
其中，dp[j]的含义是：任意取放物品，满足背包 剩余最大容量为j 的情况下能获得的最大价值。

和二维的情况一样，dp[j]可以划分为两种情况

取了下标为i的物品，其获得的最大价值为dp[j-weight[i]]+value[i]
没有取下标为i的物品，其获得的最大价值为dp[j]

首先我们思考一个问题，为什么可以状态压缩？
这是因为从二维数组的状态转移方程，我们可以知道，dp[i]的数据只依赖dp[i-1]层的数据，譬如在计算dp[3]的时候，我们就不再需要存储dp[1]的数据了。这种只依赖于有限的数据的情况，我们都可以状态压缩。在这我们压缩成两行数据，一行是dp[i-1]，一行是dp[i]。

接着我们思考这个dp数组的初始化。

j为0，代表对于下标0到i的物品，任意取放，背包最大容量为0时能获得的最大价值，毫无疑问，肯定都初始化为0。
j非零，此时因为状态转移方程中我们给dp[j]赋值时，会比较其自身。所以应该初始化为一个负值。

然后就是遍历顺序。
虽然数组只有1层了，但是因为状态转移方程里还是有i存在的，所以遍历赋值还是有两层for循环的，外层是遍历物品，内层是遍历背包容量。而且必须先遍历物品，再遍历背包容量，且背包容量需要倒序遍历。

为什么背包容量需要倒序遍历呢？
如果正序遍历，dp[j - weight[i]]可能在同一轮更新后再次被使用，导致相当于选择了同一个物品多次，这就变成了完全背包问题。倒序遍历可以确保每个物品只被使用一次。

416. 分割等和子集

在这道题虽然没有明说物品的价值，但实际上物品的价值就是等于它本身的重量。这样题目就转化为了，遍历下标从0到i的物品，任意拿取（物品只能拿取1次），满足重量为ans的情况？
为此我们想到了01背包，dp[j]表示遍历下标从0到i的物品，任意拿取，满足重量为j。当dp[j]==ans，也就是存在满足重量为ans的情况，那么返回True

代码1：最套板子的一集

class Solution:def canPartition(self, nums: List[int]) -> bool:n = len(nums)ans = 0for i in range(n):ans += nums[i]if ans%2:return Falseans=int(ans/2)dp = [0] * (ans+1) for i in range(n):for j in range(ans, nums[i]-1, -1):dp[j] = max(dp[j-nums[i]]+nums[i], dp[j])if dp[ans]==ans:return Trueelse:return False

最原始的一版，纯套板子。效率：2370ms，击败13.38%

代码2：优化外层for循环

根据上面的代码我们可以看到，其实我们不需要循环下标i，我们只需要拿到数本身就好了，所以直接用for num in nums

class Solution:def canPartition(self, nums: List[int]) -> bool:n = len(nums)ans = 0for i in range(n):ans += nums[i]if ans%2:return Falseans=int(ans/2)dp = [0] * (ans+1) for num in nums:for j in range(ans, num-1, -1):dp[j] = max(dp[j-num]+num, dp[j])if dp[ans]==ans:return Trueelse:return False

效率：2253ms，击败18.18%。

代码3：优化其他条件减少代码量

class Solution:def canPartition(self, nums: List[int]) -> bool:n = len(nums)ans = sum(nums) # 优化点1：用sum函数减少for循环if ans%2:return Falseans=ans//2 # 优化点2，用//替代int转化dp = [0] * (ans+1) for num in nums:for j in range(ans, num-1, -1):dp[j] = max(dp[j-num]+num, dp[j])if dp[ans]==ans:return Truereturn False

效率：2547ms，击败8.48%
可以看到其实效率没有说提升，但是代码量会少，看起来更简洁。

代码4：优化初始化条件（效率最高）

对于代码3，我们还可以再优化。因为我们其实并不关心dp[ans]的值具体是多少，也就是说我们并不在意最终能满足题意的方案数是多少，我们只关心能不能满足，那么初始化dp数组时就可以不用数值，而是用布尔值。注意这里，根据dp数组的含义，那么dp[0]的初始化就一定是True

class Solution:def canPartition(self, nums: List[int]) -> bool:n = len(nums)ans = sum(nums)if ans%2:return Falseans=ans//2dp = [False] * (ans+1) dp[0] = Truefor num in nums:for j in range(ans, num-1, -1):if dp[j - num]:dp[j] = Truereturn dp[ans]

效率：563ms，击败75.46%

1049.最后一块石头的重量Ⅱ

这道题转化一下思路，就可以变成和416. 分割等和子集一样的问题。
因为我们知道，如果两堆石头的重量越相近，那么相撞后可以留下的重量就越小。
也是求任取其中的石块，看背包能装下的这堆石块的最大重量是否能越靠近目标数（整体重量的一半）。

class Solution:def lastStoneWeightII(self, stones: List[int]) -> int:n = len(stones)all_sum = sum(stones)ans = all_sum//2dp = [0] * (ans+1)for stone in stones:for j in range(ans, stone-1, -1):dp[j] = max(dp[j], dp[j-stone]+stone)return abs((all_sum - dp[ans])-dp[ans])

效率：19ms，击败74.61%

494.目标和

这道题最难想的可能是不知道它和动态规划有什么关系。第一时间想的估计都是回溯去遍历每个元素取或不取。

但实际上，这道题可以将所有元素分为两类，一类是前面加+的，一类是前面加-的。那么就和1049.最后一块石头的重量Ⅱ非常类似。我们设正数集合的总和为pos，负数集合的总和为neg，那么存在以下逻辑：

pos+neg = sum
pos-neg = target

为此，推出pos = (target+sum)//2

也就是说，相当于我们要遍历所有物品，任意取放，找到满足背包容量为(target+sum)/2的情况数是多少。

所以，dp[j]的含义为，遍历前i个物品，任意取放，满足背包容量为j的情况数。

那么首先关于边界条件的判断，就有两种：

pos不是整数。因为数组都是整数，所以pos也一定是整数。
pos小于0，根据pos的定义，应该是正数集合的总和，那么不可能小于0。

代码如下：

n = len(nums)
all_sum = sum(nums)if (target+all_sum)%2: # pos不是整数return 0pos= (target+all_sum)//2if pos< 0:# pos小于0return 0

其次，关于状态转移方程，dp[j]=dp[0]+dp[1]+dp[2]+...dp[j-1]，也就是：
或者说dp[j]=dpj]+dp[j-nums[i]]或者说dp[j]+=dp[j-num]
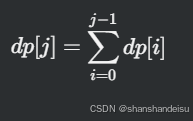
在这里插入图片描述
为什么是累加？
因为每个物品都可以选择取或不取，所以对于每个j，它的值是由所有可能的前一个状态转移而来的。具体来说，dp[j]的值是由dp[j-1]、dp[j-2]、…、dp[0]这些状态转移而来的，因为这些状态都可能在加入当前物品后达到j。

最后关于初始化，在这我们要求的dp是情况数，那么dp[0]应该是多少呢？
实际上，dp[0]应该是1。举个例子：

nums = [0]，target = 0
那么pos应该为1，因为给0前面加上一个＋是一种情况。

最后的代码如下：

class Solution:def findTargetSumWays(self, nums: List[int], target: int) -> int:n = len(nums)all_sum = sum(nums)if (target+all_sum)%2:return 0pos = (target+all_sum)//2if pos < 0:return 0dp = [0] * (pos+1)dp[0] = 1for num in nums:for j in range(pos, num-1, -1):dp[j] += dp[j-num]return dp[pos]

效率：18ms，击败87.50%

总结

对于416. 分割等和子集，题目实际上为：给定一个重量为target的背包，是否能装满这个背包，转移方程为

dp[0] = True 
for num in nums:for j in range(target, num-1, -1):if dp[j - num]:dp[j] = True

对于1049.最后一块石头的重量Ⅱ，题目实际上为：给定一个重量为target的背包，该背包能装的最大价值（价值就是重量）是多少？ 转移方程为：

dp = [0] * (target+1)
for stone in stones:for j in range(target, stone-1, -1):dp[j] = max(dp[j], dp[j-stone]+stone)

对于494.目标和，题目实际上为：给定一个重量为target的背包，求装满这个背包的方案数是多少？ 转移方程为：

dp = [0] * (target+1)
dp[0] = 1
for num in nums:for j in range(target, num-1, -1):dp[j] += dp[j-num]