当前位置：首页 > news >正文

【优先算法】专题——位运算

news 来源：原创 2025/5/11 0:59:13

在讲解位运算之前我们来总结一下常见的位运算

一、常见的位运算

1.基础为运算

<< &：有0就是0

>> |：有1就是1

~ ^：相同为0，相异位1 /无进位相加

2.给一个数 n，确定它的二进制表示中的第x 位是0还是1

n：0 1 1 0 1 0 1 0 0 1

(n >> x) & 1

3.将一个数n的二进制表示的第x位修改成1

x

0 1 1 0 1 0 1 0 1 1

0 0 0 0 0 1 0 0 0 0

0 1 1 0 1 1 1 0 1 1(使用|)

n |=(1 << x)

n = n | (1 << x)

4.将一个数n的二进制表示的第x位修改成0

x

0 1 1 0 1 0 1 1 0 0

1 1 1 1 0 1 1 1 1 1(取反得到:0 0 0 0 0 1 0 0 0 0)

0 1 1 0 0 0 1 1 0 0(使用&)

n &= (~(1<<x))

n = n &(~(1<<x))

5.位图思想

我们可以使用一个哈希表来存储我们的信息方便我们增删查改主要还是为了我们查找因为可以使用O(1)的时间复杂度来查找，但是现在我们可以使用一个int变量来进行，一个int类型4个字节32个bit位，我们可以用某一位bit位上的0或者1来表示我们的信息，0表示一个信息1表示一个信息，本质还是一个哈希表。

位图会大量用到我们2、3、4这几个操作，专门为位图服务

6.提取一个数(n)二进制中最右侧的1

n & -n 将最右侧的1，左边的区域全部变成相反

0 1 1 0 1 0 1 0 0 0(原码)

1 0 0 1 0 1 0 1 1 1(反码)

1 0 0 1 0 1 1 0 0 0(+1,补码)

0 1 1 0 1 0 1 0 0 0(原码)

0 0 0 0 0 0 1 0 0 0(原码和补码进行&)

7.干掉一个数(n)二进制表示中最右侧的1

n & (n-1)将最右侧的1，右边的区域(包含1)全部变成相反

n ： 0 1 1 0 1 0 1 0 0

n -1：0 1 1 0 1 0 0 1 1

& 0 1 1 0 1 0 1 0 0

___________________

0 1 1 0 1 0 0 0 0

8.位运算的优先级

能加括号就加括号

9.异或(^)运算的运算律

1.a ^ 0 = a

2.a ^ a = 0(消消乐)

3.a ^ b ^ c = a ^(b ^ c)

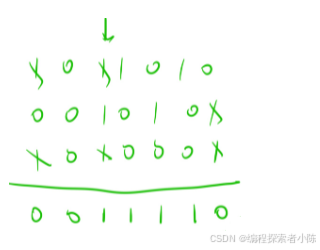
一个奇数，一堆偶数最终的结果为奇数，因为偶数抵消了为0

通过上面的总结我们可以尝试写一下如下五个题

191.位一个的个数

题目链接：位一个的个数

题目描述：

参考代码：

class Solution {
public:int hammingWeight(int n) {int count = 0;while(n != 0) {count++;n = n & (n-1);//把最低位1的右边互为相反数(包含1)}return count;}
};

338.比特位计数

题目链接：比特位计数

题目描述：

参考代码：

class Solution {
public:vector<int> countBits(int n) {vector<int>ans(n+1,0);for(int i = 1;i <= n;i++){ans[i] = ans[i>>1] + (i & 1);}return ans;}
};

461.汉明距离

题目链接：汉明距离

题目描述：

参考代码：

//对应的位置值不相同的个数。例如，假设有两个十进制数a=93和b=73，
// 如果将这两个数用二进制表示的话，有
// a=1011101
// b=1001001，
// 可以看出，二者的从右往左数的第3位、第5位不同（从1开始数）
// 因此，a和b的汉明距离是2。
class Solution {
public:int hammingDistance(int x, int y) {int s = x ^ y, ret = 0;while (s){ret += s & 1;s >>= 1;}return ret;}
};

136.只出现一次的数字

题目链接：只出现一次的数字

题目描述：

参考代码：

class Solution {
public:int singleNumber(vector<int>& nums) {int ret = 0;for(auto n :nums){ret ^= n;}return ret;}
};

260.只出现一次的数字|||

题目链接：只出现一次的数字|||

题目描述：

参考代码：

class Solution {
public:vector<int> singleNumber(vector<int>& nums) {unsigned int s = 0;for(auto n : nums){s ^= n;}int low = s & -s;//取出最右侧的1int a = 0,b = 0;for(auto n : nums){if((low & n) == low){a ^= n;}else{b ^= n;}}return vector<int>{a,b};}
};

二、判断字符是否唯一

题目链接：判断字符是否唯一

题目描述：

解法一：我们可以使用哈希表

class Solution1 {
public:bool isUnique(string astr) {unordered_set<int>hash;for (auto ch : astr){if (hash.count(ch)) return false;hash.emplace(ch);}return true;}
};

解法二：位图

我们用0表示没出现过，1表示出现过

可以利用鸽巢原理来进行优化，鸽巢原理已经在双指针那里讲过了这里就不过多赘述，一共有26个字母如果字符串的长度超过则肯定有重复字符，如果字符串的长度大于26那么直接返回false

参考代码：

class Solution {
public:bool isUnique(string astr) {//利用鸽巢原理来做的优化if (astr.size() > 26) return false;int bitMap = 0;for (auto ch : astr){int i = ch - 'a';//判断字符是否已经出现过if ((bitMap >> i) & 1 == 1) return false;//把当前字符加入位图中bitMap |= 1 << i;}return true;}
};

三、丢失的数字

题目链接：丢失的数字

题目描述：

解法一：哈希表

创建一个哈希表然后遍历数组，0出现标记一下，1出现标记一下，3出现标记一下....

解法二：高斯求和

(首项 + 尾项) * 项数 / 2这样就算出了0~5的和然后我们再减去数组里面所有数之和这样就得出来了

参考代码：

class Solution1 {
public:int missingNumber(vector<int>& nums) {int n = nums.size();int sum = n * (n + 1) / 2;int ret = 0;for (auto n : nums){ret += n;}return sum - ret;}
};

解法三：位运算(异或运算的运算律)

参考代码：

class Solution {
public:int missingNumber(vector<int>& nums){int ret = 0;for (int i = 0; i <= nums.size(); i++) ret ^= i;for (auto n : nums) ret ^= n;return ret;}
};

四、两整数之和

题目链接：两整数之和

题目描述：

在笔试中我们不讲武德直接return a + b;

解法：位运算(异或运算-无进位相加)

13+28=41

a： 0 0 1 1 0 1

b： 0 1 1 1 0 0

——————————

a^b： 0 1 0 0 0 1(a) 无进位

进位(a & b)<<1 0 1 1 0 0 0 我们进位是往前进位所以这里我们右移一位

我们继续重复如上操作，先无进位相加再进位

a：          0 1 0 0 0 1

b：          0 1 1 0 0 0

a^b：          0 0 1 0 0 1 无进位

(a & b) <<1 1 0 0 0 0 0 进位

a： 0 0 1 0 0 1

b ： 1 0 0 0 0 0

a^b： 1 0 1 0 0 1  无进位 41

(a & b) <<1 0 0 0 0 0 0 进位

进位变成0就结束了，最后的无进位相加就是我们的最终结果

参考代码：

class Solution {
public:int getSum(int a, int b) {while(b != 0){int x = a ^ b;//无进位相加unsigned carry = (unsigned)(a & b) <<1;//算出进位a = x;b = carry;}return a;}
};

五、只出现一次的数字||

题目链接：只出现一次的数字||

题目描述：

设要找的数位 ret ，由于整个数组中，需要找的元素只出现了⼀次，其余的数都出现三次，因此我们可以根据所有数的某⼀个⽐特位的总和 %3 的结果，快速定位到 ret 的⼀个⽐特位上的值是 0 还是 1 。这样，我们通过 ret 的每⼀个⽐特位上的值，就可以将 ret 给还原出来。

参考代码：

class Solution {
public:int singleNumber(vector<int>& nums) {int ret = 0;for(int i = 0;i < 32;i++){int sum = 0;for(int x : nums)if(((x>>i) & 1) == 1)sum++;sum %= 3;if(sum == 1) ret |= 1<<i;}return ret;}};

六、消失的两个数字

题目链接：消失的两个数字

题目描述：

这道题其实是丢失的数字+只出现一次的数字|||融合一起，本题的算法原理就是用到了这两道题的一个算法原理。

nums中消失了两个数字，1~N这堆数中假设a和b是消失的两个数字，nums这一堆数和1~N这一堆数异或，其他的数出现了2次a和b出现了一次，那么其实就是a ^ b

解法：位运算

1.将所有的数异或在一起，tmp

tmp = a ^ b

2.找到tmp中，比特位上为1的那一位

a^b的结果肯定不为0因为他们是不同的数，所以它们的比特位上肯定有一位是1，a和b的第x位上肯定是不同的

3.根据x位的不同，划分成两类异或

我们可以把x位是0的分为一类，x位上是1的分一类，然后对两组数据分别进行异或。

参考代码：

class Solution {
public:vector<int> missingTwo(vector<int>& nums) {//1.把所有数异或起来int tmp = 0;for(auto n : nums) tmp ^= n;for(int i = 1;i<=nums.size()+2;i++) tmp ^= i;int diff = 0;//找出a,b比特位不同的那一位while(1){if(((tmp >>diff) & 1) == 1) break;else diff++;}//3.根据diff位的不同，将所有数划分两类来异或int a = 0,b = 0;for(auto n : nums)if(((n >> diff) & 1) == 1) b ^= n;else a ^= n;for(int i = 1;i<=nums.size()+2;i++){if(((i >> diff) & 1) == 1) b ^= i;else a ^= i;}return {a,b};}
};

一、常见的位运算

1.基础为运算

2.给一个数 n，确定它的二进制表示中的第x 位是0还是1

3.将一个数n的二进制表示的第x位修改成1

4.将一个数n的二进制表示的第x位修改成0

5.位图思想

6.提取一个数(n)二进制中最右侧的1

7.干掉一个数(n)二进制表示中最右侧的1

8.位运算的优先级

9.异或(^)运算的运算律

通过上面的总结我们可以尝试写一下如下五个题

191.位一个的个数

参考代码：

338.比特位计数

参考代码：

461.汉明距离

参考代码：

136.只出现一次的数字

参考代码：

260.只出现一次的数字|||

参考代码：

二、判断字符是否唯一

参考代码：

三、丢失的数字

参考代码：

参考代码：

四、两整数之和

参考代码：

五、只出现一次的数字||

参考代码：

六、消失的两个数字

参考代码：

相关文章：