OpenGL学习笔记（六）：Transformations 变换（变换矩阵、坐标系统、GLM库应用）

---

现在我们已经知道了如何创建一个物体、着色、加入纹理。但它们都还是静态的物体，我们可以尝试着在每一帧改变物体的顶点并且重配置缓冲区从而使它们移动，但这太繁琐了，而且会消耗很多的处理时间。通常我们使用矩阵(Matrix)对象来变换一个物体。

相关图形学原理参考：GAMES101学习笔记（二）：Transformation 变换 （仿射变换、模型、视图、投影）
线性代数相关基础知识不在此介绍。本节重点关注如何使用矩阵对向量进行变换，以及GLM数学库的使用。

GLM是OpenGL Mathematics的缩写，它是一个只有头文件的库，也就是说我们只需包含对应的头文件就行了，不用链接和编译。在官网下载

向量变换

在Shader部分，我们了解了GLSL(OpenGL Shading Language)中会用到两种容器类型：向量(Vector) 和 矩阵(Matrix)。我们用向量来表示位置，表示颜色，甚至是纹理坐标。

深入了解一下向量，它其实就是一个N×1矩阵，N表示向量分量的个数（也叫N维(N-dimensional)向量）。如果我们有一个M×N矩阵，我们可以用这个矩阵乘以我们的N×1向量。

用变换矩阵和向量相乘，即完成了向量的坐标变换。单位矩阵与向量相乘向量不变，但单位矩阵通常是生成其他变换矩阵的起点。

在OpenGL中，我们通常使用4×4的变换矩阵，而其中最重要的原因就是大部分的向量都是4分量的(x, y, z, w)

齐次坐标(Homogeneous Coordinates)

• 向量的w分量也叫齐次坐标。想要从齐次向量得到3D向量，我们可以把x、y和z坐标分别除以w坐标。w分量通常是1.0。
• 如果一个向量的齐次坐标是0，这个坐标就是方向向量(Direction Vector)，因为w坐标是0，这个向量就不能位移。
• 使用齐次坐标有几点好处：它允许我们在3D向量上进行位移（如果没有w分量我们是不能位移向量的），可以用w值创建3D视觉效果。

• 缩放变换(Scaling)
  缩放是对向量的长度进行缩放，而保持它的方向不变。
  
• 位移变换(Translation)
  位移是在原始向量的基础上加上另一个向量从而获得一个在不同位置的新向量的过程，从而在位移向量基础上移动了原始向量。
  
• 旋转变换(Rotation)
  在3D空间中旋转需要定义一个角度和一个旋转轴。物体会沿着给定的旋转轴旋转特定角度。旋转矩阵在3D空间中每个单位轴都有不同定义，旋转角度用θθ表示：

可以将多个旋转矩阵复合，比如先沿着x轴旋转再沿着y轴旋转。但是这会导致一个问题——万向节死锁（Gimbal Lock）。避免万向节死锁的真正解决方案是使用四元数(Quaternion)，它不仅更安全，而且计算会更有效率。这些内容我们暂时不在这里讨论。

变换矩阵的组合
根据矩阵之间的乘法，我们可以把多个变换组合到一个矩阵中。

需要注意的是，矩阵乘法是不遵守交换律的，这意味着它们的顺序很重要。
在使用GLM创建变换矩阵时，通常的执行顺序是：缩放 -> 旋转 -> 位移。这是因为变换矩阵是按照从右到左的顺序相乘的，而每个变换都是相对于物体自身的坐标系进行的。下面解释为什么这个顺序很重要以及它是如何工作的：

• 缩放：首先应用缩放变换是因为你通常希望物体在它自己的局部坐标系中均匀或非均匀地伸缩。如果先进行了旋转或位移再缩放，那么缩放因子会同时影响物体的位置和方向，这通常不是预期的行为。
• 旋转：然后应用旋转变换，因为它是在缩放之后，物体已经处于正确的大小下进行的。旋转也是基于物体的局部坐标系，因此它可以改变物体的方向而不改变它的位置。
• 位移：最后应用位移（平移）。此时物体已经有了正确的大小和方向，所以现在可以将其移动到世界坐标系中的正确位置。

在代码中，我们的阅读顺序和实际变换顺序是相反的。

mat4 transform = mat4(1.0f);
transform = glm::translate(transform, translation); // 最后应用 (从右往左读)
transform = glm::rotate(transform, angle, axis); // 中间应用
transform = glm::scale(transform, scale); // 最先应用

使用GLM变换（缩放、旋转、位移）

我们已经了解了变换背后的所有理论，实践中将使用GLM库进行变换。这是一个抽象所有的数学细节，专门为OpenGL量身定做的数学库。我们需要的GLM的大多数功能都可以从下面这3个头文件中找到：

#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>

使用glm::translate进行位移变换

//应用示例：把一个向量(1, 0, 0)位移(1, 1, 0)个单位
glm::vec4 vec(1.0f, 0.0f, 0.0f, 1.0f);	//目标向量
glm::mat4 trans = glm::mat4(1.0f);	//单位矩阵
trans = glm::translate(trans, glm::vec3(1.0f, 1.0f, 0.0f));	//变换矩阵
vec = trans * vec;	//位移矩阵 * 目标向量
std::cout << vec.x << vec.y << vec.z << std::endl;

使用glm::rotate进行旋转变换。
使用glm::scale进行缩放变换。

//应用示例：创建变换矩阵实现先缩放0.5倍，然后逆时针旋转90度。
glm::mat4 trans = glm::mat4(1.0f);
trans = glm::rotate(trans, glm::radians(90.0f), glm::vec3(0.0, 0.0, 1.0)); 
trans = glm::scale(trans, glm::vec3(0.5, 0.5, 0.5));

我们的2维图形是在XY面上的，所以把它绕Z轴glm::vec3(0.0, 0.0, 1.0)旋转。应用旋转时，使用glm::radians将角度转化为弧度。我们trans矩阵传递给了GLM的每个函数，GLM会自动将矩阵相乘，返回的结果是一个包括了多个变换的变换矩阵。

将变换矩阵传递给着色器

修改顶点着色器 让其接收一个mat4的uniform变量。在把位置向量传给gl_Position之前，将其与变换矩阵相乘：

#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec2 aTexCoord;out vec2 TexCoord;uniform mat4 transform;void main()
{gl_Position = transform * vec4(aPos, 1.0f);TexCoord = vec2(aTexCoord.x, 1.0 - aTexCoord.y);
}

在渲染循环中把变换矩阵传递给着色器：

// get matrix's uniform location and set matrix
ourShader.use();
unsigned int transformLoc = glGetUniformLocation(ourShader.ID, "transform");
glUniformMatrix4fv(transformLoc, 1, GL_FALSE, glm::value_ptr(transform));

首先用glGetUniformLocation查询uniform变量的地址，
然后用glUniformMatrix4fv函数把矩阵数据发送给着色器。

• 第一个参数指定uniform的位置值。

• 第二个参数指定将要发送多少个矩阵，这里是1。

• 第三个参数指定是否对矩阵进行转置(Transpose)，也就是交换矩阵的行和列。

  OpenGL开发通常使用一种内部矩阵布局，叫做列主序(Column-major Ordering)布局。GLM的默认布局就是列主序，所以并不需要转置矩阵，我们填GL_FALSE。

• 第四个参数是真正的矩阵数据，但是GLM的矩阵储存与OpenGL所接受的形式不同，因此要先用GLM的自带的函数value_ptr来变换这些数据。

我们创建了一个变换矩阵，在顶点着色器中声明了一个uniform，并把矩阵发送给了着色器，着色器会变换我们的顶点坐标。此时重新编译生成就可以看到我们的图形向左侧旋转，并是原来的一半大小。

修改变换矩阵 尝试让图形 随着时间推移旋转，并移动到窗口右下角：

glm::mat4 transform = glm::mat4(1.0f); 
transform = glm::translate(transform, glm::vec3(0.5f, -0.5f, 0.0f));
transform = glm::rotate(transform, (float)glfwGetTime(), glm::vec3(0.0f, 0.0f, 1.0f));

要让箱子随着时间推移旋转，我们必须在渲染循环中更新变换矩阵，因为它在每一次渲染迭代中都要更新。我们通过glfwGetTime来获取不同时间的角度。

前面的例子中我们可以在任何地方声明变换矩阵，但是现在我们必须在每一次迭代中创建它，从而保证我们能够不断更新旋转角度。这也就意味着我们不得不在每次渲染循环的迭代中重新创建变换矩阵。

通常在渲染场景的时候，我们也会有多个需要在每次渲染迭代中都用新值重新创建的变换矩阵。

在这里我们先把箱子围绕Z轴glm::vec3(0.0f, 0.0f, 1.0f)旋转之后，我们把旋转过后的箱子位移到屏幕的右下角。

如果我们调换位移和旋转的顺序会发生什么？

int main()
{[...]while(!glfwWindowShouldClose(window)){[...]        // Create transformationsglm::mat4 transform;transform = glm::rotate(transform, (float)glfwGetTime(), glm::vec3(0.0f, 0.0f, 1.0f)); // Switched the ordertransform = glm::translate(transform, glm::vec3(0.5f, -0.5f, 0.0f)); // Switched the order               [...]}
}

结果是箱子先位移到了右下角，然后绕着屏幕中心旋转，而不是绕自身中心旋转。

/* Why does our container now spin around our screen?:
== ===================================================
Remember that matrix multiplication is applied in reverse. This time a translation is thus
applied first to the container positioning it in the bottom-right corner of the screen.
After the translation the rotation is applied to the translated container.A rotation transformation is also known as a change-of-basis transformation
for when we dig a bit deeper into linear algebra. Since we're changing the
basis of the container, the next resulting translations will translate the container
based on the new basis vectors. Once the vector is slightly rotated, the vertical
translations would also be slightly translated for example.If we would first apply rotations then they'd resolve around the rotation origin (0,0,0), but 
since the container is first translated, its rotation origin is no longer (0,0,0) making it
looks as if its circling around the origin of the scene.If you had trouble visualizing this or figuring it out, don't worry. If you
experiment with transformations you'll soon get the grasp of it; all it takes
is practice and experience.
*/

需要牢记的是，实际的变换顺序应该与阅读顺序相反：尽管在代码中我们先位移再旋转，实际的变换却是先应用旋转再是位移的。明白所有这些变换的组合，并且知道它们是如何应用到物体上是一件非常困难的事情。只有不断地尝试和实验这些变换你才能快速地掌握它们。

现在我们可以明白为什么矩阵在图形领域是一个如此重要的工具了。我们可以定义无限数量的变换，而把它们组合为仅仅一个矩阵，如果愿意的话我们还可以重复使用它。在着色器中使用矩阵可以省去重新定义顶点数据的功夫，它也能够节省处理时间，因为我们没有一直重新发送我们的数据（这是个非常慢的过程）。

坐标系统与MVP矩阵

现在，我们已经了解了如何有效地利用矩阵的变换来对所有顶点进行变换。接下来回到渲染流程中：

回顾渲染管线流程，OpenGL希望在每次顶点着色器运行后，我们可见的所有顶点都为标准化设备坐标(Normalized Device Coordinate, NDC)。我们通常会自己设定一个坐标的范围，之后再在顶点着色器中将这些坐标变换为标准化设备坐标。然后将这些标准化设备坐标传入光栅器(Rasterizer)，将它们变换为屏幕上的二维坐标或像素。

这个转化过程通常是分部进行的。顶点坐标->标准化设备坐标->屏幕坐标过程中会被转换到多个过渡坐标系统。在这些特定的坐标系统中，一些操作或运算更加方便和容易：

• 局部空间(Local Space，或者称为物体空间(Object Space))
• 世界空间(World Space)
• 观察空间(View Space，或者称为视觉空间(Eye Space))
• 裁剪空间(Clip Space)
• 屏幕空间(Screen Space)

为了将坐标从一个坐标系变换到另一个坐标系，我们需要用到几个变换矩阵，最重要的几个分别是模型(Model)、观察(View)、投影(Projection) 三个矩阵，即MVP矩阵。变换过程如图所示：

1. 局部坐标是对象相对于局部原点的坐标，也是物体起始的坐标。
2. 世界坐标是处于一个更大的空间范围的。这些坐标相对于世界的全局原点，它们会和其它物体一起相对于世界的原点进行摆放。
3. 观察坐标，通过view矩阵变换使得每个坐标都是从摄像机或者说观察者的角度进行观察的。
4. 裁剪坐标，通过projection矩阵变换将坐标处理至-1.0到1.0的范围内，并判断哪些顶点将会出现在屏幕上。
5. 最后，我们使用视口变换(Viewport Transform)将裁剪坐标变换为屏幕坐标。视口变换将位于-1.0到1.0范围的坐标变换到由glViewport函数所定义的坐标范围内。最后变换出来的坐标将会送到光栅器，将其转化为片段。

---

局部空间

局部空间是指物体所在的坐标空间，一般也是建模软件中创建模型时的坐标空间。
局部空间坐标是对象相对于局部原点的坐标，也是物体起始的坐标。

---

世界空间

当我们将多个物体导入到程序当中，它们有可能会全挤在世界的原点(0, 0, 0)上，模型会重叠在一起，这并不是我们想要的结果。我们想为每一个物体定义一个位置，从而能在更大的世界当中分别放置它们。世界空间坐标相对于世界的全局原点。物体的坐标将会由模型矩阵(Model Matrix) 从局部变换到世界空间。

模型矩阵是一种变换矩阵，它能通过对物体进行位移、缩放、旋转来将它置于它本应该在的位置或朝向。

你可以将它想像为变换一个房子，你需要先将它 缩小（它在局部空间中太大了），并将其 位移 至郊区的一个小镇，然后在y轴上往左 旋转 一点以搭配附近的房子。

---

观察空间

观察空间经常被称为OpenGL的摄像机(Camera)（有时也称为摄像机空间(Camera Space)或视觉空间(Eye Space)）。观察空间是将世界空间坐标转化为用户视野前方的坐标而产生的结果。

因此观察空间就是从摄像机的视角所观察到的空间。而这通常是由一系列的位移和旋转的组合来完成，平移/旋转场景从而使得特定的对象被变换到摄像机的前方。这些组合在一起的变换通常存储在一个 观察矩阵(View Matrix) 里，它被用来将世界坐标变换到观察空间。

Camera详解：

---

裁剪空间

在经过Model矩阵变换和View矩阵变换之后，我们还需要定义一个 投影矩阵(Projection Matrix) 将定点坐标从观察空间变换到裁剪空间。OpenGL期望所有的坐标都能落在一个特定的范围内，且任何在这个范围之外的点都应该被裁剪掉(Clipped)。

投影矩阵(Projection Matrix)指定了一个范围的坐标，比如在每个维度上的-1000到1000。投影矩阵接着会将在这个指定的范围内的坐标变换为标准化设备坐标的范围(-1.0, 1.0)。所有在范围外的坐标不会被映射到在-1.0到1.0的范围之间，所以会被裁剪掉。在上面这个投影矩阵所指定的范围内，坐标(1250, 500, 750)将是不可见的，这是由于它的x坐标超出了范围，它被转化为一个大于1.0的标准化设备坐标，所以被裁剪掉了。

如果只是图元(Primitive)，例如三角形，的一部分超出了裁剪体积(Clipping Volume)，则OpenGL会重新构建这个三角形为一个或多个三角形让其能够适合这个裁剪范围。

将特定范围内的坐标转化到标准化设备坐标系的过程 被称之为投影(Projection)，使用投影矩阵能将3D坐标投影(Project)到很容易映射到2D的标准化设备坐标系中。由投影矩阵创建的观察箱(Viewing Box)被称为平截头体(Frustum)，每个出现在平截头体范围内的坐标都会最终出现在用户的屏幕上。

一旦所有顶点被变换到裁剪空间，最终的操作——透视除法(Perspective Division) 将会执行，在这个过程中我们将位置向量的x，y，z分量分别除以向量的齐次w分量；透视除法是将4D裁剪空间坐标变换为3D标准化设备坐标的过程。这一步会在每一个顶点着色器运行的最后被自动执行。

在这一阶段之后，最终的坐标将会被映射到屏幕空间中（使用glViewport中的设定），并被变换成片段。

将观察坐标变换为裁剪坐标的投影矩阵可以为两种不同的形式，每种形式都定义了不同的平截头体。我们可以选择创建一个正射投影矩阵(Orthographic Projection Matrix)或一个透视投影矩阵(Perspective Projection Matrix)。

透视原理可以参考：GAMES101学习笔记（二）：Transformation 变换 （仿射变换、模型、视图、投影）

正射/正交投影

正射投影矩阵定义了一个类似立方体的平截头箱，它定义了一个裁剪空间，在这空间之外的顶点都会被裁剪掉。它由宽、高、近(Near)平面和远(Far)平面所指定。

使用GLM的内置函数glm::ortho创建一个正射投影矩阵：

glm::ortho(0.0f, 800.0f, 0.0f, 600.0f, 0.1f, 100.0f);

• 前两个参数指定了平截头体的左边缘和右边缘。
• 第三和第四参数指定了平截头体的底部和顶部。通过这四个参数我们定义了近平面和远平面的大小
• 第五和第六个参数定义了近平面和远平面的距离。这个投影矩阵会将处于这些x，y，z值范围内的坐标变换为标准化设备坐标。

正射投影矩阵直接将坐标映射到2D平面中，即你的屏幕，但实际上一个直接的投影矩阵会产生不真实的结果，因为这个投影没有将透视(Perspective)考虑进去。所以我们需要一个透视投影矩阵来解决这个问题。

透视投影

透视(Perspective)：在实际生活中，我们会发现离你越远的东西看起来更小，这就是透视效果。

如上图，由于透视，这两条线在很远的地方看起来会相交。这正是透视投影想要模仿的效果，它是使用透视投影矩阵来完成的。

这个投影矩阵将给定的平截头体范围映射到裁剪空间，除此之外还修改了每个顶点坐标的w值，从而使得离观察者越远的顶点坐标w分量越大。 之后作为顶点着色器的输出，透视除法会被应用到裁剪空间坐标上，即顶点坐标的每个分量都会除以它的w分量，距离观察者越远顶点坐标就会越小。这是我们在向量变换时提到的w的另一个重要作用。

最后的结果坐标就是处于标准化设备空间中的。可以在这篇文章中了解正射投影和透视投影的详细计算。

相比于正射投影，投射投影创建了一个定义了可视空间的大平截头体，一个透视平截头体可以被看作一个不均匀形状的箱子，在这个箱子内部的每个坐标都会被映射到裁剪空间上的一个点。

使用GLM库中glm::perspective方法创建一个透视投影矩阵：

glm::mat4 proj = glm::perspective(glm::radians(45.0f), (float)width/(float)height, 0.1f, 100.0f);

• 第一个参数定义了FOV的值，即视野(Field of View)，它设置了观察空间的大小。想要一个真实的观察效果，它的值通常设置为45.0f
• 第二个参数设置了宽高比，由视口的宽除以高所得。
• 第三和第四个参数设置了平截头体的近和远平面。我们通常设置近距离为0.1f，而远距离设为100.0f。所有在近平面和远平面内且处于平截头体内的顶点都会被渲染。

当使用正射投影时，每一个顶点坐标都会直接映射到裁剪空间中而不经过任何精细的透视除法（它仍然会进行透视除法，只是w分量没有被改变（它保持为1），因此没有起作用）。因为正射投影没有使用透视，远处的物体不会显得更小，所以产生奇怪的视觉效果。由于这个原因，正射投影主要用于二维渲染以及一些建筑或工程的程序，在这些场景中我们更希望顶点不会被透视所干扰。

---

屏幕坐标

我们通过Model矩阵、View矩阵、Projection矩阵将局部坐标变换到了裁剪坐标：
$$V_{clip}=M_{projection}\cdot M_{view}\cdot M_{model}\cdot V_{local}$$ 矩阵运算顺序是相反的（我们需要从右往左阅读矩阵的乘法）。最后顶点坐标被赋值到顶点着色器中的gl_Positon中，OpenGL然后对裁剪坐标执行透视除法从而将它们变换到标准化设备坐标。

视口变换：OpenGL会使用glViewPort内部的参数来将标准化设备坐标映射到屏幕坐标，每个坐标都关联了一个屏幕上的点。

光栅化原理可以参考：GAMES101学习笔记（三）：Rasterization 光栅化（三角形的离散化、抗锯齿、深度测试）

三维变换

上文中我们了解了如何将3D坐标转换为2D坐标。接下来我们就可以真正引入3D模型，进行3D绘图（前面我们一直使用的是2D的三角形或矩形）

首先创建一个模型矩阵。这个模型矩阵包含了位移、缩放与旋转操作，它们会被应用到所有物体的顶点上，以变换它们到全局的世界空间。让我们变换一下我们的平面，将其绕着x轴旋转，使它看起来像放在地上一样。这个模型矩阵看起来是这样的：

glm::mat4 model;
model = glm::rotate(model, glm::radians(-55.0f), glm::vec3(1.0f, 0.0f, 0.0f));

通过将顶点坐标乘以这个模型矩阵，我们将该顶点坐标变换到世界坐标。我们的平面看起来就是在地板上，代表全局世界里的平面。

接下来创建一个观察矩阵。我们想要在场景里面稍微往后移动，以使得物体变成可见的（当在世界空间时，我们位于原点(0,0,0)）。
想象在场景中移动：将摄像机向后移动，和将整个场景向前移动是一样的。

这正是观察矩阵所做的，我们以相反于摄像机移动的方向移动整个场景。因为我们想要往后移动，并且OpenGL是一个右手坐标系(Right-handed System)，所以我们需要沿着z轴的正方向移动。我们会通过将场景沿着z轴负方向平移来实现。它会给我们一种我们在往后移动的感觉。

就目前来说，观察矩阵是这样的：（在摄像机Camera章节中我们将会详细讨论如何在场景中移动）

glm::mat4 view;
view = glm::translate(view, glm::vec3(0.0f, 0.0f, -3.0f));	// 注意，我们将矩阵向我们要进行移动场景的反方向移动。

最后定义一个投影矩阵。我们希望在场景中使用透视投影，所以像这样声明一个投影矩阵：

glm::mat4 projection;
projection = glm::perspective(glm::radians(45.0f), screenWidth / screenHeight, 0.1f, 100.0f);

将创建的MVP变换矩阵传入着色器。
首先，让我们在顶点着色器中声明一个uniform变换矩阵然后将它乘以顶点坐标：

#version 330 core
layout (location = 0) in vec3 aPos;
...
uniform mat4 model;
uniform mat4 view;
uniform mat4 projection;void main()
{// 注意乘法要从右向左读（左乘）gl_Position = projection * view * model * vec4(aPos, 1.0);...
}

在渲染循环中将矩阵传入着色器（这通常在每次的渲染迭代中进行，因为变换矩阵会经常变动）：

int modelLoc = glGetUniformLocation(ourShader.ID, "model");
glUniformMatrix4fv(modelLoc, 1, GL_FALSE, glm::value_ptr(model));
... // 观察矩阵和投影矩阵与之类似

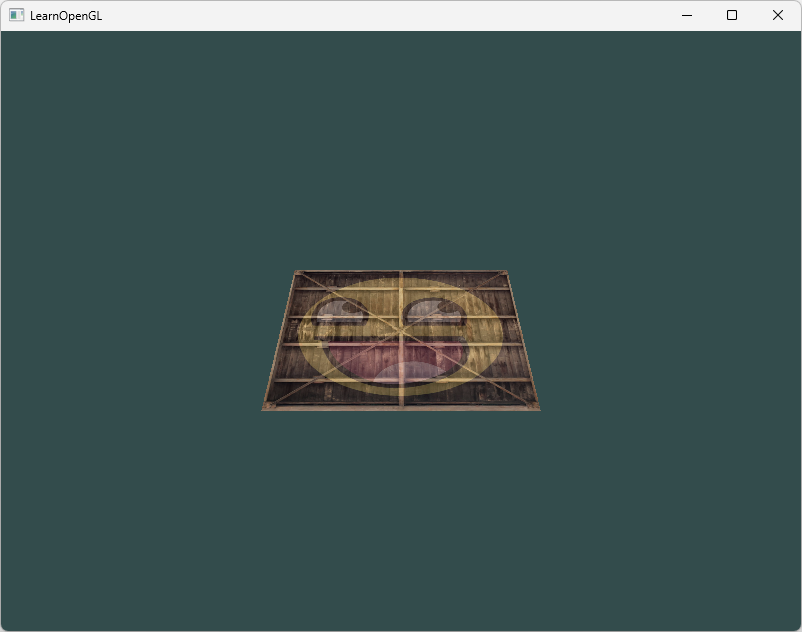
我们的顶点坐标已经使用模型、观察和投影矩阵进行变换了，最终的物体应该会：稍微向后倾斜至地板方向、离我们有一些距离、有透视效果（顶点越远，变得越小）。它看起来就像是一个3D的平面，静止在一个虚构的地板上： 源码参考

绘制3D立方体 & 深度测试（Z-buffer）

接下来拓展我们的2D平面为一个3D立方体。要想渲染一个立方体，我们一共需要36个顶点：

float vertices[] = {-0.5f, -0.5f, -0.5f,  0.0f, 0.0f,0.5f, -0.5f, -0.5f,  1.0f, 0.0f,0.5f,  0.5f, -0.5f,  1.0f, 1.0f,0.5f,  0.5f, -0.5f,  1.0f, 1.0f,-0.5f,  0.5f, -0.5f,  0.0f, 1.0f,-0.5f, -0.5f, -0.5f,  0.0f, 0.0f,-0.5f, -0.5f,  0.5f,  0.0f, 0.0f,0.5f, -0.5f,  0.5f,  1.0f, 0.0f,0.5f,  0.5f,  0.5f,  1.0f, 1.0f,0.5f,  0.5f,  0.5f,  1.0f, 1.0f,-0.5f,  0.5f,  0.5f,  0.0f, 1.0f,-0.5f, -0.5f,  0.5f,  0.0f, 0.0f,-0.5f,  0.5f,  0.5f,  1.0f, 0.0f,-0.5f,  0.5f, -0.5f,  1.0f, 1.0f,-0.5f, -0.5f, -0.5f,  0.0f, 1.0f,-0.5f, -0.5f, -0.5f,  0.0f, 1.0f,-0.5f, -0.5f,  0.5f,  0.0f, 0.0f,-0.5f,  0.5f,  0.5f,  1.0f, 0.0f,0.5f,  0.5f,  0.5f,  1.0f, 0.0f,0.5f,  0.5f, -0.5f,  1.0f, 1.0f,0.5f, -0.5f, -0.5f,  0.0f, 1.0f,0.5f, -0.5f, -0.5f,  0.0f, 1.0f,0.5f, -0.5f,  0.5f,  0.0f, 0.0f,0.5f,  0.5f,  0.5f,  1.0f, 0.0f,-0.5f, -0.5f, -0.5f,  0.0f, 1.0f,0.5f, -0.5f, -0.5f,  1.0f, 1.0f,0.5f, -0.5f,  0.5f,  1.0f, 0.0f,0.5f, -0.5f,  0.5f,  1.0f, 0.0f,-0.5f, -0.5f,  0.5f,  0.0f, 0.0f,-0.5f, -0.5f, -0.5f,  0.0f, 1.0f,-0.5f,  0.5f, -0.5f,  0.0f, 1.0f,0.5f,  0.5f, -0.5f,  1.0f, 1.0f,0.5f,  0.5f,  0.5f,  1.0f, 0.0f,0.5f,  0.5f,  0.5f,  1.0f, 0.0f,-0.5f,  0.5f,  0.5f,  0.0f, 0.0f,-0.5f,  0.5f, -0.5f,  0.0f, 1.0f
};

为了直观一点，我们将让立方体随着时间旋转：

model = glm::rotate(model, (float)glfwGetTime() * glm::radians(50.0f), glm::vec3(0.5f, 1.0f, 0.0f));

然后我们使用glDrawArrays来绘制立方体，但这一次总共有36个顶点。

glDrawArrays(GL_TRIANGLES, 0, 36);

使用glDrawArrays而不是glDrawElements，所以这个例子中没有使用EBO

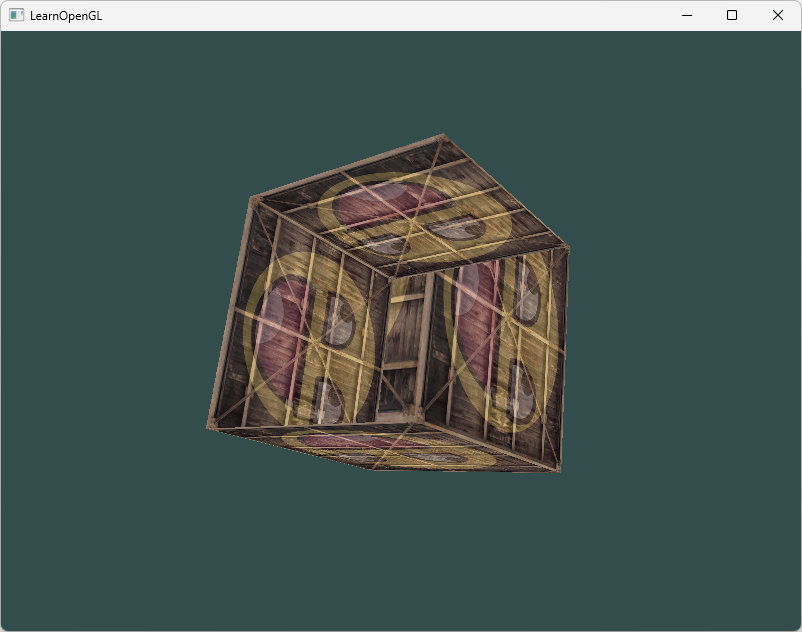
成功绘制了一个立方体，但他的面看起来相互遮挡的不正确。立方体的某些本应被遮挡住的面被绘制在了这个立方体其他面之上。之所以这样是因为OpenGL是逐个三角形绘制立方体的，所以即便之前那里有东西它也会覆盖之前的像素。因为这个原因，有些三角形会被绘制在其它三角形上面，虽然它们本不应该是被覆盖的。

这里我们就要引入Z-buffer。
OpenGL存储它的所有深度信息于一个Z缓冲(Z-buffer)中，也被称为深度缓冲(Depth Buffer)。它允许OpenGL决定何时覆盖一个像素而何时不覆盖。GLFW会自动为你生成这样一个缓冲（就像它也有一个颜色缓冲来存储输出图像的颜色）。深度值存储在每个片段里面（作为片段的z值），当片段想要输出它的颜色时，OpenGL会将它的深度值和z缓冲进行比较，如果当前的片段在其它片段之后，它将会被丢弃，否则将会覆盖。这个过程称为深度测试(Depth Testing)，它是由OpenGL自动完成的。

我们只需要告诉OpenGL启用深度测试（它默认是关闭的）

glEnable(GL_DEPTH_TEST);
//glDisable(GL_DEPTH_TEST);

因为我们使用了深度测试，我们也想要在每次渲染迭代之前清除深度缓冲（否则前一帧的深度信息仍然保存在缓冲中）。就像清除颜色缓冲一样，我们可以通过在glClear函数中指定DEPTH_BUFFER_BIT位来清除深度缓冲：

glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

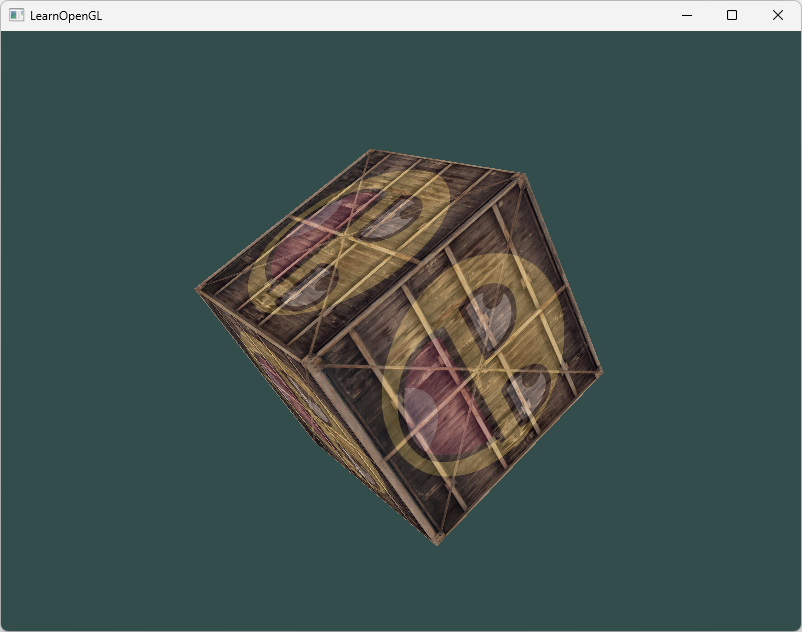
现在看起来正常了： 源码参考

练习1——更多立方体

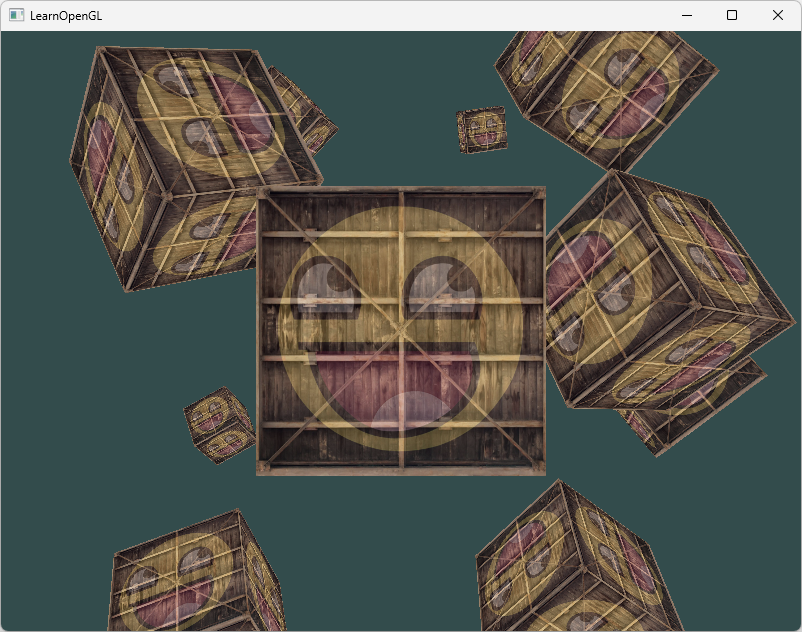
现在我们想在屏幕上显示10个立方体。每个立方体看起来都是一样的，区别在于它们在世界的位置及旋转角度不同。参考源码

立方体的图形布局已经定义好了，所以当渲染更多物体的时候我们不需要改变我们的缓冲数组和属性数组，我们唯一需要做的只是改变每个对象的模型矩阵来将立方体变换到世界坐标系中。

首先，让我们为每个立方体定义一个位移向量来指定它在世界空间的位置。我们将在一个glm::vec3数组中定义10个立方体位置：

glm::vec3 cubePositions[] = {glm::vec3( 0.0f,  0.0f,  0.0f), glm::vec3( 2.0f,  5.0f, -15.0f), glm::vec3(-1.5f, -2.2f, -2.5f),  glm::vec3(-3.8f, -2.0f, -12.3f),  glm::vec3( 2.4f, -0.4f, -3.5f),  glm::vec3(-1.7f,  3.0f, -7.5f),  glm::vec3( 1.3f, -2.0f, -2.5f),  glm::vec3( 1.5f,  2.0f, -2.5f), glm::vec3( 1.5f,  0.2f, -1.5f), glm::vec3(-1.3f,  1.0f, -1.5f)  
};

在渲染循环中，我们调用glDrawArrays 10次，但这次在我们渲染之前每次传入一个不同的模型矩阵到顶点着色器中。我们将会在渲染循环中创建一个小的循环用不同的模型矩阵渲染我们的物体10次。注意我们也对每个箱子加了一点旋转：

glBindVertexArray(VAO);
for(unsigned int i = 0; i < 10; i++)
{glm::mat4 model;model = glm::translate(model, cubePositions[i]);float angle = 20.0f * i; model = glm::rotate(model, glm::radians(angle), glm::vec3(1.0f, 0.3f, 0.5f));ourShader.setMat4("model", model);glDrawArrays(GL_TRIANGLES, 0, 36);
}