论文速读|Matrix-SSL：Matrix Information Theory for Self-Supervised Learning.ICML24

论文地址：Matrix Information Theory for Self-Supervised Learning
代码地址：https://github.com/yifanzhang-pro/matrix-ssl
bib引用：

@article{zhang2023matrix,title={Matrix Information Theory for Self-Supervised Learning},author={Zhang, Yifan and Tan, Zhiquan and Yang, Jingqin and Weiran, Huang and Yuan, Yang},journal={arXiv preprint arXiv:2305.17326},year={2023}
}

InShort

提出Matrix - SSL方法，结合矩阵信息理论统一视角，改进自监督学习，在图像和语言任务中表现优异，探讨了有效秩与维度坍缩等相关理论。

1. 研究背景
   • 对比学习与非对比学习：对比学习通过对齐相似对象、分离不相似对象学习表示；非对比学习如SimSiam、Barlow Twins等不使用负样本，最大熵编码框架为部分非对比学习方法提供统一视角。
   • 理论研究现状：对比学习的理论探索聚焦于对比损失的分解和理解；非对比学习的理论研究揭示了其与其他方法的联系。
2. 方法
   • 矩阵信息理论基础：定义矩阵熵、矩阵KL散度和矩阵交叉熵等概念，用于衡量矩阵间差异，为后续损失函数设计提供理论依据。
   • Matrix - SSL算法：提出Matrix - SSL，结合矩阵均匀性损失和矩阵对齐损失。前者使特征矩阵的交叉协方差矩阵与单位矩阵对齐，后者直接对齐自协方差矩阵，提升表示学习效果。
   • 与其他损失的关系：证明最大熵编码（MEC）损失与矩阵均匀性损失的等价性（在常数项和因子范围内），建立有效秩与矩阵KL散度的闭式关系。
3. 实验
   • 实验设置：在ImageNet数据集上进行自监督学习实验，采用ResNet50作为骨干网络，设置特定的数据增强、优化器和超参数。
   • 评估结果：在线性评估、迁移学习和半监督学习任务中，Matrix - SSL均优于SimCLR、BYOL等基线方法。在ImageNet线性评估中，100轮预训练的Matrix - SSL比SimCLR的Top - 1准确率高4.6%；在MS - COCO迁移学习任务中，400轮预训练的Matrix - SSL比MoCo v2和BYOL性能提升3%以上。
   • 消融实验：研究对齐损失比例和矩阵对数实现的泰勒展开阶数对性能影响，确定(\gamma = 1)和泰勒展开阶数为4时效果最佳。
4. 语言模型应用：提出用矩阵交叉熵损失微调大语言模型，在数学推理数据集GSM8K上，相比标准交叉熵损失，使用Matrix - LLM损失微调的Llemma - 7B模型准确率提升3.1%。
5. 结论：提供矩阵信息理论视角理解和改进自监督学习，为未来算法设计提供思路，有望推动机器学习领域发展。

---

摘要

最大熵编码框架为 SimSiam、Barlow Twins 和 MEC 等许多非对比学习方法提供了统一的视角。受该框架的启发，我们引入了 Matrix-SSL，这是一种利用矩阵信息理论将最大熵编码损失解释为矩阵均匀性损失的新方法。此外，Matrix-SSL 通过无缝整合矩阵对齐损失，直接对齐不同分支中的协方差矩阵，增强了最大熵编码方法。实验结果表明，在线性评估设置下，MatrixSSL 在 ImageNet 数据集上优于最先进的方法，在迁移学习任务中，MatrixSSL 在 MS-COCO 上的性能优于最先进的方法。具体来说，在 MS-COCO 上执行迁移学习任务时，我们的方法仅用 400 个 epoch 就比以前的 SOTA 方法（如 MoCo v2 和 BYOL）高出 3.3%，而预训练则需要 800 个 epoch。我们还尝试通过使用矩阵交叉熵损失微调 7B 模型，将表示学习引入语言建模机制，在 GSM8K 数据集上比标准交叉熵损失高出 3.1%。

Introduction

对比学习方法（Chen 等人，2020a；He 等人，2020）专注于使相似的对象紧密对齐，同时拉开不相似对象的距离。这种基于直观原则的方法带来了深刻而有趣的见解。例如，SimCLR 已被证明在相似性图上执行谱聚类（spectral clustering）（Tan 等人，2023b；HaoChen 等人，2021），并且 Wang 和 Isola（2020）强调了对比损失的两个关键方面：对齐和均匀性。

对齐损失可确保相似对象紧密映射，而均匀性损失则促进了均匀分布的输出特征空间，从而保留了最大信息。值得注意的是，许多现有的对比方法（Wu et al.， 2018;He et al.， 2020;Logeswaran & Lee， 2018;Tian et al.， 2020a;Hjelm等人，2018 年;Bachman et al.， 2019;Chen et al.， 2020a） 可以被视为这两种损失类型的具体实现，这一观点简化了对它们核心机制的理解。

同时，人们对不使用负样本的非对比学习方法越来越感兴趣，例如 BYOL（Grill 等人，2020 年）、SimSiam（Chen 和 He，2021 年）、Barlow Twins（Zbontar 等人，2021 年）、VICReg（Bardes 等人，2021 年）等。其中，Liu 等人（2022 年）提出了一个有趣的理论框架，称为最大熵编码，提议在从相同输入的不同增强中计算出的两个特征矩阵$z_1$、$z_2$之间最大化以下损失：
${\mathcal{L}}_{MEC}=-\mu logdet\left(I_d+\lambda Z_1{Z}_2^{\top }\right).$

虽然乍一看可能并不明显，但上述损失函数鼓励对特征嵌入进行最大熵编码，这与对比学习方法中的均匀性损失类似。事实证明，这种公式自然涵盖了其他几种非对比方法（如 SimSiam、Barlow Twins）的损失函数，并且由此产生的算法 MEC 在性能上超过了以前的方法（Liu 等人，2022 年）（在 BYOL 中使用的逐元素对齐损失，如(|z_1 - z_2|_2)，可以看作是这种 MEC 损失中的低阶泰勒展开项）。然而，对比方法和非对比方法的比较揭示了一些差异：

Learning Method	Loss Function
Contrastive Learning Non-contrastive Learning	Uniformity + Alignment Uniformity

这一观察自然促使我们提出一个更广泛、更具探索性的问题。在本文中，我们肯定地回答了这个问题，提出了一种方法，这种方法不仅整合了对比学习和非对比学习范式的优势，而且还增强了这些优势。

The existing maximum entropy encoding framework, however, does not explicitly differentiate between feature matrices from different branches, hindering its integration with alignment loss.
然而，现有的最大熵编码框架并没有明确区分来自不同分支的特征矩阵，这阻碍了它与对齐损失的集成。
为了弥补这一差距，我们引入了矩阵信息理论。 By extending classical concepts like entropy, Kullback–Leibler (KL) divergence, and cross-entropy to matrix analogs，我们提供了对相关损失函数的更丰富表示。值得注意的是，我们发现像 SimSiam、BYOL、Barlow Twins 和 MEC 这样的方法可以被重新解释为利用基于矩阵交叉熵（MCE）的损失函数，这是以前未被探索的联系（见定理 4.1）。

我们提出的算法 Matrix-SSL 将矩阵对齐损失纳入非对比方法中，从而提高了经验性能。这种双重关注为表示学习提供了额外的信息和更丰富的信号。
Matrix-SSL 包括 Matrix-Uniformity（矩阵均匀性）和 Matrix-Alignment（矩阵对齐）损失组件。
Matrix-Uniformity 将特征矩阵$z_1$和$z_2$的互协方差矩阵与单位矩阵$I_d$对齐，而 Matrix-Alignment 则专注于对齐它们的自协方差矩阵（见图 1）。作为副产品，我们观察到有效秩和矩阵 KL 之间的封闭形式关系，这表明有效秩可以成为衡量各种机器学习方法性能的有力指标（见第 3.4 节）。

在实验评估中，Matrix-SSL 在 ImageNet 数据集上的表现优于最先进的方法（如 SimCLR、BYOL、SimSiam、Barlow Twins、VICReg 等）。特别是在线性评估设置下，“我们的方法”仅用 100 个 epoch 的预训练就能比 SimCLR 的 100 个 epoch 预训练效果高出 4.6%。对于像 COCO 检测和 COCO 实例分割这样的迁移学习任务，“我们的方法”在仅用 400 个 epoch 的情况下比之前的最先进方法如 MoCo v2 和 BYOL 表现更好，效果高出最多达 3%，而这些对比方法需要 800 个 epoch 的预训练。

我们进一步将表示学习引入语言建模领域，并使用矩阵交叉熵损失来微调大型语言模型，在 GSM8K 数据集上的数学推理任务中取得了最先进的结果，比标准交叉熵损失的效果高出 3.1%。

贡献总结：
• 我们证明了非对比学习中 MEC 损失和矩阵均匀性损失（直至常数项和因子）的等效性，以及有效秩和矩阵 KL 之间的封闭式关系。
• 我们为对比和非对比学习方法提供了均匀性损失加对齐损失的统一视角。
• 我们在各种任务下实证验证了我们的方法，包括图像分类任务的线性评估、对象检测和实例分割任务的迁移学习，以及数学推理任务的大型语言模型微调。

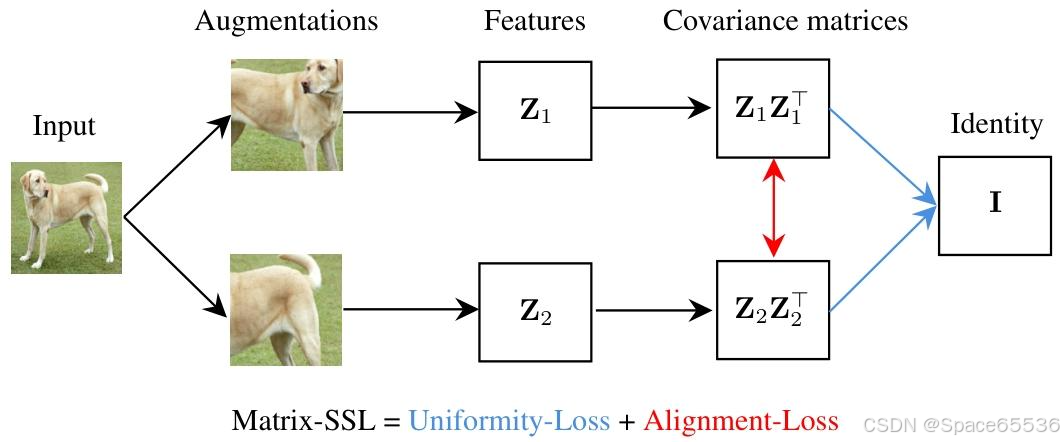
Figure 1. Illustration of the Matrix-SSL architecture. 首先是图像输入层，接着是数据增强和特征提取，然后形成协方差矩阵（$Z_1{Z}_1^{\top }$和$Z_2{Z}_2^{\top }$）。

9.结论

在本文中，我们提供了一个矩阵信息论视角，用于理解和改进自我监督学习方法。我们相信，我们的观点不仅会提供对自我监督学习方法的精致和替代理解，而且还会成为未来设计越来越健壮和有效的算法的催化剂。

补充1：关于文中提到的KL散度

论文中提及KL散度（Kullback–Leibler Divergence），主要用于衡量两个概率分布之间的差异，在矩阵信息理论的框架下，与自监督学习方法的设计、理解和优化相关。

1. 理论基础：在论文提出的矩阵信息理论中，对经典信息论概念进行拓展，定义了矩阵KL散度。对于两个正半定矩阵$P,Q\in {\mathbb{R}}^{n\times n}$，矩阵KL散度定义为$MKL(P\Vert Q)=tr(PlogP-PlogQ-P+Q)$。这一概念为对比不同矩阵提供了有力工具，是后续理论推导和损失函数设计的基础。
2. 与损失函数关系：论文证明了总编码率（TCR）损失与基于矩阵交叉熵（MCE）和矩阵KL散度的损失之间存在紧密联系。定理4.1表明，在特定条件下，TCR损失可以转化为正则化协方差矩阵与缩放单位矩阵之间的MCE/MKL损失。这种联系揭示了不同损失函数之间的内在一致性，为理解和改进自监督学习方法提供了新视角。在实际应用中，通过调整相关参数，可利用这种联系优化损失函数，提升模型性能。
3. 解释学习过程：矩阵KL散度用于解释自监督学习过程中的一些现象。有效秩与矩阵KL散度之间存在闭形式关系，命题6.1指出$erank(\frac{1}{B}Z{Z}^{\top })=\frac{d}{exp(MKL(\frac{1}{B}Z{Z}^{\top }\Vert \frac{1}{d}{I}_d))}$。在自监督学习训练中，矩阵KL散度（或MCE）会逐渐减小，意味着特征协方差矩阵$\frac{1}{B}Z{Z}^{\top }$会逐渐与$\frac{1}{d}{I}_d$对齐。这解释了为什么在训练过程中有效秩会增加，以及模型如何学习到更有效的数据表示，帮助理解自监督学习方法的收敛行为和性能提升机制。
4. 优化模型性能：在设计损失函数时，利用矩阵KL散度的最小化性质。例如，在矩阵对齐损失中，通过优化矩阵KL散度，使不同分支的协方差矩阵对齐，为模型提供更多信息和更丰富的信号，增强模型学习能力，从而提升在图像分类、目标检测、实例分割以及语言模型微调等任务中的性能。

补充2：关于论文提及的矩阵均匀性损失怎么促进特征有效分离和强化特征差异的

应用到跨模态图文对比学习中的例子：特征提取与矩阵构建、损失函数设计、联合训练与优化

1. 特征提取与矩阵构建：对于输入的图像数据，利用如ResNet等卷积神经网络进行特征提取，得到图像特征向量，进而构建图像特征矩阵；对于文本数据，使用Transformer等模型获取文本特征表示，形成文本特征矩阵。假设输入一张水果图像和一段描述水果的文本，图像经ResNet50提取特征后得到特征矩阵($Z_{1-image}$)，文本经BERT处理后得到特征矩阵($Z_{1-text}$) ，对其进行增强变换，获得另一组特征矩阵($Z_{2-image}$)和($Z_{2-text}$)。
2. 损失函数设计：在图像 - 文本对比学习中，结合矩阵均匀性损失和矩阵对齐损失进行优化。矩阵均匀性损失使图像与文本的交叉协方差矩阵与单位矩阵对齐，公式为
   ${\mathcal{L}}_{Matrix-Uniformity}(Z_{image},Z_{text})=MCE(\frac{1}{d}{I}_d,C(Z_{image},Z_{text}))$，
   以此促进特征的均匀分布。矩阵对齐损失则关注图像和文本自协方差矩阵的对齐，公式为${\mathcal{L}}_{Matrix-Alignment}(Z_{image},Z_{text})=-tr(C(Z_{image},Z_{text}))+\gamma \cdot MCE(C(Z_{image},Z_{image}),C(Z_{text},Z_{text}))$，
   通过调整(\gamma)控制对齐程度，强化特征之间的关联。
3. 联合训练与优化：将图像和文本数据同时输入模型，以矩阵均匀性损失和矩阵对齐损失之和作为总损失
   (${\mathcal{L}}_{Matrix-SSL}={\mathcal{L}}_{Matrix-Uniformity}+{\mathcal{L}}_{Matrix-Alignment}$) ，采用随机梯度下降等优化算法对模型进行训练。在训练过程中，不断调整模型参数，使损失函数最小化，从而学习到更有效的图像和文本特征表示，提升模型在跨模态任务中性能。

【关于非对比学习方法更关注特征的均匀分布】：
非对比学习方法通过设计特定的损失函数，使得模型学习到的特征在空间中尽可能均匀地分布，避免特征聚集在某些局部区域。这有助于模型捕捉到数据更全面的特征，提升其泛化能力。

• 原理：在非对比学习中，假设我们有一个图像数据集，里面包含各种不同类别的图像。以最大熵编码（MEC）损失为例，公式为(${\mathcal{L}}_{MEC}=-\mu logdet\left(I_d+\frac{d}{B{ϵ}^2}{Z}_1{Z}_2^{\top }\right)$)，其中($Z_1$)和($Z_2$)是对同一输入图像进行不同增强变换后得到的特征矩阵。这个损失函数鼓励特征嵌入的最大熵编码，本质上就是让特征在特征空间中分布得更均匀。从直观上理解，当特征均匀分布时，每个特征维度都能携带独特的信息，就像在一个二维平面上，如果所有点都聚集在一个小区域，那么很多区域的信息就被忽略了；而当这些点均匀分布时，整个平面的信息都能被充分利用。在实际的图像特征学习中，均匀分布的特征可以更好地描述图像的不同属性，使得模型对不同图像的区分能力更强。
• 示例：假设有一个包含猫、狗、汽车三类图像的数据集。使用非对比学习方法训练模型时，模型会尝试让猫的图像特征、狗的图像特征以及汽车的图像特征在特征空间中均匀分布。比如，在一个三维的特征空间中，猫的特征点不会都集中在一个角落，而是会均匀地散布在空间的某个区域；狗和汽车的特征点也会各自均匀地分布在不同区域，并且这些区域之间有明显的区分度。这样，当遇到一张新的猫的图像时，模型可以根据其特征在均匀分布的特征空间中的位置，更准确地判断它属于猫这一类。如果特征不是均匀分布，比如猫和狗的特征点有很多重叠，那么模型在区分这两类图像时就容易出错。

【假如有些猫和有些狗有相似的特征呢？比如黑猫和黑狗，这种情况学习两种辨别性特征的可行性】：
在存在相似特征的情况下，如黑猫和黑狗，该方法仍能有效学习两种视觉对象的表征，主要通过以下几个方面来实现：
矩阵均匀性损失促进特征分离：矩阵均匀性损失使得特征分布更加均匀，即便黑猫和黑狗存在相似特征，在均匀分布的特征空间中，它们也会被分配到不同的区域。以二维特征空间为例，假设一个维度代表颜色相关特征，另一个维度代表形状相关特征。虽然黑猫和黑狗在颜色（黑色）上相似，但在形状上有差异。均匀性损失会促使模型将黑猫和黑狗的特征在形状维度上充分展开，避免因颜色相似而聚集在一起，从而使模型能够区分两者。
矩阵对齐损失强化特征差异：矩阵对齐损失通过对齐不同分支的协方差矩阵，进一步突出了黑猫和黑狗之间的特征差异。模型会学习到黑猫和黑狗各自独特的特征组合模式。比如，黑猫可能具有独特的面部斑纹和体型特征，黑狗虽然颜色相同，但面部和体型特征不同。矩阵对齐损失使得模型能够捕捉到这些细微差异，在协方差矩阵层面强化这种区分，进而更好地区分黑猫和黑狗。
数据增强增加特征多样性：在训练过程中，通常会使用多种数据增强技术，如随机裁剪、颜色抖动、高斯模糊等。对于黑猫和黑狗的图像，数据增强会引入更多的差异。例如，对黑猫进行颜色抖动可能使其黑色呈现出不同的灰度变化，而对黑狗进行相同操作时，由于其毛发质地等差异，变化效果会有所不同。这些通过增强引入的差异有助于模型学习到更多区分两者的特征，即使它们原本有相似的颜色特征，也能在多样化的增强特征中找到区分点。
模型学习能力与特征挖掘：深度神经网络本身具有强大的学习能力。面对黑猫和黑狗的相似特征，模型会自动挖掘其他更具区分性的特征。如黑猫和黑狗的眼睛形状、耳朵形态等细节特征，模型在训练过程中会逐渐关注到这些特征，并将其融入到特征表示中。结合矩阵信息理论的损失函数，模型能够更有效地利用这些挖掘到的特征，从而准确地区分两种视觉对象的表征。

【或者说：那扩展到图像和文本的匹配关系：文本1：黑猫；文本2：黑狗；图像1：黑猫的图像；图像2：黑猫的图像，这种情况下应用Matrix-SSL的解释】：特征提取、矩阵构建、损失函数计算

特征提取与矩阵构建：利用预训练的图像模型（如ResNet）和文本模型（如BERT）分别对图像和文本进行特征提取。对图像1和图像2提取特征后得到图像特征矩阵$Z_{image1}$、$Z_{image2}$，对文本1和文本2提取特征后得到文本特征矩阵$Z_{text1}$、$Z_{text2}$。这些特征矩阵包含了图像和文本的语义信息，例如图像特征矩阵可能编码了黑猫的颜色、形状、姿态等视觉特征，文本特征矩阵则包含了“黑猫”“黑狗”这些词汇所蕴含的语义信息 。

矩阵均匀性损失的作用：计算图像与文本之间的矩阵均匀性损失，如${\mathcal{L}}_{Matrix-Uniformity}(Z_{image1},Z_{text1})=MCE(\frac{1}{d}{I}_d,C(Z_{image1},Z_{text1}))$。这一损失促使图像和文本的交叉协方差矩阵向单位矩阵对齐，使得特征分布更均匀。在这个例子中，对于“黑猫”的图像和文本，均匀性损失会让模型学习到两者在特征表示上的一致性，同时避免特征过于集中在某些相似维度（如“黑色”这一特征维度）。即使黑猫和黑狗在颜色上有相似性，但均匀性损失会推动模型在其他维度（如形状、品种特征等）挖掘差异，从而更准确地匹配“黑猫”的图像和文本。

矩阵对齐损失的作用：矩阵对齐损失
${\mathcal{L}}_{Matrix-Alignment}(Z_{image1},Z_{text1})=-tr(C(Z_{image1},Z_{text1}))+\gamma \cdot MCE(C(Z_{image1},Z_{image1}),C(Z_{text1},Z_{text1}))$
用于直接对齐图像和文本的自协方差矩阵。在“黑猫”的图像和文本匹配中，它帮助模型强化图像和文本特征之间的关联。比如，图像中黑猫独特的外貌特征（如绿色的眼睛、黑色的毛发质感）与文本“黑猫”所蕴含的相关语义特征通过矩阵对齐损失得到更好的匹配。而对于“黑狗”的文本和“黑猫”的图像，由于两者自协方差矩阵差异较大，矩阵对齐损失会使得模型减少对它们的匹配度，从而正确区分不同的图像 - 文本对。

整体匹配判断：通过最小化矩阵均匀性损失和矩阵对齐损失的总和
（即${\mathcal{L}}_{Matrix-SSL}={\mathcal{L}}_{Matrix-Uniformity}+{\mathcal{L}}_{Matrix-Alignment}$），模型能够学习到图像和文本之间的准确匹配关系。在这个例子中，“黑猫”的图像1与文本1之间的损失会在训练过程中逐渐减小，表明模型认为它们是匹配的；而图像1与文本2（“黑狗”）之间的损失会相对较大，模型能够识别出这两者不匹配。这样，模型就可以在图像和文本之间建立有效的匹配关系，即使存在相似特征的干扰，也能准确判断图像和文本是否对应 。

补充3：代码

参考：https://github.com/yifanzhang-pro/Matrix-SSL/blob/master/main_pretrain.py
Matrix-SSL 损失函数由 Matrix-Uniformity Loss 和 Matrix-Alignment Loss 两部分组成：
$L_{\text{Matrix-SSL}}=L_{\text{Matrix-Uniformity}}+L_{\text{Matrix-Alignment}}$
其中：

1. Matrix-Uniformity Loss 旨在使特征的协方差矩阵接近单位矩阵，以促进特征的均匀分布：
   $L_{\text{Matrix-Uniformity}}(Z_1,Z_2)=\text{MCE}\left(\frac{1}{d}{I}_d,C(Z_1,Z_2)\right)$
   其中 ( $C(Z_1,Z_2)=\frac{1}{B}{Z}_1{H}_B{Z}_2^{\top }$ )，( $H_B$ ) 是用于中心化的矩阵。

2. Matrix-Alignment Loss 通过对协方差矩阵之间的差异进行对齐：
   $L_{\text{Matrix-Alignment}}(Z_1,Z_2)=-\text{tr}(C(Z_1,Z_2))+\gamma \cdot \text{MCE}(C(Z_1,Z_1),C(Z_2,Z_2))$
   其中 ($\gamma$) 是权重因子，用于调整对齐损失的贡献。

最小化矩阵均匀性损失和矩阵对齐损失的总和：

mec_loss = (loss_func(p1, z2, lamda_inv) + loss_func(p2, z1, lamda_inv)) * 0.5 / args.m
mce_loss = (mce_loss_func(p2, z1, correlation=True, logE=False, lamda=args.mce_lambd, mu=args.mce_mu, order=args.mce_order, align_gamma=args.align_gamma)+ mce_loss_func(p1, z2, correlation=True, logE=False, lamda=args.mce_lambd, mu=args.mce_mu, order=args.mce_order, align_gamma=args.align_gamma)+ args.gamma * mce_loss_func(p2, z1, correlation=False, logE=False, lamda=args.mce_lambd, mu=args.mce_mu, order=args.mce_order, align_gamma=args.align_gamma)+ args.gamma * mce_loss_func(p1, z2, correlation=False, logE=False, lamda=args.mce_lambd, mu=args.mce_mu, order=args.mce_order, align_gamma=args.align_gamma)) * 0.5
# mec_loss = mec_loss + mce_loss * 1.
# scaled loss by lamda
# loss = -1 * mec_loss * lamda_inv
loss = mce_loss

具体来说：

1. 矩阵的均匀性损失：

mec_loss = (loss_func(p1, z2, lamda_inv) + loss_func(p2, z1, lamda_inv)) * 0.5 / args.mdef loss_func(p, z, lamda_inv, order=4):p = gather_from_all(p)z = gather_from_all(z)p = F.normalize(p)z = F.normalize(z)c = p @ z.Tc = c / lamda_inv power_matrix = csum_matrix = torch.zeros_like(power_matrix)for k in range(1, order+1):if k > 1:power_matrix = torch.matmul(power_matrix, c)if (k + 1) % 2 == 0:sum_matrix += power_matrix / kelse: sum_matrix -= power_matrix / ktrace = torch.trace(sum_matrix)return trace

2. 矩阵对齐损失：

mce_loss = (mce_loss_func(p2, z1, correlation=True, logE=False, lamda=args.mce_lambd, mu=args.mce_mu, order=args.mce_order, align_gamma=args.align_gamma)+ mce_loss_func(p1, z2, correlation=True, logE=False, lamda=args.mce_lambd, mu=args.mce_mu, order=args.mce_order, align_gamma=args.align_gamma)+ args.gamma * mce_loss_func(p2, z1, correlation=False, logE=False, lamda=args.mce_lambd, mu=args.mce_mu, order=args.mce_order, align_gamma=args.align_gamma)+ args.gamma * mce_loss_func(p1, z2, correlation=False, logE=False, lamda=args.mce_lambd, mu=args.mce_mu, order=args.mce_order, align_gamma=args.align_gamma)) * 0.5...
def mce_loss_func(p, z, lamda=1., mu=1., order=4, align_gamma=0.003, correlation=True, logE=False):p = gather_from_all(p)z = gather_from_all(z)p = F.normalize(p)z = F.normalize(z)m = z.shape[0]n = z.shape[1]# print(m, n)J_m = centering_matrix(m).detach().to(z.device)if correlation:P = lamda * torch.eye(n).to(z.device)Q = (1. / m) * (p.T @ J_m @ z) + mu * torch.eye(n).to(z.device)else:P = (1. / m) * (p.T @ J_m @ p) + mu * torch.eye(n).to(z.device)Q = (1. / m) * (z.T @ J_m @ z) + mu * torch.eye(n).to(z.device)return torch.trace(- P @ matrix_log(Q, order))

最后，总损失的计算：

total_loss = mec_loss + mce_loss
# 可以根据需要进行缩放等操作
# 例如：total_loss = -1 * total_loss * lamda_inv
loss = total_loss