当前位置：首页 > news >正文

机器学习4

news 来源：原创 2025/8/3 22:54:49

九、线性回归

1、概念

假设存在多个点，需要使用一条线来保障尽量拟合这些点，寻找这条线的过程就叫回归。

机器学习中一种有监督学习的算法,回归问题主要关注的是因变量(需要预测的值)和一个或多个数值型的自变量(预测变量)之间的关系。

2、损失函数

假设存在数据：[[4.2, 3.8]，[4.2, 2.7]，[2.7, 2.4]，[0.8, 1.0]，[3.7, 2.8]，[1.7, 0.9]，[3.2, 2.9]]

需要寻找一个直线方程 y=wx+b ，能通过因变量预测结果，这个结果最优：如下图，中间的直线最能拟合数据点。

使用一种方法（均方差）来判断目前的方程系数值能否大大最有：预测点位的y值与实际y值的差的平方的和（先求差，再求平方，再求所有结果的和）来衡量寻找的直线是否最优，这些值便成为均方差；也就是均方差越小，那么该线约优。

通过不断对直线的求解，得到很多的系数（w）值，这些值与均方差的关系函数便是损失函数。（函数最低点就是最优系数）

loss = 1/n * ${(y_1-y_1^,)^2}+{(y_2-y_2^,)^2}+....{(y_n-y_n^,)^2}$ ，

直接表述为 loss = 1/n *

得到一个二元一次方程，也就是存在最低点（均方差最小），目标为在纵坐标最小值的横坐标（也就是w值），不需要得到具体纵坐标值（值的大小并不需要，只需要是最小即可），所以可以变形为： loss = 1/2 * ，在多个特征过程内，所需要的系数也变多了，就变成了w矩阵。

3、最小二乘法MSE

3.1、原理

损失函数： loss = 1/2 *

求导结果为：loss' = $X^TXW-X^Ty$

通过导数为0，得到损失函数最小值的w值。

3.2、API

from sklearn.linear_model import LinearRegression

参数：fit_intercept 布尔值，是否计算偏置（纵轴截距）

属性：coef_ 解后的回归系数

intercept_ 解后的偏置

from sklearn.linear_model import LinearRegression
import numpy as npdata=np.array([[0,14,8,0,5,-2,9,-3,399],[-4,10,6,4,-14,-2,-14,8,-144],[-1,-6,5,-12,3,-3,2,-2,30],[5,-2,3,10,5,11,4,-8,126],[-15,-15,-8,-15,7,-4,-12,2,-395],[11,-10,-2,4,3,-9,-6,7,-87],[-14,0,4,-3,5,10,13,7,422],[-3,-7,-2,-8,0,-6,-5,-9,-309]])# 1、处理x值和y值
# x 数据为第一列到第八列所有行
x=data[:,0:8]
# y 数据为第九列所有行
y=data[:,8:]# 2、创建算法对象   
# fit_intercept 偏置
estimator=LinearRegression(fit_intercept=False)
# 传入x和y 训练
estimator.fit(x,y)print("权重系数为：\n", estimator.coef_)  #权重系数与特征数一定是同样的个数。
print("偏置为：\n", estimator.intercept_)# 3、使用新数据进行预测结果
x_new=[[11,14,8,10,5,10,8,1]]
y_predict=estimator.predict(x_new)
print("预测结果:\n",y_predict)

4、梯度下降

4.1、原理：

背景：w为矩阵情况下，逆矩阵计算量庞大，故舍弃最小二乘法，直接赋值w矩阵，通过该点的损失函数导数的值判断是否达到最优解。

$w_2$ = $w_{1}$ - a * $w_{1}$ '

$w_{1}$ 为随机取值的点

$w_{1}$ ' 为该点的损失函数导数值

学习率 a：控制每次前进距离（学习率过大，前进的步子很大，容易造成结果震荡或四处取值；学习率过小，前进的步子太小就会一直处于最优解的左或右部分），一般设置为跟着前进次数降低。

第一个点随机取值后，找到该点的导数，判断往左走还是往右走一个距离，通过多次前进，向最优系数靠近。

前进的方式为判断该点导数的正负，正则向右，前进的距离大小由该点导数值与学习率控制。

4.2、代码实现

import numpy as np
import matplotlib.pyplot as plt# 损失函数、损失函数导数、第一次的w值、学习率
# 损失函数
def loss(w):return 10*w**2 - 15.9*w +6
# 损失函数导数
def dloss(w):return 20*w-15.9
w = np.linspace(-50, 50,30)plt.plot(w, loss(w))# 数据点位的列表
x = []
y = []# 随机产生第一次点位的w值
np.random.seed(666)
w = np.random.randint(-50,50)
x.append(w)
y.append(loss(w))# 学习率
learning_rate = 0.01# 开始进行多次学习
for i in range(1,13):w = w-learning_rate*dloss(w)learning_rate -= learning_rate*0.00005x.append(w)y.append(loss(w))plt.scatter(x,y)plt.show()

5、梯度下降方法

5.1、批量梯度下降 BGD

准确率高，但是每一次的计算梯度都需要使用全部样本，计算量大且速度慢，不推荐使用

5.2、随机梯度下降 SGD

每次迭代仅使用随机单个样本，计算量不大且速度快，但是每次随机可能使用到脏数据导致梯度不降反增。

Stochastic Gradient Descent, SGD

步骤：1、挑选初始点w值；2、随机挑选训练样本；3、使用样本计算损失函数的梯度；4、更新w和学习率，再重复2、3步骤；4、达到每个样本都单独训练，算作一个epoch ；5、重复epoch，得到最优结束（或多少次后结束）。

from sklearn.linear_model import SGDRegressor

参数：loss ：损失函数，默认为'squared_error'

fit_intercept ：是否计算偏置 B

eta0 ：浮点数，学习率的初始值

learning_rate ：学习率的衰减，默认 invscaling：逆幂律衰减，eta = eta0 / pow(t, power_t)，t代表次数，power_t 默认 0.25；constant：保持不变；optimal：最优策略衰减，eta = 1.0 / (alpha * (t + t0)) ，alpha是正则化参数，t0是由 SGDRegressor 自动确定的常数；adaptive：在验证误差不再减少时降低，验证误差停止减少时，学习率会乘以一个因子（默认为0.1），直到达到最小学习率或达到最大迭代次数。

max_iter（又名epoch）：训练数据的最大次数。

penalty：正则化方法。

属性：coef_ 系数

intercept_ 偏置

from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.linear_model import SGDRegressor
from sklearn.preprocessing import StandardScaler# 获取加利福利亚住房信息
house = fetch_california_housing(data_home="../../src/")
x = house.data
y = house.target
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)# 标准化数据
scaler = StandardScaler()
x_train = scaler.fit_transform(x_train)
x_test = scaler.transform(x_test)# 生成预估器对象
sgd = SGDRegressor(loss="squared_error", alpha=0.1)
# 训练模型
sgd.fit(x_train, y_train)
# 预测结果 对比
print(sgd.predict(x_test[0:10,:]))
print(y[0:10])
# 获得决定系数， 当 决定系数 接近1时，表示模型拟合得非常好；接近0时，表示模型几乎没有解释能力；小于0时，表示模型的预测效果甚至不如常数模型（即总是预测平均值）。
print(sgd.score(x_test,y_test))
# 输出系数和偏置
print(sgd.coef_)
print(sgd.intercept_)

5.3、小批量梯度下降 MBGD

介于批量梯度下降（BGD）与随机梯度下降（SGD）之间，每次迭代使用部分数据集训练，既减少计算量，有保持梯度准确性。

步骤：1、指定每次量大小并划分多少次；2、重复传入数据到模型训练，更新w系数；

使用方式与SGD一样：from sklearn.linear_model import SGD；使用 partial_fit 继续训练。

from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.linear_model import SGDRegressor
from sklearn.preprocessing import StandardScaler
import numpy as np# 获取加利福利亚住房信息
house = fetch_california_housing(data_home="../../src/")
x = house.data
y = house.target
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)# 标准化数据
scaler = StandardScaler()
x_train = scaler.fit_transform(x_train)
x_test = scaler.transform(x_test)# 生成预估器对象
sgd = SGDRegressor(loss="squared_error", max_iter=1000, alpha=0.1, fit_intercept=True)# 设置批量大小和循环次数
batch_size = 50  # 批量大小
n_batches = len(x_train) // batch_size  # 批次数量
for epoch in range(sgd.max_iter):indices = np.random.permutation(len(x_train))  # 随机打乱样本顺序for i in range(n_batches):start_idx = i * batch_sizeend_idx = (i + 1) * batch_sizebatch_indices = indices[start_idx:end_idx]X_batch = x_train[batch_indices]y_batch = y_train[batch_indices]sgd.partial_fit(X_batch, y_batch) # 输出系数和偏置
print(sgd.coef_)
print(sgd.intercept_)# 评估
y_predict = sgd.predict(x_test)
print("得分:\n",sgd.score(x_test, y_test))
print("预测的数据集：\n", y_predict)
error = mean_squared_error(y_test, y_predict)
print("均方误差为：\n", error)

6、拟合

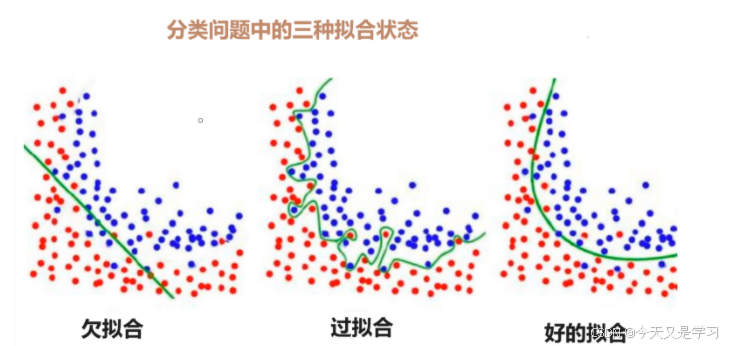
欠拟合：训练误差较高，测试误差较高

过拟合：将异常值和脏数据学习，导致复杂性过高，训练误差较低，测试误差较高

7、正则化

就是防止过拟合，增加模型的鲁棒性（耐造），所以正则化(鲁棒性调优)的本质就是牺牲模型在训练集上的正确率来提高推广、泛化能力，在原有损失函数基础上添加惩罚造成系数w降低，就是正则化。

L1：曼哈顿距离

L2：欧式距离

8、岭回归 Ridge

在原有损失函数基础上添加L2正则化：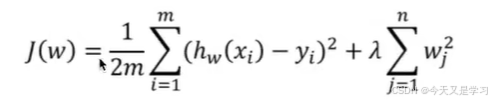

λ指惩罚型系数，又叫正则项力度。

from sklearn.linear_model import Ridge

参数：alpha ：默认1.0，正则化力度

fit_intercept：是否偏置

solver：指定求解优化问题的算法（默认auto）

normalize：默认True，数据进行标准化

max_iter：最大迭代次数，默认为15000

属性：coef_ 系数

intercept_ 偏置

from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Ridge# 获取加利福利亚住房信息
house = fetch_california_housing(data_home="../../src/")
x = house.data
y = house.target
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)# 生成预估器对象
r = Ridge(alpha=0.1,max_iter=1000,fit_intercept=True)
# 训练
r.fit(x_train, y_train)# 输出系数和偏置
print(sgd.coef_)
print(sgd.intercept_)# 评估
y_predict = r.predict(x_test)
print("预测的数据集：\n", y_predict)
print("得分:\n",r.score(x_test, y_test))

9、拉索回归 Lasso

在原有损失函数基础上添加L1正则化：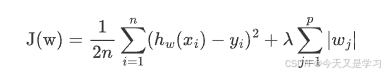

p 是特征的数量。

from sklearn.linear_model import Ridge

参数：alpha ：默认1.0，正则化力度

fit_intercept：是否偏置

precompute ：默认False，如果为 True，则使用预计算的 Gram 矩阵来加速计算。如果为数组，则使用提供的 Gram 矩阵。

copy_X ：默认True，复制数据 X

max_iter ：最大迭代次数，默认为15000

tol ：精度阈值

warm_start ：默认False，设置为 True 时，再次调用 fit 方法会重新使用之前调用 fit 方法的结果作为初始估计值，而不是清零它们。

positive ：默认False，设置为 True 时，强制系数为非负。

random_state ：随机数生成器的状态。用于随机初始化坐标下降算法中的随机选择。

selection ：默认为 'cyclic'，则按照循环顺序选择坐标，设置为 'random'，则随机选择坐标进行更新。

属性：coef_ 系数

intercept_ 偏置

n_iter_ 实际使用的迭代次数。

n_features_in_ 训练样本中特征的数量。

from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Lasso# 加载波士顿房价数据集
data = fetch_california_housing(data_home="../../src")
X, y = data.data, data.target# 划分训练集和测试集
X_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建Lasso回归模型
lasso = Lasso(alpha=0.1)  # alpha是正则化参数# 训练模型
lasso.fit(X_train, y_train)# 得出模型
print("权重系数为：\n", lasso.coef_)  #权重系数与特征数一定是同样的个数。
print("偏置为：\n", lasso.intercept_)#模型评估
y_predict = lasso.predict(x_test)
print("预测的数据集：\n", y_predict)
error = mean_squared_error(y_test, y_predict)
print("均方误差为：\n", error)

十、逻辑回归

使用回归算法计算数据，最后使用激活函数计算概率分类，实质上是分类算法

1、原理

线性回归:： $h(w)=w_1x_1+w_2x_2+....+b$

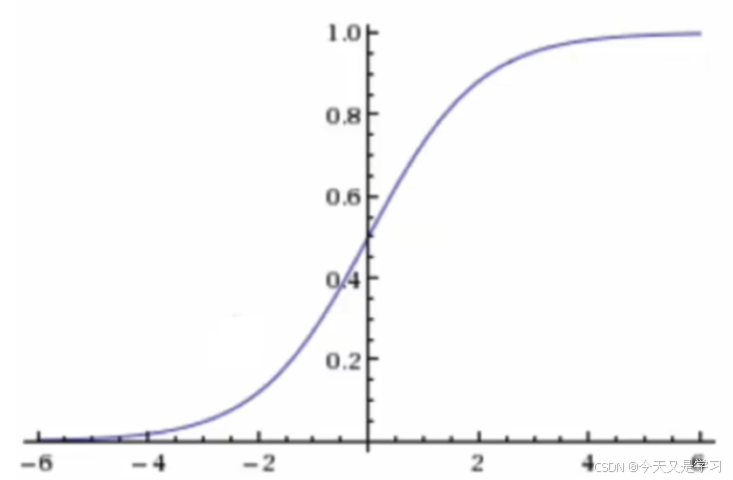
sigmoid激活函数： $f(x)=\frac{1}{1+e^{-x}}$

sigmoid函数的值是在[0,1]区间中的一个概率值,默认为0.5为阈值（可更改），大于是正例，小于是负例，也就变成分类问题。

2、API

from sklearn.linear_model import LogisticRegression()

参数：fit_intercept 是否偏置
max_iter 最大迭代次数，默认100
属性：coef_ 权重
intercept_ 偏置
predict() 预测分类
predict_proba() 预测分类(对应的概率)
score() 准确率

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression#加载数据
X,y = load_iris(return_X_y=True)# 删除第三种数据类型，形成两种分类
X=X[y!=2]
y=y[y!=2]#数据集划分
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.25,random_state=33)#逻辑回归模型
model=LogisticRegression()#训练
model.fit(X_train,y_train)#权重
print("权重系数为：\n",model.coef_)#偏置
print("偏置为：\n",model.intercept_)#预测分类
y_predict=model.predict(X_test)
print("预测结果为：\n",y_predict)
print("实际结果为：\n",y_test)#预测分类对应的概率
proba=model.predict_proba(X_test)
print("预测分类概率为：\n",proba)#评估
print("准确率为：\n",model.score(X_test,y_test))

机器学习4

九、线性回归 1、概念假设存在多个点，需要使用一条线来保障尽量拟合这些点，寻找这条线的过程就叫回归。机器学习中一种有监督学习的算法,回归问题主要关注的是因变量(需要预测的值)和一个或多个数值型的自变量(预测变量)之间的关系。 2、损失…...

编程日记 2025/8/3 22:54:49

Linux中系统的延迟任务及定时任务

一、延时任务 at 命令，即用即消如 at 11：30 rm -rf /mnt/* ctrld运行 （过一秒即可执行） -v 使用较明显的时间格式，列出at调度中的任务列表 -l 可列出目前系统上面的所有该用户的at调度 -c 可以列出后面接…...

编程日记 2025/8/3 21:29:30

从Stream的 toList() 和 collect(Collectors.toList()) 方法看Java的不可变流

环境 JDK 21Windows 11 专业版IntelliJ IDEA 2024.1.6 背景在使用Java的Stream的时候，常常会把流收集为List。假设有List list1 如下： var list1 List.of("aaa", "bbbbbb", "cccc", "d", "eeeee&qu…...

编程日记 2025/7/30 4:19:44

centos7.9单机版安装K8s

1.安装docker [rootlocalhost ~]# hostnamectl set-hostname master [rootlocalhost ~]# bash [rootmaster ~]# mv /etc/yum.repos.d/* /home [rootmaster ~]# curl -o /etc/yum.repos.d/CentOS-Base.repo http://mirrors.aliyun.com/repo/Centos-7.repo [rootmaster ~]# cu…...

编程日记 2025/8/3 13:44:26

Notepad++--在开头快速添加行号

原文网址：Notepad--在开头快速添加行号_IT利刃出鞘的博客-CSDN博客简介本文介绍Notepad怎样在开头快速添加行号。需求原文件想要的效果方法 1.添加点号 Alt鼠标左键，从首行选中首列下拉，选中需要添加序号的所有行的首列&#xff…...

编程日记 2025/7/30 2:39:13

如何在 PyCharm 中配置 HTTP 代理以确保网络连接的顺畅性

如何在 PyCharm 中配置 HTTP 代理以确保网络连接的顺畅性在配置 PyCharm 的 HTTP 代理以确保网络连接的顺畅性时，需按照一定的步骤进行设置，这不仅有助于确保 PyCharm 能够顺利访问互联网资源，还能保证插件和工具的正常更新与同步。以下是详…...

编程日记 2025/7/28 3:41:42

查找萤石云IOS Sdk中的编解码接口

2021/1/20 以前的时候，碰到的问题，想把萤石云视频介入到TRTC，但是... 萤石云的IOS接口中没有相应的解码播放库，也就是找不到PlayerSDK对应部分，怎么做呢？ 一个是坐等萤石云开放这部分接口，可能…...

编程日记 2025/7/31 4:39:45

webpack配置

4-3vue-loader测试_哔哩哔哩_bilibili 一.新建文件夹vue_todo，vscode打开二.ctrl打开终端，输入npm init -y，快速生成一个默认的package.json文件之后左边出现项目初始化文件package.json 三.接下来需要webpack完成打包，所以安装…...

编程日记 2025/7/28 12:05:09

Streamlit + AI大模型API实现视频字幕提取

简介在本文中，我将带你探讨如何使用Streamlit和AI大模型API来实现视频字幕提取的技术。Streamlit是一个开源的Python库，用于快速构建数据应用的Web界面，而AI大模型API，如OpenAI，提供了强大的语言处理能力&#xff0c…...

编程日记 2025/8/1 1:35:56

11.21 深度学习-tensor常见操作

import torch from PIL import Image from torchvision import transforms # 获取元素值 tensor.item() 返回一个数值只能是tensor里面有一个数字的 # 我们可以把单个元素tensor转换为Python数值，这是非常常用的操作 # tensor 里面超过了1个数字就不行 def g…...

编程日记 2025/7/30 21:21:40

gitlab和jenkins连接

一：jenkins 配置安装gitlab插件生成密钥 id_rsa 要上传到jenkins，id_rsa.pub要上传到gitlab cat /root/.ssh/id_rsa 复制查看的内容可以看到已经成功创建出来了对于gitlab的认证凭据二：配置gitlab cat /root/.ssh/id_rsa.pub 复制查…...

编程日记 2025/7/29 15:03:35

从视频帧生成点云数据、使用PointNet++模型提取特征，并将特征保存下来的完整实现。

文件地址 https://github.com/yanx27/Pointnet_Pointnet2_pytorch?spm5176.28103460.0.0.21a95d27ollfze Pointnet_Pointnet2_pytorch\log\classification\pointnet2_ssg_wo_normals文件夹改名为Pointnet_Pointnet2_pytorch\log\classification\pointnet2_cls_ssg "E:…...

编程日记 2025/7/31 12:54:23

vue3 + Element Plus + ts 封装全局的 message、messageBox、notification 方法

本文示例将 Element Plus 中的 ElMessage 消息提示, ElMessageBox 消息弹出框, ElNotification 消息通知方法统一封装到全局 hooks 文件中方便全局调用准备：在项目 src 目录中新建 hooks 目录、然后在 hooks 目录中新建 index.ts （如果你没有使用 ts …...

编程日记 2025/8/1 11:50:04

【人工智能】Python在机器学习与人工智能中的应用

Python因其简洁易用、丰富的库支持以及强大的社区，被广泛应用于机器学习与人工智能（AI）领域。本教程通过实用的代码示例和讲解，带你从零开始掌握Python在机器学习与人工智能中的基本用法。 1. 机器学习与AI的Python生态系统 Pyth…...

编程日记 2025/8/3 22:53:43

linux上安装docker

在 Linux 上安装 Docker 是一个相对简单的过程。以下是针对 Debian 和其他基于 Debian 的发行版（如 Ubuntu）的详细步骤。如果您使用的是其他发行版（如 CentOS 或 Fedora），也可以参考相应的官方文档进行安装。安装 Do…...

编程日记 2025/7/29 14:20:02

LeetCode:1008. 前序遍历构造二叉搜索树

目录题目描述: 代码: 第一种: 第二种: 第三种:分治法题目描述: 给定一个整数数组，它表示BST(即二叉搜索树 )的先序遍历 ，构造树并返回其根。保证对于给定的测试用例，总是有可能找到具有给定需求的二叉搜索树。二叉搜索树是一棵…...

编程日记 2025/8/3 22:54:47

开源远程桌面工具:RustDesk

在远程办公和远程学习日益普及的今天，我们经常需要远程访问办公电脑或帮助他人解决电脑问题。市面上的远程控制软件要么收费昂贵，要么需要复杂的配置，更让人担心的是数据安全问题。最近我发现了一款名为 RustDesk 的开源远程桌面工具&…...

编程日记 2025/7/30 17:47:02

nfs服务器--RHCE

一，简介 NFS（Network File System，网络文件系统）是FreeBSD支持的文件系统中的一种，它允许网络中的计算机（不同的计算机、不同的操作系统）之间通过TCP/IP网络共享资源，主要在unix系…...

编程日记 2025/7/29 1:14:08

使用 Elastic 3 步实现基于 OTel 的原生 K8s 和应用可观测性

作者：来自 Elastic Bahubali Shetti Elastic 的 OpenTelemetry 发行版现已支持 OTel Operator，可使用 EDOT SDK 自动检测应用程序，并管理 EDOT OTel Collector 的部署和生命周期以实现 Kubernetes 可观察性。了解如何通过 3 个简单步骤进行配…...

编程日记 2025/7/30 23:43:06

Vue3-小兔鲜项目出现问题及其解决方法（未写完）

基础操作 （1）使用create-vue搭建Vue3项目要保证node -v 版本在16以上 （2）添加pinia到vue项目 npm init vuelatest npm i pinia //导入creatPiniaimport {createPinia} from pinia//执行方法得到实例const pinia createPinia()…...

编程日记 2025/7/29 22:08:20

【mysql】锁机制 - 3.意向锁

意向锁（Intension Lock） 是为了提高粗粒度锁性能而设置的一种预判机制，即在一个操作发起实际资源的锁申请行为之前，先对更粗力度的资源发起一个加锁意向声明。为什么需要意向锁？ 比如对于以下操作： 事务…...

编程日记 2025/8/3 22:54:48

Nuxt3 动态路由URL不更改的前提下参数更新，NuxtLink不刷新不跳转，生命周期无响应解决方案

Nuxt3 动态路由URL不更改的前提下参数更新，NuxtLink不刷新不跳转，生命周期无响应解决方案首先说明一点，Nuxt3 的动态路由响应机制是根据 URL 是否更改，参数的更改并不会触发 Router 去更新页面，这在 Vue3 上同样存在…...

编程日记 2025/8/3 22:53:40

Spring Boot集成Redis：配置、序列化与持久化

Spring Boot集成Redis：配置、序列化与持久化一、简介什么是Redis Redis是一个开源的、基于内存的高性能键值对存储数据库，支持多种数据结构如字符串、哈希、列表、集合等。它以其卓越的性能、高可用性和持久性而广受欢迎。为什么要使用Redis Red…...

编程日记 2025/8/1 7:18:47

JAVA：探索 PDF 文字提取的技术指南

1、简述随着信息化的发展，PDF 文档成为了信息传播的重要媒介。在许多应用场景下，如数据迁移、内容分析和信息检索，我们需要从 PDF 文件中提取文字内容。JAVA提供了多种库来处理 PDF 文件，其中 PDFBox 和 iText 是最常用的两个。…...

编程日记 2025/7/30 10:02:17

当你项目服务器磁盘报警

当你们公司运维收到这样的邮件，大概率日志文件过大引起的在Linux下如何不停止服务,清空nohup.out文件呢？ nohup.out会一直一直自己增长下去，如果你的服务器硬盘不给力的话，很容易把应用也挂掉（硬盘没空间 &#xff0…...

编程日记 2025/8/3 4:10:34

SpringBoot中Maven的定义及国内源配置教程，实现自动获取Jar包

推荐一个国内镜像API网站，无需信用卡及科学上网即可调用gpt，claude3，gemini等国外模型，感兴趣的可以看下👉：https://api.atalk-ai.com/ SpringBoot中Maven的定义及国内源配置教程，实现自动获取J…...

编程日记 2025/7/31 13:55:52

LSTM 和 LSTMCell

1. LSTM 和 LSTMCell 的简介 LSTM (Long Short-Term Memory): 一种特殊的 RNN（循环神经网络），用于解决普通 RNN 中梯度消失或梯度爆炸的问题。能够捕获长期依赖关系，适合处理序列数据（如自然语言、时间序列等&…...

编程日记 2025/8/2 18:59:12

【卡尔曼滤波】数据预测Prediction观测器的理论推导及应用 C语言、Python实现（Kalman Filter）

【卡尔曼滤波】数据预测Prediction观测器的理论推导及应用 C语言、Python实现（Kalman Filter） 更新以gitee为准： 文章目录数据预测概念和适用方式线性系统的适用性数据预测算法和卡尔曼滤波公式推导状态空间方程和观测器先验估计后验估计…...

编程日记 2025/7/28 13:18:48

神经网络问题之一：梯度消失（Vanishing Gradient）

梯度消失（Vanishing Gradient）问题是深度神经网络训练中的一个关键问题，它主要发生在反向传播过程中，导致靠近输入层的权重更新变得非常缓慢甚至几乎停滞，严重影响网络的训练效果和性能。图1 在深度神经网络中容易出现…...

编程日记 2025/7/31 9:42:45

【微软：多模态基础模型】（4）统一视觉模型

欢迎关注[【youcans的AGI学习笔记】](https://blog.csdn.net/youcans/category_12244543.html）原创作品【微软：多模态基础模型】（1）从专家到通用助手【微软：多模态基础模型】（2）视觉理解【微…...

编程日记 2025/8/3 9:26:35

npm | Yarn | pnpm Node.js包管理器比较与安装

一、包管理器比较参考原文链接： 2024 Node.js Package Manager 指南：npm、Yarn、pnpm 比较 — 2024 Node.js Package Manager Guide: npm, Yarn, pnpm Compared (nodesource.com) 以下是对 Node.js 的三个包管理工具 npm、Yarn 和 pnpm 的优缺点总结&am…...

编程日记 2025/7/30 23:34:39

建造者模式

什么是建造者模式？ 建造者模式（Builder Pattern）是一种设计模式，用来一步步创建复杂的对象，而不用直接去调用复杂的构造函数或手动设置大量属性。你可以： • 按步骤“搭建”对象。 • 自由选择要设置的部…...

编程日记 2025/8/2 9:38:21

Spring Boot核心概念：应用配置

Spring Boot提供了强大的配置系统，允许开发者通过配置文件轻松管理应用的配置。支持的主要配置文件格式有两种：application.properties和application.yml。 application.properties与application.yml application.properties和application.yml是Spring…...

编程日记 2025/8/2 17:10:04

linux环境安装cuda toolkit

1 全新安装如果环境中没安装过cuda版本， 这种情况下比较简单。直接在https://developer.nvidia.com/cuda-toolkit-archive选择对应版本下载安装即可。如下为安装cuda toolkit 11.8. 2 环境中已经存在其他版本这种情况下比较复杂一些。首先要确认最高支持的版…...

编程日记 2025/8/3 21:21:51

WebSocket实战，后台修改订单状态，前台实现数据变更，提供前端和后端多种语言

案例场景： 在实际的后台中需要变更某个订单的状态，在官网中不刷新页面，可以自动更新状态在前端页面实现订单状态的实时更新（不刷新页面），可以通过 WebSocket 的方式与后台保持通信，监听订单状态…...

编程日记 2025/7/31 22:33:59

实时通信协议概述：WebRTC、RTP/RTCP、RTMP、HLS 和 FLV 的比较与应用

文章目录一、协议总览二、WebRTC2.1 时序图2.2 代码示例三、RTP/RTCP3.1 时序图3.2 代码示例四、RTMP4.1 时序图4.2 代码示例五、HLS5.1 时序图5.2 代码示例六、总结一、协议总览协议/格式细节对比适用场景用法WebRTC使用 UDP 传输协议，支持 P2P 通信&#…...

编程日记 2025/8/2 23:46:47

Vue路由

目录 1. 安装 vue-router 2. 创建 Vue 项目结构 3. 配置路由 4. 在 main.js 中使用路由 5. 在 App.vue 中添加 6. 创建组件 7. 运行你的应用在 Vue.js 2 中，路由管理通常通过 vue-router 插件来实现。vue-router 是一个官方的路由管理器，允许你…...

编程日记 2025/7/31 9:48:06

uniapp开发微信小程序笔记3-全局配置、导航栏配置、tabBar配置

前言： 本文记录的是微信小程序的全局配置、导航栏配置、tabBar配置一、全局配置： 可以直接查官方文档：pages.json 页面路由 | uni-app官网，有非常详细的文档说明都是在 pages.json里面做配置的，我们可以看到已经有…...

编程日记 2025/8/1 6:48:49

Hash table类算法【leetcode】

哈希表中关键码就是数组的索引下标，然后通过下标直接访问数组中的元素那么哈希表能解决什么问题呢，一般哈希表都是用来快速判断一个元素是否出现集合里。例如要查询一个名字是否在这所学校里。要枚举的话时间复杂度是O(n)，但如果使用哈希…...

编程日记 2025/8/3 21:06:57

多算法模型（BI-LSTM GRU Mamba ekan xgboost）实现功率预测

概述本项目旨在通过结合多算法模型网络实现功率预测。包括数据处理、特征工程、模型训练、模型推理和结果输出，最终结果以 JSON 格式返回。代码地址：代码...

编程日记 2025/8/2 22:24:53

html 图片转svg 并使用svg路径来裁剪html元素

1.png转svg 工具地址: Vectorizer – 免费图像矢量化打开svg图片,复制其中的path中的d标签的路径查看生成的svg路径是否正确在线SVG路径预览工具 - UU在线工具 2.在html中使用svg路径 <svg xmlns"http://www.w3.org/2000/svg" width"318px" height…...

编程日记 2025/7/16 15:29:33

贴代码框架PasteForm特性介绍之select,selects,lselect和reload

简介 PasteForm是贴代码推出的 “新一代CRUD” ，基于ABPvNext，目的是通过对Dto的特性的标注，从而实现管理端的统一UI，借助于配套的PasteBuilder代码生成器，你可以快速的为自己的项目构建后台管理端！目前管…...

编程日记 2025/7/29 22:51:58

【Redis】实现异步秒杀功能

一、将判断条件提前缓存到redis中将判断条件缓存到redis中，如果判断成功直接操作redis中的数据，然后将数据写入redis，如果成功返回一个值。然后根据这个值判断是否成功，如果成功把用户id，优惠卷id，订单id存…...

编程日记 2025/7/31 16:12:45

React的API✅

createContext createContext要和useContext配合使用，可以理解为 “React自带的redux或mobx” ，事实上redux就是用context来实现的。但是一番操作下来我还是感觉，简单的context对视图的更新的细粒度把控比不上mobx，除非配合memo等…...

编程日记 2025/8/1 1:33:17

2024亚太杯数学建模C题【Development Analyses and Strategies for Pet Industry 】思路详解

C：宠物行业及相关产业的发展分析与战略随着人们消费观念的发展，宠物行业作为一个新兴产业，正在全球范围内逐渐积聚势头，这得益于快速的经济发展和人均收入的提高。1992年，中国小动物保护协会成立，随后1993…...

编程日记 2025/8/2 18:28:18

使用Notepad++工具去除重复行

使用Notepad工具去除重复行参考链接：https://blog.csdn.net/londa/article/details/108981396 一、使用正则表达式 1、对文本进行排序，让重复行排在一起 2、使用正则表达式替换（注意）^(.*?)$\s?^(?.*^\1$) 在替换时选择正…...

编程日记 2025/7/17 1:22:11

Three.js + AI：AI 算法生成 3D 萤火虫飞舞效果~

AI 驱动 3D 动画大家好，我是石小石！随着 Web 技术的发展，Three.js 成为构建 3D 图形和动画的主流工具。与此同时，人工智能（AI）在图像处理、动作生成等领域表现出强大能力。将 AI 与 Three.js 结合&#x…...

编程日记 2025/8/3 7:19:52

VScode clangd插件安装

前提在VScode中写C代码时，总会用到 C/C 这个插件，也就自然而然地使用了这个插件带来的代码跳转和代码提示功能。但是当代码变地很多时，就会变得非常慢。所以经过调查后弃用C/C 插件的这个功能，使用 clangd 这个插件来提示C代码和…...

编程日记 2025/7/30 15:26:22

Swift从0开始学习对象和类 day3

类（Class） 是一种类型或模板，描述了对象的特征和行为。对象（Object） 是类的实例，实际的实体，拥有自己的数据。新入门的教学都喜欢用“人”来举例为类，在这里我也用“人”吧 //&…...

编程日记 2025/7/29 13:49:55

Linux——从命令行配置网络

1.使用nmcli添加静态网络连接 nmcli con add con-name static-addr \ ifname eth0 type ethernet ipv4.method manual ipv4.dns 172.25.250.220 \ ipv4.addresses 172.25.250.10/24 ipv4.gateway 172.25.250.254 命令概述这是一条使用 nmcli（NetworkManager 命令…...

编程日记 2025/8/3 5:33:39

九、线性回归

1、概念

2、损失函数

3、最小二乘法MSE

3.1、原理

3.2、API

4、梯度下降

4.1、原理：

4.2、代码实现

5、梯度下降方法

5.1、批量梯度下降 BGD

5.2、随机梯度下降 SGD

5.3、小批量梯度下降 MBGD

6、拟合

7、正则化

8、岭回归 Ridge

9、拉索回归 Lasso

十、逻辑回归

1、原理

2、API

相关文章：