二分查找题目:寻找峰值 II
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法
- 思路和算法
- 证明
- 代码
- 复杂度分析
题目
标题和出处
标题:寻找峰值 II
出处:1901. 寻找峰值 II
难度
7 级
题目描述
要求
一个二维网格中的峰值元素是指其值严格大于相邻值(左、右、上、下)的元素。
给定一个 m × n \texttt{m} \times \texttt{n} m×n 的矩阵 mat \texttt{mat} mat,其中任意两个相邻元素均不相等,找出任意一个峰值元素 mat[i][j] \texttt{mat[i][j]} mat[i][j] 并返回其位置 [i,j] \texttt{[i,j]} [i,j]。
可以假设整个矩阵周边环绕着一圈元素 -1 \texttt{-1} -1。
要求时间复杂度是 O(m log n) \texttt{O(m log n)} O(m log n) 或 O(n log m) \texttt{O(n log m)} O(n log m)。
示例
示例 1:
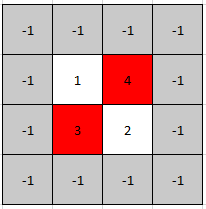
输入: mat = [[1,4],[3,2]] \texttt{mat = [[1,4],[3,2]]} mat = [[1,4],[3,2]]
输出: [0,1] \texttt{[0,1]} [0,1]
解释: 3 \texttt{3} 3 和 4 \texttt{4} 4 都是顶峰元素,所以 [1,0] \texttt{[1,0]} [1,0] 和 [0,1] \texttt{[0,1]} [0,1] 都是正确答案。
示例 2:

输入: mat = [[10,20,15],[21,30,14],[7,16,32]] \texttt{mat = [[10,20,15],[21,30,14],[7,16,32]]} mat = [[10,20,15],[21,30,14],[7,16,32]]
输出: [1,1] \texttt{[1,1]} [1,1]
解释: 30 \texttt{30} 30 和 32 \texttt{32} 32 都是顶峰元素,所以 [1,1] \texttt{[1,1]} [1,1] 和 [2,2] \texttt{[2,2]} [2,2] 都是正确答案。
数据范围
- m = mat.length \texttt{m} = \texttt{mat.length} m=mat.length
- n = mat[i].length \texttt{n} = \texttt{mat[i].length} n=mat[i].length
- 1 ≤ m, n ≤ 500 \texttt{1} \le \texttt{m, n} \le \texttt{500} 1≤m, n≤500
- 1 ≤ mat[i][j] ≤ 10 5 \texttt{1} \le \texttt{mat[i][j]} \le \texttt{10}^\texttt{5} 1≤mat[i][j]≤105
- 任意两个相邻元素均不相等
解法
思路和算法
这道题是「寻找峰值」的进阶,要求在矩阵中寻找峰值。
对于 m m m 行 n n n 列的矩阵,题目要求寻找峰值的时间复杂度是 O ( m log n ) O(m \log n) O(mlogn) 或 O ( n log m ) O(n \log m) O(nlogm),因此需要使用二分查找的做法寻找峰值。考虑矩阵每一行的最大值,其中一定存在一个最大值是峰值。在矩阵的行下标范围中执行二分查找,二分查找的次数是 O ( log m ) O(\log m) O(logm),对于矩阵的每一行可以在 O ( n ) O(n) O(n) 的时间内找到该行的最大值所在列,即每次二分查找需要 O ( n ) O(n) O(n) 的时间,总时间复杂度是 O ( n log m ) O(n \log m) O(nlogm)。
考虑矩阵 mat \textit{mat} mat 中的两个相邻行下标 i i i 和 j j j,其中 0 ≤ i , j < m 0 \le i, j < m 0≤i,j<m 且 j − i = 1 j - i = 1 j−i=1,用 c c c 表示 mat [ i ] \textit{mat}[i] mat[i] 中的最大值所在列下标。由于 mat [ i ] [ c ] ≠ mat [ j ] [ c ] \textit{mat}[i][c] \ne \textit{mat}[j][c] mat[i][c]=mat[j][c],因此 mat [ i ] [ c ] \textit{mat}[i][c] mat[i][c] 和 mat [ j ] [ c ] \textit{mat}[j][c] mat[j][c] 的大小关系是 mat [ i ] [ c ] > mat [ j ] [ c ] \textit{mat}[i][c] > \textit{mat}[j][c] mat[i][c]>mat[j][c] 或 mat [ i ] [ c ] < mat [ j ] [ c ] \textit{mat}[i][c] < \textit{mat}[j][c] mat[i][c]<mat[j][c]。
当 mat [ i ] [ c ] > mat [ j ] [ c ] \textit{mat}[i][c] > \textit{mat}[j][c] mat[i][c]>mat[j][c] 时,行下标范围 [ 0 , i ] [0, i] [0,i] 中一定存在峰值;当 mat [ i ] [ c ] < mat [ j ] [ c ] \textit{mat}[i][c] < \textit{mat}[j][c] mat[i][c]<mat[j][c] 时,行下标范围 [ j , m − 1 ] [j, m - 1] [j,m−1] 中一定存在峰值。因此可以根据 mat [ i ] [ c ] \textit{mat}[i][c] mat[i][c] 和 mat [ j ] [ c ] \textit{mat}[j][c] mat[j][c] 的大小关系判断可能存在峰值的行下标范围,并在更小的范围内查找峰值。
基于上述思路,可以使用二分查找的做法寻找峰值。
用 low \textit{low} low 和 high \textit{high} high 分别表示二分查找的行下标范围的下界和上界,初始时 low \textit{low} low 和 high \textit{high} high 分别为数组的最小行下标和最大行下标。每次查找时,取 mid \textit{mid} mid 为 low \textit{low} low 和 high \textit{high} high 的平均数向下取整,将 mat [ mid ] \textit{mat}[\textit{mid}] mat[mid] 中的最大值所在列下标记为 maxIndex \textit{maxIndex} maxIndex,比较 mat [ mid ] [ maxIndex ] \textit{mat}[\textit{mid}][\textit{maxIndex}] mat[mid][maxIndex] 和 mat [ mid + 1 ] [ maxIndex ] \textit{mat}[\textit{mid} + 1][\textit{maxIndex}] mat[mid+1][maxIndex] 的大小关系(注意当 low < high \textit{low} < \textit{high} low<high 时, mid ≤ m − 2 \textit{mid} \le m - 2 mid≤m−2,因此行下标 mid + 1 \textit{mid} + 1 mid+1 不会超出矩阵行下标范围),判断可能存在峰值的下标范围,调整查找的下标范围。
-
如果 mat [ mid ] [ maxIndex ] > mat [ mid + 1 ] [ maxIndex ] \textit{mat}[\textit{mid}][\textit{maxIndex}] > \textit{mat}[\textit{mid} + 1][\textit{maxIndex}] mat[mid][maxIndex]>mat[mid+1][maxIndex],则行下标范围 [ low , mid ] [\textit{low}, \textit{mid}] [low,mid] 中可能存在峰值,在该行下标范围中继续查找。
-
如果 mat [ mid ] [ maxIndex ] < mat [ mid + 1 ] [ maxIndex ] \textit{mat}[\textit{mid}][\textit{maxIndex}] < \textit{mat}[\textit{mid} + 1][\textit{maxIndex}] mat[mid][maxIndex]<mat[mid+1][maxIndex],则行下标范围 [ mid + 1 , high ] [\textit{mid} + 1, \textit{high}] [mid+1,high] 中可能存在峰值,在该行下标范围中继续查找。
当 low = high \textit{low} = \textit{high} low=high 时,查找结束,此时 mat [ low ] \textit{mat}[\textit{low}] mat[low] 的最大值即为峰值,找到峰值并返回其位置。
证明
为了证明上述二分查找做法的正确性,对于 0 ≤ i , j < m 0 \le i, j < m 0≤i,j<m 且 j − i = 1 j - i = 1 j−i=1, mat [ i ] [ c ] \textit{mat}[i][c] mat[i][c] 是 mat [ i ] \textit{mat}[i] mat[i] 的最大值,需要证明:当 mat [ i ] [ c ] > mat [ j ] [ c ] \textit{mat}[i][c] > \textit{mat}[j][c] mat[i][c]>mat[j][c] 时,行下标范围 [ 0 , i ] [0, i] [0,i] 中一定存在峰值;当 mat [ i ] [ c ] < mat [ j ] [ c ] \textit{mat}[i][c] < \textit{mat}[j][c] mat[i][c]<mat[j][c] 时,行下标范围 [ j , m − 1 ] [j, m - 1] [j,m−1] 中一定存在峰值。可以使用反证法证明。
当 mat [ i ] [ c ] > mat [ j ] [ c ] \textit{mat}[i][c] > \textit{mat}[j][c] mat[i][c]>mat[j][c] 时,假设行下标范围 [ 0 , i ] [0, i] [0,i] 中不存在峰值。由于 mat [ i ] [ c ] \textit{mat}[i][c] mat[i][c] 不是峰值,因此 mat [ i ] [ c ] < mat [ i − 1 ] [ c ] \textit{mat}[i][c] < \textit{mat}[i - 1][c] mat[i][c]<mat[i−1][c], mat [ i − 1 ] \textit{mat}[i - 1] mat[i−1] 的最大值一定大于 mat [ i ] \textit{mat}[i] mat[i] 的最大值。从行下标 i − 1 i - 1 i−1 向上遍历矩阵 mat \textit{mat} mat,对于每个行下标 k k k, mat [ k ] \textit{mat}[k] mat[k] 的最大值都不是峰值,因此每一行的最大值都小于上一行同列的元素,每一行的最大值都小于上一行的最大值。遍历到 mat [ 0 ] \textit{mat}[0] mat[0] 时, mat [ 0 ] \textit{mat}[0] mat[0] 的最大值严格大于其左边、右边和下边的相邻元素。由于矩阵中的元素都是正整数且矩阵周围的元素都是 − 1 -1 −1,因此 mat [ 0 ] \textit{mat}[0] mat[0] 的最大值严格大于其所有的相邻元素, mat [ 0 ] \textit{mat}[0] mat[0] 的最大值即为峰值。由此可以得到行下标范围 [ 0 , i ] [0, i] [0,i] 中一定存在峰值。
当 mat [ i ] [ c ] < mat [ j ] [ c ] \textit{mat}[i][c] < \textit{mat}[j][c] mat[i][c]<mat[j][c] 时,同理可知行下标范围 [ j , m − 1 ] [j, m - 1] [j,m−1] 中一定存在峰值。
代码
class Solution {public int[] findPeakGrid(int[][] mat) {int m = mat.length;int low = 0, high = m - 1, maxIndex = 0;while (low < high) {int mid = low + (high - low) / 2;maxIndex = getMaxIndex(mat[mid]);if (mat[mid][maxIndex] > mat[mid + 1][maxIndex]) {high = mid;} else {low = mid + 1;}}maxIndex = getMaxIndex(mat[low]);return new int[]{low, maxIndex};}public int getMaxIndex(int[] row) {int index = 0, maxNum = 0;int n = row.length;for (int i = 0; i < n; i++) {if (row[i] > maxNum) {maxNum = row[i];index = i;}}return index;}
}
复杂度分析
-
时间复杂度: O ( n log m ) O(n \log m) O(nlogm),其中 m m m 和 n n n 分别是数组 mat \textit{mat} mat 的行数和列数。二分查找的次数是 O ( log m ) O(\log m) O(logm),每次二分查找需要 O ( n ) O(n) O(n) 的时间,时间复杂度是 O ( n log m ) O(n \log m) O(nlogm)。
-
空间复杂度: O ( 1 ) O(1) O(1)。
相关文章:

二分查找题目:寻找峰值 II
文章目录 题目标题和出处难度题目描述要求示例数据范围 解法思路和算法证明代码复杂度分析 题目 标题和出处 标题:寻找峰值 II 出处:1901. 寻找峰值 II 难度 7 级 题目描述 要求 一个二维网格中的峰值元素是指其值严格大于相邻值(左、…...

调和级数不为整数的证明
文章目录 1. 问题引入2. 证明2.1 引理12.2 引理22.3 引理3:2.4 核心证明: 3. 参考 1. 问题引入 s ( n ) 1 1 2 1 3 ⋯ 1 n , n ∈ N ∗ , n ≥ 2 s(n) 1\frac{1}{2}\frac{1}{3}\cdots\frac{1}{n}, \quad \\n \in N^*, n \ge2 s(n)12131⋯n1,…...

Redis 源码分析-内部数据结构 dict
Redis 源码分析-内部数据结构 dict 在上一篇 Redis 数据库源码分析 提到了 Redis 其实用了全局的 hash 表来存储所有的键值对,即下方图示的 dict,dict 中有两个数组,其中 ht[1] 只在 rehash 时候才真正用到,平时都是指向 null&am…...

git相关操作笔记
git相关操作笔记 1. git init git init 是一个 Git 命令,用于初始化一个新的 Git 仓库。执行该命令后,Git 会在当前目录创建一个 .git 子目录,这是 Git 用来存储所有版本控制信息的地方。 使用方法如下: (1ÿ…...

STM32小实验2
定时器实验 TIM介绍 TIM(Timer)定时器 定时器可以对输入的时钟进行计数,并在计数值达到设定值时触发中断 16位计数器、预分频器、自动重装寄存器的时基单元,在72MHz计数时钟下可以实现最大59.65s的定时 不仅具备基本的定时中断…...
配置详解(2):备库安装 Oracle 软件)
Oracle Dataguard(主库为双节点集群)配置详解(2):备库安装 Oracle 软件
Oracle Dataguard(主库为双节点集群)配置详解(2):备库安装 Oracle 软件 目录 Oracle Dataguard(主库为双节点集群)配置详解(2):备库安装 Oracle 软件一、Orac…...

基于 Pod 和 Service 注解的服务发现
基于 Pod 和 Service 注解的服务发现 背景 很多应用会为 Pod 或 Service 打上一些注解用于 Prometheus 的服务发现,如 prometheus.io/scrape: "true",这种注解并不是 Prometheus 官方支持的,而是社区的习惯性用法,要使…...

操作系统之文件的逻辑结构
目录 无结构文件(流式文件) 有结构文件(记录式文件) 分类: 顺序文件 特点: 存储方式: 逻辑结构: 优缺点: 索引文件 目的: 结构: 特点…...

网络分析与监控:阿里云拨测方案解密
作者:俞嵩(榆松) 随着互联网的蓬勃发展,网络和服务的稳定性已成为社会秩序中不可或缺的一部分。一旦网络和服务发生故障,其带来的后果将波及整个社会、企业和民众的生活质量,造成难以估量的损失。 2020 年 12 月: Ak…...

vue实现虚拟列表滚动
<template> <div class"cont"> //box 视图区域Y轴滚动 滚动的是box盒子 滚动条显示的也是因为box<div class"box">//itemBox。 一个空白的盒子 计算高度为所有数据的高度 固定每一条数据高度为50px<div class"itemBox" :st…...

服务器/电脑与代码仓gitlab/github免密连接
git config --global user.name "xxxx" git config --global user.email "xxxxxx163.com" #使用注册GitHub的邮箱 生成对应邮箱的密码对 ssh-keygen -t rsa -b 4096 -C "xxxxxx163.com" 把公钥id_rsa.pub拷贝到github中 Setting----->…...

用户界面软件03
一种标准的满足不同的非功能性需求的技术是对子系统进行不同的考虑……但是一个用户 界面要求有大量的域层面的信息,以符合比较高的人机工程标准,所以,这些分开的子系统还是 紧密地耦合在一起的。 一个软件架构师的标准反应是将不同的非功能…...

年会抽奖Html
在这里插入图片描述 <!-- <video id"backgroundMusic" src"file:///D:/background.mp3" loop autoplay></video> --> <divstyle"width: 290px; height: 580px; margin-left: 20px; margin-top: 20px; background: url(D:/nianhu…...
Ubuntu20.04版本的ROS环境配置与基本概述)
(一)Ubuntu20.04版本的ROS环境配置与基本概述
前言 ROS不需要在特定的环境下进行安装,不管你是Ubuntu的什么版本或者还是虚拟机都可以按照教程进行安装。 1.安装ROS 一键安装ros及ros2 wget http://fishros.com/install -O fishros && . fishros 按照指示安装你想要的ros。 ros和ros2是可以兼容的…...

深入分析线程安全问题的本质
深入分析线程安全问题的本质 1. 并发编程背后的性能博弈2. 什么是线程安全问题?3. 源头之一:原子性问题3.1. 原子性问题示例3.2. 原子性问题分析3.3. 如何解决原子性问题? 4. 源头之二:可见性问题4.1. 为什么会有可见性问题&#…...

58. Three.js案例-创建一个带有红蓝配置的半球光源的场景
58. Three.js案例-创建一个带有红蓝配置的半球光源的场景 实现效果 本案例展示了如何使用Three.js创建一个带有红蓝配置的半球光源的场景,并在其中添加一个旋转的球体。通过设置不同的光照参数,可以观察到球体表面材质的变化。 知识点 WebGLRenderer …...

插入实体自增主键太长,mybatis-plaus自增主键
1、问题 spring-boot整合mybtais执行insert语句时,主键id为长文本数据。 2、分析问题 1)数据库主键是否自增 2)数据库主键的种子值设置的多少 3、解决问题 1)数据库主键设置的时自增 3)种子值是1 所以排查是数据库的问题 4、继…...

【利用 Unity + Mirror 网络框架、Node.js 后端和 MySQL 数据库】
要实现一个简单的1v1战斗小游戏,利用 Unity Mirror 网络框架、Node.js 后端和 MySQL 数据库,我们可以将其分为几个主要部分:客户端(Unity)、服务器(Node.js)和数据库(MySQL…...

https原理
一、基本概念 1、https概念 https(全称: Hypertext Transfer Protocol Secure,超文本传输安全协议),是以安全为目标的http通道,简单讲是http的安全版。 2、为啥说http协议不安全呢? 我们用h…...

如何处理京东商品详情接口返回的JSON数据中的缺失值?
1.在 Python 中处理缺失值 使用if - else语句进行检查和处理 假设通过requests库获取了接口返回的 JSON 数据,并使用json模块进行解析,存储在data变量中。 import json import requestsurl "YOUR_API_URL" response requests.get(url) dat…...

window对象
bom dom部分学完了,来看看bom吧~ bom是整个浏览器,本质上bom与dom是包含的关系,window是里面最大的对象 调用的方法默认对象是window,一般都会省略前面的window 创建的全局变量也是属于window的,当然window也可以省…...
ROS通信编程——参数服务器)
(五)ROS通信编程——参数服务器
前言 参数服务器在ROS中主要用于实现不同节点之间的数据共享(P2P)。参数服务器相当于是独立于所有节点的一个公共容器,可以将数据存储在该容器中,被不同的节点调用,当然不同的节点也可以往其中存储数据,关…...
)
MySQL常用命令之汇总(Summary of Commonly Used Commands in MySQL)
MySQL常用命令汇总 简介 MySQL是一个广泛使用的开源关系型数据库管理系统,由瑞典的MySQL AB公司开发,现属于Oracle公司。 MySQL支持SQL(结构化查询语言),这是数据库操作的标准语言,用户可以使用SQL进…...
)
更新至2023年,各省数字经济变量/各省数字经济相关指标数据集(20个指标)
更新至2023年,各省数字经济相关指标数据集(20个指标) 1、时间:更新至2023年,具体时间如下 2、指标:互联网宽带接入端口(万个)(2006-2023)、互联网宽带接入用户(万户)(2…...
——HDBSCAN算法详解)
聚类系列 (二)——HDBSCAN算法详解
在进行组会汇报的时候,为了引出本研究动机(论文尚未发表,暂不介绍),需要对DBSCAN、OPTICS、和HDBSCAN算法等进行详细介绍。在查询相关资料的时候,发现网络上对于DBSCAN算法的介绍非常多与细致,但…...
)
【JavaEE】—— SpringBoot项目集成百度千帆AI大模型(对话Chat V2)
本篇文章在SpringBoot项目中集成百度千帆提供的大模型接口实现Chat问答效果: 一、百度智能云 百度千帆大模型平台是百度智能云推出的一个企业级一站式大模型与AI原生应用开发及服务平台。 注册地址:https://qianfan.cloud.baidu.com/ 注册成功后&…...

一种更激进的Hook实现方案猜想
XXX原创不原创不清楚,暂定为原创。毕竟windows 大神很多XXX 昨天才发现不是原创,这种方案是VEH HOOK的一种实现方案。VEH HOOK很久很久以前都被广泛使用了。只是自己没听说过。好悲哀呀。。。。 激进的猜想: 如果VEH HOOK在内核态处理异常…...

HTML5实现好看的端午节网页源码
HTML5实现好看的端午节网页源码 前言一、设计来源1.1 网站首页界面1.2 登录注册界面1.3 端午节由来界面1.4 端午节习俗界面1.5 端午节文化界面1.6 端午节美食界面1.7 端午节故事界面1.8 端午节民谣界面1.9 联系我们界面 二、效果和源码2.1 动态效果2.2 源代码 源码下载结束语 H…...
)
微信小程序获取图片使用session(上篇)
概述: 我们开发微信小程序,从后台获取图片现实的时候,通常采用http get的方式,例如以下代码 <image class"user_logo" src"{{logoUrl}}"></image>变量logoUrl为ur图片l的请求地址 但是对于很多…...

RT-DETR融合YOLOv9的下采样模块ADown
RT-DETR使用教程: RT-DETR使用教程 RT-DETR改进汇总贴:RT-DETR更新汇总贴 《YOLOv9: Learning What You Want to Learn Using Programmable Gradient Information》 一、 模块介绍 论文链接:https://arxiv.org/abs/2402.13616 代码链接&…...

【机器学习案列】学生抑郁可视化及预测分析
🧑 博主简介:曾任某智慧城市类企业算法总监,目前在美国市场的物流公司从事高级算法工程师一职,深耕人工智能领域,精通python数据挖掘、可视化、机器学习等,发表过AI相关的专利并多次在AI类比赛中获奖。CSDN…...

CES 2025|美格智能高算力AI模组助力“通天晓”人形机器人震撼发布
当地时间1月7日,2025年国际消费电子展(CES 2025)在美国拉斯维加斯正式开幕。美格智能合作伙伴阿加犀联合高通在展会上面向全球重磅发布人形机器人原型机——通天晓(Ultra Magnus)。该人形机器人内置美格智能基于高通QC…...

Linux第一个系统程序---进度条
进度条---命令行版本 回车换行 其实本质上回车和换行是不同概念,我们用一张图来简单的理解一下: 在计算机语言当中: 换行符:\n 回车符:\r \r\n:回车换行 这时候有人可能会有疑问:我在学习C…...

黑马跟学.苍穹外卖.Day04
黑马跟学.苍穹外卖.Day04 苍穹外卖-day04课程内容1. Redis入门1.1 Redis简介1.2 Redis下载与安装1.2.1 Redis下载1.2.2 Redis安装 1.3 Redis服务启动与停止1.3.1 服务启动命令1.3.2 客户端连接命令1.3.3 修改Redis配置文件1.3.4 Redis客户端图形工具 2. Redis数据类型2.1 五种常…...

人生第一次面试之依托答辩
今天收到人生的第一场面试,是东华软件集团。答的那是依托答辩,就面了20分钟,还没考算法。其实依托答辩的效果是意料之中的,这次面试也只是想练练手。 目录 静态变量什么时候加载的? 重写和重载有什么区别࿱…...

STM32 : PWM 基本结构
这张图展示了PWM(脉冲宽度调制)的基本结构和工作流程。PWM是一种用于控制功率转换器输出电压的技术,通过调整信号的占空比来实现对负载的精确控制。以下是详细讲解: PWM 基本结构 1. 时基单元 ARR (Auto-reload register): 自动…...
面试全解】深度解析 Layer Normalization 的原理、变体及实际应用)
【大模型(LLM)面试全解】深度解析 Layer Normalization 的原理、变体及实际应用
系列文章目录 大模型(LLMs)基础面 01-大模型(LLM)面试全解:主流架构、训练目标、涌现能力全面解析 02-【大模型(LLM)面试全解】深度解析 Layer Normalization 的原理、变体及实际应用 大模型&…...

《浮岛风云》V1.0中文学习版
《浮岛风云》中文版https://pan.xunlei.com/s/VODadt0vSGdbrVOBEsW9Xx8iA1?pwdy7c3# 一款有着类似暗黑破坏神的战斗系统、类似最终幻想的奇幻世界和100%可破坏体素环境的动作冒险RPG。...

学习threejs,导入babylon格式的模型
👨⚕️ 主页: gis分享者 👨⚕️ 感谢各位大佬 点赞👍 收藏⭐ 留言📝 加关注✅! 👨⚕️ 收录于专栏:threejs gis工程师 文章目录 一、🍀前言1.1 ☘️THREE.BabylonLoader babyl…...

Django 社团管理系统的设计与实现
标题:Django 社团管理系统的设计与实现 内容:1.摘要 本文介绍了 Django 社团管理系统的设计与实现。通过分析社团管理的需求,设计了系统的架构和功能模块,并使用 Django 框架进行了实现。系统包括社团信息管理、成员管理、活动管理、财务管理等功能&…...

2025 GitCode 开发者冬日嘉年华:AI 与开源的深度交融之旅
在科技的浪潮中,AI 技术与开源探索的火花不断碰撞,催生出无限可能。2025 年 1 月 4 日,由 GitCode 联合 CSDN COC 城市开发者社区精心打造的开年首场开发者活动:冬日嘉年华在北京中关村 • 鼎好 DH3-A 座 22 层盛大举行࿰…...

嵌入式系统 tensorflow
🎬 秋野酱:《个人主页》 🔥 个人专栏:《Java专栏》《Python专栏》 ⛺️心若有所向往,何惧道阻且长 文章目录 探索嵌入式系统中的 TensorFlow:机遇与挑战一、TensorFlow 适配嵌入式的优势二、面临的硬件瓶颈三、软件优化策略四、实…...

Web无障碍
文章目录 🟢Web Accessibility-Web无障碍🟢一、Web Accessibility-Web1. web无障碍设计2. demo3.使用相关相关开源无障碍工具条(调用可能会根据网络有点慢) 如有其他更好方案,可以私信我哦✒️总结 🟢Web Accessibility-Web无障碍…...
----2.配置MySQL驱动)
Qt使用MySQL数据库(Win)----2.配置MySQL驱动
使用Everything软件,找到mysql.pro文件。并使用qt creator打开mysql.pro。 导入外部库 选择外部库 点击下一步,勾选。 为debug版本添加‘d’作为后缀取消勾选,然后点击下一步 添加后的Pro文件。 这样文件应该是改好了,选择releas…...

记录一下vue2项目优化,虚拟列表vue-virtual-scroll-list处理10万条数据
文章目录 封装BrandPickerVirtual.vue组件页面使用组件属性 select下拉接口一次性返回10万条数据,页面卡死,如何优化??这里使用 分页 虚拟列表(vue-virtual-scroll-list),去模拟一个下拉的内容…...

java 中 main 方法使用 KafkaConsumer 拉取 kafka 消息如何禁止输出 debug 日志
pom 依赖: <dependency><groupId>org.springframework.kafka</groupId><artifactId>spring-kafka</artifactId><version>2.5.14.RELEASE</version> </dependency> 或者 <dependency><groupId>org.ap…...

前端性能优化全攻略:加速网页加载,提升用户体验
前端性能优化全攻略:加速网页加载,提升用户体验 在当今互联网时代,用户对于网页的加载速度和性能要求越来越高。一个快速响应、流畅加载的网页能够极大地提升用户体验,增加用户留存率和满意度。前端性能优化是实现这一目标的关键…...

关于内网外网,ABC类地址,子网掩码划分
本文的三个关键字是:内网外网,ABC类地址,子网掩码划分。围绕以下问题展开: 如何从ip区分外网、内网?win和linux系统中,如何查询自己的内网ip和外网ip。开发视角看内外网更多是处于安全考虑,接口…...

【C++多线程编程:六种锁】
目录 普通互斥锁: 轻量级锁 独占锁: std::lock_guard: std::unique_lock: 共享锁: 超时的互斥锁 递归锁 普通互斥锁: std::mutex确保任意时刻只有一个线程可以访问共享资源,在多线程中常用于保…...
附源码 容器 子数组 数组 连续序列 三数之和(C++))
【LeetCode】力扣刷题热题100道(16-20题)附源码 容器 子数组 数组 连续序列 三数之和(C++)
目录 1.盛最多水的容器 2.和为K的子数组 3.最大子数组和 4.最长连续序列 5.三数之和 1.盛最多水的容器 给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴…...
