当前位置：首页 > news >正文

matplotlib知识

news 来源：原创 2025/7/20 18:09:24

问题与解决

1.module 'backend_interagg' has no attribute 'FigureCanvas'问题

Matplotlib 后端不兼容:

matplotlib 使用的后端（如 backend_interagg）可能与当前环境不匹配或未正确加载。

在代码中显式设置一个兼容的后端，例如 TkAgg、Qt5Agg 等

import matplotlib
matplotlib.use('TkAgg')  # 或 'Qt5Agg'
import matplotlib.pyplot as plt

功能介绍

知识点

一、基础用法

1.基础线性图

import matplotlib.pyplot as plt
import numpy as np
import matplotlib
matplotlib.use('TkAgg')x = np.linspace(-1,1,50) #在[-1，1]之间等距离取50个点，得到一个列表
y = 2*x+1 # 通过计算得到yplt.plot(x,y)# 绘制下x,y 的图片plt.show()# 显示图片

运行结果图

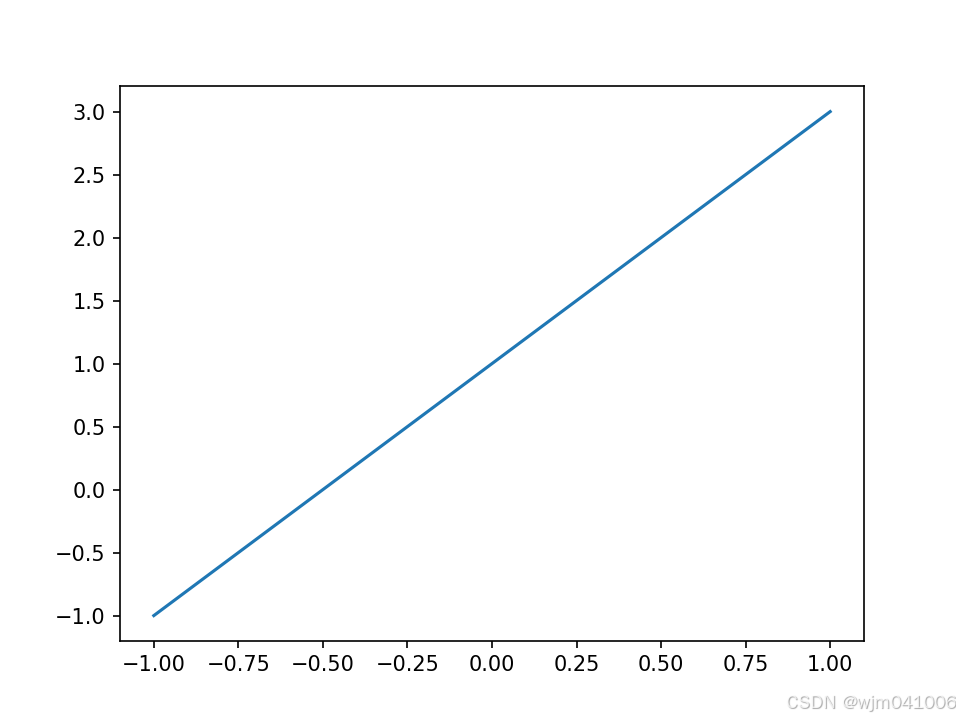
2.figure的使用

import matplotlib.pyplot as plt
import numpy as np
import matplotlib
matplotlib.use('TkAgg')# 每个fig代表一张画布x = np.linspace(-1,1,50) #在[-1，1]之间等距离取50个点，得到一个列表
y1 = 2*x+1 # 通过计算得到y
y2 = x**2plt.figure() #这个代表一个fig的开头，若想存在第二个fig，需要在下面另写，否则图片会存在一个fig中
plt.plot(x,y1)# 绘制下x,y 的图片plt.figure()
plt.plot(x,y2)plt.show()# 显示图片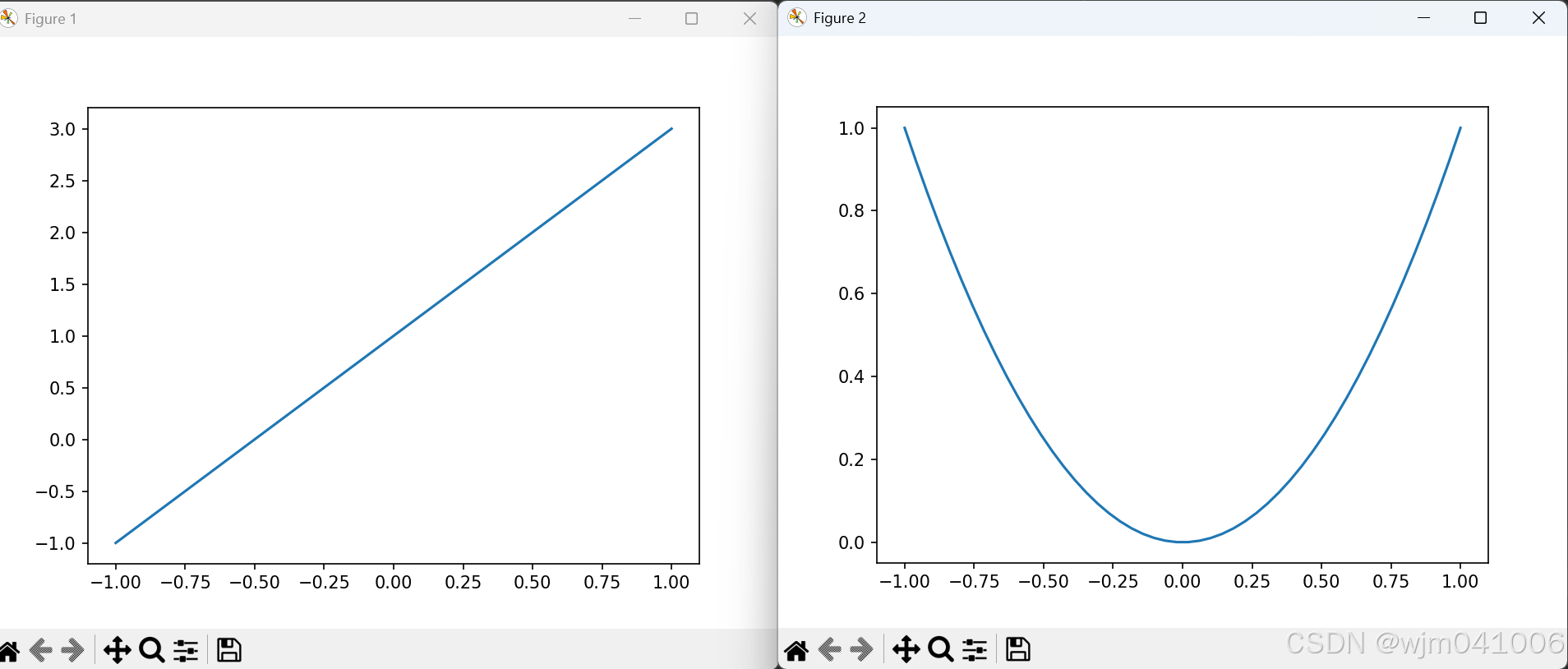

note：如果想对fig改数字，只需要使用plt.figure(num=数字)即可，还可以设置figsize，只需要plt.figure(figsize=(长，宽))

可以写在plt.plot()中的参数，颜色color，线的宽度linewidth，线的形式linestyle

3.坐标轴的设置

import matplotlib.pyplot as plt
import numpy as np
import matplotlib
matplotlib.use('TkAgg')# 每个fig代表一张画布x = np.linspace(-1,1,50) #在[-1，1]之间等距离取50个点，得到一个列表
y1 = 2*x+1 # 通过计算得到y
y2 = x**2plt.figure()
plt.plot(x,y1)
plt.plot(x,y2)
'''设置坐标轴'''
#设置x，y轴取值范围
plt.xlim((-1,5))
plt.ylim((-1,5))# 设置x，y轴标签
plt.xlabel('I am x')
plt.xlabel('I am y')# 修改x，y轴单位
new_ticks = np.linspace(-1,2,5) #将x轴的范围设置为-1到2等距离取五个数
plt.xticks(new_ticks)
#更换y的命名，一一对应
plt.yticks([-2,-1,0],['w','j','m'])plt.show()# 显示图片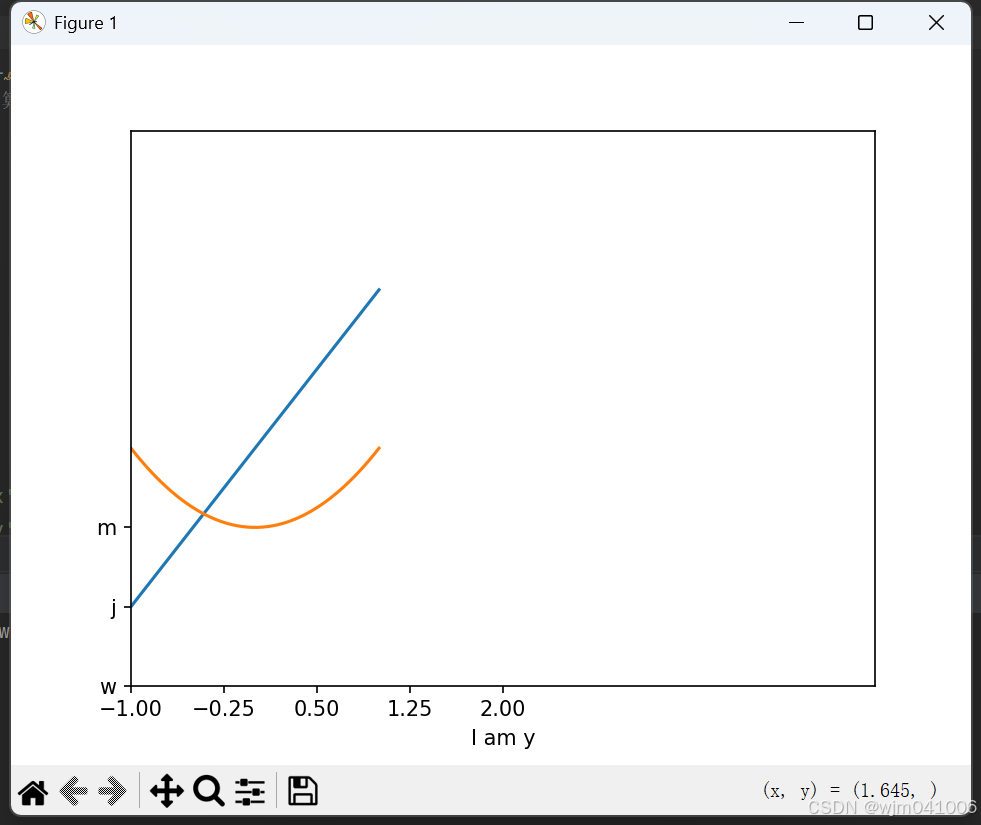

ax = plt.gca()# 拿出这张图
#使得上右的边框变为没有
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')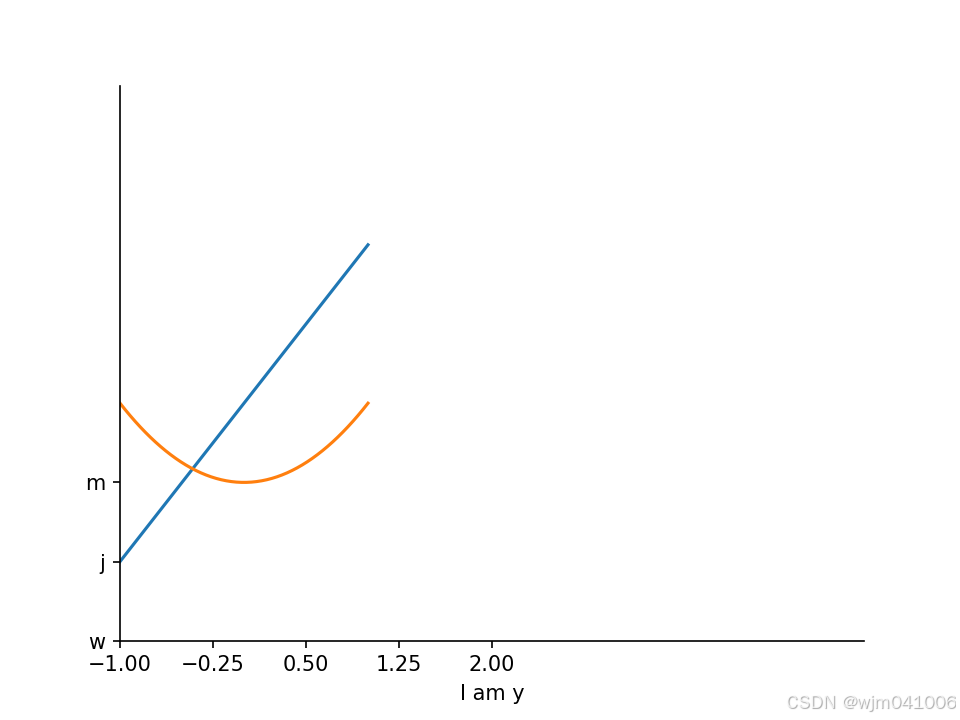

可以看到上面和下面的边框都消失了

#左侧代表y轴，下面的边框线代表x轴
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')#挪动位置,使底部的线绑定0的位置
ax.spines['bottom'].set_position(('data',0))
ax.spines['left'].set_position(('data',0))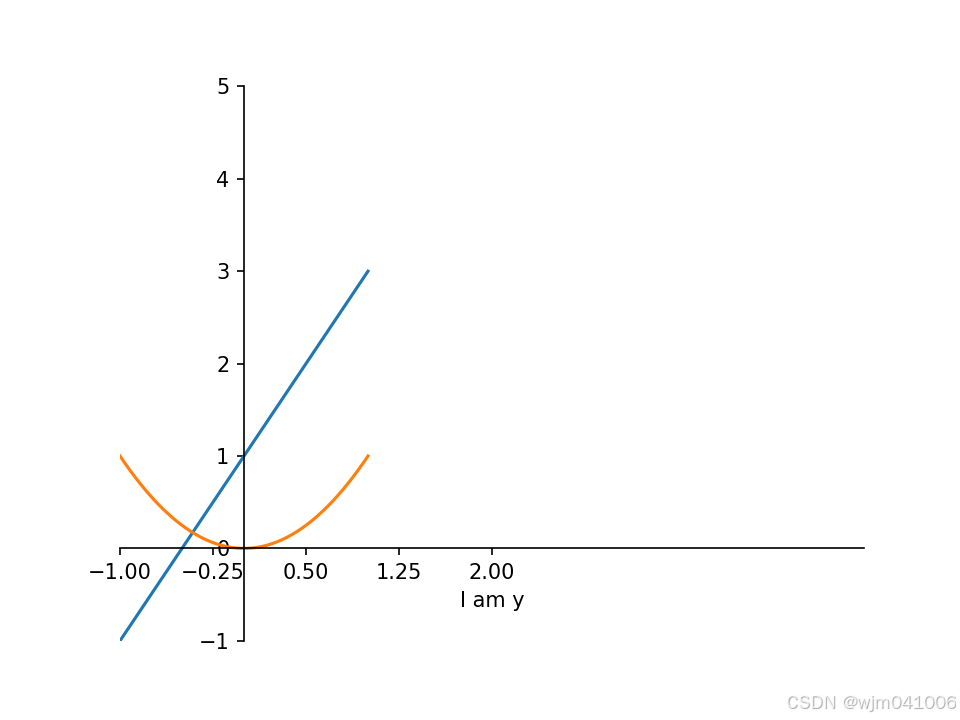

可以看到x,y绑定了对应位置

4.legend的设置

当你在plot中加上label这个参数的时候并且使用plt.legend(),就可以让你的图片出现标注

plt.plot(x,y1,label="two")
plt.plot(x,y2,label="first")
plt.legend()

而legend中也存在一些参数

handles=[]，传入的为plot的返回值，且要使用(命名,)的形式
labels=[] ，设置handles中的线的label，而不使用原来的label
loc位置，若你不想设置可以使用 'best'

5.添加注解

#添加点和线的标注
x0=1
y0=2*x0+1plt.scatter(x0,y0,s=50,color="red")
plt.plot([x0,x0],[y0,0],color="blue",linestyle="--",lw=2.5)

scatter将图形以散点形式表示

plot在两个点之间绘制直线，前面是横坐标，后面是纵坐标

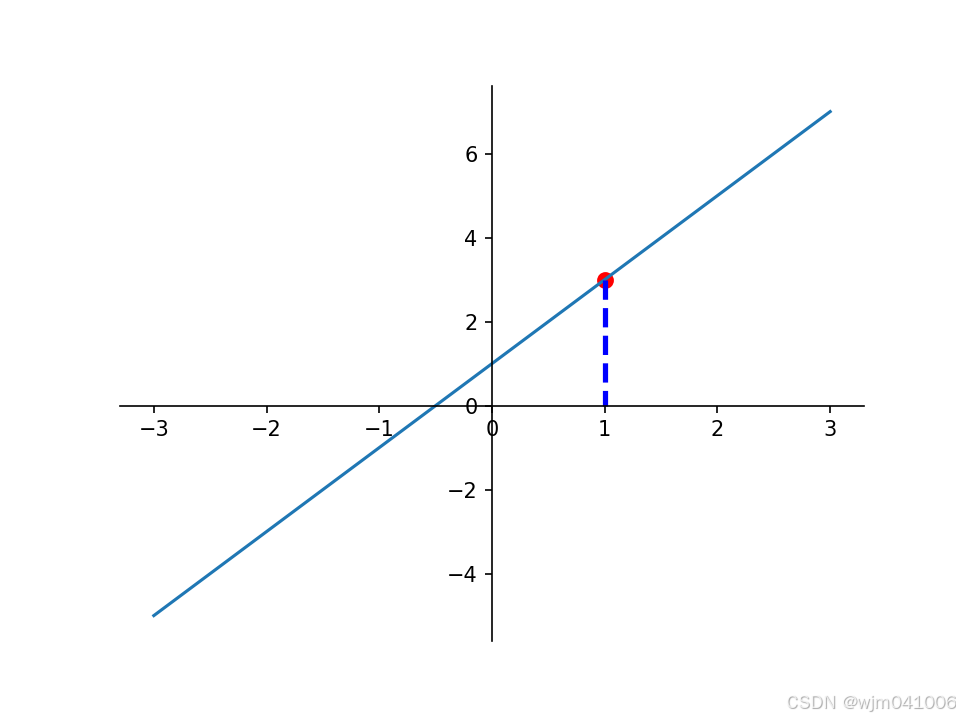
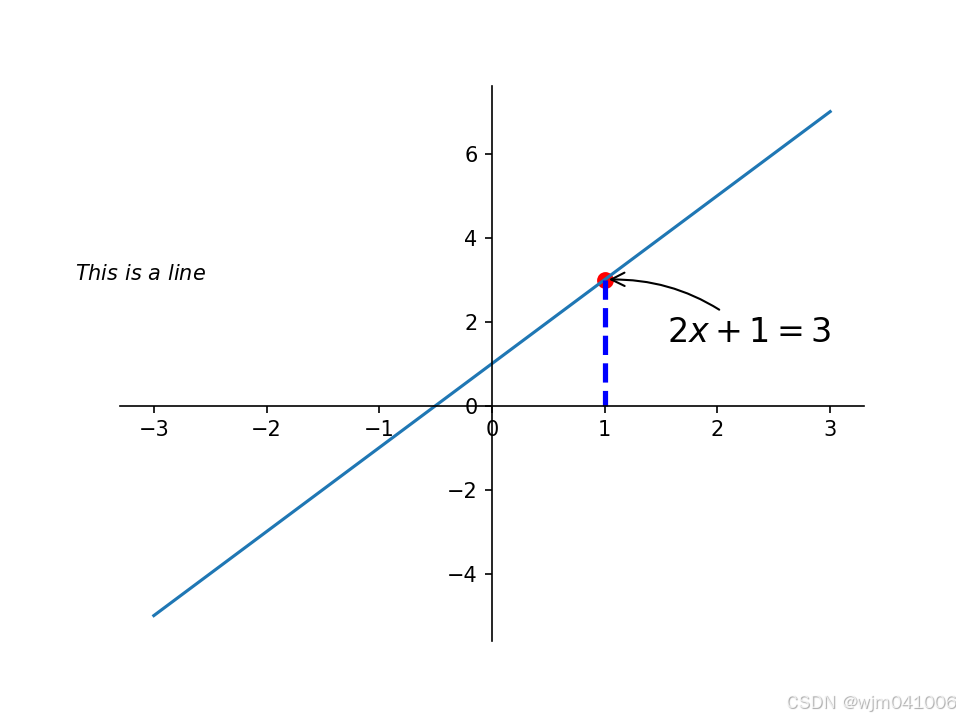
plt.annotate(r'$2x+1=%s$' % y0,xy=(x0,y0),xycoords="data",xytext=(+30,-30),textcoords='offset points',fontsize=16,arrowprops=dict(arrowstyle='->',connectionstyle='arc3,rad=.2'))

打印标注

第一个参数打印的内容，第二个参数为指向的坐标，第三个为基于该点，第四个为打印的内容和基于的点的距离，第五个是基于该店，与xytext对应，第六个是大小，第七个为形式，第八个为弧度角度。

plt.text(-3.7,3,r'$This\ is\ a\ line$')

打印文字，前面的两个参数为位置，后面为内容

5. tick设置标签样式

# facecolor代表的颜色是显示颜色，edgecolor表示边缘颜色，alpha表示不透明度
# 此代码设置所有的标签，首先从x，y轴取出标签
# label.set_fontsize(12)设置标签大小for label in ax.get_xticklabels() + ax.get_yticklabels():label.set_fontsize(12)label.set_bbox(dict(facecolor = 'r',edgecolor='b',alpha=0.3))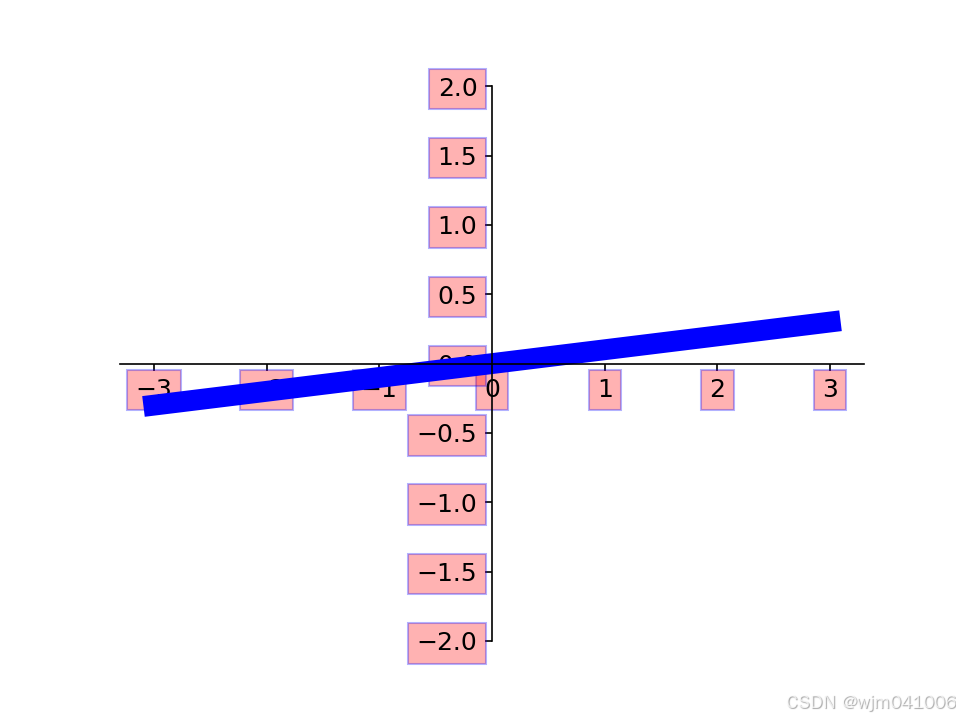

二、不同样式图像绘制

1.散点图

np.random.normal(0,1,n)平均值为0，方差为1，共随机生成n个数
plt.xticks(())把所有的标签设置为没有
plt.scatter(x,y,size=75,color=t,alpha=0.5)绘制散点图，输入为x,y，要求xy数目一致，分别对应作为点的x和y

import matplotlib.pyplot as plt
import numpy as np
import matplotlib
matplotlib.use('TkAgg')n=1024 #设置1024个数据
x=np.random.normal(0,1,n)
y=np.random.normal(0,1,n)
t = np.arctan2(y,x)plt.scatter(x,y,s=75,c=t,alpha=0.5)
plt.xlim((-1.5,1.5))
plt.ylim((-1.5,1.5))
plt.xticks(())
plt.yticks(())plt.show()# 显示图片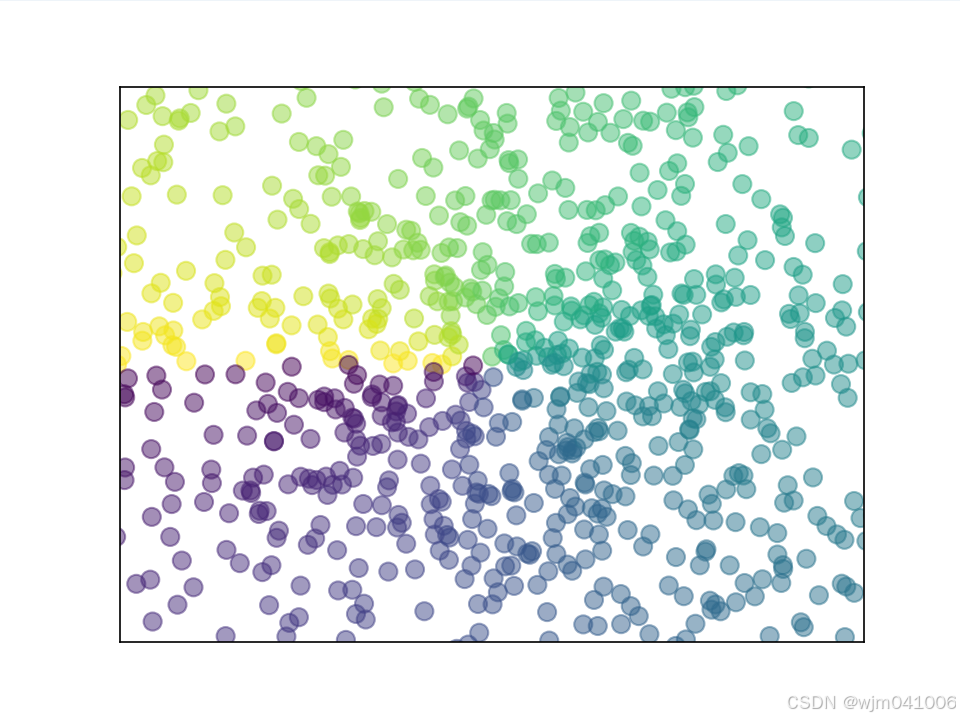

note：不要使用size和color去代表颜色和大小，matplotlib 中，scatter 函数的正确参数是 s 来设置点的大小，而不是 size，scatter 函数的正确参数是 c 来设置点的大小，而不是 color。

2.柱状图

np.random.uniform(0.5, 1.0, n)：这一部分生成了一个包含 n 个随机数的数组，随机数的范围是 [0.5, 1.0] 之间，符合均匀分布。比如可能的值为：

plt.text(x_val, y_val + 0.05, '%.2f' % y_val, ha='center', va='bottom')前面两个为文字显示位置，后面两个为对齐方式

import matplotlib.pyplot as plt
import numpy as np
import matplotlib
matplotlib.use('TkAgg')n=12
x=np.arange(n)#生成0-11的数字
y1= (1-x/float(n)) * np.random.uniform(0.5,1.0,n)
y2= (1-x/float(n)) * np.random.uniform(0.5,1.0,n)plt.bar(x,+y1,facecolor='#9999ff',edgecolor='white')
plt.bar(x,-y2,facecolor='#ff9999',edgecolor='white')# 添加文本标签
for x_val, y_val in zip(x, y1):plt.text(x_val, y_val + 0.05, '%.2f' % y_val, ha='center', va='bottom')for x_val, y_val in zip(x, y2):plt.text(x_val, -y_val - 0.05, '%.2f' % y_val, ha='center', va='top')plt.xlim((0.5,n))
plt.ylim((-1.5,1.5))
plt.xticks(())
plt.yticks(())plt.show()# 显示图片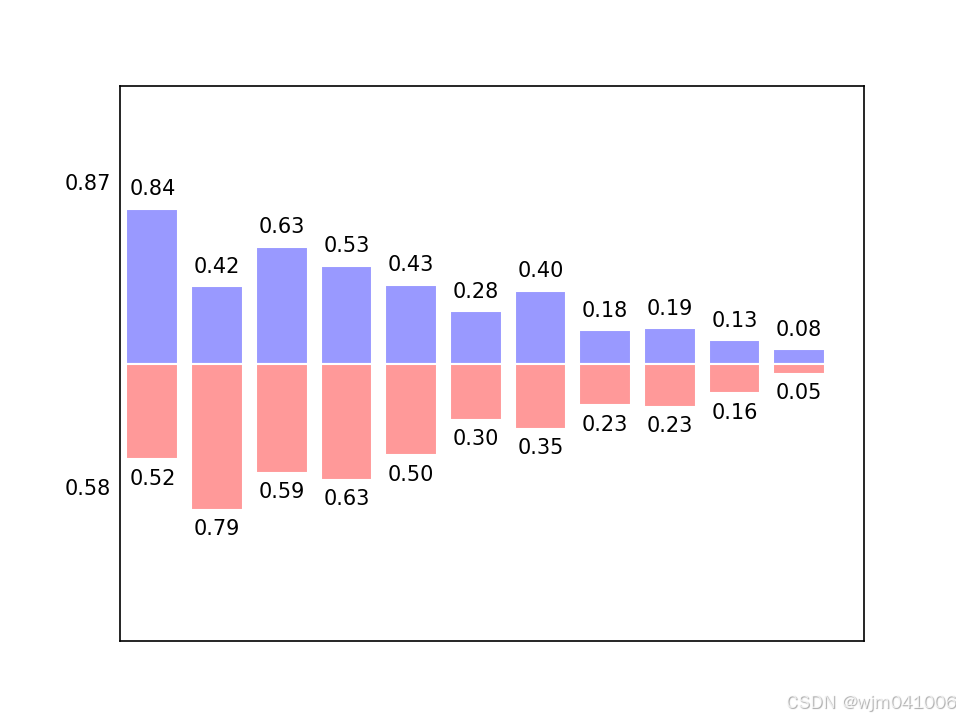

3.等高线图

x,y=np.meshgrid(x,y)

np.meshgrid 的作用：
假设你有两个一维数组（或范围），比如 x 和 y，你希望生成一个二维网格，每个网格点的坐标都是 (x, y)，然后你可以在这个网格上计算函数值。示例：
假设 x 和 y 分别是：
x = [1, 2, 3]
y = [4, 5]
1. np.meshgrid(x, y) 生成的网格：
调用 np.meshgrid(x, y) 后，会返回两个二维数组 X 和 Y，它们的形状将根据 x 和 y 的长度自动扩展。X 和 Y 将是二维数组，其中：X 是 x 的重复行，每行都是 x 数组的元素。
Y 是 y 的重复列，每列都是 y 数组的元素。
具体地，假设：
x = [1, 2, 3]
y = [4, 5]
调用 np.meshgrid(x, y) 后会生成以下两个二维数组：X, Y = np.meshgrid(x, y)
X：[[1, 2, 3],   # 第一行[1, 2, 3]]   # 第二行
Y：
[[4, 4, 4],   # 第一列[5, 5, 5]]   # 第二列

plt.contourf(x, y, z, 8, alpha=0.75, cmap=plt.cm.hot)绘制热图，plt.cm.hot表示热图颜色，主要作用为填充颜色

C = plt.contour(x, y, z, 8, colors='black', linewidths=0.5)绘制登高线，8代表等高线划分区域

plt.clabel(C, inline=False, fontsize=10)添加等高线标签

import matplotlib.pyplot as plt
import numpy as np
import matplotlib
matplotlib.use('TkAgg')# 定义函数 f(x, y)
def f(x, y):return (1 - x/2 + x**5 + y**3) * np.exp(-x**2 - y**2)# 网格点数
n = 256
x = np.linspace(-3, 3, n)  # x 从 -3 到 3 生成 n 个点
y = np.linspace(-3, 3, n)  # y 从 -3 到 3 生成 n 个点# 使用 meshgrid 生成二维网格
x, y = np.meshgrid(x, y)# 计算 Z 值
z = f(x, y)# 绘制填充的等高线图
plt.contourf(x, y, z, 8, alpha=0.75, cmap=plt.cm.hot)  # 8个颜色层
# 绘制等高线
C = plt.contour(x, y, z, 8, colors='black', linewidths=0.5)
# 添加等高线标签
plt.clabel(C, inline=False, fontsize=10)# 去掉坐标轴的刻度
plt.xticks(())
plt.yticks(())# 显示图形
plt.show()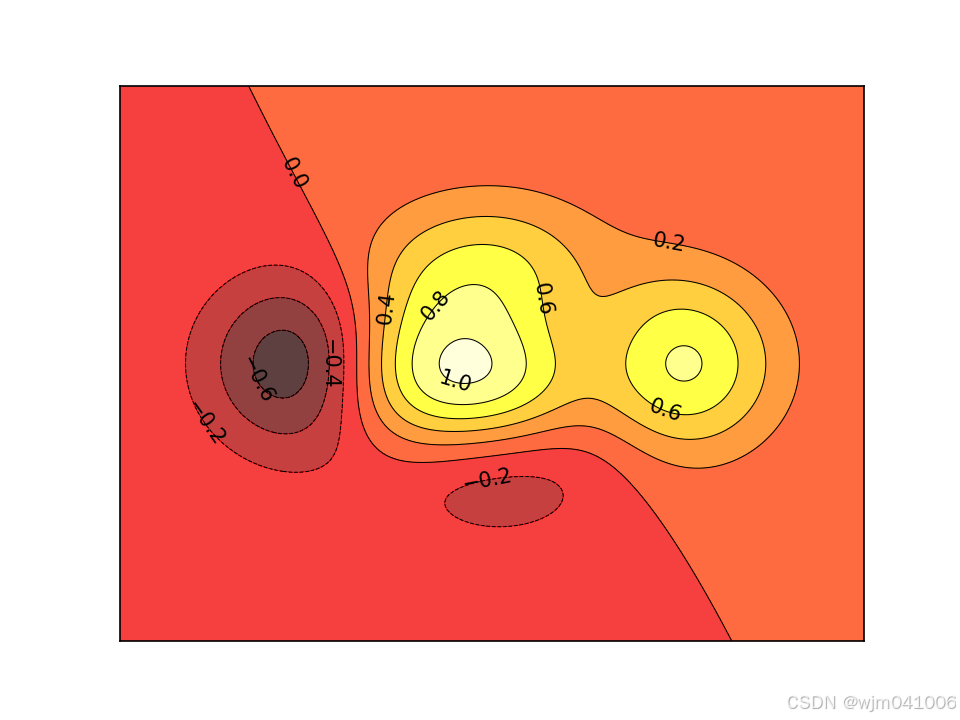

4.3D图像

首先要把这个包导入进来

from mpl_toolkits.mplot3d import Axes3D

使用 fig.add_subplot(111, projection='3d') 来初始化 3D 子图。111 表示将整个画布作为一个子图，projection='3d' 表示这将是一个 3D 图形。

ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap=plt.get_cmap('rainbow'))：使用 plot_surface 绘制 3D 曲面图。

x, y, z 是要绘制的坐标网格。
rstride 和 cstride 控制网格划分的精细程度，分别表示沿 x 和 y 方向的跨度。较小的值会增加渲染的细节，但可能使得绘制变慢。
cmap=plt.get_cmap('rainbow')：设置颜色映射（cmap），rainbow 是一个色彩渐变，从红色到紫色的色带，表示高度变化的不同区域。

绘制等高线图：

ax.contour(x, y, z, zdir='z', offset=-2, cmap='rainbow')：在 3D 曲面图上添加等高线。
- zdir='z'：指定等高线图沿 z 轴绘制，意味着这些等高线图的值将在 z 轴方向上进行投影。
- offset=-2：指定等高线图的偏移量，表示这些等高线将被绘制在 z = -2 的平面上。
- cmap='rainbow'：与曲面图相同，设置等高线的颜色映射。

import matplotlib.pyplot as plt
import numpy as np
import matplotlib
from mpl_toolkits.mplot3d import Axes3D
matplotlib.use('TkAgg')# 创建图形
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')  # 通过 add_subplot 创建 3D 图# 创建 x 和 y 数值网格
x = np.arange(-4, 4, 0.25)
y = np.arange(-4, 4, 0.25)
x, y = np.meshgrid(x, y)# 计算 r 和 z
r = np.sqrt(x**2 + y**2)
z = np.sin(r)# 绘制曲面图
ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap=plt.get_cmap('rainbow'))# 绘制等高线图 (在 z = -2 处偏移)
ax.contour(x, y, z, zdir='z', offset=-2, cmap='rainbow')# 设置 z 轴的显示范围
ax.set_zlim(-2, 2)# 去掉坐标轴的刻度
plt.xticks(())
plt.yticks(())# 显示图形
plt.show()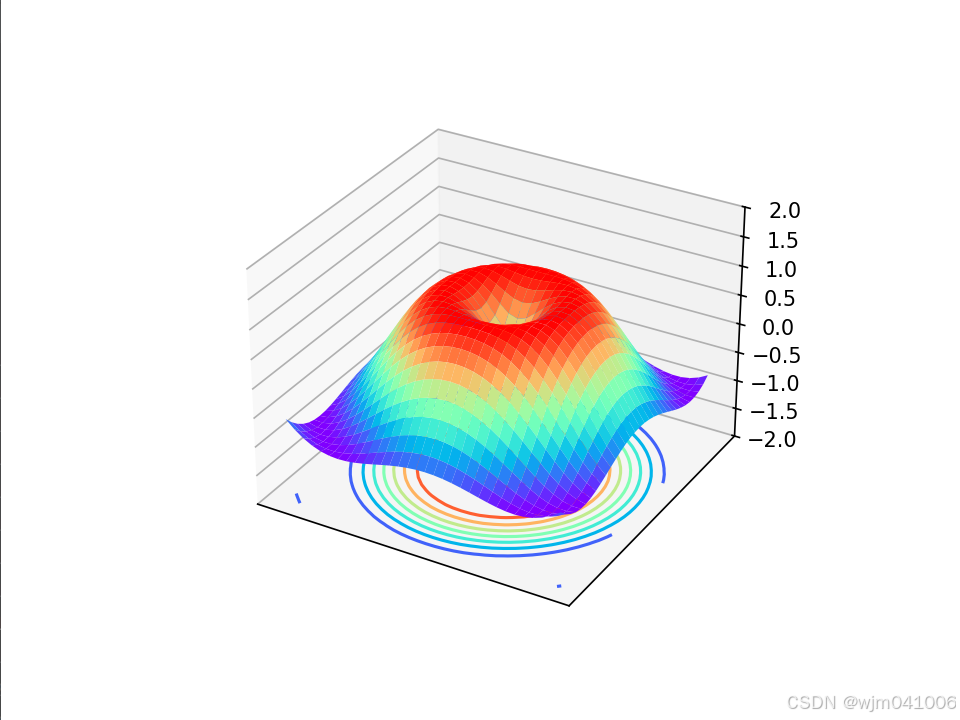

三、分格显示

plt.figure()
plt.subplot(2,2,1)
plt.plot([0,1],[0,1])plt.subplot(2,2,3)
plt.plot([0,1],[0,1])

2，2，1表示的是分为2行2列，此处为第一个模块