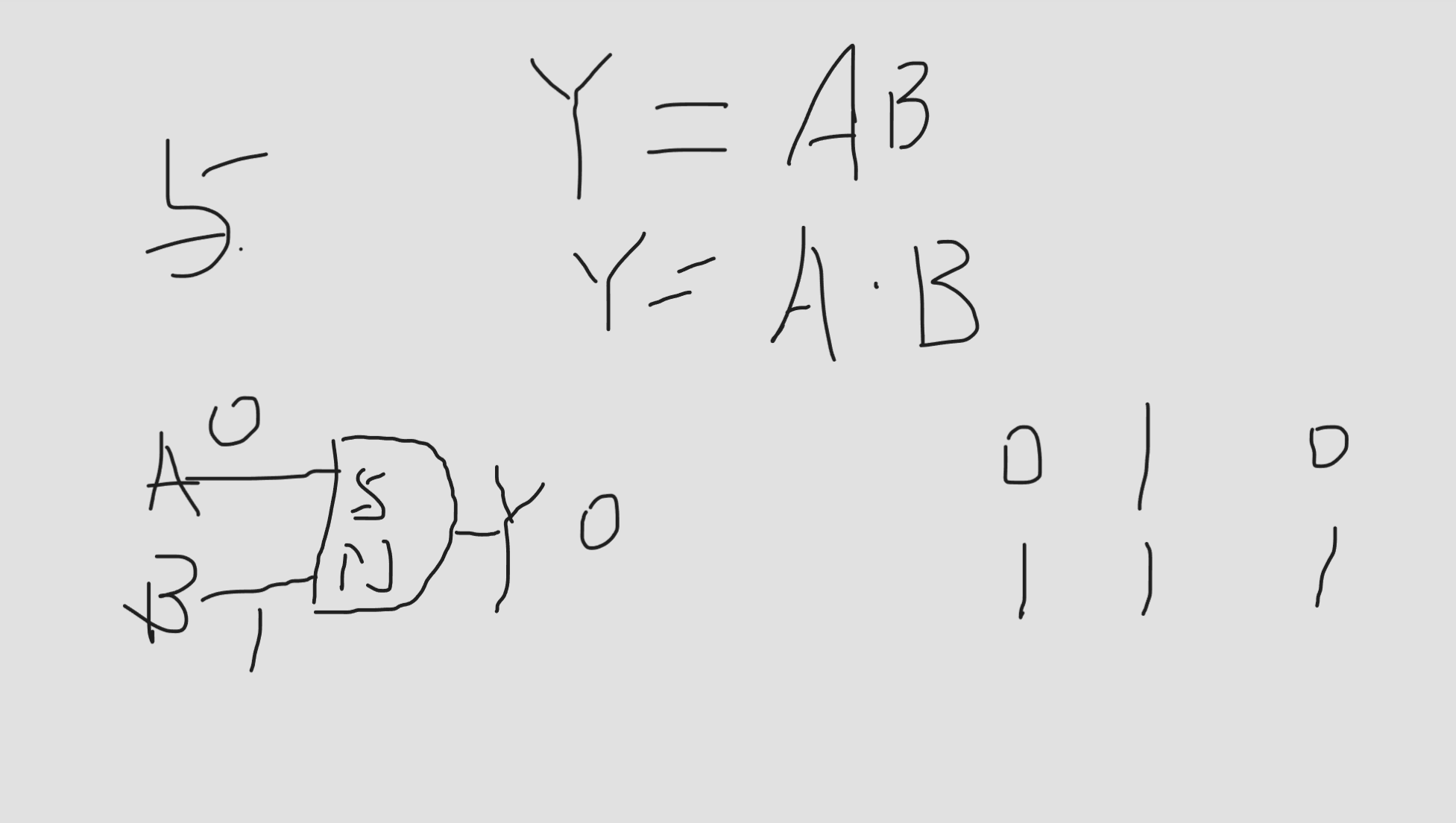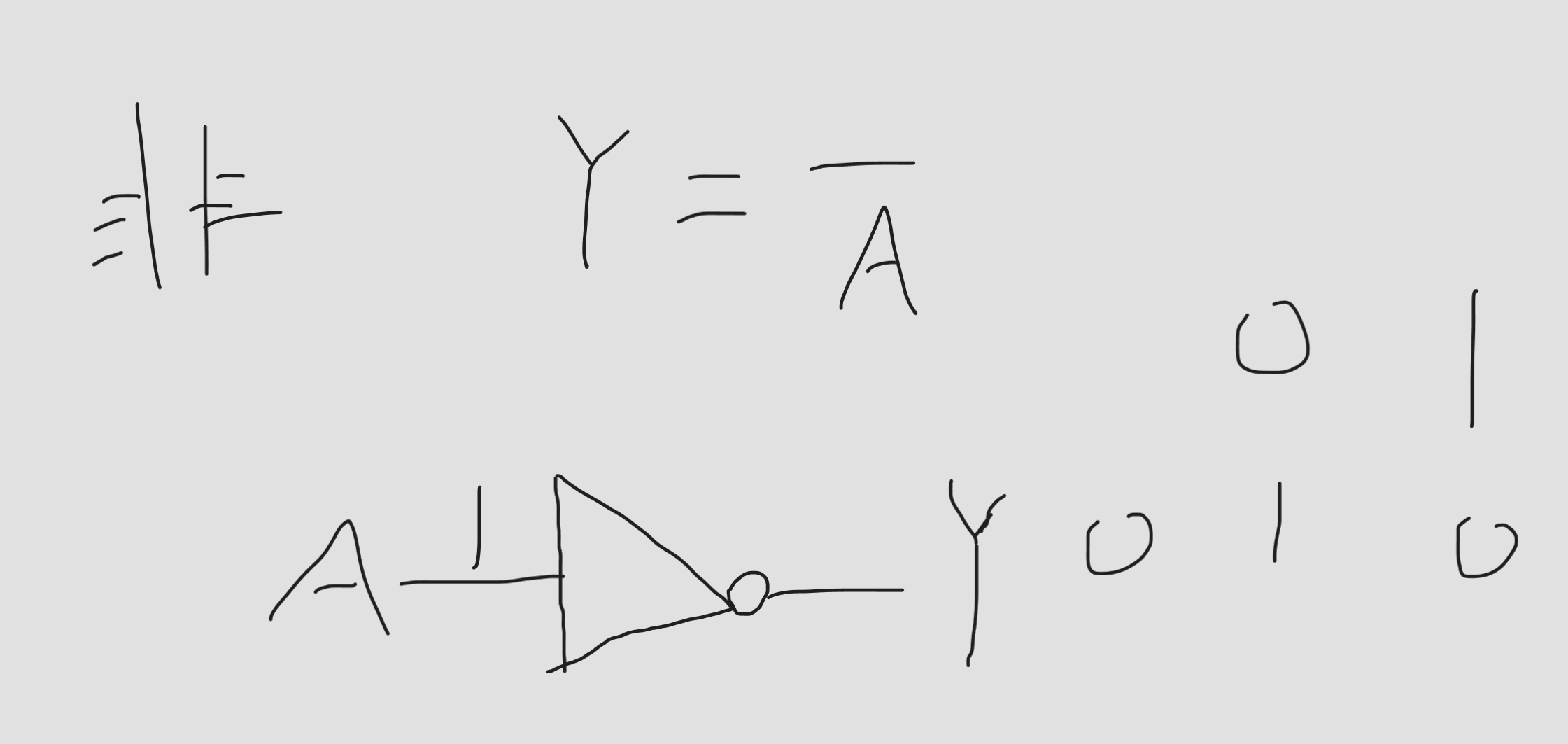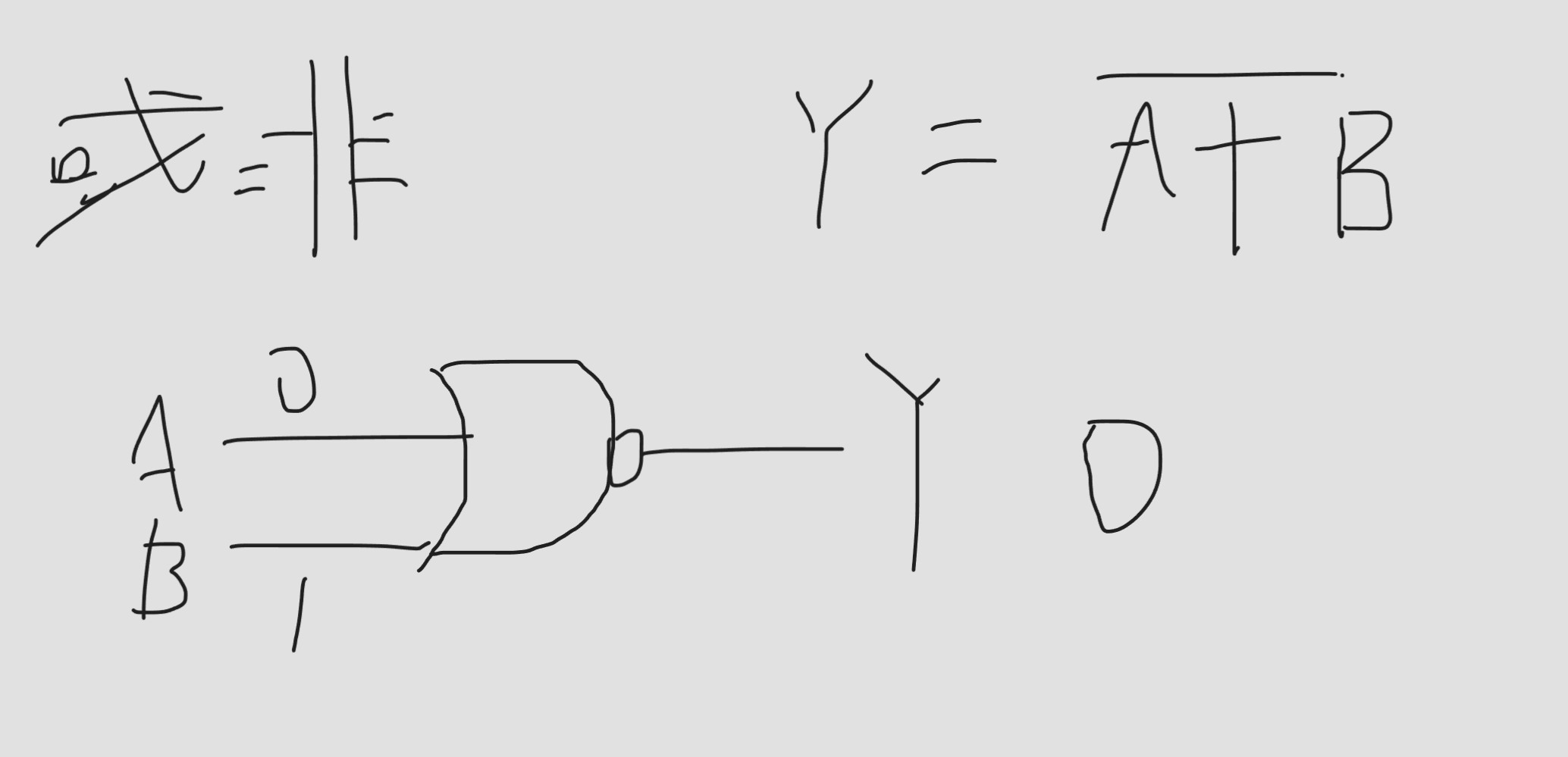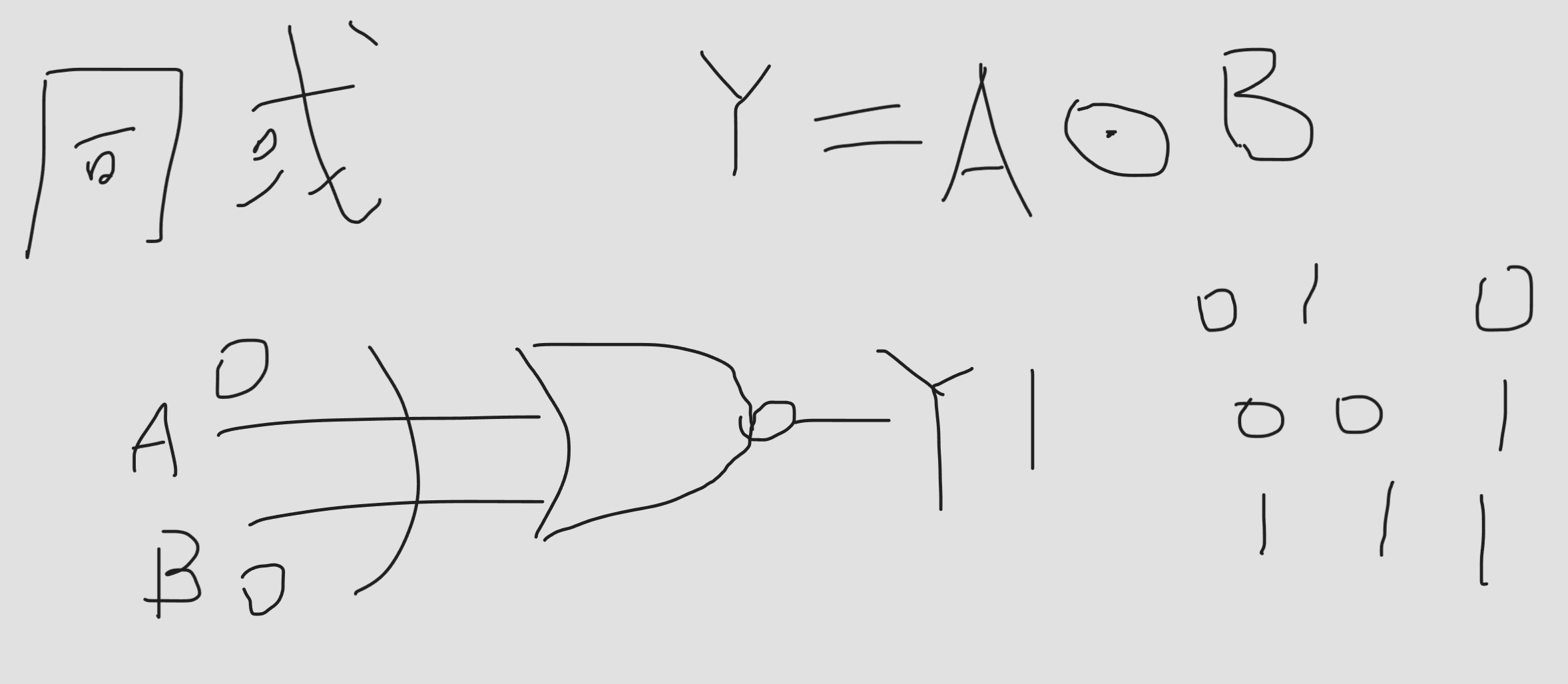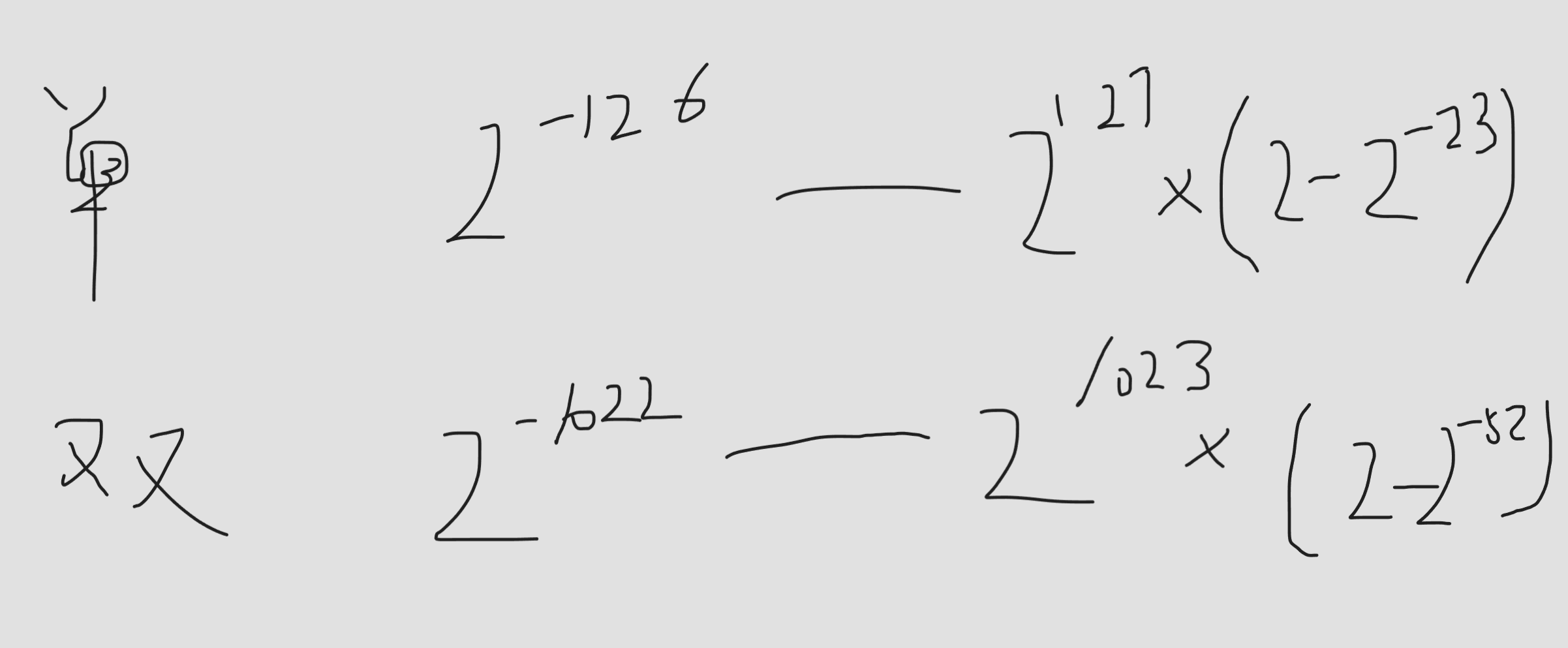数据的表示和运算
"自六月份另一个学校毕业 已经有拖三个多月的计组学习 当时其实已经已有一些学习 仅仅差了一节内容结束 也确实因为这个复杂的运算各类东西 言归正传 新的学校 新的学习 开始总结"
先看一下总的
还是分为三大块 三步走
一.数制 编码
先说数制 其实就是各类进制及其转换
- 二进制 B
- 十进制 D
- 八进制 O
- 十六进制 H(Ox)
首先说点废话:计算机采用二进制(0和1) 两个稳定状态的物理器件
至于各种进制就是逢几进一
两道类型结束 数制
1.二进制和十进制转换
二进制转换十进制:
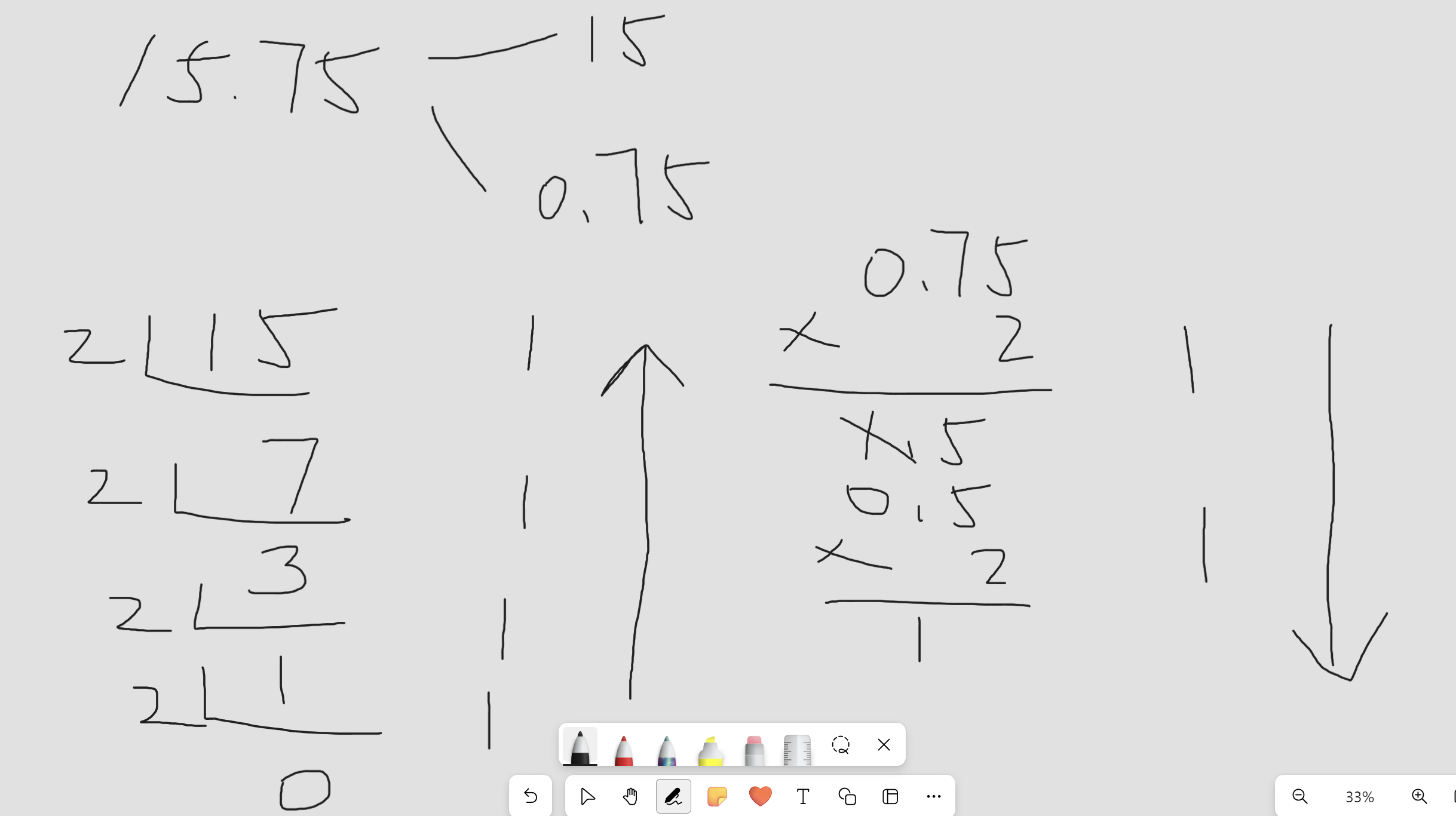
很简单 如1111.11(二进制)转换为15.75(十进制)
同样的十进制转换二进制 则是转过来
如15.75(十进制)转换为1111.11(二进制)
十变二
整数部分就一直除于二 取余数 直到1(从下到上)
小数部分就一直乘2 取整数 直到1(从上到下)
二变十
知道一个常见的就行
128 64 32 16 8 4 2 1对应二的几次方
7 6 5 4 3 2 1 0
2.二进制和八进制 十六进制转换
二进制转换其八进制和十六进制
对于 421 和 8421方法
如1111000010.01101
相反八进制 十六进制转换二进制就是把每个拆分出来
需要注意的就是划分的时候 整数从右向左 小数部分从左向右
还有就是十六进制超过10以后 有专门字母代替
A(10) B(11) C(12) D(13) E(14) F(15)
再看编码
之前是属于参加过考试比较容易掌握的计算机基础知识
接下来编码
我认为就是两个知识点
- 原反补移码
- 整数之间的转换
1.原反补移码
两个概念:
真值: +15 -8 带+ -符号的数
机器数:符号数字化 如0100 原反补码
移码:常用于表示浮点数的阶码 只能表示整数
总体来看不再一一分开
0的表示 原码 反码表示不唯一
正数的原反补码一样
整数用补码表示
取值范围
一道题来变化弄懂原反补移码的变换:
如求原码-42 的反 补 移码
2.整数
有符号整数和无符号整数
正常例如写的C语句中 int a=5;默认是有符号的 无符号修饰为unsigned
有个小注意:unsigned a =5; 默认为int型
整数之间的转换:符号 字长
- 有无符号整数之间的转换
- 不同字长整数之间的转换
#include <stdio.h>
int main(void) {short a = -4321;unsigned short b = (unsigned short) a;printf("%u", b);
}
-4321转换成无符号 字长并未改变
先求出其补码 然后其符号位不再是符号而是数值

不同字节整数之间的转换:
长 -> 短 截高位
短 -> 长 有符号 高位补1 无符号 高位补0
例如: 长 -> 短
#include <stdio.h>
int main(void) {int a = -34991;short b = (short) a;printf("%d", b);
}

短 -> 长
#include <stdio.h>
int main(void) {short a = -4321;int b = a; //有符号短 -> 长unsigned short c = (unsigned short) a;unsigned int d = c; //无符号 短 -> 长printf("%u\n %u", b, d);
}


大致第一块的内容知识 然后接下来看一些题目
8位原码能表示的不同数据有多少个

若寄存器内容10000000 若它等于-0 则为什么码
首先排除补移码 因为它们0表示唯一 不区分+ -
然后看是原码还是反码
在计算机中,通常用来表示主存地址的是 无符号数
16位补码整数0x8FA0扩展为32位应该是


小总结 对于负数比较 补码比较则是绝对值的比较 原码则是那个数的比较
二.运算
- 运算部件
- 移位运算
- 加减乘除运算
1.运算部件
之前总结过的运算器的组成:
https://www.cnblogs.com/gaodiyuanjin/p/18800302
ALU:算数逻辑单元
ACC:累加器
MQ:乘商寄存器
X:操作数寄存器
核心就是ALU的(带标志)加法器 之前我们需要搞懂几个东西 我简单介绍 然后一个总结
与 或 非 与非 或非 异或 同或
这些我们了解的用门电路图表示出来
与
或
非
与非 (就是先与 再非)
或非 (先或 再非)
异或 (没什么特殊的 跟或一样 除了 1 1为0)
同或 (跟与一样 除了 0 0为1 )
概述总结图:

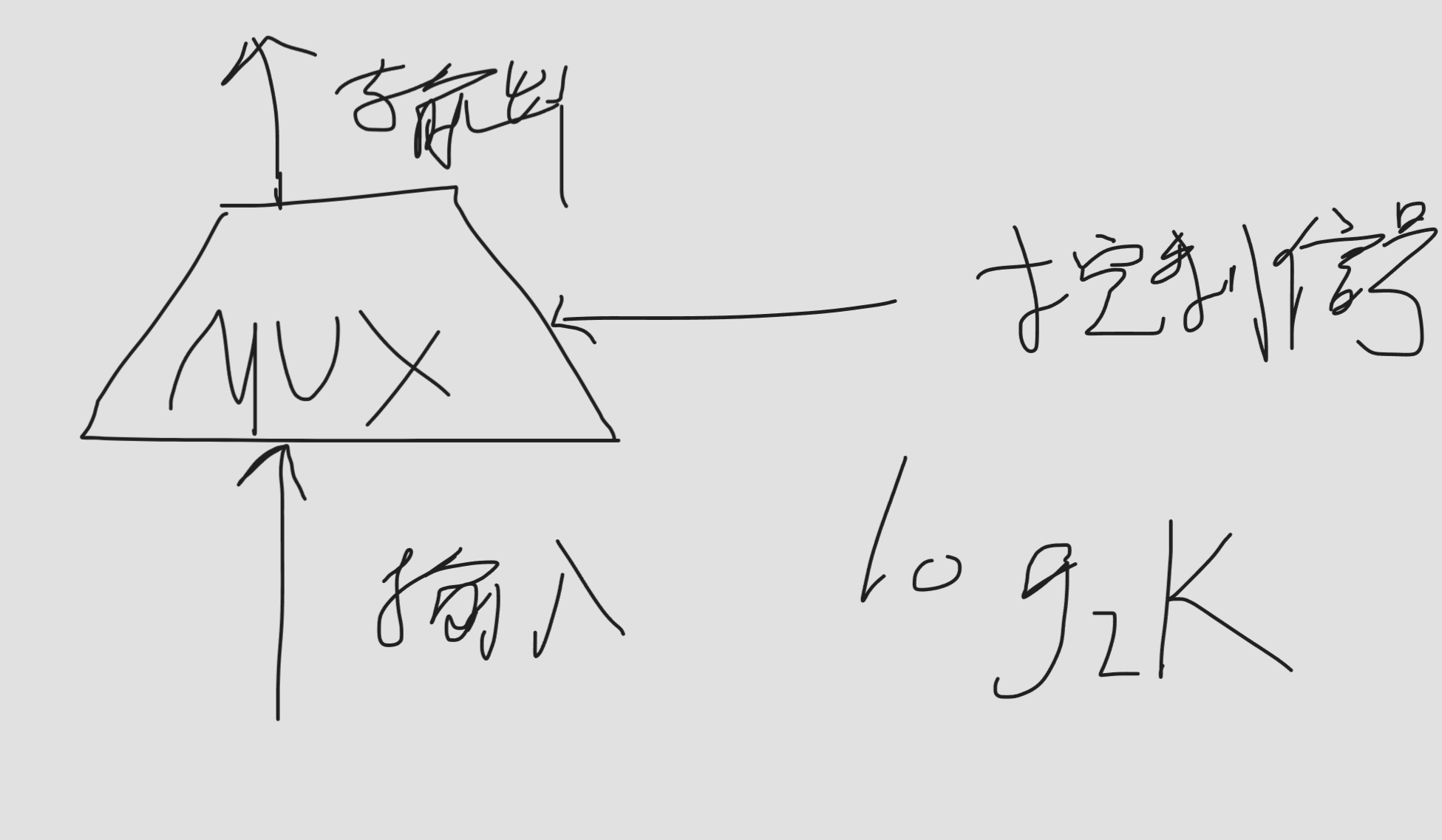
多路选择器
还有一个比较重要的新知识 拥有标志的加法器
- OF 溢出标志
- SF 符号标志
- ZF 零标志
- CF 进位/错位标志
OF=1 表溢出(有符号)
SF=0 结果为正
ZF=1 结果为0
CF=1 表溢出(无符号)
2.移位运算
逻辑移位(无符号整数) 无论左移或右移 都补0
算术移位 左移 补0 右移 补符号位
很抽象 做题弄明白
补码定点整数10010101 右移一位后的值
一般指的就是算术移位
2018统考题 整数X的机器数为 1101 1000 分别对X进行逻辑右移1位和算数右移1位操作操作 得到的机器数各是
那发生移位 肯定会伴随溢出问题
逻辑移位:只要高位的1移出 则溢出
算术移位:
左移 前后符号位变化 溢出
右移 低位1移出 丢失精度
3. 加减乘除运算
三步走 运算规则 溢出 运算电路
- 加减
[A+B]补=[A]补+[B]补
[A-B]补=[A]补+[-B]补
需要注意的就是减法当成加法运算
还有就是运算出来的符号位 要相应变化
设字长为8位 A=15,B=24,求[A+B]补 [A-B]补
溢出判断:
正+正=1符号位 得到负数溢出
负-正=0符号位 得到正数溢出一位符号位:操作的两个数符号相同 结果与原来不同 结果溢出双位符号位(运算结果为两个符号位ab):
ab=00 正数 无溢出
ab=01 正溢出
ab=10 负溢出
ab=11 负数 无溢出最高位进位和符号位进位相同 则无溢出
运算电路:
例如此电路 假设 X 0011 Y 0100
如果做加法 直接相加
若做减法 Y需要先取反 然后+1 变成1100 再相加
需要注意Sub为0时做加法 为1时做减法
无符号数大小比较:(ZF零标志 CF进/借位标志)
A=B ZF=1 CF=0
A>B ZF=0 CF=0
A<B ZF=0 CF=1
有符号数大小比较:(ZF零标志 OF溢出标志 SF符号标志)
A=B ZF=1
A>B OF=SF ZF=0
A<B OF不等于SF ZF=0
- 乘除
我认为这里更重要的是运算规则
乘除各用一道例题来学习 然后再用真实题目来理解
1.乘积的符号位由乘数符号位异或得到
2.乘积的数值位是两个乘数的绝对值之积
乘:A=-15 B=-13 A·B
使用加法和移位运算实现
被除数与除数 同号减法 异号加法
余数与除数补码 同号上商1 异号上商0
除:A=-0.1001 B=0.1101
至于数值运算:
参考deepseek
直接看真正需要掌握的题目类型
算数逻辑单元(ALU)的功能一般包括 算术运算和逻辑运算
机器运算发生溢出的根本原因是寄存器的位数有限
原码乘法先取操作数绝对值相乘 符号位单独处理
原码乘法符号位不参与运算
注意8位定点补码表示的数据范围为-128~127

需要注意 求[-啥]补码时候 负数直接取反 正数求出原码后取反
三.浮点数
不分总结了 直接上
一个重要的概念 IEEE754标准浮点数 基数都是2
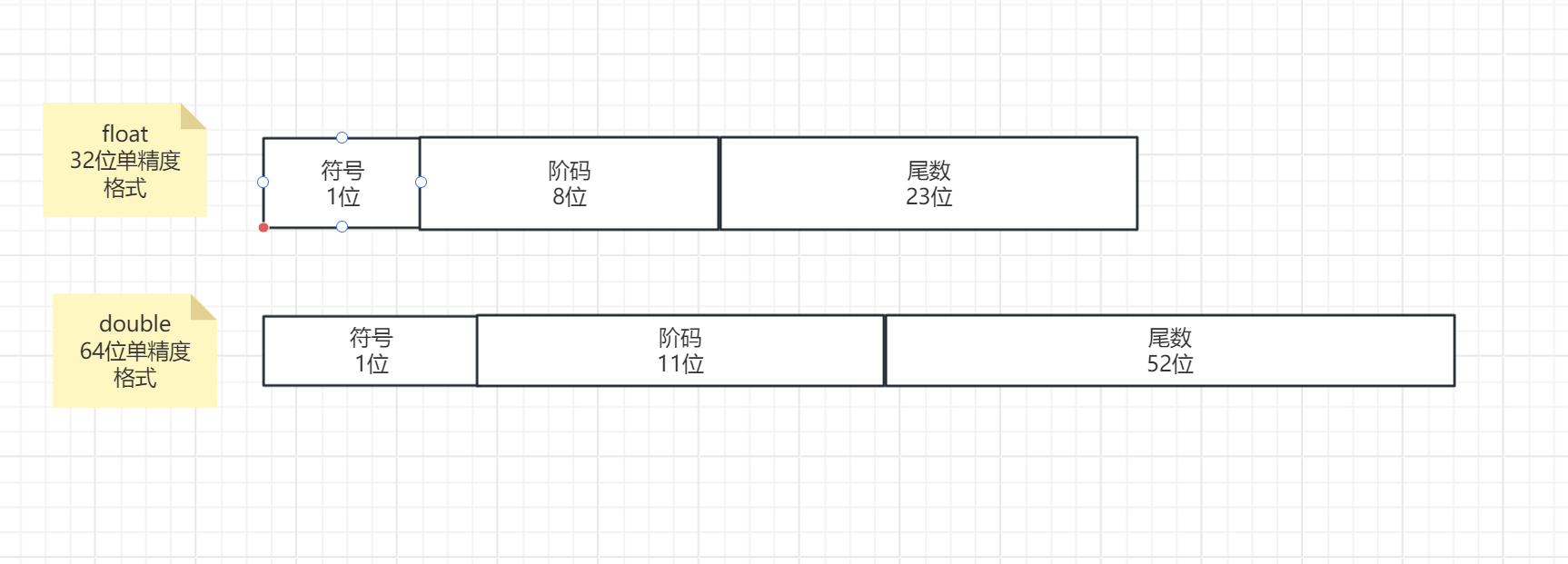
尾数用原码表示
单精度浮点数偏移值127 双精度浮点数偏移值1023
表示范围
阶码全为0或全为1时的特殊意义:
阶码 尾数
全0 全0 +0/-0
全0 非0 非规格化数 正数 2的-126次方(0.f) 负数 -2的-126次方(0.f)
全1 全0 +∞/-∞
全1 非0 非数
那么如何考察呢 就是IEEE754数的转换
将十进制数-8.25转换成IEEE754单精度浮点数格式表示
IEEE754单精度浮点数C6400000H的值
注意:IEEE754规定隐藏位1的位置在小数点之前 需要隐藏 这就是上面第一个求尾数的时候 将1隐藏 第二个求尾数的时候 将1还原出来
阶码越大 表示的数范围越大 尾数越多 精度越高
浮点数加减运算 对阶
左规和右规
左规和右规都有可能产生溢出
数据大小端和对齐存储
先弄清楚几个概念
LSB最低有效字节 表示数据的低位
MSB最高有效字节 表示数据的高位大端对齐:从高位到低位 字节顺序和原序列相同
小端对齐:从低位到高位 字节顺序和原序列相反
关于边界对齐方式存储和之前学的C语言中结构体共用体对齐一致
参考:https://www.cnblogs.com/gaodiyuanjin/p/18405937
最后一节的题目来看:
一道同类型题目
尾数规格化:
原码:最高有效位为1
正:0.1XXX
负:1.1XXX补码:小数点后一位和符号位不同
单精度浮点数 原码 补码 移码的32位机器数均为0xF0000000 从大到小顺序
移>补>原>浮
上面总结过 小阶向大阶对齐 E差多少 就右移多少
大小端对齐题目
边界对齐问题
大致这是第二章总结 应该是目前我总结写过最长的博客
下一章存储系统 再见
相关文章:

101.计组--二章
101.计组--二章数据的表示和运算 "自六月份另一个学校毕业 已经有拖三个多月的计组学习 当时其实已经已有一些学习 仅仅差了一节内容结束 也确实因为这个复杂的运算各类东西 言归正传 新的学校 新的学习 开始总结"先看一下总的还是分为三大块 三步走 一.数制 编码 先…...

LobeChat搭建
步骤 docker search lobe-chat docker pull lobehub/lobe-chat docker run -d -p 3210:3210 -e ACCESS_CODE=lobe66 --name lobe-chat lobehub/lobe-chat docker ps访问 http://localhost:3210 相关的key进入网页再配置,不必加入到docker run中。本文来自博客园,作者:潇汀…...

长园智能装备遇上利驰SuperHarness-3D,实现充电桩线束设计效率与精度双提升!
利驰数字线束软件,赋能长园智能装备充电桩线束智造。设计案例:感谢南瑞、盛弘、长园等众多充电桩龙头企业,选择利驰数字线束[抱拳][抱拳][抱拳]...

学习笔记:操作分块 / 根号重构
感谢校内模拟赛给我强行灌输了这个东西。。。 概述 操作分块 / 根号重构,又名时间轴分块,可以解决需要多次修改和查询的问题,常常难以直接维护。 借鉴序列分块的思想,我们设定一个阈值 \(B\),将连续 \(B\) 次操作视为一块。考虑一次查询操作,将对它产生影响的修改分为两类…...

url测试脚本3
#!/bin/sh . /etc/init.d/functions# 待检测的 URL 列表 array=("http://mail.163.com""http://mail.sina.com/" )# 等待效果,输出进度 wait_for_start() {echo -n "Start Curl_check"for n in 1 2 3; doecho -n " ."sleep 1doneecho…...

深入解析:linux基本知识
深入解析:linux基本知识pre { white-space: pre !important; word-wrap: normal !important; overflow-x: auto !important; display: block !important; font-family: "Consolas", "Monaco", "Courier New", monospace !important; font-size:…...

解决方案架构师是做什么
解决方案架构师 面试题 客户是怎么管理的 渠道变革变换的是哪些内容。变的是什么? 分层分级是怎么设计,价格体系是怎么制定的 marking 是怎么做的? CAP模型,是怎么管理的, 营销活动和销售是如何结合的,IT解决方案是什么 职责 懂业务,梳理解决方案。 技术架构 1 号项目。…...
:ArkTS渲染控制)
鸿蒙应用开发从入门到实战(九):ArkTS渲染控制
ArkTS拓展了TypeScript,可以结合ArkUI进行渲染控制,是的界面设计具有可编程性。本文简要描述鸿蒙应用开发中的条件渲染和循环渲染。大家好,我是潘Sir,持续分享IT技术,帮你少走弯路。《鸿蒙应用开发从入门到项目实战》系列文章持续更新中,陆续更新AI+编程、企业级项目实战…...

C# 2025年6-9月TIOBE排名增长及未来展望
根据 TIOBE 编程语言排行榜 2025 年 6 月至 9 月的公开数据,C# 的排名和市场份额变化如下(综合多个月份数据整理):一、 C# 在 2025 年 TIOBE 排行榜的连续增长趋势2025 年 6 月排名:第 5 位市场份额:4.69%2025 年 7 月排名:第 5 位市场份额:4.87%2025 年 8 月排名:第 …...

一个基于 .NET 开源、简易、轻量级的进销存管理系统
前言 最近有小伙伴在后台留言问:.NET 有值得推荐学习的进销存管理系统吗?今天大姚给大家推荐一个基于 .NET 开源、简易、轻量级的进销存管理系统:JxcLite。 项目介绍 JxcLite 是一个基于 Known 框架开发(基于 .NET Blazor 轻量级、跨平台、低代码、易扩展的插件开发框架)、…...
)
采用tree命令导出文件夹/文件的目录树(linux)
采用tree命令导出文件夹/文件的目录树(linux)pre { white-space: pre !important; word-wrap: normal !important; overflow-x: auto !important; display: block !important; font-family: "Consolas", "Monaco", "Courier New", monospace !…...
 4/12 A/F/G/M)
The 2024 ICPC Asia East Continent Online Contest (I) 4/12 A/F/G/M
M. Find the Easiest Problem 签到题,直接模拟即可点击查看代码 #include<bits/stdc++.h> #define int long long using namespace std; using pii=pair<int,int>; using ll = long long; using ull = unsigned long long; const ll inf = 1e18; const int mod = …...

深入解析 JVM 类加载机制:从字节码到运行时对象
一、概述:为什么需要类加载? Java 语言的核心特性之一是"一次编写,到处运行",这背后的关键在于 Java 虚拟机(JVM)和其类加载机制。当我们编写好 Java 代码并将其编译为 .class 字节码文件后,这些静态的字节码需要被加载到 JVM 中才能变为可执行的动态对象。类…...
)
博弈论学习(第二天)
博弈的基本理性假设: 一般来说,对于研究博弈问题,需要假设参与者具有完美理性,这分三方面,第一个就是参与者的偏好要有一定性,比如对风险的偏好,不能说一个参与者做第一个决策时属于风险接受型,而做第二个决策时就属于风险规避型。第二个就是参与者对所参与决策的问题具…...

PHP 和 Elasticsearch:给你的应用加个强力搜索引擎
PHP 和 Elasticsearch:给你的应用加个强力搜索引擎 现在做 Web 应用,搜索功能基本是标配。不管你做电商、CMS 还是社交应用,用户都希望搜索又快又准。如果你用 PHP 开发,肯定遇到过数据库搜索的瓶颈——数据一多就慢得要死。这时候 Elasticsearch 就能帮大忙了。 这篇文章会…...
--Java版 - 实践)
2025年- H146-Lc459. 重复的子字符串(字符串)--Java版 - 实践
2025年- H146-Lc459. 重复的子字符串(字符串)--Java版 - 实践pre { white-space: pre !important; word-wrap: normal !important; overflow-x: auto !important; display: block !important; font-family: "Consolas", "Monaco", "Courier New"…...

坚果云 坚果 jianguoyun 怎么收文件?
怎么收文件? 坚果云 坚果 jianguoyun 怎么收文件?注册、登录、免费的空间是 1GB。创建新的收集 https://www.jianguoyun.com/d/home#/ 查看收集结果:https://www.jianguoyun.com/#/...

mssql创建字段依赖
CREATE TABLE temp061_t ( ID INT IDENTITY(1,1) PRIMARY KEY, RoleType INT NOT NULL, isSior INT NULL ); ALTER TABLE temp061_t ADD CONSTRAINT chk_is_sior CHECK ( (RoleType = 1 AND isSior IS NULL) OR (RoleType = 2 AND isSior IN (0,1,2)) ); -- 合法插入 INSERT IN…...

AT_agc053_b [AGC053B] Taking the middle
考虑将先手最大转化为后手最小。 那么可以发现,第 \(i\) 次操作先手一定能让后手从 \([n - i + 1, n + i]\) 中选取最小的一个元素,一定可以。因为考虑先手拿的顺序不重要,一定存在构造方案,使得能让任意一个元素为中位数。...

一款多功能Linux服务器Web管理面板
为什么使用 Docker 部署 EasyNode? 正如您所说,Docker 部署具有显著优势: 环境隔离与一致性:所有依赖(Node.js, PM2等)都封装在容器内,与宿主机环境隔离,避免冲突。在任何支持 Docker 的 Linux 发行版上,体验完全一致。 简化安装:无需在主机上手动安装 Node.js、配置…...

2025.9.16 测试
2025.9.16 测试1. Problem A: 逆序对(reverse) 根据冒泡,只要逆序对个数够就有方案 经过思考,我们找到第一个操作个数大于的前缀,然后操作前一个前缀,这样前边变有序后,与当前数成逆序对一定是个后缀,然后根据需要选任意个即可 所以我们对任意方案构造出了 \(= 2\) 的解 …...

题解:P12558 [UOI 2024] Heroes and Monsters
题面: (这个没交洛谷,给学弟写的。) \(O(n^3)\) 考虑直接求出所有 \(ans_i\),前缀和回答询问。 \(a,b\) 先排序。由于我们只关心英雄的集合,所以怪兽我们贪心选择,如果我们选这个英雄那么选最前面的怪兽,否则选后面第一个能打死自己的怪兽。显然,合法方案怪兽的前缀会…...

数据分析与产品、运营、市场之间如何有效对齐 - 详解
数据分析与产品、运营、市场之间如何有效对齐 - 详解pre { white-space: pre !important; word-wrap: normal !important; overflow-x: auto !important; display: block !important; font-family: "Consolas", "Monaco", "Courier New", monosp…...
基于Java的学生托管系统的设计与实现 - 实践)
(附源码)基于Java的学生托管系统的设计与实现 - 实践
(附源码)基于Java的学生托管系统的设计与实现 - 实践pre { white-space: pre !important; word-wrap: normal !important; overflow-x: auto !important; display: block !important; font-family: "Consolas", "Monaco", "Courier New", mono…...

SVG动画优化全攻略:从设计到性能提升
本文详细介绍了如何通过清洁设计、路径简化、代码分层和元素复用等技术优化SVG动画,涵盖工具选择、结构设计到CSS动画实现的全流程,帮助开发者创建高性能的SVG动画效果。粉碎动画第四部分:优化SVG SVG动画让我回想起童年观看的汉纳-巴伯拉卡通片。像《Wacky Races》、《The …...

【GitHub每日速递 250919】MCP 生态新工具!Registry 服务器注册服务预览版,AI 开发者部署认证全流程揭秘
原文:https://mp.weixin.qq.com/s/vpm5exQj1imATtK6edQjZA gRPC-Go:高性能开源RPC框架,使用攻略及常见问题全解析 [grpc-go] 是一个基于 HTTP/2 的高性能远程过程调用(RPC)框架的 Go 语言实现。简单讲,它让不同服务能高效地通过网络互相调用函数。适用人群:Go 语言开发者…...

多元积性函数
定义:若函数 \(f(n,m)\) 满足 \(ab \perp xy \Rightarrow f(ax,by)=f(a,b)f(x,y)\),则称 \(f\) 为二元积性函数。 积性分解:将 \(x=\prod p_i^{\alpha _i},y=\prod p_i^{\beta _i}\),则有 \(f(x,y)=\prod f(p_i^{\alpha_i},p_i^{\beta_i})\)。 二元迪利克雷卷积:\((f*g)(n…...

MX 练石 2026 NOIP #7
好难好难好难好难,为数不多的罚坐了。MX 练石 2025 NOIP #6 链接:link 题解:link 时间:4h20min (2025.09.18 13:50~18:10) 题目数:4 难度:A B C D估分:50 + 10 + 10 + 10 = 80 得分:场祭 读题。 开 A,发现可以转化为 \(a_i - i \le a_j - j \land b_i - i \ge b_j - j…...

用Qt打造永远运行的程序/守护进程/程序启动器/实时监测程序运行/后台运行
一、前言说明 最近有个定制需求,希望程序能够一直运行,比如在windows上运行的程序,很可能无法保证不出故障崩溃,有时候可能是程序内部处理异常导致的崩溃,比如有些数据解析没有考虑到一些极端的情况,还有就是用户主动关闭了程序,可能是误关闭,而有些程序,又必须7*24小…...

传话游戏 题解
详细揭秘传话游戏 题解 题目描述 初始时你有一个长度为 \(m\) 的字符串 $ S_1 $ ,然后你可以进行 $ n-1 $ 次操作,每次操作修改当前字符串,形如删掉其中某些元素(可以全删,也可以都不删)。第 \(i\) 次操作得到的字符串记为 $ S_{i+1} $ ,这样得到了由 \(n\) 的字符串形成…...

智驾芯片三强对决:征程6P vs EyeQ Ultra vs Thor
微信视频号:sph0RgSyDYV47z6快手号:4874645212抖音号:dy0so323fq2w小红书号:95619019828B站1:UID:3546863642871878B站2:UID: 3546955410049087智能驾驶芯片是自动驾驶技术的「中枢神经」,其性能直接关乎车辆感知决策的精准度与响应速度。当前,全球智驾芯片市场呈现多元…...
)
0132_访问者模式(Visitor)
访问者模式(Visitor) 意图 表示一个作用于某对象结构中的各元素的操作。它使你可以在不改变各元素的类的前提下定义作用于这些元素的新操作。 UML 图优点开闭原则:容易添加新的访问者操作,无需修改元素类 单一职责原则:将相关行为集中到一个访问者对象中 灵活性:可以在运行…...

国内AI云市场:挤不进前三,生存将成问题!
微信视频号:sph0RgSyDYV47z6快手号:4874645212抖音号:dy0so323fq2w小红书号:95619019828B站1:UID:3546863642871878B站2:UID: 3546955410049087中国AI云市场已形成“一大四强”的格局,阿里云以35.8%的份额独占鳌头,而第五名之后的厂商合计市场份额不足25%,在残酷的竞争…...

P14053 [SDCPC 2019] Median 题解
P14053 [SDCPC 2019] Median 题解P14053 [SDCPC 2019] Median 题解 一道水题。 观察题意,很快我们可以发现,对于元素 \(i\),其合不合法取决于一定大于 \(i\) 的数的个数与一定小于 \(i\) 的数的个数。 这时,我们只需要统计有多少数大于 \(i\),与多少数小于 \(i\) 即可。 只…...

lQueryDef查询Evaluate报该几何不包含M值问题。
地理数据库既包括空间,又包括属性,属性类似于SQL表,理论上支持标准SQL查询。lQueryDef接口提供了高效查询方法,适用于对属性表或要素类的属性进行筛选和检索。 问题描述 一个简单的面积求和示例如下:IQueryDefFactory queryDefFactory = (IQueryDefFactory)workspace; IQu…...

我的首个RCE漏洞发现之旅:Apache ActiveMQ远程代码执行实战
本文详细讲述了作者如何通过系统化的子域名枚举和端口扫描,发现Apache ActiveMQ的CVE-2023-46604远程代码执行漏洞的全过程,包含具体的工具使用方法和实战技巧。我的首个RCE漏洞发现经历 大家好!在这篇文章中,我将分享我的第一个远程代码执行(RCE)漏洞发现经历。这次漏洞…...

北京市社保费用差额补缴计算工具
北京市社保费用差额补缴计算工具9月18日北京市发布了社会保险缴费工资基数上下限调整的通告,自2025年7月起,社保基数下限由原来的 6821元提高到7162元。 这样一来,之前已经缴了7月份社保且社保基数不到7162元的就需要补缴了。 根据我缴社保时看到的数据,我写了一个北京市社…...

使用自签名SSL证书有什么风险?
自签名SSL证书,指的是由用户自行生成密钥对并予以签名的证书,无需经由第三方权威证书颁发机构(CA)审核。鉴于其具备零成本、生成便捷的特性,该证书常被应用于个人测试、内部临时服务等非生产场景。 然而,相较于权威CA颁发的IP SSL证书,自签名证书在信任机制、安全性、兼…...

CDN可以使用iTrustSSL通配符证书吗?
CDN,即内容分发网络,它是一种通过在多个地理位置分散部署服务器节点,将网站的内容缓存并分发到离用户最近的节点上,从而显著提高网站内容的访问速度、降低延迟,并减轻源服务器负载的技术架构。借助CDN,网站能够更快地响应用户的请求,为用户提供流畅的浏览体验。而SSL证书…...

OpenCvSharp基于颜色反差规避FBA面单贴标
01 规避原理 1.抠图,根据色差或者根据固定包裹位置以及包裹尺寸抠出纸箱图片 2.色差,获取纸箱上所有背景色的灰度值 3.采图,采集大量视野相同,光源相同面单的色差灰度值,整理区间 4.取反,所有非面单灰度值区间的,都认为是纸箱背景色 02根据DPI计算1mm对应像素点。获取吸…...

【API接口】最新可用手机号归属地查询接口
最新可用手机号归属地查询接口,查询手机号码归属地、所属号段、手机卡类型、运营商等信息 使用之前您需要先去注册下key 申请地址: https://www.52api.cn 接口地址:https://www.52api.cn/api/mobile_location 返回格式:application/json 请求方式:GET/POST 请求示例:htt…...

【API接口】最新可用IP地址查询接口
最新可用IP地址查询接口,精准定位IPV4地址的地理位置信息,包括国家、城市、地区、运营商等详细数据,内置双线路来确保数据可用性 使用之前您需要先去注册下key 申请地址: https://www.52api.cn 接口地址:https://www.52api.cn/api/ip_query 返回格式:application/json 请…...

UE5创建的对象无法用ai操控
UE5创建的对象无法用ai操控记得更改这个设置...

【API接口】最新可用喜马拉雅接口
最新可用番茄畅听接口,支持搜索、详情解析、音频链接解析功能,助您快速构建您的专属听书客户端 使用之前您需要先去注册下key 申请地址: https://www.52api.cn 接口地址:https://www.52api.cn/api/xmly 返回格式:application/json 请求方式:GET/POST 请求示例:https://…...

25/09/18 小结
第三期ccb CF519E 2100 虽然是一道2100的题,但还是比较好想的。在树上找到最短距离,明显需要用到公共祖先之类的算法,并且,还要明确的知道节点往上走几步会到哪个节点。因此,学习了dfn序求LCA的方法。 具体来说在dfs序中,两个节点之间的dfn一定会遍历到lca的儿子节点,而…...

【API接口】最新可用番茄畅听接口
最新可用番茄畅听接口,支持搜索、详情解析、音频链接解析功能,助您快速构建您的专属听书客户端 使用之前您需要先去注册下key 申请地址: https://www.52api.cn 接口地址:https://www.52api.cn/api/fanqie_ct 返回格式:application/json 请求方式:GET/POST 请求示例:htt…...

【API接口】最新可用七猫短剧接口
最新可用七猫短剧接口,支持短剧搜索、短剧详情解析、短剧播放链接解析功能,助您快速构建您的专属短剧客户端 使用之前您需要先去注册下key 申请地址: https://www.52api.cn 接口地址:https://www.52api.cn/api/qm_duanju 返回格式:application/json 请求方式:GET/POST 请…...
)
磁盘分析工具推荐(Wiztree)
前言 磁盘空间占满了真难受,但是又像仓鼠一样不愿意删除,怎么找到有效的办法呢? (买买买!只要磁盘够大,都不是问题!) 但是买买买也是有上限的(除非你一直用机械硬盘去备份保存,物理存储) 所以还是需要删除文件的 那么,问题来了,怎么删除更有效呢? 那当然是,删除…...

用FastAPI和Streamlit实现一个ChatBot
用FastAPI+Streamlit实现一个流式响应的ChatBot前言 本文使用FastAPI+Streamlit实现一个流式响应类ChatGPT的LLM应用,这里只是一个demo,后续会基于此实现一个完整的MCP Client + MCP Server的MCP应用。 Streamlit是专为机器学习和数据科学项目打造的开源Python库,它允许开发…...
:Apache Solr — 企业级搜索的开源先锋)
搜索百科(2):Apache Solr — 企业级搜索的开源先锋
大家好,我是 INFINI Labs 的石阳。 欢迎回到 《搜索百科》 专栏!每天 5 分钟,带你速览一款搜索相关的技术或产品,同时还会带你探索它们背后的技术原理、发展故事及上手体验等。 上一篇我们认识了搜索技术的基石 Apache Lucene,今天我们将继续这个旅程,了解基于 Lucene 构…...