数据结构初阶——红黑树的实现（C++） - 教程

目录

平衡搜索二叉树

红黑树的相关概念

红黑树的性质

红黑树节点的定义

红黑树的插入

红黑树的验证

红黑树的查找

红黑树的删除

红黑树对比AVL树

红黑树的整体实现

---

平衡搜索二叉树

我们常见的平衡搜索二叉树有AVL树、红黑树和B树（及其变种B+树），我们这里所讨论的就是红黑树了，这个结构比较的抽象，但是我们要明白一点：我们的平衡搜索二叉树的本质就是平衡，也就是通过一种自平衡的机制使得树可以不退化为链表。友情提醒：红黑树的实现还是很复杂的，一般的公司笔面对这个的要求就是了解即可。

红黑树的相关概念

我们这里的红黑树就是用到了红色和黑色的节点的树（字面意思），我们用的是两种区分的节点的数量根据一套规则来控制树的平衡性的，这里的区分也可以是别的东西，我们这里的平衡不像AVL树那么的严格，而是保证没有一条从根节点到叶节点的路径比其他任意路径长出两倍，这就是一种近似的平衡效果，如图：

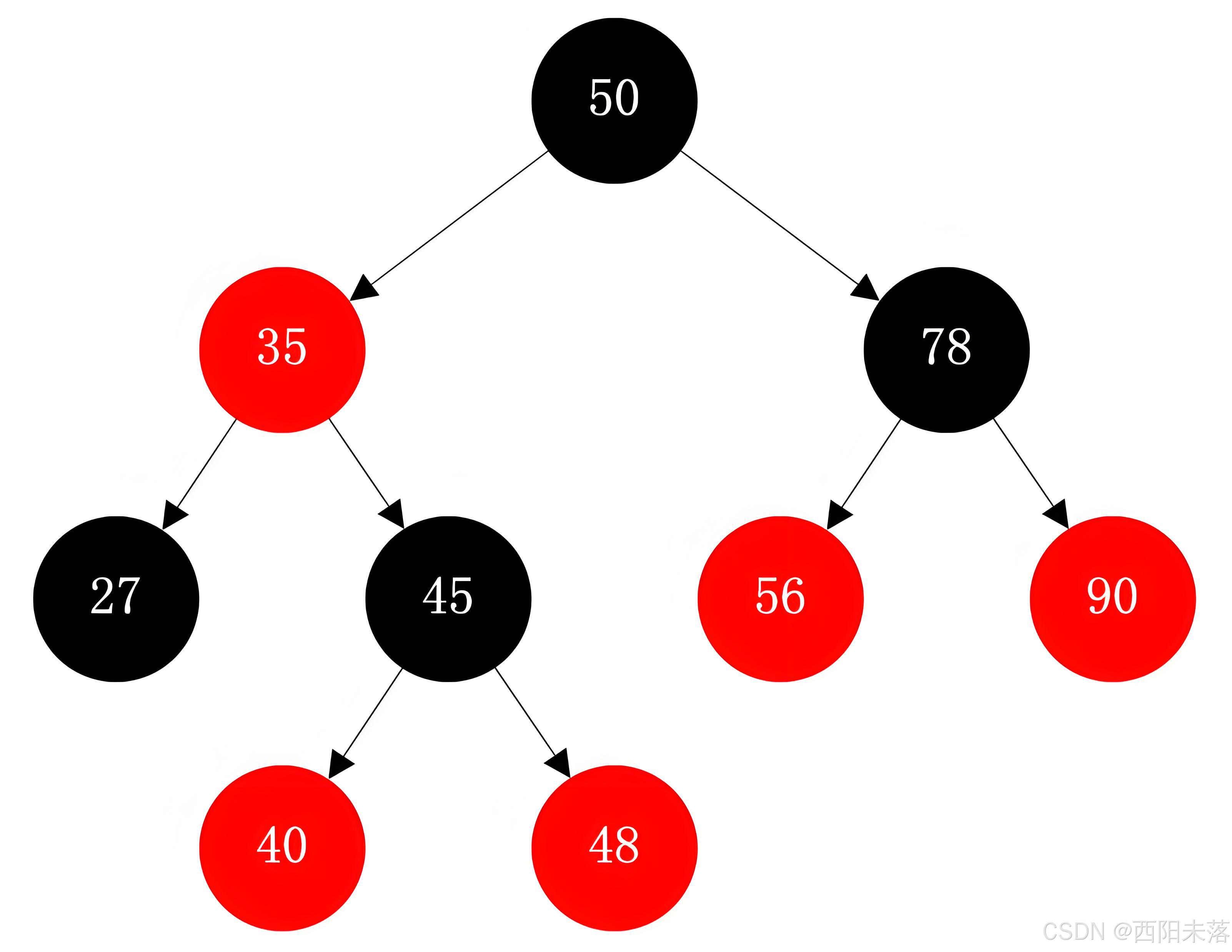
红黑树的性质

我们想实现红黑树就必须要了解它的相关性质，我们总结了红黑的4点性质：

1、除了根节点是黑色的，每个节点不是红色就是黑色。

2、一个节点是红色，那么它的两个孩子就是黑色的。

3、对于每一个节点，从这个节点到其所有后代的叶子节点的路径上包含相同数目的黑色节点。

4、每一个叶子节点都是黑色的。

我们怎么理解从根节点到叶子节点的最长路径不会超过最短路径的两倍呢？

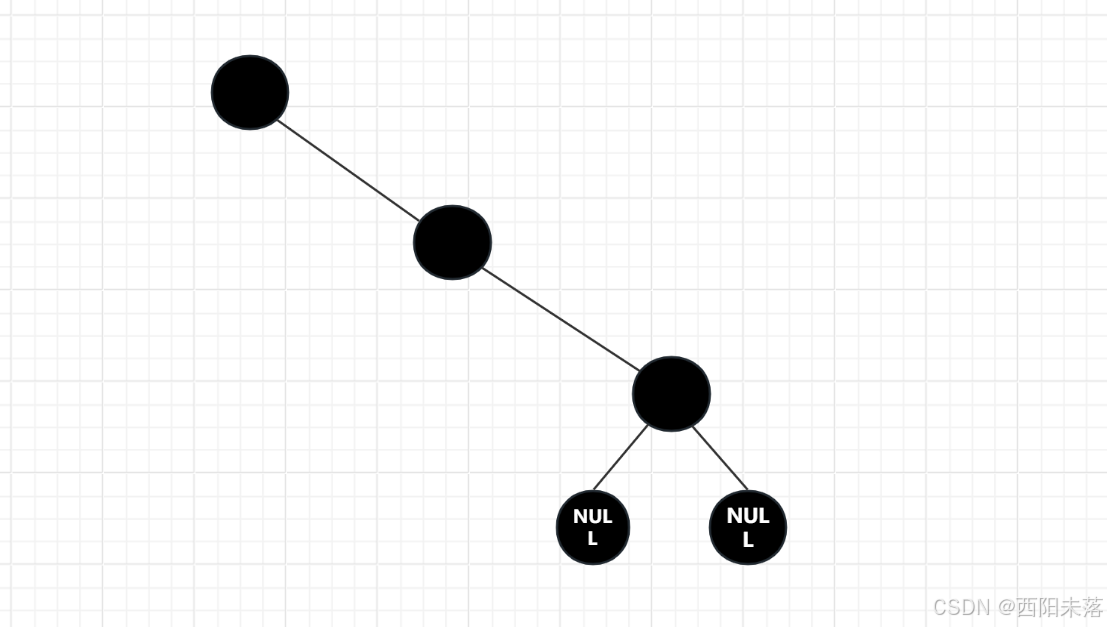
我们想要验证这个结论就需要指出我们根据上面的性质所能实现的最长和最短路径了：

我们首先假设我们所有路径上包含的黑色节点数量是N个，最短路径就是将这N个节点连起来， 长度是N：

我们的最长路径就是一个黑色一个红色，让红色节点尽量的多，我们这个路径的黑色节点和红色节点的数目相同长度是2N：

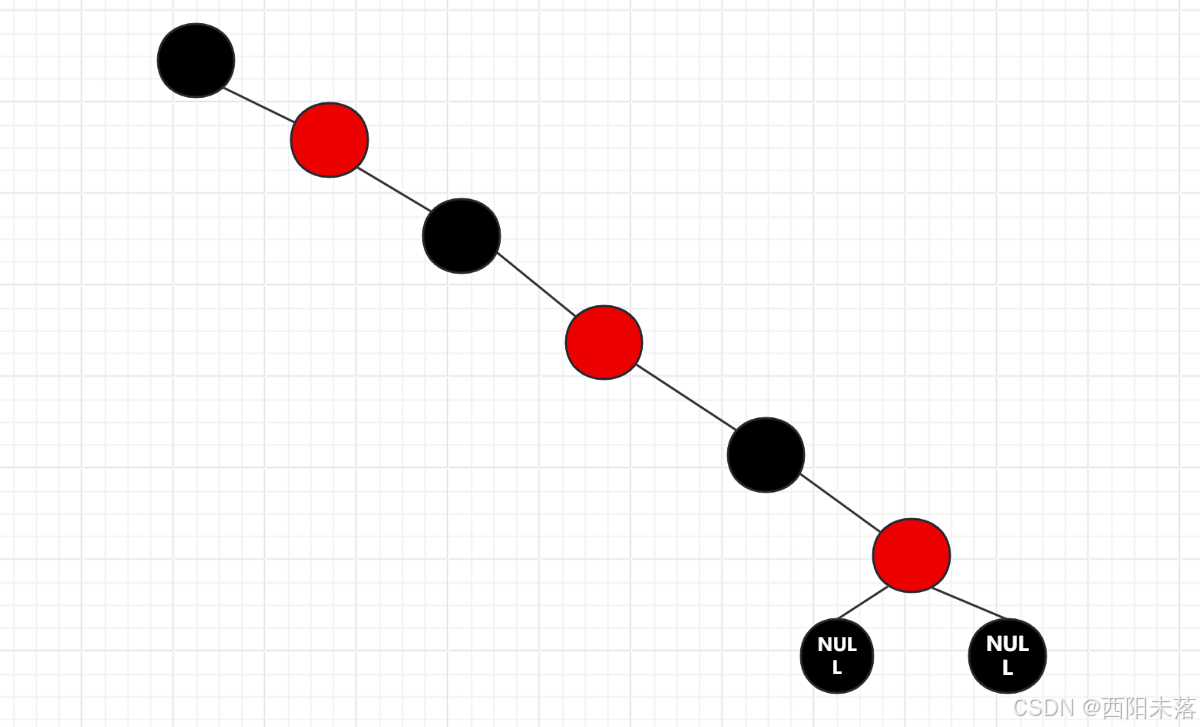
我们这里算长度没有算叶节点，这样我们就说明我们是可以保证我们的近似平衡条件的。

红黑树节点的定义

我们这里的红黑树的节点定义为三分叉的结构，然后再加入颜色这一成员：

enum Colour {
RED,
BLACK
};
template
struct RBTreeNode {
RBTreeNode* _left;
RBTreeNode* _right;
RBTreeNode* _parent;
pair _kv;
int _col;
RBTreeNode(const pair& kv)
:_left(nullptr),
_right(nullptr),
_parent(nullptr),
_kv(kv),
_col(RED) {}
};

我们这里默认将节点的颜色设置成了红色的，我们这里可以分析一下设置成黑色和红色会出现的情况：

• 如果我们将这个节点默认设置成了黑色的，那么我们一上来就破坏了性质3的条件，这个时候我们就需要对树进行调整了。
• 如果我们将这个节点设置成了红色的，我们就会有两种情况了，第一种情况就是这个节点的父节点是红色的，那也就表明破坏了性质2的条件，但是如果该节点的父节点是黑色的就不会有什么差错。

所以综上所述我们优先考虑将节点默认设置成了红色。

红黑树的插入

我们插入节点分成下面三个步骤：

1、我们根据二叉搜索树的插入方式找到我们要插入的位置。

2、将插入的节点插入到树中。

3、如果插入的父节点是红色的，就要对红黑树进行调整了。

我们这里最重要的还是最后一个步骤，因为这里会有很多的情况发生。

我们插入节点后应该怎么调整呢？

我们这里插入节点主要是针对插入节点后的父节点为红色进行判断的，因为黑色不需要调整。

我们这里先说明一个情况的必要，那就是我们的祖父节点（父亲的父亲）一定是存在的，因为根节点不可能是红色（性质1）。

我们这里的调整主要是看插入节点的叔叔节点（插入节点的父节点的兄弟节点），根据插入节点的叔叔的不同，我们将红黑树的调整分成了下面三种情况：

第一种情况：插入节点有叔叔节点，且叔叔节点是红色的。

这个时候为了使得不出现连续的红色节点，我们将父节点变成黑色，但是为了保持黑色节点的数目不变，我们将祖父节点变成红色，然后将叔叔节点也变成黑色：

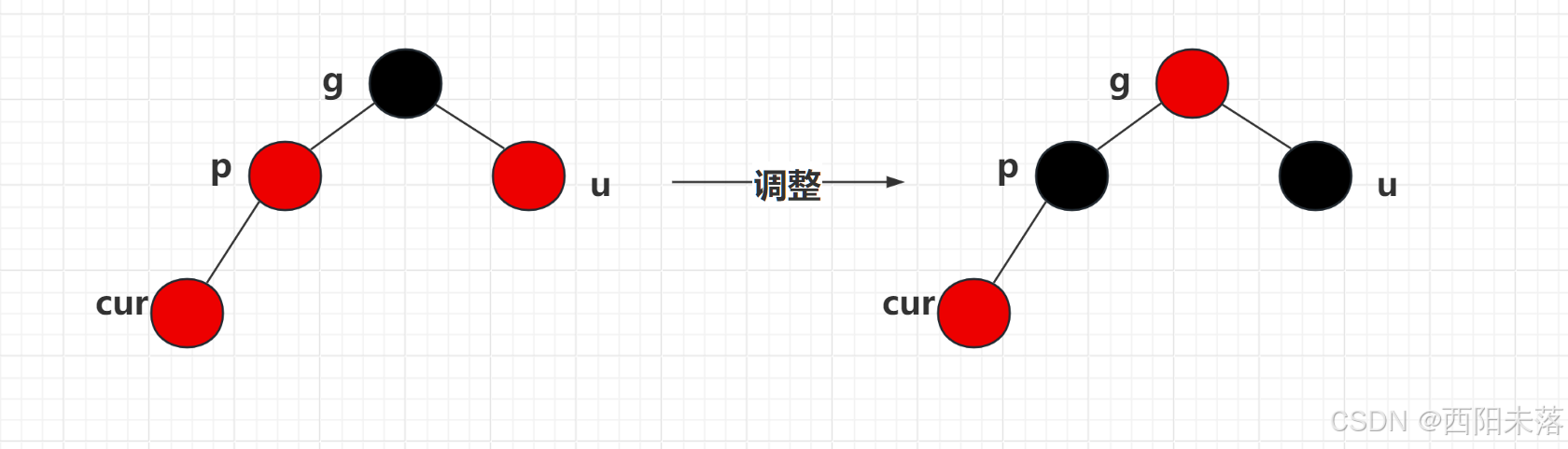
但是我们还没有结束，因为我们的祖父节点有可能是根节点，这个时候我们就要将祖父节点变成黑色，这个时候就相当于每一条路径上都增加了一个黑色的节点。

但是如果祖父节点不是根节点，我们就需要将祖父节点作为新插入的节点，再次重复上面的操作了。

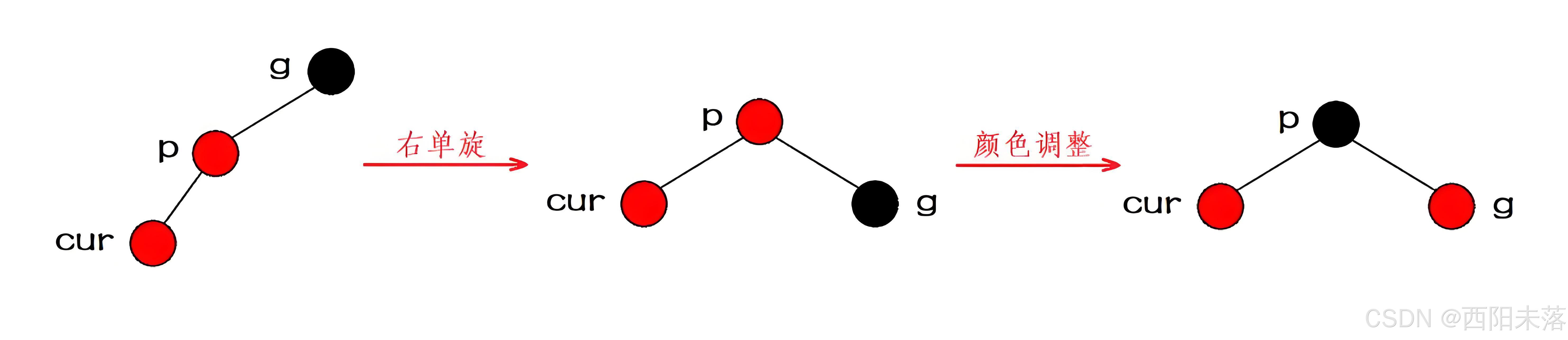
第二种情况：插入节点的叔叔节点存在，且叔叔节点是黑色。

这种情况的cur一定不是新插入的节点，而是第一种情况中的向上调整的过程的祖父节点的重新插入如图：

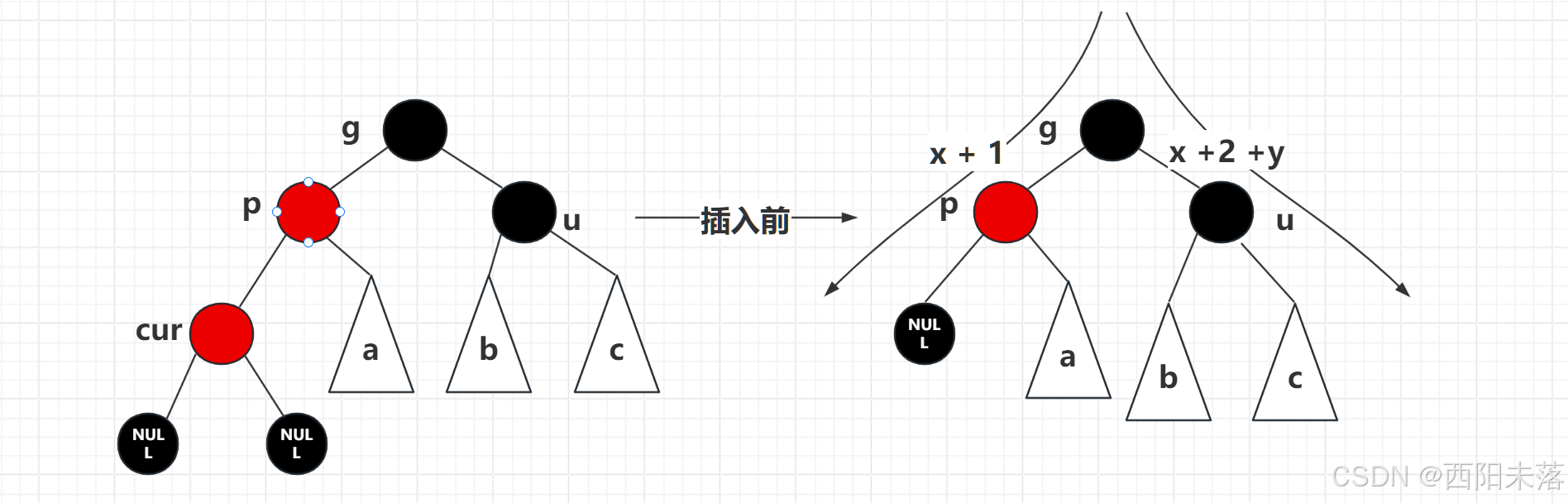
我们这里讲插入之前的祖父节点上面黑色节点的数量设置成x，将叔叔节点下面黑色节点的数量设置为y，那么就会出现图示的两条路经的节点数量为x + 1 和 x + y + 2的情况，我们很明显地发现x + 2 + y是要大于x + 1的，这样就不会满足红黑树的要求，再因为我们的情况2和3都只是循环处理，不会向上调整，所以我们的这一情况只能是情况1来的。

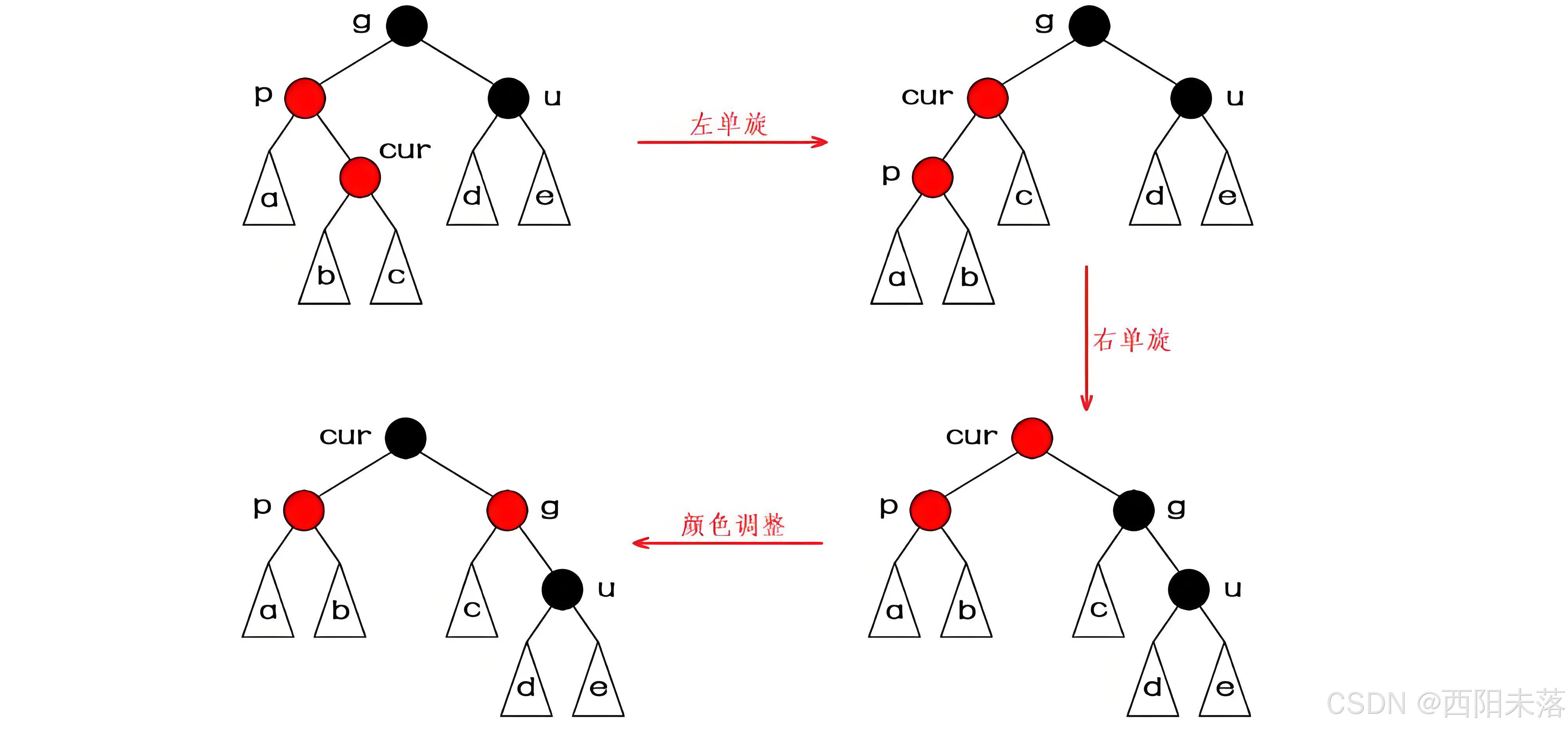
这种情况下，我们单纯的使用变色是不能实现我们要的效果的，我们需要像实现AVL一样使用旋转的方式来进行处理，如果我们的祖孙三代是直线关系也就是（cur、parent和grandfather这三个节点在同一条直线上面），这个时候我们就要进行单旋的操作了，然后才是调整颜色。

这里还是要说明一下，我们这里的直线关系就是p是g的右孩子，cur是parent的右孩子时需要进行左单旋的操作，再进行颜色的调整。

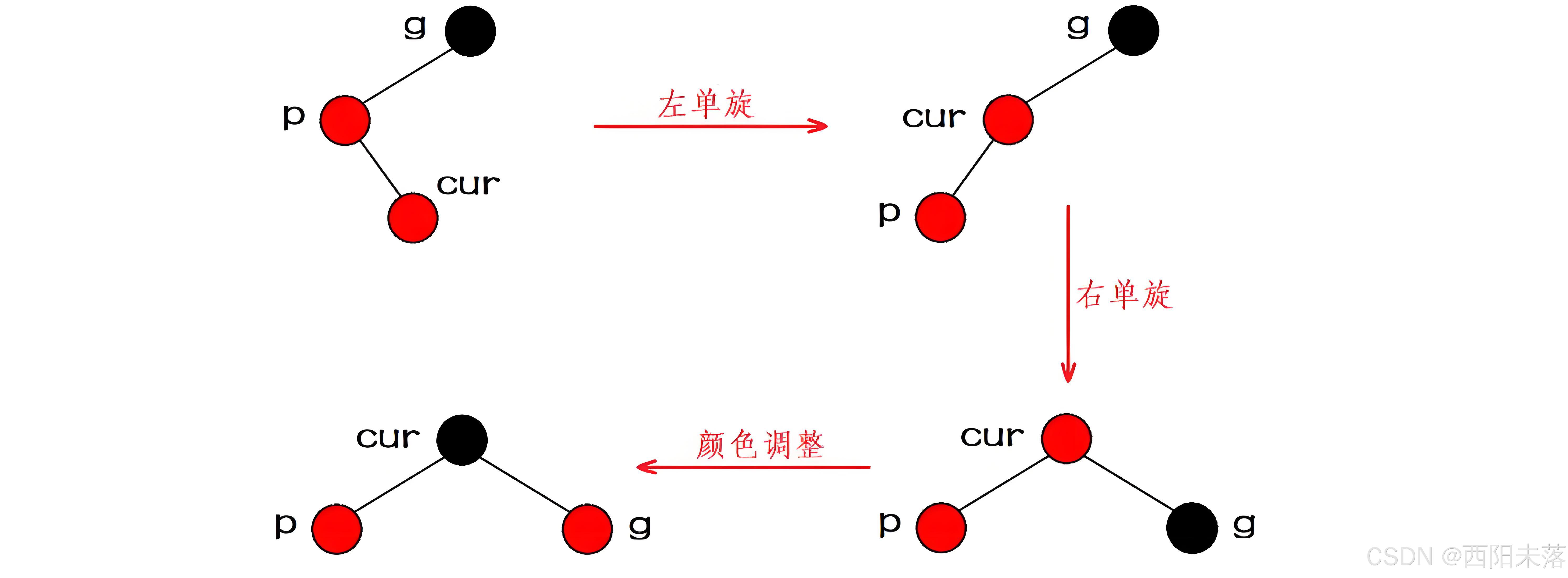
如果祖孙三代的关系是折线的关系，我们就要进行双旋的操作了，然后再进行颜色的调整。

第三种情况：插入节点的叔叔节点不存在

这样的情况一定是新插入的节点，不可能是情况以来的，因为叔叔节点都不存在了说明节点的数量就是祖父节点往上的数量，不可能是包括了下面的。

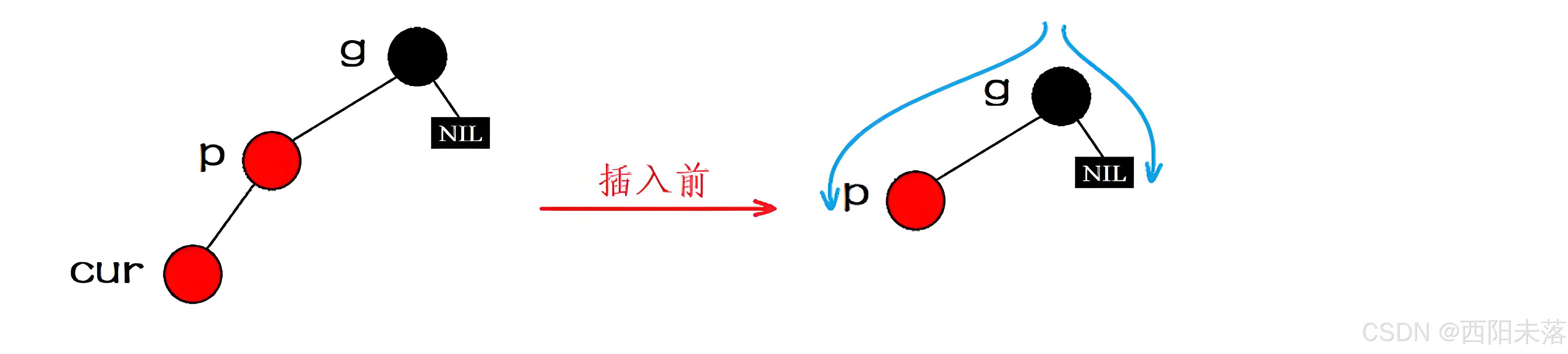
和第二种情况一样我们也是分成了两种线性的关系来讨论的，如果是祖孙三代的关系是直线的话，我们就要进行单旋然后再是进行颜色的调整，这样操作之后我们的根节点就是黑色的了，就不需要进行向上的处理了。

如果是折线的关系，和上面的情况2是一样的进行双旋之后，再进行颜色的调整，调整完了之后就没有其他的操作了。

实现代码如下：

bool insert(const pair& kv) {
if(_root == nullptr) {
_root = new Node(kv);
_root->_col = BLACK;
}
return true;
Node* parent = nullptr;
Node* cur = _root;
// 查看有没有这个值
while(cur) {
if(cur->_kv.first _right;
}else if(cur->_kv.first > kv.first) {
parent = cur;
cur = cur->_left;
}else {
return false;
}
}
cur = new Node(kv);
if(parent->_kv.first _right = cur;
}else {
parent->_left = cur;
}
cur->_parent = parent;
// 我们要处理的是父亲是红色的
while(parent && parent->_col == RED) {
Node* grandfather = parent->_parent;
if(parent == grandfather->_left) {
// 这个情况
//  g
//p   u
Node* uncle = grandfather->_right;
// 有uncle且为红色，变颜色继续处理
if(uncle && uncle->_col == RED) {
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
// 继续处理上面
cur = grandfather;
parent = cur->_parent;
}else { // uncle为黑色，旋转变颜色
if(cur == parent->_left) {
//    g
//  p   u
//c
RotateR(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}else {
//     g
// p     u
//   c
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}else { // 在右边
Node* uncle = grandfather->_left;
// 有叔叔且是红色
if(uncle && uncle->_col == RED) {
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
}else { // 不存在叔叔，或者是为黑色
//    g
// u     p
//          c
if(cur == parent->_right) {
RotateL(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}else {
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
}
_root->_col = BLACK; // 这里可能被情况1变成了红色
return true;
}
void RotateR(Node* parent) {
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if(subLR) {
subLR->_parent = parent;
}
Node* pParent = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if(parent == _root) {
_root = subL;
subL->_parent = nullptr;
}else {
if(pParent->_left == parent) {
pParent->_left = subL;
}else {
pParent->_right = subL;
}
subL->_parent = pParent;
}
}
void RotateL(Node* parent) {
Node* subR = parent->_right;
Node* subRL = subR->_left;
if(subRL) {
subRL->_parent = parent;
}
Node* pParent = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
if(pParent == nullptr) {
_root = subR;
subR->_parent = nullptr;
}else {
if(parent == pParent->_left) {
pParent->_left = subR;
}else {
pParent->_right = subR;
}
subR->_parent = pParent;
}
}

敲黑板：

这里重点要注意的是我们的根节点很有可能被设置成了红色的，所以我们这里统一的最后强制置为黑色的。

红黑树的验证

我们实现完了红黑树之后，如何判断是否合格呢？首先我们要判断它是不是满足二叉搜索树的，其次再判断是不是满足我们上面写到的几点性质。

第一步：满足二叉搜索树

代码如下：

void InOrder() {
_InOrder(_root);
cout _left);
cout _kv.first _kv.second _right);
}

第二步：是不是满足我们的性质

bool IsBalance() {
if(_root == nullptr) {
return true;
}
if(_root->_col == RED) {
return false;
}
// 我们首先要拿到一个参考的值
int refNum = 0;
Node* cur = _root;
while(cur) {
if(cur->_col == BLACK) {
++refNum;
}
cur = cur->_left;
}
return Check(_root, 0, refNum);
}
bool Check(Node* root, int num, const int refNUm) {
if(root == nullptr) {
if(num != refNUm) {
cout _col == RED && root->_parent->_col == RED) {
cout _kv.first _col == BLACK) {
num++;
}
return Check(root->_left, num, refNUm) && Check(root->_right, num, refNUm);
}

红黑树的查找

红黑树的查找的实现和我们的二叉搜索树的查找几乎没什么两样，逻辑如下：

1、如果是空树，那么查找失败返回nullptr。

2、如果是key值小于当前节点的值，就到该节点的左子树中找。

3、如果是key值大于当前节点的值，就到该节点的右子树中找。

4、如果是key值等于当前节点的值，查找就成功了，就返回对应的节点。

代码如下：

Node* Find(const K& key) {
Node* cur = _root;
while(cur) {
if(cur->_kv.first _left;
}else if(cur->_kv.first > key) {
cur = cur->_right;
}else {
return cur;
}
}
return nullptr;
}

红黑树的删除

这里就不实现了，因为这个操作有点困难并且考到的概率极低，有兴趣的友友可以去小破站上找找视频。

红黑树对比AVL树

我们的红黑树和AVL树都是比较高效的平衡二叉树，增删改查的时间复杂度都是O(logN)，但是这两个树控制控制平衡的方式很不一样：

• AVL树是通过控制左右高度差不超过1来实现的。
• 红黑树是通过控制不同颜色的节点，来使得最长路径不超过最短路径的2倍的，其实是一种近似的平衡。

由于我们的红黑树实现的是近似平衡，所以红黑树降低了插入节点时需要进行的旋转的次数，所以在经常进行增删的结构中红黑树的性能更好，实际的运用中也是红黑树居多。

红黑树的整体实现

#include
enum Colour
{
RED,
BLACK
};
template
struct RBTreeNode
{
// 这里更新控制平衡也要加入parent指针
T _data;
RBTreeNode* _left;
RBTreeNode* _right;
RBTreeNode* _parent;
Colour _col;
RBTreeNode(const T& data)
:_data(data)
, _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
{}
};
template
struct RBTreeIterator
{
typedef RBTreeNode Node;
typedef RBTreeIterator Self;
Node* _node;
Node* _root;
RBTreeIterator(Node* node, Node* root)
:_node(node)
,_root(root)
{}
Self operator++()
{
if (_node->_right)
{
// 右不为空，中序下一个访问的节点是右子树的最左(最小)节点
Node* min = _node->_right;
while (min->_left)
{
min = min->_left;
}
_node = min;
}
else
{
// 右为空，祖先里面孩子是父亲左的那个祖先
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && cur == parent->_right)
{
cur = parent;
parent = cur->_parent;
}
_node = parent;
}
return *this;
}
Self operator--()
{
if (_node == nullptr)  // --end()
{
// --end()，特殊处理，走到中序最后一个结点，整棵树的最右结点
Node* rightMost = _root;
while (rightMost && rightMost->_right)
{
rightMost = rightMost->_right;
}
_node = rightMost;
}
else if (_node->_left)
{
// 左子树不为空，中序左子树最后一个
Node* rightMost = _node->_left;
while (rightMost->_right)
{
rightMost = rightMost->_right;
}
_node = rightMost;
}
else
{
// 孩子是父亲右的那个祖先
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && cur == parent->_left)
{
cur = parent;
parent = cur->_parent;
}
_node = parent;
}
return *this;
}
Ref operator*()
{
return _node->_data;
}
Ptr operator->()
{
return &_node->_data;
}
bool operator!= (const Self& s) const
{
return _node != s._node;
}
bool operator== (const Self& s) const
{
return _node == s._node;
}
};
template
class RBTree
{
typedef RBTreeNode Node;
public:
typedef RBTreeIterator Iterator;
typedef RBTreeIterator ConstIterator;
Iterator Begin()
{
Node* cur = _root;
while (cur && cur->_left)
{
cur = cur->_left;
}
return Iterator(cur, _root);
}
Iterator End()
{
return Iterator(nullptr, _root);
}
ConstIterator Begin() const
{
Node* cur = _root;
while (cur && cur->_left)
{
cur = cur->_left;
}
return ConstIterator(cur, _root);
}
ConstIterator End() const
{
return ConstIterator(nullptr, _root);
}
pair Insert(const T& data)
{
if (_root == nullptr)
{
_root = new Node(data);
_root->_col = BLACK;
//return pair(Iterator(_root, _root), true);
return { Iterator(_root, _root), true };
}
KeyOfT kot;
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (kot(cur->_data) _right;
}
else if (kot(cur->_data) > kot(data))
{
parent = cur;
cur = cur->_left;
}
else
{
return { Iterator(cur, _root), false };
}
}
cur = new Node(data);
Node* newnode = cur;
cur->_col = RED;
if (kot(parent->_data) _right = cur;
}
else
{
parent->_left = cur;
}
// 链接父亲
cur->_parent = parent;
// 父亲是红色，出现连续的红色节点，需要处理
while (parent && parent->_col == RED)
{
Node* grandfather = parent->_parent;
if (parent == grandfather->_left)
{
//   g
// p   u
Node* uncle = grandfather->_right;
if (uncle && uncle->_col == RED)
{
// 变色
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
// 继续往上处理
cur = grandfather;
parent = cur->_parent;
}
else
{
if (cur == parent->_left)
{
//     g
//   p    u
// c
RotateR(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
//      g
//   p    u
//     c
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
else
{
//   g
// u   p
Node* uncle = grandfather->_left;
// 叔叔存在且为红，-》变色即可
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
// 继续往上处理
cur = grandfather;
parent = cur->_parent;
}
else // 叔叔不存在，或者存在且为黑
{
// 情况二：叔叔不存在或者存在且为黑
// 旋转+变色
//   g
// u   p
//       c
if (cur == parent->_right)
{
RotateL(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
}
_root->_col = BLACK;
return { Iterator(newnode, _root), true };
}
void RotateR(Node * parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
Node* pParent = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if (parent == _root)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
if (pParent->_left == parent)
{
pParent->_left = subL;
}
else
{
pParent->_right = subL;
}
subL->_parent = pParent;
}
}
void RotateL(Node * parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
Node* parentParent = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
if (parentParent == nullptr)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (parent == parentParent->_left)
{
parentParent->_left = subR;
}
else
{
parentParent->_right = subR;
}
subR->_parent = parentParent;
}
}
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_kv.first _right;
}
else if (cur->_kv.first > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
int Height()
{
return _Height(_root);
}
int Size()
{
return _Size(_root);
}
private:
int _Height(Node* root)
{
if (root == nullptr)
return 0;
int leftHeight = _Height(root->_left);
int rightHeight = _Height(root->_right);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
int _Size(Node* root)
{
if (root == nullptr)
return 0;
return _Size(root->_left) + _Size(root->_right) + 1;
}
private:
Node* _root = nullptr;
};