题目描述
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 31 [3 -1 -3] 5 3 6 7 31 3 [-1 -3 5] 3 6 7 51 3 -1 [-3 5 3] 6 7 51 3 -1 -3 [5 3 6] 7 61 3 -1 -3 5 [3 6 7] 7
示例 2:
输入:nums = [1], k = 1
输出:[1]
提示:
1 <= nums.length <= 105-104 <= nums[i] <= 1041 <= k <= nums.length
解法一
思路:
记录当前窗口中的最大值,当窗口右移时,新的元素进入窗口,同时也要删除元素,左侧删除的元素可能就是最大值的位置,那么就要重新选择最大值,若删除的元素不是最大值,则直接删除,在比较新的元素的大小。
代码:
class Solution {public int[] maxSlidingWindow(int[] nums, int k) {//记录最大值windowMaxint windowMax = Integer.MIN_VALUE;//记录窗口位置int left=0;int[] res = new int[nums.length-k+1];int count=0;//对于第一个窗口进行处理for(int i=0;i<k;i++){if(windowMax<nums[i])windowMax=nums[i];}res[count++] = windowMax;for(int i=k; i<nums.length; i++) {//如果移除的数据是最大值,就需要重新确定最大值if(nums[left]==windowMax&&nums[left+1]!=windowMax){windowMax=Integer.MIN_VALUE;for(int j=left+1;j<i+1;j++){if(windowMax<nums[j])windowMax=nums[j];}}if(windowMax<nums[i]) windowMax=nums[i];res[count++] = windowMax;left++;}return res;}
}public class leetcode_010 {public static int subarraySum(int[] nums, int k) {int ans=0;int tempSum=0;for(int i=0;i<nums.length;i++){tempSum+=nums[i];if(tempSum==k)ans++;for (int j=i+1;j<nums.length;j++){tempSum+=nums[j];if(tempSum==k)ans++;}tempSum=0;}return ans;}public static void main(String[] args) {Scanner sc = new Scanner(System.in);String[] line = sc.nextLine().split(",");int[] nums= Arrays.stream(line).mapToInt(Integer::parseInt).toArray();int k = sc.nextInt();int res = subarraySum(nums,k);System.out.println(res);}
}
注意:
若是采用stream流的方式来寻找最大值,那么这样比单层循环更加的耗时。
解法二
思路:
来自官方的解答,采用优先队列。
java的优先队列就是堆结构(大根堆),窗口右移,一个元素进入优先队列中,此时,判断当前的队首元素是否还在窗口中,若还在,那么就是当前最大值,否则就要移除队首元素,直至新的队首元素在窗口中。
代码:
class Solution {public int[] maxSlidingWindow(int[] nums, int k) {int n = nums.length;//队列中存储的是数组,第一个元素是值,第二个元素是索引PriorityQueue<int[]> pq = new PriorityQueue<int[]>(new Comparator<int[]>() {public int compare(int[] pair1, int[] pair2) {//若值不想等,则按值降序排列,否则按索引降序排列return pair1[0] != pair2[0] ? pair2[0] - pair1[0] : pair2[1] - pair1[1];}});for (int i = 0; i < k; ++i) {pq.offer(new int[]{nums[i], i});}int[] ans = new int[n - k + 1];ans[0] = pq.peek()[0];for (int i = k; i < n; ++i) {pq.offer(new int[]{nums[i], i});while (pq.peek()[1] <= i - k) {pq.poll();}ans[i - k + 1] = pq.peek()[0];}return ans;}
}
解法三
思路:
来自官方的解答,采用双端队列。
由于我们需要求出的是滑动窗口的最大值,如果当前的滑动窗口中有两个下标 i 和 j,其中 i 在 j 的左侧(i<j),并且 i 对应的元素不大于 j 对应的元素(nums[i]≤nums[j]),那么会发生什么呢?
当滑动窗口向右移动时,只要 i 还在窗口中,那么 j 一定也还在窗口中,这是 i 在 j 的左侧所保证的。因此,由于 nums[j] 的存在,nums[i] 一定不会是滑动窗口中的最大值了,我们可以将 nums[i] 永久地移除。
因此我们可以使用一个队列存储所有还没有被移除的下标。在队列中,这些下标按照从小到大的顺序被存储,并且它们在数组 nums 中对应的值是严格单调递减的。
当滑动窗口向右移动时,我们需要把一个新的元素放入队列中。为了保持队列的性质,我们会不断地将新的元素与队尾的元素相比较,如果新加入的元素比队尾元素大,那么队尾元素永远不会成为最大值,因为,新加入的元素一定在窗口中,可以直接删除队尾元素,再与新的队尾元素进行比较,若是新加入的元素比队尾元素小,那么直接加入队尾。此时在判断队首元素是否在窗口中,不在就移除。
代码:
class Solution {public int[] maxSlidingWindow(int[] nums, int k) {int n = nums.length;//双端队列,采用LinkedList实现Deque<Integer> deque = new LinkedList<Integer>();for (int i = 0; i < k; ++i) {while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {deque.pollLast();}deque.offerLast(i);}int[] ans = new int[n - k + 1];ans[0] = nums[deque.peekFirst()];for (int i = k; i < n; ++i) {while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {deque.pollLast();}deque.offerLast(i);while (deque.peekFirst() <= i - k) {deque.pollFirst();}ans[i - k + 1] = nums[deque.peekFirst()];}return ans;}
}
解法四
思路:
来自官方的解答,采用分块的思想。
我们可以将数组nums从左到右按照 k 个一组进行分组,最后一组中元素的数量可能会不足 k 个。如果我们希望求出 nums[i] 到 nums[i+k−1] 的最大值,就会有两种情况:
-
如果
i是k的倍数,那么nums[i]到nums[i+k−1]恰好是一个分组。我们只要预处理出每个分组中的最大值,即可得到答案; -
如果
i不是k的倍数,那么nums[i]到nums[i+k−1]会跨越两个分组,占有第一个分组的后缀以及第二个分组的前缀。假设j是k的倍数,并且满足i<j≤i+k−1,即j是两个分组的边界且j属于第二个分组的起始,那么nums[i]到nums[j−1]就是第一个分组的后缀,nums[j]到nums[i+k−1]就是第二个分组的前缀。如果我们能够预处理出每个分组中的前缀最大值以及后缀最大值,同样可以在 O(1) 的时间得到答案。
因此我们用 prefixMax[i] 表示下标i对应的分组中,以 i 结尾的前缀最大值;suffixMax[i] 表示下标i对应的分组中,以 i 开始的后缀最大值。它们分别满足如下的递推式
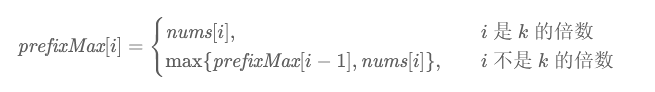
以及
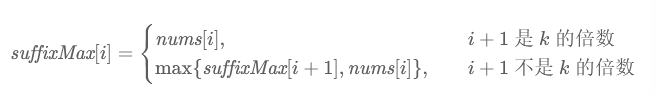
需要注意在递推 suffixMax[i] 时需要考虑到边界条件 suffixMax[n−1]=nums[n−1],而在递推 prefixMax[i] 时的边界条件 prefixMax[0]=nums[0] 恰好包含在递推式的第一种情况中,因此无需特殊考虑。
在预处理完成之后,对于 nums[i] 到 nums[i+k−1] 的所有元素,如果i不是 k 的倍数,那么窗口中的最大值为 suffixMax[i] 与 prefixMax[i+k−1]中的较大值;如果i是k的倍数,那么此时窗口恰好对应一整个分组,suffixMax[i] 和 prefixMax[i+k−1] 都等于分组中的最大值,因此无论窗口属于哪一种情况,
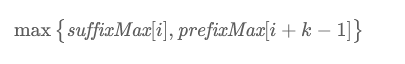
即为答案。
代码:
class Solution {public int[] maxSlidingWindow(int[] nums, int k) {int n = nums.length;int[] prefixMax = new int[n];int[] suffixMax = new int[n];for (int i = 0; i < n; ++i) {if (i % k == 0) {prefixMax[i] = nums[i];}else {prefixMax[i] = Math.max(prefixMax[i - 1], nums[i]);}}for (int i = n - 1; i >= 0; --i) {if (i == n - 1 || (i + 1) % k == 0) {suffixMax[i] = nums[i];} else {suffixMax[i] = Math.max(suffixMax[i + 1], nums[i]);}}int[] ans = new int[n - k + 1];for (int i = 0; i <= n - k; ++i) {ans[i] = Math.max(suffixMax[i], prefixMax[i + k - 1]);}return ans;}
}


;)






和SpawnActorOfClass())



二分搜索)






(IP地址、子网和公网、NAPT、代理))




)
)

)






)














