当前位置：首页 > news >正文

原假设的选择准则：总损失视角的假设检验

news 来源：原创 2025/9/17 12:38:20

在假设检验中，原假设（𝐻0）与备择假设（𝐻1）的设定是统计推断的核心。原假设通常代表“无效应”或“现状维持”，提供可操作的基准，例如总体均值等于某特定值，其保守性有助于控制第一类错误。备择假设则体现研究者关注的效应或差异，如治疗是否显著改善疾病，其形式影响检验方法的选择和统计功效。两者的设定需结合研究目的、理论背景及实际代价权衡，例如临床试验中，为降低对患者风险，原假设通常设为“治疗无效”。合理设定假设不仅保证推断科学性，也使检验结果更具解释性和决策价值。

一、引言

在统计推断与实际决策中，依据的是小概率原理，误判错误是不可避免的。以司法案例为例，法官和陪审团必须基于有限证据判断被告有无罪；在医学诊断中，医生需根据化验结果决定患者是否患病；在金融分析中，分析师则通过历史数据判断市场是否异常波动。尽管领域不同，本质上这些问题都可以抽象为假设检验：通过对零假设 $H_0$ 与备择假设 $H_1$ 的检验，作出是否拒绝 $H_0$ 的决策。
假设检验不可避免地涉及两类错误：一类错误（Type I Error）是当 $H_0$ 为真时错误地拒绝它，可能导致“虚假发现”；二类错误（Type II Error）是当 $H_1$ 为真时错误地接受 $H_0$，可能导致错失重要效应。在 Neyman-Pearson 框架下，研究者重点控制一类错误率 $\alpha$，并尽量降低二类错误率 $\beta$，以实现稳健决策；而在贝叶斯框架下，决策不仅考虑错误概率，还通过损失函数量化不同类型错误的严重程度，使得检验结果更符合实际风险与代价。
本文将围绕假设检验的理论与实践展开：首先从错误的条件概率出发，阐明其统计意义；随后引入损失函数，解释如何衡量总体风险；最后讨论原假设的选取原则，并结合直观示例加深理解，帮助读者在科研或实际问题中科学设定假设并合理决策。

二、假设检验的基本逻辑

2.1 零假设与备择假设

在统计推断中，假设检验的首要步骤是明确零假设 $H_0$ 与备择假设 $H_1$。零假设通常代表“无效应”或“现状维持”的情况，例如司法中“被告无罪”、医学中“患者健康”、金融中“市场无异常”。它提供了一个稳定的基准，用于与样本数据进行比较。备择假设 $H_1$ 则体现研究者或决策者真正关注的现象或效应，例如“被告有罪”“患者患病”“市场存在异常”，通常是希望通过数据证据加以支持的结论。
假设的设定不仅决定检验的方向，也影响检验方法的选择，例如单尾或双尾检验。科学合理地设定 $H_0$ 与 $H_1$ 是保证统计推断有效性和可靠性的前提。设定过程中需要考虑实际代价、研究目标和潜在风险，使检验既符合统计学理论，也满足实际决策需求。

2.2 决策与四种结果

在假设检验中，基于样本数据做出的判决有两类：“未拒绝 $H_0$”或“拒绝 $H_0$”。同时，真实情况可能为 $H_0$ 为真或 $H_1$ 为真。这两类维度的交叉产生了四种可能结果：

实际情况 \ 判决结果	判无罪（未拒绝 $H_0$）	判有罪（拒绝 $H_0$）
被告无罪（$H_0$ 为真）	正确判决 $1-\alpha$	一类错误 $\alpha$
被告有罪（$H_1$ 为真）	二类错误 $\beta$	正确判决 $1-\beta$

其中，一类错误（Type I Error）指错误拒绝真实的 $H_0$，其概率为 $\alpha$；二类错误（Type II Error）指未能拒绝 $H_0$ 而接受 $H_0$，即在 $H_1$ 为真时未能发现效应，其概率为 $\beta$。通过控制 $\alpha$，我们可以设定检验的严格程度，而通过样本量设计、效应大小估计等方法，则可以尽可能降低 $\beta$。

这种四象限逻辑不仅帮助我们理解假设检验的风险与决策权衡，也为进一步引入损失函数和总体风险分析奠定了基础，使统计推断能够与实际决策紧密结合。

三、损失函数框架下的总体风险

3.1 条件概率表达

在假设检验中，判决结果与真实状态的关系可以通过条件概率清晰刻画。基于前述四种可能性，我们有：

判决结果 \ 实际情况	$H_0$ 为真	$H_1$ 为真
未拒绝 $H_0$（判无罪）	$P(\text{未拒绝 } H_0 \mid H_0) = 1 - \alpha$	$P(\text{未拒绝 } H_0 \mid H_1) = \beta$
拒绝 $H_0$（判有罪）	$P(\text{拒绝 } H_0 \mid H_0) = \alpha$	$P(\text{拒绝 } H_0 \mid H_1) = 1 - \beta$

这种表达方式清晰展示了决策（拒绝或不拒绝 $H_0$）在不同真实状态下的正确性与错误概率，为进一步量化损失提供基础。

3.2 损失函数的引入

在实际问题中，不同错误的后果差异显著。例如：

在司法判决中，“冤枉无辜”（一类错误）的社会成本远高于“放走罪犯”（二类错误）；
在医学诊断中，严重疾病的“漏诊”（二类错误）可能造成更大损失。

为反映这种差异，引入损失函数 $\lambda(\alpha_i, \omega_j)$，表示在真实状态为 $\omega_j$ 时采取行动 $\alpha_i$ 所产生的损失。在两类状态、两类判决下，损失矩阵为：

实际情况 \ 判决结果	$\alpha_1$ = 判无罪（不拒绝 $H_0$）	$\alpha_2$ = 判有罪（拒绝 $H_0$）
$\omega_1$ = 被告无罪 ($H_0$ 为真)	$\lambda_{11} = 0$	$\lambda_{12} = L_0$
$\omega_2$ = 被告有罪 ($H_1$ 为真)	$\lambda_{21} = L_{1}$	$\lambda_{22} = 0$

其中 $L_0$ 与 $L_{1}$ 分别表示一类和二类错误的损失，体现“错误才产生代价，正确判决不产生损失”。

3.3 总体期望损失（风险函数）

基于损失函数，我们可以定义总体期望损失或风险函数：

\[R = \underset{j}{\sum} P \left(\right. H_{j} \left.\right) \textrm{ } \mathbb{E} \left[\right. \lambda \left(\right. \alpha , \omega_{j} \left.\right) \mid H_{j} \left]\right. . \]

代入损失矩阵后得到：

\[R = P \left(\right. H_{0} \left.\right) \left[\right. \lambda_{11} \left(\right. 1 - \alpha \left.\right) + \lambda_{12} \alpha \left]\right. + P \left(\right. H_{1} \left.\right) \left[\right. \lambda_{21} \beta + \lambda_{22} \left(\right. 1 - \beta \left.\right) \left]\right. . \]

由于 $\lambda_{11} = \lambda_{22} = 0$，可简化为：

\[R = P \left(\right. H_{0} \left.\right) L_{0} \alpha + P \left(\right. H_{1} \left.\right) L_{1} \beta . \]

这一公式表明总体风险取决于三个核心因素：

先验概率 $P(H_0), P(H_1)$；
错误概率 $\alpha, \beta$；
错误损失 $L_0, L_{1}$。

通过这一框架，可以在 Neyman-Pearson 方法与贝叶斯决策理论之间建立桥梁，实现对统计显著性、错误控制与实际代价的综合考量，为科学决策提供量化依据。

四、基于总损失的原假设选择与判断准则

4.1 判断准则

在统计决策理论中，选择原假设不仅关乎形式上的统计推断，更涉及总体损失最小化的问题。总体期望损失（风险函数）定义为：

\[R = P \left(\right. H_{0} \left.\right) L_{0} \alpha + P \left(\right. H_{1} \left.\right) L_{1} \beta , \]

其中：

$P \left(\right. H_{0} \left.\right)$、$P \left(\right. H_{1} \left.\right)$ 分别为原假设与备择假设成立的先验概率；
$L_{0}$、$L_{1}$ 分别为一类错误（Type I Error）和二类错误（Type II Error）的损失；
$\alpha$ 和 $\beta$ 分别为一类错误率和二类错误率。

基于这一公式，判断原假设设定的准则可以总结为：

先验概率权衡
若某一状态在总体中占绝对多数，则该状态适合作为原假设。原因在于：总损失中 $P \left(\right. H_{0} \left.\right) L_{0} \alpha$ 项占主导，若误判概率较小，则可有效降低总体损失。
错误损失权衡
当某类错误的损失极大时，即便其发生概率很小，也必须谨慎考虑原假设的设定和检验设计，以降低高损失事件的发生概率。
风险最小化
原假设的选择应使得在给定显著性水平 $\alpha$α 下，总体期望损失 $R$R 尽可能小，即在概率与损失权衡下，控制总体风险。
实际可操作性
原假设的选择应符合现实判断的直觉与可操作性，使统计决策易于实施，并能结合后续补救措施调整风险。

4.2 案例1：产品抽检

情境设定：

$H_{0}$：产品为合格；
$H_{1}$：产品为不合格。

现实中绝大多数产品是合格的，即 $P(H_{0}) \gg P(H_{1})$。若将不合格产品设为原假设，则总损失主要由大量合格产品被误判引起的 $L_{0} \alpha$ 决定。这不仅会导致生产延误，还会增加质检成本、仓储压力和客户投诉等社会成本。
相反，将合格产品设为原假设：

一类错误（误将合格产品判为不合格）发生概率 $\alpha$ 较小，损失 $L_{0}$ 可以接受；
二类错误（不合格产品未被发现）损失 $L_{1}$ 较大，但可通过强化抽检比例、改进检测技术或增加复检程序降低 $\beta$。

风险分析：

\[R = P \left(\right. H_{0} \left.\right) L_{0} \alpha + P \left(\right. H_{1} \left.\right) L_{1} \beta \]

由于 $P(H_{0})$ 较大，将“合格产品”作为原假设可显著降低 $R$ 的主导部分，并通过合理设计抽检程序控制二类错误，平衡质量风险与生产效率。

4.3 案例2：疫情核酸检测

情境设定：

$H_{0}$：个体未感染（健康者）；
$H_{1}$：个体已感染（携带病毒）。

一类错误（$\alpha$）：健康者被误判为阳性，损失 $L_{0}$（隔离、复查、心理压力等）；
二类错误（$\beta$）：感染者被误判为健康，损失 $L_{1}$（病毒传播、公共卫生风险）。

在疫情场景中：

先验概率 $P \left(\right. H_{1} \left.\right)$ 较小，即感染者比例低；
然而二类错误损失 $L_{1} \gg L_{0}$，即漏检可能带来严重公共卫生后果；
即使 $\beta$ 较小，$P \left(\right. H_{1} \left.\right) L_{1} \beta$ 也可能远超 $P \left(\right. H_{0} \left.\right) L_{0} \alpha$。

总损失公式：

\[R = P \left(\right. H_{0} \left.\right) L_{0} \alpha + P \left(\right. H_{1} \left.\right) L_{1} \beta \]

为了最小化 $R$：

选择“未感染”为原假设，便于大规模筛查；
通过增加检测频率、扩大样本量来降低 $\beta$，减少二类错误的风险；
即使增加少量健康者的误判（小的 $L_{0} \alpha$），也能显著降低总体损失。

实践体现：大规模核酸检测政策正是基于这种风险最小化思路，即通过降低二类错误来控制公共健康风险，从而优化社会总体损失。

4.4 综合分析

从上述两个案例可以看出，原假设的选择不是随意设定，而是基于概率分布、损失权重与总体风险最小化的综合考虑：

先验概率分布
- 若某种状态在总体中占绝对多数，则该状态适合作为原假设。
- 在产品抽检中，绝大多数产品合格，因此将“合格产品”设为原假设可减少大量误判合格产品的损失；
- 在疫情核酸检测中，未感染者占绝大多数，因此将“未感染”为原假设便于大规模筛查。
错误损失权重
- 一类错误和二类错误的损失大小直接影响风险函数 $R$ 的主导项。
- 在产品抽检中，误判合格产品（$L_{0}$）的损失相对可控，而漏检不合格产品（$L_{1}$）的损失较大，但可通过提高抽检比例降低二类错误率 $\beta$；
- 在疫情检测中，二类错误（漏检感染者）的损失远大于一类错误，即使感染者比例小，也需要通过提高检测频率和样本量降低 $\beta$，以最小化总体损失。
风险函数最小化
- 原假设的设定应在概率分布和损失权重的综合作用下，使总体期望损失 $R$ 尽可能小。
- 产品抽检和疫情检测的实践均体现了这一原则：通过合理选择原假设，并配合补救措施（复检、强化检测、随机抽检），实现风险控制与效率优化的平衡。

合理选择原假设应综合考虑总体占比、错误损失及风险函数大小。在不同场景中，虽然最常见状态通常被设为原假设，但针对高损失事件（如漏检不合格产品或感染者），必须通过优化检验设计降低二类错误率，从而实现总体损失最小化和社会效益最大化。

五、样本量n的影响分析

5.1 样本量为10的功效函数

条件设定

原假设：$H_0: \mu = 0$
备择假设：$H_1: \mu = 1$
总体分布：$X_i \sim N(\mu, 1)$，方差 $\sigma^2 = 1$
样本量：$n = 10$

样本均值分布

样本均值：

\[\bar{X} = \frac{1}{n}\sum_{i=1}^n X_i \sim N\left(\mu, \frac{1}{n}\right) \]

在 $H_0$ 下：$\bar{X} \sim N(0, 1/10), \sigma_{\bar{X}} \approx 0.316$
在 $H_1$ 下：$\bar{X} \sim N(1, 1/10)$

检验统计量

右尾检验：

\[Z = \frac{\bar{X} - 0}{1/\sqrt{10}} \sim N(0,1) \quad (H_0 \text{下}) \]

拒绝域

显著性水平 $\alpha$：

\[Z > z_{1-\alpha} \quad \Leftrightarrow \quad \bar{X} > \frac{z_{1-\alpha}}{\sqrt{10}} \]

功效计算

在 $H_1$ 下：

\[1-\beta = P_{H_1}\left(\bar{X} > \frac{z_{1-\alpha}}{\sqrt{10}}\right) = 1 - \Phi\left(\frac{\frac{z_{1-\alpha}}{\sqrt{10}} - 1}{1/\sqrt{10}}\right) \]

举例数值

$\alpha = 0.05, z_{0.95} \approx 1.645$
临界值：

\[\bar{X}_{\text{临界}} = \frac{1.645}{\sqrt{10}} \approx 0.52 \]

功效：

\[1-\beta = 1 - \Phi\left(\frac{0.52 - 1}{0.316}\right) = 1 - \Phi(-1.52) \approx 0.935 \]

结论：样本量 $n=10$ 时，$\alpha=0.05$ 可较好地区分 $\mu=0$ 与 $\mu=1$。

5.2 Python程序

import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
import matplotlib# 中文显示设置
matplotlib.rcParams['font.sans-serif'] = ['SimHei']  # 设置中文字体为黑体
matplotlib.rcParams['axes.unicode_minus'] = False    # 正确显示负号# 参数设定
mu0 = 0       # 原假设均值
mu1 = 1       # 备择假设均值
sigma = 1     # 总体标准差
alpha = 0.05  # 显著性水平# 样本量
n_values = np.array([5, 10, 15, 20, 25, 30, 35, 40])
powers = []for n in n_values:# 样本均值标准差sigma_xbar = sigma / np.sqrt(n)# 临界值（右尾检验）z_alpha = stats.norm.ppf(1 - alpha)xbar_crit = mu0 + z_alpha * sigma_xbar# 功效计算power = 1 - stats.norm.cdf(xbar_crit, loc=mu1, scale=sigma_xbar)powers.append(power)# 输出结果
for n, power in zip(n_values, powers):print(f"样本量 n={n}, 功效={power:.4f}")# 作图
plt.figure(figsize=(8,5))
plt.plot(n_values, powers, marker='o', linestyle='-', color='b')
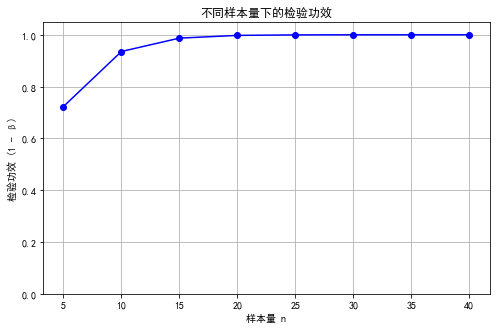
plt.title('不同样本量下的检验功效')
plt.xlabel('样本量 n')
plt.ylabel('检验功效 (1 - β)')
plt.ylim(0,1.05)
plt.grid(True)
plt.show()

总结

在假设检验中，核心在于根据样本数据对原假设 $H_{0}$ 与备择假设 $H_{1}$ 做出判断，同时量化可能的错误。通过条件概率可以清晰地表达四种结果：正确接受 $H_{0}$、一类错误、二类错误、正确拒绝 $H_{0}$。一类错误（Type I Error）由显著性水平 $\alpha$ 控制，而二类错误（Type II Error）与样本量、效应大小及检验设计相关。引入损失函数后，可以结合实际决策场景赋予不同错误以不同权重，形成总体期望损失（风险函数） $$R = P \left(\right. H_{0} \left.\right) L_{0} \alpha + P \left(\right. H_{1} \left.\right) L_{1} \beta$$，从而实现统计显著性与实际代价的综合考量。以均值检验为例，样本均值的分布随样本量变化，显著性水平确定临界值，进一步可计算功效$1-\beta$，评估检验在备择假设下正确拒绝 $H_{0}$ 的概率。通过对不同样本量的功效计算与可视化，可以直观地观察样本量对检验能力的影响，从而为实验设计、样本量选择提供量化依据。这一分析框架既适用于经典 Neyman-Pearson 方法，也可以拓展到贝叶斯决策背景，实现统计推断与实际应用的有机结合。

参考文献

Casella, G., & Berger, R. L. (2002). Statistical Inference (2nd ed.). Duxbury.
经典统计推断教材，详细介绍假设检验、显著性水平及功效分析，适合作为理论基础参考。
Lehmann, E. L., & Romano, J. P. (2005). Testing Statistical Hypotheses (3rd ed.). Springer.
深入讲解 Neyman-Pearson 定理与功效函数设计，提供原假设选择与风险分析的方法论。
Hogg, R. V., McKean, J., & Craig, A. T. (2019). Introduction to Mathematical Statistics (8th ed.). Pearson.
系统介绍条件概率表达、一类和二类错误及样本量对功效的影响，配合例题易于理解。
Wasserman, L. (2004). All of Statistics: A Concise Course in Statistical Inference. Springer.
以简明方式覆盖统计推断全景，包括损失函数与总体风险分析，适合快速入门与应用。
Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences (2nd ed.). Lawrence Erlbaum.
重点介绍功效分析与样本量计算方法，提供社会科学实验设计与功效可视化的实用指导。

实际情况 \ 判决结果	判无罪（未拒绝 \(H_0\)）	判有罪（拒绝 \(H_0\)）
被告无罪（\(H_0\) 为真）	正确判决 \(1-\alpha\)	一类错误 \(\alpha\)
被告有罪（\(H_1\) 为真）	二类错误 \(\beta\)	正确判决 \(1-\beta\)

判决结果 \ 实际情况	\(H_0\) 为真	\(H_1\) 为真
未拒绝 \(H_0\)（判无罪）	\(P(\text{未拒绝 } H_0 \mid H_0) = 1 - \alpha\)	\(P(\text{未拒绝 } H_0 \mid H_1) = \beta\)
拒绝 \(H_0\)（判有罪）	\(P(\text{拒绝 } H_0 \mid H_0) = \alpha\)	\(P(\text{拒绝 } H_0 \mid H_1) = 1 - \beta\)

实际情况 \ 判决结果	\(\alpha_1\) = 判无罪（不拒绝 \(H_0\)）	\(\alpha_2\) = 判有罪（拒绝 \(H_0\)）
\(\omega_1\) = 被告无罪 (\(H_0\) 为真)	\(\lambda_{11} = 0\)	\(\lambda_{12} = L_0\)
\(\omega_2\) = 被告有罪 (\(H_1\) 为真)	\(\lambda_{21} = L_{1}\)	\(\lambda_{22} = 0\)

目录