实用指南：Git分支管理：从创建到合并冲突解决（二）

git分支

master：默认的分支名称或是主分支（现在很多项目已改用 main），本质是一个存储最新提交commit ID的文件。

通过打印master中的内容，可以得到最新提交的commit ID。
在打印这个ID的信息 git cat-file -p 6dcef86b56b8a8934fc28605b67ef9892674a5ad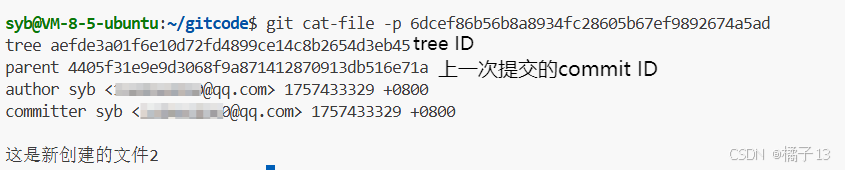

我们可以得到tree ID与上一次parent ID，而这个parent ID实际上就是上一次提交commit ID。
然后再打印这个commit ID，又会得到上上次的commit ID…… 以此类推。
我们最终得到一条时间线，这就是master的提交时间线。
通过命令git log --pretty=oneline 可以看到master中所有提交的commit ID 的历史记录（这里记录比较少，因为我提交次数少）。

master提交时间线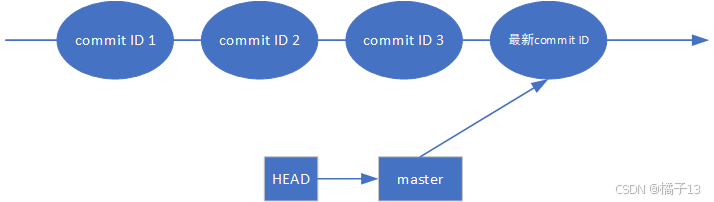

查看所有分支

git branch

这里只有master分支，master前有个星号，说明HEAD指向master，master是正在工作的分支。

HEAD可以指向其他分支，被指向的分支就是当前正在工作的分支。

创建分支

git branch 分支名称

例子：创建dev分支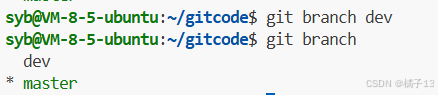

通过tree .git命令，我们可以看到所有的分支在路径 .git/refs/heads/ 下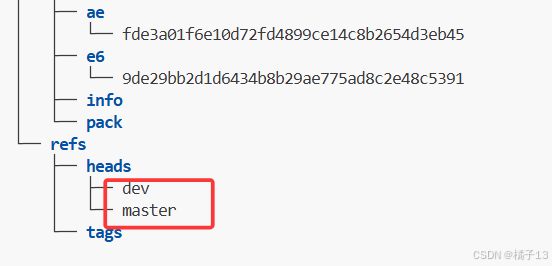

创建的dev分支实际上存的是最新的commit ID，即master所存的commit ID。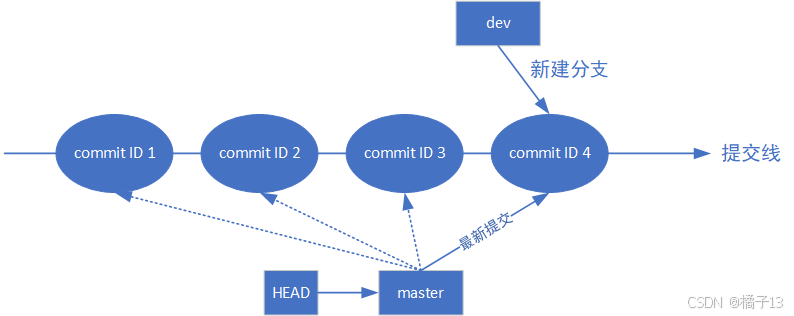

切换分支

git checkout 分支名称
git checkout -b 新分支名称 # 新建并切换到新的分支

例子：切换到dev分支
使用git checkout dev切换分支。

cat .git/HEAD打印一下HEAD指针。

此时HEAD确实指向了dev分支。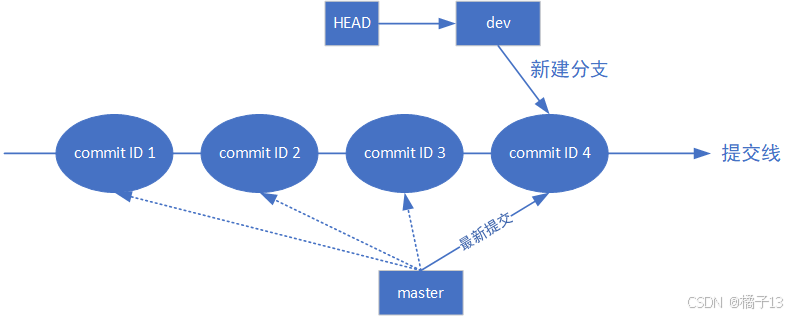

若哦我们再进行提交，master会进行更新，而master不会，原因是dev是当前的工作分支。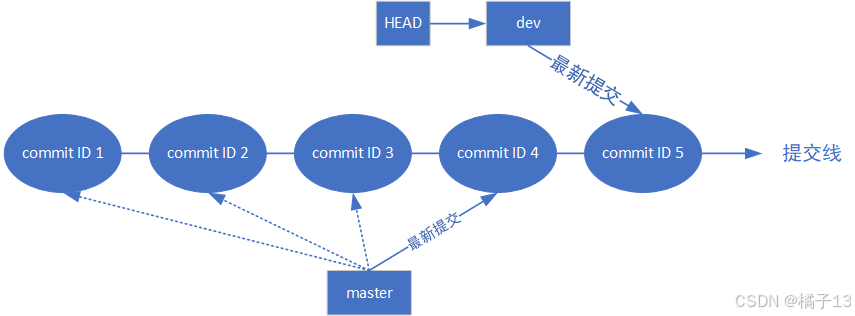

合并分支

git merge 分支名称

仍以上面为例：
使用git checkout master先切换回master分支。
使用命令git merge dev #将dev分支合并到当前的master分支进行合并分支。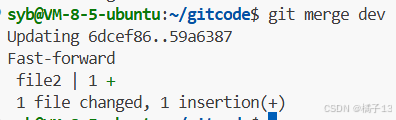

这里默认使用的是快速合并模式，就是直接将master中存储dev中最新的commit ID。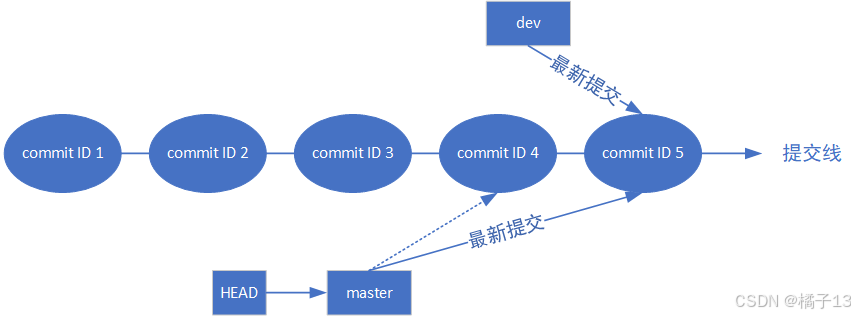

选项：
–no-ff：全称是 “no fast-forward”（不使用快进模式），用于控制合并分支时的提交历史记录方式。

git merge --no-ff #分支名称 -m "合并描述"

默认情况下，当 Git 发现可以通过「快进合并」（fast-forward）完成分支合并时（即目标分支没有新提交，能直接指向源分支的最新提交），会直接移动分支指针，不产生新的合并提交。
而 --no-ff 选项强制 Git 无论是否能快进合并，都创建一个新的合并提交，明确记录这次分支合并的操作。
例子：
假设存在分支关系：master 分支落后于 dev分支（main 没有新提交）：

A---B---C dev
/
D---E master

1. 快速模式（默认模式）

git merge dev # 在master分支下进行

结果：master 指针直接移动到 C（注意：这里没有进行新的提交，仅仅只是master指针进行移动），无新提交，历史记录线性化：

D---E---A---B---C master, dev

2. 使用 --no-ff 合并：

git merge --no-ff dev -m "合并描述" #强烈建议加上 -m “合并描述” 明确此次合并做了什么

结果：创建一个新的合并提交 M（注意：这里又进行了一次提交），明确记录合并操作，保留分支历史：

A---B---C dev
/ \
D---E-----------M main

优势：会在历史中清晰留下 “合并功能分支” 的标记。

删除分支

git branch -d 分支名称 # -d（delete）
git branch -D 分支名称 # 强行删除

注意事项

1. 无法删除当前所在分支
   必须先切换到其他分支（如 git checkout main），才能删除目标分支。否则会提示：
   error: Cannot delete branch ‘feature/login’ checked out at ‘/path/to/your/project’

2. 仅删除本地分支，不影响远程分支
   git branch -d 只操作本地仓库的分支。如果需要删除远程分支，需使用：

git push origin --delete 远程分支名称 # 例如 git push origin --delete feature/login

3. 删除后的恢复方式
   如果误删了包含未合并代码的分支，可通过 git reflog 找回分支的最后一次提交，再重新创建分支：

# 1. 查找被删除分支的最后一次提交记录（找到对应的 commit ID，如 a1b2c3d）
git reflog
# 2. 基于该提交重新创建分支，恢复代码
git branch feature/login a1b2c3d

注：因为创建，合并和删除分支非常快，所以git鼓励你使用分支完成某个任务，合并后再删掉分支，这和直接在master分支上工作效果是一样的，但过程更安全。

合并冲突问题

syb@VM-8-5-ubuntu:~/gitcode$ touch conflict
syb@VM-8-5-ubuntu:~/gitcode$ vim conflict #在mater主分支下添加内容
syb@VM-8-5-ubuntu:~/gitcode$ git add .
syb@VM-8-5-ubuntu:~/gitcode$ git commit -m "新建文件conflict在master下"
[master 81bf776] 新建文件conflict在master下
1 file changed, 1 insertion(+)
create mode 100644 conflict
syb@VM-8-5-ubuntu:~/gitcode$ git checkout -b dev1
Switched to a new branch 'dev1'
syb@VM-8-5-ubuntu:~/gitcode$ vim conflict #在dev1分支下进行修改
syb@VM-8-5-ubuntu:~/gitcode$ git add .
syb@VM-8-5-ubuntu:~/gitcode$ git commit -m "在dev1分支下修改confict"
[dev1 641cfef] 在dev1分支下修改confict
1 file changed, 1 insertion(+), 1 deletion(-)
syb@VM-8-5-ubuntu:~/gitcode$ git checkout master
Switched to branch 'master'
syb@VM-8-5-ubuntu:~/gitcode$ vim conflict #在master分支下进行修改
syb@VM-8-5-ubuntu:~/gitcode$ git add .
syb@VM-8-5-ubuntu:~/gitcode$ git commit -m "在master分支下修改confict"
[master 3ff2624] 在master分支下修改confict
1 file changed, 1 insertion(+), 1 deletion(-)

这样我们创造出这样的情况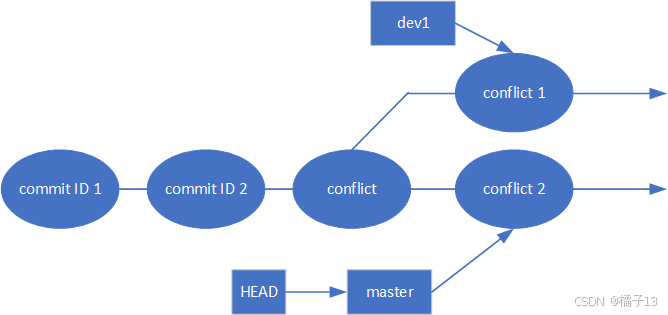

这是我们进行合并

git merge dev1

这时 git 无法自动合并，会提示冲突。解决方法如下：

1. 打开冲突文件,手动解决标记为<<<<<<<、========、>>>>>>> 的冲突部分
2. 解决后执行git add <冲突文件> 标记为已解决
3. 最后执行 git commit 完成合并（Git 会自动生成合并提交信息）

通过命令可以形象看出合并冲突

git log --graph --abbrev-commit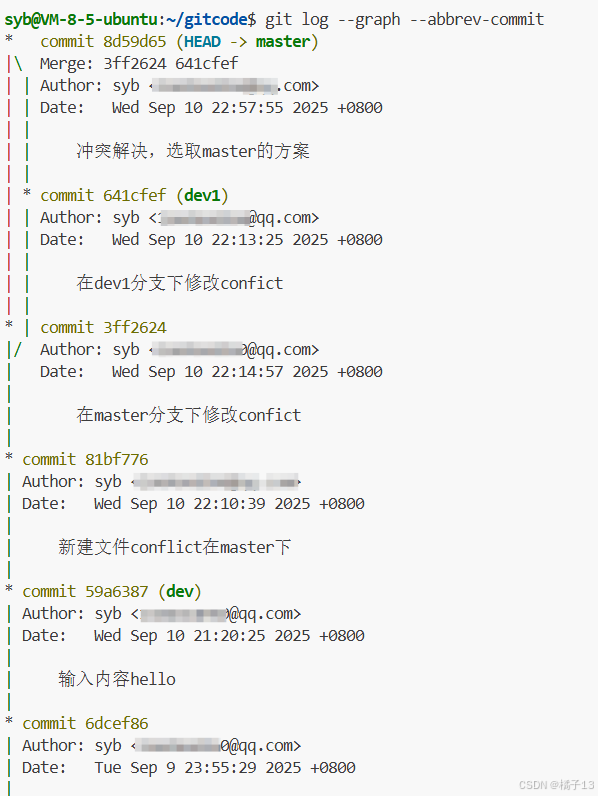

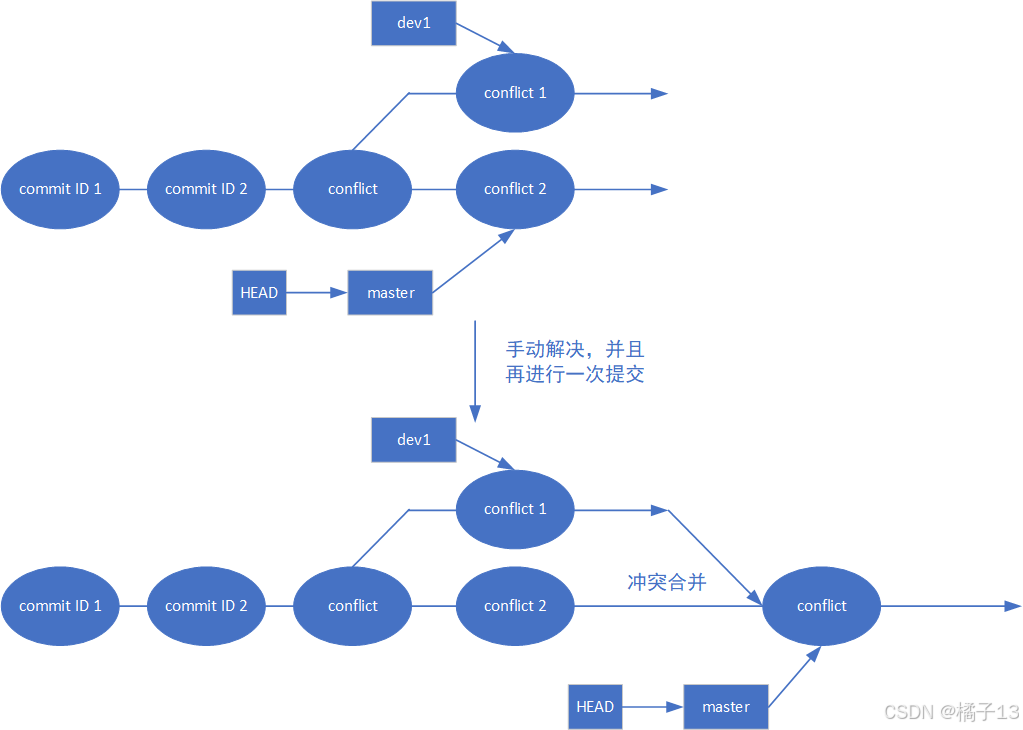
补充常用参数：

–abort：放弃当前合并过程，恢复到合并前的状态（解决冲突时遇到问题可用）

git merge --abort

总结：

快进合并（Fast-forward）
如果目标分支没有新提交，而被合并分支（如 dev）是基于目标分支最新提交开发的，Git 会直接将目标分支指针移动到被合并分支的最新提交，不会创建新提交。
示例：

# 合并前
A <- B <- C (main)
\
D <- E (feature)
# 合并后（Fast-forward）
A <- B <- C <- D <- E (main, feature)

三方合并（Three-way merge）
如果目标分支和被合并分支都有新提交，Git 会基于两者的共同祖先，创建一个新的「合并提交」，整合两边的修改。
示例：

# 合并前
A <- B <- C <- F (master)
\
D <- E (dev)
# 合并后（产生新的合并提交 G）
A <- B <- C <- F <- G (master)
\ /
D <- E <- (dev)

合并冲突（Merge conflict）
如果两边修改了同一文件的同一部分，Git 无法自动合并，会提示冲突。此时需要：
打开冲突文件，手动解决标记为 <<<<<<<、=======、>>>>>>> 的冲突部分
解决后执行 git add <冲突文件> 标记为已解决
最后执行 git commit 完成合并（Git 会自动生成合并提交信息）

切换分支时的安全问题

git stash 是 Git 中一个非常实用的命令，用于临时保存工作区和暂存区的修改，让你可以在不提交当前变更的情况下，切换到其他分支或进行其他操作。

作用：
当你正在一个分支上开发，突然需要切换到另一个分支处理问题，但当前工作还没完成、不想提交（因为提交可能不完整或不符合规范）时，git stash 可以帮你：

• 把工作区和暂存区的修改 “暂存” 起来（存入 Git 的 “栈” 中）
• 让工作区回到干净状态（与最近一次提交保持一致）
• 之后可以随时从 “栈” 中恢复之前的修改

一系列命令：

1. 保存当前修改：git stash 或 git stash save "描述"

# 简单保存（默认描述）
git stash
# 带描述保存（推荐，方便后续识别）
git stash save "完善用户登录逻辑：未完成密码加密部分"

注意：
会保存：工作区的修改 + 暂存区已 git add 的内容
不会保存：未跟踪的新文件（需用 -u 选项）、已忽略的文件

git stash -u -m "包含新添加的xxx文件"

2. 查看 stash 列表：git stash list

git stash list

输出示例：

stash@{
0
}: On feature/login: 相关描述yyy
stash@{
1
}: On dev: 相关描述xxx（临时保存）

注：stash@{n} 是 stash 的标识符，n 越小表示越新保存的内容

3. 恢复 stash 内容：git stash apply 或 git stash pop

# 恢复最近一次 stash（stash@{0}），但不删除 stash 记录
git stash apply
# 恢复指定 stash（如 stash@{1}）
git stash apply stash@{
1
}
# 恢复最近一次 stash 并删除该 stash 记录（推荐，避免堆积）
git stash pop

恢复后，修改会回到工作区（之前暂存的内容会变回暂存状态）

4. 删除 stash 记录：git stash drop 或 git stash clear

# 删除最近一次 stash
git stash drop
# 删除指定 stash
git stash drop stash@{
1
}
# 清空所有 stash 记录（谨慎使用）
git stash clear

5. 查看 stash 具体修改内容：git stash show

# 查看最近一次 stash 的修改摘要
git stash show
# 查看详细修改（类似 git diff）
git stash show -p

Git 切换分支（git checkout/git switch）时，会做两件事：
把当前工作区、暂存区的内容 “重置” 为目标分支的最新提交状态；
同时，尝试保留你未提交的修改—— 但前提是：这些修改 “不干扰” 目标分支的文件（即修改的文件在目标分支中没有冲突）。
如果未提交修改与目标分支的文件有冲突，Git 会直接拒绝切换分支，避免文件内容被覆盖或丢失；但如果没有冲突，未提交文件会 “跟随” 你切换到新分支，此时风险才会出现。

关于未提交的文件，在切换分支后是否安全？

场景 1：未提交文件是「已跟踪文件」（曾 git add 过，即使本次没 add）
安全情况：目标分支中，这些文件的内容与当前分支的 “最近一次提交” 完全一致（无冲突）。
结果：该文件的修改会保留在工作区，切换后仍能看到。
危险情况：目标分支中，这些文件的内容与当前分支的 “最近一次提交” 不同（有冲突）。
结果：git 直接报错拒绝切换，提示 “本地修改会被合并覆盖”，不会丢失文件。

场景 2：未提交文件是「未跟踪文件」（从未 git add 过，如新建的xxx文件）
安全情况：目标分支中不存在同名文件。
结果：xxx文件会保留在工作区，切换后仍在。
危险情况：目标分支中存在同名文件，且内容与当前未跟踪文件不同。
结果：git 会覆盖你的未跟踪文件（用目标分支的xxx文件替换你新建的xxx文件），且不会提前警告！你的修改会直接丢失，无法恢复。

为什么推荐先 git stash 再切换分支？

虽然大部分情况下 Git 会保护已跟踪文件，但未跟踪文件的覆盖风险是 “隐形” 的—— 你可能不知道目标分支是否有同名文件，一旦覆盖就无法挽回。

安全操作流程：
切换分支前，用 git status 查看未提交文件（区分已跟踪 / 未跟踪）； 用 git stash -u（-u包含未跟踪文件）临时保存所有修改：
bash git stash -u -m "暂存当前修改：包含新添加的xxx文件"
切换分支（此时工作区干净，无任何风险）；
回到原分支后，用 git stash pop 恢复修改。