当前位置：首页 > news >正文

AVL 树

news 来源：原创 2025/7/21 22:31:47

1.AVL树的概念

AVL树是最先发明的自平衡二叉查找树，AVL树可以是一棵空树，或者具有以下性质的树：左右子树都是AVL树。且左右子树的高度差的绝对值不超过1。
AVL树是一颗高度平衡搜索二叉树，通过控制高度去控制平衡。

AVL树的发明者是G. M. Adelson-Velsky和E. M. Landis，故命名为AVL树，他们在1962年的论文《An algorithm for the organization of information》中提到了AVL树的概念。

为了方便观察和控制树是否平衡，引入一个叫做平衡因子的概念，每一个结点都有一个平衡因子，任何结点的平衡因子等于右子树高度 - 左子树高度，结合AVL树中左右子树高度绝对值不超过1的特点，可以得出，任何结点的平衡因子等于 -1、0、1，不会是其他值（AVL树不一定必须要平衡因子，只是为了便于观察）。

AVL树是高度平衡搜索二叉树，要求的高度差是不超过1，按道理来说要求高度差是0，会更平衡，这里是因为这样的想法在有些情况下实现不了，比如说只有2个结点的时候，4个结点的时候，高度差无法做到是0，最好的情况下就是1。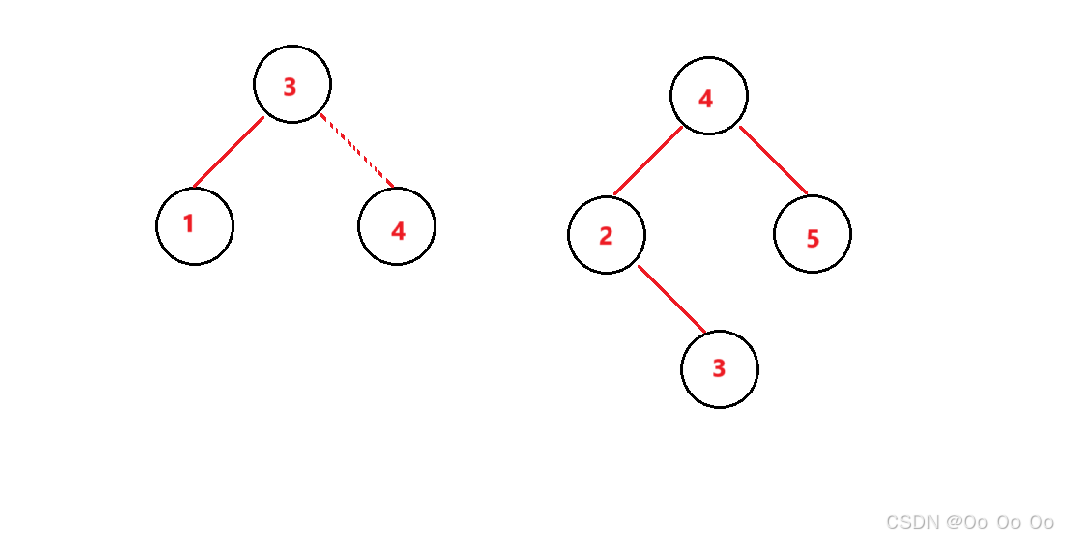

AVL树整体结点数量分布和完全二叉树完全类似，高度可以控制在logN，其增删查改的效率也可以控制在O(logN)，相比起二叉搜索树就有了质的提升。

2.AVL树的实现

2.1AVL树的结构

template<class K, class V>
struct AVLTreeNode
{AVLTreeNode(pair<K, V> kv):_bf(0),_parent(nullptr),_left(nullptr),_right(nullptr),_kv(kv){}int _bf;// 平衡因子AVLTreeNode* _parent;// 需要建立子结点和父结点的联系AVLTreeNode* _left;AVLTreeNode* _right;pair<K, V> _kv;
};
template<class K,class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:private:Node* _root = nullptr;
};

2.2AVL树的插入

2.2.1插入的大概过程

插入的过程稍微有点复杂，先来看看大概的过程，然后再细分讨论

AVL树的插入和搜索二叉树按照相同的规则插入，都是小的值往左边插入，大的值往右边插入。
新增结点以后，只会影响祖先结点的高度，换句话说，可能会影响到部分祖先结点的平衡因子，所以更新结点的平衡因子，最坏情况下要更新到根结点，有些情况下更新到中间就可以停止，具体情况插入的时候分析讨论
更新平衡因子过程中没有出现问题（也就是平衡因子都是平衡的），则插入结束
更新平衡因子过程中出现不平衡，对不平衡子树进行旋转，旋转的作用就是调节平衡，同时可以降低子树的高度，旋转后不会影响上一层，就插入结束

2.2.2平衡因子的更新

平衡因子的更新原则是：

只有子树高度变化才会影响当前结点平衡因子；
新增结点在parent的右子树，parent的平衡因子 ++
新增结点在parent左子树，parent平衡因子 --
parent所在的子树的高度是否变化决定了是否要继续向上更新

更新停止的条件：

若更新后parent的平衡因子等于0，那么更新中parent的平衡因子变化情况就只有两种：-1--->0或者1--->0，说点明更新前parent的子树一边高一边低，新增结点是插入在低的那一边，插入后parent所在的子树高度不变，不会影响parent的父亲结点的平衡因子，更新结束
若更新后的平衡因子等于1或-1，那么更新中parent的平衡因子变换情况也只有两种：0--->-1或者0--->-1，说明更新前parent子树两边一样高，新增结点插入后，导致parent所在的子树一边高一边低，不过parent所在的子树任然符合平衡要求，但是高度增加了1，会影响parent的父亲结点的平衡因子，所以要向上更新
更新后的平衡因子等于2或-2，更新前更新中parent的平衡因子变换情况也是两种：1--->2或-1--->-2，说明更新前parent所在的子树一边高一边低，新增结点是插入在高的那一边，parent所在的子树高的那边更高了，破坏了平衡，很明显，parent所在的子树不符合平衡要求，这个时候就需要旋转处理了，旋转的目的有两个：1、把parent所在的子树旋转平衡；2、降低parent所在子树高度，降低或恢复到插入结点前的高度。旋转以后就不用继续往上更新（因为高度不变）
不断更新，更新到根节点，根节点的平衡因子是1或-1就停止了

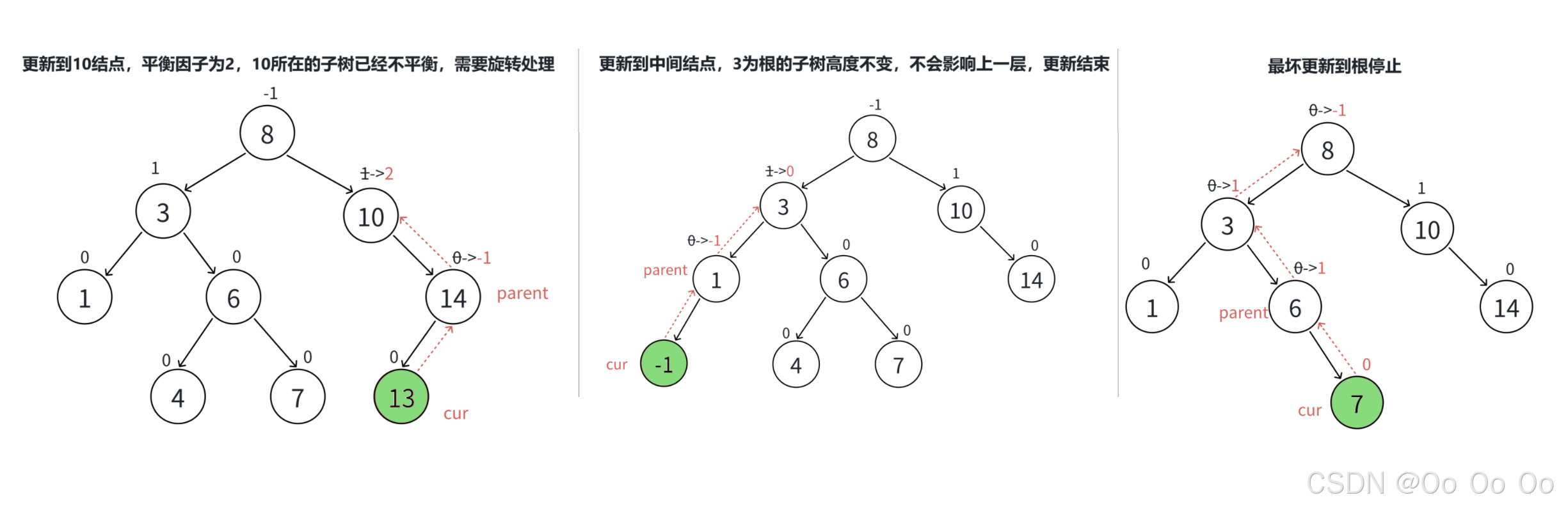
2.2.3插入结点及平衡因子更新的代码实现

	bool Insert(const pair<K, V> kv){if (root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = cur;while (cur){// 小于往左边走if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}// 大于往右边走else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);// 大于在右边if (kv.first > parent->_kv.first){parent->_right = cur;}// 小于在左边else{parent->_left = cur;}// 链接父子关系cur->_parent = parent;// 处理平衡因子while (parent){// 插在在左边--if (parent->_left == cur){parent->_bf--;}// 插在在右边++else{parent->_bf++;}// 等于0就不用向上更新if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){// 旋转处理}else{//当出现其他情况时，处理错误assert(false);}}return false;}

2.3旋转

2.3.1旋转的原则

保持搜索树的规则
将旋转的树从不平衡变平衡，降低旋转树的高度

旋转的方式有四种：左单旋、右单旋、左右双旋、右左双旋。

2.3.2右单旋

图中展示的根节点为10的AVL树抽象图，a、b、c均为三颗高度为h的子树(h>=0)，a、b、c均符合AVL树的要求，10可能是整棵树的根，也可能是一整棵树中局部的子树的根。通过抽象图的方式进行一种概括抽象的表示，其代表了所有右单旋的场景，但是实际上的右单旋的具体形态有很多种。
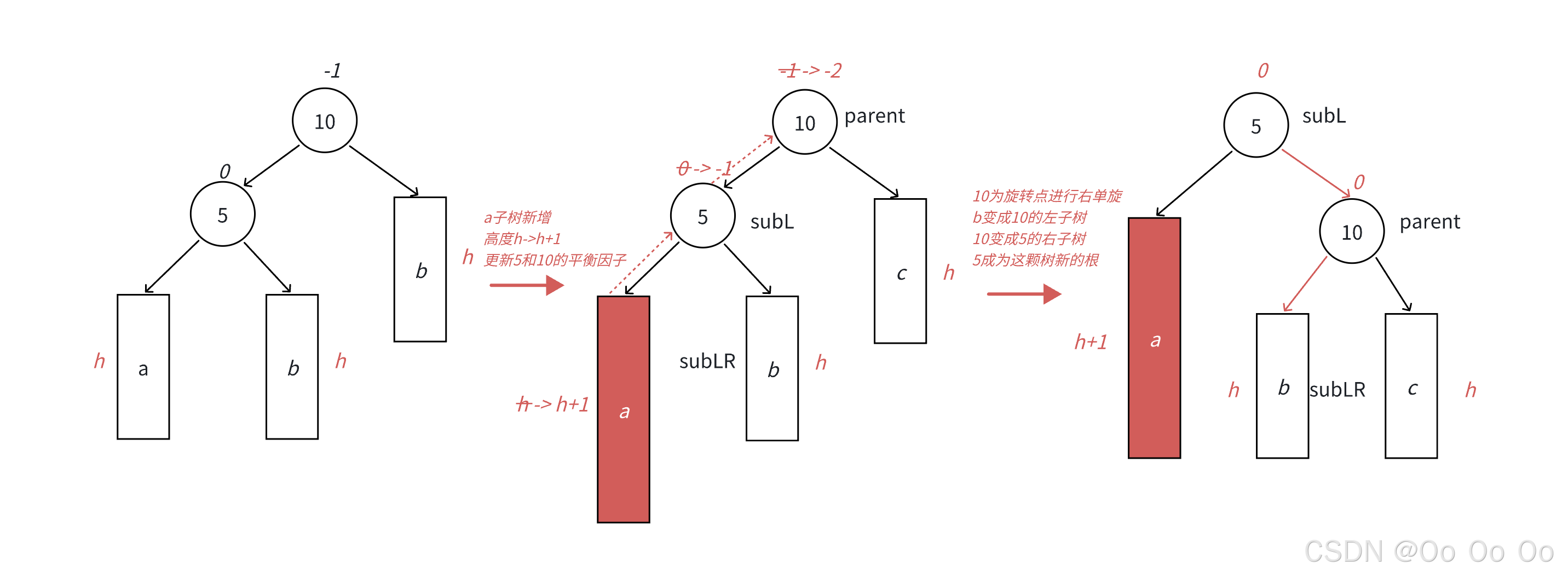
在a子树中插入一个新结点，导致a子树的高度从h变为h+1，不断向上更新平衡因子，导致结点10的平衡因子从-1变为-2，10为根的树左右高度差超过1，违反了平衡规则，10为根的树的左边太高了，需要往右边旋转，以控制两棵树的平衡。
旋转的核心步骤：因为 5 < b子树的值 < 10，这个时候将b变成10的左子树，10变成5的右子树，5变成这棵树新的根，既符合搜索树的规则，控制了平衡，同时又将这棵树的高度恢复到插入之前的h+2。如果结点10是整棵树的局部子树，那么通过这样的旋转方式也不会影响上一层，所以插入就到此结束了。

具体的a、b、c高度讨论：

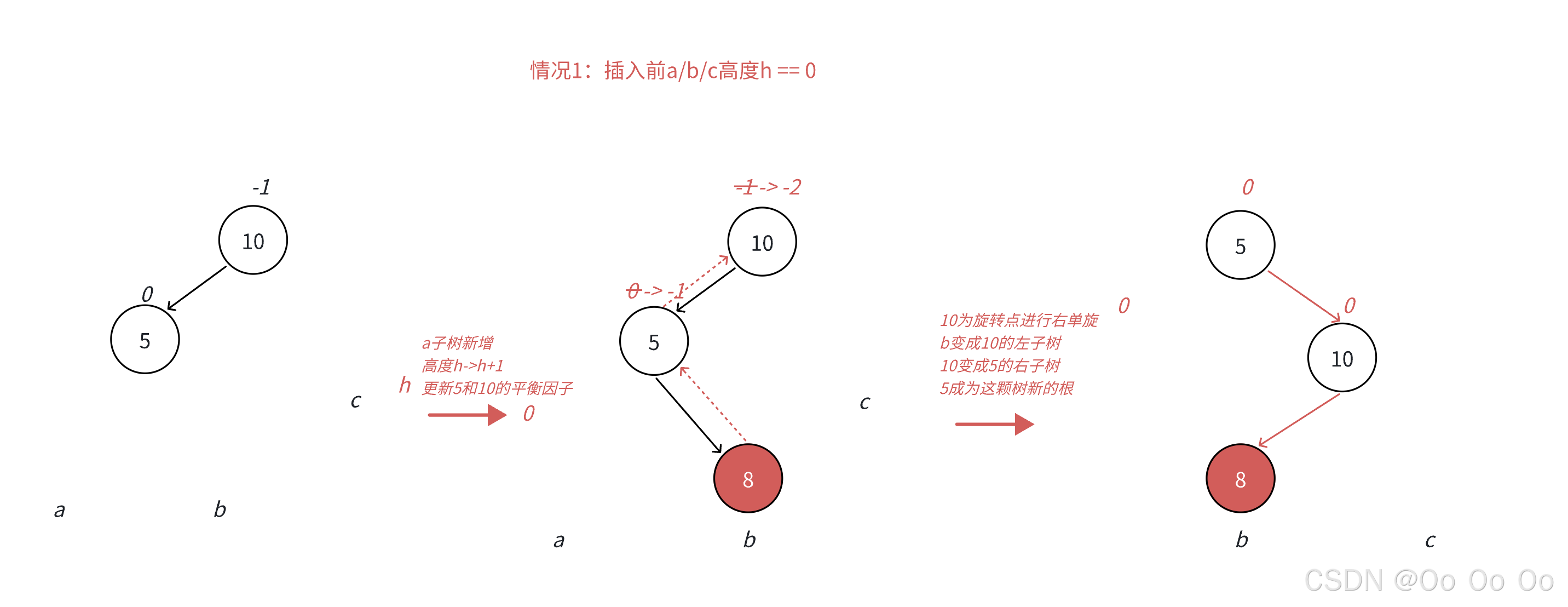
当h等于0的时候，这种时候很简单，只需要将5作为新的根，10放到其右边即可
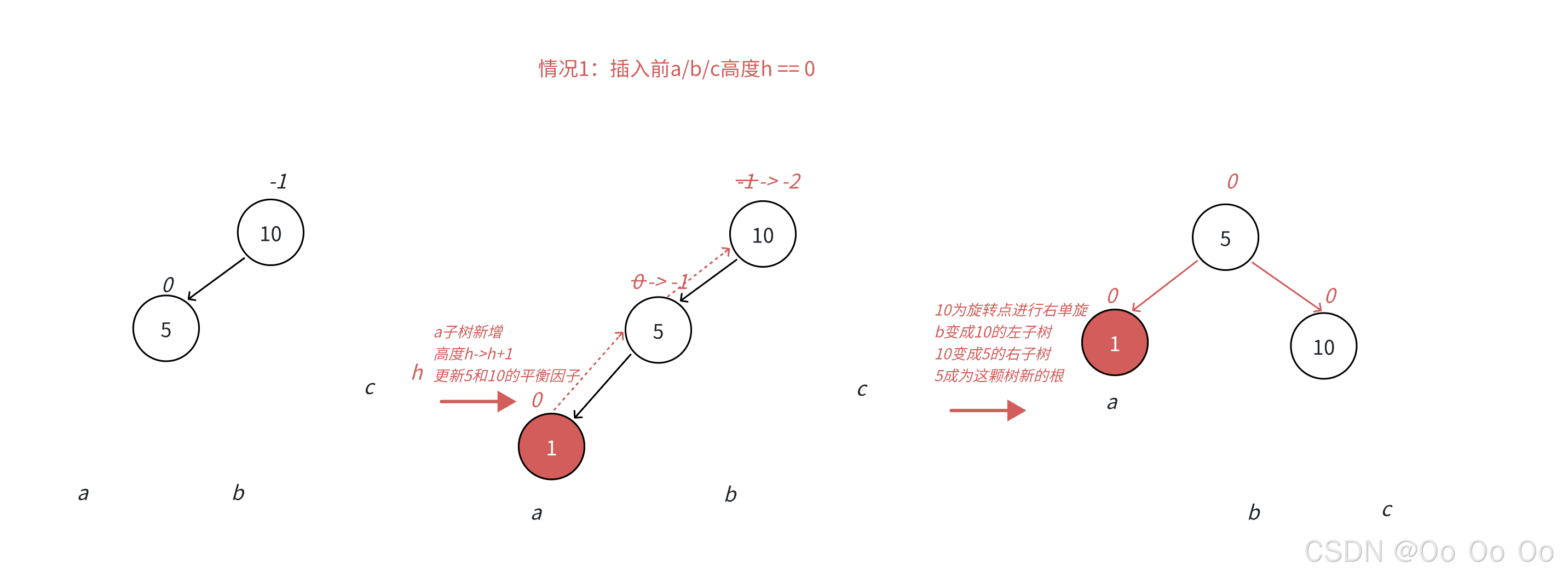
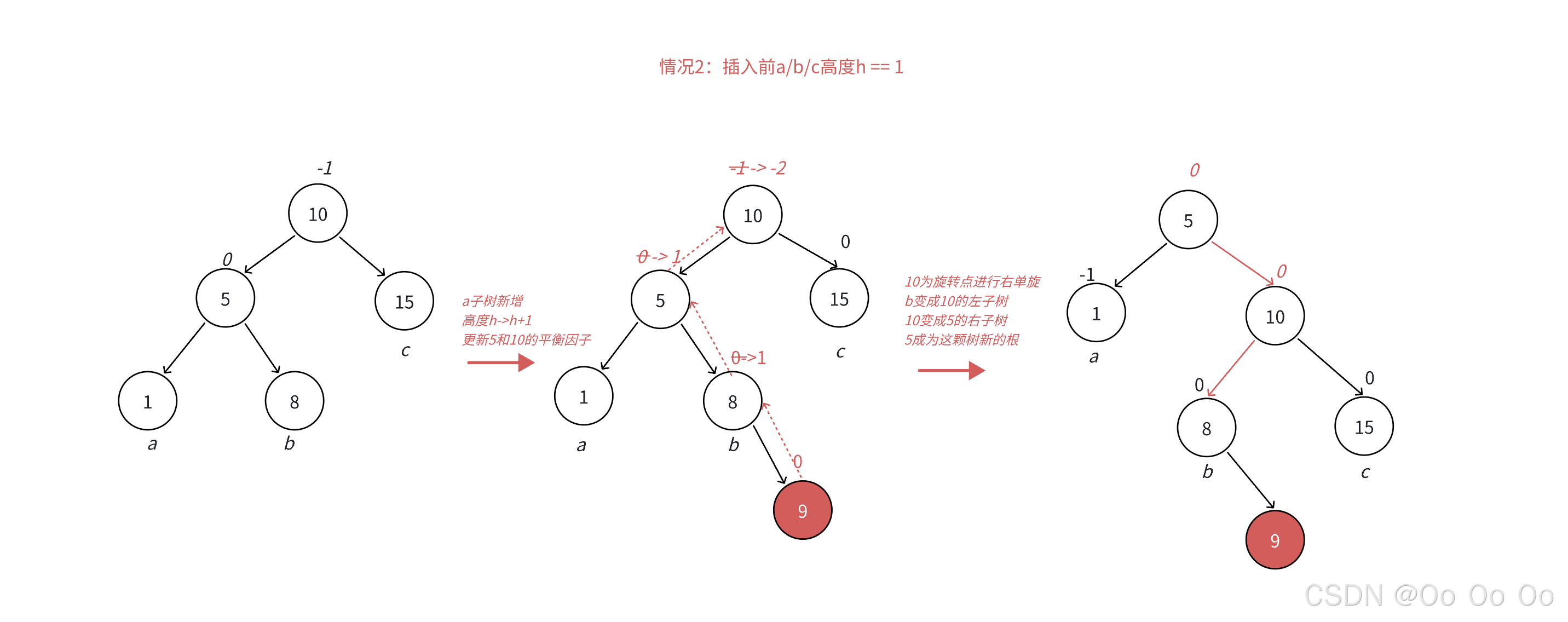
当h等于1的时候，同样的，一样的方式进行旋转
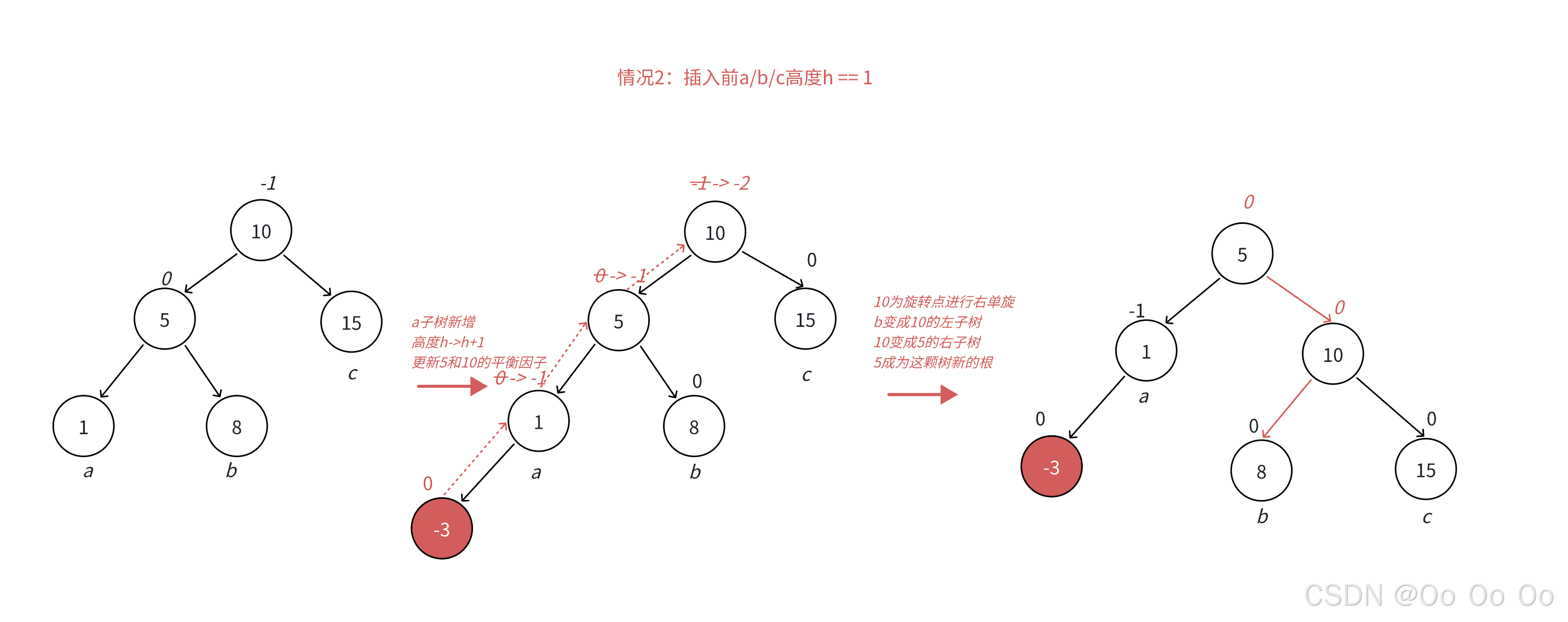
当h等于2的时候，AVL子树的情况要加以注意(以a、b、c为x的形状进行分析)
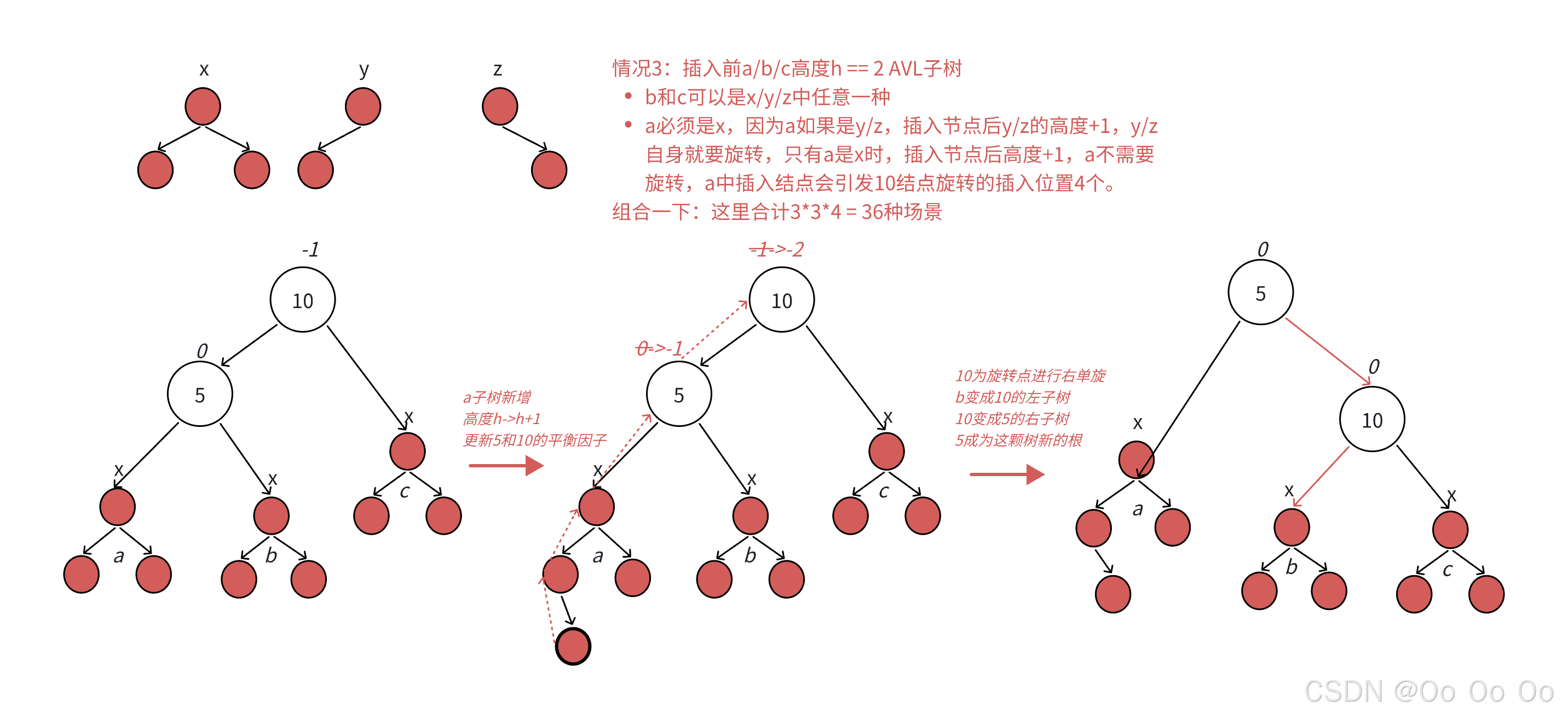
当h等于3的时候，可能出现的情况就更多，也更加复杂

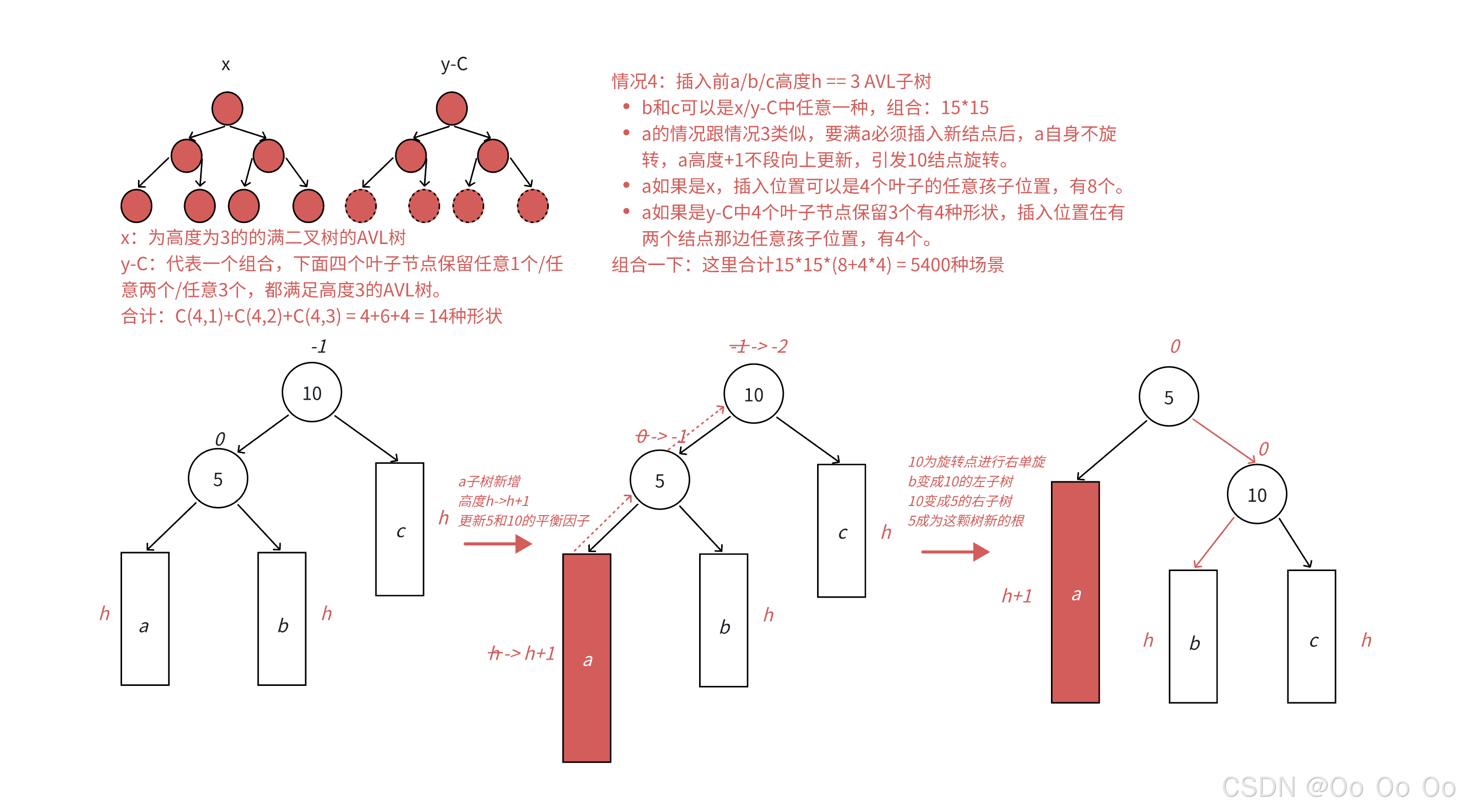
通过这样的推导可以看出抽象图的重要性，在后面的右旋和双旋部分都主要以抽象图来讨论。

右单旋代码实现：

void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;Node* ppNode = parent->_parent;// 链接结点,注意不要漏了_parent也要正确连接parent->_left = subLR;if (subLR){subLR->_parent = parent;}subL->_right = parent;parent->_parent = subL;// parent的上面还有结点，parent只是整棵树中的一棵子树if (ppNode){if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}// parent就是根结点，更新根结点else{_root = subL;_root->_parent = nullptr;}// 处理平衡因子,需要更改的只有parent和subL(因为只有他们两个的子树发生了改变)parent->_bf = 0;subL->_bf = 0;
}

2.3.3左单旋

左单旋和右单旋非常相似。图中展示的根节点为10的AVL树抽象图，a、b、c均为三颗高度为h的子树(h>=0)，a、b、c均符合AVL树的要求，10可能是整棵树的根，也可能是一整棵树中局部的子树的根。通过抽象图的方式进行一种概括抽象的表示，其代表了所有左单旋的场景，但是实际上的左单旋的具体形态有很多种(同右单旋)。
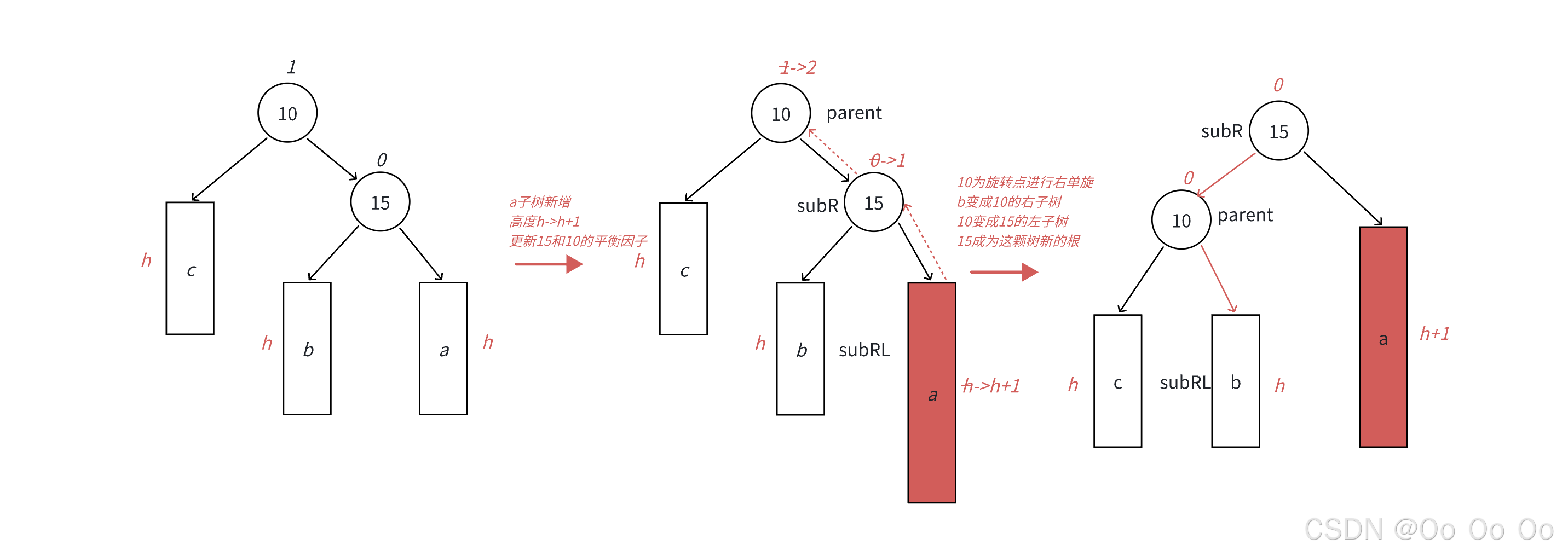
在a子树中插入一个新结点，导致a子树的高度从h变为h+1，不断向上更新平衡因子，导致结点10的平衡因子从1变为2，结点10为根的树左右高度差超过1，违反了平衡规则。结点10为根的树右边太高了，需要左往左边旋转，以控制两棵树的平衡
旋转核心步骤：因为5 < b子树 <10，将b变成10的左子树，10变为5的右子树，5变为这棵树新的根，既符合搜索树的规则，控制了平衡，同时又将这棵树的高度恢复到插入之前的h+2。如果结点10是整棵树的局部子树，那么通过这样的旋转方式也不会影响上一层，所以插入就到此结束了。

左单旋的代码实现：

	void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;Node* ppNode = parent->_parent;parent->_right = subRL;if (subRL){subRL->_parent = parent;}subR->_left = parent;parent->_parent = subR;if (ppNode){if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}else{_root = subR;subR->_parent = nullptr;}parent->_bf = 0;subR->_bf = 0;}

2.3.4左右双旋

简单的观察不难发现，左单旋和右单旋都几乎是一条直线上的插入，这就导致有些场景不适用，需要其他的方法结合才能实现平衡

如图中显示，当左边高的时候，如果插入的位置不是a子树，而是插入在b子树，b子树的高度从h变为h+1，引发旋转，但是这个时候用右单旋无法解决问题，右单旋后，树依旧不平衡。因为右单旋是纯粹的解决左边高，但是插入在b子树中，结点10为根的子树不再是简单的左边高，对于10来说是左边高，但是对于结点5来说，是右边高，这时就需要两次旋转才能解决问题，以5为旋转点进行一个左单旋，再以10为旋转点进行一个右单旋，这棵树就平衡了。

下面同样的还是通过抽象图的方式具体分析

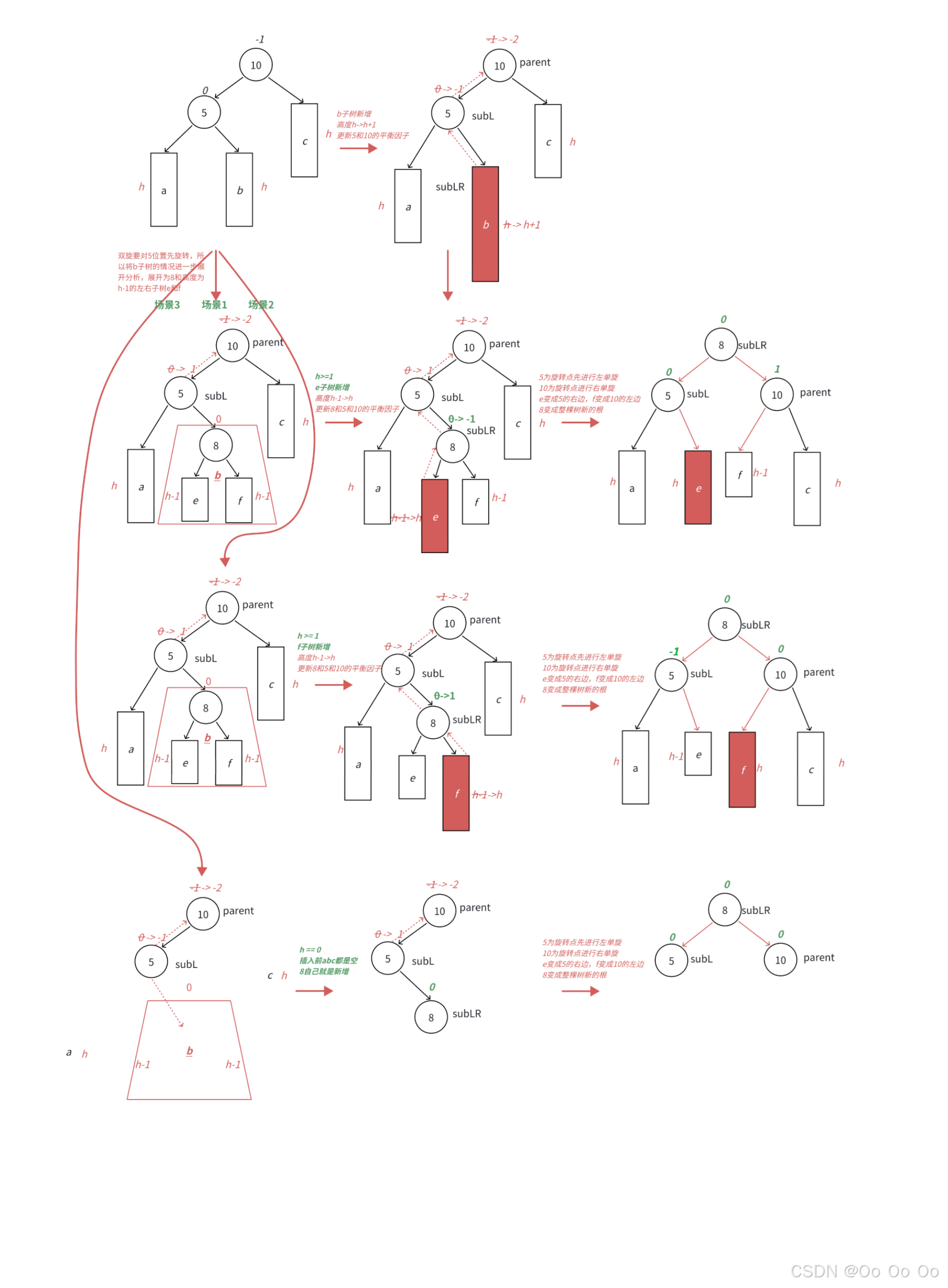
图中将b子树进一步分为8(不一定是8，只是8符合这里的AVL树，可以是大于5小于10的值)和左子树高度为h-1的e和f子树，因为要对b的父亲结点5为旋转点进行左单旋，左单旋需要动b子树中的左子树。b子树中新增结点的位置不同，平衡因子更新的细节也不同，分为下面三种情况讨论：

情况1：h>=1时，新增结点插入在e子树，e子树高度从h-1变为h，并不断更新8---->5--->10平衡因子，引发旋转，旋转后8的平衡因子从-1变为了0，结点10的平衡因子从-2变为1，结点5的平衡因子从1变为0
情况2：h>=1时，新增结点插入在f子树，f子树高度从h-1变为h，并不断更新8---->5--->10平衡因子，引发旋转，旋转后8的平衡因子从1变为0，结点10的平衡因子从-2变为0，结点5的平衡因子从1变为-1
情况3：h==0时，a、b、c都是空树，b自己就是一个新增结点，不断更新5--->10平衡因子，引发旋转，旋转后8的平衡因子还是0，结点5的平衡因子从1变为0，10的平衡因子从-2变为0

左右双旋代码实现

void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;// 提前存储平衡因子，左单旋和右单旋之后就变了//RotateL(subL);RotateL(parent->_left);RotateR(parent);if (bf == 0){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 0;}// 新增在subLR左边else if (bf == -1){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 1;}// 新增在subLR右边else if (bf == 1){subL->_bf = -1;subLR->_bf = 0;parent->_bf = 0;}else{assert(false);}
}

2.3.5右左双旋

类似于左右双旋，将a、b、c子树抽象为高度为h的AVL子树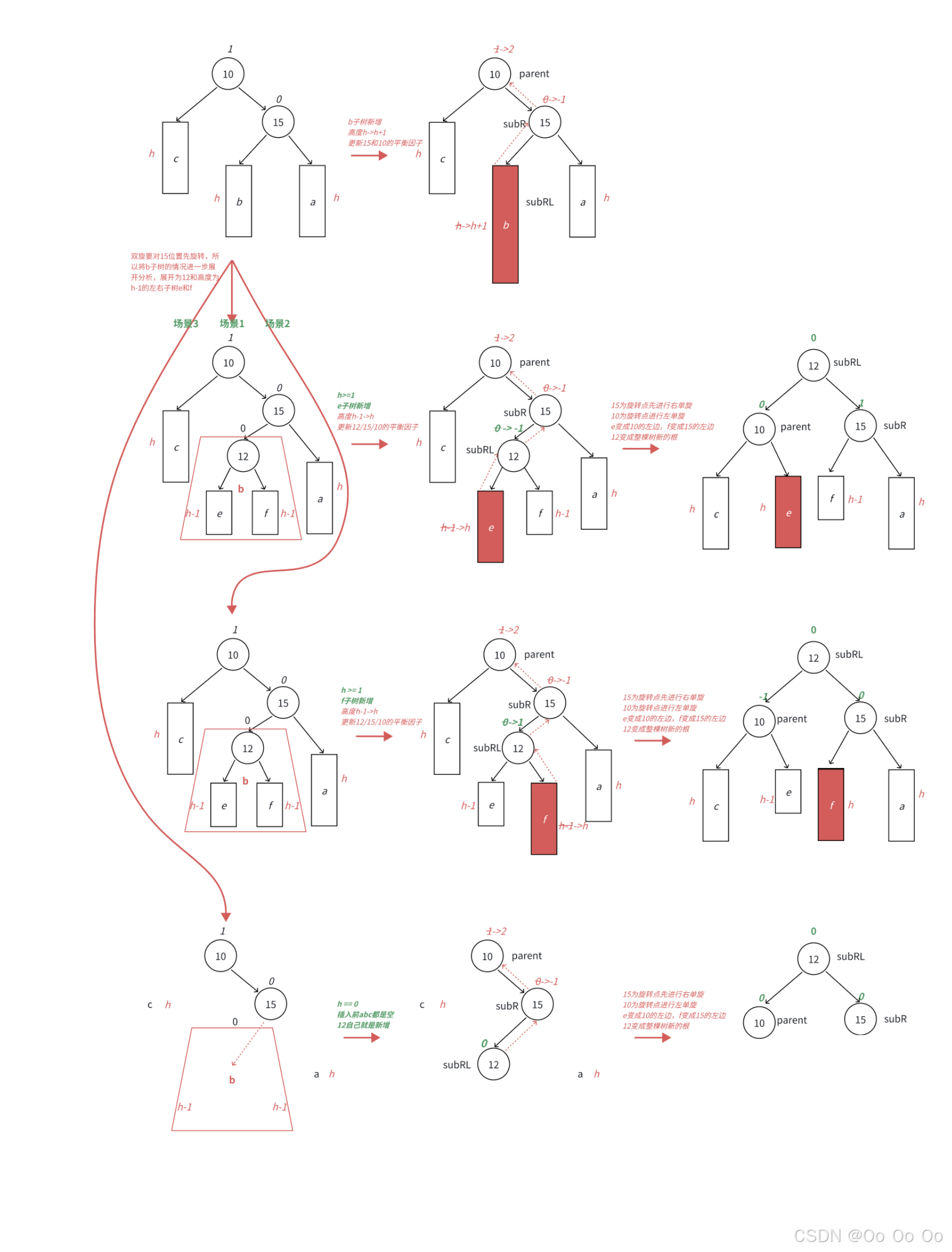

将b子树进一步分为12(不一定是12，只是12符合这里的AVL树，可以是大于10小于15的值)和左子树高度为h-1的e和f子树，因为要对b的父亲结点5为旋转点进行右单旋，右单旋需要动b子树中的左子树。b子树中新增结点的位置不同，平衡因子更新的细节也不同，分为下面三种情况讨论：

情况1：h>=1时，新增结点插入在e子树，e子树高度从h-1变为h，并不断更新12---->15--->10平衡因子，引发旋转，旋转后12的平衡因子从-1变为了0，结点15的平衡因子从-1变为1，结点10的平衡因子从2变为0
情况2：h>=1时，新增结点插入在f子树，f子树高度从h-1变为h，并不断更新12---->15--->10平衡因子，引发旋转，旋转后12的平衡因子从1变为0，结点15的平衡因子从-1变为0，结点10的平衡因子从2变为-1
情况3：h==0时，a、b、c都是空树，b自己就是一个新增结点，不断更新15--->10平衡因子，引发旋转，旋转后12的平衡因子还是0，结点15的平衡因子从-1变为0，10的平衡因子从2变为0

右左双旋代码实现

	void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;//RotateR(subR);RotateR(parent->_right);RotateL(parent);if (bf == 0){subR->_bf = 0;subRL->_bf = 0;parent->_bf = 0;}else if (bf == -1){subR->_bf = 1;subRL->_bf = 0;parent->_bf = 0;}else if (bf == 1){subR->_bf = 0;subRL->_bf = 0;parent->_bf = -1;}else{assert(false);}}

2.4AVL树的查找

AVL树的查找和二叉搜索树一样，按照规进行查找即可，效率是O(logN)

	Node* Find(K k){Node* cur = _root;while (cur){if (cur->_kv.first == k){return cur;}else if (k < cur->_kv.first){cur = cur->_left;}else if (k > cur->_kv.first){cur = cur->_right;}else{assert(false);}}return nullptr;}

2.5AVL树的平衡检测

在写完AVL树的时候，如果要检测是否平衡，不能通过直接遍历结点的平衡因子来判断是否平衡，要通过计算每颗子树的高度差来判断；因为要是本来这棵树内部平衡因子的计算方式就是有问题的，就会判断错误了。

	int Height(){return _Height(_root);}void IsBalnceAVLTree(){if (_IsBalnceAVLTree(_root)){cout << "此树是平衡的AVL树" << endl;}}
private:bool _IsBalnceAVLTree(Node* root){if (root == nullptr){return true;}int LeftTreeHeight = _Height(root->_left);int RightTreeHeight = _Height(root->_right);int SubBc = RightTreeHeight - LeftTreeHeight;if (abs(SubBc) >= 2){cout << "高度差异常" << endl;}else if (root->_bf != SubBc){cout << "平衡因子异常" << endl;}return _IsBalnceAVLTree(root->_left) && _IsBalnceAVLTree(root->_right);}int _Height(Node* root){if (root == nullptr){return 0;}int leftheight = _Height(root->_left);int rightheight = _Height(root->_right);return max(leftheight, rightheight) + 1;}

AVL树的删除后面有再时间补充...