当前位置：首页 > news >正文

实验五时域采样与频域采样

news 来源：原创 2025/7/27 17:23:29

时域采样理论的验证

【实例3-1】近似绘制x (n) = R4n = 在(0,2 $\pi$ ) 上的幅频响应曲线( $FT [x (n)]$ )。

x = [1, 1, 1, 1];
N = 64;
xk = fft(x, N);
figure;
subplot(2, 1, 1);
stem(0:3, x, '.');
subplot(2, 1, 2);
k = 0:N-1;
plot(2*k/N, abs(xk));
title('|FT(x[n])|');
xlabel('\omega/\pi');

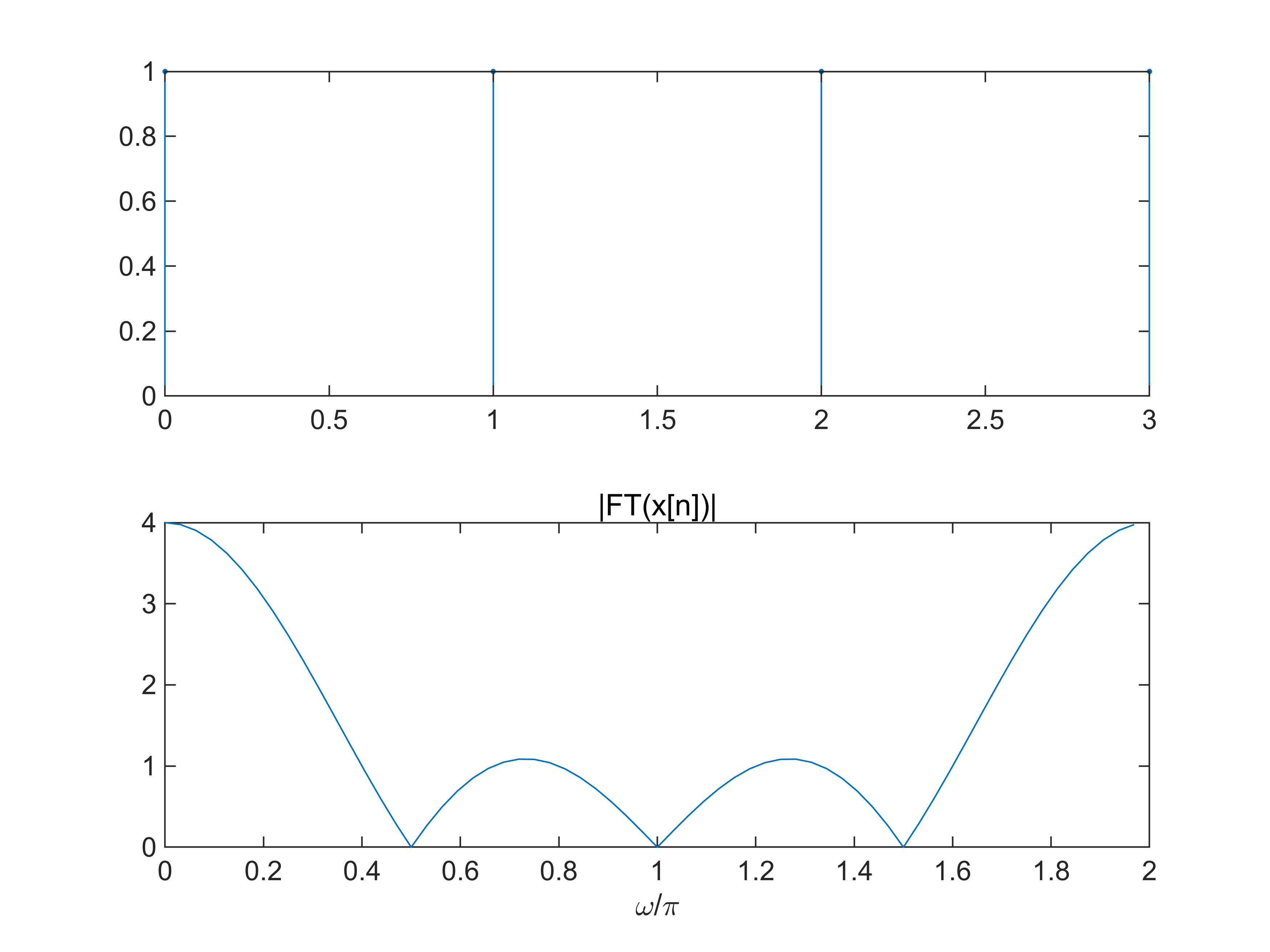
编写实验程序，计算 x1(n) 、x2(n) 和 x3(n) 的幅度特性，并绘图显示。观察分析频谱混叠失真。

% 参数定义
A = 444.128;
alpha = 50 * sqrt(2) * pi;
Omega_0 = 50 * sqrt(2) * pi;
Fs_values = [1000, 300, 200]; % 采样频率：1kHz, 300Hz, 200Hz
T_p = 64e-3; % 采样周期
t = 0:T_p:1; % 时间区间
x_t = A * exp(-alpha * t) .* sin(Omega_0 * t) .* (t >= 0); % 原信号
figure;
% 计算各个采样信号并计算FFT
for i = 1:length(Fs_values)Fs = Fs_values(i); % 当前采样频率T = 1 / Fs;  % sN = ceil(T_p * Fs); % 计算变换点数并确保是整数N = 2^nextpow2(N); % 确保 N 是 2 的幂，方便 FFT 计算n = 0:floor(N)-1; % 离散时间序列% 生成采样信号xn = A .* exp(-alpha * n * T) .* sin(Omega_0 * n * T);% 计算FFTXk = fft(xn, N); % 计算频域信号f = (0:N-1) * Fs / N; % 频率轴% 绘图subplot(3,2,2*i-1);stem(n,xn,'.');axis autotitle(['Fs = ', num2str(Fs), ' Hz']);subplot(3,2,2*i);plot(f, abs(Xk)*T);axis 'auto x'title(['T*|FT(x',num2str(i),'[n])|','，Fs = ', num2str(Fs), ' Hz']);xlabel('频率 (Hz)');ylabel('幅度');
end

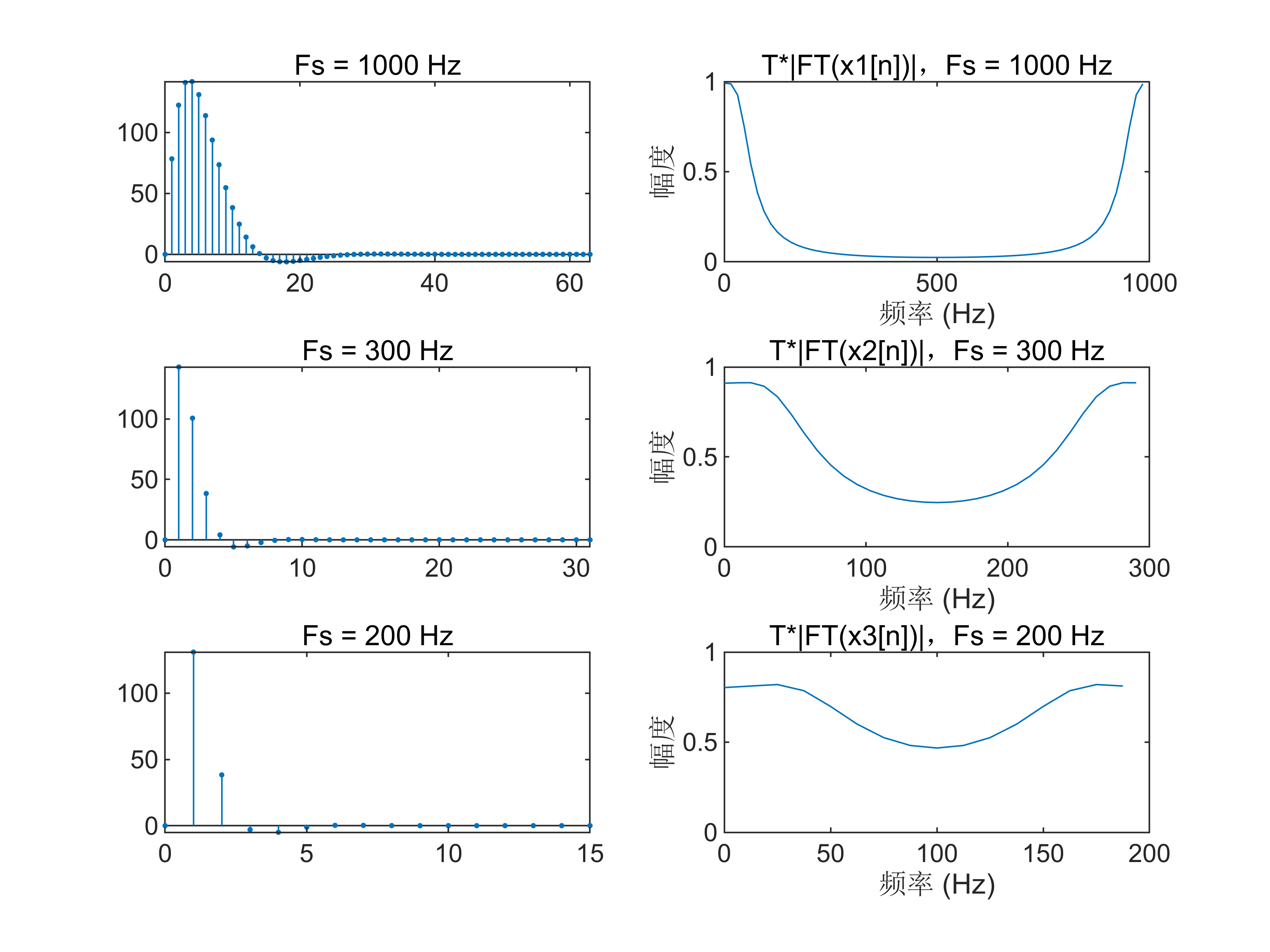
频域采样理论的验证

【实例3-2】抽取信号x (k )= {1, 2, 3, 4, 4, 3, 2,1} 信号中的k 为偶数的信号点出来。

x1=[1 2 3 4 4 3 2 1];
N=1:2:7;
x2=x1(N)

x2 = 1x4    1     3     4     2

给定信号如下：

$x(n)=\left\lbrace \begin{array}{ll} n+1, & 0\le n\le 13\newline 27-n, & 14\le n\le 26\newline 0, & \textrm{其他} \end{array}\right.$

编写程序分别对频谱函数 $X(e^{j\omega } )=\textrm{FT}[x(n)]$ 在区间 $[0,2\pi ]$ 上等间隔采样32和16点，得到 $X_{32} (k)$ 和 $X_{16} (k)$ ：

% 定义信号 x(n)
n = 0:31;
x = zeros(1, length(n));
x(1:14) = n(1:14) + 1; % 0 <= n <= 13
x(15:27) = 27 - n(15:27); % 14 <= n <= 26xn = x;
% 计算32点和16点FFT
Xk = fft(x, 1024);
N32 = 1:32:1024;% xk抽样得到32个点
Xk32 = Xk(N32);
N16=1:64:1024;% xk抽样得到16个点
Xk16 = Xk(N16); % 计算32点和16点IFFT
xn32 = ifft(Xk32, 32); 
xn16 = ifft(Xk16, 16);
% Xejw
figure;
subplot(3, 2, 1);
plot(linspace(0, 1, 256), abs(Xk(1:256)));
xlabel('ω/π');
ylabel('|X(e^{jω})|');
title('(a)FT[x(n)]');subplot(3, 2, 2);
stem(n,xn,'.');
xlabel('n');
ylabel('x(n)');
title('(b)三角波序列');% Xk16
subplot(3, 2, 3);
stem(0:15, abs(Xk16),'.');
xlabel('k');
ylabel('|X_{16}(k)|');
title('(c)16点频域采样');subplot(3, 2, 4);
stem(0:15,xn16,'.');
axis([0 32 0 15])
xlabel('n');
ylabel('x(n)');
title('(d)16点IDFT[X_{16}(k)]');% Xk32
subplot(3, 2, 5);
stem(0:31, abs(Xk32),'.');
xlabel('k');
ylabel('|X_{32}(k)|');
title('(e)32点频域采样');subplot(3, 2, 6);
stem(n,xn32,'.');
xlabel('n');
ylabel('x(n)');
title('(f)32点IDFT[X_{32}(k)]');

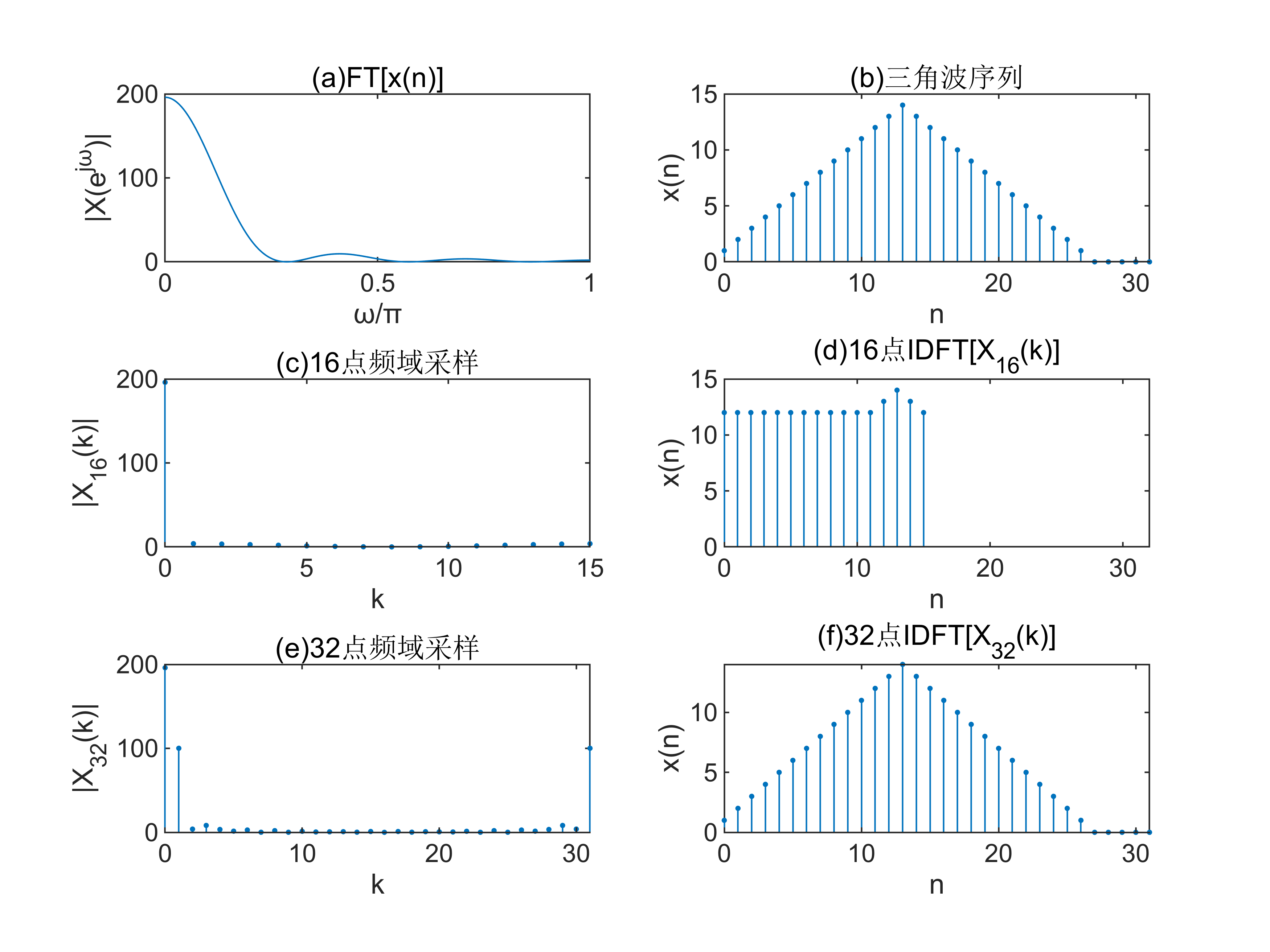
语音信号整数倍抽取后的频谱的分析

读取motherland.wav 语音文件，截取第1000 至2999 共2000 个采样点。

（1）分析这2000 采样点的幅度频谱（采用实验四的代码）；

close;clear;
% 读取音频文件
[audio,fs] = audioread(...".\2024-2025（1）《信号处理实验》资料（请拷贝到u盘中，每次试验带到实验室）\实验中用到的一些函数和音频图像文件\motherland.wav"...
);% 截取1~2秒的音频数据
audioSegment = audio(1000:2999, :);N=1024;   
t = (0:1999)/fs;
xk=fft(audioSegment,N);f = linspace(0, fs, N);
% 绘制幅度谱
figure;
subplot(2,1,1);
plot(t, audioSegment);
title('原信号时域波形');
xlabel('t(s)');
ylabel('');
subplot(2,1,2);
plot(f, abs(xk));
title('原信号幅度谱');
xlabel('f(Hz) ');
ylabel('幅度');

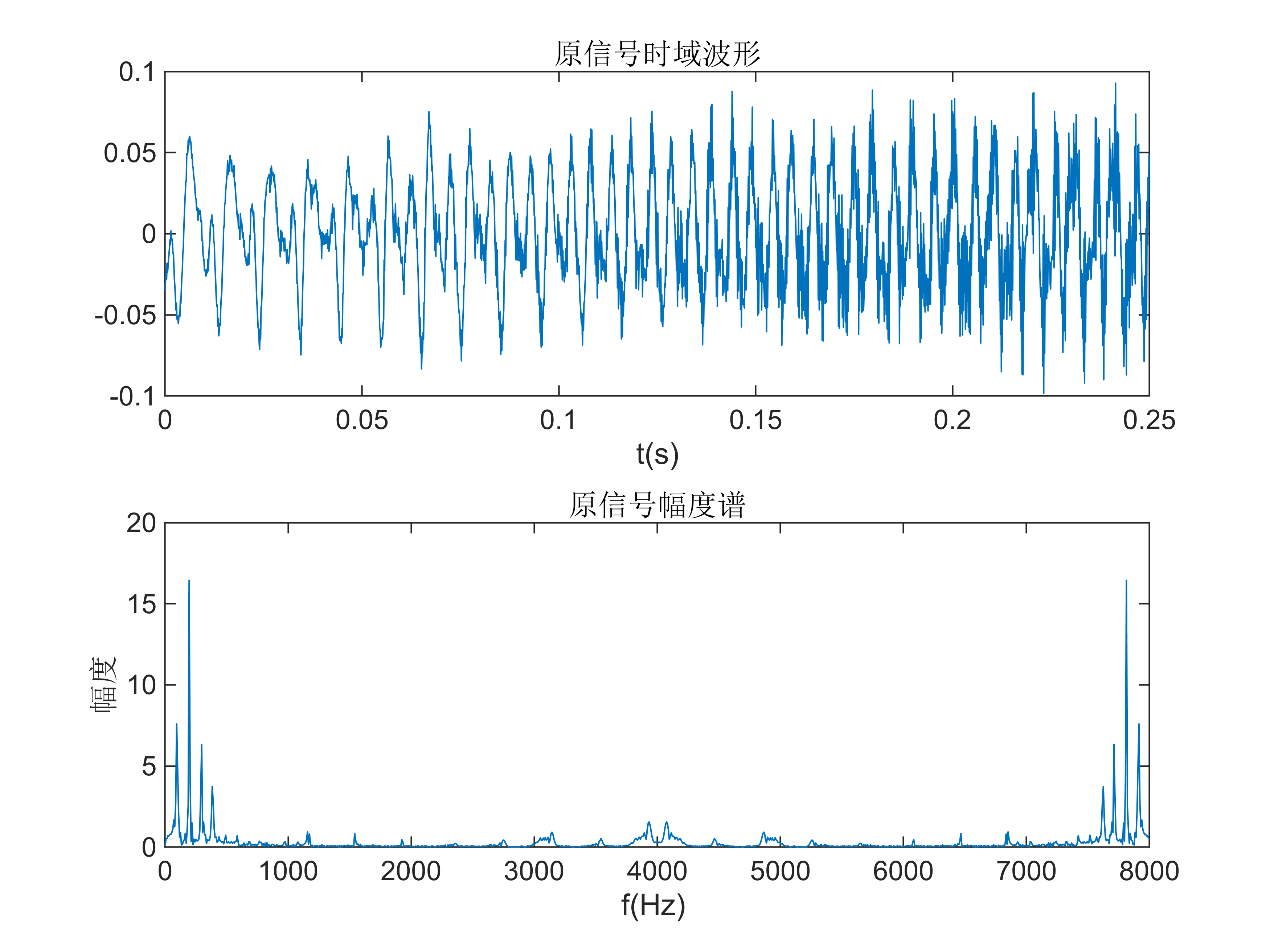
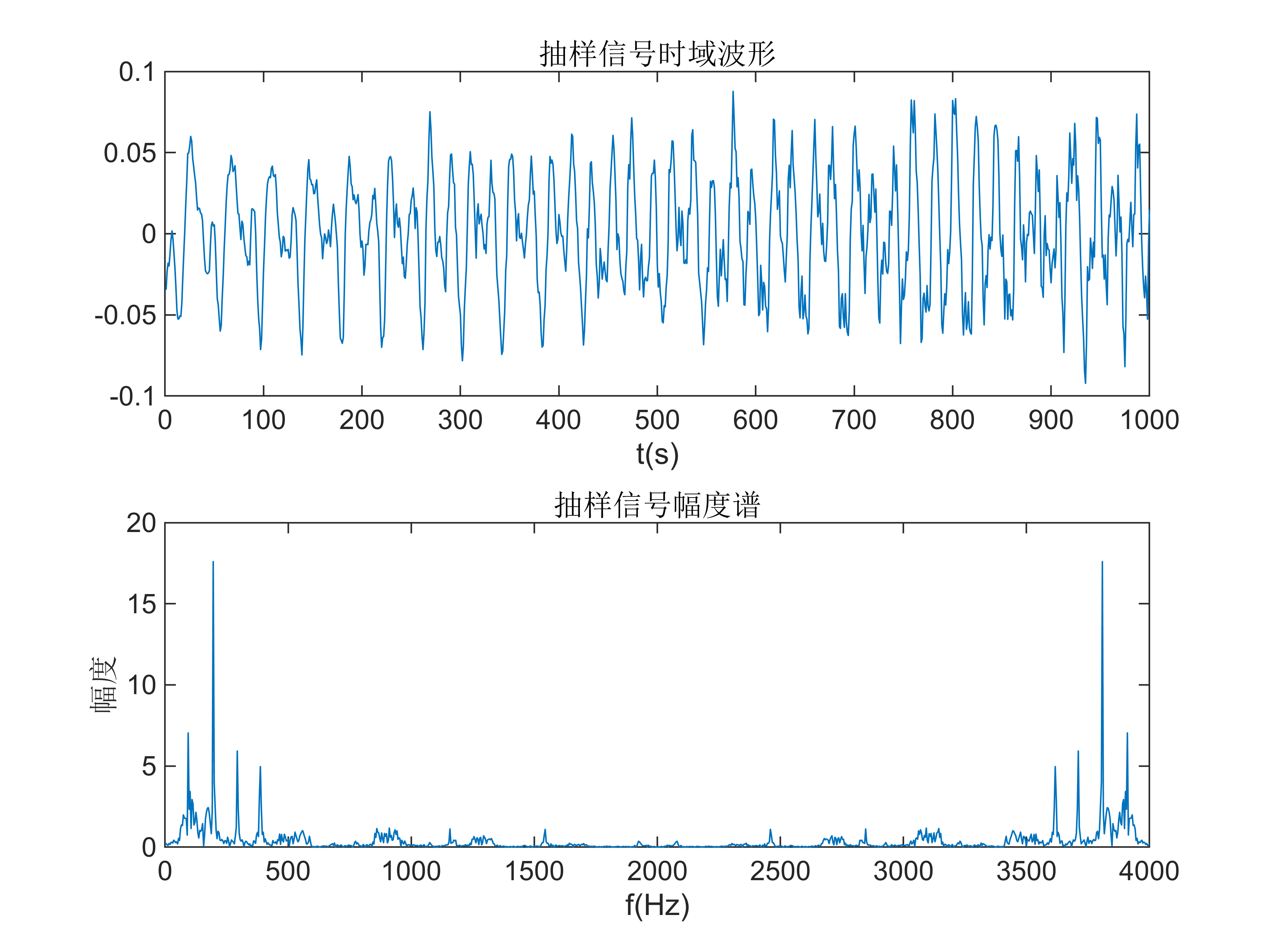
（2）对这2000 采样点数据，每2 个点抽取1 点，得到1000 点数据，画出这1000 个采样点的幅度频谱。

n=1:2:1999;
% 每2个点抽取1点
sample=audioSegment(n);%抽样信号fft
xk1=fft(sample,N);
f = linspace(0, fs/2, N);figure;
subplot(2,1,1);
plot(1:1000, sample);
title('抽样信号时域波形');
xlabel('t(s)');
ylabel('');
subplot(2,1,2);
plot(f, abs(xk1));
title('抽样信号幅度谱');
xlabel('f(Hz)');
ylabel('幅度');

思考题

1. 如果序列x(n)的长度为M，希望得到其频谱 $X(e^{j\omega } )$ 在 $[0,2\pi )$ 上的N 点等间隔采样，当N<M 时，如何用一次最少点数的DFT 得到该频谱采样？

n<m时，频域抽样不够密，（x）n以周期进行延拓，频域产生混叠，抽样信号不能还原原信号。

可将m分为n长度的k段，不足时域补零。分段进行DFT。此时DFT点数最少为N次。

2. 对采样后的语音信号，每2 个样点抽取1 点，语音信号会发生频谱混叠吗？

如果发生会发生频谱混叠，原因是什么？以实验内容3.3 为例进行说明。

当每2 个样点抽取1 点时，相当于对信号进行了降采样，即将采样率降低为原来的一半。如果在降采样之前没有适当的低通滤波器来滤除高于新采样率一半的频率分量，根据奈奎斯特采样定理，信号中高频成分就会折叠到低频部分，导致频谱混叠。

在本题中，信号的中高频成分分量较少，观察不到混叠现象。