第3周作业-1层隐藏层的神经网络分类二维数据

1层隐藏层的神经网络分类二维数据¶

1. 导入包¶

① numpy是Python科学计算的基本包。

② sklearn提供了用于数据挖掘和分析的简单有效的工具。

③ matplotlib是在Python中常用的绘制图形的库。

④ testCases提供了一些测试示例用以评估函数的正确性。

⑤ planar_utils提供了此作业中使用的各种函数。

In [2]:

import sys 
import numpy 
import matplotlib
import sklearn   #安装 pip install scikit-learn
print(sys.version)             # 打印 python 版本号
print(numpy.__version__)        # 打印 numpy 包 版本号
print(matplotlib.__version__)   # 打印 matplotlib 包 版本号
print(sklearn.__version__)         # 打印 h5py 包 版本号

3.12.4 (tags/v3.12.4:8e8a4ba, Jun  6 2024, 19:30:16) [MSC v.1940 64 bit (AMD64)]
2.2.3
3.10.1
1.6.1

需要的文件

需要的testCases.py和planar_utils.py文件下载链接：

下载:https://wwyy.lanzouu.com/iekB72wste9a 密码:htp0

In [128]:

# Package imports
import numpy as np
import matplotlib.pyplot as plt
from testCases import *
import sklearn
import sklearn.datasets
import sklearn.linear_model
from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets%matplotlib inline# 设置一个固定的随机种子，以保证接下来的步骤中我们的结果是一致的。
np.random.seed(1) 

2. 数据集¶

2.1 导入数据集¶

① 首先，让我们获取要使用的数据集。

② 以下代码会将花的图案的2类数据集加载到变量X和Y中。

In [129]:

X, Y = load_planar_dataset() 

2.2 查看数据集图案¶

① 把数据集加载完成了，然后使用matplotlib可视化数据集。

② 数据看起来像一朵由红色（y = 0）和蓝色（y = 1）的数据点组成的花朵图案。

③ 我们的目标是建立一个适合该数据的分类模型。

In [130]:

# 绘制散点图
plt.scatter(X[0, :], X[1, :], c=Y.reshape(X[0,:].shape), s=40, cmap=plt.cm.Spectral)  

Out[130]:

<matplotlib.collections.PathCollection at 0x24af4ea8ce0>

2.3 查看数据集维度¶

① 现在，我们已经有了以下的东西：

1. X：一个numpy的矩阵，包含了这些数据点的数值
2. Y：一个numpy的向量，对应着的是X的标签【0 | 1】（红色:0 ， 蓝色 :1）

② 我们继续来仔细地看数据。

In [131]:

shape_X = X.shape
shape_Y = Y.shape
m = shape_X[1]  # 训练集里面的数量print ('X的维度为: ' + str(shape_X))
print ('Y的维度为: ' + str(shape_Y))
print ("数据集里面的数据有：" + str(m) + " 个")

X的维度为: (2, 400)
Y的维度为: (1, 400)
数据集里面的数据有：400 个

3. Logistic回归¶

3.1 Logistic回归简介¶

① 在构建完整的神经网络之前，先让我们看看逻辑回归在这个问题上的表现如何。

② 我们可以使用sklearn的内置函数来做到这一点， 运行下面的代码来训练数据集上的逻辑回归分类器。

3.2 Logistic回归模型¶

In [133]:

# Train the logistic regression classifier
clf = sklearn.linear_model.LogisticRegressionCV();
# clf.fit(X.T, Y.T);  #这个会报错
clf.fit(X.T, Y.T.ravel()); # 或 Y.T.flatten()

代码解释：

sklearn.linear_model.LogisticRegressionCV()

• 这是 scikit-learn 库中用于逻辑回归的类，带有交叉验证功能。
• LogisticRegressionCV 是逻辑回归分类器的实现，它会通过交叉验证自动选择最佳的正则化参数（如 L1 或 L2 正则化）。
• clf 是这个分类器的实例。

clf.fit(X.T, Y.T.ravel())

• clf.fit 是逻辑回归分类器的训练方法，用于拟合模型。
• X.T 和 Y.T 是数据矩阵 X 和目标向量 Y 的转置。
• Y.T.ravel() 是对 Y.T 进行处理，将其从列向量（二维数组）转换为一维数组。

3.3 绘制边界¶

① 现在，你可以运行下面的代码以绘制此模型的决策边界：

相关知识

1. NumPy 的形状问题

• Y 和 LR_predictions 的形状必须是一致的，并且是一维数组（形状为 (n_samples,)）。
• 如果 Y 是一个二维数组（形状为 (n_samples, 1)），需要将其转换为一维数组。

2. 计算准确性的公式

准确性公式是：

KaTeX parse error: Undefined control sequence: \* at position 35: …确预测的数量}{总样本数量} \̲*̲100\%

在代码中，np.dot(Y, LR_predictions) 和 np.dot(1 - Y, 1 - LR_predictions) 的结果应该是一个标量，表示正确预测的数量。

3. NumPy 的 np.dot

np.dot 用于计算两个数组的点积。

• 如果输入是一维数组，结果是一个标量。
• 如果输入是二维数组，结果是一个数组。

4. NumPy 的 np.mean

• np.mean 用于计算数组的均值。
• 可以用它来计算准确率，因为准确率本质上是正确预测的比例。

In [135]:

# Plot the decision boundary for logistic regression
# 绘制决策边界                       
plot_decision_boundary(lambda x: clf.predict(x), X, Y) 
# 图标题
plt.title("Logistic Regression") # 打印准确性
LR_predictions = clf.predict(X.T)# LR_predictions = clf.predict(X.T).ravel()  #展平为一维数组
Y = Y.ravel()  #展平为一维数组
print ('逻辑回归的准确性：%d ' % float((np.dot(Y,LR_predictions) + np.dot(1-Y,1-LR_predictions))/float(Y.size)*100) +'% ' + "(正确标记的数据点所占的百分比)") 

逻辑回归的准确性：47 % (正确标记的数据点所占的百分比)

② 由于数据集不是线性可分类的，因此逻辑回归效果不佳。让我们试试是否神经网络会做得更好吧！

4. 神经网络模型¶

4.1 神经网络简介¶

① 从上面我们可以得知Logistic回归不适用于“flower数据集”。

② 现在你将训练带有单个隐藏层的神经网络。

③ 这是我们的模型：

4.2 神经网络数学模型¶

① 数学原理：
例如对第$i$个样本$x^{(i)}$，执行以下操作：

• KaTeX parse error: \tag works only in display equations
• KaTeX parse error: \tag works only in display equations
• KaTeX parse error: \tag works only in display equations
• KaTeX parse error: \tag works only in display equations
• KaTeX parse error: Undefined control sequence: \mbox at position 43: …gin{cases} 1 & \̲m̲b̲o̲x̲{if } a^{[2](i)…

② 根据所有的预测数据，你还可以如下计算损失J:

KaTeX parse error: \tag works only in display equations

4.3 建立神经网络方法¶

① 建立神经网络的一般方法是：

1. 定义神经网络结构（输入单元数，隐藏单元数等）。
2. 初始化模型的参数
3. 循环：

• 3.1 实施前项传播
• 3.2 计算损失
• 3.3 实现后向传播
• 3.4 更新参数（梯度下降）

② 我们通常会构建辅助函数来计算第（1）-（3）步，然后将它们合并为nn_model()函数。

③ 一旦构建了 nn_model() 并学习了正确的参数，就可以对新数据进行预测。

4.4 定义神经网络结构¶

① 在构建神经网络之前，我们要先把神经网络的结构给定义好。

② 定义三个变量：

1. n_x：输入层的大小
2. n_h：隐藏层的大小（将其设置为4）
3. n_y：输出层的大小

note：使用shape来找到n_x和n_y。 另外，将隐藏层大小硬编码为4。

In [136]:

def layer_sizes(X, Y):"""参数：X - 输入数据集,维度为（输入的数量，训练/测试的数量）Y - 标签，维度为（输出的数量，训练/测试数量）返回：n_x - 输入层的数量n_h - 隐藏层的数量n_y - 输出层的数量"""# 输入层大小n_x = X.shape[0] # 隐藏层大小n_h = 4# 输出层大小n_y = Y.shape[0] return (n_x, n_h, n_y)

In [137]:

# 测试一下 layer_sizes 函数
print("=========================测试layer_sizes=========================")
X_assess, Y_assess = layer_sizes_test_case()
(n_x, n_h, n_y) = layer_sizes(X_assess, Y_assess)
print("The size of the input layer is: n_x = " + str(n_x))
print("The size of the hidden layer is: n_h = " + str(n_h))
print("The size of the output layer is: n_y = " + str(n_y))

=========================测试layer_sizes=========================
The size of the input layer is: n_x = 5
The size of the hidden layer is: n_h = 4
The size of the output layer is: n_y = 2

4.5 初始化模型的参数¶

① 在这里，我们要实现函数initialize_parameters()。

② 我们要确保我们的参数大小合适。

③ 我们将会用随机值初始化权重矩阵。

• np.random.randn(a，b) * 0.01来随机初始化一个维度为(a，b)的矩阵。
• np.zeros((a，b))用零初始化矩阵（a，b）。将偏向量初始化为零。

In [138]:

def initialize_parameters(n_x, n_h, n_y):"""参数：n_x - 输入层节点的数量n_h - 隐藏层节点的数量n_y - 输出层节点的数量返回：parameters - 包含参数的字典：W1 - 权重矩阵,维度为（n_h，n_x）b1 - 偏向量，维度为（n_h，1）W2 - 权重矩阵，维度为（n_y，n_h）b2 - 偏向量，维度为（n_y，1）"""# 设置一个种子，这样你的输出与我们的匹配，尽管初始化是随机的。np.random.seed(2) W1 = np.random.randn(n_h,n_x) * 0.01b1 = np.zeros((n_h,1))W2 = np.random.randn(n_y,n_h) * 0.01b2 = np.zeros((n_y,1))# 使用断言确保我的数据格式是正确的assert(W1.shape == ( n_h , n_x ))assert(b1.shape == ( n_h , 1 ))assert(W2.shape == ( n_y , n_h ))assert(b2.shape == ( n_y , 1 ))parameters = {"W1": W1,"b1": b1,"W2": W2,"b2": b2}return parameters

In [139]:

#测试一下 initialize_parameters 函数
print("=========================测试initialize_parameters=========================")    
n_x, n_h, n_y = initialize_parameters_test_case()
parameters = initialize_parameters(n_x, n_h, n_y)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))

=========================测试initialize_parameters=========================
W1 = [[-0.00416758 -0.00056267][-0.02136196  0.01640271][-0.01793436 -0.00841747][ 0.00502881 -0.01245288]]
b1 = [[0.][0.][0.][0.]]
W2 = [[-0.01057952 -0.00909008  0.00551454  0.02292208]]
b2 = [[0.]]

4.6 循环¶

4.6.1 前向传播¶

① 我们现在要实现前向传播函数forward_propagation()。

② 我们可以使用sigmoid()函数，也可以使用np.tanh()函数。

③ 步骤如下：

• 使用字典类型的parameters（它是initialize_parameters() 的输出）检索每个参数。
• 实现前向传播，计算$Z^{[1]},A^{[1]},Z^{[2]}$和$A^{[2]}$（所有训练数据的预测结果向量）。
• 反向传播所需的值存储在cache中，cache将作为反向传播函数的输入。

步骤及相关解释

1. 前向传播（Forward Propagation）

前向传播是神经网络中从输入层到输出层的计算过程。它包括以下步骤：

• 输入层：接收输入数据。
• 隐藏层：对输入数据进行加权求和和非线性变换。
• 输出层：生成最终的预测结果。

在前向传播中，每个神经元的输出可以表示为：
$$Z=W\cdot X+b$$
$$A=g(Z)$$
其中：

• ( Z ) 是加权输入。
• ( W ) 是权重矩阵。
• ( X ) 是输入数据。
• ( b ) 是偏置项。
• ( g ) 是激活函数（如 Sigmoid、ReLU 等）。
• ( A ) 是激活后的输出。

2. 缓存（Cache）

在神经网络的实现中，cache 是一个字典，用于存储中间计算结果。这些结果在反向传播中会被用到。例如：

• Z1：第一个隐藏层的加权输入。
• A1：第一个隐藏层的激活输出。
• Z2：输出层的加权输入。
• A2：输出层的激活输出。

3. 测试用例（Test Case）

forward_propagation_test_case() 是一个测试函数，用于生成测试数据：

• X_assess：测试输入数据。
• parameters：测试模型的参数（包括权重和偏置）。

这些测试数据用于验证 forward_propagation 函数的正确性。

4. NumPy 的 np.mean

np.mean 用于计算数组的均值。在这段代码中，np.mean 被用来计算 cache 中各个变量的均值，以便验证输出是否与预期一致。

5. 打印结果

通过打印 cache 中各个变量的均值，可以直观地检查 forward_propagation 函数的输出是否正确。

In [171]:

def forward_propagation(X, parameters):"""参数：X - 维度为（n_x，m）的输入数据。parameters - 初始化函数（initialize_parameters）的输出返回：A2 - 使用sigmoid()函数计算的第二次激活后的数值cache - 包含“Z1”，“A1”，“Z2”和“A2”的字典类型变量"""# 从字典 “parameters” 中检索每个参数W1 = parameters["W1"]b1 = parameters["b1"]W2 = parameters["W2"]b2 = parameters["b2"]# 实现前向传播计算A2(概率)Z1 = np.dot(W1,X) + b1A1 = np.tanh(Z1)Z2 = np.dot(W2,A1) + b2A2 = sigmoid(Z2)# 确保 A2 的形状为 (1, n_samples)A2 = A2.reshape(1, -1)#使用断言确保我的数据格式是正确的assert(A2.shape == (1,X.shape[1]))cache = {"Z1": Z1,"A1": A1,"Z2": Z2,"A2": A2}return A2, cache

In [141]:

# 测试一下 forward_propagation 函数
print("=========================测试forward_propagation=========================") 
X_assess, parameters = forward_propagation_test_case()
A2, cache = forward_propagation(X_assess, parameters)
# 我们在这里使用均值只是为了确保你的输出与我们的输出匹配。
print(np.mean(cache['Z1']) ,np.mean(cache['A1']),np.mean(cache['Z2']),np.mean(cache['A2']))

=========================测试forward_propagation=========================
-0.0004997557777419913 -0.000496963353231779 0.00043818745095914653 0.500109546852431

4.6.2 计算成本¶

① 现在，我们已经计算了$A^{[2]}$

② $a^{[2](i)}$包含了训练集里每个数值，现在我们可以构建成本函数了。

③ 我们的成本选择交叉熵损失，计算成本的公式如下：
KaTeX parse error: \tag works only in display equations

In [142]:

def compute_cost(A2, Y, parameters):"""计算方程（7）中给出的交叉熵成本，参数：A2 - 使用sigmoid()函数计算的第二次激活后的数值Y - "True"标签向量,维度为（1，数量）parameters - 一个包含W1，B1，W2和B2的字典类型的变量返回：成本 - 交叉熵成本给出方程（7）"""# 样本数量m = Y.shape[1] # 计算交叉熵代价epsilon = 1e-5  # 一个非常小的值logprobs = Y * np.log(A2 + epsilon) + (1 - Y) * np.log(1 - A2 + epsilon)  #防止为0# logprobs = Y*np.log(A2) + (1-Y)* np.log(1-A2)cost = -1/m * np.sum(logprobs)# 确保损失是我们期望的维度# 例如，turns [[17]] into 17 cost = np.squeeze(cost)     assert(isinstance(cost, float))return cost

In [143]:

# 测试一下 compute_cost 函数
print("=========================测试compute_cost=========================") 
A2, Y_assess, parameters = compute_cost_test_case()print("cost = " + str(compute_cost(A2, Y_assess, parameters)))

=========================测试compute_cost=========================
cost = 0.6928998985200261

① 使用正向传播期间计算的cache，现在可以利用它实现反向传播。

② 现在我们要开始实现函数backward_propagation（）。

4.6.3 后向传播¶

① 反向传播通常是深度学习中最难（数学意义）部分，为了帮助你，这里有反向传播讲座的幻灯片。

② 由于我们正在构建向量化实现，因此我们将需要使用这下面的六个方程：

③ 要计算$d{z}^{[1]}$，你首先需要计算$g^{[1{]}^{\prime }}(Z^{[1]})$。

④ $g^{[1]}(...)$ 是tanh激活函数，因此如果$a=g^{[1]}(z)$则$g^{[1{]}^{\prime }}(z)=1-a^2$。

⑤ 所以我们需要使用(1 - np.power(A1, 2))计算$g^{[1{]}^{\prime }}(Z^{[1]})$。

In [144]:

def backward_propagation(parameters, cache, X, Y):"""使用上述说明搭建反向传播函数。参数：parameters - 包含我们的参数的一个字典类型的变量。cache - 包含“Z1”，“A1”，“Z2”和“A2”的字典类型的变量。X - 输入数据，维度为（2，数量）Y - “True”标签，维度为（1，数量）返回：grads - 包含W和b的导数一个字典类型的变量。"""m = X.shape[1]# 首先，从字典“parameters”中检索W1和W2。W1 = parameters["W1"]W2 = parameters["W2"]# 还可以从字典“cache”中检索A1和A2。A1 = cache["A1"]A2 = cache["A2"]# 反向传播:计算 dW1、db1、dW2、db2。dZ2= A2 - YdW2 = 1 / m * np.dot(dZ2,A1.T)db2 = 1 / m * np.sum(dZ2,axis=1,keepdims=True)dZ1 = np.dot(W2.T,dZ2) * (1-np.power(A1,2))dW1 = 1 / m * np.dot(dZ1,X.T)db1 = 1 / m * np.sum(dZ1,axis=1,keepdims=True)grads = {"dW1": dW1,"db1": db1,"dW2": dW2,"db2": db2}return grads 

In [145]:

# 测试一下 backward_propagation 函数
print("=========================测试backward_propagation=========================")
parameters, cache, X_assess, Y_assess = backward_propagation_test_case()
grads = backward_propagation(parameters, cache, X_assess, Y_assess)
print ("dW1 = "+ str(grads["dW1"]))
print ("db1 = "+ str(grads["db1"]))
print ("dW2 = "+ str(grads["dW2"]))
print ("db2 = "+ str(grads["db2"])) 

=========================测试backward_propagation=========================
dW1 = [[ 0.01018708 -0.00708701][ 0.00873447 -0.0060768 ][-0.00530847  0.00369379][-0.02206365  0.01535126]]
db1 = [[-0.00069728][-0.00060606][ 0.000364  ][ 0.00151207]]
dW2 = [[ 0.00363613  0.03153604  0.01162914 -0.01318316]]
db2 = [[0.06589489]]

⑥ 反向传播完成了，我们开始对参数进行更新。

4.6.4 更新参数¶

① 我们需要使用（dW1，db1，dW2，db2）更新（W1，b1，W2，b2）。

② 更新算法如下：
$ \theta = \theta - \alpha \frac{\partial J }{ \partial \theta }$

③ 其中：

1. $\alpha$ 代表学习率
2. $\theta$ 代表一个参数。

④ 我们需要选择一个良好的学习速率，我们可以看一下下面这两个图(图由Adam Harley提供)。

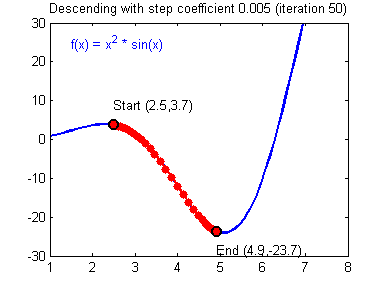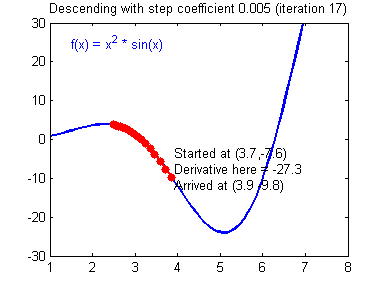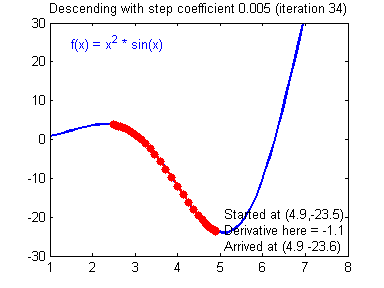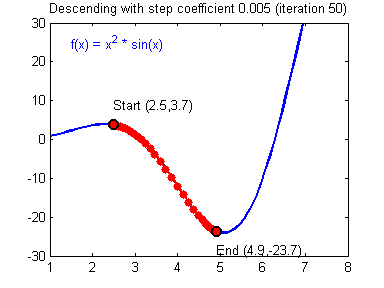
⑤ 上面两个图分别代表了具有良好学习速率（收敛）和不良学习速率（发散）的梯度下降算法。

In [146]:

def update_parameters(parameters, grads, learning_rate = 1.2):"""使用上面给出的梯度下降更新规则更新参数参数：parameters - 包含参数的字典类型的变量。grads - 包含导数值的字典类型的变量。learning_rate - 学习速率返回：parameters - 包含更新参数的字典类型的变量。"""# 从字典“parameters”中检索每个参数W1 = parameters["W1"]b1 = parameters["b1"]W2 = parameters["W2"]b2 = parameters["b2"]# 从字典“梯度”中检索每个梯度dW1 = grads["dW1"]db1 = grads["db1"]dW2 = grads["dW2"]db2 = grads["db2"]# 每个参数的更新规则W1 = W1 - learning_rate * dW1b1 = b1 - learning_rate * db1W2 = W2 - learning_rate * dW2b2 = b2 - learning_rate * db2parameters = {"W1": W1,"b1": b1,"W2": W2,"b2": b2}return parameters

In [147]:

# 测试一下 update_parameters 函数
print("=========================测试update_parameters=========================")
parameters, grads = update_parameters_test_case()
parameters = update_parameters(parameters, grads)print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))

=========================测试update_parameters=========================
W1 = [[-0.00643025  0.01936718][-0.02410458  0.03978052][-0.01653973 -0.02096177][ 0.01046864 -0.05990141]]
b1 = [[-1.02420756e-06][ 1.27373948e-05][ 8.32996807e-07][-3.20136836e-06]]
W2 = [[-0.01041081 -0.04463285  0.01758031  0.04747113]]
b2 = [[0.00010457]]

4.7 整合¶

① 我们现在把上面的东西整合到nn_model()中，神经网络模型必须以正确的顺序使用先前的功能。

In [208]:

def nn_model(X, Y, n_h, num_iterations = 10000, print_cost=False):"""参数：X - 数据集,维度为（2，示例数）Y - 标签，维度为（1，示例数）n_h - 隐藏层的数量num_iterations - 梯度下降循环中的迭代次数print_cost - 如果为True，则每1000次迭代打印一次成本数值返回：parameters - 模型学习的参数，它们可以用来进行预测。"""    # 初始化参数，然后检索 W1, b1, W2, b2。输入:“n_x, n_h, n_y”。np.random.seed(3)n_x = layer_sizes(X, Y)[0]n_y = layer_sizes(X, Y)[2]# 初始化参数，然后检索 W1, b1, W2, b2。# 输入:“n_x, n_h, n_y”。输出=“W1, b1, W2, b2，参数”。parameters = initialize_parameters(n_x, n_h, n_y)W1 = parameters["W1"]b1 = parameters["b1"]W2 = parameters["W2"]b2 = parameters["b2"]# 循环(梯度下降)for i in range(0, num_iterations):# 前项传播A2, cache = forward_propagation(X, parameters)# 计算成本cost = compute_cost(A2, Y, parameters)# 反向传播grads = backward_propagation(parameters, cache, X, Y)# 更新参数parameters = update_parameters(parameters, grads)# 每1000次迭代打印成本if print_cost and i % 1000 == 0:print ("Cost after iteration %i: %f" %(i, cost))return parameters

In [210]:

# 测试一下 nn_model 函数
print("=========================测试nn_model=========================")
X_assess, Y_assess = nn_model_test_case()
parameters = nn_model(X_assess, Y_assess, 4, num_iterations=10000, print_cost=False)print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))

=========================测试nn_model=========================

C:\Users\86158\AppData\Local\Temp\ipykernel_10044\499126413.py:10: RuntimeWarning: divide by zero encountered in loglogprobs = np.multiply(np.log(A2), Y) + np.multiply(np.log(1 - A2), (1 - Y))
C:\Users\86158\AppData\Local\Temp\ipykernel_10044\499126413.py:6: RuntimeWarning: overflow encountered in expreturn 1/(1+np.exp(-z))

W1 = [[-4.18501964  5.33203231][-7.53803638  1.20755888][-4.19301361  5.32615356][ 7.53798951 -1.2075854 ]]
b1 = [[ 2.32933188][ 3.81002159][ 2.33009153][-3.8101016 ]]
W2 = [[-6033.82354742 -6008.14298684 -6033.08777738  6008.07944581]]
b2 = [[-52.67924992]]

4.8 预测¶

① 构建predict()来使用模型进行预测。

② 使用正向传播来预测结果。

note：$y\_prediction=1\text{activation > 0.5}=\{\begin{array}{ll}1& \text{if}activation>0.5\\ 0& \text{otherwise}\end{array}$

note：如果你想基于阈值将矩阵X设为0和1，则可以执行以下操作： X_new = (X > threshold)

In [151]:

def predict(parameters, X): """使用学习的参数，为X中的每个示例预测一个类参数：parameters - 包含参数的字典类型的变量。X - 输入数据（n_x，m）返回predictions - 我们模型预测的向量（红色：0 /蓝色：1）"""# 使用前向传播计算概率，并使用 0.5 作为阈值将其分类为 0/1。A2, cache = forward_propagation(X, parameters)predictions = np.round(A2)return predictions

③ 现在运行模型以查看其如何在二维数据集上运行。

④ 运行以下代码以使用含有$n\_h$隐藏单元的单个隐藏层测试模型。

In [152]:

# 测试一下 predict 函数
print("=========================测试predict=========================")
parameters, X_assess = predict_test_case()predictions = predict(parameters, X_assess)
print("预测的平均值= " + str(np.mean(predictions)))

=========================测试predict=========================
预测的平均值= 0.6666666666666666

⑤ 现在我们把所有的东西基本都做完了，我们开始正式运行。

5. 正式运行¶

5.1 构建训练模型¶

In [216]:

# 用 n_h 维隐藏层构建一个模型
X, Y = load_planar_dataset()parameters = nn_model(X, Y, n_h = 4, num_iterations = 10000, print_cost=True)

Cost after iteration 0: 0.693048
Cost after iteration 1000: 0.288083
Cost after iteration 2000: 0.254385
Cost after iteration 3000: 0.233864
Cost after iteration 4000: 0.226792
Cost after iteration 5000: 0.222644
Cost after iteration 6000: 0.219731
Cost after iteration 7000: 0.217504
Cost after iteration 8000: 0.219447
Cost after iteration 9000: 0.218605

5.2 绘制决策边界¶

In [217]:

# 绘制决策边界
# Y = Y.ravel()  #确保 Y为一维数组
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
plt.title("Decision Boundary for hidden layer size " + str(4))

Out[217]:

Text(0.5, 1.0, 'Decision Boundary for hidden layer size 4')

5.3 打印准确率¶

In [221]:

# 打印准确率
predictions = predict(parameters, X)# print ('准确率: %d' % float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%')
accuracy = np.mean(predictions == Y) * 100  #当前版本推荐的公式
print ("准确率: {} %".format(accuracy))

准确率: 90.5 %

① 与Logistic回归相比，准确性确实更高。

② 该模型学习了flower的叶子图案！与逻辑回归不同，神经网络甚至能够学习非线性的决策边界。

5.4 调节隐藏层节点数量¶

① 现在，让我们尝试几种不同的隐藏层大小。

② 调整隐藏层大小（可选练习）运行以下代码（可能需要1-2分钟），你将观察到不同大小隐藏层的模型的不同表现。

In [222]:

plt.figure(figsize=(16, 32))
hidden_layer_sizes = [1, 2, 3, 4, 5, 10, 20] # 隐藏层数量# X, Y = load_planar_dataset()  #重新加入初识数据集即可解决报错问题
for i, n_h in enumerate(hidden_layer_sizes):plt.subplot(5, 2, i+1)plt.title('Hidden Layer of size %d' % n_h)parameters = nn_model(X, Y, n_h, num_iterations = 5000)plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)predictions = predict(parameters, X)# accuracy = float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100)accuracy = np.mean(predictions == Y) * 100  #当前版本推荐的公式print ("隐藏层的节点数量： {}  ，准确率: {} %".format(n_h, accuracy))

隐藏层的节点数量： 1  ，准确率: 67.5 %
隐藏层的节点数量： 2  ，准确率: 67.25 %
隐藏层的节点数量： 3  ，准确率: 90.75 %
隐藏层的节点数量： 4  ，准确率: 90.5 %
隐藏层的节点数量： 5  ，准确率: 91.25 %
隐藏层的节点数量： 10  ，准确率: 90.25 %
隐藏层的节点数量： 20  ，准确率: 90.5 %

③ 较大的模型（具有更多隐藏单元）能够更好地适应训练集，直到最终的最大模型过度拟合数据。

④ 最好的隐藏层大小似乎在n_h = 5附近。实际上，这里的值似乎很适合数据，而且不会引起过度拟合。

⑤ 我们还将在后面学习有关正则化的知识，它允许我们使用非常大的模型（如n_h = 50），而不会出现太多过度拟合。