当前位置：首页 > news >正文

高阶数据结构——红黑树实现

news 来源：原创 2025/7/4 19:23:34

1.红黑树的概念

1.1 红黑树的规则：

1.2 红黑树的效率

2.红黑树的实现

2.1 红黑树的结构

2.2 红黑树的插入

2.2.1 不旋转只变色（无论c是p的左还是右，p是g的左还是右，都是一样的变色处理方式）

2.2.2 单旋+变色

2.2.3 双旋+变色

2.2.4 插入代码+总结：

2.3 红黑树的查找

2.4 红黑树的验证

1.红黑树的概念

咱们之前已经学过AVL树了，其实红黑树是一种能够控制平衡的二叉搜索树。咱们之前学习的AVL树，也是一种控制平衡的二叉搜索树，但是，AVL树，是通过平衡因子这个风向标来判断需不需要进行控制平衡，所以，AVL树的平衡很严格。但是红黑树就不一样了，红黑树有它的平衡判断原则，但是，这个的平衡的条件肯定比AVL树要松一些。可以想象为，AVL是一根绷紧的弦线，但是红黑树是一根比较松散的弦线。

红黑树是⼀棵二叉搜索树，他的每个结点增加⼀个存储位来表示结点的颜色，可以是红色或者黑色。通过对任何⼀条从根到叶子的路径上各个结点的颜色进行约束，红黑树确保没有⼀条路径会比其他路径长出2倍，因而是接近平衡的。

1.1 红黑树的规则：

那么咱们是如何判断一个树是红黑树的呢？

1. 每个结点不是红色就是黑色。

2. 根结点是黑色的。

3. 如果⼀个结点是红色的，则它的两个孩⼦结点必须是黑色的，也就是说任意⼀条路径不会有连续的红色结点。（但是可以有连续的两个黑色节点）。

4. 对于任意⼀个结点，从该结点到其所有NULL结点的简单路径上，均包含相同数量的黑色结点。

只要控制住了这四点规则，也就控制住了最长路径<=2*最短路径，也就控制住了红黑树的平衡

这里讲一下路径的问题：

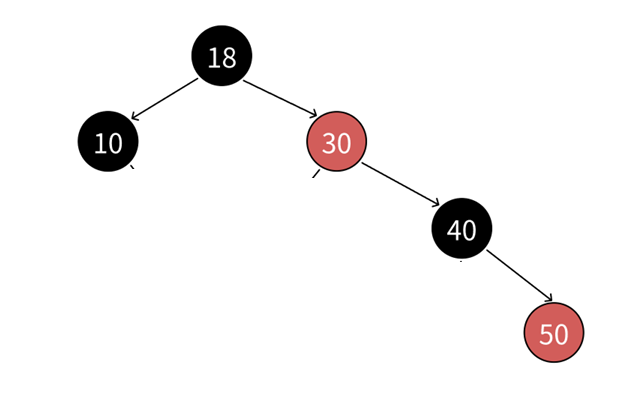
请问这个红黑树有几条路径呢？

大家会不会说是2条？啊，恭喜大家，答错了。这里的路径是一定要把下面的空节点也给算上的！

而有些书上为了好让大家区分，就定义了一个NIL的黑色节点，这个其实就是代替了空节点，只不过更好数了而已。

并且，某一条路径上面，节点有几个，那么这条路径的长度就是几。

所以，这个红黑树是不是有6个路径啊！

那么，还是这个图，再来看一个问题：最短路径是多少？最长路径是多少？最短路径是2（18-10），最长路径是3 （18-30-40）。所以，咱们可以发现：

1.最短路径全是黑色节点。

2.最长路径一定小于等于最短路径的2倍。（当然在这幅图中，最长路径是小于最短路径的2倍的）。但是有一种极端的情况，他俩会相等。咱们待会说。

【1】关于上面的1.，如果一条路径全是黑色节点，那么这个路径一定是最短路径。但是，最短路径不一定是全黑节点。

所以，他俩的关系是这种。

【2】关于第二点：

• 由规则4可知，从根到NULL结点的每条路径都有相同数量的黑色结点，所以极端场景下，最短路径就就是全是黑色结点的路径，假设最短路径长度为bh(blackheight)。

• 由规则2和规则3可知，任意⼀条路径不会有连续的红色结点，所以极端场景下，最长的路径就是⼀黑⼀红间隔组成，那么最长路径的长度为2*bh。

• 综合红黑树的4点规则而言，理论上的全黑最短路径和⼀黑⼀红的最长路径并不是在每棵红黑树都存在的。假设任意⼀条从根到NULL结点路径的长度为h，那么bh<=h<=2*bh。

1.2 红黑树的效率

假设N是红黑树树中结点数量，h最短路径的长度，那么2h-1<=N<=2²*h-1，由此推出h ≈logN，也就是意味着红黑树增删查改最坏也就是走最长路径2 *logN，那么时间复杂度还是O(logN)。

红黑树的表达相对AVL树要抽象⼀些，AVL树通过高度差直观的控制了平衡。红黑树通过4条规则的颜色约束，间接的实现了近似平衡，他们效率都是同⼀档次，但是相对而言，插⼊相同数量的结点，红黑树的旋转次数是更少的，因为他对平衡的控制没那么严格。

2.红黑树的实现

2.1 红黑树的结构

 // 枚举值表⽰颜⾊enum Colour{RED,BLACK};// 这⾥我们默认按key/value结构实现template<class K, class V>struct RBTreeNode{// 这⾥更新控制平衡也要加⼊parent指针pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Colour _col;RBTreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr){}};template<class K, class V>class RBTree{typedef RBTreeNode<K, V> Node;public:private:Node* _root = nullptr;};

来看一下红黑的大体的代码逻辑，这里与前面AVL树大体不同的是：这里没有了平衡因子bf了，取而代之的是颜色Colour，并且，枚举出两个颜色。

2.2 红黑树的插入

1. 插入⼀个值按二叉搜索树规则进行插入，插入后我们只需要观察是否符合红黑树的4条规则。

2. 如果是空树插入，新增结点是黑色结点。如果是非空树插入，新增结点必须红色结点，因为非空树插入，新增黑色结点就破坏了规则4，规则4是很难维护的。

3. 非空树插入后，新增结点必须红色结点，如果父亲结点是黑色的，则没有违反任何规则，插入结束

4. 非空树插入后，新增结点必须红色结点，如果父亲结点是红色的，则违反规则3。进⼀步分析，c是红色，p为红，g必为黑，这三个颜色都固定了（这句话很关键），关键的变化看u的情况，需要根据u分为以下几种情况分别处理。

总的来说，插入黑色需要维护每条路径上的黑色节点数量，成本很大，所以插入红色节点。

说明：下图中假设我们把新增结点标识为c(cur)，c的父亲标识为p(parent)，p的父亲标识为 g(grandfather)，p的兄弟标识为u（uncle）。

2.2.1 不旋转只变色（无论c是p的左还是右，p是g的左还是右，都是一样的变色处理方式）

c为红，p为红，g为黑，u存在且为红，则将p和u变黑，g变红。在把g当做新的c，继续往上更新。

分析：因为p和u都是红色，g是黑色，把p和u变黑，左边子树路径各增加⼀个黑色结点，g再变红，相当于保持g所在子树的黑色结点的数量不变，同时解决了c和p连续红色结点的问题，需要继续往上更新是因为，g是红色，如果g的父亲还是红色，那么就还需要继续处理（因为不可以有连续的两个红色节点）；如果g的父亲是黑色，则处理结束了；如果g就是整棵树的根，再把g变回黑色。

咱们先来看一种简单的情况：

上图就是简单的变色不需要旋转。

来看这种情况的抽象图：

这是抽象图：这里c只能是原来就存在的节点，a,b,d,e,f均为抽象表示，说明其中还有节点是不固定的。所以这里的c不是新增，这样就可以与下面的节点圆一下，使得各个路径的黑色节点数量一致。但是若是c为新增，那么c下面的a，b可就啥都没了，那么这样的话，各个路径的黑色节点很难控制一致。

所以，这里的c为红色节点，是因为，你插入的时候，插入在了c的其中一个孩子节点的下面，再通过只变色不旋转的情况，使得c变成了红色节点。

【1】h==0

d/e/f代表每条路径拥有hb个黑色结点的子树，a/b代表每条路径拥有hb-1个黑色结点的根为红的子树，hb>=0。

这里，c就一定是新增的节点了。如果这里c不是新增，那么要保持各个路径的黑色节点一致，很明显，如果，这儿为黑，不可以，因为右边路径的黑色节点只有一个。为红，也不可以，因为不能有连续的两个红色节点。

【2】h==1

【3】h==2

以上分别展示了hb==0/hb==1/hb==2的具体情况组合分析，当hb等于2时，这里组合情况上百亿种，这些样例是帮助我们理解，不论情况多少种，多么复杂，处理方式⼀样的，变色再继续往上处理即可，所以我们只需要看抽象图即可。

所以，殊途同归，这种情况的处理方式都是一样的，所以，不需要过多的关注底层，多看看上面，即可判断出该用什么方法。

这里还是要提一嘴，不管c位于p的左还是右，p位于g的左还是右，处理方式都是一样的。但是这个只限于uncle存在且为红的情况。因为后面，这些不同，他们的处理方式是不同的。

2.2.2 单旋+变色

c为红，p为红，g为黑，u不存在或者u存在且为黑，u不存在，则c⼀定是新增结点，u存在且为黑，则 c⼀定不是新增，c之前是黑色的，是在c的子树中插入，符合情况1，变色将c从黑色变成红色，更新上来的。（原因同上）

之前，uncle存在且为红是一种情况，且只有一种处理方式，但是这种uncle不存在或者uncle存在且为黑，是一种情况，这种情况会由于c，p的位置的不同而产生不同的解决办法，在这里，咱们先介绍单旋+变色，最后总结的时候再来总结其他的方法。

分析：p必须变黑，才能解决，连续红色结点的问题，u不存在或者是黑色的，这里单纯的变色无法解决问题，需要旋转+变色。

看这个形态，像不像右单旋的形态呢？没错，很像，没错，这里的解决办法就是右单旋。

如果p是g的左，c是p的左，那么以g为旋转点进行右单旋，再把p变黑，g变红即可。p变成课这颗树新的根，这样子树黑色结点的数量不变，没有连续的红色结点了，且不需要往上更新，因为p的父亲是黑色还是红色或者空都不违反规则。（上面是黑节点，可以有两个连续的黑节点，上面是红节点，黑红相接，没有任何问题。）

这个形态像不像左单旋的形态模型，没错，很像，所以用左单旋来解决。

如果p是g的右，c是p的右，那么以g为旋转点进行左单旋，再把p变黑，g变红即可。p变成课这颗树新的根，这样子树黑色结点的数量不变，没有连续的红色结点了，且不需要往上更新，因为p的父亲是黑色还是红色或者空都不违反规则。

看这个，uncle不存在的情况，如果只用单个的变色，无法解决问题，因为变色变到最后，根节点成红色的了。

来看uncle存在且为黑的抽象图：

hb==1：
也是一样，不需要太去关注底层的节点有多复杂啥的，多看看上面的形态是啥样的。

2.2.3 双旋+变色

c为红，p为红，g为黑，u不存在或者u存在且为黑，u不存在，则c⼀定是新增结点，u存在且为黑，则 c⼀定不是新增，c之前是黑色的，是在c的子树中插入，符合情况1，变色将c从黑色变成红色，更新上来的。

这个看着像不像咱们的那个先左后右双旋？没错，这个也是同样的解决办法：

如果p是g的左，c是p的右，那么先以p为旋转点进行左单旋，再以g为旋转点进行右单旋，再把c变黑，g变红即可。c变成课这颗树新的根，这样子树黑色结点的数量不变，没有连续的红色结点了，且不需要往上更新，因为c的色亲是黑色还是红色或者空都不违反规则。

这个像咱们的先右后左双旋转模型，没错，这个的处理方法也是这种：

如果p是g的右，c是p的左，那么先以p为旋转点进行右单旋，再以g为旋转点进行左单旋，再把c变黑，g变红即可。c变成课这颗树新的根，这样子树黑色结点的数量不变，没有连续的红色结点了，且不需要往上更新，因为c的父亲是黑色还是红色或者空都不违反规则。

2.2.4 插入代码+总结：

OK，那么接下来来看关键的代码：

//插入
bool Insert(const pair<k, v>& kv)
{if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;//别忘了根节点必须是黑色的return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else{return false;//这个是return false，不是assert(false)}}//插入红节点cur = new Node(kv);cur->_col = RED;if (kv.first > parent->_kv.first){parent->_right = cur;}else if (kv.first < parent->_kv.first){parent->_left = cur;}cur->_parent = parent;//现在才是真正的插入后调节红黑树的平衡的时候while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left)//先分parent是grandfather的左还是右这一大类//这样才可以确定uncle是grandfather的左还是右//之后，由于c的位置在哪都可以，所以不用讨论c的情况//但是若是uncle为空或者为黑色，就需要讨论c的位置了{Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED){//  g//p   u//	cparent->_col = uncle->_col = RED;grandfather->_col = BLACK;cur = grandfather;parent = cur->_parent;//如果此时的cur就是根节点//那么这个程序这个继续往上判断就没有必要了，别忘了根节点是黑色}else if(uncle==nullptr||uncle->_col==BLACK){//    g//p        u//   c      if (cur == parent->_left){RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}//    g//p        u//         celse if (cur == parent->_right){RotateL(parent);RotateR(grandfather);parent->_col = grandfather->_col = RED;cur->_col = BLACK;}}break;}else if (parent == grandfather->_right){Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){//  g//u   p//			cparent->_col = uncle->_col = RED;grandfather->_col = BLACK;cur = grandfather;parent = cur->_parent;//如果此时的cur就是根节点//那么这个程序这个继续往上判断就没有必要了，所以才要判空// 但要是这样的话，根节点此时就是红色的呀，这好办，在最后加一个// 总的：将根节点的颜色置为黑色即可。（虽然很暴力，但是很有用）//别忘了根节点是黑色}else if (uncle == nullptr || uncle->_col == BLACK){//    g//u       p//           cif (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}//    g//u        p//         celse if (cur == parent->_right){RotateR(parent);RotateL(grandfather);parent->_col = grandfather->_col = RED;cur->_col = BLACK;}}}break;}_root->_col = BLACK;return true;
}

大家看这代码，听我来给大家总结一下：

以上这两张图，是我认为本章最核心的部分，就是理清楚各个情况即可。

2.3 红黑树的查找

按二叉搜索树逻辑实现即可，搜索效率为 O(logN)。

Node* Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_kv.first < key){cur = cur->_right;}else if (cur->_kv.first > key){cur = cur->_left;}else{return cur;}}return nullptr;
}

2.4 红黑树的验证

这⾥获取最长路径和最短路径，检查最长路径不超过最短路径的2倍是不可行的，因为就算满足这个条件，红黑树也可能颜色不满足规则，当前暂时没出问题，后续继续插入还是会出问题的。所以我们还是去检查4点规则，满足这4点规则，⼀定能保证最长路径不超过最短路径的2倍。 （因为咱们前面说过，只有保证4点规则，才可以保证接下来的一切）

1.规则1枚举颜色类型，天然实现保证了颜色不是黑色就是红色。

2.规则2直接检查根即可。（如果根是红色，就直接返回false即可）

3.规则3前序遍历检查，遇到红色结点查孩子不太方便，因为孩子有两个，且不⼀定存在，反过来检查父亲的颜色就方便多了。

4.规则4前序遍历，遍历过程中用形参记录跟到当前结点的blackNum(黑色结点数量)，前序遍历遇到黑色结点就++blackNum，走到空就计算出了⼀条路径的黑色结点数量。再任意⼀条路径黑色结点数量作为参考值，依次比较即可。

接下来来看代码：

bool Check(Node* root, int blackNum, const int refNum)
{if (root == nullptr){// 前序遍历走到空时，意味着一条路径走完了if (blackNum != refNum){cout << "存在黑色结点的数量不相等的路径" << endl;return false;}return true;}// 检查孩子不太方便，因为孩子有两个，且不一定存在，反过来检查父亲就方便多了if (root->_col == RED && root->_parent->_col == RED){cout << root->_kv.first << "存在连续的红色结点" << endl;return false;}if (root->_col == BLACK){++blackNum;}return Check(root->_left, blackNum, refNum) && Check(root->_right, blackNum, refNum);
}
bool IsBalanceTree()
{if (_root == nullptr)return true;if (_root->_col == RED)return false;// 参考值int refNum = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){++refNum;}cur = cur->_left;}return Check(_root, 0, refNum);
}

OK，还有一个红黑树的删除，还是一样，在这就不做讲解了，大家有兴趣的，可以下去自行研究。

本篇完...............

1.红黑树的概念

1.1 红黑树的规则：

1.2 红黑树的效率

2.红黑树的实现

2.1 红黑树的结构

2.2 红黑树的插入

2.2.1 不旋转只变色（无论c是p的左还是右，p是g的左还是右，都是一样的变色处理方式）

2.2.2 单旋+变色

2.2.3 双旋+变色

2.2.4 插入代码+总结：

2.3 红黑树的查找

2.4 红黑树的验证

相关文章：