当前位置：首页 > news >正文

[概率论基本概念1]什么是经验分布

news 来源：原创 2025/7/19 5:11:26

一、说明

描述一个概率模型，有密度函数很好描述。如果写不出密度函数，退而用分布函数也能完整刻画，因此，分布函数表示比密度函数表示更加宽泛普适。本片讲述经验分布拟合分布函数的基础概念。

二、经验分布直观解释

在统计学中，经验分布函数（又称经验累积分布函数，eCDF ）是与样本的经验测度相关的分布函数。该累积分布函数是一个阶跃函数，在n 个数据点处，其值在每个数据点上都以1/ n 的幅度跃升。对于任何指定的测量变量值，其值是该测量变量观测值中小于或等于该指定值的比率。
在这里插入图片描述
绿色曲线渐近地接近0和1的高度，但未达到这两个高度，它是标准正态分布的真实累积分布函数。
灰色线段表示从该分布中抽取的特定样本的观测值，蓝色阶跃函数的水平阶跃（包括每一步的最左侧点，但不包括最右侧点）构成了该样本的经验分布函数。（单击此处加载新图表。）

经验分布函数是生成样本点的累积分布函数的估计值。根据格利文科-坎泰利定理，它以概率 1 收敛到该基础分布。目前有许多结果可以量化经验分布函数向基础累积分布函数的收敛速度。

三、经验分布解析表述

设( X 1 , …, X n )为独立同分布的实随机变量，具有共同的累积分布函数 F ( t )。则经验分布函数定义为[
在这里插入图片描述
在这里 $1_A$ 是事件A的指标,对于给定的t，指标 $\mathbf {1} _{X_{i}\leq t}$ 是参数为 $p = F (t)$ 的伯努利随机变量；因此
$n{\widehat {F}}_{n}(t)$ 是一个二项式随机变量，均值为 $n F (t)$ ，方差为 $n F (t) (1 - F (t))$ 。这意味着 ${\widehat {F}}_{n}(t)$ 是F ( t )的无偏估计量。

然而，在一些教科书中，其定义如下
在这里插入图片描述

四、渐进性质

由于当 $n$ 趋向无穷大时，比率 $(n + 1) / n$ 趋近于 1 ，因此上面给出的两个定义的渐近性质是相同的。

根据强大数定律，估计量
$\scriptstyle {\widehat {F}}_{n}(t)$ 对于t的每一个值，当n → ∞时几乎肯定收敛于F ( t )：
在这里插入图片描述
因此估计量 $\scriptstyle {\widehat {F}}_{n}(t)$ 是一致的。该表达式断言了经验分布函数逐点收敛于真实的累积分布函数。有一个更强的结论，称为格利文科-坎泰利定理，它指出收敛实际上在t上均匀发生：

这个表达式中的 sup-norm 称为Kolmogorov–Smirnov 统计量，用于检验经验分布之间的拟合优度
$\scriptstyle {\widehat {F}}_{n}(t)$ 以及假设的真实累积分布函数F。这里可以合理地使用其他范数函数来代替 sup 范数。例如，L2范数可以推导出Cramér–von Mises 统计量。

渐近分布可以用几种不同的方式进一步刻画。首先，中心极限定理指出，逐点 $\scriptstyle {\widehat {F}}_{n}(t)$ 具有渐近正态分布，标准 ${\sqrt {n}}$ 收敛速度：
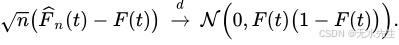
在这里插入图片描述
这个结果由Donkser定理扩展。该定理断言经验过程 $\scriptstyle {\sqrt {n}}({\widehat {F}}_{n}-F)$ ，被视为一个函数，索引为 $\scriptstyle t\in \mathbb {R}$ ，在Skorokhod 空间中分布收敛 $\scriptstyle D[-\infty ,+\infty ]$ 均值零高斯过程格 $\scriptstyle G_{F}=B\circ F$ 其中B是标准布朗桥。

一、说明

二、经验分布直观解释

三、经验分布解析表述

四、渐进性质

相关文章：