dijkstra算法加训上 之 分层图最短路
来几个分层图的题练习下哈
P4568 [JLOI2011] 飞行路线
P4568 [JLOI2011] 飞行路线 - 洛谷![]() https://www.luogu.com.cn/problem/P4568
https://www.luogu.com.cn/problem/P4568
题目描述
Alice 和 Bob 现在要乘飞机旅行,他们选择了一家相对便宜的航空公司。该航空公司一共在 n 个城市设有业务,设这些城市分别标记为 0 到 n−1,一共有 m 种航线,每种航线连接两个城市,并且航线有一定的价格。
Alice 和 Bob 现在要从一个城市沿着航线到达另一个城市,途中可以进行转机。航空公司对他们这次旅行也推出优惠,他们可以免费在最多 k 种航线上搭乘飞机。那么 Alice 和 Bob 这次出行最少花费多少?
输入格式
第一行三个整数 n,m,k,分别表示城市数,航线数和免费乘坐次数。
接下来一行两个整数 s,t,分别表示他们出行的起点城市编号和终点城市编号。
接下来 m 行,每行三个整数 a,b,c,表示存在一种航线,能从城市 a 到达城市 b,或从城市 b 到达城市 a,价格为 c。
输出格式
输出一行一个整数,为最少花费。
输入输出样例
输入 #1复制
5 6 1 0 4 0 1 5 1 2 5 2 3 5 3 4 5 2 3 3 0 2 100输出 #1复制
8说明/提示
数据规模与约定
对于 30% 的数据,2≤n≤50,1≤m≤300,k=0。
对于 50% 的数据,2≤n≤600,1≤m≤6×103,0≤k≤1。
对于 100% 的数据,2≤n≤104,1≤m≤5×104,0≤k≤10,0≤s,t,a,b<n,a=b,0≤c≤103。
另外存在一组 hack 数据。
思路
就是增加了一个考虑情况,有k个路线可以免费,嘶,这个看代码仔细思考,然后把走的每个路的情况在脑子里过,应该能想明白我语言描述不出来、
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+10;
const int M=5e4+10;
using tiii=tuple<int,int,int>;
vector<pair<int,int>>graph[N];
vector<vector<int>>distance_(N,vector<int>(15,INT_MAX));
int n,m,k,s,t;
int main(){cin>>n>>m>>k>>s>>t;while(m--){int u,v,w;cin>>u>>v>>w;graph[u].push_back({v,w});graph[v].push_back({u,w});}priority_queue<tiii,vector<tiii>,greater<tiii>>pq;pq.push({0,s,0});//第一个是花费,中间是节点 ,第二个是花费次数distance_ [s][0]=0;while(!pq.empty()){int dist=get<0>(pq.top());int u=get<1>(pq.top());int num=get<2>(pq.top());pq.pop();if(u==t) {cout<<dist;return 0;}if(dist>distance_[u][num]) continue;for(auto edge:graph[u]){int v=edge.first;int w=edge.second;if(num<k&&dist<distance_[v][num+1]){distance_[v][num+1]=dist;pq.push({distance_[v][num+1],v,num+1});} if(dist+w<distance_[v][num]){distance_[v][num]=dist+w;pq.push({distance_[v][num],v,num});}}}cout<<-1;return 0;
}LCP 35. 电动车游城市
LCP 35. 电动车游城市 - 力扣(LeetCode)![]() https://leetcode.cn/problems/DFPeFJ/description/?envType=problem-list-v2&envId=tZEK0x2Y
https://leetcode.cn/problems/DFPeFJ/description/?envType=problem-list-v2&envId=tZEK0x2Y
小明的电动车电量充满时可行驶距离为
cnt,每行驶 1 单位距离消耗 1 单位电量,且花费 1 单位时间。小明想选择电动车作为代步工具。地图上共有 N 个景点,景点编号为 0 ~ N-1。他将地图信息以[城市 A 编号,城市 B 编号,两城市间距离]格式整理在在二维数组paths,表示城市 A、B 间存在双向通路。初始状态,电动车电量为 0。每个城市都设有充电桩,charge[i]表示第 i 个城市每充 1 单位电量需要花费的单位时间。请返回小明最少需要花费多少单位时间从起点城市start抵达终点城市end。示例 1:
输入:paths = [[1,3,3],[3,2,1],[2,1,3],[0,1,4],[3,0,5]], cnt = 6, start = 1, end = 0, charge = [2,10,4,1]输出:43解释:最佳路线为:1->3->0。 在城市 1 仅充 3 单位电至城市 3,然后在城市 3 充 5 单位电,行驶至城市 0。 充电用时共 3*10 + 5*1= 35 行驶用时 3 + 5 = 8,此时总用时最短 43。
示例 2:
输入:paths = [[0,4,2],[4,3,5],[3,0,5],[0,1,5],[3,2,4],[1,2,8]], cnt = 8, start = 0, end = 2, charge = [4,1,1,3,2]输出: 38 解释:最佳路线为:0->4->3->2。 城市 0 充电 2 单位,行驶至城市 4 充电 8 单位,行驶至城市 3 充电 1 单位,最终行驶至城市 2。 充电用时 4*2+2*8+3*1 = 27 行驶用时 2+5+4 = 11,总用时最短 38。提示:
1 <= paths.length <= 200paths[i].length == 32 <= charge.length == n <= 1000 <= path[i][0],path[i][1],start,end < n1 <= cnt <= 1001 <= path[i][2] <= cnt1 <= charge[i] <= 100- 题目保证所有城市相互可以到达
思路
分层图最短路的核心在于将节点扩展为多个状态,每个状态包含当前城市和剩余电量。通过优先队列(小根堆)进行Dijkstra算法,每次处理时间最小的状态,确保找到最优解。
状态定义:每个状态由当前城市、剩余电量和到达该状态的时间组成。
充电处理:在当前城市充电,每次增加一格电量,消耗对应充电时间。
移动处理:移动到相邻城市,消耗电量(等于路径长度),时间增加路径耗时。
其实和上面那个差不多,要仔细比对一下细节,题多给一个状态,所以我们每次进行操作时候也要判断那个状态,distance其实记录的就是状态,之前一维数组是因为只记录一个状态,现在分层图最短路,多一个状态所以要用二维,然后我们就又多了许多判断的条件,这是要注意的
class Solution {
public:struct Node{int x;int y;int cost;bool operator>(const Node& other) const{return cost>other.cost;//小根堆}};
int electricCarPlan(vector<vector<int>>& paths, int cnt, int start, int end, vector<int>& charge) {int n = charge.size();//n个城市//建图vector<vector<pair<int, int>>> graph(n);for (auto& path : paths) {graph[path[0]].emplace_back(path[1], path[2]);graph[path[1]].emplace_back(path[0], path[2]);//无向图所以添加两次,保证连接性}//这种题,节点不是真正的点,而是点+当前状态,在该题状态就是电量vector<vector<int>> distance(n, vector<int>(cnt + 1, INT_MAX));//节点+状态distance[start][0] = 0;//小根堆,priority_queue<Node, vector<Node>, greater<Node>> heap;heap.emplace(start, 0, 0);//往里面先添加当前到达位置,到达当前城市电量为0,到达当前城市花费的时间,也就是代价,小根堆也是靠这个参数来排序//接下来就是核心代码,从小根堆里得到每次走最短的路所到的城市while (!heap.empty()) {auto [u, cur_charge, t] = heap.top();//u是当前所到达的城市,cur是当前城市充电花的时间,t是到达这个城市花费的时间 heap.pop();if (u == end) return t;//到end一定是最短路所以直接返回tif (t>distance[u][cur_charge]) continue; //当想走向下一个城市,我们有两条路//1,选择充电先充一格电///2,不充电直接走向下一个城市for (auto& [v, cost] : graph[u]) {// 1充电(如果当前电量不满)if (cur_charge < cnt) {//当前的电只要没充满久一直一格一格的充电int new_charge = cur_charge + 1;//加一格电int new_time = t + charge[u];//到达这个城市后的时间也就也加charge[u]if (new_time < distance[u][new_charge]) {//如果选择充电然后判断到达这个状态是不是更小了distance[u][new_charge] = new_time;//冲完电后的状态heap.emplace(u, new_charge, new_time);//然后扔进堆里}}if (cur_charge >= cost) {//如果当前的电够去下一个城市就去int remaining = cur_charge - cost;//剩下的电if (t + cost < distance[v][remaining]) {//之前花的时间+这次去下一个城市的时间如果更小就更新当前状态到达下一条路的代价distance[v][remaining] = t + cost;heap.emplace(v, remaining, t + cost);}}}}return -1; // 无法到达
}
};787. K 站中转内最便宜的航班
787. K 站中转内最便宜的航班![]() https://leetcode.cn/problems/cheapest-flights-within-k-stops/
https://leetcode.cn/problems/cheapest-flights-within-k-stops/
有
n个城市通过一些航班连接。给你一个数组flights,其中flights[i] = [fromi, toi, pricei],表示该航班都从城市fromi开始,以价格pricei抵达toi。现在给定所有的城市和航班,以及出发城市
src和目的地dst,你的任务是找到出一条最多经过k站中转的路线,使得从src到dst的 价格最便宜 ,并返回该价格。 如果不存在这样的路线,则输出-1。示例 1:
输入: n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1 输出: 700 解释: 城市航班图如上 从城市 0 到城市 3 经过最多 1 站的最佳路径用红色标记,费用为 100 + 600 = 700。 请注意,通过城市 [0, 1, 2, 3] 的路径更便宜,但无效,因为它经过了 2 站。示例 2:
输入: n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1 输出: 200 解释: 城市航班图如上 从城市 0 到城市 2 经过最多 1 站的最佳路径标记为红色,费用为 100 + 100 = 200。示例 3:
输入:n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0 输出:500 解释: 城市航班图如上 从城市 0 到城市 2 不经过站点的最佳路径标记为红色,费用为 500。提示:
1 <= n <= 1000 <= flights.length <= (n * (n - 1) / 2)flights[i].length == 30 <= fromi, toi < nfromi != toi1 <= pricei <= 104- 航班没有重复,且不存在自环
0 <= src, dst, k < nsrc != dst
思路
整体就是个dijkstra,但是这次相当于分层图最短路了,分层图就是现在又有个另一个限制,我们要保证在k次转飞机路线内才行,所以我们就把distance数组变成二维记录走到每个节点时已经转运了几次,还有堆里面也加上这玩意,就行了,还是很有意思的哈哈
class Solution {
public:using tiii=tuple<int, int, int>;int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {//建图 vector<vector<pair<int,int>>> graph(n);for(auto &edge:flights){graph[edge[0]].push_back({edge[1],edge[2]});}//建堆priority_queue<tiii,vector<tiii>,greater<>>pq;//distance_表vector<vector<int>> distance_(n,vector<int>(k+2,INT_MAX));//初始化distance_[src][k+1]=0;pq.push({0,src,k+1});int ans=0;while(!pq.empty()){auto [dist,u,remain]=pq.top();pq.pop();if(u==dst) return dist;if(remain==0) continue;if(dist>distance_[u][remain]) continue; for(auto [v,w]:graph[u]){int new_remain=remain-1;if(dist+w<distance_[v][new_remain]){distance_[v][new_remain]=dist+w;pq.push({distance_[v][new_remain],v,new_remain});}}}return -1;}
};864. 获取所有钥匙的最短路径
864. 获取所有钥匙的最短路径![]() https://leetcode.cn/problems/shortest-path-to-get-all-keys/
https://leetcode.cn/problems/shortest-path-to-get-all-keys/
给定一个二维网格
grid,其中:
- '.' 代表一个空房间
- '#' 代表一堵墙
- '@' 是起点
- 小写字母代表钥匙
- 大写字母代表锁
我们从起点开始出发,一次移动是指向四个基本方向之一行走一个单位空间。我们不能在网格外面行走,也无法穿过一堵墙。如果途经一个钥匙,我们就把它捡起来。除非我们手里有对应的钥匙,否则无法通过锁。
假设 k 为 钥匙/锁 的个数,且满足
1 <= k <= 6,字母表中的前k个字母在网格中都有自己对应的一个小写和一个大写字母。换言之,每个锁有唯一对应的钥匙,每个钥匙也有唯一对应的锁。另外,代表钥匙和锁的字母互为大小写并按字母顺序排列。返回获取所有钥匙所需要的移动的最少次数。如果无法获取所有钥匙,返回
-1。
示例 1:
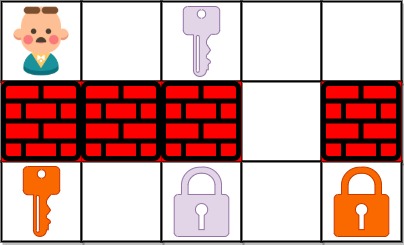
输入:grid = ["@.a..","###.#","b.A.B"] 输出:8 解释:目标是获得所有钥匙,而不是打开所有锁。示例 2:
输入:grid = ["@..aA","..B#.","....b"] 输出:6示例 3:
输入: grid = ["@Aa"] 输出: -1
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 30grid[i][j]只含有'.','#','@','a'-'f'以及'A'-'F'- 钥匙的数目范围是
[1, 6]- 每个钥匙都对应一个 不同 的字母
- 每个钥匙正好打开一个对应的锁
思路
这题也是很有意思的,状态就是带几把钥匙,我们可以利用位运算来代表此时状态手里有几把钥匙哈哈,这题的状态就是坐标和钥匙个数,所以我们的队列里面就要存这俩状态。虽然这题是用bfs但其实核心思路还是一样的
class Solution {#define mxn 31
public:
int move[5]={-1,0,1,0,-1};int shortestPathAllKeys(vector<string>& grid) {vector<vector<vector<bool>>>visited(mxn,vector<vector<bool>>(mxn,vector<bool>(1<<6)));vector<vector<int>>q(mxn*mxn*(1<<6),vector<int>(3));//x,y,状态int l=0,r=0,key=0;int m=grid.size();int n=grid[0].size();for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(grid[i][j]=='@'){q[r][0]=i;q[r][1]=j;q[r++][2]=0;//代表还没拿到钥匙}if(grid[i][j]>='a'&&grid[i][j]<='f'){key|=(1<<(grid[i][j]-'a'));}}}int level=1;while(l<r){int size=r-l;for(int k=0,x,y,s;k<size;k++){x=q[l][0];y=q[l][1];s=q[l++][2];//状态for(int i=0,nx,ny,ns;i<4;i++){nx=x+move[i];ny=y+move[i+1];ns=s;if(nx<0||ny<0||nx==m||ny==n||grid[nx][ny]=='#')continue;if(grid[nx][ny]>='A'&&grid[nx][ny]<='F'&&!(s & (1 << (grid[nx][ny] - 'A')))){continue;//遇到锁但是没有对应钥匙}if(grid[nx][ny]>='a'&&grid[nx][ny]<='f'){ns|=(1<<(grid[nx][ny]-'a'));}//换状态if(ns==key)return level;if(!visited[nx][ny][ns]){visited[nx][ny][ns]=true;q[r][0]=nx;q[r][1]=ny;q[r++][2]=ns;}}}level++;}return -1;}
};总结
小总结一下哈
分层最短路思想总结
分层最短路是一种将状态和位置结合的多维搜索方法,核心思想是将传统图中的节点扩展为“位置+状态”的复合节点,通过状态的分层处理,解决带有约束条件的最短路径问题。其本质是构建一个状态空间图,通过搜索该图找到最优解。记好对每个状态都要判断此时是不是最优路
核心思想
-
状态分层:
-
将问题中影响路径选择的动态变量(如电量、钥匙持有状态、剩余步数等)作为“状态维度”。
-
每个节点由
(位置, 状态)唯一标识,例如:-
电动车问题:
(城市, 剩余电量) -
钥匙问题:
(坐标, 已持有钥匙掩码)
-
-
-
状态转移:
-
在搜索过程中,状态会随着操作(移动、充电、拾取钥匙等)动态变化。
-
例如:从
(x, y, 钥匙掩码)移动到相邻格子后,可能更新钥匙掩码或触发锁的检查。
-
-
最优性保证:
-
使用 BFS(无权图) 或 Dijkstra(带权图) 逐层扩展,确保首次到达目标状态时的路径最短。
-
通用步骤
1. 问题分析与状态定义
-
确定约束条件:找出影响路径选择的动态变量(如电量、钥匙、剩余使用次数等)。
-
状态表示:将约束条件编码为状态变量。例如:
-
电量:整数(0~最大容量)
-
钥匙:位掩码(如
101表示持有钥匙a和c)
-
2. 构建状态空间图
-
节点:每个节点为
(位置, 状态),例如(x, y, mask)。 -
边:
-
移动边:从
(x, y, s)到相邻位置(nx, ny, s),需满足移动条件(如不撞墙、有钥匙开锁等)。 -
状态转移边:在特定位置触发状态更新(如充电、拾取钥匙)。
-
3. 初始化与数据结构
-
队列/优先队列:
-
BFS:普通队列(无权图,每步代价相同)。
-
Dijkstra:优先队列(按代价排序,如时间、距离)。
-
-
访问标记数组:记录
(位置, 状态)是否已被访问,避免重复处理。
4. 搜索过程
-
起点入队:初始位置和初始状态(如电量0、无钥匙)。
-
逐层扩展:
-
取出当前节点,检查是否达到终止条件(如到达终点、收集所有钥匙)。
-
对当前节点进行状态转移(如充电、拾取钥匙)和移动操作,生成新节点。
-
若新节点未被访问过且路径更优,则更新并加入队列。
-
-
终止条件:
-
找到目标状态(如所有钥匙收集完毕)。
-
队列为空时返回无解。
-
关键优化点
-
状态压缩:
-
使用位掩码(Bitmask)表示离散状态(如钥匙),将状态空间从指数级压缩到多项式级。
-
例如:6把钥匙可用
6位二进制数(0~63)表示。
-
-
剪枝策略:
-
若
(位置, 状态)已以更优代价访问过,跳过当前路径。 -
例如:在电动车问题中,若
到达城市u的电量5的时间已经比当前路径更短,则无需处理当前节点。
-
-
分层队列管理:
-
BFS按层扩展,天然保证最短路径;Dijkstra按代价排序,确保优先处理更优路径。
-
这个是ai帮我总结的,偷懒了一下,但我看他说的还是可以的,我对图这玩意实在用语言说不出,只能脑子里想象出,当然也可以画图画出来,但不太好弄就没弄,仔细看看应该就能会哈哈
相关文章:

dijkstra算法加训上 之 分层图最短路
来几个分层图的题练习下哈 P4568 [JLOI2011] 飞行路线 P4568 [JLOI2011] 飞行路线 - 洛谷https://www.luogu.com.cn/problem/P4568 题目描述 Alice 和 Bob 现在要乘飞机旅行,他们选择了一家相对便宜的航空公司。该航空公司一共在 n 个城市设有业务,设这…...

赋予AI更强的“思考”能力
刚刚!北大校友、OpenAI前安全副总裁Lilian Weng最新博客来了:Why We Think 原文链接:Why We Think by Lilian Weng 这篇文章关注:如何让AI不仅仅是“知道”答案,更能“理解”问题并推导出答案。通过赋予AI更强的“思…...
)
微服务项目->在线oj系统(Java版 - 1)
相信自己,终会成功 目录 C/S架构与B/S架构 C/S架构(Client/Server,客户端/服务器架构) 特点: 优点: 缺点: 典型应用: B/S架构(Browser/Server,浏览器/服务器架构&a…...
)
【深度学习】使用块的网络(VGG)
虽然 AlexNet 证明深层神经网络卓有成效,但它没有提供一个通用的模板来指导后续的研究人员设计新的网络。 也就是说尽管我知道了更深更大的网络更有效,但是不清楚怎么让它更深更大,从而起到一个更好的效果。 于是,研究人员开始从单…...

Python数据可视化 - Pyecharts绘图示例
文章目录 一、Pyecharts简介及安装1. Pyecharts简介2. 安装Pyecharts 二、准备数据三、饼图示例1. 初始化选项配置2. 饼图相关设置3. 全局配置项3.1 标题配置项3.2 图例配置项3.3 提示框配置项3.4 工具箱配置项3.5 视觉映射配置项 4. 系列配置项4.1 标签选项配置4.2 图元样式配…...

Day29
复习日 知识点回顾 类的装饰器装饰器思想的进一步理解:外部修改、动态类方法的定义:内部定义和外部定义 作业:复习类和函数的知识点,写下自己过去29天的学习心得,如对函数和类的理解,对python这门工具的理…...

Python列表全面解析:从入门到精通
文章目录 Python列表全面解析:从入门到精通一、列表基础1. 什么是列表?2. 列表特性总结表 二、列表的基本操作(基础)1. 访问元素2. 修改列表 三、列表的常用方法(基础)1. 添加元素的方法2. 删除元素的方法3. 查找和统计方法4. 排序和反转 四、列表的高级…...

Nacos数据写入流程
在 3 节点的 Nacos 集群中,数据写入流程和主节点(Leader)的角色基于 Nacos 的分布式一致性协议(通常使用 Raft 协议)来实现。以下以 Markdown 格式详细说明 3 节点 Nacos 集群的数据写入流程以及主节点的角色和确定方式…...

《P4551 最长异或路径》
题目描述 给定一棵 n 个点的带权树,结点下标从 1 开始到 n。寻找树中找两个结点,求最长的异或路径。 异或路径指的是指两个结点之间唯一路径上的所有边权的异或。 输入格式 第一行一个整数 n,表示点数。 接下来 n−1 行,给出…...

Ansible模块——文件属性查看,文件或目录创建和属性修改
ansible.builtin.stat 可以查看文件信息。 选项 类型 默认值 描述 pathstrnull 要检查的文件或目录的完整路径(必需)。 followboolfalse 如果是符号链接,是否跟随到目标路径上获取其状态。 get_attributesbooltrue 是否返回扩展属性&#…...

【图像生成大模型】Wan2.1:下一代开源大规模视频生成模型
Wan2.1:下一代开源大规模视频生成模型 引言Wan2.1 项目概述核心技术1. 3D 变分自编码器(Wan-VAE)2. 视频扩散 Transformer(Video Diffusion DiT)3. 数据处理与清洗 项目运行方式与执行步骤1. 环境准备2. 安装依赖3. 模…...
:LangChain提示词模版)
AGI大模型(25):LangChain提示词模版
我们也可以创建prompt template, 并引入一些变量到prompt template中,这样在应用的时候更加灵活。 1 代码实现 # 我们也可以创建prompt template, 并引入一些变量到prompt template中,这样在应用的时候更加灵活 from langchain_core.prompts import ChatPromptTemplate from…...

mybatis中的resultMap的association及collectio的使用
目录 1.reusltmap的说明 2.association的使用 3.collection的使用 4.总结 1.reusltmap的说明 resultmap定义了数据库的结果映射到java对象的规则,resultmap包含4个属性: id: ResultMap 的唯一标识 type: 映射到的 Java 类型(全限定类名或…...

静态网站部署:如何通过GitHub免费部署一个静态网站
GitHub提供的免费静态网站托管服务可以无需担心昂贵的服务器费用和复杂的设置步骤,本篇文章中将一步步解如何通过GitHub免费部署一个静态网站,帮助大家将创意和作品快速展现给世界。 目录 了解基础情况 创建基础站点 在线调试站点 前端项目部署 部署…...

Android 手写签名功能详解:从原理到实践
Android 手写签名功能详解 1. 引言2. 手写签名核心实现:SignatureView 类3. 交互层实现:MainActivity 类4. 布局与配置5. 性能优化与扩展方向 1. 引言 在电子政务、金融服务等移动应用场景中,手写签名功能已成为提升用户体验与业务合规性的关…...
笔记-9】WKWebView无法访问网络)
【iOS(swift)笔记-9】WKWebView无法访问网络
对于iOS 在info中添加App Transport Security Settings,然后在App Transport Security Settings里添加Allow Arbitrary Loadstrue 对于macOS 除了上面的操作,还需在项目信息的App Sandbox里有个Network打钩选项...

Adapter适配器模式
Adapter适配器模式是一种结构设计模式,用于解决接口不兼容的问题,通过适配器类,可以将一个类的接口转换为客户渴望的另一个接口,从而使原来无法协作的对象能够一起工作。 角色和职责: 目标接口(Target&…...

七、xlib窗口渲染
文章目录 1.渲染图片2.双缓冲3.混合图片4.渐变窗口 1.渲染图片 在上篇文章中的最后,我们使用libpng加载了一个png图片,并显示到窗口上,但是我们可以看到显示到窗口的图片周边有黑色的背景。原因是在我测试的操作系统下使用xlib创建的窗口默认…...

python中http.cookiejar和http.cookie的区别
在Python中,http.cookiejar和http.cookie(通常指http.cookies模块)是两个不同的模块,它们的主要区别如下: 1. 功能定位 http.cookiejar 用于管理HTTP客户端的Cookie,提供自动化的Cookie存储、发送和接收功…...

架构设计模式:构建健壮、可扩展的 Serverless 应用
架构设计模式:构建健壮、可扩展的 Serverless 应用 到目前为止,我们已经掌握了 Serverless 的基本概念,了解了 FaaS 和 BaaS 如何协同工作,学会了使用框架进行开发部署,并知道了如何监控和排查问题。现在,是时候从“能用”向“好用”迈进了。 仅仅将代码部署到 Lambda 函…...

2- PyTorch
文章目录 1. Overview2. 线性模型 1. Overview 在人的智能中,最经常做的事情是推理和预测,在机器学习中也是如此。我们在以往的算法课中,所接触的穷举、贪心、分治和动规等算法都是由人设计的,而在机器学习中,算法是由…...

MinIO:从入门到精通,解锁云原生存储的奥秘
一、引言:为什么 MinIO 正在重塑存储世界? 在云计算和大数据时代,传统存储系统面临扩展性差、成本高、兼容性不足等挑战。MinIO 凭借其 S3 兼容性、分布式架构、高性能存储 等特性,成为企业构建现代化存储基础设施的首选。 本文…...
(Go语言版))
【LeetCode 热题100】739:每日温度(详细解析)(Go语言版)
🌡️ LeetCode 739:每日温度(详解 单调栈 多种思路对比) 📌 题目描述 给定一个整数数组 temperatures,表示每天的温度,返回一个数组 answer,其中 answer[i] 是指在第 i 天之后&am…...

Linux学习笔记|GCC编译指令基础|静动态库|makefile
一、GCC 编译指令基础 基本编译命令 gcc -o code code.c和gcc code.c -o code:这两条命令功能相同,都是使用 GCC 编译器将code.c源文件编译成名为code的可执行文件。-o选项用于指定输出文件名,选项位置在源文件前后不影响最终结果。 编译过程…...
(Go语言版))
【LeetCode 热题100】17:电话号码的字母组合(详细解析)(Go语言版)
☎️ LeetCode 17. 电话号码的字母组合(回溯 DFS 详解) 📌 题目描述 给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按任意顺序返回。 数字到字母的映射如下(与电话按键相同)…...

C++学习:六个月从基础到就业——C++17:std::optional/variant/any
C学习:六个月从基础到就业——C17:std::optional/variant/any 本文是我C学习之旅系列的第四十七篇技术文章,也是第三阶段"现代C特性"的第九篇,主要介绍C17引入的三个重要工具类型:std::optional、std::varia…...

Go语言中函数 vs 方法
函数(Function):不属于任何类型,是全局可调用的。 方法(Method):绑定在某个类型上的函数,调用时依赖于这个类型的值或指针。 一、函数(Function) func 函数…...

代码随想录算法训练营第六十五天| 图论10—卡码网94. 城市间货物运输 I,95. 城市间货物运输 II
被学校课程轰炸了一周,回过头发现训练营已经要结束了,抓紧时间补完。不过算法这边也很难,感觉每天都是勉强理解在干什么的状态。 94. 城市间货物运输 I 94. 城市间货物运输 I SPFA算法,也是Bellman_ford 队列优化算法 优化原理…...

TDengine 在新能源领域的价值
能源数据的定义 能源数据是指记录和描述能源产业各个方面的信息,包括能源生产、供应、消费、储备、价格、排放以及相关政策和技术的数据。这些数据可以通过各种途径收集和整理,如能源企业的统计报表、政府部门的调查和监测、国际组织的发布数据等。 能…...

浅谈Frida 检测与绕过
目录 ptrace 占位与进程名检测端口检测与 D-Bus 协议通信扫描 /proc 目录(maps、task、fd)定位 so 中的 SVC syscall内存动态释放代码 1. ptrace 占位与进程名检测 检测方式 遍历运行进程列表,检查是否存在 frida-server 或相关进程名&…...

WaterStamp —— 一个实用的网页水印生成器开发记
我正在参加CodeBuddy「首席试玩官」内容创作大赛,本文所使用的 CodeBuddy 免费下载链接:腾讯云代码助手 CodeBuddy - AI 时代的智能编程伙伴 最近,我和 CodeBuddy 一起完成了一个名为 WaterStamp 的网页水印生成器项目。这个小工具主要用于给…...

【MySQL】存储过程,存储函数,触发器
目录 准备工作 一. 存储过程 1.1.什么是存储过程 1.2.创建存储过程 1.3.创建只显示大于等于指定值的记录的存储过程 1.4.显示,删除存储过程 二. 存储函数 2.1.什么是存储函数 2.2.使用存储函数 2.2.1.使用存储函数之前 2.2.2.使用存储函数计算标准体重 …...

python打卡第29天
知识点回顾 类的装饰器装饰器思想的进一步理解:外部修改、动态类方法的定义:内部定义和外部定义 作业:复习类和函数的知识点,写下自己过去29天的学习心得,如对函数和类的理解,对python这门工具的理解等&…...

vim - v
在 Vim 中,使用 可视模式(Visual Mode) 可以选中文本并进行复制、剪切、粘贴等操作。以下是详细的使用方法: 1. 进入可视模式 命令功能v字符可视模式(按字符选择)V(大写)行可视模式…...
)
Linux 线程(上)
前言:大家早上中午晚上好!!今天来学习一下linux系统下所谓的线程吧!!! 一、重新理解进程,什么是进程? 1.1 图解 其中黑色虚线部分一整块就是进程,注意:一整…...
报错:“没有主清单属性” 的解决方法)
# 终端执行 java -jar example.jar 时(example.jar为项目jar包)报错:“没有主清单属性” 的解决方法
终端执行 java -jar example.jar 时(example.jar为项目jar包)报错:“没有主清单属性” 的解决方法 在Java中,一个JAR文件必须包含一个主清单属性(Main-Class属性)才能在命令行中直接运行。如果你在尝试运行…...

4:OpenCV—保存图像
将图像和视频保存到文件 在许多现实世界的计算机视觉应用中,需要保留图像和视频以供将来参考。最常见的持久化方法是将图像或视频保存到文件中。因此,本教程准备解释如何使用 OpenCV C将图像和视频保存到文件中。 将图像保存到文件 可以学习如何保存从…...

[C++面试] const相关面试题
1、非 const 的引用必须指向一个已存在的变量 int main() {int &a 20; // 错误const int &b 30; } 字面量 20 是临时值(右值),没有明确的内存地址。非常量引用(左值引用)不能直接绑定到右值(如…...
Redis当中的消息队列)
#Redis黑马点评#(六)Redis当中的消息队列
目录 Redis当中的消息队列 一 基于List 二 基于PubSub 三 基于Stream 单消费模式 消费者组 Redis当中的消息队列 消息队列,字面意思就是存放消息的队列。最简单的消息队列模型包括3个角色: 消息队列:存储和管理消息,也称为…...

Git基础原理和使用
Git 初识 一、版本管理痛点 在日常工作和学习中,我们经常遇到以下问题: - 通过不断复制文件来保存历史版本(如报告-v1、报告-最终版等) - 版本数量增多后无法清晰记住每个版本的修改内容 - 项目代码管理存在同样问题 二、版本控…...
)
Java程序员学AI(一)
一、前言 最近刷技术圈,满眼都是 GPT、DeepSeek、QWen 这些 AI 名词。看着同行们在群里聊 AI 写代码、做数据分析,我这个摸了 Java 老程序员突然慌了 —— 再不出手,怕是真要被时代落下了! 作为一个 Java 死忠粉,学 …...
)
《Python星球日记》 第91天:端到端 LLM 应用(综合项目:医疗文档助手)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 目录 一、项目概述与需求分析1. 项目背景2. 项目目标3. 技术栈概览二、数据准备与处理1. 文档收集策略2. 文本预处理流程3. 向量化与知识库构建三、模…...

目前主流的AI测试工具推荐
以下是目前备受关注的AI测试工具及平台,涵盖功能测试、视觉测试、性能测试及国产化解决方案等多个领域,结合其核心特性与适用场景进行综合推荐: 一、主流AI测试工具推荐 Testim 核心功能:基于AI的动态元素定位技术,…...
)
vscode优化使用体验篇(快捷键)
本文章持续更新中 最新更新时间为2025-5-18 1、方法查看方法 1.1当前标签跳到新标签页查看方法实现 按住ctrl 鼠标左键点击方法。 1.2使用分屏查看方法实现(左右分屏) 按住ctrl alt 鼠标左键点击方法。...

uniprot中PTM数据的下载
首先是PTM的介绍: 参考:https://en.wikipedia.org/wiki/Post-translational_modification 蛋白质的翻译后修饰(PTM)通过改变氨基酸残基的化学结构,显著影响其带电性质,从而调控蛋白质的功能、定位和相互作…...

【QGIS二次开发】地图编辑-04
系列目录: 【QGIS二次开发】地图显示与交互-01_qgis二次开发加载地图案例-CSDN博客 【QGIS二次开发】地图显示与交互-02_setlayerlabeling-CSDN博客 【QGIS二次开发】地图符号与色表-03-CSDN博客 4 地图编辑 4.1 添加点要素 功能演示: 运行程序后…...
)
Qt 信号和槽-核心知识点小结(11)
目录 小结表格索引 disconnect函数 lambda表达式 啥是耦合,啥是内聚 简介:这是Qt信号和槽的最后一篇文章,最主要的是总结该信号和槽的核心知识点。以及该核心知识点的文章索引(表格太长了,手机可能看不完整&#…...

React响应事件中onClick={handleClick} 的结尾有没有小括号的区别
你可以通过在组件中声明 事件处理 函数来响应事件: function MyButton() {function handleClick() {alert(You clicked me!);}return (<button onClick{handleClick}>点我</button>);} 注意,onClick{handleClick} 的结尾没有小括号&#x…...

React-Query使用react-testing-library进行测试
1.测试react-query首先我们必须得拥有queryClient,所以我们初始化queryClient,因为默认是重试三次,这意味着如果想测试错误的查询,测试可能会超时。所以可以在初始化时关闭 const createWrapper () > {const queryClient new…...

软件设计师CISC与RISC考点分析——求三连
一、考点分值占比与趋势分析(CISC与RISC) 综合知识分值统计表 年份考题数量分值分值占比考察重点2018111.33%指令特征对比2019111.33%控制器实现方式2020222.67%寄存器数量/流水线技术2021111.33%寻址方式对比2022222.67%指令复杂度/译码方式2023111.3…...