当前位置：首页 > news >正文

2025年- H27-Lc135- 239.滑动窗口最大值（自定义双端队列）---java版

news 来源：原创 2025/6/7 12:05:45

1.题目描述

在这里插入图片描述

2.思路

（1）双端队列可以移除最左边的元素，也可以移除最右边的元素（两端移除）
（2）在最右边插入元素（右边加入）
（3）队列单调性（保持队列是单调递减）
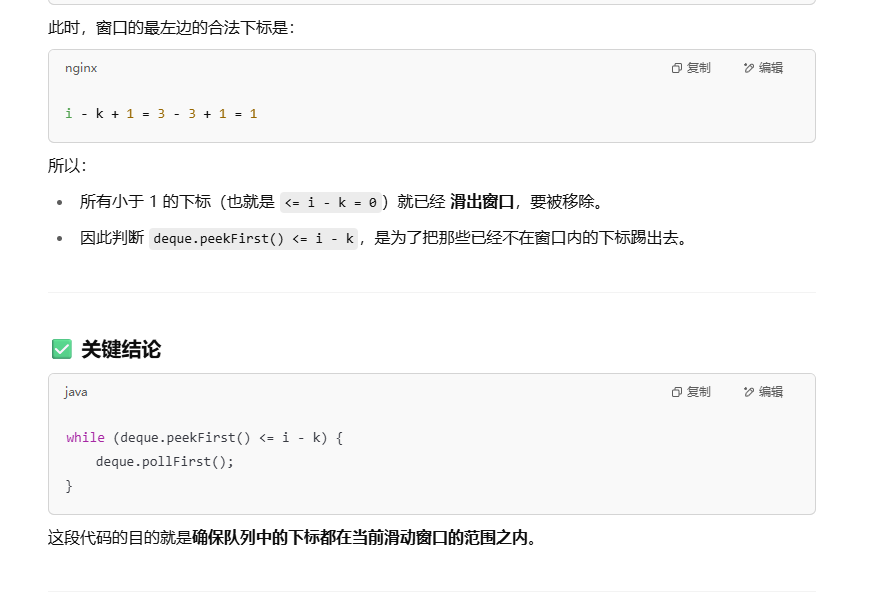
在这里插入图片描述

3.代码实现

import java.util.Arrays;
import java.util.Deque;
import java.util.LinkedList;public class H239 {public int[] maxSlidingWindow(int[] nums, int k) {//1.获取数组的长度int n=nums.length;//2.创建一个双端队列,存储的是数组的下标Deque<Integer> dq=new LinkedList<>();//3.// 初始化前 k 个元素，准备好第一个滑动窗口for(int i=0;i<k;i++) {//用while循环，队列不为空且当前元素nums[i]要大于队尾元素while (!dq.isEmpty() && nums[i]>=nums[dq.peekLast()]) {dq.pollLast(); //4.将队尾元素pop移出}//5. 将当前元素下标加入队尾，从队尾插入元素！！！！忘记了dq.offerLast(i);}//6.创建一个结果数组用来保存每次滑动窗口的最大值int[] res=new int[n-k+1];//7.结果数组的第一个元素是当前最大的元素。res[0]=nums[dq.peekFirst()];for(int i=k;i<n;++i){//8.判断队首元素是不是滑出当前的滑动窗口，判断队列的第一个元素是否过期，小于等于索引0 ，则移出while(!dq.isEmpty()&&dq.peekFirst()<=i-k){dq.pollFirst();}// 关键：移除所有小于当前元素的尾部元素!!!忘记了while (!dq.isEmpty() && nums[i] >= nums[dq.peekLast()]) {dq.pollLast();}dq.offerLast(i);// 加入当前元素的下标//9.当前窗口的最大值就是队首元素对应的值，将每次滑动窗口的队首元素都加入到结果数组中。res[i-k+1]=nums[dq.peekFirst()];}//10.返回结果数组return res;}public static void main(String[] args){H239 test=new H239();int[] nums={1,3,-1,-3,5,3,6,7};int k=3;int[] res= test.maxSlidingWindow(nums,k);
//System.out.println("输出滑动窗口的最大值："+res); 不会输出数组内容.Java中直接打印数组会输出的是对象地址，比如 [I@5e2de80c。System.out.println("输出滑动窗口的最大值："+ Arrays.toString(res));}
}

2025年- H27-Lc135- 239.滑动窗口最大值（自定义双端队列）---java版

1.题目描述 2.思路 （1）双端队列可以移除最左边的元素，也可以移除最右边的元素（两端移除） （2）在最右边插入元素（右边加入） （3）队列单调性&#xf…...

编程日记 2025/5/27 15:27:26

EKS 工作节点的集群网络架构

AWS EKS（弹性 Kubernetes 服务）是亚马逊提供的托管 Kubernetes 服务，一旦配置完成，即可像变魔术一样运行。但这通常是 EKS 的默认设置。如果您打算根据组织的设计、合规性标准和隐私要求进行自定义，该怎么办&#xff1…...

编程日记 2025/6/3 11:07:29

【技海登峰】Kafka漫谈系列（十一）SpringBoot整合Kafka之消费者Consumer

【技海登峰】Kafka漫谈系列（十一）SpringBoot整合Kafka之消费者Consumer spring-kafka官方文档： https://docs.spring.io/spring-kafka/docs/2.8.10/reference/pdf/spring-kafka-reference.pdf KafkaTemplate API： https://docs.spring.io/spring-kafka/api/org/springframe…...

编程日记 2025/5/29 16:24:56

Python字符串格式化(一）：三种经典格式化方法

文章目录一、% operator：C语言风格的初代格式化方案（Python 2.0引入）1. 语法核心：占位符与类型码2. 进阶用法：格式修饰符3. 致命缺陷：类型严格匹配的陷阱4. 适用场景：旧代码维护的兼容性选择二…...

编程日记 2025/5/31 14:30:18

浅谈无服务器WebSocket的优势

实际上，一个实用的解决方案是将构建业务关键型实时平台的复杂性卸载到专门的云服务中。完全托管的无服务器 WebSocket 解决方案为事件驱动的消息传递提供了基础结构;它使底层基础设施成为一种商品。客户端使用提供程序服务发送/接收低延迟消息，并专注于…...

编程日记 2025/5/29 8:51:51

10.7 LangChain v0.3架构大升级：模块化设计+多阶段混合检索，开发效率飙升3倍！

LangChain v0.3 技术生态与未来发展关键词：LangChain Chains, Agents 架构, Retrieval Strategy, LangGraph, 模块化设计 3. LangChain 项目：Chains, Agents, Retrieval Strategy LangChain v0.3 通过 Chains-Agents-Retrieval 三位一体的技术栈，构建起完整的大模型应用开…...

编程日记 2025/5/29 9:52:09

GLPK(GNU线性规划工具包)中建模语言MathProg的使用

GNU MathProg是一种用于描述线性数学规划模型的建模语言。用GNU MathProg语言编写的模型描述由一组语句和数据块组成。在MathProg中，模型以集合、参数、变量、约束和目标(sets, parameters, variables, constraints, objectives称为模型对象)的形式进行描述。在Ma…...

编程日记 2025/5/29 13:57:48

系统思考：IT企业项目困境分析

最近遇到一家快速发展的IT技术公司，遭遇了项目进度滞后、团队沟通不畅和资源分配不合理等一系列挑战。虽然他们拥有一支技术强大的团队，但在项目管理和团队协作上却显得力不从心。结果，多个项目超预算、交期延迟，客户满意度直线下…...

编程日记 2025/5/29 18:59:18

计算机网络 - 2.基础协议

1.TCP协议 1.TCP(Transmission Control Protocol)：传输控制协议2.TCP协议是一种面向连接的、可靠的、基于字节流的传输层通信协议 1.面向连接：两个使用TCP协议的应用（通常一个客户和一个服务器）在彼此交换数据包之前必须先建立一个TCP连接2.可靠的 1.数据传输之前都要建立…...

编程日记 2025/5/31 18:23:12

go语法大赏

前些日子单机房稳定性下降，找了好一会才找到真正的原因。这里面涉及到不少go语法细节，正好大家一起看一下。一、仿真代码这是仿真之后的代码 package mainimport ("fmt""go.uber.org/atomic""time" )type StopSignal…...

编程日记 2025/5/29 13:31:23

运行vscode编辑器源码

距离上次二次开发vscode已经是三年前的事了，当时是1.60.0版本，目前vscode已升级到了1.99.2版本，里面改动很大，最近下载下来了新版源码跑起来看看准备node、python 源码里面node版本做了限制 2025-01-27 09:53:00.450 [info] Fo…...

编程日记 2025/5/29 18:18:19

ShenNiusModularity项目源码学习（26：ShenNius.Admin.Mvc项目分析-11）

本文学习并分析ShenNiusModularity项目中商城系统模块的小程序用户页面、用户收货地址页面。 1、小程序用户页面小程序用户页面用于检索、浏览使用商城系统的用户数据（保存在shop_appuser表内，系统用户保存在sys_user表内），该页…...

编程日记 2025/5/27 5:37:15

C#中的成员常量：编译时的静态魔法

在C#编程中，常量(const)是一个强大而特殊的语言特性，特别是当它们作为类的成员时。本文将深入探讨成员常量的特性、使用场景以及与静态量的区别。成员常量的基本特性成员常量是声明在类内部的常量，具有以下核心特点： 声明位置…...

编程日记 2025/5/27 6:08:42

C# 深入理解类(成员常量)

成员常量成员常量类似前一章所述的局部常量，只是它们被声明在类声明中而不是方法内，如下面的示例： 与局部常量类似，用于初始化成员肯量的值在编译时必须是可计算的，而且通常是一个预定义简单类型或由它们组成的表达…...

编程日记 2025/5/29 11:08:38

服务端HttpServletRequest、HttpServletResponse、HttpSession

一、概述在JavaWeb 开发中，获取客户端传递的参数至关重要。http请求是客户端向服务端发起数据传输协议，主要包含包含请求行、请求头、空行和请求体四个部分，在这四部分中分别携带客户端传递到服务端的数据。常见的http请求方式有get、post、…...

编程日记 2025/5/29 8:46:21

有哪些GIF图片转换的开源工具

以下是关于GIF图片转换的开源工具的详细总结，涵盖功能特点、适用场景及用户评价： 1. FFmpeg 功能特点：作为开源命令行工具，FFmpeg支持视频转GIF、调整帧率、分辨率、截取片段等操作，可通过脚本批量处理。适用场景：适合开发者或技术用户进行高效批处理，常用于服务器端自…...

编程日记 2025/5/27 4:48:45

Vue.js教学第五章：计算属性与侦听器详解

Vue.js 之计算属性与侦听器详解一、计算属性（一）概念计算属性（Computed Properties）是 Vue.js 中的一个核心概念。它允许我们基于一个或多个数据属性来定义一个新的属性，该属性的值会根据其依赖的数据属性的变化而自动更新。这就好像是一个 “智能” 属性，它的值不是…...

编程日记 2025/5/27 7:45:19

第三章：UI 系统架构拆解与动态界面管理实录

还记得我们第二章刚跑通主场景，那时候是不是觉得“终于见到界面了”？但请等等，你看到的只是冰山一角，下面藏着的是 UIManager 的地狱之门。本章我们将深入探讨： UI 界面如何加载（Prefab 动态加载机制&…...

编程日记 2025/5/29 12:44:07

第四章：WebSocket 通信机制全解与客户端发包实录

如果你以为一个游戏启动后只靠本地逻辑运转，那你真是低估了网络通信的存在感。在互动组件项目里，WebSocket 才是真正的灵魂通道——UI 再好看，没包发出去也等于白搭。本章我们深入讲解 WebSocket 在安卓前端项目中的应用，从封装结…...

编程日记 2025/5/29 18:19:45

pnpm项目内网迁移

pnpm项目内网迁移文章目录 pnpm项目内网迁移0.前言1.基础环境安装2.构建pnpm离线安装包3.使用pnpm重新安装项目依赖4.项目迁移参考链接： 0.前言要将一个依赖pnpm的项目迁移到内网离线环境下进行开发。 1.基础环境安装要保证NodeJS版本一致，否则执行…...

编程日记 2025/5/29 18:20:38

C++23 放宽范围适配器以允许仅移动类型（P2494R2）

文章目录引言背景与动机提案内容与实现细节提案 P2494R2实现细节编译器支持对开发者的影响提高灵活性简化代码向后兼容性示例代码总结引言 C23 标准中引入了许多重要的改进，其中一项值得关注的特性是放宽范围适配器（range adaptors）以允…...

编程日记 2025/5/27 4:56:34

[ctfshow web入门] web119

信息收集 import requestsurl "http://51a7e437-2e66-4742-bbfe-e4cce44e360b.challenge.ctf.show/" for i in range(255):data {"code": f"{chr(i)}"}response requests.post(url, datadata)# print(len(response.text))# print(response.t…...

编程日记 2025/5/29 15:38:36

vector--OJ3

链接: [link](链接: link) class Solution { public: vector<string> str{ "","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz" };void CB(string& …...

编程日记 2025/5/29 18:53:55

第6章实战案例：基于 STEVAL-IDB011V1 板级 CI/CD 全流程

在前五章中，我们完成了嵌入式 CI/CD 从环境搭建、编译自动化、测试自动化、发布分发到监控回归的全技术链条。本章将以 STEVAL-IDB011V1（搭载 BlueNRG-355）评估板为实战载体，手把手演示如何在 GitLab CI（或 Jenkins）上，构建一条从 Git Push → 编译 → 测试 → 刷写 → …...

编程日记 2025/5/29 16:18:12

逆变器的输出外特性分析

VSG 并网状态下，考虑到弱电网下线路阻抗不能忽略，VSG 的功率传输模型可以表示为 VSG 的输出电压经过线路阻抗后串联至电网（考虑滤波电感，且忽略滤波电容作用）。设 U 为 VSG 输出电压的幅值，Ug为电网电压的幅…...

编程日记 2025/5/19 0:50:14

如何给PSCAD添加库文件

1、点击Options 2、选择蓝色的选项 3、查看Intel(R) Visual Fortran Compiler XE 的版本 4、打开原文件的Library 5、打开 6、点击这个文件的右键 7、然后选择第一项project setting 9、先把第8步中link里面原有的路径删除，再点browes[A1] ，然后选择 [A…...

编程日记 2025/5/19 0:24:50

基于simulink搭建的模块化多电平MMC仿真模型

1. 模块化多电平换流器的运行原理 1.1模块化多电平换流器的拓扑结构 MMC共由6个桥臂构成。其中每个桥臂由若干个串联且结构相同的子模块(Sub-Module, SM)与一个电抗器L串联…...

编程日记 2025/5/25 19:58:30

基于simulink的LCC-HVDC输电模型

1.本模型基于simulink搭建常规直流输电模型，运行稳定。有需要交流或者模型的可在CSDN上留言...

编程日记 2025/5/18 23:42:42

PWM整流器双闭环PI参数的整定

1. 整流侧电路拓扑图整流电路由交流侧电源、线路电阻、线路电抗、整流器、滤波电容以及负载组成。整体电路图如图1所示。图 1 整流电路拓扑图其中，IGBT的开关状函数如下式所示根据图 1 列出 KVL 公式如下，电流的正方向是从左到右对于每一相的IGBT相…...

编程日记 2025/6/1 14:22:43

柔性直流输电系统介绍及simulink模型的搭建

1. 柔性直流输电的运行原理柔性直流输电系统由电压源型换流器与直流输电线路构成, 图 1‑1所示为单端电压源型换流器原理图。柔性直流输电系统的功率可以双向流动,即换流器既可以作为整流站将从交流系统接收的功率通过直流线路输送出去,也可以作为逆变站将通过直流…...

编程日记 2025/5/18 23:02:28

matlab求矩阵的逆、行列式、秩、转置

inv - 计算矩阵的逆用途：计算一个可逆矩阵的逆矩阵。 D [1, 2; 3, 4]; % 定义一个2x2矩阵 D_inv inv(D); % 计算矩阵D的逆 disp(D_inv);det - 计算矩阵的行列式用途：计算方阵的行列式。 E [1, 2; 3, 4]; determinant det(E); % 计算行列式 disp…...

编程日记 2025/5/26 23:16:46

如何在纷杂的环境当中保持保持独立思考能力？

引言当你在人群当中时，你是否经常容易受到身边人的干扰，而丢失自己原有的想法，其实在环境纷杂当中，我们很容易产生“从众效应”而丢失了自己对这件事独立思考的能力。拥有不受外界影响，独立思考的能力可以让我们更加…...

编程日记 2025/5/18 21:46:47

Linux：计算机的层状结构

1.冯诺依曼体系结构我们常见的计算机，如笔记本、台式机。我们不常见的计算机，如服务器，大部分都遵守冯诺依曼体系结构。 CPU：运算器和控制器组成。运算器主要工作是做算术运算和逻辑运算。控制器主要工作是协调设备之间信息流动的…...

编程日记 2025/5/18 21:21:09

注册表设置windows背景护眼色

方法一： CtrlR，输入regedit打开注册表 HKEY_CURRENT_USER\Control Panel\Colors 右侧窗口Windows键值由255 255 255改为202 234 206。方法二： 还是注册表 HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Windows\CurrentVersion\Themes\DefaultColo…...

编程日记 2025/5/18 21:09:37

《算法导论(第4版)》阅读笔记：p82-p82

《算法导论(第4版)》学习第 17 天，p82-p82 总结，总计 1 页。一、技术总结 1. Matrix Matrices(矩阵) (1)教材因为第 4 章涉及到矩阵，矩阵属于线性代数(linear algebra)范畴，如果不熟悉，可以看一下作者推荐的两本…...

编程日记 2025/5/18 21:06:29

政府数据开放试点企业如何抢占特许经营协议黄金席位

首席数据官高鹏律师团队《中共中央办公厅国务院办公厅关于加快公共数据资源开发利用的意见》的落地，标志着数据从“封闭管理的行政资源”正式转变为“可流通的市场要素”。但机遇与风险从来是一枚硬币的两面——特许经营协议的黄金席位背后，隐藏着…...

编程日记 2025/5/18 20:37:54

Spring之Bean的初始化 Bean的生命周期全站式解析

目录导图步骤第一步实例化第二步属性赋值第三步初始化 aware 接口 BeanPostProcessor 接口 InitializingBean 和 init-method 第四步使用第五步使用后销毁描述一下 Bean 的生命周期导图步骤总体上可以分为五步首先是 Bean 的实例化Bean 在进行实例…...

编程日记 2025/5/18 20:22:52

exit耗时高

背景：程序退出发现被强制退出，而不是正常的退出。正常退出是发送15信号，而异常退出是发送信号9，强制退出。退出机制是先发送信号15，然后6s内没有退出完成，会发送信号9。通过查看退出流程，是将初…...

编程日记 2025/5/18 20:10:03

密文搜索-map容器+substr

https://www.luogu.com.cn/problem/P8630 ///因为密码是打乱顺序的，所以只要字母个数对上就行 ///用map存字母种类和个数 ///vector存每行密码 ///不用set，每行独立再考察一个字符串分割函数substr，map自动比较 #include<bits/stdc.h…...

编程日记 2025/5/18 20:06:55

从专家编码到神经网络学习：DTM 的符号操作新范式

1st author: Paul Soulos paper: Differentiable Tree Operations Promote Compositional Generalization ICML 2023 code: psoulos/dtm: Differentiable Tree Machine 1. 问题与思路现代深度学习在连续向量空间中取得了巨大成功，然而在处理具有显式结构&#x…...

编程日记 2025/5/18 20:01:36

江协科技GPIO输入输出hal库实现

首先先介绍一下GPIO在hal库里面的函数 GPIOhal库函数介绍 GPIO在hal库里面有两个文件，一个hal_gpio.h一个hal_gpio_ex.h 第一个文件主要存放的就是hal库里面对gpio的相关函数以及GPIO配置的结构体，还有hal库与标准库的一大区别回调函数。以及一些对gp…...

编程日记 2025/5/18 19:42:37

软件设计师教程—— 第二章程序设计语言基础知识（上）

前言在竞争激烈的就业市场中，证书是大学生求职的重要加分项。中级软件设计师证书专业性强、认可度高，是计算机相关专业学生考证的热门选择，既能检验专业知识，又有助于职业发展。本教程将聚焦核心重点，以点带面构建知…...

编程日记 2025/5/18 19:39:27

Java 快速转 C# 教程

以下是一个针对 Java 开发者快速转向 C# 的简明教程，重点对比 Java 与 C# 的异同，帮助你快速上手。项目结构： .sln ：解决方案文件，管理多个项目之间的依赖关系。.csproj ：项目文件，定义目标框…...

编程日记 2025/5/18 19:39:26

Linux面试题集合（5）

把文件1的内容追加到文件2 cat 文件1>>文件2 把文件1和文件2合并成文件3 cat 文件1 文件2>文件3 使用less查看文件时，搜寻ab字符 /ab 用more和less如何查看文件 more： CtrlF -- 向下滚动一屏 CtrlB -- 返回上一屏 f -- 向下翻屏 b -- 向上翻屏 …...

编程日记 2025/5/18 19:38:19

OpenCV 光流估计：从原理到实战

在计算机视觉领域，光流估计（Optical Flow Estimation）是一项至关重要的技术，它能够通过分析视频序列中图像像素的运动信息，捕捉物体和相机的运动情况。OpenCV 作为强大的计算机视觉库，为我们提供了高效实现…...

编程日记 2025/5/29 10:27:35

星火杯大模型应用创新赛学习笔记——datawhale

背景——赛事任务聚焦大学生真实应用场景，围绕阅读、写作、搜索、聊天、问答等方向，聚焦口语学习、面试招聘、论文写作、学习笔记等一个或多个细分应用场景，完成具有创新性、实用性的应用方案，呈现可演示、可落地、具备商业价值…...

编程日记 2025/5/18 19:21:20

Ulyssess Ring Attention

https://zhuanlan.zhihu.com/p/689067888https://zhuanlan.zhihu.com/p/689067888DeepSpeed Ulysess：切分Q、K、V序列维度，核心卖点保持通信复杂度低，和GPU数无关，和序列长度呈线性关系。 Ring-Attention：切分Q、K、V序…...

编程日记 2025/5/18 19:16:05

c++重要知识点汇总（不定期更新）

前言真心希望各位dalao点赞收藏~ 树状数组作用：高效求出区间前缀和，允许进行修改操作。举个栗子： 刚开始有8项，分别为1-8。首先构建二叉树： 1-8/ |/ |/ |/ |/ |1-4 5-8/ | / |/ | / |1-…...

编程日记 2025/5/18 19:16:03

重排序模型解读 mxbai-rerank-base-v2 强大的重排序模型

mxbai-rerank-base-v2 强大的重排序模型模型介绍benchmark综合评价安装模型介绍 mxbai-rerank-base-v2 是 Mixedbread 提供的一个强大的重排序模型，旨在提高搜索相关性。该模型支持多语言，特别是在英语和中文方面表现出色。它还支持代码和 SQL 排序&a…...

编程日记 2025/5/18 19:12:54

电子电路：到底该怎么理解电容器的“通交流阻直流”？

电容器“通交流，阻直流”的特性源于其对不同频率电信号的响应差异，具体可通过以下步骤理解： 一、电容器的基本结构与充放电机制结构：由两个导体极板（如金属）和中间的绝缘介质组成。充放电过程&#xff1a…...

编程日记 2025/5/18 18:55:53

1.题目描述

2.思路

3.代码实现

相关文章：