【C++】18.二叉搜索树

由于map和set的底层是红黑树，同时后面要讲的AVL树(高度平衡二叉搜索树)，为了方便理解，我们先来讲解二叉搜索树，因为红黑树和AVL树都是在二叉搜索树的前提下实现的

在之前的C语言数据结构章节中，我们讲过二叉树，这次就来认识一下二叉搜索树

1. 二叉搜索树的概念

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

• 若它的左子树不为空，则左子树上所有结点的值都小于等于根结点的值

• 若它的右子树不为空，则右子树上所有结点的值都大于等于根结点的值

• 它的左右子树也分别为二叉搜索树

• 二叉搜索树中可以支持插入相等的值，也可以不支持插入相等的值，具体看使用场景定义，后续我们学习map/set/multimap/multiset系列容器底层就是二叉搜索树，其中map/set不支持插入相等值，multimap/multiset支持插入相等值

---

2. 二叉搜索树的性能分析

最优情况下，二叉搜索树为完全二叉树(或者接近完全二叉树)，其高度为： log2 N

最差情况下，二叉搜索树退化为单支树(或者类似单支)，其高度为： N

所以综合而言二叉搜索树增删查改时间复杂度为： O(N)

那么这样的效率显然是无法满足我们需求的，我们后续章节需要继续讲解二叉搜索树的变形，平衡二叉搜索树AVL树和红黑树，才能适用于我们在内存中存储和搜索数据。

另外需要说明的是，二分查找也可以实现 O(log2 N) 级别的查找效率，但是二分查找有两大缺陷：

1. 需要存储在支持下标随机访问的结构中，并且有序。

2. 插入和删除数据效率很低，因为存储在下标随机访问的结构中，插入和删除数据一般需要挪动数据。

这里也就体现出了平衡二叉搜索树的价值

---

3. 二叉搜索树的实现

template<class K>
struct BSTreeNode
{BSTreeNode(const K& key):_key(key),_left(nullptr),_right(nullptr){}K _key;BSTreeNode<K>* _left;BSTreeNode<K>* _right;
};template<class K>
class BSTree
{//typedef BSTreeNode<K> Node;using Node = BSTreeNode<K>;
public:
private:Node* _root = nullptr;
};

首先我们要管理每个节点的数据以及它的左右孩子，所以我们先封装一个树节点类，用来管理节点的数据和左右孩子，其次我们要把每个树节点统一管理，所以还需要再封装一个树类，用来管理所有节点。

BSTreeNode:

这里我们模板参数使用K（表示key的意思），模板参数并不是只能是T

和之前list一样，只需要写构造，原因如下：

I. 节点类的核心需求

二叉搜索树的节点通常需要强制初始化关键值（如节点的值 val），并将子节点指针（left 和 right）初始化为空。
通过定义带参数的构造函数，可以确保：

• 值必须显式初始化：节点必须有值，不能存在未初始化的节点。

• 子节点指针默认置空：左右子节点指针默认初始化为 nullptr，避免野指针问题。

---

II. C++ 构造函数规则

• 默认构造函数：如果用户没有定义任何构造函数，编译器会生成一个默认构造函数。但如果用户定义了带参数的构造函数，编译器不再生成默认构造函数。此时若尝试无参创建对象会报错，符合“节点必须有值”的逻辑。

• 拷贝构造函数：若未显式定义，编译器会生成一个浅拷贝构造函数。对于树节点来说，浅拷贝通常是危险的（可能导致重复释放同一内存），但二叉搜索树的操作一般通过指针传递节点，不涉及拷贝节点对象本身，因此可以暂时忽略拷贝构造函数的需求。若需要更严格的控制，可显式删除拷贝构造函数。

---

III. 为什么其他构造函数可以不写？

• 默认构造函数：
  已通过带参构造函数禁用，确保节点必须有初始值。

• 拷贝构造函数：
  树节点通常通过指针操作，不需要拷贝节点对象。若需要复制整棵树（深拷贝），应在树结构中实现，而非节点类中。

• 移动构造函数：
  对于简单的值类型（如 int 和指针），默认生成的移动操作已足够。

• 析构函数：
  节点类的子节点指针是“原始指针”，但二叉搜索树的释放通常由树结构统一管理（如递归删除子树），因此节点类可以不显式定义析构函数。

---

BSTree:

我们先将BSTreeNode<K>类型typedef一下（类型太长了不好写），但是我们这里使用using，在现阶段using和typedef功能是一样的，具体差异后面章节会讲，不过using取别名的用法有点不一样；由于我们要管理树，将所有节点联系起来，所以我们可以提供一个指向根节点的指针_root作为成员变量，方便我们管理

---

3.1 二叉搜索树的插入

插入的具体过程如下：

1. 树为空，则直接新增结点，赋值给root指针

2. 树不空，按二叉搜索树性质，插入值比当前结点大往右走，插入值比当前结点小往左走，找到空位置，插入新结点。

3. 如果支持插入相等的值，插入值跟当前结点相等的值可以往右走，也可以往左走，找到空位置，插入新结点。（要注意的是要保持逻辑一致性，插入相等的值不要一会往右走，一会往左走）

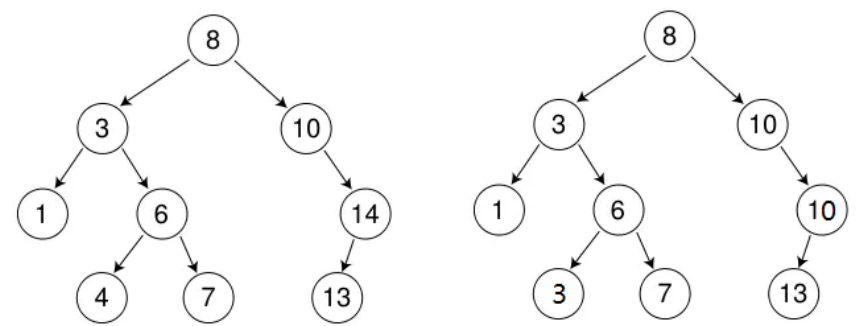
int a[] = { 8 , 3 , 1 , 10 , 6 , 4 , 7 , 14 , 13 };

以这组数据为例来画图演示一下：

插入不相等的值

插入相等的值

代码实现：

代码实现分别可以用递归和非递归两种方法来实现，这里我们采用非递归，递归太深的情况会栈溢出，同时我们这里默认不允许插入相等的值。

第一步：处理空树的特殊情况

• 若树为空（_root == nullptr），直接创建根节点并初始化值为 key，返回 true 表示插入成功。

  if (_root == nullptr) {_root = new Node(key);return true;
  }

---

第二步：查找插入位置

1. 初始化指针：

   • parent 记录当前节点的父节点（初始为 nullptr）。

   • cur 从根节点 _root 开始遍历。

   Node* parent = nullptr;
   Node* cur = _root;

2. 循环遍历树：

   • 若 key 大于当前节点的值，向右子树移动。

   • 若 key 小于当前节点的值，向左子树移动。

   • 若遇到重复值（key 已存在），返回 false 表示插入失败。

   while (cur) {if (cur->_key < key) {parent = cur;cur = cur->_right;} else if (cur->_key > key) {parent = cur;cur = cur->_left;} else {return false; // 重复值，插入失败}
   }

---

第三步：创建新节点并链接到父节点

1. 创建新节点：
   循环结束后，cur 指向 nullptr，此时 parent 是待插入位置的父节点。创建新节点 cur。

   cur = new Node(key);

2. 确定插入方向：
   根据 key 与父节点值的比较结果，将新节点链接为父节点的左子节点或右子节点。

   if (parent->_key < key) {parent->_right = cur; // 插入右子树
   } else {parent->_left = cur;  // 插入左子树
   }

代码如下：

bool Insert(const K& key)
{if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;
}

如果想要允许插入相等的值，只需要在第二步插入位置时，判断条件修改一下为cur->_key <= key或者cur->_key >= key，然后去掉else语句——遇到重复值（key 已存在），返回 false 表示插入失败。

---

3.2 打印测试

这里我们采用中序遍历的方式，将数据打印出来

void InOrder(Node* root)
{if (root == nullptr) return;InOrder(root->_left);cout << root->_key << " ";InOrder(root->_right);
}

使用上面图示数据模拟：

void Test()
{int a[] = { 8,3,1,10,6,4,7,14,13 };BSTree<int> t;for (auto x : a){t.Insert(x);}t.InOrder(_root);
}

显然这么写是错的，编译一下可以看到

我们知道_root是私有成员变量，在类外我们是访问不了的，但是我们中序遍历需要传根节点指针，那应该怎么办呢？

我们可以实现一个类外可以访问的访问根节点的成员函数GetRoot()，但是这么写不太好，我们可以这么写

public:void InOrder(){_InOrder(_root);cout << endl;}
private:void _InOrder(Node* root){if (root == nullptr) return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}

我们直接将中序遍历私有，然后在公有下把中序遍历封装在另一个函数中，这样我们就可以在类外无参的使用中序遍历

运行结果：

---

3.3 二叉搜索树的查找

1. 从根开始比较，查找x，x比根的值大则往右边走查找，x比根值小则往左边走查找。

2. 最多查找高度次，走到空，还没找到，这个值不存在。

3. 如果不支持插入相等的值，找到x即可返回

4. 如果支持插入相等的值，意味着有多个x存在，一般要求查找中序的第一个x。如下图，查找3，要找到1的右孩子的那个3返回

代码实现：

查找非常简单，和插入的思路一样

bool Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return true;//找到了}}//没找到return false;
}

---

3.4 二叉搜索树的删除

首先查找元素是否在二叉搜索树中，如果不存在，则返回false。

如果查找元素存在则分以下四种情况分别处理：（假设要删除的结点为N）

1. 要删除的结点N左右孩子均为空

2. 要删除的结点N左孩子为空，右孩子结点不为空

3. 要删除的结点N右孩子为空，左孩子结点不为空

4. 要删除的结点N左右孩子结点均不为空

对应以上四种情况的解决方案：

1. 把N结点的父亲对应孩子指针指向空，直接删除N结点（情况1可以当成2或者3处理，效果是一样的）

2. 把N结点的父亲对应孩子指针指向N的右孩子，直接删除N结点

3. 把N结点的父亲对应孩子指针指向N的左孩子，直接删除N结点

4. 无法直接删除N结点，因为N的两个孩子无处安放，只能用替换法删除。找N左子树的值最大结点R(最右结点)或者N右子树的值最小结点R(最左结点)替代N，因为这两个结点中任意一个，放到N的位置，都满足二叉搜索树的规则。替代N的意思就是N和R的两个结点的值交换，转而变成删除R结点，R结点符合情况2或情况3，可以直接删除。

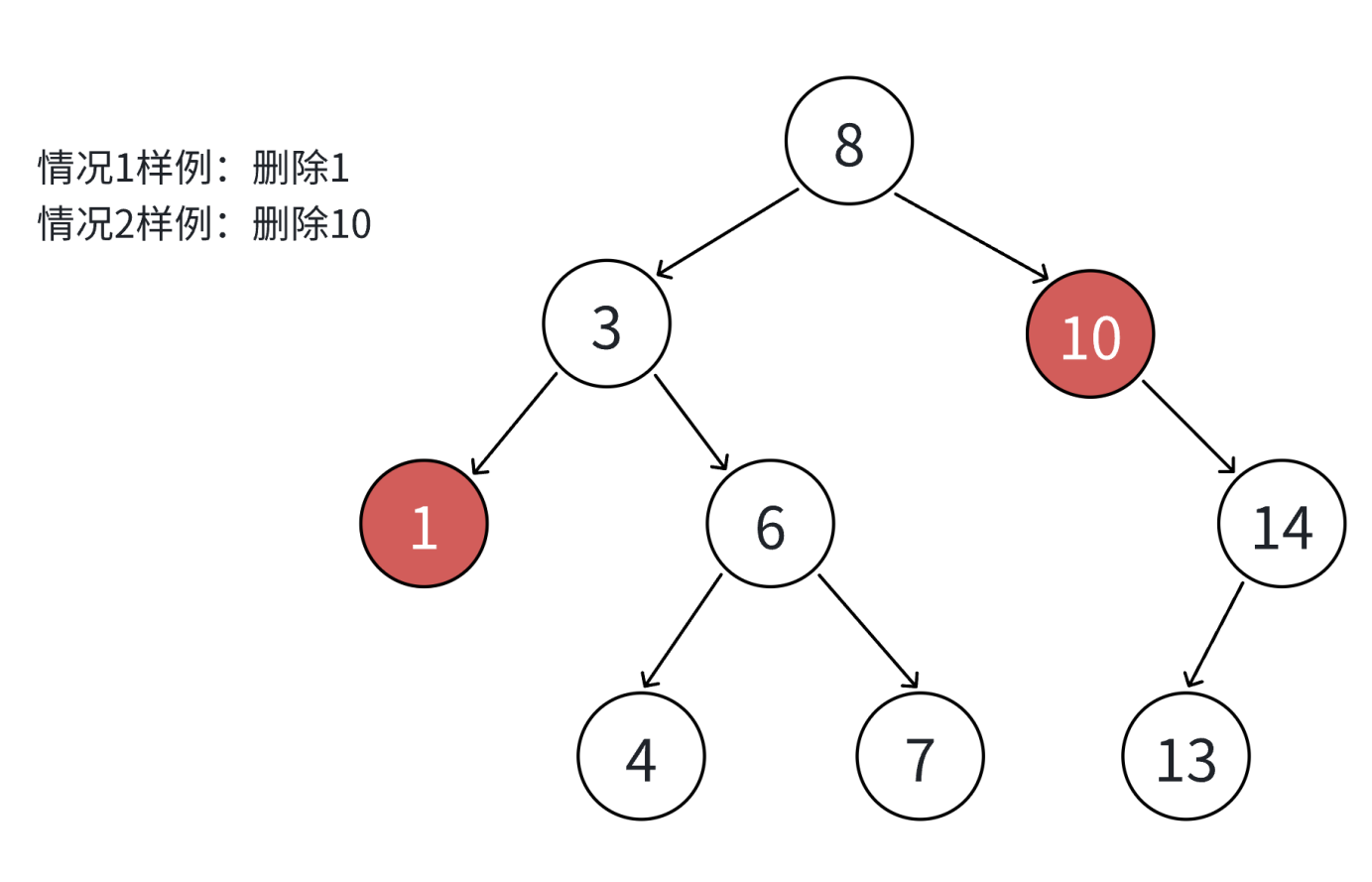
代码实现：

第1步. 查找待删除节点

• 初始化指针：
  parent 记录当前节点的父节点（初始为 nullptr），cur 从根节点 _root 开始遍历。

• 遍历搜索：
  根据 key 与当前节点值的比较，向左或向右子树移动，直到找到目标节点或遍历结束。

  while (cur) {if (cur->_key < key) { ... }    // 向右子树移动else if (cur->_key > key) { ... } // 向左子树移动else { ... }                      // 找到目标节点，进入删除逻辑
  }

• 未找到处理：
  若遍历结束未找到 key，返回 false 表示删除失败。

---

第2步. 根据子节点情况删除节点

(1) 左子节点为空（或右子节点为空）

• 直接替换：

  • 若左子节点为空，用右子节点 cur->_right 替代当前节点。

  • 若右子节点为空，用左子节点 cur->_left 替代当前节点。

• 处理根节点：
  若删除的是根节点（cur == _root），直接更新 _root 为对应的子节点。

• 链接父节点：
  根据 cur 是父节点的左/右子节点，更新父节点的指针指向 cur 的子节点。

  // 左子节点为空的情况
  if (cur->_left == nullptr) {if (cur == _root) {_root = cur->_right; // 更新根节点} else {if (parent->_right == cur) {parent->_right = cur->_right;} else {parent->_left = cur->_right;}}delete cur;
  }

(2) 左右子节点均存在

• 替换法删除：

  • 找到右子树的最小节点：从 cur->_right 出发，循环找到最左侧节点 replace（即右子树的最小节点）。

  • 替换值：将 replace->_key 赋值给 cur->_key。

  • 删除替换节点：

    • 若 replace 是其父节点的左子节点，将父节点的左指针指向 replace 的右子节点。

    • 若 replace 是其父节点的右子节点（即右子树没有左子节点），将父节点的右指针指向 replace 的右子节点。

    • 删除 replace 节点。

  else {// 找右子树的最小节点Node* replaceParent = cur;Node* replace = cur->_right;while (replace->_left) {replaceParent = replace;replace = replace->_left;}// 替换值cur->_key = replace->_key;// 删除替换节点if (replace == replaceParent->_left) {replaceParent->_left = replace->_right;} else {replaceParent->_right = replace->_right;}delete replace;
  }

---

第3步. 返回结果

• 删除成功：
  在找到并删除节点后，立即返回 true。

• 删除失败：
  若循环结束未找到节点，返回 false。

---

总结步骤

1. 查找目标节点：遍历树找到待删除节点。

2. 处理删除逻辑：

   • 单子节点：直接用子节点替换，更新父节点或根节点指针。

   • 双子节点：替换法删除（右子树最小节点），调整指针关系。

3. 释放内存：删除节点并返回操作结果。

代码如下：

bool Erase(const K& key)
{Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 找到了删除if (cur->_left == nullptr) // 左孩子为空{if (cur == _root){_root = cur->_right;}else{if (parent->_right == cur){// 此时cur->_key > parent->_keyparent->_right = cur->_right;}else //parent->_left == cur{// 此时cur->_key < parent->_keyparent->_left = cur->_right;}}delete cur;}else if (cur->_right == nullptr) // 右孩子为空{if (cur == _root){_root = cur->_left;}else{if (parent->_right == cur){// 此时cur->_key > parent->_keyparent->_right = cur->_left;}else //parent->_left == cur{// 此时cur->_key < parent->_keyparent->_left = cur->_left;}}delete cur;}else // 两个孩子都不为空{// 替换法删除节点——右子树最小节点替换Node* replaceParent = cur;// 要考虑删除根节点时，不能置为nullptrNode* replace = cur->_right;while (replace->_left){replaceParent = replace;replace = replace->_left;}cur->_key = replace->_key;if (replace == replaceParent->_left){replaceParent->_left = replace->_right;}else //replace == replaceParent->_right{// 此时第一个右孩子就是右子树最小节点replaceParent->_right = replace->_right;}delete replace;}//成功删除return true;}}//没找到，删除失败return false;
}

---

4. 二叉搜索树key和key/value使用场景

4.1 key搜索场景：

只有key作为关键码，结构中只需要存储key即可，关键码即为需要搜索到的值，搜索场景只需要判断key在不在。key的搜索场景实现的二叉树搜索树支持增删查，但是不支持修改，修改key破坏搜索树结构了。

场景1：小区无人值守车库，小区车库买了车位的业主车才能进小区，那么物业会把买了车位的业主的车牌号录入后台系统，车辆进入时扫描车牌在不在系统中，在则抬杆，不在则提示非本小区车辆，无法进入。

场景2：检查一篇英文章单词拼写是否正确，将词库中所有单词放入二叉搜索树，读取文章中的单 词，查找是否在二叉搜索树中，不在则波浪线标红提示

---

4.2 key/value搜索场景：

每一个关键码key，都有与之对应的值value，即<key, value>，value可以是任意类型对象。树的结构中(结点)除了需要存储key还要存储对应的value，增/删/查还是以key为关键字走二叉搜索树的规则进行比较，可以快速查找到key对应的value。key/value的搜索场景实现的二叉树搜索树支持修改，但是不支持修改key，修改key破坏搜索树性质了，可以修改value。

I. 键（Key）与值（Value）的定义

• 键（Key）
  键是用于唯一标识数据的标识符。它类似于字典中的“词条”，用于快速查找、插入或删除对应的值。

  • 特性：唯一性（在同一个容器中，键不能重复）、可比较性（必须支持比较或哈希操作）。

  • 示例：学号、身份证号、用户名等。

• 值（Value）
  值是与键关联的实际数据。它可以是任意类型，存储具体的业务信息。

  • 特性：允许重复、无特殊约束（除非业务需要）。

  • 示例：学生成绩、用户详细信息、缓存的数据等。

---

II. 键与值的核心差异

特性	键（Key）	值（Value）
唯一性	必须唯一	可以重复
作用	快速定位数据	存储实际数据
约束	必须可比较或可哈希	无特殊约束（类型灵活）
修改性	通常不可修改（需删除后重新插入）	可直接修改

---

场景1：简单中英互译字典，树的结构中(结点)存储key(英文)和vlaue(中文)，搜索时输入英文，则同时查找到了英文对应的中文。

场景2：商场五日值守车库，入口进场时扫描车牌，记录车牌和入场时间，出口离场时，扫描车牌，查找入场时间，用当前时间-入场时间计算出停车时长，计算出停车费用，缴费后抬杆，车辆离场。

场景3：统计一篇文章中单词出现的次数，读取一个单词，查找单词是否存在，不存在这个单词说明第一次出现，（单词，1），单词存在，则++单词对应的次数。

代码实现：

我们只需要在之前二叉搜索树的增删查代码的基础上简单修改即可，增加一个模板参数V，此时我们节点中存储的数据就是键值对<key, value>，所以在树节点类中需要新增一个V类型的成员变量，同时构造函数中也需要增加一个V类型的形参

Insert: 只需增加一个V类型的形参，因为在插入新的树节点时，要new一个<key, value>类型的树节点，其余操作不需要改变

Find：只需要查找键，修改返回值，我们返回树节点，就可以通过树节点得到里面的值

Erase：不需要修改

namespace key_value
{template<class K, class V>struct BSTreeNode{BSTreeNode(const K& key, const V& value):_key(key),_value(value), _left(nullptr), _right(nullptr){}// 不写默认构造函数、拷贝构造函数等// 编译器会自动禁用默认构造函数（因为用户已定义其他构造函数）// 若需要禁用拷贝，可显式删除K _key;V _value;BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;};template<class K, class V>class BSTree{//typedef BSTreeNode<K> Node;using Node = BSTreeNode<K, V>;public:bool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key, value);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false; //重复值插入失败}}cur = new Node(key, value);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return cur;//找到了}}//没找到return nullptr;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 找到了删除if (cur->_left == nullptr) // 左孩子为空{if (cur == _root){_root = cur->_right;}else{if (parent->_right == cur){// 此时cur->_key > parent->_keyparent->_right = cur->_right;}else //parent->_left == cur{// 此时cur->_key < parent->_keyparent->_left = cur->_right;}}delete cur;}else if (cur->_right == nullptr) // 右孩子为空{if (cur == _root){_root = cur->_left;}else{if (parent->_right == cur){// 此时cur->_key > parent->_keyparent->_right = cur->_left;}else //parent->_left == cur{// 此时cur->_key < parent->_keyparent->_left = cur->_left;}}delete cur;}else // 两个孩子都不为空{// 替换法删除节点——右子树最小节点替换Node* replaceParent = cur;// 要考虑删除根节点时，不能置为nullptrNode* replace = cur->_right;while (replace->_left){replaceParent = replace;replace = replace->_left;}cur->_key = replace->_key;if (replace == replaceParent->_left){replaceParent->_left = replace->_right;}else //replace == replaceParent->_right{// 此时第一个右孩子就是右子树最小节点replaceParent->_right = replace->_right;}delete replace;}//成功删除return true;}}//没找到，删除失败return false;}void InOrder(){_InOrder(_root);cout << endl;}private:void _InOrder(Node* root){if (root == nullptr) return;_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}private:Node* _root = nullptr;};}

---

我们这里还要显式实现一下拷贝构造和析构，因为这里需要深拷贝资源，且在析构时要把每个new出来的树节点都要释放掉。

拷贝构造:

通过调用 Copy(t._root)，复制原树 t 的根节点，并将新树的根节点 _root 指向复制后的根节点。

因为拷贝构造没有返回值，独立函数 Copy 将递归逻辑封装为一个“黑盒”，只需关注输入（原树的根节点）和输出（新树的根节点），同时：

• Copy 函数通常设为私有，因为它是类内部的实现细节，外部无需知道如何复制一棵树。

• 隐藏实现细节，避免用户误用，同时提高类的封装性。

    BSTree(const BSTree& t){_root = Copy(t._root);}
private:Node* Copy(Node* root){if (root == nullptr) return nullptr;Node* newNode = new Node(root->_key, root->_value);newNode->_left = Copy(root->_left);newNode->_right = Copy(root->_right);return newNode;}

---

构造函数：

当我们自己显式定义了拷贝构造函数时，编译器就不会自动生成默认的无参构造函数

这样的话我们的根节点_root就不能实现初始化了，所以我们这里可以手动实现，也可以强制编译器生成默认构造

手动实现：

BSTree() {}

强制编译器生成：

BSTree() = default;//C++11起

---

赋值重载：

BSTree& operator=(BSTree tmp)
{swap(tmp._root, _root);return *this;
}

这里直接使用现代写法来实现

---

析构函数：

    ~BSTree(){Destroy(_root);_root = nullptr;}
private:void Destroy(Node* root){if (root == nullptr) return;Destroy(root->_left);Destroy(root->_right);delete root;}

这里和拷贝构造一样，封装一个Destroy()函数，递归销毁每个树节点

---

模拟测试一下场景1：

void test1()
{BSTree<string, string> dict;dict.Insert("left", "左边");dict.Insert("right", "右边");dict.Insert("insert", "插入");dict.Insert("string", "字符串");string str;while (cin >> str){auto ret = dict.Find(str);if (ret){cout << "->" << ret->_value << endl;}else{cout << "无此单词，请重新输入" << endl;}}
}

运行结果：

---

模拟测试一下场景3：

void test2()
{string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };BSTree<string, int> countTree;for (const auto& str : arr){// 先查找水果在不在搜索树中// 1、不在，说明水果第一次出现，则插入<水果, 1>// 2、在，则查找到的结点中水果对应的次数++//BSTreeNode<string, int>* ret = countTree.Find(str);auto ret = countTree.Find(str);if (ret == NULL){countTree.Insert(str, 1);}else{ret->_value++;}}countTree.InOrder();
}

运行结果：

代码：

namespace key
{template<class K>struct BSTreeNode{BSTreeNode(const K& key):_key(key), _left(nullptr), _right(nullptr){}// 不写默认构造函数、拷贝构造函数等// 编译器会自动禁用默认构造函数（因为用户已定义其他构造函数）// 若需要禁用拷贝，可显式删除：// BSTreeNode(const BSTreeNode<K>&) = delete;// BSTreeNode& operator=(const BSTreeNode<K>&) = delete;K _key;BSTreeNode<K>* _left;BSTreeNode<K>* _right;};template<class K>class BSTree{//typedef BSTreeNode<K> Node;using Node = BSTreeNode<K>;public:bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false; //重复值插入失败}}cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return true;//找到了}}//没找到return false;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 找到了删除if (cur->_left == nullptr) // 左孩子为空{if (cur == _root){_root = cur->_right;}else{if (parent->_right == cur){// 此时cur->_key > parent->_keyparent->_right = cur->_right;}else //parent->_left == cur{// 此时cur->_key < parent->_keyparent->_left = cur->_right;}}delete cur;}else if (cur->_right == nullptr) // 右孩子为空{if (cur == _root){_root = cur->_left;}else{if (parent->_right == cur){// 此时cur->_key > parent->_keyparent->_right = cur->_left;}else //parent->_left == cur{// 此时cur->_key < parent->_keyparent->_left = cur->_left;}}delete cur;}else // 两个孩子都不为空{// 替换法删除节点——右子树最小节点替换Node* replaceParent = cur;// 要考虑删除根节点时，不能置为nullptrNode* replace = cur->_right;while (replace->_left){replaceParent = replace;replace = replace->_left;}cur->_key = replace->_key;if (replace == replaceParent->_left){replaceParent->_left = replace->_right;}else //replace == replaceParent->_right{// 此时第一个右孩子就是右子树最小节点replaceParent->_right = replace->_right;}delete replace;}//成功删除return true;}}//没找到，删除失败return false;}void InOrder(){_InOrder(_root);cout << endl;}private:void _InOrder(Node* root){if (root == nullptr) return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}private:Node* _root = nullptr;};void Test(){int a[] = { 8,3,1,10,6,4,7,14,13 };BSTree<int> t;for (auto x : a){t.Insert(x);}t.InOrder();for (auto x : a){t.Erase(x);t.InOrder();}}
}namespace key_value
{template<class K, class V>struct BSTreeNode{BSTreeNode(const K& key, const V& value):_key(key),_value(value), _left(nullptr), _right(nullptr){}// 不写默认构造函数、拷贝构造函数等// 编译器会自动禁用默认构造函数（因为用户已定义其他构造函数）// 若需要禁用拷贝，可显式删除K _key;V _value;BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;};template<class K, class V>class BSTree{//typedef BSTreeNode<K> Node;using Node = BSTreeNode<K, V>;public://BSTree() {}BSTree() = default;//C++11起BSTree(const BSTree& t){_root = Copy(t._root);}BSTree& operator=(BSTree tmp){swap(tmp._root, _root);return *this;}~BSTree(){Destroy(_root);_root = nullptr;}bool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key, value);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false; //重复值插入失败}}cur = new Node(key, value);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return cur;//找到了}}//没找到return nullptr;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 找到了删除if (cur->_left == nullptr) // 左孩子为空{if (cur == _root){_root = cur->_right;}else{if (parent->_right == cur){// 此时cur->_key > parent->_keyparent->_right = cur->_right;}else //parent->_left == cur{// 此时cur->_key < parent->_keyparent->_left = cur->_right;}}delete cur;}else if (cur->_right == nullptr) // 右孩子为空{if (cur == _root){_root = cur->_left;}else{if (parent->_right == cur){// 此时cur->_key > parent->_keyparent->_right = cur->_left;}else //parent->_left == cur{// 此时cur->_key < parent->_keyparent->_left = cur->_left;}}delete cur;}else // 两个孩子都不为空{// 替换法删除节点——右子树最小节点替换Node* replaceParent = cur;// 要考虑删除根节点时，不能置为nullptrNode* replace = cur->_right;while (replace->_left){replaceParent = replace;replace = replace->_left;}cur->_key = replace->_key;if (replace == replaceParent->_left){replaceParent->_left = replace->_right;}else //replace == replaceParent->_right{// 此时第一个右孩子就是右子树最小节点replaceParent->_right = replace->_right;}delete replace;}//成功删除return true;}}//没找到，删除失败return false;}void InOrder(){_InOrder(_root);cout << endl;}private:void Destroy(Node* root){if (root == nullptr) return;Destroy(root->_left);Destroy(root->_right);delete root;}Node* Copy(Node* root){if (root == nullptr) return nullptr;Node* newNode = new Node(root->_key, root->_value);newNode->_left = Copy(root->_left);newNode->_right = Copy(root->_right);return newNode;}void _InOrder(Node* root){if (root == nullptr) return;_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}private:Node* _root = nullptr;};void test1(){BSTree<string, string> dict;dict.Insert("left", "左边");dict.Insert("right", "右边");dict.Insert("insert", "插入");dict.Insert("string", "字符串");string str;while (cin >> str){auto ret = dict.Find(str);if (ret){cout << "->" << ret->_value << endl;}else{cout << "无此单词，请重新输入" << endl;}}}void test2(){string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };BSTree<string, int> countTree;for (const auto& str : arr){// 先查找水果在不在搜索树中// 1、不在，说明水果第一次出现，则插入<水果, 1>// 2、在，则查找到的结点中水果对应的次数++//BSTreeNode<string, int>* ret = countTree.Find(str);auto ret = countTree.Find(str);if (ret == NULL){countTree.Insert(str, 1);}else{ret->_value++;}}countTree.InOrder();}
}