当前位置：首页 > news >正文

数据结构*优先级队列(堆)

news 来源：原创 2025/6/8 20:03:14

什么是优先级队列(堆)

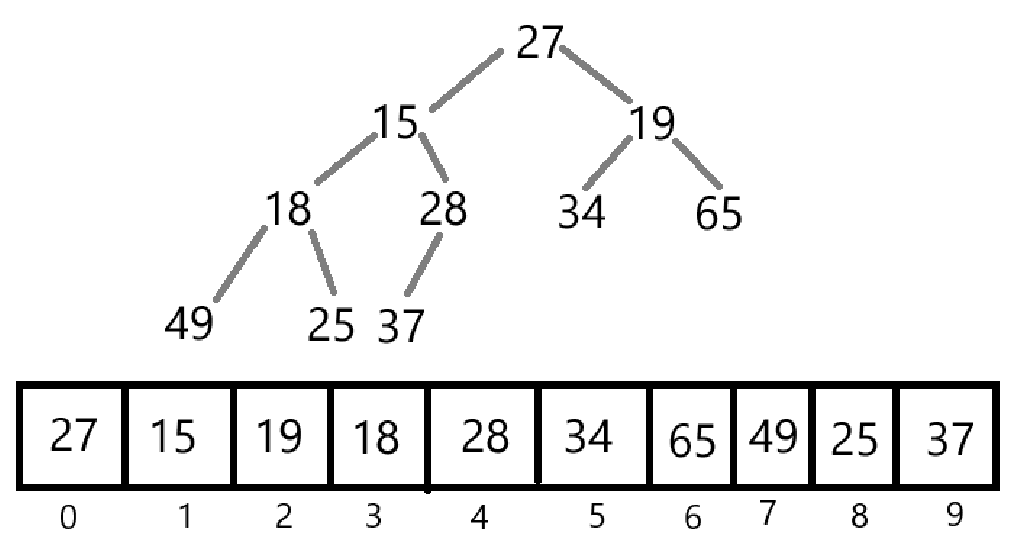
优先级队列一般通过堆（Heap）这种数据结构来实现，堆是一种特殊的完全二叉树，其每个节点都满足堆的性质。如下图所示就是一个堆：
在这里插入图片描述

堆的存储方式

由于堆是一棵完全二叉树，所以也满足二叉树的性质：
1、一颗非空二叉树的第i层上最多有2^(i-1)个结点。
2、一颗深度为k的二叉树，其树的最大结点为2^k-1
3、由第二条性质推出，具有n个结点的完全二叉树的深度k = log(n+1) [以2为底的log] 向上取整。
4、对于任意一颗二叉树，其叶子结点为n0(结点度为0)，度为2的结点个数为n2，则n0 = n2 + 1。
5、对于具有n个结点的完全二叉树，按照从上到下、从左到右的顺序从0开始编号，则对于序号i的结点：
左孩子结点下标为2i + 1，当2i + 1 > n 时，就不存在左孩子结点。
右孩子结点下标为2i + 2，当2i + 2 > n 时，就不存在右孩子结点。
其父亲结点的下标为(i - 1) / 2。i == 0时，其结点为根节点，没有父亲结点。
当元素存入数组后，需要利用性质5来完成一些功能，完成对数组的访问。

最大堆或最小堆

对于一个完全二叉树来说：每个节点的值都大于或等于其子节点的值，堆顶元素是整个堆中的最大值，被称为最大堆；
在这里插入图片描述
每个节点的值都小于或等于其子节点的值，堆顶元素就是堆中的最小值，被称为最小堆。

对于最大堆或者最小堆来说，数组是最常用的实现方式。数组存储堆中的值是以层序遍历的方式来存储的。

最大堆或最小堆的创建

根据数组来创建最大堆或最小堆。以下图为例：
在这里插入图片描述
下面代码实现了最大堆

public void createHeapMAX() {//需要对每棵子树进行调整，调整方式是一样的。//parent是从最后一个孩子的父亲结点开始的，每次parent--来访问其他的树。//当parent为根节点调整完了，说明完成了最大堆的创建for (int parent = ((useSize - 1) - 1) / 2; parent >= 0; parent--) {//每个初始parent的树的向下调整siftDownMAX(parent,useSize);//传useSize的目的是为了，在parent和child交换后，parent需要到child位置在判断下一个结点是否满足最大堆，//对应的每棵树结束的标志是child下标超过useSize}
}
/*** 向下调整，让节点的值不断向下调整* @param parent* @param useSize*/
private void siftDownMAX(int parent,int useSize){//1、定义child下标int child = parent * 2 + 1;while(child < useSize) {//2、比较左右子树的值，child谁是最大值if(child + 1 < useSize && elem[child + 1] > elem[child]) {child++;}//3、判断是否交换if(elem[parent] < elem[child]) {swap(parent,child);//当前父节点变为子节点，继续检查其新的子节点(检查子树的子树)parent = child;child = parent * 2 + 1;}else {return;//如果当前父节点已经大于其子节点，那么其子树必然已经是合法的最大堆（因为构建过程是自底向上的）}}
}
private void swap(int parent,int child){int temp = elem[parent];elem[parent] = elem[child];elem[child] = temp;
}

在这里插入图片描述
和上述逻辑差不多，就是更改了比较符号。下面是实现最小堆的代码：

public void createHeapMIN() {for (int parent = ((useSize - 1) - 1) / 2; parent >= 0; parent--) {siftDownMIN(parent,useSize);}
}
private void siftDownMIN(int parent,int useSize){int child = parent * 2 + 1;while(child < useSize) {if(child + 1 < useSize && elem[child + 1] < elem[child]) {child++;}if(elem[parent] > elem[child]) {swap(parent,child);parent = child;child = parent * 2 + 1;}else {return;}}
}
private void swap(int parent,int child){int temp = elem[parent];elem[parent] = elem[child];elem[child] = temp;
}

在这里插入图片描述
上述代码的总时间复杂度为O(N)。单个siftDownMAX和siftDownMIN的时间复杂度为O(logN)

堆的删除与插入

堆的删除

在堆中删除一定是删除堆顶的元素，也就是根节点。
实现的方法是：
1、将最后一个叶子节点和根节点交换。
2、此时再删除最后一个叶子节点(原根节点)。
3、进行向下调整

public int poll() {if(isEmpty()) {return -1;}swap(0,useSize - 1);useSize--;siftDownMAX(0,useSize);return elem[0];
}

堆的插入

实现的方法是：
1、将添加的数据放在最底层。
2、在进行向上调整

public void offer(int value) {if(isFull()){elem = Arrays.copyOf(elem,2*elem.length);}elem[useSize] = value;useSize++;int child = useSize - 1;siftUp(child);
}
/*** 实现的是最大堆* @param child*/
private void siftUp(int child){int parent = (child - 1) / 2;while (child > 0) {if(elem[parent] < elem[child]) {swap(parent,child);child = parent;//向上调整parent = (child - 1) / 2;}else {break;}}
}
private void swap(int parent,int child){int temp = elem[parent];elem[parent] = elem[child];elem[child] = temp;
}

上述代码的总时间复杂度为O(N*logN)。单个siftUp的时间复杂度为O(logN)。
显然较上面创建的最大堆的时间复杂度大一些。

获取堆顶元素

实现的方法是：
直接返回数组首元素即可

public int peek() {if(isEmpty()) {return -1;}return elem[0];
}
private boolean isEmpty() {return useSize == 0;
}

堆的集合类

对于堆的集合类有两种PriorityQueue 和 PriorityBlockingQueue。PriorityBlockingQueue属于线程安全的，PriorityQueue属于线程不安全的。
我们先学习PriorityQueue类
1、由于在堆的实现过程中需要进行比较，所以放置的元素一定要能比较。像对象就不能进行比较，也就不能成为元素。
2、不能传入null
3、可以任意插入多个元素，类有自动扩容的机制

public class TestPriorityQueue {public static void main(String[] args) {PriorityQueue<Student> priorityQueue = new PriorityQueue<>();PriorityQueue<Integer> priorityQueueAge = new PriorityQueue<>();Student student = new student();priorityQueueAge.offer(Student.age);//没有错误，比较的是int类型priorityQueue.offer(new Student());//会抛出ClassCastException异常priorityQueue.offer(null);//会抛出NullPointerException异常}
}
class Student {public int age;
}

构造方法

构造方法	功能
PriorityQueue()	创建一个空的优先级队列，初始容量为11
PriorityQueue(int initialCapacity)	初始优先级队列的容量，但不能传小于1的数字
PriorityQueue(Collection<? extends E> c)	传入一个集合类来创建堆
PriorityQueue(Comparator<? super E> comparator)	传入比较器，按照比较器的方法完成堆的排序
PriorityQueue(int initialCapacity,Comparator<? super E> comparator)	传入比较器和初始容量

public static void main(String[] args) {PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();priorityQueue.offer(10);priorityQueue.offer(3);priorityQueue.offer(4);System.out.println(priorityQueue.peek());//输出：3
}

//传入一个集合类
public static void main(String[] args) {ArrayList<Integer> arrayList = new ArrayList<>();arrayList.add(10);arrayList.add(3);arrayList.add(4);PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(arrayList);System.out.println(priorityQueue.peek());//输出：3
}

通过上述代码和PriorityQueue类的源码，发现，当没有传入比较器时，堆默认是按最小堆来排的。要实现最大堆就需要传入一个比较器。
1、通过实现Comparator接口（完整类），来创建一个比较器

class Compare implements Comparator<Integer> {@Overridepublic int compare(Integer o1, Integer o2) {return o2 - o1;//此时是按最大堆来建立的//return o2.compareTo(o1);//此时也是按最大堆来建立的//Integer类继承了Comparable接口//return o1 - o2;就是按最小堆来建立的}
}

public static void main(String[] args) {Compare compare = new Compare();PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(compare);priorityQueue.offer(10);priorityQueue.offer(3);priorityQueue.offer(4);System.out.println(priorityQueue.peek());//输出：10
}

2、使用匿名内部类，在需要比较器的地方直接创建匿名内部类，无需定义独立的类。

public static void main(String[] args) {PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new Comparator<Integer>() {@Overridepublic int compare(Integer o1, Integer o2) {return o2 - o1;}});priorityQueue.offer(10);priorityQueue.offer(3);priorityQueue.offer(4);System.out.println(priorityQueue.peek());//输出：10
}

常用方法

方法	功能
boolean offer(E e)	添加数据
E peek()	获取堆顶的元素
E poll()	删除优先级最高的元素并返回
int size()	获取有效元素个数
void clear()	清空元素
boolean isEmpty()	判断是否为空

在官方中插入元素（offer()）的时间复杂度为O(logN)，用的是向上调整，创建堆（批量插入N个元素）的时间复杂度为O(N*logN)。使用构造方法传入集合类时，时间复杂度为O(N)，用的是向下调整。
删除堆顶的元素（poll()）的时间复杂度为O(logN)，用的是向下调整。

关于堆的一些问题

top-K问题

代码展示：

代码一：

/*** 总时间复杂度为：O((N+k)*logN)* @param array* @param k* @return*/
public int[] topK1(int[] array,int k) {int[] ret = new int[k];if(array == null || k <= 0) {return ret;}PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(array.length);//将所有元素放到堆中，offer方法自动按照最小堆排序for (int i = 0;i < array.length;i++) {priorityQueue.offer(array[i]);}//将堆中前三个元素放到ret数组中。for (int i = 0;i < k;i++) {ret[i] = priorityQueue.poll();}return ret;
}

代码二：

/*** 总时间复杂度为：O(N*logK)* @param array* @param k* @return*/
public int[] topK(int[] array,int k) {int[] ret = new int[k];if(array == null || k <= 0) {return ret;}//根据最大根创建优先级队列PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(k, new Comparator<Integer>() {@Overridepublic int compare(Integer o1, Integer o2) {return o2 - o1;}});//创建有K个元素的堆//时间复杂度为：O(K * logK)for (int i = 0; i < k; i++) {priorityQueue.offer(array[i]);}//遍历后面的数组元素//时间复杂度为：O((N-K) * logK)for (int i = k; i < array.length; i++) {//当数组元素大于堆顶的元素，说明这个元素不是前K个最小的元素if(array[i] < priorityQueue.peek()){priorityQueue.poll();priorityQueue.offer(array[i]);}}//将堆中的前k放到ret数组中//时间复杂度为：O(K * logK)   几乎可以忽略for (int i = 0; i < k; i++) {ret[i] = priorityQueue.poll();}return ret;
}

代码解释：

对于代码一来说，是将所有元素全部放到堆中，进行堆排。如果有大量数据，会导致有很多次进行调整，时间复杂度高，为O((N+k)logN)。
对于代码二来说，只是对前K个元素进行了堆排，降低了时间复杂度，为O(NlogK)。

堆排序

如果是按照从小到大来排序，是要创建最大堆，反之创建最小堆。
以从小到大来排序为例。当创建最大堆后，将堆顶的元素和最后一个元素交换，再对剩余元
素进行调整为最大堆。重复这操作，直到整个数组有序。

这里为什么不创建最小堆呢？

当创建的是最小堆时，需要再创建一个数组，用来存放最小堆的堆顶，再对剩余元
素进行调整为最小堆。这样相比于创建最大堆，其空间复杂就会大一些。

代码展示：

/*** 从小到大排序* 时间复杂度为：O(N*logN)* 空间复杂度为：O(1)* @param array*/
public void heapSort(int[] array) {//先创建一个最大堆，时间复杂度为：O(N)for (int parent = ((array.length - 1) - 1) / 2; parent >= 0 ; parent--) {shiftDown(array,parent,array.length);}int end = array.length - 1;//进行排序，时间复杂度为：O(N*logN) <---- 有N次调整，每次调整的时间复杂度为：O(logN)while (end > 0) {swap(array,0,end);end--;shiftDown(array,0,end + 1);}
}
private void swap(int[] array,int a,int b) {int temp = array[a];array[a] = array[b];array[b] = temp;
}
private void shiftDown(int[] array ,int parent,int useSize) {int child = 2 * parent + 1;while (child < useSize) {if(child + 1 <useSize && array[child] < array[child + 1]) {child++;}if(array[parent] < array[child]) {swap(array,parent,child);parent = child;child = 2 * parent + 1;}else {break;}}
}

代码解释：

在这里插入图片描述

数据结构*优先级队列(堆)

什么是优先级队列(堆) 优先级队列一般通过堆（Heap）这种数据结构来实现，堆是一种特殊的完全二叉树，其每个节点都满足堆的性质。如下图所示就是一个堆： 堆的存储方式由于堆是一棵完全二叉树，所以也满足二…...

编程日记 2025/5/27 8:01:01

Windows本地化部署Dify完整指南

编程日记 2025/5/26 18:30:18

全局异常处理：如何优雅地统一管理业务异常

在软件开发中，异常处理是保证系统健壮性的重要环节。一个良好的异常处理机制不仅能提高代码的可维护性，还能为使用者提供清晰的错误反馈。本文将介绍如何通过全局异常处理和业务异常统一处理来编写更加优雅的代码。一、传统异常处理的痛点 1.1 典型问…...

编程日记 2025/6/4 5:08:45

AI517 AI本地部署 docker微调（失败）

本地部署AI 计划使用OLLAMA进行本地部署修改DNS 访问github 刷新缓存配置环境变量 OLLAMA安装成功部署成功计划使用docker进行微调下载安装docker 虚拟化已开启开启上面这些准备下载ubuntu docker ragflow dify 用git去泡...

编程日记 2025/5/28 16:11:08

C++（初阶）（十八）——AVL树

AVL树 AVL树概念实现AVL树的结点插入插入方法平衡因子更新更新停止条件旋转右单旋左单旋左右双旋右左双旋遍历AVL平衡检测完整代码概念 1，AVL树是最先发明的⾃平衡⼆叉查找树，AVL树是⼀颗⾼度平衡搜索⼆叉树， 通过控制高度差去控制平衡。…...

编程日记 2025/5/23 22:16:49

2022河南CCPC（前四题）

签到题目 #include <bits/stdc.h> using namespace std; #define int long long #define PII pair<int,int> #define fi first #define se second #define endl \n #define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);void solve() {int n;cin>>…...

编程日记 2025/5/26 11:57:05

【滑动窗口】LeetCode 1658题解 | 将 x 减到 0 的最小操作数

将 x 减到 0 的最小操作数一、题目链接二、题目三、题目解析四、算法原理五、编写代码六、时空复杂度一、题目链接将 x 减到 0 的最小操作数二、题目三、题目解析以示例1为例： 四、算法原理像"题目解析"中正面删除并修改数组元素的操作太困难&…...

编程日记 2025/5/27 5:26:54

电机试验平台：创新科技推动电动机研究发展

电机试验平台是电机制造和研发过程中不可或缺的重要设备，其功能涵盖了电机性能测试、电机寿命测试、电机质量评估等多个方面。随着科技的不断发展和电机应用领域的日益扩大，对电机试验平台的要求也越来越高。本文将从现代化电机试验平台的设计与应用两个…...

编程日记 2025/5/24 19:39:15

linux-软件的安装与部署、web应用部署到阿里云

一、软件安装方式概述 CentOS安装软件的方式主要包括： - 源码安装 - rpm安装（二进制安装） - yum安装（在线安装） 1.源码安装： 源码包是指C等语言所开发的源代码文件的一个压缩包，通常压缩为.…...

编程日记 2025/6/1 17:43:12

Qt Widgets模块功能详细说明，基本控件：QLabel（一）

一、基本控件（Widgets） Qt 提供了丰富的基本控件，如按钮、标签、文本框、复选框、单选按钮、列表框、组合框、菜单、工具栏等。 1、QLabel 1.1、概述 (用途、继承关系) QLabel 是 Qt 框架中用于显示文本、图像或动画的控件，属…...

编程日记 2025/6/3 18:07:01

Ubuntu 安装 squid

1. 安装Squid及工具 Debian/Ubuntu sudo apt update sudo apt install squid apache2-utils CentOS/RHEL sudo yum install squid httpd-tools 2. 创建用户名密码文件创建密码文件（首次使用 -c 参数，后续添加用户省略） sudo htpasswd…...

编程日记 2025/5/29 11:59:53

中药药效成分群的合成生物学研究进展-文献精读130

Advances in synthetic biology for producing potent pharmaceutical ingredients of traditional Chinese medicine 中药药效成分群的合成生物学研究进展摘要中药是中华民族的文化瑰宝，也是我国在新药创制领域的重要驱动力。许多中药材来源于稀缺物种&#xf…...

编程日记 2025/5/29 19:04:48

芯片生态链深度解析（三）：芯片设计篇——数字文明的造物主战争

【开篇：设计——数字文明的“造物主战场”】当英伟达的H100芯片以576TB/s显存带宽重构AI算力边界，当阿里平头哥倚天710以RISC-V架构实现性能对标ARM的突破，这场围绕芯片设计的全球竞赛早已超越技术本身，成为算法、架构与生态标准…...

编程日记 2025/6/1 5:24:14

Echart地图数据源获取

DataV.GeoAtlas地理小工具系列选择需要的区域地图，选中后输出即可：地图钻取代码 <!DOCTYPE html> <html lang="en"> <head><meta charset="UTF-8"><title>map</title><style>html, body, #map{margin: 0;…...

编程日记 2025/6/1 9:54:42

【C++ - 仿mudou库one thread one loop式高并发服务器实现】

文章目录项目介绍项目模块和服务器主要设计模式项目主要流程前置知识1.bind函数2.定时器任务TimerTask和时间轮思想TimerWheel3.正则表达式4.通用型容器Any类服务器设计模式1）单Reactor单线程模式2）单Reactor多线程模式3）多Reactor多线程模…...

编程日记 2025/5/28 18:00:42

本地缓存更新方案探索

文章目录本地缓存更新方案探索1 背景2 方案探索2.1 初始化2.2 实时更新2.2.1 长轮询2.2.1.1 client2.2.2.2 server 本地缓存更新方案探索 1 背景大家在工作中是否遇到过某些业务数据需要频繁使用，但是数据量不大的情况，一般就是几十条甚至几百条这种…...

编程日记 2025/5/29 19:02:20

Java—异常体系

Java的异常体系是Java语言中用于处理程序运行过程中可能出现的错误的机制。通过异常处理，程序可以在遇到问题时自动反馈，从而避免程序崩溃。Java异常体系中包含两大类：错误(Error)和异常(Exception)。一、错误（Error&#xff09…...

编程日记 2025/5/27 7:44:17

深度学习（第3章——亚像素卷积和可形变卷积）

前言： 本章介绍了计算机识别超分领域和目标检测领域中常常使用的两种卷积变体，亚像素卷积（Subpixel Convolution）和可形变卷积（Deformable Convolution），并给出对应pytorch的使用。亚像素卷积…...

编程日记 2025/5/26 7:42:07

5.15 学习日志

1.SST（总平方和）、SSR（回归平方和）、SSE（残差平方和）之间的关系。在使用线性回归模型时，经常提到的统计量MSE（Mean Squared Error、均方误差）：是 SSE 的平均…...

编程日记 2025/5/26 9:54:08

重排序模型解读：gte-multilingual-reranker-base 首个GTE系列重排模型诞生

模型介绍 gte-multilingual-reranker-base 模型是 GTE 模型系列中的第一个 reranker 模型，由阿里巴巴团队开发。模型特征： Model Size: 306MMax Input Tokens: 8192 benchmark 关键属性： 高性能：与类似大小的 reranker 模型…...

编程日记 2025/5/29 13:12:15

计算机发展的历程

计算机系统的概述一, 计算机系统的定义计算机系统的概念计算机系统硬件软件硬件的概念计算机的实体, 如主机, 外设等计算机系统的物理基础决定了计算机系统的天花板瓶颈软件的概念由具有各类特殊功能的程序组成决定了把硬件的性能发挥到什么程度软件的分类…...

编程日记 2025/6/2 11:18:46

【通用智能体】Search Tools：Open Deep Research 项目实战指南

Open Deep Research 项目实战指南一、项目运行方式（一）运行环境要求（二）运行方式（三）传统本地运行（四）Docker 容器运行二、操作步骤（一）使用搜索功能&#…...

编程日记 2025/6/3 1:34:56

nodejs 文件的复制

在 Node.js 中，文件复制操作可以通过多种方式实现，具体取决于文件大小、性能需求以及是否需要保留文件元数据（如权限、时间戳等）。以下是几种常见的文件复制方法及其示例代码： 1. 使用 fs.copyFile（简单高…...

编程日记 2025/5/25 9:59:36

GO语言学习（三）

GO语言学习（三） GO语言的独特接口可以实现内容和面向对象组织的更加方便，我们从这里来详细的讲解接口，让大家感受一下interface的魅力 interface定义首先接口是一组方法签名的组合，我们通过接口来实现定义对象的一…...

编程日记 2025/5/27 8:08:28

高频面试题（含笔试高频算法整理）基本总结回顾61

干货分享，感谢您的阅读！ （暂存篇---后续会删除，完整版和持续更新见高频面试题基本总结回顾（含笔试高频算法整理）） 备注：引用请标注出处，同时存在的问题请在相关博客留言…...

编程日记 2025/6/3 10:21:30

C++:C++内存管理

C 内存分区 C 内存分为 5 个主要区域： 栈 (Stack)：存储局部变量、函数参数和返回地址。由编译器自动分配和释放，效率高但空间有限。堆 (Heap)：动态分配的内存区域，需手动管理（new/delete 或 malloc/free…...

编程日记 2025/5/26 7:44:16

目标跟踪相关综述文章

文章年份会议/引用量IFObject tracking:A survery20067618Object Tracking Methods:A Review2019554Multiple object tracking: A literature review20201294Deep learning for multiple object tracking: a survey2019145Deep Learning for Visual Tracking:A Comprehensive S…...

编程日记 2025/5/28 7:39:39

JavaScript【6】事件

1.概述： 在 JavaScript 中，事件（Event）是浏览器或 DOM（文档对象模型）与 JavaScript 代码之间交互的一种机制。它代表了在浏览器环境中发生的特定行为或者动作，比如用户点击鼠标、敲击键盘、页面…...

编程日记 2025/5/26 7:18:01

Python训练打卡Day26

函数专题1：函数定义与参数知识点回顾： 函数的定义变量作用域：局部变量和全局变量函数的参数类型：位置参数、默认参数、不定参数传递参数的手段：关键词参数传递参数的顺序：同时出现三种参数类型时到目前为…...

编程日记 2025/5/29 10:41:58

通俗版解释CPU、核心、进程、线程、协程的定义及关系

通俗版解释（比喻法） 1. CPU 和核心 CPU 一个工厂（负责干活的总部）。核心工厂里的车间（比如工厂有4个车间，就能同时处理4个任务）。 2. 进程进程一家独立运营的公司（比如一家…...

编程日记 2025/5/29 12:55:17

微积分基本规则及示例解析

微积分中的基本规则是构成微积分理论和应用的基石。以下是一些微积分中的基本规则，我将用简单的例子来解释它们，以便小学生也能理解。 1. **极限规则**： - 常数的极限：\(\lim_{x \to a} c c\) - 例如，\(\lim…...

编程日记 2025/6/3 9:15:46

Baklib知识中台构建企业智能服务新引擎

知识中台构建智能服务新范式随着企业数字化转型进入深水区，传统知识管理模式的局限性日益显现——分散的文档系统、低效的信息检索以及割裂的业务场景，严重制约着组织效能的释放。在此背景下，Baklib提出的知识中台解决方案，通过…...

编程日记 2025/5/27 1:22:44

Python实例题：Python百行制作登陆系统

目录 Python实例题题目 python-login-systemPython 百行登录系统脚本代码解释用户数据库： 注册功能： 登录功能： 主程序： 运行思路注意事项 Python实例题题目 Python百行制作登陆系统 python-login-systemPython…...

编程日记 2025/5/29 13:15:44

Java求职面试：从核心技术到大数据与AI的场景应用

面试场景： 在某互联网大厂的面试间，一位严肃的面试官正准备对面前的求职者谢飞机进行技术面试。谢飞机虽然有些紧张，但他相信凭借自己的机智和幽默能够顺利通过。第一轮提问：核心语言与平台的基础问题面试官：“谢…...

编程日记 2025/5/29 17:50:24

系统架构设计（六）：面向对象设计

核心概念概念含义说明对象（Object）现实世界事物的抽象表示，包含属性（状态）和方法（行为）类（Class）一类对象的抽象模板继承（Inheritance）子类继承…...

编程日记 2025/5/26 20:47:51

国内AWS CloudFront与S3私有桶集成指南：安全访问静态内容

在现代web应用架构中，将静态内容存储在Amazon S3中并通过CloudFront分发是一种常见且高效的做法。本指南将详细介绍如何创建私有S3桶，配置CloudFront分配，并使用Origin Access Identity (OAI)来确保安全访问。步骤1：创建S3桶首先，我们需要创建一个名为"b-static&…...

编程日记 2025/6/1 9:46:45

MATLAB进行深度学习网络训练

文章目录前言环境配置一、环境部署二、数据准备三、训练配置与执行四、模型评估与优化五、高级技巧六、实战案例：COVID-19 肺部 CT 图像分类前言在 MATLAB 中进行深度学习网络训练主要分为数据准备、网络构建、训练配置和模型评估四个核心步骤。以下是详细教程&…...

编程日记 2025/5/26 4:16:04

jvm安全点(三)openjdk17 c++源码垃圾回收之安全点结束，唤醒线程

1. VMThread::inner_execute() - 触发安全点 cpp 复制 void VMThread::inner_execute(VM_Operation* op) { if (op->evaluate_at_safepoint()) { SafepointSynchronize::begin(); // 进入安全点，阻塞所有线程 // ...执行GC等操作... SafepointSynchronize::…...

编程日记 2025/5/26 7:23:20

局部放大maya的视图HUD文字大小的方法

一、问题描述： 有网友问：有办法局部放大maya的字体吗比如hud中currenttime打开之后画面右下角有个frame 想放大一下能做到吗？ 在 Maya 中，可以通过自定义 HUD（Heads-Up Display）元素的字体大小来局部放大特…...

编程日记 2025/5/26 7:14:31

Vue.js 教学第三章：模板语法精讲，插值与 v-bind 指令

Vue.js 模板语法精讲：插值与 v-bind 指令在 Vue.js 开发中，模板语法是构建动态用户界面的核心。本文将深入讲解两大基础模板语法：插值（{{ }}）和 v-bind 指令，通过大量实例帮助你掌握这些关键概念。一、插值语法：双花括号的魔法 1.1 基础文本插值双花括号是最简单的…...

编程日记 2025/5/30 3:41:30

系统架构设计师案例分析题——软件架构设计篇

重中之重，本题争取拿下25满分~ 目录一.核心知识 1.什么是架构风格 2.RUP的9个核心工作流 3.企业应用集成方式 4.软件质量属性 5.SySML系统建模语言9种图 6.云计算架构 7.中间件 8.构件、连接件、软件重用 9.层次型架构的缺点 10.架构开发方法ADM 11.微…...

编程日记 2025/5/28 16:29:38

系统架构设计（十一）：架构风格总结2

架构风格汇总架构风格核心特点应用场景分层架构（Layered）将系统划分为多个层次，每层只依赖于下一层企业应用、MIS 系统、三层架构客户端-服务器（C/S）分为服务端与客户端，服务集中，客户端请求数…...

编程日记 2025/5/29 16:49:46

泛微对接金蝶云星空实战案例技术分享

前言在企业信息化建设中，OA系统与ERP系统对接往往是一个复杂而关键的环节。OA系统通常具有高度的自定义性，其基础资料和单据可能与ERP系统存在字段不一致等问题。同时，OA系统涉及审批流程及流程发起方定义，增加了对接的复杂性。…...

编程日记 2025/5/27 17:49:49

Predict Podcast Listening Time-(回归+特征工程+xgb)

Predict Podcast Listening Time 题意： 给你没个播客的信息，让你预测观众的聆听时间。数据处理： 1.构造新特征收听效率进行分组 2.对数据异常处理 3.对时间情绪等进行数值编码 4.求某特征值求多项式特征 5.生成特征组合 6.交叉验证并enc…...

编程日记 2025/5/30 17:14:58

Java并发编程的挑战：从理论到实战

在现代软件开发中，随着多核处理器的普及和系统性能要求的提高，并发编程已经成为Java开发者必须掌握的核心技能之一。然而，Java并发编程不仅仅是“创建多个线程”那么简单，它涉及到线程安全、资源竞争、死锁、通信机制、性能优化等多个复杂问题。本文将围绕Java并发编程中…...

编程日记 2025/6/1 10:00:16

大麦（Hordeum vulgare）中 BAHD 超家族酰基转移酶-文献精读129

Systematic identification and expression profiles of the BAHD superfamily acyltransferases in barley (Hordeum vulgare) 系统鉴定与大麦（Hordeum vulgare）中 BAHD 超家族酰基转移酶的表达谱分析摘要 BAHD 超家族酰基转移酶在植物中催化和调控次…...

编程日记 2025/5/28 17:03:45

信任的进阶：LEI与vLEI协同推进跨境支付体系变革

在全球经济版图加速重构的背景下，跨境支付体系正经历着前所未有的变革。2022年全球跨境支付规模突破150万亿美元，但平均交易成本仍高达6.04%，支付延迟超过2.7天。这种低效率背后，隐藏着复杂的身份识别困境：超过40%的…...

编程日记 2025/5/28 15:43:38

当语言模型学会犯错和改正：搜索流(SoS)方法解析

引言语言模型的能力日新月异，但它们在执行复杂规划任务时仍面临着明显的局限。这是因为大多数训练数据只展示了最终的"正确答案"，而非解决问题的完整过程。想象一下，如果我们只能看到数学题的最终答案，而从不知道解题…...

编程日记 2025/5/28 15:56:26

Centos7.9同步外网yum源至内网

curl -o /etc/yum.repos.d/CentOS-Base.repo https://mirrors.aliyun.com/repo/Centos-7.repo curl -o /etc/yum.repos.d/epel.repo http://mirrors.aliyun.com/repo/epel-7.repo yum makecache yum repolist安装软件 yum install -y yum-utils createrepo # yum-utils包含re…...

编程日记 2025/5/27 7:10:49

OTA与boot loader

OTA指的是无线升级，通常用于更新设备的固件或软件，用户不用手动操作，非常方便。而bootloader是启动时加载操作系统的程序，负责硬件初始化和启动流程。首先，OTA是如何通过bootloader工作的。OTA下载更新包后&#xff0…...

编程日记 2025/6/4 16:38:17

什么是优先级队列(堆)

堆的存储方式

最大堆或最小堆

最大堆或最小堆的创建

堆的删除与插入

堆的删除

堆的插入

获取堆顶元素

堆的集合类

构造方法

常用方法

关于堆的一些问题

top-K问题

代码展示：

代码解释：

堆排序

代码展示：

代码解释：

相关文章：