【数据结构】_二叉树

1.二叉树链式结构的实现
1.1 前置说明
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入,为了降低大家学习成本,此处
手动快速创建一棵简单的二叉树,快速进入二叉树操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。
typedef int BTDataType;typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->_left = node2;node1->_right = node4;node2->_left = node3;node4->_left = node5;node4->_right = node6;return node1;
}
❗❗❗注意:上述代码并不是创建二叉树的方式,真正创建二叉树方式后序详解重点讲解。
再看二叉树基本操作前,再回顾下二叉树的概念,二叉树是:
1.空树
2.非空:根节点,根节点的左子树、根节点的右子树组成的。
从概念中可以看出,二叉树定义是
递归式的,因此后序基本操作中基本都是按照该概念实现的。
2.二叉树的遍历
2.1 前序、中序以及后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照
某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
- 前序遍历——访问根结点的操作发生在遍历其左右子树之前。(
根 左子树 右子树) - 中序遍历——访问根结点的操作发生在遍历其左右子树之中。(左 根 右)
- 后序遍历——访问根结点的操作发生在遍历其左右子树之后。(左 右 根)
任何一个二叉树,都要看做三个部分
根节点、左子树、右子树
🤗🤗🤗下面我们来看看这三种的遍历顺序叭
-
前序遍历

-
中序遍历

-
后序遍历

-
层序遍历

判断一个树是不是完全二叉树可以用
层序遍历
因为假设D没有,那么就会是ABC null E…这样会有一个null隔开来
2.2前序遍历实现
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>typedef char BTDataType;
typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;}BTNode;//前序遍历
void PrevOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%c ", root->_data);//打印根PrevOrder(root->_left);PrevOrder(root->_right);
}//求二叉树的结点个数
int TreeSize(BTNode* root)//传的是根结点的指针
{return 0;
}//创建树
BTNode* GreateNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));node->_data = x;node->_left = NULL;node->_right = NULL;return node;
}int main()
{BTNode* A = GreateNode('A');BTNode* B = GreateNode('B');BTNode* C = GreateNode('C');BTNode* D = GreateNode('D');BTNode* E = GreateNode('E');A->_left = B;A->_right = C;B->_left = D;B->_right = E;PrevOrder(A);return 0;
}
运行结果:

前序遍历递归展开过程:

2.3中序遍历的实现
由前序遍历我们可以知道交换根左右那个递归代码的顺序就能退出中、后续遍历,只用改变这一个递归的顺序
//中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->_left);printf("%c ", root->_data);//打印根InOrder(root->_right);
}
2.4后序遍历的实现
//后续遍历
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->_left);PostOrder(root->_right);printf("%c ", root->_data);//打印根
}
2.5求二叉树的结点个数
在很多时候,我们会直接这样写,但是我们会发现最后的结果是错误的,原因就是每一个递归里面都有一个size,这个size始终都加不到一个size上面,就只能加一次,这个size是局部变量,我们就要思考一下如何加到同一个size上面呢??
错误写法:
//求二叉树的结点个数
int TreeSize(BTNode* root)//传的是根结点的指针
{if (root == NULL){return 0;}int size = 0;size++;TreeSize(root->_left);TreeSize(root->_right);return size;
}
运行结果:
TreeSize=1(是错误的)
方法一:
修改成全局变量
//求二叉树的结点个数
int size = 0;
int TreeSize(BTNode* root)//传的是根结点的指针
{if (root == NULL){return 0;}size++;TreeSize(root->_left);TreeSize(root->_right);return size;
}//int main函数里面
printf("TreeSize:%d\n", TreeSize(A));
printf("TreeSize:%d\n", TreeSize(A));但这里存在一个缺陷,就是再次调用时会相互影响

方法二:
//求二叉树的结点个数
void TreeSize(BTNode* root,int* psize)//传的是根结点的指针
{if (root == NULL){return;}else{(*psize)++;}TreeSize(root->_left, psize);TreeSize(root->_right, psize);}//int main函数里面
int sizea = 0;
TreeSize(A, &sizea);
printf("TreeSize:%d\n", sizea);int sizeb = 0;
TreeSize(B, &sizeb);
printf("TreeSize:%d\n", sizeb);

方法三:
//求二叉树的结点个数
int TreeSize(BTNode* root)
{//空树if (root == NULL){return 0;}else{return 1 + TreeSize(root->_left) + TreeSize(root->_right);}
}
这里就不会相互影响
2.6求叶子结点个数
//求叶子结点个数
int TreeLeafSize(BTNode* root)
{//空树if (root == NULL){return 0;//如果传入的节点指针为NULL,表示这是一个空树或空子树//空树没有叶子节点,所以返回0}if (root->_left == NULL && root->_right == NULL){//如果一个节点的左右子节点都为NULL,那么这个节点就是叶子节点return 1;//每找到一个叶子节点就返回1}return TreeSize(root->_left) + TreeSize(root->_right);//对于非叶子节点,递归计算其左子树和右子树的叶子节点数量//将左右子树的叶子节点数量相加,得到当前子树的叶子节点总数
}
运行结果:

2.7二叉树第k层节点个数
当前树的第
k层节点数,等于其左子树的第k-1层节点数加上右子树的第k-1层节点数。
层数=1时就不需要再分解
这句话的意思就是:
从根节点 A(k=3)的视角看
A 的第3层节点,其实是A的左子树(根为 B)的第2层节点和右子树(根为 C)的第2层节点之和。
为什么?因为:
左子树(B 为根)的第1层是B自己(对应原树的第 2 层),第2层是B的子节点(D、E,对应原树的第3层)。
右子树(C 为根)的第1层是C自己(对应原树的第 2 层),第2层是C的子节点 F(对应原树的第3层)。
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL){return 0;//如果当前节点为空,说明该路径上没有节点,返回 0}if (k == 1){return 1;//当层数 k 递减到 1 时,表示当前节点就是目标层的节点,返回 1}return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}
main函数中调用:

画图解释:

运行结果:

2.8二叉树查找值为x的节点
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;//如果当前节点为空,返回 NULL}if (root->_data == x){return root;//如果当前节点的值等于 x,返回当前节点}//这里我们用的前序遍历//没找到 我们就找左BTNode* node = BinaryTreeFind(root->_left, x);if (node){return node;//否则递归查找左子树,若找到则返回该节点}node = BinaryTreeFind(root->_right, x);if (node){return node;//若左子树未找到,递归查找右子树,找到则返回}return NULL;//若左右子树均未找到,返回 NULL
}2.9销毁二叉树
//销毁树
void DestoryTree(BTNode* root)
{if (root == NULL){return;}//用后续销毁DestoryTree(root->_left);DestoryTree(root->_right);free(root);
}
2.10二叉树的层序遍历
画图解释层序遍历的原理:

层序遍历的实现原理:
层序遍历的目标是
从上到下、从左到右依次访问二叉树的每个节点。实现这一目标的关键在于利用队列的先进先出特性:
- 根节点入队:首先将
根节点放入队列。 - 循环处理队列:只要队列不为空,就执行以下操作:
- 出队当前节点:
取出队列头部的节点并访问(打印数据)。 - 子节点入队:将
当前节点的左子节点和右子节点(如果存在)依次加入队列。 - 重复步骤 2:由于队列的
先进先出特性,下层的节点会在当前层的所有节点处理完毕后才被处理,从而保证了层序遍历的顺序。
其在Queue.h文件中需要声明:
//声明一下
struct BinaryTreeNode;
typedef struct BinaryTreeNode* QDataType;
代码分析:
//二叉树的层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);// 初始化队列if (root == NULL)// 处理空树的情况{return;}QueuePush(&q, root);// 将根节点入队while (!QueueEmpty(&q)) // 当队列不为空时循环{BTNode* front = QueueFront(&q); // 获取队头节点QueuePop(&q); // 队头节点出队printf("%c ", front->_data); // 访问当前节点(打印数据)if (front->_left)// 如果左子节点存在,将其入队{QueuePush(&q, front->_left);}if (front->_right)// 如果右子节点存在,将其入队{QueuePush(&q, front->_right);}}QueueDestory(&q); // 销毁队列,释放资源printf("\n");
}关键步骤解析
- 队列初始化与根节点入队:
-
- 创建队列并初始化,若根节点不为空则将其入队。这是遍历的起点。
- 循环处理队列:
-
- 出队并访问当前节点:每次从队列头部取出节点并打印其数据。
-
- 子节点入队:按左、右顺序将子节点加入队列。由于队列的 FIFO 特性,这些子节点会在当前层的所有节点处理完毕后才被处理。
- 队列管理:
-
- 空队列检测:循环条件
!QueueEmpty(&q)确保所有节点都被处理后终止循环。
- 空队列检测:循环条件
-
- 资源释放:遍历结束后销毁队列,避免内存泄漏。
运行结果:

2.11判断二叉树是否是完全二叉树
本题运用的是层序遍历
是完全二叉树返回1,不是返回0

// 判断二叉树是否是完全二叉树
//是返回1 不是返回0
int BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);// 初始化队列if (root == NULL)// 处理空树的情况{return 1;// 空树被视为完全二叉树}QueuePush(&q, root);// 将根节点入队while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q); // 获取队头节点QueuePop(&q); // 队头节点出队//只要出来为空 咱就break// 只要出队节点为空,立即终止循环if (front == NULL){break;}//把左右录进去(无论是否为空)QueuePush(&q, front->_left);QueuePush(&q, front->_right);}//下面只要有一个非空就不是完全二叉树// 检查队列中剩余的节点while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q); // 获取队头节点QueuePop(&q); // 队头节点出队// 若发现非空节点,则不是完全二叉树if (front){QueueDestory(&q);//防止内存泄露return 0;}}QueueDestory(&q);return 1;
}
关键点解析:
- 队列的使用:通过队列实现层序遍历,确保节点按层级顺序处理。
- 首次遇到空节点:当层序遍历中首次遇到空节点时,立即终止第一层循环。
- 剩余节点检查:检查队列中剩余的所有节点。若存在非空节点,则二叉树不是完全二叉树。
- 内存管理:在返回结果前销毁队列,避免内存泄漏。
运行结果:

3.二叉树的相关OJ题
3.1二叉树的前序遍历
要求:Note: The returned array must be malloced, assume caller calls free().
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;}BTNode;int TreeSize(BTNode* root)
{if (root == NULL){return 0;}return 1 + TreeSize(root->_left) + TreeSize(root->_right);
}//辅助递归函数
void _preorderTraversal(BTNode* root, int* array, int* pi)//数组,数组里面第几个数
{if (root == NULL){return;//如果当前节点为空,直接返回}//否则将当前节点的值存入数组array的当前位置*piarray[(*pi)++] = root->_data;//然后递归遍历左子树和右子树_preorderTraversal(root->_left, array, pi);_preorderTraversal(root->_right, array, pi);//注意:pi是一个指向整数的指针,用于跟踪当前存储位置,每次存入后会递增
}//对外接口函数
int* preorderTraversal(BTNode* root, int* returnSize)
{//首先调用TreeSize计算树的节点数int size = TreeSize(root);//定义一个数组int* array = (int*)malloc(sizeof(int) * size);//动态分配足够的内存来存储遍历结果//下标int i = 0;//初始化索引i为 0_preorderTraversal(root, array, &i);//调用辅助函数进行实际的遍历*returnSize = size;//设置返回的大小,并返回存储结果的数组指针return array;
}int main()
{// 构建二叉树节点BTNode* node1 = (BTNode*)malloc(sizeof(BTNode));node1->_data = 1;node1->_left = NULL;node1->_right = NULL;BTNode* node2 = (BTNode*)malloc(sizeof(BTNode));node2->_data = 2;node2->_left = NULL;node2->_right = NULL;BTNode* node3 = (BTNode*)malloc(sizeof(BTNode));node3->_data = 3;node3->_left = NULL;node3->_right = NULL;node1->_right = node2;node2->_right = node3;// 调用前序遍历函数int returnSize;int* result = preorderTraversal(node1, &returnSize);//以二叉树的根节点node1作为参数调用preorderTraversal函数//该函数会返回存储前序遍历结果的数组指针//同时通过&returnSize获取结果数组的大小 以便后续输出结果// 输出前序遍历结果printf("前序遍历结果: ");for (int i = 0; i < returnSize; i++){printf("%d ", result[i]);//遍历存储前序遍历结果的数组result 按照顺序输出数组中的元素}printf("\n");// 释放动态分配的内存free(node1);free(node2);free(node3);free(result);return 0;
}
这道题目的意思其实就是,
通过前序的方法把二叉树的有效值放到我们自己开辟的动态数组里面。
简单来说就是我们原先学了前序遍历,其有一个排序,将这个排好的顺序存储到数组里面,再通过数组遍历出来;就是先动态开辟一个数组 也就是preorderTraversal,然后再调用_preorderTraversal排序 ,相当于之前的前序遍历去遍历出来,再把它存到数组里面,最后再用*returnSize = size这个size在int main里面遍历出这个数组
结果:

3.2单值二叉树
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;}BTNode;//创建树
BTNode* GreateNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));node->_data = x;node->_left = NULL;node->_right = NULL;return node;
}bool isUnivalTree(BTNode* root)
{if (root == NULL){return true;}//当前树if (root->_left && root->_data != root->_left->_data){return false;}if (root->_right && root->_data != root->_right->_data){return false;}//递归判断左右子树return isUnivalTree(root->_left) && isUnivalTree(root->_right);
}int main()
{BTNode* A = GreateNode('1');BTNode* B = GreateNode('1');BTNode* C = GreateNode('1');BTNode* D = GreateNode('1');BTNode* E = GreateNode('1');BTNode* F = GreateNode('1');A->_left = B;A->_right = C;B->_left = D;B->_right = E;C->_right = F;if (isUnivalTree(A) == true){printf("是单值二叉树:true");}else{printf("不是单值二叉树:false");}
}
核心代码的详细分析
bool isUnivalTree(BTNode* root)
{if (root == NULL){return true;}//当前树if (root->_left && root->_data != root->_left->_data){return false;}if (root->_right && root->_data != root->_right->_data){return false;}//递归判断左右子树return isUnivalTree(root->_left) && isUnivalTree(root->_right);
}
- 1.空树处理
如果根节点为空(root == NULL),直接返回true。
这是因为空树被视为单值二叉树(没有节点,自然不存在值不同的节点) - 2.当前节点与子节点的比较
-
- 检查左子节点:如果左子节点
存在(root->_left != NULL),且其值不等于当前节点的值(root->_data != root->_left->_data),则返回false。
- 检查左子节点:如果左子节点
-
- 检查右子节点:同理,如果右子节点存在且值不同,也返回
false。
- 检查右子节点:同理,如果右子节点存在且值不同,也返回
关键点:只要当前节点的
任一子节点值与当前节点不同,整棵树就不是单值二叉树,立即返回false。
- 递归检查左右子树
-
- 递归检查左子树:调用
isUnivalTree(root->_left)判断左子树是否为单值。
- 递归检查左子树:调用
-
- 递归检查右子树:调用
isUnivalTree(root->_right)判断右子树是否为单值。
- 递归检查右子树:调用
-
- 返回结果:只有左右子树都为单值二叉树时,整棵树才是单值二叉树,因此用
&&连接两个递归结果。
- 返回结果:只有左右子树都为单值二叉树时,整棵树才是单值二叉树,因此用
总结
这个函数通过递归的方式,从根节点开始逐层检查每个节点的值是否与子节点相同,确保整棵树所有节点的值一致。只要有任何一个节点的值与子节点不同,就会立即终止递归并返回 false。
3.3二叉树的最大深度
题意:该题求的是二叉树有多少层
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;}BTNode;//创建树
BTNode* GreateNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));node->_data = x;node->_left = NULL;node->_right = NULL;return node;
}//二叉树的最大深度
int maxDepth(BTNode* root)
{if (root == NULL){return 0;}int leftDepth = maxDepth(root->_left);int rightDepth = maxDepth(root->_right);return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;}int main()
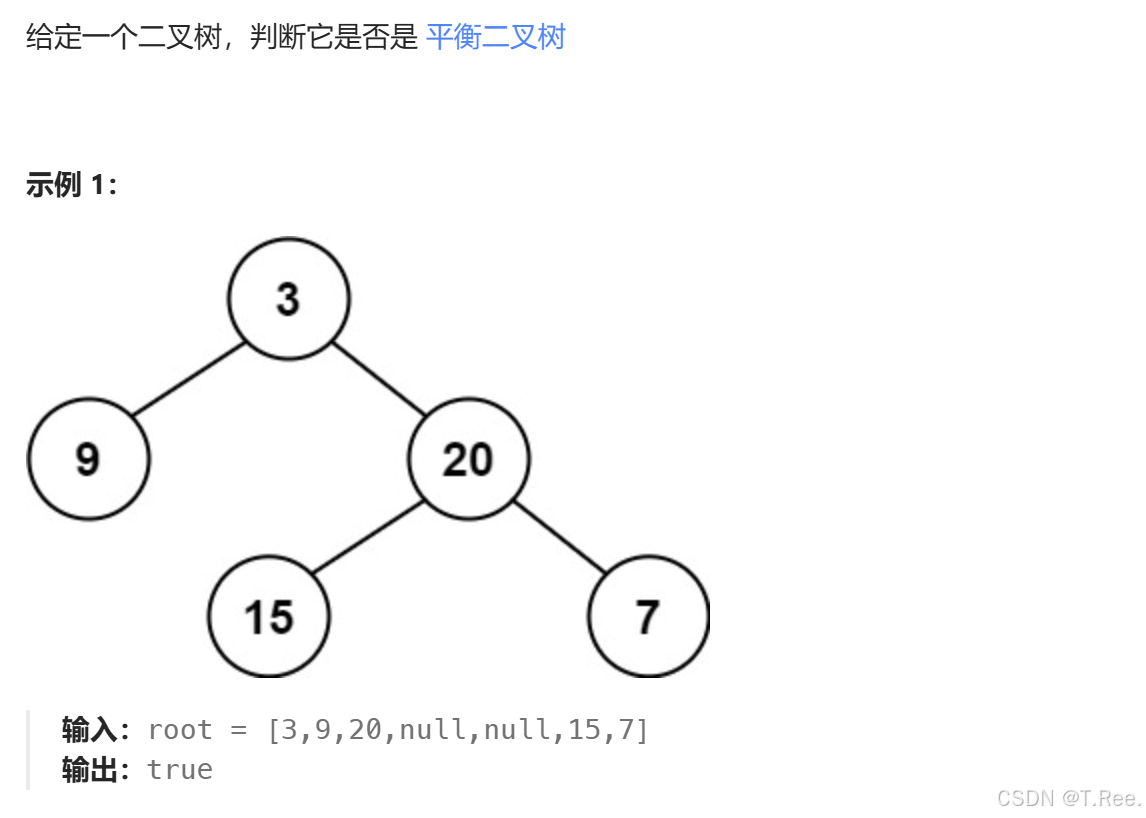
{BTNode* A = GreateNode('3');BTNode* B = GreateNode('9');BTNode* C = GreateNode('20');BTNode* D = GreateNode('15');BTNode* E = GreateNode('7');A->_left = B;A->_right = C;C->_left = D;C->_right = E;int depth = maxDepth(A);printf("该二叉树的深度是:%d", depth);return 0;
}
运行结果:

核心代码分析:
//二叉树的最大深度
int maxDepth(BTNode* root)
{if (root == NULL){return 0;}int leftDepth = maxDepth(root->_left);int rightDepth = maxDepth(root->_right);return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;}
-
当当前节点为
NULL时(即到达叶子节点的子节点),返回深度0。
作用:防止无限递归,并为后续递归计算提供基准值。 -
左子树深度:递归调用
maxDepth(root->_left)计算左子树的最大深度。
右子树深度:递归调用maxDepth(root->_right)计算右子树的最大深度。 -
比较左右子树的深度,取较大值加
1(当前节点自身的深度)
最后的return它的作用是返回当前节点的最大深度;因为当前节点本身也算一层深度,所以需要在子树的最大深度基础上 +1
这个返回语句的本质是:当前节点的最大深度 = 左右子树的最大深度 + 1,通过递归回溯的方式从叶子节点向上逐层计算,最终得到整棵树的最大深度。
3.4翻转二叉树
- 前序遍历方法
思维流程图:

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;}BTNode;//创建树
BTNode* GreateNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));node->_data = x;node->_left = NULL;node->_right = NULL;return node;
}// 前序遍历打印树(用于验证)
void preOrderPrint(BTNode* root)
{if (root == NULL){return;}printf("%c ", root->_data);preOrderPrint(root->_left);preOrderPrint(root->_right);
}//翻转一个二叉树
BTNode* flipTree(BTNode* root)
{if (root == NULL){return NULL;}else{BTNode* tmp = root->_left;root->_left = root->_right;root->_right = tmp;flipTree(root->_left);flipTree(root->_right);return root;}
}int main()
{BTNode* A = GreateNode('5');BTNode* B = GreateNode('7');BTNode* C = GreateNode('9');BTNode* D = GreateNode('8');BTNode* E = GreateNode('3');BTNode* F = GreateNode('2');BTNode* G = GreateNode('4');A->_left = B;A->_right = C;B->_left = D;B->_right = E;C->_left = F;C->_right = G;printf("原树前序遍历: \n");preOrderPrint(A);printf("\n");// 翻转二叉树BTNode* flippedRoot = flipTree(A);printf("翻转后树前序遍历: \n");preOrderPrint(flippedRoot);return 0;
}
运行结果:

- 中序遍历方法
BTNode* flipTree(BTNode* root)
{if (root == NULL){return NULL;}else{BTNode* right = root->_right;//保存原始右子树指针root->_right = flipTree(root->_left);// 递归翻转左子树,并将结果赋给右子树root->_left = flipTree(right); // 递归翻转原始右子树(保存在right中),并将结果赋给左子树return root;}
}- 保存原始右子树:
避免在递归过程中丢失右子树指针。 - 翻转左子树:递归调用
flipTree(root->_left),并将返回的翻转后的左子树赋给当前节点的右子树。 - 翻转右子树:递归调用
flipTree(right)(原始右子树),并将返回的翻转后的右子树赋给当前节点的左子树。
🤔🤔🤔思考:为什么要返回root?
返回root的核心目的是维持树的结构连贯性:
- 递归连接子树:在递归调用中,需要将子树的
根节点回给父节点,以便父节点能正确指向翻转后的子树。
例如,当root->_right = flipTree(root->_left)时,flipTree(root->_left)返回的是翻转后的左子树的根节点,该节点需要被赋给当前节点的右子树指针。 - 统一接口:无论树的结构如何,函数始终返回当前处理节点的指针,使得递归调用可以
嵌套进行。 - 避免断链:若不返回
root,上层节点将无法得知子树的新根节点,导致树结构断裂。
3.5相同的树
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;}BTNode;//创建树
BTNode* GreateNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));node->_data = x;node->_left = NULL;node->_right = NULL;return node;
}//相同的树
bool isSameTree(BTNode* p, BTNode* q)
{if (p == NULL && q == NULL){return true;}//结构不同if (p == NULL && q != NULL){return false;}//结构不同if (p != NULL && q == NULL){return false;}//值不同if (p->_data != q->_data){return false;}//比较左右子树return isSameTree(p->_left, q->_left) && isSameTree(p->_right, q->_right);
}int main()
{BTNode* A = GreateNode('5');BTNode* B = GreateNode('7');BTNode* C = GreateNode('9');BTNode* D = GreateNode('5');BTNode* E = GreateNode('7');BTNode* F = GreateNode('9');//BTNode* G = GreateNode('4');A->_left = B;A->_right = C;D->_left = E;D->_right = F;bool result = isSameTree(A, D);printf("TreeA 和 TreeD 是否相同: %s\n", result ? "是" : "否");return 0;
}
运行结果:

3.6对称二叉树
// 辅助函数:递归判断两个子树是否镜像对称
bool isMirror(BTNode* t1, BTNode* t2) {if (t1 == NULL && t2 == NULL){return true;}if (t1 == NULL || t2 == NULL){return false;}return (t1->_data == t2->_data) && isMirror(t1->_left, t2->_right) && isMirror(t1->_right, t2->_left);
}//判断二叉树是否轴对称
bool isSymmetric(BTNode* root)
{if (root == NULL){return true;}return isMirror(root->_left, root->_right);
}3.7另一个树的子树
root跟subRoot中每一颗子树都进行比较,如果有相同的,则满足
//相同的树
bool isSameTree(BTNode* p, BTNode* q)
{if (p == NULL && q == NULL){return true;}//结构不同if (p == NULL && q != NULL){return false;}//结构不同if (p != NULL && q == NULL){return false;}//值不同if (p->_data != q->_data){return false;}//比较左右子树return isSameTree(p->_left, q->_left) && isSameTree(p->_right, q->_right);
}//另一棵树的子树
bool isSubtree(BTNode* root, BTNode* subRoot)
{// 基准情况:如果主树root为空,显然不可能包含任何子树,返回falseif (root == NULL){return false;}// 检查当前节点为根的子树是否与subRoot完全相同if (isSameTree(root, subRoot))//判断里面用的是上面的函数{return true;}// 如果当前节点不匹配,则递归检查左子树和右子树return isSubtree(root->_left, subRoot) || isSubtree(root->_right, subRoot);
}
3.7平衡二叉树
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点的左右两个子树的高度差的绝对值不超过1。
前序方法:
//辅助函数
int TreeDepth(BTNode* root)
{if (root == NULL){return 0;}int leftDepth = TreeDepth(root->_left);//左树深度int rightDepth = TreeDepth(root->_right);//右树深度return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;}//平衡二叉树
bool isBalanced(BTNode* root)
{if (root == NULL){return true;}int gap = TreeDepth(root->_left) - TreeDepth(root->_right);if (abs(gap) > 1)//abs是求绝对值函数{return false;}return isBalanced(root->_left) && isBalanced(root->_right);
}
注意:为什么那个abs那里的
if不要else呢?
- 当
abs(gap) <=1时,不要直接返回true,而是继续递归检查左右子树; - 将最后的递归检查移至
if条件之后,确保当前节点平衡时,仍会检查其子树的平衡性。
逻辑流程:
1.如果当前节点为空,返回true。
2.计算左右子树的高度差gap:
- 如果
abs(gap) > 1,返回false(当前节点不平衡)。 - 否则,递归检查左右子树是否平衡,并返回结果。
优化时间复杂度最好是O(n);
后序方法:(优化了时间复杂度)
判断的同时把高度带给上一层的父亲
bool _isBalanced(BTNode* root ,int* pDepth)
{if (root == NULL){*pDepth = 0;return true;}else{//判断左树,不满足int leftDepth = 0;if (_isBalanced(root->_left, &leftDepth ) == false){return false;}//判断右树,不满足int rightDepth = 0; if (_isBalanced(root->_right, &rightDepth) == false){return false;}//判断当前树,不满足if (abs(leftDepth - rightDepth) > 1){return false;}//满足*pDepth = leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;return true;}
}bool isBalanced(BTNode* root)
{int depth = 0;return _isBalanced(root, &depth);
}
main函数中调用:
// 调用isBalanced函数判断是否平衡
int balanced = isBalanced(A);// 输出结果
if (balanced)
{printf("这是一棵平衡二叉树。\n");
}
else
{printf("这不是一棵平衡二叉树。\n");
}
这串代码中的*pDepth = leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;与计算最大深度的逻辑完全一致。这里的*pDepth同样是记录当前节点的最大深度,但其核心目的是为了辅助判断二叉树是否平衡。
这样优化后其实就类似于上面求深度的函数直接在里面写
举个例子:

总结:
方法一 简单直观,但存在大量重复计算,效率较低。
方法二 通过后序遍历和深度传递,将时间复杂度优化到 O (n),是更优的解法。
建议:在实际应用中优先选择方法二,尤其是处理大规模数据时。
3.8重建二叉树
本题题意:这道题就说类似的把数组内容放到二叉树中通过前序遍历方法进行存储,也就是按照前序遍历的方法 照着数组内容进行存储;之前我们展开过二叉树遍历的数据,反过来就说 把数组里面的内容还原回去阿

//定义二叉树的节点结构
typedef struct TreeNode
{BTDataType _data;struct TreeNode* _left;struct TreeNode* _right;}TreeNode;//构建二叉树
TreeNode* CreateTree(char* str, int* pi)
{if (str[*pi] == '#'){(*pi)++;return NULL;}//不是#构建‘根’else{TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));root->_data = str[*pi];(*pi)++;//因为前面那个i已经构建了root->_left = CreateTree(str, pi);root->_right = CreateTree(str,pi);return root;}
}//中序遍历
void InOrder(TreeNode* root)
{if (root == NULL){return;}InOrder(root->_left);printf("%c ", root->_data);InOrder(root->_right);}int main()
{char str[100];scanf("%s", str);//str数组名即首元素地址int i = 0;//下标TreeNode* root = CreateTree(str, &i);InOrder(root);return 0;
}
运行结果:

画图解析:
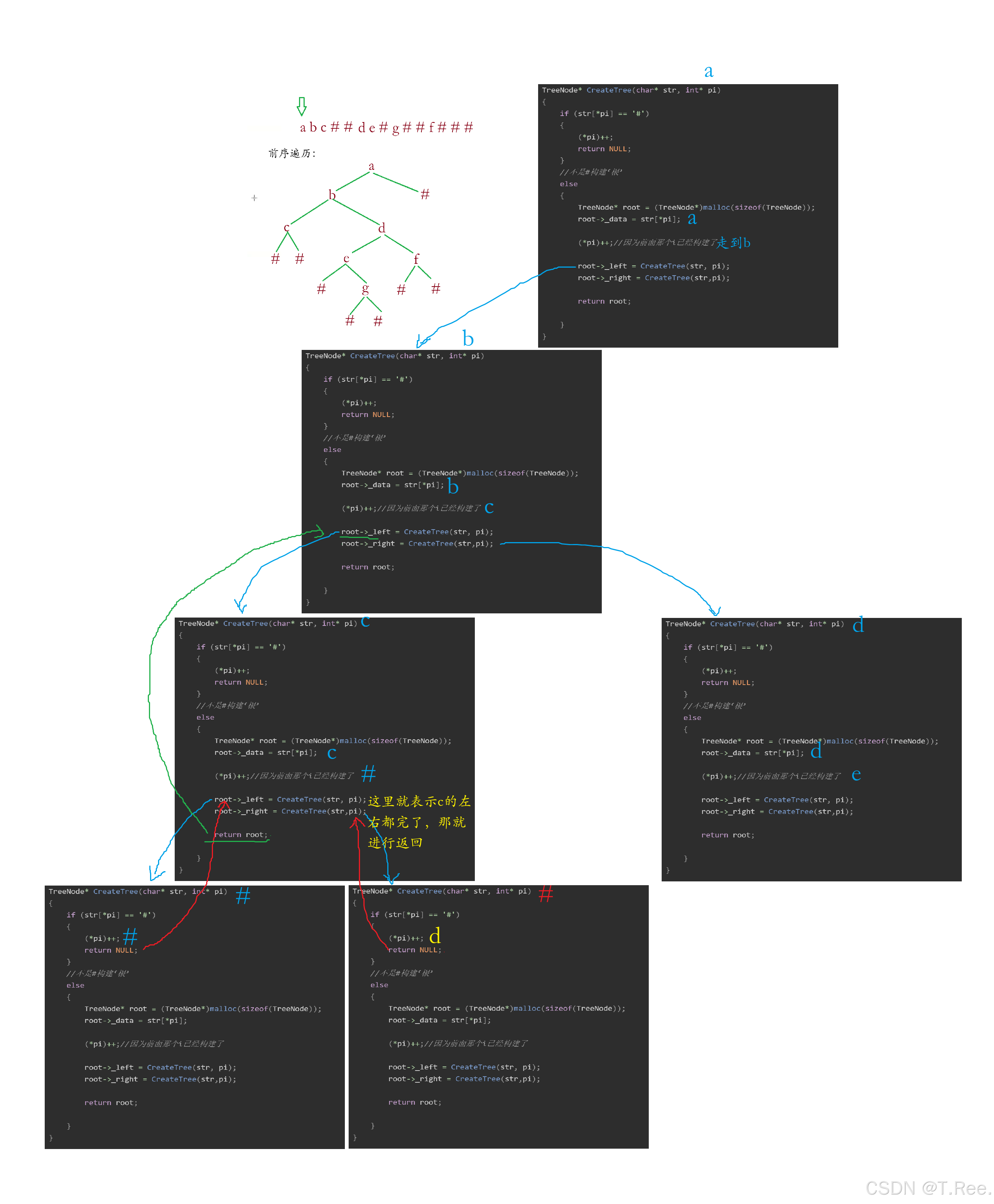
这里传指针是为了在同一个i上加加
CreateTree函数的工作流程是:
- 检查当
前字符是否为#,如果是则表示该节点为空,指针后移并返回NULL - 如果不是
#,则创建新节点并设置数据 - 递归构建左子树和右子树
- 返回构建好的节点
注意:这里的关键是使用指针
pi来跟踪当前处理的字符位置,确保递归调用时位置信息能被正确传递和更新。
思考:🤔🤔🤔
为什么需要传递
&i(地址)?
核心问题:递归函数需要在多层调用之间共享和修改同一个变量(即字符位置)。
每次递归调用都会创建独立的函数栈帧,其中的局部变量(包括参数)是相互独立的。如果直接传递int i,每次递归调用都会得到i的一个副本。当内层递归修改i时,外层递归的i值不会改变,导致所有递归调用都从同一位置开始解析字符串,最终造成无限循环或错误构建。(简单来讲呢就是:把数组里面的内容还原回去,首先要一个指针才能移动,从而指向数组里面不同的位置,实现遍历),通过传递&i,*pi指向的是主函数中的变量i,任何递归层对*pi的修改都会直接反映到这个共享变量上。
🎉🎉🎉
到这里本章就结束啦~
友友们
我们下期见咯~

相关文章:

【数据结构】_二叉树
1.二叉树链式结构的实现 1.1 前置说明 在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入,为了降低大家学习成本,此处手动快速创建一棵简单的二叉树&#x…...

ALIENTEK精英STM32F103开发板 实验0测试程序详解
#include "sys.h" #include "usart.h" #include "delay.h" //ALIENTEK精英STM32F103开发板 实验0 //新建工程 实验 //技术支持:www.openedv.com //广州市星翼电子科技有限公司 int main(void) { u8 t0; //见注释1 St…...

LeetCode 33. 搜索旋转排序数组:二分查找的边界艺术
文章目录 问题描述解决思路代码实现关键点解析1. 为什么用 nums[left] < nums[mid]?2. 示例分析案例 1:数组 [3, 1],目标值 1案例 2:数组 [5],目标值 5 边界条件处理1. 单元素数组2. 完全有序数组3. 严格递增与重复…...

Rust 学习笔记:关于 HashMap 的练习题
Rust 学习笔记:关于 HashMap 的练习题 Rust 学习笔记:关于 HashMap 的练习题以下代码能否通过编译?若能,输出是?以下代码能否通过编译?若能,输出是? Rust 学习笔记:关于 …...
—6.1 葡萄酒评论分析报告(project))
(头歌作业)—6.1 葡萄酒评论分析报告(project)
第1关:葡萄酒评论分析报告——国家列表和平均分 任务描述 本关任务:编写程序,多维度分析葡萄酒数据。 相关知识 葡萄酒评论分析报告描述 winemag-data.csv 文件 winemag-data.csv 包含 编号、国家、描述、评分、价格、省份 等 6列 和12974…...

下集:一条打包到底的静态部署之路
说完坑,再来讲正经操作。 这次我决定写得明明白白,清清楚楚,把那条“Spring Boot 扛着 Next.js 上线”的路子掰碎了揉细了告诉你。 无废话、无迷信、无AI幻觉。 第一步:Next.js 静态导出 项目根目录下的 next.config.js 要写得…...

多商户商城系统源码解析:开发直播电商APP的技术底层实战详解
随着直播电商的火爆,越来越多的创业者和企业都在寻求打造自己的多商户商城系统,以实现“人、货、场”三者的深度融合。然而,从一个简单的电商平台到一个功能完善的直播电商APP,其技术底层架构和实现过程并非一蹴而就。本文将从架构…...

每日Prompt:生成自拍照
提示词 帮我生成一张图片:图片风格为「人像摄影」,请你画一张及其平凡无奇的iPhone对镜自拍照,主角是穿着JK风格cos服的可爱女孩,在自己精心布置的可按风格的房间内的落地镜前用后置摄像头随手一拍的快照。照片开启了闪光灯&…...
(技巧)(暴力解法;哈希集合;二分查找))
LeetCode 热题 100_寻找重复数(100_287_中等_C++)(技巧)(暴力解法;哈希集合;二分查找)
LeetCode 热题 100_寻找重复数(100_287_中等_C) 题目描述:输入输出样例:题解:解题思路:思路一(暴力解法):思路二(哈希集合):思路三&am…...
—— ROPE位置编码:从理论到实践)
多模态学习(三)—— ROPE位置编码:从理论到实践
ROPE位置编码:从理论到LLaMA的实践 一、前言 ROPE(Rotary Positional Embedding,旋转位置编码)是一种通过旋转矩阵将位置信息融入Token Embedding的编码方法。相比传统Transformer的绝对位置编码,ROPE能更灵活地建模…...

Redis——过期删除策略和内存
过期删除策略 Redis可以对key设置过期时间,因此需要有相应的机制将已过期的键值对删除 设置了过期时间的key会存放在过期字典中,可以用presist命令取消key过期时间 过期字典存储在redisDb结构中: typedef struct redisDb {dict *dict; …...

Selenium无法定位元素的几种解决方案详解
🍅 点击文末小卡片,免费获取软件测试全套资料,资料在手,涨薪更快 1、frame/iframe表单嵌套 WebDriver只能在一个页面上对元素识别与定位,对于frame/iframe表单内嵌的页面元素无法直接定位。 解决方法: …...

开源项目实战学习之YOLO11:12.3 ultralytics-models-sam-encoders.py源码分析
👉 点击关注不迷路 👉 点击关注不迷路 👉 另外,前些天发现了一个巨牛的AI人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。感兴趣的可以点击相关跳转链接。 点击跳转到网站。 ultralytics-models-sam 1.sam-modules-encoders.pyblocks.py: 定义模型中的各…...

Bitmap原理及Hive去重方式对比
1. 什么是 Bitmap? Bitmap(位图)是一种用位(bit)来表示数据集合的数据结构。每个位代表一个元素是否存在,比如: 一个长度为N的bitmap,每一位对应一个元素的状态(0或1&a…...
)
力扣-比特位计数(统计一个数二进制下1的个数)
下面是题面 1.用c的内置函数__builtin_popcount() 语法:__builtin_popcount(int x),函数会返回一个二进制下x所含的1的个数 2.直接数位枚举 这是最慢也是暴力做法,写法也很简单 用一个while循环…...

开源项目实战学习之YOLO11:12.2 ultralytics-models-sam-decoders.py源码分析
👉 点击关注不迷路 👉 点击关注不迷路 👉 另外,前些天发现了一个巨牛的AI人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。感兴趣的可以点击相关跳转链接。 点击跳转到网站。 ultralytics-models-sam 1.sam-modules-decoders.pyblocks.py: 定义模型中的各…...

Python训练营打卡Day28
浙大疏锦行 DAY 28 类的定义和方法 知识点回顾: 1.类的定义 2.pass占位语句 3.类的初始化方法 4.类的普通方法 5.类的继承:属性的继承、方法的继承 作业 题目1:定义圆(Circle)类 要求: 1.包含属性&#x…...
)
【前端基础】HTML元素隐藏的四个方法(display设置为none、visibikity设置为hidden、rgba设置颜色、opacity设置透明度)
HTML元素隐藏的四个方法 1、display设置为none 元素不显示出来。不占位置,也没有任何空间。就不存在一样。 2、visibility设置为hidden 默认:visible。元素可见设置为hidden:元素不可见,但是会占据这个元素应该占用的空间。 3、…...

STM32中的DMA
DMA介绍 什么是DMA? DMA(Direct Memory Access,直接存储器访问)提供在外设与内存、存储器和存储器之间的高速数据传输使用。它允许不同速度的硬件装置来沟通,而不需要依赖于CPU,在这个时间中,CPU对于内存…...

小型气象站应用之鱼塘养殖方案
概述 "看天吃饭",在农村经常听到这句话,鱼塘也不例外。天气的急剧变化,或连续的不利天气都有可能造成鱼类"浮头",甚至"翻肚子",更甚至"翻塘",一年白忙活了。 鱼塘…...

Makefile变量冲突与包含关系解析
Nuttx makefile每层独立,除非显示的通过include的方式包含。 Makefile调试技巧 打印变量 $(info CSRCS$(CSRCS))查看变量赋值过程 make --debugv在 Makefile 中,变量的作用域和可见性取决于 包含关系(include) 和 递归调用&…...

2025/517学习
对离群值怎么操作。这个就是拟合操作的。用更弯曲的曲线去拟合,如常见函数log 多元回归和单元回归 如题,如果我有多个自变量,来对一个因变量进行OLS回归,有没有operator可以做到?(ts_regression似乎只支持一个…...

浅谈前端架构设计与工程化
引言 在当今快速发展的Web开发领域,前端已经从简单的页面展示演变为复杂的应用程序开发。随着项目规模的扩大和团队协作的需求增加,良好的前端架构设计和工程化实践变得至关重要。本文将探讨如何构建可维护、可扩展的前端架构,并介绍现代前端…...

JMeter 教程:编写 POST 请求脚本访问百度
目录 ✅ 教程目的 🛠️ 环境要求 📄 实操步骤 第一步:启动 JMeter 第二步:添加测试计划和线程组 1.右键左侧 Test Plan(测试计划) 2.选择 Add → Threads (Users) → Thread Group(线程组…...
)
Typescript学习教程,从入门到精通,TypeScript 函数语法知识点及案例代码(5)
TypeScript 函数语法知识点及案例代码 TypeScript 提供了丰富的函数语法特性,使得函数定义更加灵活和强大。以下将详细介绍 TypeScript 中函数的相关语法,包括函数定义、可选参数、默认参数、剩余参数、重载函数、递归函数、匿名函数、箭头函数以及回调…...

【51单片机定时器/计数器】
目录 简介 定时器配置流程 1.配置定时器工作方式寄存器TMOD 2.配置中断寄存器TCON 3.定时时间计算公式 4.配置中断允许寄存器IE 5.使用中断函数完成中断 简介 定时器/计数器本质都是对脉冲信号进行计数,区别在于作为定时器时的脉冲信号来自于晶振12分频&…...

Oracle 的 ASSM 表空间
Oracle 的 ASSM(Automatic Segment Space Management)表空间 是一种自动管理段空间的技术,通过位图(Bitmap)机制跟踪数据块的使用情况,替代传统的手动管理(MSSM,即 Freelist 管理&am…...

C++学习:六个月从基础到就业——C++11/14:auto类型推导
C学习:六个月从基础到就业——C11/14:auto类型推导 本文是我C学习之旅系列的第四十一篇技术文章,也是第三阶段"现代C特性"的第三篇,主要介绍C11/14中的auto类型推导机制。查看完整系列目录了解更多内容。 引言 在现代C…...

select语句的书写顺序
一.MySQL SELECT语句的执行顺序 MySQL中SELECT语句的执行顺序与SQL语句的书写顺序不同,理解这个执行顺序对于编写高效查询非常重要。 1.标准SELECT语句的执行顺序 FROM子句(包括JOIN操作) 首先确定数据来源表执行表连接操作 WHERE子句 对F…...

OpenWebUI新突破,MCPO框架解锁MCP工具新玩法
大家好,Open WebUI 迎来重要更新,现已正式支持 MCP 工具服务器,但 MCP 工具服务器需由兼容 OpenAPI 的代理作为前端。mcpo 是一款实用代理,经测试,它能让开发者使用 MCP 服务器命令和标准 OpenAPI 服务器工具ÿ…...

【Day28】
总结: Python 通过缩进来定义代码块的结构。当解释器遇到像 def, class, if, for 这样的语句,并且后面跟着冒号 : 时,它就期望接下来会有一个或多个缩进的语句来构成这个代码块。如果它没有找到任何缩进的语句(即代码块是空的&am…...

STM32 | FreeRTOS 消息队列
01 一、概述 队列又称消息队列,是一种常用于任务间通信的数据结构,队列可以在任务与任务间、中断和任务间传递信息,实现了任务接收来自其他任务或中断的不固定长度的消息,任务能够从队列里面读取消息,当队列中的消…...

Vue-事件修饰符
事件修饰符 prevent (阻止默认事件) 超链接 点击事件 代码 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><title>事件修饰符</title><!-- 引入Vue --><script …...

c++函数调用运算符及类型转换运算符重载
author: hjjdebug date: 2025年 05月 17日 星期六 14:44:48 CST descrip: c函数调用运算符及类型转换运算符重载 文章目录 0. 前言. 运算符包括以下运算符.1. 运算符重载语句一般格式:2. 函数调用运算符:3. 类型转换运算符: 例如 int(); double(); bool(…...

如何在 Windows 10 或 11 中安装 PowerShellGet 模块?
PowerShell 是微软在其 Windows 操作系统上提供的强大脚本语言,可用于通过命令行界面自动化各种任务,适用于 Windows 桌面或服务器环境。而 PowerShellGet 是 PowerShell 中的一个模块,提供了用于从各种来源发现、安装、更新和发布模块的 cmdlet。 本文将介绍如何在 PowerS…...

84.评论日记
原链接 这个视频我发了四五条评论。评论内容甚至和下面这个视频内的其他评论一样。 找了另外的账号也发了。 发现,无论是我这个账号,还是其他的账号,评论都无法看到。 我大胆猜测有一种机制,某些官号会被设置成一种高检测的等…...

一周学会Pandas2 Python数据处理与分析-Pandas2数据添加修改删除操作
锋哥原创的Pandas2 Python数据处理与分析 视频教程: 2025版 Pandas2 Python数据处理与分析 视频教程(无废话版) 玩命更新中~_哔哩哔哩_bilibili 对数据的修改、增加和删除在数据整理过程中时常发生。修改的情况一般是修改错误,还有一种情况是格式转换…...

荷兰国旗问题 之 指针划分区间问题
文章目录 首先介绍一下什么是荷兰国旗问题?问题描述为:给定一个由红色、白色和蓝色三种颜色组成的无序数组,将数组元素按颜色排序,使得所有红色元素在前,白色元素居中,蓝色元素在后。这里的 “颜色” 通常用…...

冒泡排序-java
public class BubbleSort{ public static void bubbleSort(int[] arr) { int n arr.length; boolean swapped; // 外层循环控制遍历的轮数 for (int i 0; i < n - 1; i) { swapped false; for (int j 0; …...

进阶-数据结构部分:2、常用排序算法
飞书文档https://x509p6c8to.feishu.cn/wiki/FfpIwIPtviMMb4kAn3Sc40ABnUh 常用排序算法 这几种算法都是常见的排序算法,它们的优劣和适用场景如下: 冒泡排序(Bubble Sort):简单易懂,时间复杂度较高&…...

人工智能-自然语言与语音产品实现
一、语义相似度 (一)、文本向量化 1、文本向量化(Text Vectorization) 是自然语言处理(NLP)中的核心预处理步骤,旨在将人类语言的文本转换为计算机可处理的数值向量(数学表达&…...

阿里巴巴开源移动端多模态LLM工具——MNN
MNN 是一个高效且轻量级的深度学习框架。它支持深度学习模型的推理和训练,并在设备端的推理和训练方面具有行业领先的性能。目前,MNN 已集成到阿里巴巴集团的 30 多个应用中,如淘宝、天猫、优酷、钉钉、闲鱼等,覆盖了直播、短视频…...

SpringBootAdmin:全方位监控与管理SpringBoot应用
监控的意义 1. 监控服务状态是否宕机 2. 监控服务运行指标 (内存,虚拟机,线程,请求等) 3. 监控日志 4. 管理服务 (服务下线) 可视化监控平台 Spring Boot Admin, 开源社区项目, 用于管理和监控SpringBoot应用程序. 客户端注册到服务端, 通过HTTP请求方式, 服务端定期从客…...

SAP HCM 0008数据存储逻辑
0008信息类型:0008信息类型是存储员工基本薪酬的地方,因为很多企业都会都薪酬带宽,都会按岗定薪,所以在上线前为体现工资体系的标准化,都会在配置对应的薪酬关系,HCM叫间接评估,今天我们就分析下…...
】Config配置中心-ConfigServer端与Git通信(含源代码)(十三))
【springcloud学习(dalston.sr1)】Config配置中心-ConfigServer端与Git通信(含源代码)(十三)
该系列项目整体介绍及源代码请参照前面写的一篇文章【springcloud学习(dalston.sr1)】项目整体介绍(含源代码)(一) springcloud学习(dalston.sr1)系统文章汇总如下: 【springcloud学习(dalston…...

2020CCPC河南省赛题解
A. 班委竞选 签到题,模拟。 #include <bits/stdc.h> #define x first #define y second #define int long long //#define double long doubleusing namespace std; typedef unsigned long long ULL ; typedef pair<int,int> PII ; typedef pair<d…...

C语言输入函数对比解析
目录 C语言输入函数全家福(和它们的秘密)fgetsgetsscanfgetcharfscanf函数对比表灵魂总结 哈哈,看来你正在和C语言的输入函数们玩“大家来找茬”!放心,我会用最接地气的方式给你讲明白,保证比看《甄嬛传》还…...

python四则运算计算器
python四则运算计算器 是谁说,python不好写计算器的,我亲自写个无ui的计算器功能,证明这是谣言 step1:C:\Users\wangrusheng\Downloads\num.txt 15 - 4 * 3 10 / 2(5 3) * 2 6 / 31/2 * 8 3/4 * 4 - 0.52.5 * (4 1.6) - 9 / 3-6 12 * (…...

BUUCTF——Nmap
BUUCTF——Nmap 进入靶场 类似于一个nmap的网站 尝试一下功能 没什么用 看看数据包 既然跟IP相关 伪造一个XXF看看 拼接了一下没什么用 果然没这么简单 尝试一下命令注入 构造payload 127.0.0.1 | ls 应该有过滤 加了个\ 直接构造个php木马上传试试 127.0.0.1 | <?…...

【Changer解码头详解及融入neck层数据的实验设计】
Changer解码头详解 ChangerEx中的 Changer 解码头(定义在 [changer.py](file://opencd\models\decode_heads\changer.py))是基于双时相输入的,用于遥感变化检测任务。下面我将详细解释: 🎯 一、解码头输入数据来源 输…...