【DAY21】 常见的降维算法
内容来自@浙大疏锦行python打卡训练营
@浙大疏锦行
目录
PCA主成分分析
t-sne降维
线性判别分析 (Linear Discriminant Analysis, LDA)
作业:
什么时候用到降维
降维的主要应用场景
知识点回顾:
- PCA主成分分析
- t-sne降维
- LDA线性判别
通常情况下,我们提到特征降维,很多时候默认指的是无监督降维,这种方法只需要特征数据本身。但是实际上还包含一种有监督的方法。



# 先运行之前预处理好的代码
import pandas as pd
import pandas as pd #用于数据处理和分析,可处理表格数据。
import numpy as np #用于数值计算,提供了高效的数组操作。
import matplotlib.pyplot as plt #用于绘制各种类型的图表
import seaborn as sns #基于matplotlib的高级绘图库,能绘制更美观的统计图形。
import warnings
warnings.filterwarnings("ignore")# 设置中文字体(解决中文显示问题)
plt.rcParams['font.sans-serif'] = ['SimHei'] # Windows系统常用黑体字体
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
data = pd.read_csv('data.csv') #读取数据# 先筛选字符串变量
discrete_features = data.select_dtypes(include=['object']).columns.tolist()
# Home Ownership 标签编码
home_ownership_mapping = {'Own Home': 1,'Rent': 2,'Have Mortgage': 3,'Home Mortgage': 4
}
data['Home Ownership'] = data['Home Ownership'].map(home_ownership_mapping)# Years in current job 标签编码
years_in_job_mapping = {'< 1 year': 1,'1 year': 2,'2 years': 3,'3 years': 4,'4 years': 5,'5 years': 6,'6 years': 7,'7 years': 8,'8 years': 9,'9 years': 10,'10+ years': 11
}
data['Years in current job'] = data['Years in current job'].map(years_in_job_mapping)# Purpose 独热编码,记得需要将bool类型转换为数值
data = pd.get_dummies(data, columns=['Purpose'])
data2 = pd.read_csv("data.csv") # 重新读取数据,用来做列名对比
list_final = [] # 新建一个空列表,用于存放独热编码后新增的特征名
for i in data.columns:if i not in data2.columns:list_final.append(i) # 这里打印出来的就是独热编码后的特征名
for i in list_final:data[i] = data[i].astype(int) # 这里的i就是独热编码后的特征名# Term 0 - 1 映射
term_mapping = {'Short Term': 0,'Long Term': 1
}
data['Term'] = data['Term'].map(term_mapping)
data.rename(columns={'Term': 'Long Term'}, inplace=True) # 重命名列
continuous_features = data.select_dtypes(include=['int64', 'float64']).columns.tolist() #把筛选出来的列名转换成列表# 连续特征用中位数补全
for feature in continuous_features: mode_value = data[feature].mode()[0] #获取该列的众数。data[feature].fillna(mode_value, inplace=True) #用众数填充该列的缺失值,inplace=True表示直接在原数据上修改。# 最开始也说了 很多调参函数自带交叉验证,甚至是必选的参数,你如果想要不交叉反而实现起来会麻烦很多
# 所以这里我们还是只划分一次数据集data.drop(columns=['Id'], inplace=True) # 删除 Loan ID 列
data.info() # 查看数据集的信息,包括数据类型和缺失值情况输出:(目前有31个特征,我们看看降维后的特征个数是多少)
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 7500 entries, 0 to 7499
Data columns (total 31 columns):# Column Non-Null Count Dtype
--- ------ -------------- ----- 0 Home Ownership 7500 non-null int64 1 Annual Income 7500 non-null float642 Years in current job 7500 non-null float643 Tax Liens 7500 non-null float644 Number of Open Accounts 7500 non-null float645 Years of Credit History 7500 non-null float646 Maximum Open Credit 7500 non-null float647 Number of Credit Problems 7500 non-null float648 Months since last delinquent 7500 non-null float649 Bankruptcies 7500 non-null float6410 Long Term 7500 non-null int64 11 Current Loan Amount 7500 non-null float6412 Current Credit Balance 7500 non-null float6413 Monthly Debt 7500 non-null float6414 Credit Score 7500 non-null float6415 Credit Default 7500 non-null int64 16 Purpose_business loan 7500 non-null int32 17 Purpose_buy a car 7500 non-null int32 18 Purpose_buy house 7500 non-null int32 19 Purpose_debt consolidation 7500 non-null int32 20 Purpose_educational expenses 7500 non-null int32 21 Purpose_home improvements 7500 non-null int32 22 Purpose_major purchase 7500 non-null int32 23 Purpose_medical bills 7500 non-null int32 24 Purpose_moving 7500 non-null int32 25 Purpose_other 7500 non-null int32 26 Purpose_renewable energy 7500 non-null int32 27 Purpose_small business 7500 non-null int32 28 Purpose_take a trip 7500 non-null int32 29 Purpose_vacation 7500 non-null int32 30 Purpose_wedding 7500 non-null int32
dtypes: float64(13), int32(15), int64(3)
memory usage: 1.3 MBfrom sklearn.model_selection import train_test_split
X = data.drop(['Credit Default'], axis=1) # 特征,axis=1表示按列删除
y = data['Credit Default'] # 标签from sklearn.model_selection import train_test_split
X = data.drop(['Credit Default'], axis=1) # 特征,axis=1表示按列删除
y = data['Credit Default'] # 标签
# 按照8:2划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # 80%训练集,20%测试集from sklearn.ensemble import RandomForestClassifier #随机森林分类器from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score # 用于评估分类器性能的指标
from sklearn.metrics import classification_report, confusion_matrix #用于生成分类报告和混淆矩阵
import warnings #用于忽略警告信息
warnings.filterwarnings("ignore") # 忽略所有警告信息
# --- 1. 默认参数的随机森林 ---
# 评估基准模型,这里确实不需要验证集
print("--- 1. 默认参数随机森林 (训练集 -> 测试集) ---")
import time # 这里介绍一个新的库,time库,主要用于时间相关的操作,因为调参需要很长时间,记录下会帮助后人知道大概的时长
start_time = time.time() # 记录开始时间
rf_model = RandomForestClassifier(random_state=42)
rf_model.fit(X_train, y_train) # 在训练集上训练
rf_pred = rf_model.predict(X_test) # 在测试集上预测
end_time = time.time() # 记录结束时间print(f"训练与预测耗时: {end_time - start_time:.4f} 秒")
print("\n默认随机森林 在测试集上的分类报告:")
print(classification_report(y_test, rf_pred))
print("默认随机森林 在测试集上的混淆矩阵:")
print(confusion_matrix(y_test, rf_pred))
# umap-learn 是一个用于降维和可视化的库,特别适合处理高维数据。它使用了一种基于流形学习的算法,可以有效地将高维数据嵌入到低维空间中,同时保持数据的局部结构。
# !pip install umap-learn -i https://pypi.tuna.tsinghua.edu.cn/simple# 确保这些库已导入,你的原始代码中可能已经包含了部分
import time
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler # 特征缩放
from sklearn.decomposition import PCA # 主成分分析
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA # 线性判别分析
# UMAP 需要单独安装: pip install umap-learn
import umap # 如果安装了 umap-learn,可以这样导入from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report, confusion_matrix# 你的 X_train, X_test, y_train, y_test 应该已经根据你的代码准备好了
# 我们假设你的随机森林模型参数与基准模型一致,以便比较降维效果
# rf_params = {'random_state': 42} # 如果你的基准模型有其他参数,也在这里定义
# 为了直接比较,我们使用默认的 RandomForestClassifier 参数,除了 random_statePCA主成分分析
可以将PCA视为:
1. 对数据进行均值中心化。
2. 对中心化后的数据进行SVD。
3. 使用SVD得到的右奇异向量 `V` 作为主成分方向。
4. 使用奇异值 `S` 来评估每个主成分的重要性(解释的方差)。
5. 使用 U*S(或 X_centered * V)来获得降维后的数据表示。
PCA主要适用于那些你认为最重要的信息可以通过数据方差来捕获,并且数据结构主要是线性的情况。
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report, confusion_matrix
import time
import numpy as np # 确保numpy导入# 假设 X_train, X_test, y_train, y_test 已经准备好了print(f"\n--- 2. PCA 降维 + 随机森林 (不使用 Pipeline) ---")# 步骤 1: 特征缩放
scaler_pca = StandardScaler()
X_train_scaled_pca = scaler_pca.fit_transform(X_train)
X_test_scaled_pca = scaler_pca.transform(X_test) # 使用在训练集上fit的scaler# 步骤 2: PCA降维
# 选择降到10维,或者你可以根据解释方差来选择,例如:
pca_expl = PCA(random_state=42)
pca_expl.fit(X_train_scaled_pca)
cumsum_variance = np.cumsum(pca_expl.explained_variance_ratio_)
n_components_to_keep_95_var = np.argmax(cumsum_variance >= 0.95) + 1
print(f"为了保留95%的方差,需要的主成分数量: {n_components_to_keep_95_var}")

# 我们测试下降低到10维的效果
n_components_pca = 10
pca_manual = PCA(n_components=n_components_pca, random_state=42)X_train_pca = pca_manual.fit_transform(X_train_scaled_pca)
X_test_pca = pca_manual.transform(X_test_scaled_pca) # 使用在训练集上fit的pcaprint(f"PCA降维后,训练集形状: {X_train_pca.shape}, 测试集形状: {X_test_pca.shape}")
start_time_pca_manual = time.time()
# 步骤 3: 训练随机森林分类器
rf_model_pca = RandomForestClassifier(random_state=42)
rf_model_pca.fit(X_train_pca, y_train)# 步骤 4: 在测试集上预测
rf_pred_pca_manual = rf_model_pca.predict(X_test_pca)
end_time_pca_manual = time.time()print(f"手动PCA降维后,训练与预测耗时: {end_time_pca_manual - start_time_pca_manual:.4f} 秒")print("\n手动 PCA + 随机森林 在测试集上的分类报告:")
print(classification_report(y_test, rf_pred_pca_manual))
print("手动 PCA + 随机森林 在测试集上的混淆矩阵:")
print(confusion_matrix(y_test, rf_pred_pca_manual))
t-sne降维
这是一种与PCA截然不同的降维算法,尤其在理解其核心思想和适用场景上。
t-SNE:保持高维数据的局部邻域结构,用于可视化
PCA 的目标是保留数据的全局方差,而 t-SNE 的核心目标是在高维空间中相似的数据点,在降维后的低维空间中也应该保持相似(即彼此靠近),而不相似的点则应该相距较远。它特别擅长于将高维数据集投影到二维或三维空间进行可视化,从而揭示数据中的簇结构或流形结构。---深度学习可视化中很热门

总结一下:t-SNE是一种强大的非线性降维技术,主用于高维数据的可视化。它通过在低维空间中保持高维空间中数据点之间的局部相似性(邻域关系)来工作。与PCA关注全局方差不同,t-SNE 更关注局部细节。理解它的超参数(尤其是困惑度)和结果的正确解读方式非常重要。
from sklearn.manifold import TSNE
from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report, confusion_matrix
import time
import numpy as np
import matplotlib.pyplot as plt # 用于可选的可视化
import seaborn as sns # 用于可选的可视化# 假设 X_train, X_test, y_train, y_test 已经准备好了
# 并且你的 X_train, X_test 是DataFrame或Numpy Arrayprint(f"\n--- 3. t-SNE 降维 + 随机森林 ---")
print(" 标准 t-SNE 主要用于可视化,直接用于分类器输入可能效果不佳。")# 步骤 1: 特征缩放
scaler_tsne = StandardScaler()
X_train_scaled_tsne = scaler_tsne.fit_transform(X_train)
X_test_scaled_tsne = scaler_tsne.transform(X_test) # 使用在训练集上fit的scaler# 步骤 2: t-SNE 降维
# 我们将降维到与PCA相同的维度(例如10维)或者一个适合分类的较低维度。
# t-SNE通常用于2D/3D可视化,但也可以降到更高维度。
# 然而,降到与PCA一样的维度(比如10维)对于t-SNE来说可能不是其优势所在,
# 并且计算成本会显著增加,因为高维t-SNE的优化更困难。
# 为了与PCA的 n_components=10 对比,我们这里也尝试降到10维。
# 但请注意,这可能非常耗时,且效果不一定好。
# 通常如果用t-SNE做分类的预处理(不常见),可能会选择非常低的维度(如2或3)。# n_components_tsne = 10 # 与PCA的例子保持一致,但计算量会很大
n_components_tsne = 2 # 更典型的t-SNE用于分类的维度,如果想快速看到结果# 如果你想严格对比PCA的10维,可以将这里改为10,但会很慢# 对训练集进行 fit_transform
tsne_model_train = TSNE(n_components=n_components_tsne,perplexity=30, # 常用的困惑度值n_iter=1000, # 足够的迭代次数init='pca', # 使用PCA初始化,通常更稳定learning_rate='auto', # 自动学习率 (sklearn >= 1.2)random_state=42, # 保证结果可复现n_jobs=-1) # 使用所有CPU核心
print("正在对训练集进行 t-SNE fit_transform...")
start_tsne_fit_train = time.time()
X_train_tsne = tsne_model_train.fit_transform(X_train_scaled_tsne)
end_tsne_fit_train = time.time()
print(f"训练集 t-SNE fit_transform 完成,耗时: {end_tsne_fit_train - start_tsne_fit_train:.2f} 秒")# 对测试集进行 fit_transform
# 再次强调:这是独立于训练集的变换
tsne_model_test = TSNE(n_components=n_components_tsne,perplexity=30,n_iter=1000,init='pca',learning_rate='auto',random_state=42, # 保持参数一致,但数据不同,结果也不同n_jobs=-1)
print("正在对测试集进行 t-SNE fit_transform...")
start_tsne_fit_test = time.time()
X_test_tsne = tsne_model_test.fit_transform(X_test_scaled_tsne) # 注意这里是 X_test_scaled_tsne
end_tsne_fit_test = time.time()
print(f"测试集 t-SNE fit_transform 完成,耗时: {end_tsne_fit_test - start_tsne_fit_test:.2f} 秒")print(f"t-SNE降维后,训练集形状: {X_train_tsne.shape}, 测试集形状: {X_test_tsne.shape}")start_time_tsne_rf = time.time()
# 步骤 3: 训练随机森林分类器
rf_model_tsne = RandomForestClassifier(random_state=42)
rf_model_tsne.fit(X_train_tsne, y_train)# 步骤 4: 在测试集上预测
rf_pred_tsne_manual = rf_model_tsne.predict(X_test_tsne)
end_time_tsne_rf = time.time()print(f"t-SNE降维数据上,随机森林训练与预测耗时: {end_time_tsne_rf - start_time_tsne_rf:.4f} 秒")
total_tsne_time = (end_tsne_fit_train - start_tsne_fit_train) + \(end_tsne_fit_test - start_tsne_fit_test) + \(end_time_tsne_rf - start_time_tsne_rf)
print(f"t-SNE 总耗时 (包括两次fit_transform和RF): {total_tsne_time:.2f} 秒")print("\n手动 t-SNE + 随机森林 在测试集上的分类报告:")
print(classification_report(y_test, rf_pred_tsne_manual))
print("手动 t-SNE + 随机森林 在测试集上的混淆矩阵:")
print(confusion_matrix(y_test, rf_pred_tsne_manual))
线性判别分析 (Linear Discriminant Analysis, LDA)
1. 核心定义与目标:
线性判别分析 (LDA) 是一种经典的有监督降维算法,也常直接用作分类器。作为降维技术时,其核心目标是找到一个低维特征子空间(即原始特征的线性组合),使得在该子空间中,不同类别的数据点尽可能地分开(类间距离最大化),而同一类别的数据点尽可能地聚集(类内方差最小化)。
2. 工作原理简述:
LDA 通过最大化“类间散布矩阵”与“类内散布矩阵”之比的某种度量(例如它们的行列式之比)来实现其降维目标。它寻找能够最好地区分已定义类别的投影方向。
3. 关键特性:
* 有监督性 (Supervised): 这是 LDA 与 PCA 最根本的区别。LDA 在降维过程中必须使用数据的类别标签 (y) 来指导投影方向的选择,目的是优化类别的可分离性。
* 降维目标维度 (Number of Components): LDA 降维后的维度(即生成的判别特征的数量)有一个严格的上限:min(n_features, n_classes - 1)。
* n_features:原始特征的数量。
* n_classes:类别标签 (y) 中不同类别的数量。
* 这意味着,例如,对于一个二分类问题 (n_classes = 2),LDA 最多能将数据降至 1 维。如果有 5 个类别,最多能降至 4 维(前提是原始特征数不少于4)。这个特性直接源于其优化目标。
* 线性变换 (Linear Transformation):与 PCA 类似,LDA 也是一种线性方法。它找到的是原始特征的线性组合来形成新的、具有判别能力的低维特征(称为判别向量或判别成分)。
* 数据假设 (Assumptions):
* 理论上,LDA 假设每个类别的数据服从多元高斯分布。
* 理论上,LDA 假设所有类别具有相同的协方差矩阵。
* 在实践中,即使这些假设不完全满足,LDA 通常也能表现良好,尤其是在类别大致呈椭球状分布且大小相似时。
4. 输入要求:
* 特征 (X):数值型特征。如果存在类别型特征,通常需要先进行预处理(如独热编码)。
* 标签 (y):一维的、代表类别身份的数组或 Series(例如 [0, 1, 0, 2, 1])。LDA 不需要标签进行独热编码。标签的类别数量直接决定了降维的上限。
5. 与特征 (X) 和标签 (y) 的关系:
* LDA 的降维过程和结果直接由标签y中的类别结构驱动。它试图找到最能区分这些由 y 定义的类别的特征组合。
* 原始特征 X 提供了构建这些判别特征的原材料。特征 X 的质量和相关性会影响 LDA 的效果,但降维的“方向盘”是由 y 控制的。
6. 优点:
* 直接优化类别可分性,非常适合作为分类任务的预处理步骤,往往能提升后续分类器的性能。
* 计算相对高效。
* 生成的低维特征具有明确的判别意义。
7. 局限性与注意事项:
* 降维的维度受限于 n_classes - 1,这可能比 PCA 能达到的降维程度低很多,尤其是在类别数较少时。
* 作为线性方法,可能无法捕捉数据中非线性的类别结构。如果类别边界是非线性的,LDA 效果可能不佳。
* 对数据的高斯分布和等协方差假设在理论上是存在的,极端偏离这些假设可能影响性能。
* 如果类别在原始特征空间中本身就高度重叠,LDA 的区分能力也会受限。
8. 适用场景:
* 当目标是提高后续分类模型的性能时,LDA 是一个强有力的降维工具。
* 当类别信息已知且被认为是区分数据的主要因素时。
* 当希望获得具有良好类别区分性的低维表示时,尤其可用于数据可视化(如果能降到2D或3D)。
简而言之,LDA 是一种利用类别标签信息来寻找最佳类别分离投影的降维方法,其降维的潜力直接与类别数量挂钩。
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report, confusion_matrix
import time
import numpy as np
# 假设你已经导入了 matplotlib 和 seaborn 用于绘图 (如果需要)
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D # 如果需要3D绘图
import seaborn as snsprint(f"\n--- 4. LDA 降维 + 随机森林 ---")# 步骤 1: 特征缩放
scaler_lda = StandardScaler()
X_train_scaled_lda = scaler_lda.fit_transform(X_train)
X_test_scaled_lda = scaler_lda.transform(X_test) # 使用在训练集上fit的scaler# 步骤 2: LDA 降维
n_features = X_train_scaled_lda.shape[1]
if hasattr(y_train, 'nunique'):n_classes = y_train.nunique()
elif isinstance(y_train, np.ndarray):n_classes = len(np.unique(y_train))
else:n_classes = len(set(y_train))max_lda_components = min(n_features, n_classes - 1)# 设置目标降维维度
n_components_lda_target = 10if max_lda_components < 1:print(f"LDA 不适用,因为类别数 ({n_classes})太少,无法产生至少1个判别组件。")X_train_lda = X_train_scaled_lda.copy() # 使用缩放后的原始特征X_test_lda = X_test_scaled_lda.copy() # 使用缩放后的原始特征actual_n_components_lda = n_featuresprint("将使用缩放后的原始特征进行后续操作。")
else:# 实际使用的组件数不能超过LDA的上限,也不能超过我们的目标(如果目标更小)actual_n_components_lda = min(n_components_lda_target, max_lda_components)if actual_n_components_lda < 1: # 这种情况理论上不会发生,因为上面已经检查了 max_lda_components < 1print(f"计算得到的实际LDA组件数 ({actual_n_components_lda}) 小于1,LDA不适用。")X_train_lda = X_train_scaled_lda.copy()X_test_lda = X_test_scaled_lda.copy()actual_n_components_lda = n_featuresprint("将使用缩放后的原始特征进行后续操作。")else:print(f"原始特征数: {n_features}, 类别数: {n_classes}")print(f"LDA 最多可降至 {max_lda_components} 维。")print(f"目标降维维度: {n_components_lda_target} 维。")print(f"本次 LDA 将实际降至 {actual_n_components_lda} 维。")lda_manual = LinearDiscriminantAnalysis(n_components=actual_n_components_lda, solver='svd')X_train_lda = lda_manual.fit_transform(X_train_scaled_lda, y_train)X_test_lda = lda_manual.transform(X_test_scaled_lda)print(f"LDA降维后,训练集形状: {X_train_lda.shape}, 测试集形状: {X_test_lda.shape}")start_time_lda_rf = time.time()
# 步骤 3: 训练随机森林分类器
rf_model_lda = RandomForestClassifier(random_state=42)
rf_model_lda.fit(X_train_lda, y_train)# 步骤 4: 在测试集上预测
rf_pred_lda_manual = rf_model_lda.predict(X_test_lda)
end_time_lda_rf = time.time()print(f"LDA降维数据上,随机森林训练与预测耗时: {end_time_lda_rf - start_time_lda_rf:.4f} 秒")print("\n手动 LDA + 随机森林 在测试集上的分类报告:")
print(classification_report(y_test, rf_pred_lda_manual))
print("手动 LDA + 随机森林 在测试集上的混淆矩阵:")
print(confusion_matrix(y_test, rf_pred_lda_manual))

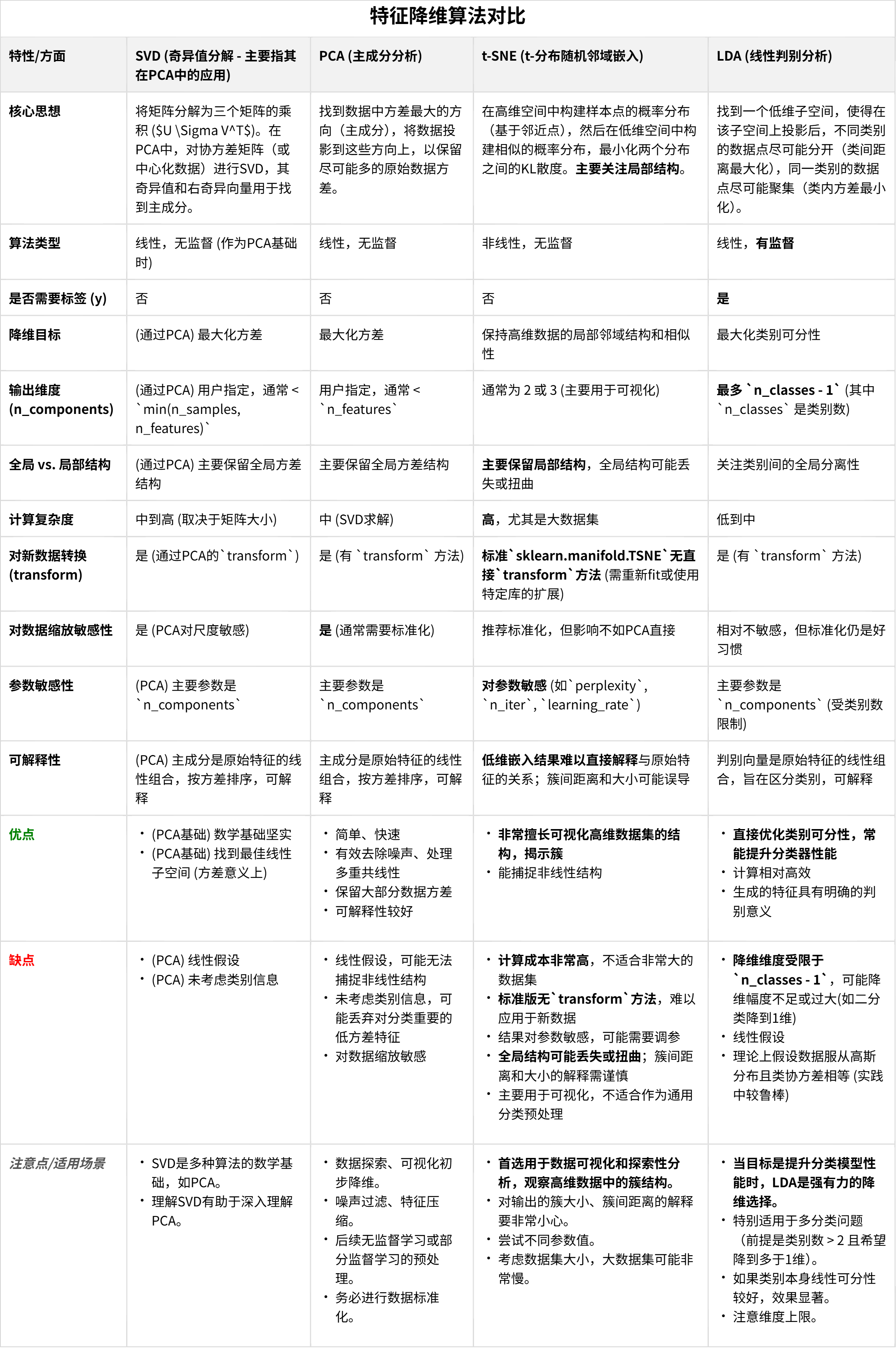
还有一些其他的降维方式,也就是最重要的词向量的加工,我们未来再说
作业:
自由作业:探索下什么时候用到降维?降维的主要应用?或者让ai给你出题,群里的同学互相学习下。可以考虑对比下在某些特定数据集上t-sne的可视化和pca可视化的区别。
降维(Dimensionality Reduction)是机器学习和数据分析中的关键技术,主要用于解决高维数据带来的计算复杂度、噪声干扰和可视化难题。
什么时候用到降维
-
高维数据导致计算成本高
当特征维度极高(如文本、图像、基因数据)时,模型训练速度显著下降,降维可减少计算资源消耗。 -
缓解维度灾难(Curse of Dimensionality)
高维空间中数据稀疏,模型容易过拟合,降维可提升模型泛化能力。 -
数据可视化需求
将高维数据压缩到2D/3D,便于人类直观理解数据分布(如客户分群、异常检测)。 -
特征相关性高或冗余
当多个特征高度相关(如温度与季节)时,降维可提取核心信息。 -
数据去噪
通过保留主要成分(如PCA),过滤噪声或无关特征。
降维的主要应用场景
1. 数据可视化
目标:将高维数据映射到 2D/3D 空间,直观展示数据分布。
药物场景:
-
使用 t-SNE 或 UMAP 将药物的成分、剂型、强度等特征降维,可视化不同聚类的药物群体。
-
示例:横轴表示主成分 1(如 “抗生素类成分”),纵轴表示主成分 2(如 “口服剂型”),可清晰区分不同类型药物的聚集区域,发现空白领域(如 “注射型抗生素” vs “口服降压药”)。
2. 特征去噪与压缩
目标:去除冗余特征,保留关键信息,提升模型效率。
药物场景:
-
主成分分析(PCA):对文本向量化后的高维特征(如 TF-IDF 矩阵)进行降维,保留前 100 个主成分,减少计算量。
-
应用:
-
加速 K-Means 聚类,避免因高维导致的 “距离失效” 问题。
-
提升随机森林等模型的训练速度,同时避免过拟合。
-
3. 无监督学习前预处理
目标:为聚类、异常检测等无监督任务提供更优质的特征空间。
药物场景:
-
K-Means 聚类前降维:
-
对 “成分 + 剂型 + 强度” 的高维特征降维后,聚类结果更聚焦于核心差异(如 “高剂量注射剂” vs “低剂量片剂”)。
-
-
异常检测:
-
使用 Autoencoder 降维后,在低维空间中更容易识别罕见药物配方(如成分独特的复方制剂)。
-
4. 特征相关性分析
目标:揭示特征间的潜在关联,辅助业务洞察。
药物场景:
-
因子分析(FA):发现隐藏的 “因子”(如 “抗炎因子” 由多个成分共同构成),解释药物分类的本质驱动因素。
-
应用:
-
识别核心成分组合(如 “布洛芬 + 对乙酰氨基酚” 常出现在止痛药中),指导新药配方设计。
-
5. 推荐系统与市场空白挖掘
目标:在低维空间中计算药物 / 制造商的相似性,预测潜在需求。
药物场景:
-
矩阵分解:将 “制造商 - 药物” 高维交互矩阵降维,预测制造商未生产但可能相关的药物类型。
-
示例:某制造商擅长生产 “口服抗生素片剂”,降维后发现其邻近区域存在 “注射型抗生素” 空白,可作为研发方向。
相关文章:

【DAY21】 常见的降维算法
内容来自浙大疏锦行python打卡训练营 浙大疏锦行 目录 PCA主成分分析 t-sne降维 线性判别分析 (Linear Discriminant Analysis, LDA) 作业: 什么时候用到降维 降维的主要应用场景 知识点回顾: PCA主成分分析t-sne降维LDA线性判别 通常情况下,…...
)
Linux面试题集合(3)
一秒刷新一次某个进程的状况 top -d 1 -p pid ’显示pid为1、2、3的进程的状况 top -p 1,2,3(按上键选择某个进程) 强制杀死进程 kill -9 pid 说一下ps和top命令的区别 ps命令只能显示执行瞬间的进程状态 top命令实时跟进进程状态 你在工作中什么情况下…...

Pytorch实现常用代码笔记
Pytorch实现常用代码笔记 基础实现代码其他代码示例Network ModulesLossUtils 基础实现代码 参考 深度学习手写代码 其他代码示例 Network Modules Pytorch实现Transformer代码示例 Loss PyTorch实现CrossEntropyLoss示例 Focal Loss 原理详解及 PyTorch 代码实现 PyTorc…...

vscode vue 项目 css 颜色调色版有两个
vue 项目 css 颜色调色版有两个,不知道是哪个插件冲突了。 这个用着很别扭,一个个插件删除后发现是 Vue - Official 这个插件问题,删了就只有一个调色版了。...

MySQL刷题相关简单语法集合
去重 distinct 关键字 eg. :select distinct university from user_profile 返回行数限制: limit关键字 eg. :select device_id from user_profile limit 2 返回列重命名:as 关键字 eg.:select device_id as user_in…...

MySQL多条件查询深度解析
一、业务场景引入 在数据分析场景中,我们经常会遇到需要从多个维度筛选数据的需求。例如,某教育平台运营团队希望同时查看"山东大学"的所有学生以及所有"男性"用户的详细信息,包括设备ID、性别、年龄和GPA数据ÿ…...
调度逻辑)
RT Thread FinSH(msh)调度逻辑
文章目录 概要FinSH功能FinSH调度逻辑细节小结 概要 RT-Thread(Real-Time Thread)作为一款开源的嵌入式实时操作系统,在嵌入式设备领域得到了广泛应用。 该系统不仅具备强大的任务调度功能,还集成了 FinSH命令行系统,…...

安装nerdctl和buildkitd脚本命令
#!/bin/bash set -euo pipefail # 检查是否以root权限运行 if [ "$(id -u)" -ne 0 ]; then echo "错误:请使用root权限或sudo运行本脚本" >&2 exit 1 fi # 检测openEuler系统(兼容大小写) detect_distrib…...

HTTP与HTTPS协议的核心区别
HTTP与HTTPS协议的核心区别 数据传输安全性 HTTP采用明文传输,数据易被窃听或篡改(如登录密码、支付信息),而HTTPS通过SSL/TLS协议对传输内容加密,确保数据完整性并防止中间人攻击。例如,HTTPS会生成对称加…...

51单片机仿真突然出问题
最近发现仿真出问题了,连最简单的程序运行结果都不对,比如,左移位<<,如果写P1 << 1;则没有问题,但写成P1 << cnt;就不对(cnt已经定义过,而且赋了初值&…...
超市管理系统 (正式版)(指针)(数据结构)(清屏操作)(文件读写)(网页版预告)(html)(js)(json))
(C语言)超市管理系统 (正式版)(指针)(数据结构)(清屏操作)(文件读写)(网页版预告)(html)(js)(json)
目录 前言: 源代码: product.h product.c fileio.h fileio.c main.c json_export.h json_export.c tasks.json idex.html script.js 相关步骤: 第一步: 第二步: 第三步: 第四步: 第五步…...

uni-app小程序登录后…
前情 最近新接了一个全新项目,是类似商城的小程序项目,我负责从0开始搭建小程序,我选用的技术栈是uni-app技术栈,其中就有一个用户登录功能,小程序部分页面是需要登录才可以查看的,对于未登录的用户需要引…...

从零开始理解Jetty:轻量级Java服务器的入门指南
目录 一、Jetty是什么?先看一个生活比喻 二、5分钟快速入门:搭建你的第一个Jetty服务 步骤1:Maven依赖配置 步骤2:编写简易Servlet(厨房厨师) 步骤3:组装服务器(餐厅开业准备&am…...

如何免费在线PDF转换成Excel
咱们工作中是不是经常遇到这种头疼事儿?辛辛苦苦从别人那里拿到PDF文件,想改个数据调个格式,结果发现根本没法直接编辑! 数据被困住:PDF表格无法直接计算/筛选,手动录入太反人类! 格式大崩坏&…...

StarRocks MCP Server 开源发布:为 AI 应用提供强大分析中枢
过去,开发者要让大模型(LLM)使用数据库查询数据,往往需要开发专属插件、设计复杂的接口或手动构建 Prompt,这不仅费时费力,而且很难在不同模型之间复用。StarRocks MCP Server 提供了一个“通用适配器”接口…...

Vue百日学习计划Day21-23天详细计划-Gemini版
总目标: 在 Day 21-23 完成 Vue.js 的介绍学习、环境搭建,并成功运行第一个 Vue 3 项目,理解其基本结构。 Day 21: Vue.js 介绍与概念理解 (~3 小时) 本日目标: 理解 Vue.js 是什么、渐进式框架的概念以及选择 Vue 的原因。初步了解 Vite 是什么及其作用…...

JS逆向-某易云音乐下载器
文章目录 介绍下载链接Robots文件搜索功能JS逆向**函数a:生成随机字符串****函数b:AES-CBC加密****函数c:RSA公钥加密** 歌曲下载总结 介绍 在某易云音乐中,很多歌曲听是免费的,但下载需要VIP,此程序旨在“…...

Qt与Hid设备通信
什么是HID? HID(Human Interface Device)是直接与人交互的电子设备,通过标准化协议实现用户与计算机或其他设备的通信,典型代表包括键盘、鼠标、游戏手柄等。 为什么HID要与qt进行通信? 我这里的应…...

QT使用QXlsx读取excel表格中的图片
前言 读取excel表格中的图片的需求比较小众,QXlsx可以操作excel文档,进行图片读取、插入操作,本文主要分享单独提取图片和遍历表格提取文字和图片。 源码下载 github 开发环境准备 把下载的代码中的QXlsx目录,整个拷贝到所创建…...

二叉树进阶
一、二叉搜索树 1.二叉搜索树的概念 二叉搜索树又称二叉排序树,它也可以是一棵空树,或是具备以下性质的树: 1.1 若它的左子树不为空,则它左子树上所有节点的值都小于根节点的值。 1.2 若它的右子树不为空,则它右子…...

腾讯 CodeBuddy 杀入 AI 编程赛道,能否撼动海外工具霸主地位?
在 AI 编程助手领域,海外的 Cursor 等工具风头正劲,如今腾讯带着 CodeBuddy 隆重登场,国产 AI 编程助手能否借其之力崛起?让我们一探究竟。 官网: 腾讯云代码助手 CodeBuddy - AI 时代的智能编程伙伴 实战安装教程 …...
——海康威视相机测试)
项目QT+ffmpeg+rtsp(二)——海康威视相机测试
文章目录 前言一、验证RTSP地址的有效性1.1 使用VLC播放器验证1.2 使用FFmpeg命令行验证1.3 使用Python代码检查网络连接1.4 检查摄像头Web界面1.5 使用RTSP客户端工具二、关于IPV4的地址2.1 原来2.1.1 原因2.2 解决2.3 显示前言 昨晚拿到一个海康威视的相机,是连接上了交换机…...

vscode用python开发maya联动调试设置
如何在VScode里编写Maya Python脚本_哔哩哔哩_bilibili1 包括1,maya的python全面在vscode支持,2,通过mayacode发送到maya,3同步调试 import maya.cmds as cmds 1、让 maya.cmds编译通过 下载Autodesk_Maya_2018_6_Update_DEVK…...

Postman遇到脚本不支持replaceIn函数
目录: 1、问题现象2、代码处理3、执行结果 1、问题现象 2、代码处理 function replaceVariables(template) {// 获取所有变量(环境变量全局变量)const variables pm.environment.toObject();const globalVars pm.globals.toObject();const…...
:移情阶段的用户触达策略——从社交平台到精准访谈)
精益数据分析(64/126):移情阶段的用户触达策略——从社交平台到精准访谈
精益数据分析(64/126):移情阶段的用户触达策略——从社交平台到精准访谈 在创业的移情阶段,精准找到目标用户并开展深度访谈是验证需求的关键。今天,我们结合《精益数据分析》中的方法论,探讨如何利用Twit…...

turn.js与 PHP 结合使用来实现 PDF 文件的页面切换效果
将 Turn.js 与 PHP 结合使用来实现 PDF 文件的页面切换效果,你需要一个中间步骤将 PDF 转换为 Turn.js 可以处理的格式(如 HTML 页面或图片)。以下是实现这一功能的步骤和示例代码: 步骤 1: 安装必要的库 首先,你需要…...

SQL Server 与 Oracle 常用函数对照表
一、字符串处理函数 SQL Server 函数SQL Server 实例Oracle 函数Oracle 实例输出结果CONCATSELECT CONCAT(A, B, C);CONCATSELECT CONCAT(A, B) FROM DUAL;ABC(SQL) AB(Oracle)SUBSTRINGSELECT SUBSTRING(Hello, 2, 3);SUBSTRSEL…...

数据治理新纪元:全面解读TSDDITAI系列评估规范
在数字化转型的浪潮中,数据已成为驱动业务增长和创新的核心要素。然而,如何确保大数据产品、企业、人才及数据资源的优质与合规,成为了摆在行业面前的重大课题。为此,TSDDITAI系列评估规范应运而生,为大数据产业的健康…...

电子电路:什么是色环电阻器,怎么识别和计算阻值?
识别和计算色环电阻的阻值需要掌握颜色编码规则和基本步骤。以下是具体方法及窍门: 一、色环电阻的基本规则 色环数量: 4环电阻:前2环为有效数字,第3环为倍乘(10ⁿ),第4环为误差。5环电阻:前3环为有效数字,第4环为倍乘,第5环为误差。6环电阻(较少见):前3环为有效数…...

UE中的各种旋转
1 直接修改第三人称玩家的角度 注意不是修改玩家的actor或者pawn,而是修改controller的旋转 这只会修改相机的方向,不会修改角色的方向,因为第三人控制器的根物体不受controller控制,而相机弹簧臂受controller控制 如果修改角色…...

游戏引擎学习第289天:将视觉表现与实体类型解耦
回顾并为今天的工作设定基调 我们正在继续昨天对代码所做的改动。我们已经完成了“脑代码(brain code)”的概念,它本质上是一种为实体构建的自组织控制器结构。现在我们要做的是把旧的控制逻辑迁移到这个新的结构中,并进一步测试…...

NestJS——日志、NestJS-logger、pino、winston、全局异常过滤器
个人简介 👀个人主页: 前端杂货铺 🙋♂️学习方向: 主攻前端方向,正逐渐往全干发展 📃个人状态: 研发工程师,现效力于中国工业软件事业 🚀人生格言: 积跬步…...

list重点接口及模拟实现
list功能介绍 c中list是使用双向链表实现的一个容器,这个容器可以实现。插入,删除等的操作。与vector相比,vector适合尾插和尾删(vector的实现是使用了动态数组的方式。在进行头删和头插的时候后面的数据会进行挪动,时…...

Linux | mdadm 创建软 RAID
注:本文为 “Linux mdadm RAID” 相关文章合辑。 略作重排,未整理去重。 如有内容异常,请看原文。 Linux 下用 mdadm 创建软 RAID 以及避坑 喵ฅ・ﻌ・ฅ Oct 31, 2023 前言 linux 下组软 raid 用 mdadm 命令,multi…...

迁移学习:解锁AI高效学习与泛化能力的密钥
前言 在人工智能(AI)技术日新月异的今天,迁移学习(Transfer Learning)作为一项革命性技术,正深刻改变着机器学习领域的格局。 它不仅让模型能够像人类一样“举一反三”,更在加速模型开发、提升性…...

前端-HTML元素
目录 HTML标签是什么? 什么是HTML元素? HTML元素有哪些分类方法? 什么是HTML头部元素 更换路径 注:本文以leetbook为基础 HTML标签是什么? HTML标签是HTML语言中最基本单位和重要组成部分 虽然它不区分大小写&a…...

STM32之蜂鸣器和按键
一、蜂鸣器的原理与应用 基本概念 蜂鸣器是一种一体化结构的电子讯响器,采用直流电压供电,广泛应用于计算机、打印机、复印机、报警器、电子玩具、汽车电子设备、电话机、定时器等电子产品中作发声器件。 工作原理 蜂鸣器一般分为两类:有源…...

H3C UIS 超融合管理平台原理解读以及日常运维实操与故障处理
前言:超融合(Hyper-Converged Infrastructure, HCI)是将计算、存储、网络和虚拟化资源整合到统一硬件平台中,并通过软件定义技术实现资源池化与灵活管理的架构。H3C(新华三)和华为作为国内领先的ICT厂商&am…...

【强化学习】#5 时序差分学习
主要参考学习资料:《强化学习(第2版)》[加]Richard S.Suttion [美]Andrew G.Barto 著 文章源文件:https://github.com/INKEM/Knowledge_Base 缩写说明 DP:动态规划GPI:广义策略迭代MC:蒙特卡洛…...

Day119 | 灵神 | 二叉树 | 二叉树的最近共公共祖先
Day119 | 灵神 | 二叉树 | 二叉树的最近共公共祖先 236.二叉树的最近共公共祖先 236. 二叉树的最近公共祖先 - 力扣(LeetCode) 思路: 二叉树的最近公共祖先【基础算法精讲 12】_哔哩哔哩_bilibili 首先我们采用后序遍历 递归函数返回值…...

Elasticsearch 性能优化面试宝典
Elasticsearch 性能优化面试宝典 🚀 目录 设计调优 🏗️写入调优 ⚡查询调优 🔍综合设计 💎总结 📝设计调优 🏗️ 面试题1:索引设计优化 题目: 假设需要设计一个电商商品索引,日增数据量1TB,要求支持多维度查询(名称、分类、价格区间)。请说明索引设计的关…...

mysql数据库-中间件MyCat
1. MyCat简介 在整个 IT 系统架构中,数据库是非常重要,通常又是访问压力较大的一个服务,除了在程序开发的本身做优化,如: SQL 语句优化、代码优化,数据库的处理本身优化也是非常重要的。主从、热备、分表分…...

制作大风车动画
这个案例的风车旋转应用了图形变换来实现,速度和缩放比例应用slider来实现,其中图片的速度,图片大小的信息通过State来定义变量管理,速度和和缩放比例的即时的值通过Prop来管理。 1. 案例效果截图 2. 案例运用到的知识点 2.1. 核…...

嘉立创EDA成图:文件管理
在 工程 文 件夹 中 新建 一 个以 自 己选 手 编号 后 8 位 命名 的 项目 工 程文 件 按要求名字命名(这里以日期命名) 选择半离线或者全离线 添加路径 1. 新建 图 纸文 件 ,文 件 名为 moban.elibz; 点击保存之后打开文件夹有这…...

Vim编辑器命令模式操作指南
Vim 的命令模式(即 Normal 模式)是 Vim 的核心操作模式,用于执行文本编辑、导航、搜索、保存等操作。以下是命令模式下的常用操作总结: 1. 模式切换 进入命令模式:在任何模式下按 Esc 键(可能需要多次按&a…...
openjdk17 c++源码垃圾回收安全点信号函数处理线程阻塞)
jvm安全点(一)openjdk17 c++源码垃圾回收安全点信号函数处理线程阻塞
1. 信号处理入口 JVM_HANDLE_XXX_SIGNAL 是 JVM 处理信号的统一入口,负责处理 SIGSEGV、SIGBUS 等信号。javaSignalHandler 是实际注册到操作系统的信号处理函数,直接调用 JVM_HANDLE_XXX_SIGNAL。 2. 安全点轮询页的识别 …...
)
手机打电话时由对方DTMF响应切换多级IVR语音应答(二)
手机打电话时由对方DTMF响应切换多级IVR语音应答(二) --本地AI电话机器人 一、前言 前面的篇章《手机打电话时由对方DTMF响应切换多级IVR语音应答(一)》中,我们从理论的角度论述了“根据对方按下DTMF值响应多级IVR”…...
)
【Java ee初阶】HTTP(2)
一、HTTP的方法 方法 说明 支持的HTTP协议版本 GET 获取资源 1.0、1.1 POST 传输实体主体 1.0、1.1 PUT 传输文件 1.0、1.1 HEAD 获得报文首部 1.0、1.1 DELETE 删除文件 1.0、1.1 OPTIONS 询问支持的方法 1.1 TRACE 追踪路径 1.1 CONNECT 要求用隧道…...
)
计算机视觉与深度学习 | Python实现EMD-SSA-VMD-LSTM-Attention时间序列预测(完整源码和数据)
EMD-SSA-VMD-LSTM-Attention 一、完整代码实现二、代码结构解析三、关键数学公式四、参数调优建议五、性能优化方向六、工业部署建议 以下是用Python实现EMD-SSA-VMD-LSTM-Attention时间序列预测的完整解决方案。该方案结合了四层信号分解技术与注意力增强的深度学习模型&#…...

Java 应用如何实现 HTTPS:加密数据传输的实用指南
Java 应用如何实现 HTTPS:加密数据传输的实用指南 在当今的互联网环境中,数据安全至关重要,HTTPS 作为加密的数据传输协议,为 Java 应用提供了安全通信的保障。本文将深入探讨 Java 应用如何实现 HTTPS,通过详细代码实…...
