数据结构进阶:AVL树与红黑树
目录
前言
AVL树
定义
结构
插入
AVL树插入的大致过程
更新平衡因子
旋转
右单旋
左单旋
左右双旋
右左双旋
实现
红黑树
定义
性质
结构
插入
实现
总结
前言
在学习了二叉搜索树之后,我们了解到其有个致命缺陷——当树的形状呈现出一边倒的情况时,搜索的效率会退化,由O(logN)退化到O(N)。

为了解决这个问题,前人发明了AVL树和红黑树用以解决这个问题,
二者本质就是时刻注意将树调整为平衡或近似平衡的状态,以保证二叉的结构,从而确保其功能的效率。区别就在于平衡的实现逻辑不同。
AVL树
定义
AVL树是一棵高度平衡的二叉树,要么是一棵空树,
要么是具备以下性质的二叉搜索树:左右子树都是AVL树,左右子树高度差的绝对值<=1。
为了方便计算高度差,我们在实现时引入了平衡因子(balance factor),用以记录左右子树的高度差。平衡因子 = 右子树高度 - 左子树高度。所以平衡因子的值就只能为0 / 1 / -1;分别表示平衡、右子树高一层、左子树高一层。当然平衡因子不是必须的,但有了它我们能够更好的观察AVL树。
为什么不要求高度差为0呢?显然,假如只有两个结点,就不可能存在此情况。
AVL树因其完全平衡性,使得其效率能够保持在O(logN),这就是控制平衡的回报,往下我们将学习插入时如何控制平衡。
结构
AVL树是BSTree(二叉搜索树)的改进,所以大体结构与前文是一致的,只不过需要在结点中维护一个平衡因子的变量,可直接参考实现即可。
插入
AVL树插入的大致过程
1.根据二叉搜索树的插入方法插入结点;
2.更新平衡因子;(新增结点影响祖先结点的高度,因此要从下往上更新到根的平衡因子。但未必会走到根,在中间就可能结束,具体情况具体分析)
2.更新过程中检查平衡因子是否有异常,有异常就要进行旋转,否则插入结束。(旋转的本质就是调整平衡,让较高的子树高度下降一层)
更新平衡因子
平衡因子 = 右子树高度 - 左子树高度(即在parent的左子树插入就-1,右子树插入就+1)。
更新后的结果决定是否继续向上更新。
【1】更新后为0,意味着原来是-1->0或1->0,即原来是一边高一边低,并且是在低的位置插入结点,对于parent而言子树高度不变,更新就结束了。
【2】更新后结果为1或-1,则意味着0->1或0->-1,即在parent两边高度相同的情况下插入,插入后仍符合要求,但parent的高度相当于增加1,会影响其祖先的左右子树高度差,于是需要继续向上更新。
【3】更新后结果为2或-2,则意味着1->2或-1->-2,即原来是一边高一边低,却在高的位置插入结点,此时parent的左右子树高度差不符合要求,要进行旋转调节平衡。旋转的本质是通过降低较高子树的一层高度而使左右高度差回到插入前的平衡状态,这样相当于parent子树高度不变,不会影响祖先,所以旋转后不需要再向上更新,可以直接结束。
【4】在【2】的情况不断向上更新直到根,根为+-1就结束了,为+-2则要旋转。
【2】【3】情况结合。

更新到根。

更新到中间位置结束。

旋转
旋转既要保持原来的结构,还要降低被旋树的高度。
但到底要怎么旋?还需分具体情况而论,共有四种情况:左/右单旋,左右/右左双旋。
插入后需要旋转的位置总共就4个,先分出两种大情况:要么在左子树,要么在右子树。
最后就可分为左子树的左,左子树的右,右子树的左,右子树的右。
看起来好像是笔者在自嗨,这总结的情况有点太抽象了。下面用图来展示。
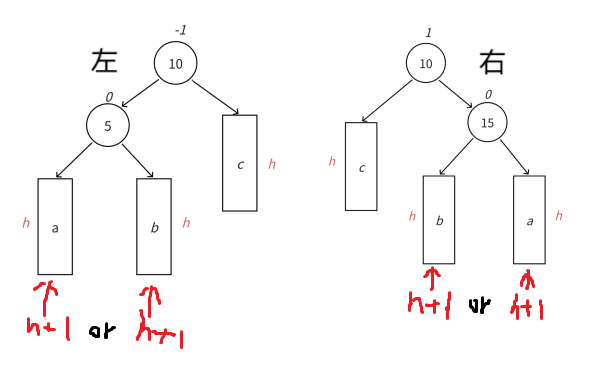
当然这还是抽象图,但至少能够直观看出4种情况了。(如若还是看不清,可以假设只有两个结点,把子树abc当作空结点来看)
具体怎么操作?君且安坐,听笔者慢慢道来。
右单旋
右单旋本质是以parent为根的右树往下压一层。
右单旋一共就三步,先以10为parent,5为subL,先把subL的右孩子subLR给parent的左,
再让parent作为subL的右孩子,
最后调整subL与parent->parent的关系。
本例较为简单,parent为根,根的父亲为空,调整步骤简单未在图中显示。
上述步骤在写代码时仍有许多细节问题,请读者自行探索。

左单旋
左单旋本质是以parent为根的左树往下压一层。
左单旋一共就三步,先以10为parent,5为subR,先把subR的右孩子subRL给parent的左,
再让parent作为subR的右孩子,
最后调整subR与parent->parent的关系。
本例较为简单,parent为根,根的父亲为空,调整步骤简单未在图中显示。
上述步骤在写代码时仍有许多细节问题,请读者自行探索。

左右双旋
双旋的本质是把subLR推举成根,让subL和parent分别做其左右孩子,然后自己的孩子也分别交给他们。(这里的subLR是8)
步骤:先左单旋subL,再右单旋parent。
无论新结点插入在e或f,最终e或f都要交给别人的,不影响旋转逻辑。

右左双旋
与左右双旋同理,
先右单旋subR,再左单旋parent
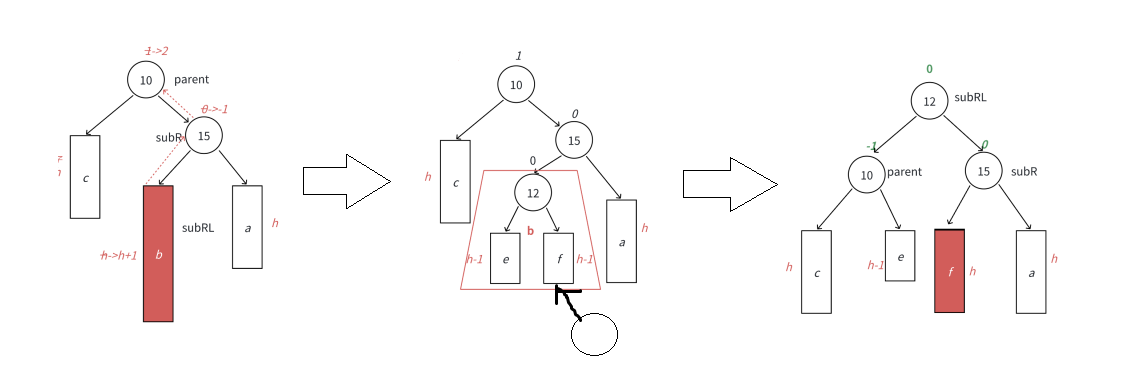
实现
#pragma once
#include <iostream>
#include <assert.h>
using namespace std;template<class K, class V>
struct AVLTree_Node
{typedef AVLTree_Node<K, V> Node;pair<K, V> _kv;Node* _left;Node* _right;Node* _parent;int _bf;AVLTree_Node(const pair<K, V> kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}
};template<class K, class V>
class AVLTree
{typedef AVLTree_Node<K, V> Node;public:bool insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = cur;while (cur){if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (kv.first < parent->_kv.first){parent->_left = cur;cur->_parent = parent;}else if (kv.first > parent->_kv.first){parent->_right = cur;cur->_parent = parent;}parent = cur->_parent;while (parent){if (parent->_left == cur)parent->_bf--;else if (parent->_right == cur)parent->_bf++;if (parent->_bf == 0)break;else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);return true;}else if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);return true;}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);return true;}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);return true;}}else{assert(false);}}return true;}bool find(const K& k){Node* cur = _root;while (cur){if (k < cur->_kv.first){cur = cur->_left;}else if (k > cur->_kv.first){cur = cur->_right;}else{return true;}}return false;}void Inorder(){_inorder(_root);}int Height(){return _Height(_root);}bool IsBalanceTree(){return _IsBalanceTree(_root);}
private:bool _IsBalanceTree(Node* root){// 空树也是AVL树if (nullptr == root)return true;// 计算pRoot结点的平衡因⼦:即pRoot左右⼦树的⾼度差int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);int diff = rightHeight - leftHeight;// 如果计算出的平衡因⼦与pRoot的平衡因⼦不相等,或者// // pRoot平衡因⼦的绝对值超过1,则⼀定不是AVL树if (abs(diff) >= 2){cout << root->_kv.first << "高度差异常" << endl;return false;} if(root->_bf != diff){cout << root->_kv.first << "平衡因子异常" << endl;return false;} // pRoot的左和右如果都是AVL树,则该树⼀定是AVL树return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);}void _inorder(Node* root){if (root == nullptr)return;_inorder(root->_left);cout << root->_kv.first<<" ";_inorder(root->_right);}int _Height(Node* root){if (root == nullptr)return 0;int left_height = _Height(root->_left);int right_height = _Height(root->_right);return left_height > right_height ? left_height + 1 : right_height + 1;}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if(subLR)subLR->_parent = parent;Node* pp = parent->_parent;subL->_right = parent;parent->_parent = subL;if (pp == nullptr){_root = subL;subL->_parent = nullptr;}else{if (pp->_left == parent){pp->_left = subL;}else if (pp->_right == parent){pp->_right = subL;}subL->_parent = pp;}parent->_bf = subL->_bf = 0;}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if(subRL)subRL->_parent = parent;Node* pp = parent->_parent;subR->_left = parent;parent->_parent = subR;if (pp == nullptr){_root = subR;subR->_parent = nullptr;}else{if (pp->_left == parent){pp->_left = subR;}else if (pp->_right == parent){pp->_right = subR;}subR->_parent = pp;}parent->_bf = subR->_bf = 0;}void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(subL);RotateR(parent);if (bf == 0){parent->_bf = 0;subL->_bf = 0;subLR->_bf = 0;}else if (bf == -1){parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}else if (bf == 1){subL->_bf = -1;parent->_bf = 0;subLR->_bf = 0;}else{assert(false);}}void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(subR);RotateL(parent);if (bf == 0){parent->_bf = 0;subR->_bf = 0;subRL->_bf = 0;}else if (bf == 1){parent->_bf = -1;subR->_bf = 0;subRL->_bf = 0;}else if (bf == -1){parent->_bf = 0;subR->_bf = 1;subRL->_bf = 0;}else{assert(false);}}
private:Node* _root = nullptr;
};
红黑树
红黑树是一棵更抽象一点的二叉搜索树,它既没有AVL树那么直观,平衡也不如AVL树那么完美,可是我们使用的map、set等容器底层都是用红黑树实现的。
这就很奇怪了,接下来便让我们一探究竟。
定义
红黑树是一棵空树或是一颗满足以下原则的二叉搜索树:
【1】结点不是红色就是黑色
【2】根节点必须为黑色
【3】红色结点的孩子必须是黑色结点或空,即红色不能连续
【4】从任意结点出发,到达其所有NULL结点的简单路径上,黑色结点数量相同
性质
上面的条件决定了红黑树的性质:
【1】最长路径的长度 <= 最短路径的长度的2倍
先根据[原则4]极端假设,最短路径有bh个黑色结点
再根据[原则2][原则3]可知,红色不能连续,极端场景下,最长路径由一黑一红间隔构成,那么最长路径上的结点个数就为2*bh
最后综合所有原则,理论上最短路径皆为黑色,最长路径一黑一红,不是每棵树都能有的极端情况。假设任意路径上的结点个数为x,则bh <= x <= 2*bh
 (假设极端情况)
(假设极端情况)
【2】插入时只能插入红色结点
假设插入的是黑色,那么根据[原则4],任意结点出发到其所有null的路径上,黑色结点数量相同。在某一支单独插入结点,会影响到各支上的黑色结点个数相等的情况,难以调整。
而反之插入红色结点,不违反[原则4],但可能违反[原则3]红色结点不能连续。但此时,并不会影响到其他支,只需要在本支上调整颜色即可。
为了不大动干戈,调整所有分支,因此不能插入黑色结点,只能插入影响规模小,易于调整的红色结点。而且若在黑色结点下插入,符合任一原则,不需要进行任何调整,也能提高效率。
【3】效率
已知最长路径<=最短路径的2倍,那么如果N为结点总个数,最短路径的高度为h,最长路径的高度为2*h,则满足2^h - 1 <= N <= 2^2h - 1。可推出 h = logN,最坏情况走最长路径也只为2*logN,所以时间复杂度还是O(logN)。
红⿊树的表达相对AVL树要抽象⼀些,AVL树通过⾼度差直观的控制了平衡。红⿊树通过4条规则的颜⾊约束,间接的实现了近似平衡,但二者效率仍在同⼀档次,相对⽽⾔,插⼊相同数量的结点,红⿊树的旋转次数是更少的,因为他对平衡的控制没那么严格。而旋转次数少了就使得效率上优于AVL树,多往下走几层并不会显著影响其效率。所以,也就回答了刚开始的疑问,set、map当然是用更高效的红黑树实现了。
结构
结点需要新增一个记录颜色的成员,可以用枚举来实现。
详情见实现。
插入
红黑树虽然因规则多,看起来抽象,但理解之后会发现,其插入确实比AVL树方便。
一共就分为两大种情况,红插黑,红插红。(只插入红色结点,上文有解释)
红插黑是最简单的情况,无需任何处理。
红插红就稍微麻烦点,但大体也只有三种情况。不过在了解这三种情况之前,还需要知道一件事情,——此时,插入的结点记作child, 被插入的记作parent,那么已知child、parent都为红,可以知道parent->_parent即grandparent必为黑(或空)因为插入前树完好,应符合原则。既然child,parent,grandparent的颜色都是确定的,现在唯一的未知量就是uncle了(grandparent的另一个孩子)。
uncle分为不存在,存在黑色,存在红色三种情况。(实际上uncle不存在和存在且为黑是可以合并的一种情况。)
【1】uncle存在且为红:变色
将p和u由红变黑,g变红。这样既能确保红黑相间,又能保持两分支黑色结点数相同。

但有个问题是,g变红后,g的parent也为红(原g为黑),这样又红红连续了,因此还要继续向上变色,直到g的parent为黑或是为根结点时停下。
注意这里插在p的左右是无所谓的。
【2】uncle不存在或存在且为黑:变色+旋转(旋转的转法和AVL树的转法是一致的,可以直接copy。)
(1)变色+单旋
在p外侧插入(只显示了p的新孩子,若有另一个孩子必为黑,按单旋规则给g没问题)
调整方法:单旋g,p变黑,g变红,结束调整。

(2)变色+双旋
在p的内侧插入就要双旋,把c推举成根,并把c变黑,g变红,就结束调整了。
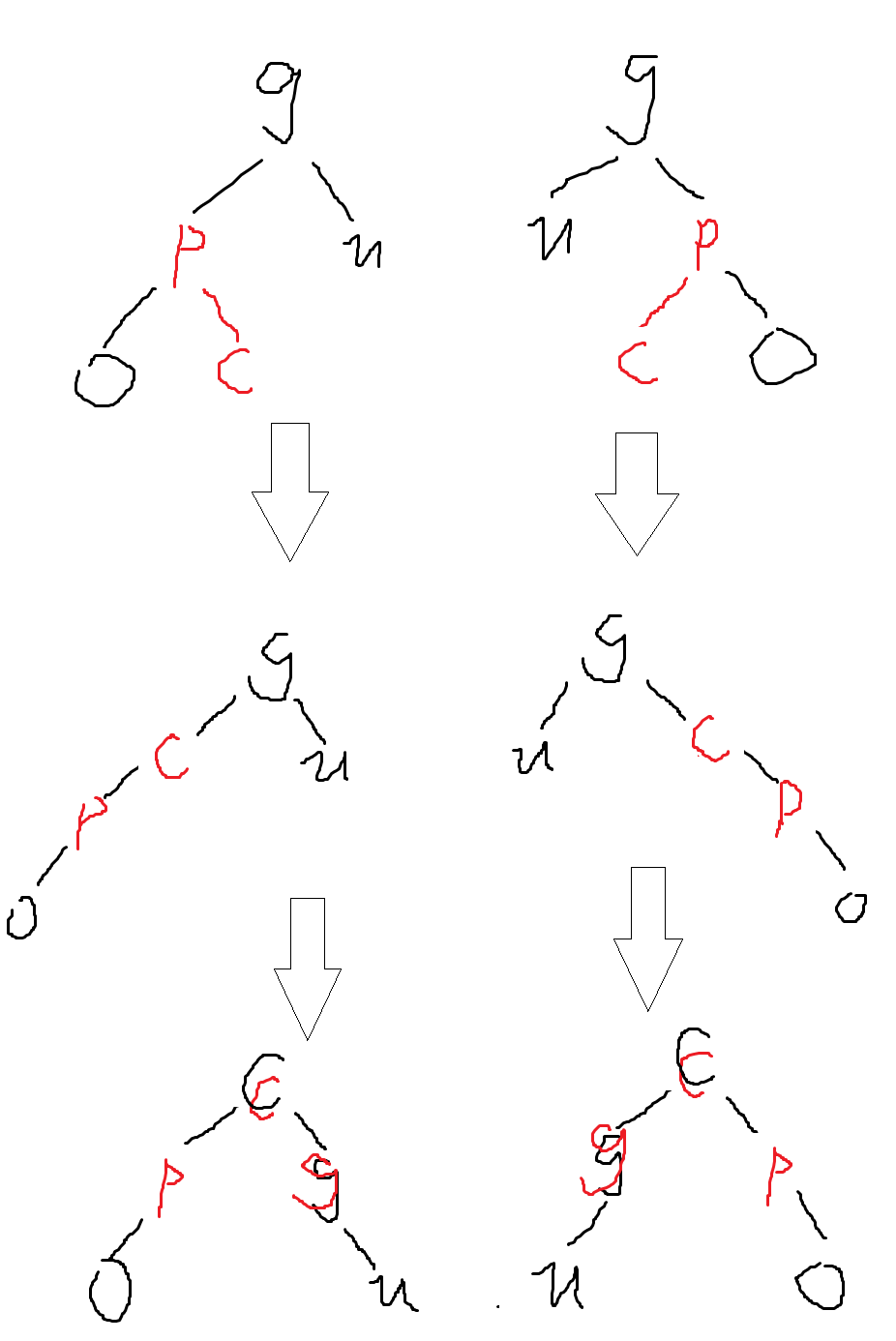
总结一下,就这两种大情况,理解后其实是要比AVL树还更好理解的(滑稽)
实现
#pragma once
#include<iostream>using namespace std;enum Color{Red,Black
};template<class K,class V>
struct RBTree_Node
{typedef RBTree_Node Node;RBTree_Node(const pair<K,V>& kv):_kv(kv), _parent(nullptr), _left(nullptr), _right(nullptr),_col(Red){}pair<K, V> _kv;Node* _parent;Node* _left;Node* _right;Color _col;
};//---------------------------------------------------------------------------------------template<class K,class V>
class RBTree
{typedef RBTree_Node<K,V> Node;public:bool insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = Black;return true;}Node* cur = _root;Node* parent = cur;while (cur){if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else{return false;}}Node* node = new Node(kv);node->_col = Red;if (kv.first < parent->_kv.first){parent->_left = node;}else{parent->_right = node;}node->_parent = parent;while (parent && parent->_col == Red){Node* grandparent = parent->_parent;if (parent && parent == grandparent->_left){Node* uncle = grandparent->_right;if (uncle && uncle->_col == Red){parent->_col = uncle->_col = Black;if(grandparent!=_root)grandparent->_col = Red;cur = grandparent;parent = cur->_parent;}else if (uncle == nullptr || uncle->_col == Black){if (cur == parent->_left){RotateR(grandparent);parent->_col = Black;grandparent->_col = Red;}else if (cur == parent->_right){RotateL(parent);RotateR(grandparent);cur->_col = Black;grandparent->_col = Red;}else{return false;}break;}}else if (parent && parent == grandparent->_right){Node* uncle = grandparent->_left;if (uncle && uncle->_col == Red){parent->_col = uncle->_col = Black;grandparent->_col = Red;cur = grandparent;parent = cur->_parent;}else if (uncle == nullptr || uncle->_col == Black){if (cur == parent->_right){RotateL(grandparent);parent->_col = Black;grandparent->_col = Red;}else if (cur == parent->_left){RotateR(parent);RotateL(grandparent);cur->_col = Black;grandparent->_col = Red;}else{return false;}break;}}else{return false;}}return true;}bool Find(const K& key){Node* cur = _root;while (cur){if (key < cur->_kv.first){cur = cur->_left;}else if (key > cur->_kv.first){cur = cur->_right;}else{return true;}}return false;}void Inorder(){_Inorder(_root);}int Height(){return _Height(_root);}bool isRBTree(){if (_root == nullptr){return true;}if (_root->_col == Red){return Red;}int refBN = 0;Node* cur = _root;while (cur){if (cur->_col == Black){refBN++;}cur = cur->_left;}return check(_root, 0, refBN);}
private:bool check(Node* root, int curBN, int refBN){if (root == nullptr){if (curBN != refBN){cout << "存在路径黑结点数异常" << endl;return false;}return true;}if (root->_col == Red && root->_parent && root->_parent->_col == Red){cout << root->_kv.first << "存在连续红结点" << endl;return false;}if (root->_col == Black)curBN++;return check(root->_left, curBN, refBN)&& check(root->_right, curBN, refBN);}int _Height(Node* root){if (root == nullptr)return 0;int lh = _Height(root->_left);int rh = _Height(root->_right);return lh > rh ? lh + 1 : rh + 1;}void _Inorder(Node* root){if (root == nullptr)return;_Inorder(root->_left);cout << root->_kv.second<<" ";_Inorder(root->_right);}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* pp = parent->_parent;subL->_right = parent;parent->_parent = subL;if (pp == nullptr){_root = subL;subL->_parent = nullptr;}else{if (pp->_left == parent){pp->_left = subL;}else if (pp->_right == parent){pp->_right = subL;}subL->_parent = pp;}}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* pp = parent->_parent;subR->_left = parent;parent->_parent = subR;if (pp == nullptr){_root = subR;subR->_parent = nullptr;}else{if (pp->_left == parent){pp->_left = subR;}else if (pp->_right == parent){pp->_right = subR;}subR->_parent = pp;}}private:Node* _root = nullptr;
};总结
AVL树比较直观,红黑树比较抽象。但二者都是能够被理解的。
重点在于不断去模拟二者不同的控制平衡的逻辑,当然也考察了二叉树的知识。
二者都涉及了旋转,怎么旋是好理解的,可实现代码时还有诸多细节,算是很好的锻炼。
不要求手撕,但其本质还是要熟悉的。
(附:未涉及删除操作,有兴趣可以参考相关数据结构教材)
相关文章:

数据结构进阶:AVL树与红黑树
目录 前言 AVL树 定义 结构 插入 AVL树插入的大致过程 更新平衡因子 旋转 右单旋 左单旋 左右双旋 右左双旋 实现 红黑树 定义 性质 结构 插入 实现 总结 前言 在学习了二叉搜索树之后,我们了解到其有个致命缺陷——当树的形状呈现出一边倒…...

AI人工智能在交通物流领域的应用
AI人工智能在交通物流领域的应用 AI人工智能在交通物流领域有着广泛而深入的应用,正推动着该领域的深刻变革,以下是详细介绍: 交通领域 智能驾驶 自动驾驶汽车:依靠深度学习算法、计算机视觉、激光雷达和传感器融合技术&#x…...

牛客网NC22222:超半的数
牛客网NC22222:超半的数 题目描述 输入输出格式 输入格式: 第一行包含一个整数 n (1 ≤ n ≤ 1000)第二行包含 n 个整数 a_i (1 ≤ a_i ≤ 10^9) 输出格式: 输出一个整数,表示出现次数超过一半的那个数 解题思路 这道题目有多种解法&a…...
)
在服务器上安装AlphaFold2遇到的问题(2)
如何删除已安装的cuDNN 1. 通过包管理器卸载(推荐) RHEL/CentOS (dnf/yum) #查看已安装的 cuDNN 包 sudo dnf list installed | grep cudnn #卸载 cuDNN 运行时和开发包 sudo dnf remove -y libcudnn* libcudnn8* libcudnn-devel* Ubuntu/Debian (ap…...
)
【2025年软考中级】第一章1.5 输入输出技术(外设)
文章目录 输入输出技术(外设)I/O设备总线结构输入输出控制程序控制方式中断方式直接内存存取(DMAC)方式IO通道方式和外围处理机(IOP)方式 数据传输方式生物特征认证技术 输入输出技术(外设&…...

2025 家用投影新标杆:雷克赛恩 CyberPro1 如何重新定义客厅观影体验
目录 一、家庭影音升级:从 “看得清” 到 “看得精” 的需求之变 (一)传统投影的痛点突围 (二)技术参数背后的用户价值 二、全天候观影无忧:亮度与环境光的博弈艺术 (一)真实亮…...

[基础] HPOP、SGP4与SDP4轨道传播模型深度解析与对比
HPOP、SGP4与SDP4轨道传播模型深度解析与对比 文章目录 HPOP、SGP4与SDP4轨道传播模型深度解析与对比第一章 引言第二章 模型基础理论2.1 历史演进脉络2.2 动力学方程统一框架 第三章 数学推导与摄动机制3.1 SGP4核心推导3.1.1 J₂摄动解析解3.1.2 大气阻力建模改进 3.2 SDP4深…...

12 web 自动化之基于关键字+数据驱动-反射自动化框架搭建
文章目录 一、如何实现一条用例,实现覆盖所有用例的测试1、结合数据驱动:编辑一条用例,外部导入数据实现循环测试2、用例体:实现不同用例的操作步骤对应的断言 二、实战1、项目路径总览2、common 文件夹下的代码文件3、keywords 文…...

学习状态不佳时的有效利用策略
当学习状态不佳时,可以尝试以下策略,将这段时间转化为有意义的活动,既不勉强自己又能为后续高效学习铺路: 1. 整理与规划:低精力高回报任务 整理学习环境:收拾书桌、归类资料、清理电脑文件,减…...

Spring Cloud深度实践:从服务发现到弹性智能API网关全景解析
引言 大家好!继初步搭建了微服务基础架构后,我们进一步深入到服务调用的优化、系统的弹性构建以及API网关的高级应用。本文将全面回顾这一进阶阶段的实践成果,通过更丰富的图解,力求清晰展现各核心组件的工作原理与协同方式。 项…...

第J1周:ResNet-50算法实战与解析
🍨 本文为🔗365天深度学习训练营 中的学习记录博客 🍖 原作者:K同学啊 我的环境 语言环境:Python3.8 编译器:Jupyter Lab 深度学习环境:Pytorchtorch1.12.1cu113 torchvision0.13.1cu113 一、准备工作 二、导入数据 三、划分数据…...

PCL 计算一条射线与二次曲面的交点
文章目录 一、简介二、实现代码三、实现效果一、简介 对于二次曲面而言,其一般方程可以写为: z = a 0 + a 1 x + a 2 y + a...

Executors类详解
Executors类详解 Executors 是Java中用于快速创建线程池的工具类,提供了一系列工厂方法,简化了 ThreadPoolExecutor 和 ScheduledThreadPoolExecutor 的配置。以下是其核心方法、实现原理及使用注意事项: 1. 常用线程池工厂方法 (1) newFixedThreadPool 作用:创建固定大小…...

学习alpha
(sign(ts_delta(volume, 1)) * (-1 * ts_delta(close, 1))) 这个先用sign操作符 sign.如果输入NaN则返回NaN 在金融领域,符号函数 sign(x) 与 “基础”(Base)的组合概念可结合具体场景解读,以下从不同金融场景分析其潜在意义&…...

6种方式来探究数据集的的方法worldquant
覆盖率百分比 指金融数据字段(如股价、成交量、财务指标)在时间或空间上的有效数据比例。 时间维度:数据在历史周期内的完整度(如:某股票过去 1 年中,95% 的交易日有收盘价)。空间维度…...

MiniMax语音模型Speech-02近日登顶多个全球榜单,详细技术解析
MiniMax最新发布的Speech-02把TTS领域传统巨头OpenAI、ElevenLabs拉下马来,直接登顶智能语音权威榜单Artificial Arena,不管是WER(字错率),还是SIM(声纹相似度)等客观指标都领先国外顶级模型&am…...

JavaScript 时间转换:从 HH:mm:ss 到十进制小时及反向转换
关键点 JavaScript 可以轻松实现时间格式(HH:mm:ss 或 HH:mm)与十进制小时(如 17.5)的相互转换。两个函数分别处理时间字符串到十进制小时,以及十进制小时到时间字符串的转换,支持灵活的输入和输出格式。这…...

前端面经 手写Promise
核心功能 仿Promise对象需要接收包含两个变量的回调函数 构造函数 <script>class myPromise {constructor(func){const resolve (result)>{console.log(resolve执行了)}const reject (result)>{console.log(reject执行了)}func(resolve,reject)}}// Promise的…...

JavaSE基础语法之方法
方法 一、方法入门 1.方法定义 方法是一种语法结构,它可以把一段代码封装成一个功能,以便重复调用。 2.方法的格式 修饰符 返回值类型 方法名( 形参列表 ){方法体代码(需要执行的功能代码) }示例: public static int sum ( int a ,…...

在 Neo4j 中实现向量化存储:从文本到高效语义搜索
在当今数据驱动的时代,图数据库因其强大的关系表达能力和高效的查询性能,逐渐成为处理复杂数据结构的首选工具之一。Neo4j 作为领先的图数据库,不仅支持传统的图数据存储和查询,还通过向量化存储功能,为语义搜索和推荐…...

三格电子上新了——IO-Link系列集线器
一、产品概述 1.1产品用途 IO-Link系列集线器是一系列数字量输入输出I/O设备,可以将标准开关量信号接入到此设备。通过此集线器方便的将大量的I/O点位接入到IO-Link主站,进而接入到PLC控制系统。 IO-Link通信接口和8个I/O接口(16个IO点位)均采用M12规…...

记一次从windows连接远程Linux系统来控制设备采集数据方法
文章目录 0 引入1、方法2、优化Process使用 3、引用 0 引入 最近使用的探测器是老外的,老外的探测器需要在centos系统上,在这系统上有相应的指令或者软件控制,但是我们的软件在windwons上,所以目前的困难是:如何在Win…...

鸿蒙 ArkTS 常用的数组和字符串 操作方法
数组的常用方法 方法名功能描述concat(value0, ?value1, /* … ,*/ ?valueN)合并两个或多个数组。此方法不会更改现有数组,而是返回一个新数组copyWithin(target, ?start, ?end)浅复制数组的一部分到同一数组中的另一个位置,并返回它,不…...

Web性能优化的未来:边缘计算、AI与新型渲染架构
一、边缘计算与性能优化深度整合 1.1 边缘节点计算卸载策略 • 智能任务分割:将非关键路径计算卸载到边缘节点 // 客户端代码 const edgeTask = new EdgeTask(image-processing); edgeTask.postMessage(imageData, {transfer...

Python字符串常用内置函数详解
文章目录 Python字符串常用内置函数详解一、基础字符串函数1. len() - 获取字符串长度2. ord() - 获取字符的Unicode码点3. chr() - 通过Unicode码点获取字符4. ascii() - 获取字符的ASCII表示 二、类型转换函数1. str() - 将对象转为字符串2. repr() - 获取对象的官方字符串表…...

2025程序设计天梯赛补题报告
2025程序设计天梯赛补题报告 仅包含L1 L2 L1-6 这不是字符串题 题目描述 因为每年天梯赛字符串题的解答率都不尽如人意,因此出题组从几年前开始决定:每年的天梯赛的 15 分一定会有一道字符串题,另外一道则一定不是字符串题。 小特现在有…...
【未完】)
【GNN笔记】Signed Graph Convolutional Network(12)【未完】
视频链接:《图神经网络》 Signed Graph Convolutional Network 之前介绍的GNN模型主要集中在无符号的网络(或仅由正链接组成的图)上,符号 图带来的挑战,主要集中在于 否定链接,与正链接相比,它不…...

CSR、SSR与ISR的奇妙之旅
网页渲染三剑客:CSR、SSR与ISR的奇妙之旅 三种渲染方式的核心本质 CSR(客户端渲染)让浏览器成为"厨师",SSR(服务器端渲染)让服务器担任"厨师",而ISR(增量静态再生)则是一位兼具"提前备餐"和"即时烹饪"能力的"超级厨师"…...
开发)
YOLO+UI(C#)开发
接Windows目标检测程序开发(YOLO(python推理)界面开发(C#)) C#作为软件界面,推理、前处理、后处理逻辑全部python,接任何功能定制...

生产级JVM参数优化
Spring Boot 应用性能提升 300% 当你的 Spring Boot 应用响应迟缓,且已采用缓存、数据库索引和异步处理优化后,下一个优化方向在哪里?我的答案是 JVM 本身。 经过性能分析和深入研究,我发现合理配置 JVM 参数可以带来显著的性能…...

什么是SMBus
一、SMBus的定义与背景 基本概念 SMBus(System Management Bus,系统管理总线) 是一种基于IC(Inter-Integrated Circuit)协议的轻量级两线制串行通信总线,由Intel于1995年提出,主要用于低带宽系统…...

[Unity]AstarPathfindingProject动态烘焙场景
需求 项目是MMO大场景,按地块划分了10x10的大格子。角色移动时动态更新周边场景,且角色还有传送功能。 项目中寻路用了AstarPathfindingProject的Grid。因此需要动态烘焙寻路信息。 核心代码 private void bakeAStarPath(){AstarPath astarPath Astar…...

Go语言处理HTTP下载中EOFFailed
在 Go 语言中使用 HTTP 下载文件时遇到 EOF 或 Failed 错误,通常是由于网络连接问题、服务器中断、未正确处理响应体或并发写入冲突等原因导致的。以下是详细的解决方案: 1. 检查错误类型并重试 io.EOF 错误可能表示连接被服务器关闭,而 Fai…...
)
React学习(一)
React 基础概念 组件:React 应用的基本构建块,可以是类组件或函数组件。JSX:JavaScript 的语法扩展,允许在 JavaScript 中写 HTML 结构。Props:组件的输入参数,用于父组件向子组件传递数据。State…...

QML 属性动画、行为动画与预定义动画
目录 引言相关阅读本文使用的动画属性工程结构示例解析示例1:属性动画应用示例2:行为动画实现示例3:预定义动画 总结工程下载 引言 QML动画系统为界面元素提供了流畅的过渡效果。本文通过三个示例,结合属性动画(PropertyAnimatio…...
)
UML活动图零基础入门:1 分钟掌握核心逻辑(附实战模板)
想快速搞懂UML活动图怎么用?别担心!作为软件开发和业务流程设计的动态流程图,UML活动图能直观展现系统操作步骤、决策逻辑和并行流程,是团队协作中沟通需求、优化流程的必备工具。无论是产品经理梳理业务流程,还是开发…...

临床决策支持系统的提示工程优化路径深度解析
引言 随着人工智能技术在医疗领域的迅猛发展,临床决策支持系统(CDSS)正经历从传统规则引擎向智能提示工程的范式转变。在这一背景下,如何构建既符合循证医学原则又能适应个体化医疗需求的CDSS成为医学人工智能领域的核心挑战。本报告深入剖析了临床决策支持系统中提示工程的…...

[模型部署] 3. 性能优化
👋 你好!这里有实用干货与深度分享✨✨ 若有帮助,欢迎: 👍 点赞 | ⭐ 收藏 | 💬 评论 | ➕ 关注 ,解锁更多精彩! 📁 收藏专栏即可第一时间获取最新推送🔔…...

使用 LSTM/GRU 预测设备异常的模型
LSTM(Long Short-Term Memory) 是一种特殊的循环神经网络(RNN)架构,旨在解决传统 RNN 在处理长序列数据时的梯度消失和梯度爆炸问题。它通过引入门控机制和单元状态来更好地控制信息的流动,使得网络能够学习到长期依赖关系。以下是其主要特点: 门控机制:包括遗忘门、输…...
)
八股文--JVM(1)
⭐️⭐️JVM内存模型 程序计数器:可以看作是当前线程所执行的字节码的行号指示器,用于存储当前线程正在执行的 Java 方法的 JVM 指令地址。如果线程执行的是 Native 方法,计数器值为 null。是唯一一个在 Java 虚拟机规范中没有规定任何 OutOf…...

BM25 算法与关键词提取在向量数据库中的实践优化
BM25 算法与关键词提取在向量数据库中的实践优化 在实际构建问答系统或语义检索场景中,向量数据库(如 Weaviate)提供了基于语义匹配的检索能力,然而我们发现 BM25 关键词检索效果不理想,甚至出现了召回率过低、查询必…...

济南超算研究所面试问题
1.自我介绍 2.java抽象类与接口的区别 3.抽象类能否实例化 4.在项目中用的抽象类偏多还是接口偏多 5.抽象类用的场景介绍一下 6.java中数据结构有哪些 7.数据的基本类型 8.引用类型,包装类型 9.是一个场景题,在查询数据库中的数据时,…...

“多维像素”可赋能具身智能非凡感知力——昱感微参加2025松山湖中国IC创新高峰论坛
5月13日,由中国半导体行业协会集成电路设计分会、芯原微电子(上海)股份有限公司联合主办的第十五届松山湖中国IC创新高峰论坛在东莞松山湖举行。本届松山湖论坛以“面向‘具身智慧机器人’的创新IC新品推介”为主题,吸引了许多知名…...

解决CLion控制台不能及时显示输出的问题
CLion 2025版本可以免费用于非商业用途了,下载来试用了一下,与JB的其它 IDE一样的资源占用比较大,流畅度不及VSCode。 在Windows下创建了一个简单的控制台应用程序,使用printf和std::cout输出字符串,发现CLion的控制台…...

多尺度对比度调整
一、背景介绍 受到了前面锐化算法实现的启发,对高频层做增强是锐化,那么对中低频一起做增强,就应该能有局域对比度增强效果。 直接暴力实现了个基本版本,确实有对比度增强效果。然后搜了下关键字,还真找到了已经有人这…...

虹桥前湾印象城MEGA品牌大会灵感迸发,共绘湾系生活新章
前言:当千年水韵流淌至上海前湾,当苏州河的生态肌理转化为商业空间的呼吸脉络……上海虹桥前湾印象城MEGA“漫漫而来”。 5月15-16日,以“灵感新章 Wave of Megagination”为主题的虹桥前湾印象城MEGA品牌大会成功举办,正式掀开长…...

新京东,正在成为一种生活方式
出品|何玺排版|叶媛 一个新京东,正在从“心”诞生。 2025年2月11日之前,如果问京东是做什么的,相信大多数人会回答京东是电商平台,卖家电数码日用百货的。现在,如果问京东是做什么的,相信大家的回答不在是…...

读论文alexnet:ImageNet Classification with Deep Convolutional Neural Networks
https://zhuanlan.zhihu.com/p/13694329885 1, 公式 卷积层输出尺寸: o ⌊(i 2p - k) / s⌋ 1 式中,i:输入尺寸;o:输出尺寸;p:padding;k: kernel_size;s: stride。⌊…⌋表示向下取整。 2, 推导过程 …...

操作系统|| 虚拟内存页置换算法
题目 写一个程序来实现 FIFO 和 LRU 页置换算法。首先,产生一个随机的页面引用序列,页面数从 0~9。将这个序列应用到每个算法并记录发生的页错误的次数。实现这个算法时要将页帧的数量设为可变。假设使用请求调页。可以参考所示的抽象类。 抽象类&…...
:下载模型到本地之ModelScope(魔搭社区))
AGI大模型(19):下载模型到本地之ModelScope(魔搭社区)
1 安装模块 魔塔社区提供了下载的模块,如下: pip install modelscope -i https://pypi.tuna.tsinghua.edu.cn/simple 2 模型下载 from modelscope import snapshot_download model_dirsnapshot_download(LLM-Research/Meta-Llama-3-8B,cache_dirrD:\…...
