当前位置：首页 > news >正文

math toolkit for real-time development读书笔记一-三角函数快速计算(1)

news 来源：原创 2025/6/18 23:09:38

一、基础知识

根据高中知识我们知道，很多函数都可以用泰勒级数展开。正余弦泰勒级数展开如下：

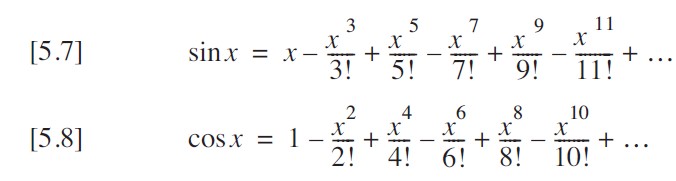
将其进一步抽象为公式可知：

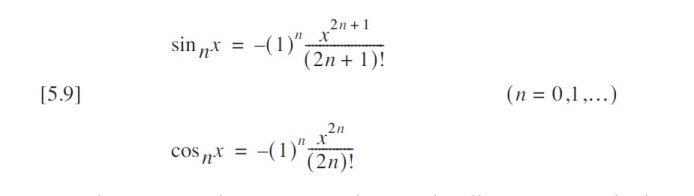
正弦和余弦的泰勒级数具有高度结构化的模式，可拆解为以下核心特征：

1. 符号交替特性

正弦级数：项的符号以 $(-1)^{n}$ 交替，即 +,−,+,−,…
余弦级数：符号同样由 $(-1)^{n}$ 控制，但首项为正（n=0 时），即 +,−,+,−,…
作用：正负项交替抵消了部分累积误差，避免数值无意义地发散（如大角度场景中，若所有项同号，和会迅速溢出）。

2. 幂次规律

正弦：包含 x 的奇次幂（ $x^{1},x^{3},x^{5},$ …），对应通项中的 2n+1。
余弦：包含 x 的偶次幂（ $x^{0},x^{2},x^{4}$ …），对应通项中的 2n（注意 $x^{0}$ =1 为首项）。
直观理解：正弦是奇函数（仅含奇次幂），余弦是偶函数（仅含偶次幂），与函数的奇偶性代数定义一致。

3. 分母的阶乘主导

分母为分子指数的阶乘，即奇次幂项分母为 (2n+1)!，偶次幂项为 (2n)!。
阶乘的超指数增长：例如 10!=3,628,800，20!≈ $2.43*10^{18}$ ，远快于 $x^{n}$ 的增长（即使 x 较大）。
关键作用：确保级数对任意 x 收敛，且小角度下项值急剧衰减（如 x=π/6 时，第 3 项已小于 $2*10^{-4}$ ）。

在任何计算机数学的教科书或手册中，你也都会找到这些函数的定义和相关性质。然而仅有公式并不足以在实际应用中解决问题。公式是基础，但只有结合计算特性的优化，才能真正解决现实问题。

如果直接利用泰勒级数进行计算，将遇到几方面的问题：

阶乘的计算边界：在编程中，n! 很快会超出数值类型范围（如 32 位整数最大表示 20!），需使用浮点类型或大数库，或通过递推避免显式计算阶乘。
机器精度的限制：计算机无法表示无限精度，当项值小于机器的最小精度时，其对总和的贡献在数值上为零，此时截断级数是合理的。

无穷级数的问题在于它们…… 嗯…… 是无穷的。如果我有一台无限算力的计算机和无限的时间，我现在就可以结束跳过后续的内容，关上电脑愉快的下班各回各家各找各妈了。

但在现实世界中，你不可能等待计算无穷多项。计算机也无法处理无限项计算。以 sin(1000) 为例，直接展开需数千项才能使阶乘主导项衰减，而单精度浮点数在计算前几项时就会因 xn 过大而溢出（如 $1000^{10}$ = $10^{30}$ ，已接近单精度上限 $3.4*10^{38}$ ）。幸运的是，你也不需要无限的精度。计算机中的任何实数都只是一个近似值，受限于计算机的字长。当计算机依次计算级数中的高阶项时，这些项最终会变得小于计算机的位分辨率。在那之后，计算更多的项就毫无意义了。

在这个级数中，随着 n 的增大，各项变得越来越小，但级数的和却是无穷大。数学家们必然且确实会关注幂级数的收敛性；不过请放心，如果有人给出一个如 sin (x) 这样的函数的级数展开式，他们必定已确保其收敛性。对于正弦和余弦函数，符号交替的特性确保了小项不会累积成大的数值。

如果高阶项变得可以忽略不计，你可以截断级数以获得多项式近似。处理任何无穷级数时都必须这样做。有时你可以估算引入的误差，但大多数情况下，程序员只需保留足够多的项，以确保误差控制在合理范围内。

通过一个例子来理解可能更直观。表 5.1计算了 x=30∘（即 π/6 弧度）的正弦和余弦值。在所示的精度范围内，两个级数在第五项后均已收敛（由于余弦项的每一项比正弦项少一个 x 的幂次，其收敛速度通常稍慢）。正如预期，由于分母中阶乘的存在，各项的绝对值迅速减小。

表5.1
项数n	正弦项 $(-1)^{n}\frac{x^{2n+1}}{(2n+1)!}$	正弦项累加和
0	$(-1)^{0}\frac{(\pi /6)^{20+1}}{(20+1)!} =\frac{\pi }{6}\approx 0.52359878$	0.52359878
1	$(-1)^{1}\frac{(\pi /6)^{21+1}}{(21+1)!} =-1*\frac{\frac{\pi }{6}^{3}}{3!}\approx -0.02379643$	0.49980235
2	$(-1)^{2}\frac{(\pi /6)^{22+1}}{(22+1)!} =1*\frac{\frac{\pi }{6}^{5}}{5!}\approx 0.00033462$	0.50013697
3	$(-1)^{3}\frac{(\pi /6)^{23+1}}{(23+1)!} =-1*\frac{\frac{\pi }{6}^{7}}{7!}\approx- 0.00000257$	0.50013440
4	$(-1)^{2}\frac{(\pi /6)^{24+1}}{(24+1)!} =1*\frac{\frac{\pi }{6}^{9}}{9!}\approx 0.00000001$	0.50013441
真实值	sin(π/6)=0.5	误差： $1.34*10^{-5}$

项数n	余弦项 $(-1)^{n}\frac{x^{2n}}{(2n)!}$	余弦项累加和
0	$(-1)^{0}\frac{(\pi /6)^{20}}{(20)!} =\frac{\pi }{6}^{0}= 1$	1
1	$(-1)^{1}\frac{(\pi /6)^{21}}{(21)!} =-1*\frac{\frac{\pi }{6}^{2}}{2!}\approx -0.13707187$	0.86292813
2	$(-1)^{2}\frac{(\pi /6)^{22}}{(22)!} =1*\frac{\frac{\pi }{6}^{4}}{4!}\approx 0.00279031$	0.86571844
3	$(-1)^{3}\frac{(\pi /6)^{23}}{(23)!} =-1*\frac{\frac{\pi }{6}^{6}}{6!}\approx- 0.00003298$	0.86568546
4	$(-1)^{2}\frac{(\pi /6)^{24}}{(24)!} =1*\frac{\frac{\pi }{6}^{8}}{8!}\approx -0.00000039$	0.86568585
真实值	cos(π/6)=0.8660254	误差： $3.39*10^{-5}$

对于三角函数的任何实际计算，最终结果都要求我必须限制 x 的范围，就像我对平方根函数所做的那样。显然，范围越小，所需的项数就越少。我还没有向你展示如何限制范围，但暂时假设这是可以做到的。那么需要多少项呢？

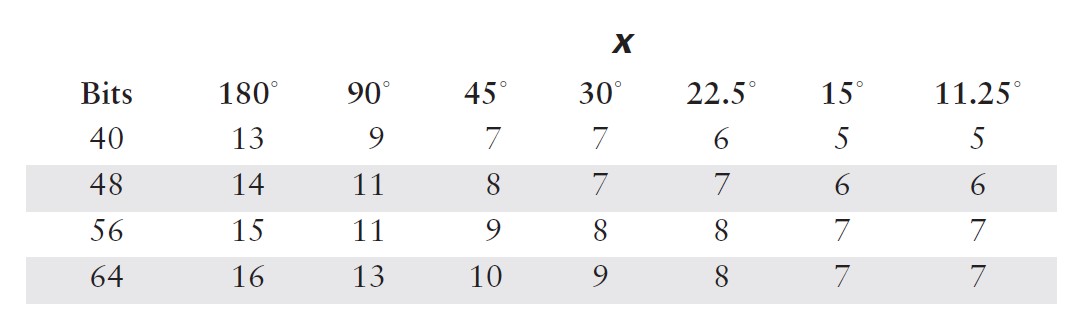
在这种情况下，计算所需的项数相当直接。由于级数中的项具有交替的符号，我不必担心诸如许多小数项累加为大数之类的潜在问题。正如你在表 5.1 中看到的，中间结果围绕最终结果振荡。因此，我可以确定误差总是小于（有时远小于）第一个被忽略项的大小。我需要做的就是为角度范围的代表性值计算方程中每个项的值，然后将结果与我所使用的数值表示中的最低有效位（LSB）精度进行比较。由于我无法预先知道你可能使用的数值格式，因此最好将这两个步骤分开。项值如表 5.2 和 5.3 所示。请注意，对于更小的范围，误差减小得有多显著。

在表 5.4 和 5.5 中，我使用这些结果计算了典型计算机表示所需的项数。通常，预期尾数范围为 24 位（32 位浮点数）或 56 位（C 语言双精度使用的八字节格式）。较小的数值有时在专用嵌入式系统中有用，而最大的数值对应双精度和数值协处理器的字长。同样，只需看一眼这些表格，你就会相信，花一些计算能力来减少输入参数的范围是值得的。

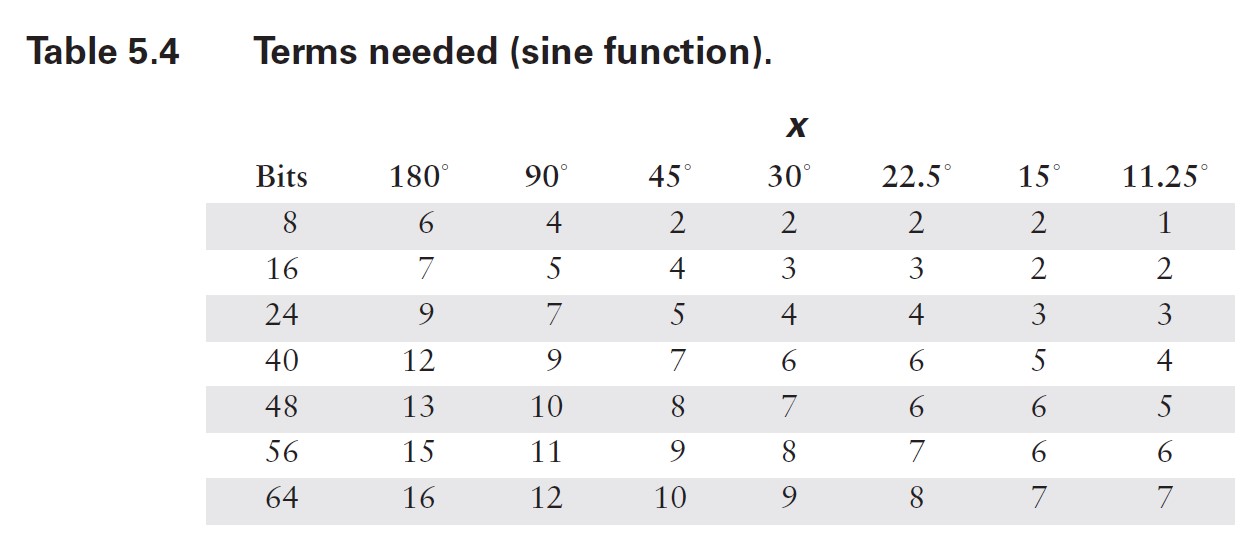
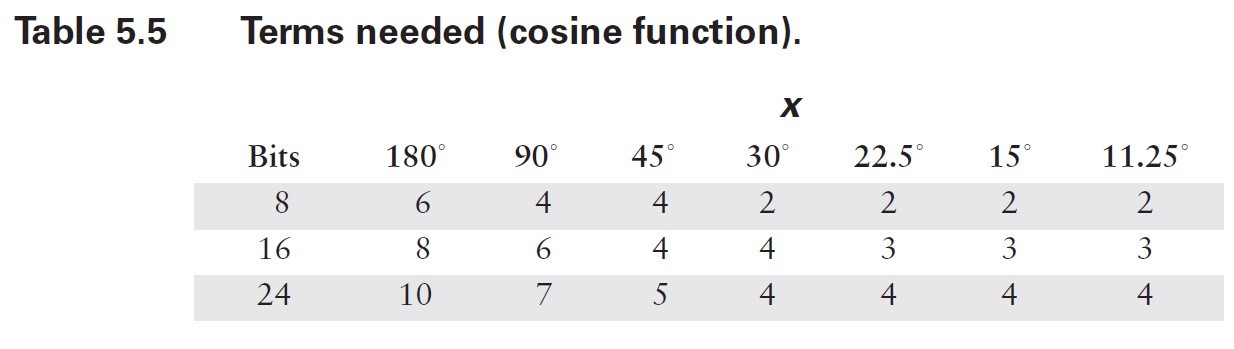
既然我已经知道需要在截断级数中包含多少项，接下来仍需设计代码对其进行计算。缺乏经验的程序员可能会直接按方程 [5.7] 的写法进行编程，为每一项反复计算 $x^{n}$ 和n!。一个简单的停止准则可能只是将每一项的值与某个误差准则进行比较（在这种情况下，表 5.2 至 5.5 并非必需）。

事实上，这正是我最初实现该函数的方式，只是为了证明自己能够做到。这是一个糟糕的实现，因为它需要反复将x提升到越来越高的幂次，更不用说为每一项调用两个耗时函数的开销了。诚然，该函数对任何输入（无论多大）都能给出正确答案，但付出的运行时性能代价却非常高昂。

double factorial(unsigned long n){
double retval = 1.0;
for(; n>1; --n)
retval *= (double)n;
return retval;
}
double sine(double x){
double first_term;
double next_term = x;
double retval = x;
double sign = 1.0;
double eps = 1.0e-16;
int n = 1;do{
cout << next_term << endl;
first_term = next_term;
n += 2;
sign *= -1.0;
next_term = sign * pow(x, n)/factorial(n);
retval += next_term;
}
while((abs(next_term) > eps));
return retval;
}

通过观察到每一项都可以由前一项递推计算，我们可以显著优化代码效率。回顾方程 [5.9] 中正弦函数的通项公:

该级数的下一项时：

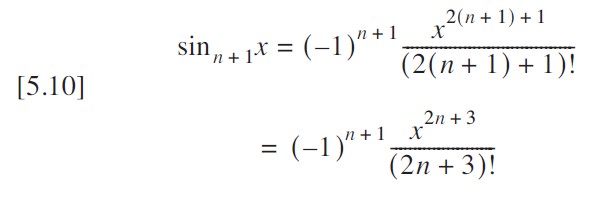
前后项相比知;

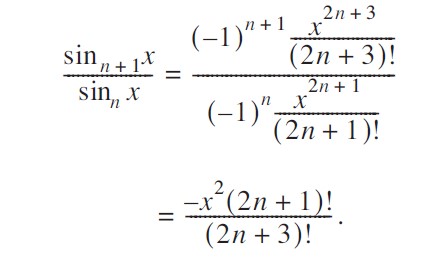
我们以 $R_{n+1}$ 代表其比值：

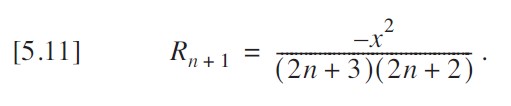
改进版本消除了对 pow () 和 factorial () 的调用。此版本如下代码所示。

double sine(double x){
double last = x;
double retval = x;
double eps = 1.0e-16;
long n = 1;
do{
n += 2;
last *= (-x * x/((double)n * (double)(n-1)));
retval += last;
}
while((abs(last) > eps));
return retval;
}

如上中的代码效率尚可，许多人可能想就此打住。然而，这个函数的实现方式仍然相当糟糕。我可以通过仅计算一次 x² 来稍作改进，但还有一种更好的方法 —— 方程 [5.11] 中的关系给出了线索：每一项都是下一项的一个因子。事实上，这甚至包括值 x，它存在于每一项中。因此，我可以将方程 [5.7] 和 [5.8] 因式分解为:

这种公式化方法被称为霍纳法则，它几乎是计算该级数的最优方式。请注意，每一步的分母都是两个连续整数的乘积 —— 在正弦级数中为 2×3、4×5、6×7，等等。一旦你发现这一规律，就能凭记忆写出这些函数的计算式。如果无法使用现成的正弦函数，而你又急需一个，直接对这两个方程进行编码其实相当不错。

不过仍有几个细节需要解决。首先，我遇到一个小问题：由于必须保存所有中间结果，所示方法会占用大量栈空间。如果你的编译器是高度优化的，或者你不介意栈空间消耗，这不会有问题。但如果你使用的是简单编译器和 80x87 数学协处理器，你会像我一样很快发现，协处理器可能会发生栈溢出。

式5-12可以重新改写为：

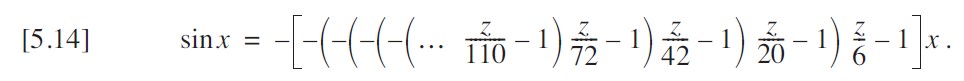
但对于计算机实现而言，我可以通过另一轮变换消除一半的符号变化。这可能并不明显，但如果我仔细地将所有前导负号折叠到括号内的表达式中，就能得到等效的形式。

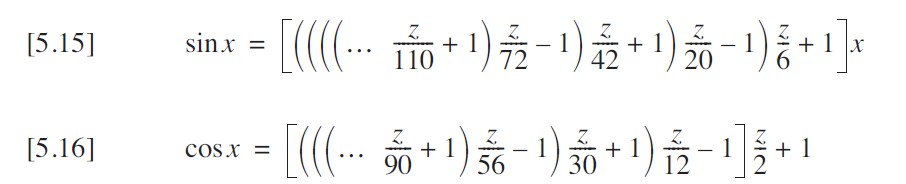
这已经是相当高效的实现方式了。这些方程虽然看起来不简洁，但计算速度非常快。就像我可以在方程 [5.12] 和 [5.13] 的右侧添加更多项一样，也可以在方程 [5.15] 和 [5.16] 的左侧添加项。只需记住，这次符号是交替变化的，从右端显示的正号开始。

如下代码展示了这些方程的直接实现。所使用的项数适用于 32 位浮点精度和 ±45° 的范围。由于大多数计算机执行乘法的速度比除法快，我通过将常数存储为其倒数来调整了算法（不用担心涉及常数的表达式，大多数编译器会对这些部分进行优化）。注意名称前添加的下划线，这是为了强调（双关语）这些函数仅在有限范围内有用的事实。我会在后面的全范围版本中使用这些函数。

// Find the Sine of an Angle <= 45
double _sine(double x){
double s1 = 1.0/(2.0*3.0);
double s2 = 1.0/(4.0*5.0);
double s3 = 1.0/(6.0*7.0);
double s4 = 1.0/(8.0*9.0);
double z = x * x;
return ((((s4*z-1.0)*s3*z+1.0)*s2*z-1.0)*s1*z+1.0)*x;
}
// Find the Cosine of an Angle <= 45
double _cosine(double x){
double c1 = 1.0/(1.0*2.0);
double c2 = 1.0/(3.0*4.0);
double c3 = 1.0/(5.0*6.0);
double c4 = 1.0/(7.0*8.0);
double z = x * x;
return (((c4*z-1.0)*c3*z+1.0)*c2*z-1.0)*c1*z+1.0;
}

第二个细节？我悄悄省去了一个用于判断使用多少项的测试。由于必须从内到外计算霍纳法则，你必须知道 “内部” 从哪里开始。这意味着你不能在计算过程中测试各项；必须预先知道需要多少项。在这种情况下，对于小的 x 值，霍纳法则的额外效率抵消了跳过内部项计算可能获得的任何收益。这一结果与第 4 章中关于平方根的讨论得出的结论相似：有时固定次数地计算某些内容会更简单（而且通常更快），而不是测试某个终止条件。如果这能让你更放心，可以为 x 非常接近零的特殊情况添加一个测试；否则，最好计算完整的表达式。

你可能想知道，既然我已经在方程 [5.5] 中表明余弦可以由正弦推导而来，为什么还要同时包含正弦和余弦函数。原因很简单：即使你只对其中一个函数感兴趣，实际上也需要能够计算这两个函数。当结果接近零时，一种近似最准确；当结果接近一时，另一种近似最准确。根据输入值的不同，你最终会使用其中一种或另一种。

霍纳法则的计算必须从内到外逐层展开，这意味着无法在循环中动态判断项数，必须预先确定需要计算的项数。这一限制带来两个关键问题：

1. 为何放弃动态项数测试？

霍纳法则的结构性限制：其嵌套乘法形式（如 sin(x)=x⋅(1−3!x2⋅(1−5×4x2⋅(⋯)))）要求先计算最内层项，再向外逐层展开。若在计算中动态判断是否终止（如 “当项值小于误差阈值时停止”），需存储所有中间层结果，这会抵消霍纳法则的空间优化优势。
小角度场景的效率平衡：对于小 x（如 x≈0），级数收敛极快，理论上只需 1-2 项即可满足精度。但预定义固定项数（如 4 项）的计算成本可能低于动态测试的判断开销（如条件分支、浮点比较）。正如第 4 章平方根计算的结论：固定次数的计算有时比动态终止更高效。

为何同时实现正弦与余弦函数？

尽管余弦可通过正弦推导（cos(x)=sin(2π−x)），但独立实现两者仍有必要：

1. 精度互补性

正弦在 0 附近更精确：当 x≈0 时，正弦级数首项 x 直接逼近真实值，而余弦级数首项为 1，次项 −2x2 对小 x 的修正量极小，需更多项才能达到同等精度。
余弦在 2π 附近更精确：当 x≈2π 时，余弦值接近 0，其级数收敛更快；而正弦值接近 1，需更多项修正首项 x 的较大偏差。

2. 输入范围的动态选择

根据输入 x 的范围选择计算路径：
- 若 x 靠近 kπ（正弦主导区间），优先计算正弦，再通过三角恒等式推导余弦。
- 若 x 靠近 kπ+2π（余弦主导区间），直接计算余弦更高效。
避免大角度误差累积：例如，计算 cos(179∘) 时，若通过 sin(1∘) 推导，需先将 179∘ 约简为 1∘，再调用正弦函数。此过程可能引入额外的约简误差，而直接计算余弦可避免中间步骤

至此，我已证明如果输入参数的范围可以限制，就能实现一个良好且高效的正弦函数。接下来需要说明的是，我确实可以限制范围。

一、基础知识

为何同时实现正弦与余弦函数？

1. 精度互补性

2. 输入范围的动态选择

相关文章：