day 17 无监督学习之聚类算法

一、聚类流程

1. 利用聚类发现数据模式

无监督算法中的聚类，目的就是将数据点划分成不同的组或 “簇”，使得同一簇内的数据点相似度较高，而不同簇的数据点相似度较低，从而发现数据中隐藏的模式。

2. 对聚类后的类别特征进行可视化

通过可视化，比如使用散点图、柱状图、热力图等，能够更直观地理解每个聚类所包含的数据特征。例如，如果是数值型数据，可以通过可视化展示不同聚类在各个特征维度上的分布情况，像均值、中位数、标准差等统计量的差异。

3. 得到新特征并赋予实际含义

通过聚类和可视化分析，可以提取出新的特征。比如，根据聚类结果，可以为每个数据点添加一个 “簇标签” 特征，这个特征表示该数据点所属的聚类类别。同时，结合对聚类类别特征的理解，可以赋予这些新特征实际含义。

二、聚类评估指标介绍

以下是三种常用的聚类效果评估指标，分别用于衡量聚类的质量和簇的分离与紧凑程度：

1. 轮廓系数 (Silhouette Score)

定义：轮廓系数衡量每个样本与其所属簇的紧密程度以及与最近其他簇的分离程度。

计算过程：对每个样本，首先计算它到同簇内其他样本的平均距离（记为 a），这代表了样本与自己所在簇的紧密程度；然后计算它到其他簇的最小平均距离（记为 b），b 反映了样本与最近其他簇的分离程度。对所有样本的轮廓系数求平均，就得到了整个数据集的轮廓系数。

取值范围：[-1, 1]

• 轮廓系数越接近 1，表示样本与其所属簇内其他样本很近，与其他簇很远，聚类效果越好。
• 轮廓系数越接近 -1，表示样本与其所属簇内样本较远，与其他簇较近，聚类效果越差（可能被错误分类）。
• 轮廓系数接近 0，表示样本在簇边界附近，聚类效果无明显好坏。

使用建议：选择轮廓系数最高时的 k 值作为最佳簇数量。

---

2. CH 指数 (Calinski-Harabasz Index)

定义：CH 指数是簇间分散度与簇内分散度之比，用于评估簇的分离度和紧凑度。

计算过程：涉及到簇间的协方差矩阵和簇内的协方差矩阵。先计算簇间的平方和（SSB）与簇内的平方和（SSW），SSB 反映了簇间的分散程度，值越大表示簇间差异越大；SSW 反映了簇内的分散程度，值越小表示簇内越紧凑。

其中 k 是簇的数量，n 是样本总数。

取值范围：[0, +∞)

• CH 指数越大，表示簇间分离度越高，簇内紧凑度越高，聚类效果越好。
• 没有固定的上限，值越大越好。

使用建议：选择 CH 指数最高时的 k 值作为最佳簇数量。

---

3. DB 指数 (Davies-Bouldin Index)

定义：DB 指数衡量簇间距离与簇内分散度的比值，用于评估簇的分离度和紧凑度。

计算过程：对于每个簇，先计算它与其他簇的相似度（基于簇内平均距离和簇间距离），然后取所有簇相似度的平均值作为 DB 指数。

取值范围：[0, +∞)

• DB 指数越小（“麻烦指数”），表示簇间分离度越高，簇内紧凑度越高，聚类效果越好。
• 没有固定的上限，值越小越好。

使用建议：选择 DB 指数最低的 k 值作为最佳簇数量。

三、常见聚类算法

# 先运行之前预处理好的代码
import pandas as pd
import pandas as pd    #用于数据处理和分析，可处理表格数据。
import numpy as np     #用于数值计算，提供了高效的数组操作。
import matplotlib.pyplot as plt    #用于绘制各种类型的图表
import seaborn as sns   #基于matplotlib的高级绘图库，能绘制更美观的统计图形。
import warnings
warnings.filterwarnings("ignore")# 设置中文字体（解决中文显示问题）
plt.rcParams['font.sans-serif'] = ['SimHei']  # Windows系统常用黑体字体
plt.rcParams['axes.unicode_minus'] = False    # 正常显示负号
data = pd.read_csv('data.csv')    #读取数据# 先筛选字符串变量 
discrete_features = data.select_dtypes(include=['object']).columns.tolist()
# Home Ownership 标签编码
home_ownership_mapping = {'Own Home': 1,'Rent': 2,'Have Mortgage': 3,'Home Mortgage': 4
}
data['Home Ownership'] = data['Home Ownership'].map(home_ownership_mapping)# Years in current job 标签编码
years_in_job_mapping = {'< 1 year': 1,'1 year': 2,'2 years': 3,'3 years': 4,'4 years': 5,'5 years': 6,'6 years': 7,'7 years': 8,'8 years': 9,'9 years': 10,'10+ years': 11
}
data['Years in current job'] = data['Years in current job'].map(years_in_job_mapping)# Purpose 独热编码，记得需要将bool类型转换为数值
data = pd.get_dummies(data, columns=['Purpose'])
data2 = pd.read_csv("data.csv") # 重新读取数据，用来做列名对比
list_final = [] # 新建一个空列表，用于存放独热编码后新增的特征名
for i in data.columns:if i not in data2.columns:list_final.append(i) # 这里打印出来的就是独热编码后的特征名
for i in list_final:data[i] = data[i].astype(int) # 这里的i就是独热编码后的特征名# Term 0 - 1 映射
term_mapping = {'Short Term': 0,'Long Term': 1
}
data['Term'] = data['Term'].map(term_mapping)
data.rename(columns={'Term': 'Long Term'}, inplace=True) # 重命名列
continuous_features = data.select_dtypes(include=['int64', 'float64']).columns.tolist()  #把筛选出来的列名转换成列表# 连续特征用中位数补全
for feature in continuous_features:     mode_value = data[feature].mode()[0]            #获取该列的众数。data[feature].fillna(mode_value, inplace=True)          #用众数填充该列的缺失值，inplace=True表示直接在原数据上修改。# 最开始也说了 很多调参函数自带交叉验证，甚至是必选的参数，你如果想要不交叉反而实现起来会麻烦很多
# 所以这里我们还是只划分一次数据集
from sklearn.model_selection import train_test_split
X = data.drop(['Credit Default'], axis=1)  # 特征，axis=1表示按列删除
y = data['Credit Default'] # 标签
# # 按照8:2划分训练集和测试集
# X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)  # 80%训练集，20%测试集import numpy as np
import pandas as pd
from sklearn.cluster import KMeans, DBSCAN, AgglomerativeClustering
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import seaborn as sns# 标准化数据（聚类前通常需要标准化）
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

K-Means 算法

KMeans 是一种基于距离的聚类算法，需要预先指定聚类个数，即 `k`。

---

核心步骤：

1. 随机选择 `k` 个样本点作为初始质心（簇中心）。

2. 计算每个样本点到各个质心的距离，将样本点分配到距离最近的质心所在的簇。

3. 更新每个簇的质心为该簇内所有样本点的均值。

4. 重复步骤 2 和 3，直到质心不再变化或达到最大迭代次数为止。

---

肘部法（Elbow Method）

它是一种常用的确定 k 值的方法。

原理：通过计算不同 k 值下的簇内平方和（Within-Cluster Sum of Squares, WCSS），绘制 k 与 WCSS 的关系图。

选择标准：在图中找到“肘部”点，即 WCSS 下降速率明显减缓的 k 值，通常认为是最佳簇数。这是因为增加 k 值带来的收益（WCSS 减少）在该点后变得不显著。

本质：K - Means 算法就是通过不断迭代，最小化簇内平方和（WCSS），让每个簇内的样本尽可能紧密地聚集在一起，使得这个值收敛到一个相对最小的值 。

---

优点：

简单高效：算法实现简单，计算速度快，适合处理大规模数据集。

适用性强：对球形或紧凑的簇效果较好，适用于特征空间中簇分布较为均匀的数据。

易于解释：簇中心有明确意义。例如在客户聚类中，簇中心可以代表该类客户的典型特征。

缺点：

需预先指定 `k` 值：对簇数量 `k` 的选择敏感。若选择不当，k 值过大，会导致每个簇的数据过少，聚类过于细碎；k值过小，又会使不同类的数据被合并到一起，无法准确反映数据真实结构。

对初始质心敏感：初始质心的随机选择可能导致结果不稳定或陷入局部最优，无法得到全局最优的聚类（可通过 KMeans++ 初始化方法缓解）。

对噪声和异常值敏感：异常值可能会显著影响质心的位置，导致聚类结果失真。 

不适合非球形簇：对非线性可分或形状复杂的簇效果较差，无法处理簇密度不均的情况。

---

代码实例：

import numpy as np
import pandas as pd
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.metrics import silhouette_score, calinski_harabasz_score, davies_bouldin_score
import matplotlib.pyplot as plt
import seaborn as sns# 评估不同 k 值下的指标
k_range = range(2, 11)  # 测试 k 从 2 到 10
inertia_values = []
silhouette_scores = []
ch_scores = []
db_scores = []for k in k_range:kmeans = KMeans(n_clusters=k, random_state=42)kmeans_labels = kmeans.fit_predict(X_scaled)# 惯性表示每个样本到其所属簇中心的距离平方和，用于肘部法则来选择最优k值。inertia_values.append(kmeans.inertia_)  silhouette = silhouette_score(X_scaled, kmeans_labels)  # 轮廓系数silhouette_scores.append(silhouette)ch = calinski_harabasz_score(X_scaled, kmeans_labels)  # CH 指数ch_scores.append(ch)db = davies_bouldin_score(X_scaled, kmeans_labels)  # DB 指数db_scores.append(db)print(f"k={k}, 惯性: {kmeans.inertia_:.2f}, 轮廓系数: {silhouette:.3f}, CH 指数: {ch:.2f}, DB 指数: {db:.3f}")# 绘制评估指标图
plt.figure(figsize=(15, 10))# 肘部法则图（Inertia）
plt.subplot(2, 2, 1)
plt.plot(k_range, inertia_values, marker='o')
plt.title('肘部法则确定最优聚类数 k（惯性值越小越好）')
plt.xlabel('聚类数 (k)')
plt.ylabel('惯性')
plt.grid(True)# 轮廓系数图
plt.subplot(2, 2, 2)
plt.plot(k_range, silhouette_scores, marker='o', color='orange')
plt.title('轮廓系数确定最优聚类数 k（越大越好）')
plt.xlabel('聚类数 (k)')
plt.ylabel('轮廓系数')
plt.grid(True)# CH 指数图
plt.subplot(2, 2, 3)
plt.plot(k_range, ch_scores, marker='o', color='green')
plt.title('Calinski-Harabasz 指数确定最优聚类数 k（越大越好）')
plt.xlabel('聚类数 (k)')
plt.ylabel('CH 指数')
plt.grid(True)# DB 指数图
plt.subplot(2, 2, 4)
plt.plot(k_range, db_scores, marker='o', color='red')
plt.title('Davies-Bouldin 指数确定最优聚类数 k（越小越好）')
plt.xlabel('聚类数 (k)')
plt.ylabel('DB 指数')
plt.grid(True)plt.tight_layout()
plt.show()

1. 肘部法则图： 找下降速率变慢的拐点，这里都差不多。
2. 轮廓系数图：找局部最高点，这里选6不能选7。
3. CH指数图： 找局部最高点，这里选7之前的都还行。
4. DB指数图：找局部最低点，这里选6、7、9、10都行。

为什么选择局部最优点：该点处样本整体聚类效果在不同 k 值下相对最佳，聚类结构更合理。

# 提示用户选择 k 值
selected_k = 6# 使用选择的 k 值进行 KMeans 聚类
kmeans = KMeans(n_clusters=selected_k, random_state=42)
kmeans_labels = kmeans.fit_predict(X_scaled)
# 在原始特征数据集 X 中添加新列 KMeans_Cluster，值为样本对应的 KMeans 聚类标签
X['KMeans_Cluster'] = kmeans_labels# 使用 PCA 降维到 2D 进行可视化
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)# KMeans 聚类结果可视化
plt.figure(figsize=(6, 5))
sns.scatterplot(x=X_pca[:, 0], y=X_pca[:, 1], hue=kmeans_labels, palette='viridis')
plt.title(f'KMeans Clustering with k={selected_k} (PCA Visualization)')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.show()# 打印 KMeans 聚类标签的前几行
print(f"KMeans Cluster labels (k={selected_k}) added to X:")
print(X[['KMeans_Cluster']].value_counts())

DBSCAN算法 

DBSCAN（Density - Based Spatial Clustering of Applications with Noise）是一种基于密度的空间聚类算法，无需预先指定聚类个数。

---

核心步骤：

1.定义参数：确定两个关键参数，邻域半径（eps）和最小点数（minPts）。邻域半径 eps 定义了一个点的邻域范围，最小点数 minPts 规定了在一个点的 eps 邻域内最少需要包含的点数，以确定该点是否为核心点。

2.标记核心点：对于数据集中的每个点，计算在其 eps 邻域内的点数。如果点数大于或等于 minPts，则将该点标记为核心点；否则，标记为非核心点。

3.形成簇：从任意一个核心点出发，将其 eps 邻域内的所有点（包括核心点和非核心点）划分为一个簇。对于这些邻域内的核心点，再继续扩展其邻域内的点，不断将相邻的核心点及其邻域点合并到同一个簇中，直到没有新的点可以加入该簇。

4.标记噪声点：所有不属于任何簇的点被标记为噪声点。

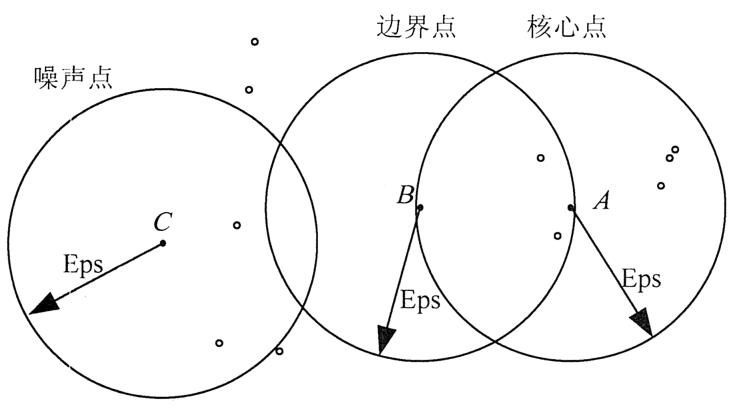
DBSCAN 无需像 K - Means 那样专门确定聚类个数，算法会根据数据的密度分布自动发现不同的簇。每个簇都是基于核心点及其邻域关系自然形成的，聚类个数由数据本身的分布决定。

本质：DBSCAN 通过基于密度的连接性来识别数据集中的簇，将密度相连的数据点归为同一簇，并将低密度区域中的点识别为噪声点，从而实现对数据分布的聚类分析。

---

优点：

无需指定簇数量：能够根据数据的固有结构自动发现合适的簇数，这在很多实际应用场景中更具灵活性，因为事先往往很难准确预估数据应有的类别数量。

能识别噪声点：可以有效识别数据集中的噪声点，将那些处于低密度区域的数据点标记为噪声，而不是强行将它们划分到某个簇中，这使得聚类结果更能反映数据的真实分布情况，对于包含噪声的数据具有更好的鲁棒性。

适应任意形状簇：对任意形状的簇都能较好地识别，不像 K - Means 假设簇是球形或凸形的。DBSCAN 基于密度连接来定义簇，因此可以处理诸如环形、不规则形状等复杂形状的簇，适用于更广泛的数据分布类型。

缺点：

参数选择敏感：对邻域半径 eps 和最小点数 minPts 这两个参数非常敏感。不同的参数设置可能会导致截然不同的聚类结果。

计算密度复杂：在高维数据集中，计算点的密度（即 eps 邻域内的点数）变得更加复杂和耗时。

不适用于密度变化大的数据：如果数据集中不同簇的密度差异较大，DBSCAN 可能无法很好地处理。因为单一的 eps 和 minPts 参数难以同时适应不同密度区域的簇划分，可能会在低密度区域过度合并，而在高密度区域过度分割。

---

代码实例：

import numpy as np
import pandas as pd
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.metrics import silhouette_score, calinski_harabasz_score, davies_bouldin_score
import matplotlib.pyplot as plt
import seaborn as snseps_range = np.arange(0.3, 0.8, 0.1)  # 测试不同邻域半径
min_samples_range = range(3, 8)  # 测试不同最小样本数
results = []for eps in eps_range:for min_samples in min_samples_range:dbscan = DBSCAN(eps=eps, min_samples=min_samples)dbscan_labels = dbscan.fit_predict(X_scaled)# 计算簇的数量（排除噪声点：噪声点标签为-1）n_clusters = len(np.unique(dbscan_labels)) - (1 if -1 in dbscan_labels else 0)# 计算噪声点数量n_noise = list(dbscan_labels).count(-1)# 只有当簇数量大于 1 且有有效簇时才计算评估指标if n_clusters > 1:# 排除噪声点后计算评估指标mask = dbscan_labels != -1if mask.sum() > 0:  # 确保有非噪声点silhouette = silhouette_score(X_scaled[mask], dbscan_labels[mask])ch = calinski_harabasz_score(X_scaled[mask], dbscan_labels[mask])db = davies_bouldin_score(X_scaled[mask], dbscan_labels[mask])results.append({'eps': eps,'min_samples': min_samples,'n_clusters': n_clusters,'n_noise': n_noise,'silhouette': silhouette,'ch_score': ch,'db_score': db})print(f"eps={eps:.1f}, min_samples={min_samples}, 簇数: {n_clusters}, 噪声点: {n_noise}, "f"轮廓系数: {silhouette:.3f}, CH 指数: {ch:.2f}, DB 指数: {db:.3f}")else:print(f"eps={eps:.1f}, min_samples={min_samples}, 簇数: {n_clusters}, 噪声点: {n_noise}, 无法计算评估指标")# 将结果转为 DataFrame 以便可视化和选择参数
results_df = pd.DataFrame(results)
results_df

# 绘制评估指标图
plt.figure(figsize=(15, 10))
# 轮廓系数图
plt.subplot(2, 2, 1)
for min_samples in min_samples_range:# 固定min_samples参数，才可以专注研究eps参数变化时各项评估指标的变化趋势subset = results_df[results_df['min_samples'] == min_samples] # plt.plot(subset['eps'], subset['silhouette'], marker='o', label=f'min_samples={min_samples}')
plt.title('轮廓系数确定最优参数（越大越好）')
plt.xlabel('eps')
plt.ylabel('轮廓系数')
plt.legend()
plt.grid(True)# CH 指数图
plt.subplot(2, 2, 2)
for min_samples in min_samples_range:subset = results_df[results_df['min_samples'] == min_samples]plt.plot(subset['eps'], subset['ch_score'], marker='o', label=f'min_samples={min_samples}')
plt.title('Calinski-Harabasz 指数确定最优参数（越大越好）')
plt.xlabel('eps')
plt.ylabel('CH 指数')
plt.legend()
plt.grid(True)# DB 指数图
plt.subplot(2, 2, 3)
for min_samples in min_samples_range:subset = results_df[results_df['min_samples'] == min_samples]plt.plot(subset['eps'], subset['db_score'], marker='o', label=f'min_samples={min_samples}')
plt.title('Davies-Bouldin 指数确定最优参数（越小越好）')
plt.xlabel('eps')
plt.ylabel('DB 指数')
plt.legend()
plt.grid(True)# 簇数量图
plt.subplot(2, 2, 4)
for min_samples in min_samples_range:subset = results_df[results_df['min_samples'] == min_samples]plt.plot(subset['eps'], subset['n_clusters'], marker='o', label=f'min_samples={min_samples}')
plt.title('簇数量变化')
plt.xlabel('eps')
plt.ylabel('簇数量')
plt.legend()
plt.grid(True)plt.tight_layout()
plt.show()

# 选择 eps 和 min_samples 值（根据图表选择最佳参数）
selected_eps = 0.6 
selected_min_samples = 6  # 使用选择的参数进行 DBSCAN 聚类
dbscan = DBSCAN(eps=selected_eps, min_samples=selected_min_samples)
dbscan_labels = dbscan.fit_predict(X_scaled)
X['DBSCAN_Cluster'] = dbscan_labels# 使用 PCA 降维到 2D 进行可视化
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)# DBSCAN 聚类结果可视化
plt.figure(figsize=(6, 5))
sns.scatterplot(x=X_pca[:, 0], y=X_pca[:, 1], hue=dbscan_labels, palette='viridis')
plt.title(f'DBSCAN Clustering with eps={selected_eps}, min_samples={selected_min_samples} (PCA Visualization)')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.show()# 打印 DBSCAN 聚类标签的分布
print(f"DBSCAN Cluster labels (eps={selected_eps}, min_samples={selected_min_samples}) added to X:")
print(X[['DBSCAN_Cluster']].value_counts())

在 DBSCAN 聚类结果中，标签为 -1 的样本数量高达 7452，而其他簇（标签 0 - 5 ）样本数极少 。标签 -1 在 DBSCAN 中代表噪声点，说明大部分样本被判定为噪声，少数簇样本量少，这表明聚类效果不佳，可能存在问题：

参数不合适：eps（邻域半径）和 min_samples（最小样本数）设置不当。eps 过小，会使样本难以形成簇，大量样本被划分为噪声；min_samples 过大，也会导致簇难以生成。

数据特性：数据分布可能不适合 DBSCAN 算法。DBSCAN 适用于样本分布有明显密度差异的情况，若数据分布较为均匀或不存在明显的密度相连区域，该算法就难以有效聚类。

---

层次聚类算法

层次聚类算法是一种基于簇间相似度构建树形聚类结构的算法，不需要预先指定聚类个数，但在实际应用中，常根据具体需求从生成的聚类结构中确定聚类数。

---

核心步骤：

主要分为凝聚式（自底向上）和分裂式（自顶向下）两种，这里以常用的凝聚式层次聚类为例：

初始化：将每个数据点视为一个单独的簇。此时，簇的数量等于数据点的数量。

计算簇间距离：计算每两个簇之间的距离。常用的距离度量方法有单链接（两个簇中距离最近的两个点之间的距离）、完全链接（两个簇中距离最远的两个点之间的距离）、平均链接（两个簇中所有点对之间距离的平均值）等。

合并簇：找出距离最近的两个簇，并将它们合并为一个新簇。

重复步骤 2 和 3：不断重复计算簇间距离和合并簇的过程，直到所有的数据点都在一个簇中，或者达到某个终止条件（例如簇的数量达到预期值）。这样就生成了一个树形结构，称为树状图（dendrogram）。

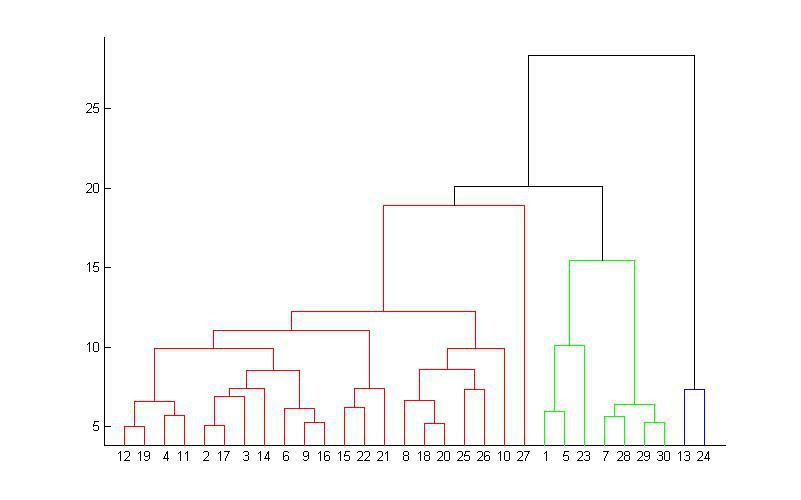在实际应用中，从生成的树状图确定聚类个数并没有一个固定的标准方法，常见思路有：

基于先验知识：根据业务背景或数据特点，预先知道大概的聚类数量，然后在树状图上选择合适的层次进行切割，得到相应数量的簇。

观察树状图：直观地观察树状图，选择在树状图上簇间距离变化较大的位置进行切割，使得切割后得到的簇相对合理。

本质：通过逐步合并（凝聚式）或分裂（分裂式）数据点或簇，构建出一个反映数据点之间亲疏关系的树形结构。

---

优点：

无需预先指定聚类数：与 K - Means 不同，层次聚类不需要事先确定聚类的数量，而是生成一个包含所有可能聚类情况的树形结构，用户可以根据实际需求在事后灵活选择聚类数。

能够发现数据的层次结构：该算法可以揭示数据内在的层次关系，这对于理解数据的组织结构非常有帮助。例如在生物学中对物种进行分类，层次聚类可以展现出物种之间从低级到高级的分类层次。

对数据分布适应性较好：相对 K - Means 对球形簇的假设，层次聚类可以处理各种形状的数据分布，因为它是基于数据点之间的相似度或距离逐步构建聚类结构，而不是基于质心。

缺点：

计算复杂度高：每一步合并都需要重新计算所有簇之间的距离，随着数据量的增大，计算量会急剧增加，因此不太适合处理大规模数据集。

结果不可逆：一旦两个簇合并（或一个簇分裂），在后续步骤中无法撤销这个操作。如果在某个阶段做出了不恰当的合并（或分裂）决策，可能会导致最终聚类结果不佳。

对噪声敏感：由于是基于距离进行簇的合并或分裂，噪声点可能会对簇间距离的计算产生较大影响，进而干扰聚类结果。例如，噪声点可能会使原本不应合并的簇被合并在一起。

确定聚类数主观性强：从树状图中选择合适的聚类数主要依赖于用户的主观判断，不同的人可能会因为观察角度不同而选择不同的聚类数，缺乏客观统一的标准。

---

代码实例：

import numpy as np
import pandas as pd
from sklearn.cluster import AgglomerativeClustering
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.metrics import silhouette_score, calinski_harabasz_score, davies_bouldin_score
import matplotlib.pyplot as plt
import seaborn as sns# 标准化数据
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 评估不同 n_clusters 下的指标
n_clusters_range = range(2, 11)  # 测试簇数量从 2 到 10
silhouette_scores = []
ch_scores = []
db_scores = []for n_clusters in n_clusters_range:# 指定聚类数量为当前循环的n_clusters，并使用ward链接准则来合并簇。agglo = AgglomerativeClustering(n_clusters=n_clusters, linkage='ward')  agglo_labels = agglo.fit_predict(X_scaled)# 计算评估指标silhouette = silhouette_score(X_scaled, agglo_labels)ch = calinski_harabasz_score(X_scaled, agglo_labels)db = davies_bouldin_score(X_scaled, agglo_labels)silhouette_scores.append(silhouette)ch_scores.append(ch)db_scores.append(db)print(f"n_clusters={n_clusters}, 轮廓系数: {silhouette:.3f}, CH 指数: {ch:.2f}, DB 指数: {db:.3f}")# 绘制评估指标图
plt.figure(figsize=(15, 5))# 轮廓系数图
plt.subplot(1, 3, 1)
plt.plot(n_clusters_range, silhouette_scores, marker='o')
plt.title('轮廓系数确定最优簇数（越大越好）')
plt.xlabel('簇数量 (n_clusters)')
plt.ylabel('轮廓系数')
plt.grid(True)# CH 指数图
plt.subplot(1, 3, 2)
plt.plot(n_clusters_range, ch_scores, marker='o')
plt.title('Calinski-Harabasz 指数确定最优簇数（越大越好）')
plt.xlabel('簇数量 (n_clusters)')
plt.ylabel('CH 指数')
plt.grid(True)# DB 指数图
plt.subplot(1, 3, 3)
plt.plot(n_clusters_range, db_scores, marker='o')
plt.title('Davies-Bouldin 指数确定最优簇数（越小越好）')
plt.xlabel('簇数量 (n_clusters)')
plt.ylabel('DB 指数')
plt.grid(True)plt.tight_layout()
plt.show()

# 提示用户选择 n_clusters 值（这里可以根据图表选择最佳簇数）
selected_n_clusters = 10  # 示例值，根据图表调整# 使用选择的簇数进行 Agglomerative Clustering 聚类
agglo = AgglomerativeClustering(n_clusters=selected_n_clusters, linkage='ward')
agglo_labels = agglo.fit_predict(X_scaled)
X['Agglo_Cluster'] = agglo_labels# 使用 PCA 降维到 2D 进行可视化
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)# Agglomerative Clustering 聚类结果可视化
plt.figure(figsize=(6, 5))
sns.scatterplot(x=X_pca[:, 0], y=X_pca[:, 1], hue=agglo_labels, palette='viridis')
plt.title(f'Agglomerative Clustering with n_clusters={selected_n_clusters} (PCA Visualization)')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.show()# 打印 Agglomerative Clustering 聚类标签的分布
print(f"Agglomerative Cluster labels (n_clusters={selected_n_clusters}) added to X:")
print(X[['Agglo_Cluster']].value_counts())

# 层次聚类的树状图可视化
from scipy.cluster import hierarchy
import matplotlib.pyplot as plt# 假设 X_scaled 是标准化后的数据
# 计算层次聚类的链接矩阵
Z = hierarchy.linkage(X_scaled, method='ward')  # 'ward' 是常用的合并准则# 绘制树状图
plt.figure(figsize=(10, 6))
hierarchy.dendrogram(Z, truncate_mode='level', p=3)  # p控制显示的层次深度，显示最后3层
# hierarchy.dendrogram(Z, truncate_mode='level')  # 不用p这个参数，可以显示全部的深度
plt.title('Dendrogram for Agglomerative Clustering')
plt.xlabel('Cluster Size')
# 纵轴反映在聚类过程中，不同样本或簇合并时的距离度量值。距离越大，差异越大。
plt.ylabel('Distance')
plt.show()

@浙大疏锦行