【C++】AVL树实现

目录

前言

一、AVL树的概念

二、AVL树的实现

1.基本框架

2.AVL树的插入

三、旋转

1.右单旋

2.左单旋

3.左右双旋

4.右左双旋

四、AVL树的查找

五、AVL树的平衡检测

六、AVL树的删除

总结

---

---

前言

        本文主要讲解AVL树的插入，AVL树是在二叉搜索树的基础上，更加实用的一种数据结构，它拥有自平衡的特性，来保证它的搜索效率，本文就来探究它是如何实现自平衡的。

---

温馨提醒：本文所有代码中父节点我拼写成了perent，正确拼写应该是parent，不好意思，望周知(✪ω✪)。 

一、AVL树的概念

• AVL 树是最先发明的自平衡二叉查找树，AVL是一颗空树，或者具备下列性质的二叉搜索树：它的左右子树都是AVL树，且左右子树的高度差的绝对值不超过1。AVL树是⼀颗高度平衡搜索二叉树， 通过控制高度差去控制平衡。
• AVL树得名于它的发明者G.M.Adelson-Velsky和E.M.Landis是两个前苏联的科学家，他们在1962 年的论文《Analgorithmfortheorganizationofinformation》中发表了它。
• AVL树实现这里我们引入一个平衡因子(balancefactor)的概念，每个结点都有一个平衡因子，任何结点的平衡因子等于右子树的高度减去左子树的高度，也就是说任何结点的平衡因子等于0/1/-1， AVL树并不是必须要平衡因子，但是有了平衡因子可以更方便我们去进行观察和控制树是否平衡， 就像一个风向标一样。
• 思考一下为什么AVL树是高度平衡搜索二叉树，要求高度差不超过1，而不是高度差是0呢？0不是更好的平衡吗？画画图分析我们发现，不是不想这样设计，而是有些情况是做不到高度差是0的。比如一棵树是2个结点，4个结点等情况下，高度差最好就是1，无法做到高度差是0。如下图一棵AVL树，它的平衡因子绝对值不超过1.
• 
• 反之，如果平衡因子绝对值大于1，就不是AVL树，如下图：
• AVL树整体结点数量和分布和完全二叉树类似，高度可以控制在logN，那么增删查改的效率也可以控制在O(logN)，相比二叉搜索树有了本质的提升。效率计算如下图：
• 

温馨提醒：本章节需要有二叉搜索树的基础，主页有哦，AVL树就是在二叉搜索树上增加了自平衡机制，调整子树高度差，保证查找效率。

---

二、AVL树的实现

1.基本框架

#pragma once
#include <assert.h>template<class K, class V>
struct AVLTreeNode
{pair<K, V> _kv;//k:v结构AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _perent;int _bf;//平衡因子AVLTreeNode(const pair<K, V>& kv)//构造:_kv(kv), _left(nullptr), _right(nullptr), _perent(nullptr), _bf(0){}
};template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;//重命名
public:private:Node* _root = nullptr;//根节点
};

• AVL树的基本框架与搜索二叉树有点不同，主要是节点定义的区别：

1. 节点的数据结构采用 key:value 结构，也就是使用pair保存数据。
2. 节点采用三叉链结构，即有左孩子节点指针、右孩子节点指针、父节点指针。
3. 增加成员变量 _bf，也就是平衡因子，用于检测每一个节点是否符合AVL树的特征（左右子树高度差不超过1）。

• 然后，AVL树的模版参数K,V，分别控制数据key:value的数据类型。类只有一个变量_root，也就是根节点。

温馨提醒：不要忘记了搜索二叉树的特性：对于不支持相等值的搜索二叉树，每个节点的左子树的数据全小于根节点，右子树的数据全大于根节点。

---

2.AVL树的插入

AVL树插入一个值的大概过程：

1. 插入一个值按二叉搜索树规则进行插入。
2. 新增结点以后，只会影响祖先结点的高度，也就是可能会影响部分祖先结点的平衡因子，所以更新从新增结点 -> 根结点路径上的平衡因子，实际中最坏情况下要更新到根节点，有些情况更新到中间就可以停止了，具体情况我们下面再详细分析。
3. 更新平衡因子过程中没有出现问题，则插入结束。
4. 更新平衡因子过程中出现不平衡，对不平衡子树旋转，旋转后调平衡的同时，本质降低了子树的高度，不会再影响上⼀层，所以插入结束。

我们先不管更新平衡因子和旋转，先把前面的代码写出来：

    //插入bool Insert(const pair<K, V>& kv){//树为空if (_root == nullptr){_root = new Node(kv);return true;}//树不为空Node* cur = _root;Node* perent = nullptr;while (cur){if (kv.first > cur->_kv.first){perent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){perent = cur;cur = cur->_left;}else{return false;}}//插入cur = new Node(kv);if (kv.first > perent->_kv.first){perent->_right = cur;}else{perent->_left = cur;}cur->_perent = perent;//更新平衡因子//...return true;}

• 这些就基本和搜索二叉树一致，这里就不赘述了。
• 需要注意的是插入新节点后记得更新新节点的父节点指针，毕竟是三叉链。

---

1.平衡因子更新：

更新原则：

• 平衡因子=右子树⾼度-左子树高度
• 只有子树高度变化才会影响当前结点平衡因子。
• 插入结点，会增加高度，所以新增结点在parent的右子树，parent的平衡因子++，新增结点在parent的左子树，parent平衡因子--。
• parent所在子树的高度是否变化决定了是否会继续往上更新。

我们先看一些实际情况：来了解什么时候可以停止向上更新平衡因子

（1）

• 如上图，新增节点13，在节点14的左边，所以14的平衡因子--，14的平衡因子变化就可能会引起其父节点平衡因子变化。因为14节点的平衡因子是由0变化到-1，所以它高度一定是加1，14的父节点是节点10，14在10的右边，所以14的平衡因子要++，此时对于节点10来说，平衡因子绝对值大于1了，需要旋转处理。（先不管如何旋转）
• 我们继续观察节点14，它的平衡因子原来是0，现在变成-1，说明它原来的子树高度差为0，插入一个节点后导致它高度差变化，所以，在插入节点操作中如果平衡因子变为-1，说明它一定是由0变化过来的，并且需要继续向上更新父节点的平衡因子。同理我们也能得出，如果插入操作导致平衡因子变为-1，说明它一定是从0变过来的，而且也需要继续向上更新平衡因子。
• 得出一条结论：更新后parent的平衡因子等于1或-1，更新前更新中parent的平衡因子变化为 0->1 或者 0->-1，说明更新前 parent 子树两边⼀样高，新增的插入结点后，parent所在的子树一边高一边低，parent所在的子树符合平衡要求，但是高度增加了1，会影响parent的父亲结点的平衡因子，所以要继续向上更新。
• 我们继续观察节点10，它的平衡因子变化是因为右子树新增一个节点，导致它的平衡因子从1变为2，此时它已经不满足AVL树了，需要进行旋转操作，我们先不管怎么旋转，我们先了解旋转的结果，旋转的目标有两个：1、把 parent子树旋转平衡。2、降低parent子树的高度，恢复到插入结点以前的高度。这样一来，相当于节点10的平衡因子没有发生变化，所以此时不需要向上更新平衡因子。同理当平衡因子从-1变为-2，我们也不需要向上更新父节点的平衡因子。
• 得出第二条结论：更新后parent的平衡因子等于2或-2，更新前更新中parent的平衡因子变化为1->2或者-1->-2，说明更新前parent子树一边高一边低，新增的插入结点在高的那边，parent所在的子树高的那边更高了，破坏了平衡，parent所在的子树不符合平衡要求，需要旋转处理，旋转的目标有两个：1、把 parent子树旋转平衡。2、降低parent子树的高度，恢复到插入结点以前的高度。所以旋转后也不需要继续往上更新，插入结束。

（2）

• 如上图，这次插入节点-1，位于父节点1的左子树，所以父节点1的平衡因子--，此时因为节点1的平衡因子发生变化，所以需要继续向上更新，节点1的父节点3的平衡因子此时从1变为0，这说明新增节点导致节点3的左右子树高度平衡了，这时我们还需要继续向上更新平衡因子吗？答案是不用了，因为平衡因子变为0说明它一定是从-1或者1变过来的，变化前高度差为1，变化后高度差为0，这对于其父节点来说高度没变化，所以不需要继续向上更新平衡因子了。
• 得出结论：更新后parent的平衡因子等于0，更新中parent的平衡因子变化为-1->0或者1->0，说明更新前 parent 子树一边高一边低，新增的结点插入在低的那边，插入后parent所在的子树高度不变，不会影响parent的父亲结点的平衡因子，更新结束。

（3）

• 插入节点7，节点6的平衡因子加1，节点3的平衡因子加1，根节点8的平衡因子也要加1。所以这就是最后一种情况也是最坏的情况，需要我们一路向上更新的根节点。
• 总结：如果平衡因子变为1或者-1，继续向上更新，如果一直到根节点平衡因子还是1或者-1，则停止更新。

---

2.总结：平衡因子更新停止条件

1. 更新后parent的平衡因子等于0，更新中parent的平衡因子变化为-1->0或者1->0，说明更新前 parent 子树一边高一边低，新增的结点插入在低的那边，插入后parent所在的子树高度不变，不会影响parent的父亲结点的平衡因子，更新结束。
2. 更新后parent的平衡因子等于1或-1，更新前更新中parent的平衡因子变化为 0->1 或者 0->-1，说明更新前 parent 子树两边⼀样高，新增的插入结点后，parent所在的子树一边高一边低，parent所在的子树符合平衡要求，但是高度增加了1，会影响parent的父亲结点的平衡因子，所以要继续向上更新。
3. 更新后parent的平衡因子等于2或-2，更新前更新中parent的平衡因子变化为1->2或者-1->-2，说明更新前parent子树一边高一边低，新增的插入结点在高的那边，parent所在的子树高的那边更高了，破坏了平衡，parent所在的子树不符合平衡要求，需要旋转处理，旋转的目标有两个：1、把 parent子树旋转平衡。2、降低parent子树的高度，恢复到插入结点以前的高度。所以旋转后也不需要继续往上更新，插入结束。
4. 如果平衡因子变为1或者-1，继续向上更新，如果一直到根节点平衡因子还是1或者-1，则停止更新。（最坏情况）

更新平衡因子代码：

//插入
bool Insert(const pair<K, V>& kv)
{//树为空if (_root == nullptr){_root = new Node(kv);return true;}//树不为空Node* cur = _root;Node* perent = nullptr;while (cur){if (kv.first > cur->_kv.first){perent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){perent = cur;cur = cur->_left;}else{return false;}}//插入cur = new Node(kv);if (kv.first > perent->_kv.first){perent->_right = cur;}else{perent->_left = cur;}cur->_perent = perent;//更新平衡因子while (perent){if (cur == perent->_left)//插入节点位于左边{--perent->_bf;//平衡因子--}else//插入节点位于右边{++perent->_bf;//平衡因子++}if (perent->_bf == 0)//平衡因子等于0{break;//直接结束}else if (perent->_bf == -1 || perent->_bf == 1)//平衡因子需要继续向上更新{cur = perent;//更新cur为父节点perent = perent->_perent;//更新父节点为父父节点}else if (perent->_bf == -2 || perent->_bf == 2)//不满足AVL树，需要旋转处理{//旋转//...break;//旋转完直接结束}else//平衡因子出现其它值，说明存在bug{assert(false);//说明出现bug，报错处理}}return true;
}

• 以上就是插入节点时关于平衡因子更新的代码，应该不难理解。
• 接下来就是关于旋转怎么操作的问题了。

---

三、旋转

旋转的原则：

1. 保持搜索树的规则
2. 让旋转的树从不满足平衡变平衡，其次降低旋转树的高度，恢复到以前的高度（注意不是平衡因子）

旋转总共分为四种：左单旋/右单旋/左右双旋/右左双旋。

1.右单旋

• 以上就是一个完整的右单旋过程，看不懂没关系，我们一步一步来。
• 上图展示的是10为根的树，有a/b/c抽象为三棵高度为h的子树(h>=0)，a/b/c均符合AVL树的要求。10可能是整棵树的根，也可能是一个整棵树中局部的子树的根。这里a/b/c是高度为h的子树， 是一种概括抽象表示，他代表了所有右单旋的场景，实际右单旋形态有很多种。
• 这里首先的问题就是为啥 a，b，c 要抽象成三个子树，而不是具体的节点，我们通过下面几个案例就会明白了。

（1）h=0

• 当 a，b，c 为h=0的三颗子树时，那么就只有两个节点，此时在 a 位置插入节点1，这时，根节点10的平衡因子变为-2，然后进行旋转操作，平衡了高度差。
• 所以当h=0时，右单旋只有一种情况。

---

（2）h=1

• h=1时，a,b,c就是一个节点的子树，此时也只有一种情况。
• 我们先不管如何旋转，先观察插入位置，插入位置都是最左边最高处。

---

（3）h=2

• h=2，h=2的子树有3种情况，如上图中的 X，Y，Z。
• 这里需要注意，子树a只能是X这一种情况，子树b,c可以是这三种任意一种，为什么呢？因为是在子树a插入新节点，然后需要保证影响到根节点10以此触发旋转操作，如果a树为Y,Z一种，那么新插入节点后a要么平衡要么不平衡，a平衡不会影响到根节点的平衡因子，a不平衡则自身会触发旋转操作，最终也不会影响根节点的平衡因子。所以a只能是X。
• 通过计算，h=2时，一共有36种情况，而这些情况都可以经过右单旋恢复平衡。

（4）h=3

• h=3时，高度为3的子树就有非常多的情况了，可以分为上图中X和y-C，y-C表示最后一层四个叶子结点保留任意1个/任意2个/任意3个的子树。
• 同h=2，这里a子树也只能是X这种情况，计算下来，一共有5400种情况，以至于画图时不得不使用抽象的子树a,b,c来表示。
• 所以你应该明白了为什么a,b,c要使用抽象的子树表示吧，就是因为有无数种情况，无数种情况都可以抽象成a,b,c来表示。

---

 理解了a,b,c的含义，我们接下来观察旋转如何实现：

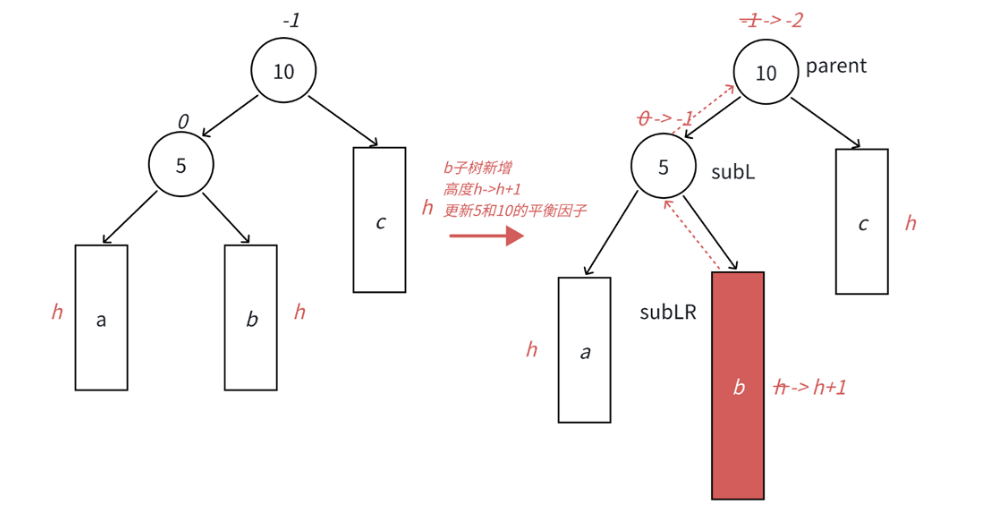
• 如图，在a子树中插入一个新结点，导致a子树的高度从h变成h+1，不断向上更新平衡因子，导致10的平衡因子从-1变成-2，10为根的树左右高度差超过1，违反平衡规则。10为根的树左边太高了，需要往右边旋转，控制两棵树的平衡。
• 旋转核心步骤，因为5 < b子树的值 < 10，将b变成10的左子树，10变成5的右子树，5变成这棵树新的根，符合搜索树的规则，控制了平衡，同时这棵树的高度恢复到了插入之前的h+2，符合旋转原则。如果插入之前根节点为10的整棵树是一个局部子树，旋转后不会再影响上一层，插入结束了。
• 简单点说，为什么可以这样旋转，因为b和10节点都大于节点5，所以b和10节点都能作为5的右子树。因为b一开始是10的左边，所以让b直接成为10的左子树。最后整棵树的高度恢复了到了h+1，这样就平衡了高度差。
• 我们通过观察上面h=0,1,2,3的案例，就能发现，只要出现根节点的左孩子平衡因子变为-1，导致根节点平衡因子变为-2，就可以使用右单旋进行调整了。

（1）右单旋的代码实现：

//右单旋
void RotateR(Node* perent)
{Node* subL = perent->_left;//左孩子Node* subLR = subL->_right;//左孩子的右孩子//旋转过去perent->_left = subLR;subL->_right = perent;Node* ppNode = perent->_perent;//记录父父节点//更新父节点指针if (subLR)subLR->_perent = perent;perent->_perent = subL;if (perent == _root)//判断根节点{_root = subL;subL->_perent = nullptr;}else{if (ppNode->_left == perent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_perent = ppNode;}//更新平衡因子subL->_bf = perent->_bf = 0;
}

代码解释： 

• 
• 因为右单旋受影响的节点有根节点、根节点的左孩子、左孩子的右子树。所以如上图，我们将根节点命名parent，左孩子命名subL，左孩子右子树命名subLR
• 首先第一步就是将b（subLR）旋转过去作为根节点（parent）的左子树，然后将parent点作为左孩子（subL）的右孩子。
• 然后因为是三叉链，所以我们还需要更新subLR和parent的父节点指针，这里需要注意的是subLR可能为0，如h=0时，所以我们需要if判断一下。
• 其次就是根节点的更新，因为可能是局部子树也可能是整棵树，所以在更新父节点指针前，先保存parent的父节点指针ppNode。我们先判断parent是不是根节点，是：我们就更新subL为新根节点然后令subL的父节点指针为空，因为根节点没有父节点。否：说明是局部子树，所以我们先判断parent是ppNode的哪个孩子节点，然后调整ppNode的该孩子节点指向subL，最后令subL的父节点指针指向ppNode。这样就完成了根节点的更新。
• 最后就是更新平衡因子了。我们根据上面和上上面的图就能得知，平衡因子受影响的只有parent和subL，a,b,c子树是作为整体不受影响，并且，parent和subL的平衡因子经过旋转后就一定为0，这一点通过图就能直观的得出来。

完成右单旋代码后，我们就可以更新一下插入函数了：

//插入
bool Insert(const pair<K, V>& kv)
{//树为空if (_root == nullptr){_root = new Node(kv);return true;}//树不为空Node* cur = _root;Node* perent = nullptr;while (cur){if (kv.first > cur->_kv.first){perent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){perent = cur;cur = cur->_left;}else{return false;}}//插入cur = new Node(kv);if (kv.first > perent->_kv.first){perent->_right = cur;}else{perent->_left = cur;}cur->_perent = perent;//更新平衡因子while (perent){if (cur == perent->_left)//插入节点位于左边{--perent->_bf;//平衡因子--}else//插入节点位于右边{++perent->_bf;//平衡因子++}if (perent->_bf == 0)//平衡因子等于0{break;//直接结束}else if (perent->_bf == -1 || perent->_bf == 1)//平衡因子需要继续向上更新{cur = perent;//更新cur为父节点perent = perent->_perent;//更新父节点为父父节点}else if (perent->_bf == -2 || perent->_bf == 2)//不满足AVL树，需要旋转处理{//旋转if (perent->_bf == -2 && cur->_bf == -1)//左边高{RotateR(perent);//右单旋}//剩余情况//...break;//旋转完直接结束}else{assert(false);//说明出现bug，报错处理}}return true;
}

• 右旋转，顾名思义就是朝右边旋转。
• 
• 条件：纯粹的左边高，观察上面的图，也就是根节点（parent）的左孩子节点（cur）的左子树高（a），导致根节点平衡因子超了。
• 注意：根节点的左孩子节点的左子树，也就是a，a的形状是不确定的，所以只关注cur的平衡因子。
• 所以右旋转条件写成代码就是：perent->_bf == -2 && cur->_bf == -1

---

2.左单旋

理解了右单旋，左单旋就好说了。

• 如上图展示的是10为根的树，有a/b/c抽象为三棵高度为h的子树(h>=0)，a/b/c均符合AVL树的要求。10可能是整棵树的根，也可能是一个整棵树中局部的子树的根。这里a/b/c是高度为h的子树， 是一种概括抽象表示，他代表了所有右单旋的场景，实际右单旋形态有很多种，具体跟上面左旋类似。
• 在a子树中插入一个新结点，导致a子树的高度从h变成h+1，不断向上更新平衡因子，导致10的平衡因子从1变成2，10为根的树左右高度差超过1，违反平衡规则。10为根的树右边太高了，需要往左边旋转，控制两棵树的平衡。
• 旋转核心步骤，因为10 < b子树的值 <15，将b变成10的右子树，10变成15的左子树，15变成这棵树新的根，符合搜索树的规则，控制了平衡，同时这棵的高度恢复到了插入之前的h+2，符合旋转原则。如果插入之前10整棵树是一个局部子树，旋转后不会再影响上一层，插入结束了。最后树的高度依旧恢复到了h+1
• 总体上说就是右单旋的反方向版，受影响的3个位置：根节点（parent）、右孩子节点（subR）、右孩子的左子树（subRL）。

（1）左单旋代码实现

//左单旋
void RotateL(Node* perent)
{Node* subR = perent->_right;Node* subRL = subR->_left;//旋转过去perent->_right = subRL;subR->_left = perent;Node* ppNode = perent->_perent;//父父节点//更新父节点指针if (subRL)subRL->_perent = perent;perent->_perent = subR;//判断父父节点if (perent == _root){_root = subR;subR->_perent = nullptr;}else{if (ppNode->_left == perent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_perent = ppNode;}subR->_bf = perent->_bf = 0;
}

• 和右单旋一样，先将b旋转过去，将subRL变成parent的右子树，将parent变为subR的左孩子，随后更新父节点指针，然后更新根节点，最后更新parent和subR的平衡因子。

完成左单旋后可以更新一下插入函数：

//插入
bool Insert(const pair<K, V>& kv)
{//树为空if (_root == nullptr){_root = new Node(kv);return true;}//树不为空Node* cur = _root;Node* perent = nullptr;while (cur){if (kv.first > cur->_kv.first){perent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){perent = cur;cur = cur->_left;}else{return false;}}//插入cur = new Node(kv);if (kv.first > perent->_kv.first){perent->_right = cur;}else{perent->_left = cur;}cur->_perent = perent;//更新平衡因子while (perent){if (cur == perent->_left)//插入节点位于左边{--perent->_bf;//平衡因子--}else//插入节点位于右边{++perent->_bf;//平衡因子++}if (perent->_bf == 0)//平衡因子等于0{break;//直接结束}else if (perent->_bf == -1 || perent->_bf == 1)//平衡因子需要继续向上更新{cur = perent;//更新cur为父节点perent = perent->_perent;//更新父节点为父父节点}else if (perent->_bf == -2 || perent->_bf == 2)//不满足AVL树，需要旋转处理{//旋转if (perent->_bf == -2 && cur->_bf == -1)//左边高{RotateR(perent);//右单旋}else if (perent->_bf == 2 && cur->_bf == 1)//右边高{RotateL(perent);//左单旋}//其他情况...break;//旋转完直接结束}else{assert(false);//说明出现bug，报错处理}}return true;
}

•  perent->_bf == 2 && cur->_bf == 1，也就是只有parent平衡因子为2并且subR（cur）平衡因子为1的情况，也就是纯粹的右边高，这时使用左单旋。

---

3.左右双旋

（1）问题引入

• 通过上面两图可以看到，左边高时，如果插入位置不是在a子树，而是插入在b子树，b子树高度从h变成h+1，引发旋转，右单旋无法解决问题，右单旋后，我们的树依旧不平衡。右单旋解决的是纯粹的左边高，但是插入在b子树中，10为跟的子树不再是单纯的左边高，对于10是左边高，但是对于5是右边高，这时需要用两次旋转才能解决。
• 判断是不是纯粹的左边高或者右边高，根据图，从新插入节点出发到根节点，如果是一条直线那么就是纯粹的一边高，如果是折线就不是。

（2）解决方法

首先我们子树的表示就直接用抽象图，前面已经解释过了，其实抽象子树最好一点就是其平衡因子不会发生变化，因为是当成一个整体移动。

• 第一步：将子树b拆分，拆分成一个具体节点（比5大比10小）和两棵抽象子树e和f

• 第二步：节点5为首的左子树，单独对这个左子树进行左单旋，将整棵树变为纯粹的左边高。

• 第三步：对整棵树进行右单旋，注意此时需要将上图中节点5的子树和子树f视为两颗抽象子树

因为先进行左单旋，后进行右单旋，所以取名左右双旋

（3）平衡因子更新 

其实旋转过程很简单，只需要调用上面已经写好的单旋函数即可。真正难点是更新平衡因子，因为子树b被拆分成了e和f，那么新插入节点就有可能位于e也可能位于f，根据上图，e和f最终成为了根节点的左右孩子节点的右左子树。所以就会影响到根节点和左右孩子节点的平衡因子。

• 第一种：插入在e
• 此时parent=1，subL=0，subLR=0
• 第二种：插入在f
• 此时parent=0，subL=-1，subLR=0
• 其实还有第三种：b子树高度h=0，也就是b就是新插入节点
• 此时parent=0，subL=0，subLR=0
• 现在问题是如何判断插入位置？我们可以根据subLR的平衡因子进行判断，subLR=-1说明左边插入，subLR=1说明右边插入，subLR=0说明自己就是新增节点。

（5）左右双旋代码实现

//左右双旋
void RotateLR(Node* perent)
{Node* subL = perent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;//单旋前先记录平衡因子RotateL(perent->_left);//先对左子树进行左单旋RotateR(perent);//对整体进行右单旋if (bf == -1)//左边高{perent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}else if (bf == 1)//右边高{perent->_bf = 0;subL->_bf = -1;subLR = 0;}else if (bf == 0)//自己就是新增节点{perent->_bf = 0;subL->_bf = 0;subLR = 0;}else//如果真走到这里说明有bug{assert(false);}
}

• 首先需要注意的是，调用单旋会把平衡因子更新为0，所以需要提前记录subLR的平衡因子。
• 然后，既然调用单旋会把平衡因子更新为0，那为什么还需要写bf==0的情况，这其实是一个好习惯，因为写了bf==0的情况那么无论单旋函数会不会将平衡因子变为0，都不会影响双旋函数更新平衡因子，这就是降低耦合性。

最后，我们继续完善一下插入函数代码中的旋转条件：

//插入
bool Insert(const pair<K, V>& kv)
{//树为空if (_root == nullptr){_root = new Node(kv);return true;}//树不为空Node* cur = _root;Node* perent = nullptr;while (cur){if (kv.first > cur->_kv.first){perent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){perent = cur;cur = cur->_left;}else{return false;}}//插入cur = new Node(kv);if (kv.first > perent->_kv.first){perent->_right = cur;}else{perent->_left = cur;}cur->_perent = perent;//更新平衡因子while (perent){if (cur == perent->_left)//插入节点位于左边{--perent->_bf;//平衡因子--}else//插入节点位于右边{++perent->_bf;//平衡因子++}if (perent->_bf == 0)//平衡因子等于0{break;//直接结束}else if (perent->_bf == -1 || perent->_bf == 1)//平衡因子需要继续向上更新{cur = perent;//更新cur为父节点perent = perent->_perent;//更新父节点为父父节点}else if (perent->_bf == -2 || perent->_bf == 2)//不满足AVL树，需要旋转处理{//旋转if (perent->_bf == -2 && cur->_bf == -1)//左边高{RotateR(perent);//右单旋}else if (perent->_bf == 2 && cur->_bf == 1)//右边高{RotateL(perent);//左单旋}else if (perent->_bf == -2 && cur->_bf == 1)//左的中间高{RotateLR(perent);//左右双旋}//剩余情况...break;//旋转完直接结束}else{assert(false);//说明出现bug，报错处理}}return true;
}

• 
• 根据图就能发现，需要左右双旋的条件就是，subL的平衡因子=1.
• 也就是：perent->_bf == -2 && cur->_bf == 1

---

4.右左双旋

同理，我们先对右子树进行右单旋，再对整树进行左单旋。然后分三种情况讨论平衡因子的更新

• 
• 
• 
• 
• 跟左右双旋类似，下面我们将a/b/c子树抽象为高度h的AVL子树进行分析，另外我们需要把b子树的细节进⼀步展开为12和左子树高度为h-1的e和f子树，因为我们要对b的父亲15为旋转点进行右单旋，右单旋需要动b树中的右子树。b子树中新增结点的位置不同，平衡因子更新的细节也不同，通过观察12的平衡因子不同，这里我们要分三个场景讨论。
• 场景1：h>=1时，新增结点插入在e子树，e子树高度从h-1变为h并不断更新12->15->10平衡因子，引发旋转，其中12的平衡因子为-1，旋转后10和12平衡因子为0，15平衡因子为1。
• 场景2：h>=1时，新增结点插入在f子树，f子树高度从h-1变为h并不断更新12->15->10平衡因子， 引发旋转，其中12的平衡因子为1，旋转后15和12平衡因子为0，10平衡因子为-1。
• 场景3：h==0时，a/b/c都是空树，b自己就是⼀个新增结点，不断更新15->10平衡因子，引发旋转，其中12的平衡因子为0，旋转后10和12和15平衡因子均为0

（1）右左双旋代码实现

//右左双旋
void RotateRL(Node* perent)
{Node* subR = perent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;//先记录平衡因子RotateR(perent->_right);//先右单旋RotateL(perent);//再左单旋if (bf == -1){perent->_bf = 0;subR->_bf = 1;subRL->_bf = 0;}else if (bf == 1){perent->_bf = -1;subR->_bf = 0;subRL->_bf = 0;}else if (bf == 0){perent->_bf = 0;subR->_bf = 0;subRL->_bf = 0;}else{assert(false);}
}

（2）插入函数最终版

//插入
bool Insert(const pair<K, V>& kv)
{//树为空if (_root == nullptr){_root = new Node(kv);return true;}//树不为空Node* cur = _root;Node* perent = nullptr;while (cur){if (kv.first > cur->_kv.first){perent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){perent = cur;cur = cur->_left;}else{return false;}}//插入cur = new Node(kv);if (kv.first > perent->_kv.first){perent->_right = cur;}else{perent->_left = cur;}cur->_perent = perent;//更新平衡因子while (perent){if (cur == perent->_left)//插入节点位于左边{--perent->_bf;//平衡因子--}else//插入节点位于右边{++perent->_bf;//平衡因子++}if (perent->_bf == 0)//平衡因子等于0{break;//直接结束}else if (perent->_bf == -1 || perent->_bf == 1)//平衡因子需要继续向上更新{cur = perent;//更新cur为父节点perent = perent->_perent;//更新父节点为父父节点}else if (perent->_bf == -2 || perent->_bf == 2)//不满足AVL树，需要旋转处理{//旋转if (perent->_bf == -2 && cur->_bf == -1)//左边高{RotateR(perent);//右单旋}else if (perent->_bf == 2 && cur->_bf == 1)//右边高{RotateL(perent);//左单旋}else if (perent->_bf == -2 && cur->_bf == 1)//左的中间高{RotateLR(perent);//左右双旋}else if (perent->_bf == 2 && cur->_bf == -1)//右的中间高{RotateRL(perent);//右左双旋}else{assert(false);}break;//旋转完直接结束}else{assert(false);//说明出现bug，报错处理}}return true;
}

最后稍微总结一下双旋的思想：

• 由于插入位置不是纯粹的一边高，所以先针对插入节点的那棵子树，使用单旋将其调整为纯粹的一边高，最终对整体再进行一次单旋即可。

---

四、AVL树的查找

查找逻辑和普通的二叉搜索树一样，这里不再赘述

//查找
Node* Find(const K& key)
{Node* cur = _root;while (cur){if (key > cur->_kv.first){cur = cur->_right;}else if (key < cur->_kv.first){cur = cur->_left;}else{return cur;}}return nullptr;
}

---

五、AVL树的平衡检测

主要是检查我们写的代码有没有bug

• 为此，我们需要实现中序遍历：

void _InOrder(Node* root)//中序遍历
{if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_InOrder(root->_right);
}

• 当然，和搜索二叉树一样，为了方便使用，选择封装一层，将上面的中序遍历代码放到类的private私有成员中。
• 再将以下封装代码放在类的public共用成员中：

//中序遍历
void InOrder()
{_InOrder(_root);
}

• 这样直接调用无参的中序遍历就可以使用了，避免了传参。

 

---

（1）简单的初步测试

测试代码：

#include <iostream>
#include "AVLTree.h"
using namespace std;void TestAVLTree1()
{AVLTree<int, int> t;//常规测试用例：int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };//特殊的需要双旋场景的测试用例：// int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };//插入for (auto e : a){t.Insert({ e,e });}//中序遍历t.InOrder();
}int main()
{TestAVLTree1();return 0;
}

运行结果：

• 很明显，数据都是从小到大排序的，符号二叉搜索树的特性，说明大方向没问题。
• 但是现在还不能完全保证代码正确，因为有序只能说明是搜索树，不能说明树是平衡的。
• 为此我们还需要写一个程序检查树是否平衡。

---

（2）平衡检测

​​​​​​​

• 首先，判断一棵搜索树是否平衡，我们能使用平衡因子判断吗？答案是不能的，因为平衡因子本身就可能是错的，毕竟平衡因子是我们自己进行更新的。
• 这时，我们就需要使用朴实的方法进行检测，如上图，我们需要计算每棵子树的高度，使用高度差来判断树是否平衡，比如上面根节点8，我们先计算出它的左右子树高度，判断高度差的绝对值是否大于2，顺带可以与节点8的平衡因子进行比较判断平衡因子本身是否正确。
• 使用这种方法判断每个节点的左右子树。

实现方法：

• 我们首先需要实现计算高度的函数Height，这个在树的章节详细解释过。

int _Height(Node* root)//计算高度
{if (root == nullptr)return 0;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

• 然后就是判断平衡的IsBalanceTree函数，这个就是通过计算的左右子树高度，递归来判断树是否平衡，很好理解。比较好的一点就是可以指出出现异常的节点。

bool _IsBalanceTree(Node* root)//判断是否为AVL树
{//空树也是AVL树if (nullptr == root)return true;//计算pRoot结点的平衡因子：即pRoot左右子树的高度差int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);int diff = rightHeight - leftHeight;// 如果计算出的平衡因子与pRoot的平衡因子不相等，或者// pRoot平衡因子的绝对值超过1，则⼀定不是AVL树if (abs(diff) >= 2){cout << root->_kv.first << "高度差异常" << endl;return false;}if (root->_bf != diff){cout << root->_kv.first << "平衡因子异常" << endl;return false;}//pRoot的左和右如果都是AVL树，则该树⼀定是AVL树return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);
}

• 这两个函数我们都可以套一层使用，避免传参。

//判断是否为AVL树
bool IsBalanceTree()
{return _IsBalanceTree(_root);
}//计算高度
int Height()
{return _Height(_root);
}

测试方法：

我们使用十万个随机值进行插入，然后判断树是否平衡。

void TestAVLTree2()
{const int N = 100000;//测试用例个数vector<int> v;v.reserve(N);//提前扩容srand(time(0));//设置随机数种子for (size_t i = 0; i < N; i++)//生成随机值{v.push_back(rand() + i);}AVLTree<int, int> t;int begin1 = clock();//记录时间for (auto e : v){t.Insert({ e,e });//插入随机值}int end1 = clock();cout << "Insert: " << end1 - begin1 << "（毫秒）" << endl;if (t.IsBalanceTree())//判断平衡{cout << "平衡，是AVL树" << endl;}else{cout << "不平衡，不是AVL树" << endl;}cout << "Hight: " << t.Height() << "（层）" << endl;//计算树的高度cout << "Size: " << t.Size() << "（个）" << endl;//计算树的大小int begin2 = clock();//测试一下查找效率for (size_t i = 0; i < N; i++){t.Find(rand() + i);}int end2 = clock();cout << "Find: " << end2 - begin2 << "（毫秒）" << endl;
}

补充一下size方法：

public://计算大小int Size(){return _Size(_root);}
private:int _Size(Node* root){if (root == nullptr)return 0;int left = _Size(root->_left);int right = _Size(root->_right);return left + right + 1;}

运行结果：

• 你可能发现树的大小只有6万多个，这是因为我们实现的AVL树不支持重复数据。

---

六、AVL树的删除

关于删除部分，本文章没有做出详解，原因是它比插入部分更加复杂，像笔试面试一般也不会考：

删除大致分为以下三步：

1. 按照二叉搜索树树的方式进行删除（主页有）
2. 更新平衡因子
3. 旋转

有兴趣的可以参考：《殷人昆 数据结构：用面向对象方法与C++语言描述》中有讲解

---

总结

        以上就是本文的全部内容了，感谢支持！