PyTorch API 9 - masked, nested, 稀疏, 存储

---

torch.random

---

torch.random.fork_rng(devices=None, enabled=True, _caller='fork_rng', _devices_kw='devices', device_type='cuda')

---

复制 RNG 的状态，使得在返回时 RNG 会被重置到之前的状态。

参数

• devices (可迭代的设备ID集合) – 需要复制 RNG 状态的设备。CPU 的 RNG 状态总是会被复制。默认情况下，fork_rng() 会作用于所有设备，但如果机器上有大量设备时会发出警告，因为在这种情况下该函数运行会很慢。

如果显式指定了设备，这个警告会被抑制

• enabled (布尔值) – 如果设为 False，则不会复制 RNG 状态。这是一个便捷参数，可以轻松禁用上下文管理器而无需删除它并取消其下 Python 代码的缩进。
• device_type (字符串) – 设备类型字符串，默认为 cuda。关于自定义设备，详见[注：支持使用 privateuse1 的自定义设备]

返回类型：Generator

---

torch.random.get_rng_state()

---

返回随机数生成器的状态，以torch.ByteTensor形式表示。

注意：返回的状态仅针对CPU上的默认生成器。

另请参阅：torch.random.fork_rng()。

返回类型：Tensor

---

torch.random.initial_seed()

---

返回用于生成随机数的初始种子，以 Python 长整型表示。

注意：返回的种子仅适用于 CPU 上的默认生成器。

返回类型：int

---

torch.random.manual_seed(seed)

---

为所有设备设置生成随机数的种子。返回一个 torch.Generator 对象。

参数

• seed ( int ) – 期望的种子值。该值必须在闭区间 [-0x8000_0000_0000_0000, 0xffff_ffff_ffff_ffff] 范围内，否则会抛出 RuntimeError。负数输入会通过公式 0xffff_ffff_ffff_ffff + seed 映射为正值。

返回类型：Generator

---

torch.random.seed()

---

为所有设备设置随机数生成种子，使用非确定性随机数。返回一个用于初始化随机数生成器(RNG)的64位数值。

返回值类型：int

---

torch.random.set_rng_state(new_state)

---

设置随机数生成器状态。

注意：此函数仅适用于CPU。对于CUDA，请使用torch.manual_seed()，该函数同时适用于CPU和CUDA。

参数

• new_state (torch.ByteTensor) – 期望的状态

---

torch.masked

---

简介

---

动机

---

警告：PyTorch 的掩码张量 API 目前处于原型阶段，未来可能会发生变更。

MaskedTensor 作为 torch.Tensor 的扩展，为用户提供以下能力：

• 支持任意掩码语义（例如变长张量、nan* 运算符等）
• 区分 0 梯度和 NaN 梯度
• 适用于多种稀疏场景（参见下方教程）

在 PyTorch 中，"指定值"和"未指定值"长期缺乏正式语义定义且存在不一致性。事实上，MaskedTensor 的诞生正是为了解决原生 torch.Tensor 类无法妥善处理的诸多问题。因此，MaskedTensor 的主要目标是成为 PyTorch 中"指定值"和"未指定值"的权威实现，使其成为一等公民而非事后补救方案。

这将进一步释放稀疏张量的潜力，提供更安全、更一致的运算符，同时为用户和开发者带来更流畅、更直观的使用体验。

---

什么是 MaskedTensor？

MaskedTensor 是一种张量子类，由两部分组成：1) 输入数据（data），2) 掩码（mask）。掩码用于指示输入中的哪些条目应被包含或忽略。例如，假设我们希望屏蔽所有值为 0 的元素（以灰色表示），并计算最大值：

---

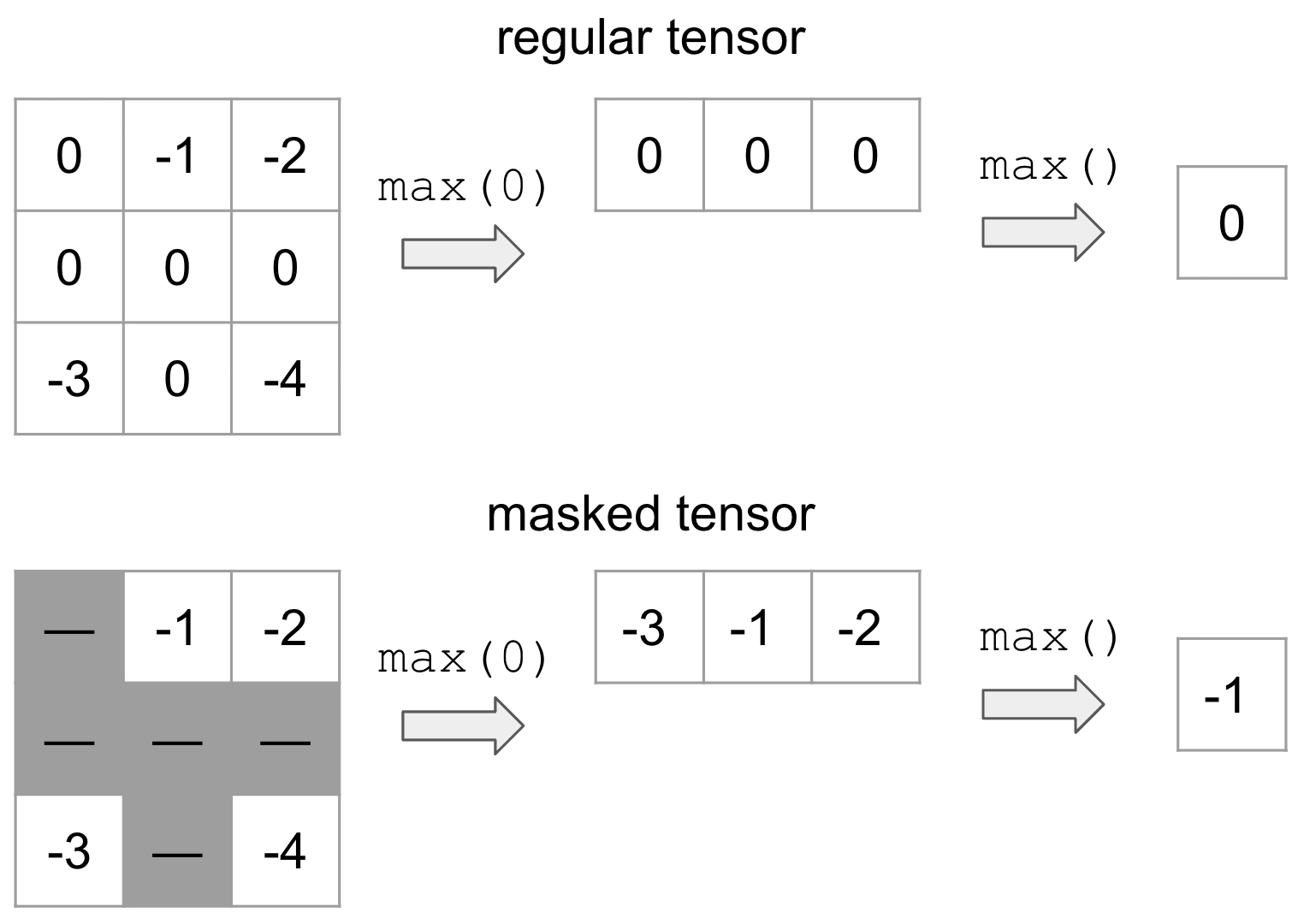
上方是普通张量的示例，而下方是 MaskedTensor 的示例，其中所有 0 值均被屏蔽。显然，是否使用掩码会导致不同的结果。这种灵活的结构允许用户在计算过程中系统地忽略任何他们希望排除的元素。

我们已编写了多个现有教程来帮助用户快速上手，例如：

• 概述 - 新用户的起点，讨论如何使用 MaskedTensor 及其价值
• 稀疏性 - MaskedTensor 支持稀疏 COO 和 CSR 数据及掩码张量
• Adagrad 稀疏语义 - 展示 MaskedTensor 如何简化稀疏语义和实现的实用案例
• 高级语义 - 探讨设计决策原因（如要求二进制/归约操作的掩码匹配）、与 NumPy 的 MaskedArray 的差异，以及归约语义

---

支持的运算符

---

一元运算符

一元运算符是指仅包含单个输入的运算符。将其应用于MaskedTensor相对简单：如果数据在给定索引处被掩码，我们应用该运算符；否则，数据将继续保持掩码状态。

可用的单目运算符包括：

abs	计算input中每个元素的绝对值。
absolute	torch.abs()的别名
acos	计算input中每个元素的反余弦值。
arccos	torch.acos()的别名。
acosh	返回一个新张量，包含input元素的反双曲余弦值。
arccosh	torch.acosh()的别名。
angle	计算给定input张量各元素的相位角（弧度制）。
asin	返回一个新张量，包含input元素的反正弦值。
arcsin	torch.asin()的别名。
asinh	返回一个新张量，包含input元素的反双曲正弦值。
arcsinh	torch.asinh()的别名。
atan	返回一个新张量，包含input元素的反正切值。
arctan	torch.atan()的别名。
atanh	返回一个新张量，包含input元素的反双曲正切值。
arctanh	torch.atanh()的别名。
bitwise_not	计算输入张量的按位取反值。
ceil	返回一个新张量，包含对input各元素向上取整的结果（即大于等于该元素的最小整数）。
clamp	将input中所有元素限制在范围[min, max]内。
clip	torch.clamp()的别名。
conj_physical	计算给定input张量各元素的物理共轭值。
cos	返回一个新张量，包含input元素的余弦值。
cosh	返回一个新张量，包含input元素的双曲余弦值。
deg2rad	返回一个新张量，将input各元素从角度制转换为弧度制。
digamma	torch.special.digamma()的别名。
erf	torch.special.erf()的别名。
erfc	torch.special.erfc()的别名。
erfinv	torch.special.erfinv()的别名。
exp	返回一个新张量，包含输入张量input各元素的指数值。
exp2	torch.special.exp2()的别名。
expm1	torch.special.expm1()的别名。
fix	torch.trunc()的别名
floor	返回一个新张量，包含对input各元素向下取整的结果（即小于等于该元素的最大整数）。
frac	计算input中每个元素的小数部分。
lgamma	计算input各元素绝对值的伽玛函数的自然对数。
log	返回一个新张量，包含input各元素的自然对数值。
log10	返回一个新张量，包含input各元素的以10为底的对数值。
log1p	返回一个新张量，包含(1 + input)的自然对数值。
log2	返回一个新张量，包含input各元素的以2为底的对数值。
logit	torch.special.logit()的别名。
i0	torch.special.i0()的别名。
isnan	返回一个布尔型张量，表示input各元素是否为NaN。
nan_to_num	将input中的NaN、正无穷和负无穷值分别替换为nan、posinf和neginf指定的值。
neg	返回一个新张量，包含input各元素的负值。
negative	torch.neg()的别名
positive	返回input本身。
pow	对input各元素取exponent次幂，返回结果张量。
rad2deg	返回一个新张量，将input各元素从弧度制转换为角度制。
reciprocal	返回一个新张量，包含input各元素的倒数。
round	将input各元素四舍五入到最接近的整数。
rsqrt	返回一个新张量，包含input各元素的平方根的倒数。
sigmoid	torch.special.expit()的别名。
sign	返回一个新张量，包含input各元素的符号。
sgn	此函数是torch.sign()对复数张量的扩展。
signbit	检测input各元素的符号位是否被设置。
sin	返回一个新张量，包含input各元素的正弦值。
sinc	torch.special.sinc()的别名。
sinh	返回一个新张量，包含input各元素的双曲正弦值。
sqrt	返回一个新张量，包含input各元素的平方根。
square	返回一个新张量，包含input各元素的平方值。
tan	返回一个新张量，包含input各元素的正切值。
tanh	返回一个新张量，包含input各元素的双曲正切值。
trunc	返回一个新张量，包含input各元素的截断整数值。

---

可用的原地(inplace)一元运算符包括上述所有运算符除以下外：

angle	计算给定input张量各元素的相位角（弧度制）。
positive	返回input本身。
signbit	检测input各元素的符号位是否被设置。
isnan	返回一个布尔型张量，表示input各元素是否为NaN。

---

二元运算符

正如教程中所示，MaskedTensor 也实现了二元运算，但有一个前提条件：两个 MaskedTensor 的掩码必须匹配，否则会引发错误。如错误提示所述，如果您需要支持特定运算符或对其行为有其他语义建议，请在 GitHub 上提交问题。目前，我们选择了最保守的实现方式，以确保用户清楚了解操作过程，并在处理掩码语义时做出明确决策。

可用的二元运算符包括：

add	将 other 乘以 alpha 后加到 input 上
atan2	逐元素计算 inputi/otheri\text{input}{i} / \text{other}{i}inputi​/otheri​ 的反正切值，并考虑象限
arctan2	torch.atan2() 的别名
bitwise_and	计算 input 和 other 的按位与
bitwise_or	计算 input 和 other 的按位或
bitwise_xor	计算 input 和 other 的按位异或
bitwise_left_shift	计算 input 左移 other 位的算术结果
bitwise_right_shift	计算 input 右移 other 位的算术结果
div	将 input 的每个元素除以 other 的对应元素
divide	torch.div() 的别名
floor_divide
fmod	逐元素应用 C++ 的 std::fmod
logaddexp	计算输入指数和的对数
logaddexp2	计算以 2 为底的输入指数和的对数
mul	将 input 乘以 other
multiply	torch.mul() 的别名
nextafter	逐元素返回 input 向 other 方向的下一个浮点数值
remainder	逐元素计算 Python 的模运算
sub	从 input 中减去 other 乘以 alpha 的结果
subtract	torch.sub() 的别名
true_divide	torch.div() 的别名，rounding_mode=None
eq	逐元素计算相等性
ne	逐元素计算 input≠other\text{input} \neq \text{other}input=other
le	逐元素计算 input≤other\text{input} \leq \text{other}input≤other
ge	逐元素计算 input≥other\text{input} \geq \text{other}input≥other
greater	torch.gt() 的别名
greater_equal	torch.ge() 的别名
gt	逐元素计算 input>other\text{input} \text{other}input>other
less_equal	torch.le() 的别名
lt	逐元素计算 input<other\text{input} < \text{other}input<other
less	torch.lt() 的别名
maximum	逐元素计算 input 和 other 的最大值
minimum	逐元素计算 input 和 other 的最小值
fmax	逐元素计算 input 和 other 的最大值
fmin	逐元素计算 input 和 other 的最小值
not_equal	torch.ne() 的别名

可用的原地二元运算符包括上述所有运算符，但不包括：

logaddexp	计算输入指数和的对数
logaddexp2	计算以 2 为底的输入指数和的对数
equal	如果两个张量大小和元素相同则为 True，否则为 False
fmin	逐元素计算 input 和 other 的最小值
minimum	逐元素计算 input 和 other 的最小值
fmax	逐元素计算 input 和 other 的最大值

---

归约操作

以下归约操作均支持自动求导功能。如需了解更多信息，概述教程展示了一些归约操作的具体示例，而高级语义教程则深入探讨了我们如何确定某些归约操作的语义。

sum	返回输入张量 input 中所有元素的和。
mean
amin	返回输入张量 input 在给定维度 dim 上每一切片的最小值。
amax	返回输入张量 input 在给定维度 dim 上每一切片的最大值。
argmin	返回展平张量或沿某一维度的最小值索引。
argmax	返回输入张量 input 中所有元素的最大值索引。
prod	返回输入张量 input 中所有元素的乘积。
all	测试输入张量 input 中所有元素是否均为 True。
norm	返回给定张量的矩阵范数或向量范数。
var	计算指定维度 dim 上的方差。
std	计算指定维度 dim 上的标准差。

---

查看与选择函数

我们还提供了一系列查看和选择函数。直观地说，这些运算符会同时作用于数据和掩码，然后将结果封装在MaskedTensor中。举个简单例子，比如select()函数：

>>> data = torch.arange(12, dtype=torch.float).reshape(3, 4)
>>> data
tensor([[0., 1., 2., 3.], [4., 5., 6., 7.], [8., 9., 10., 11.]])
>>> mask = torch.tensor([[True, False, False, True], [False, True, False, False], [True, True, True, True]])
>>> mt = masked_tensor(data, mask)
>>> data.select(0, 1)
tensor([4., 5., 6., 7.])
>>> mask.select(0, 1)
tensor([False, True, False, False])
>>> mt.select(0, 1)
MaskedTensor([    --, 5.0000,   --,   --]
)

---

当前支持以下操作：

atleast_1d	将零维输入张量转换为1维视图
broadcast_tensors	根据广播语义广播给定张量
broadcast_to	将input广播至shape指定的形状
cat	沿指定维度拼接tensors序列中的张量
chunk	尝试将张量分割为指定数量的块
column_stack	通过水平堆叠tensors中的张量创建新张量
dsplit	沿深度方向将三维及以上的input张量按indices_or_sections分割
flatten	将input展平为一维张量
hsplit	沿水平方向将一维及以上的input张量按indices_or_sections分割
hstack	水平（按列）顺序堆叠张量
kron	计算input与other的Kronecker积（记作⊗\otimes⊗）
meshgrid	通过attr:tensors中的一维输入创建坐标网格
narrow	返回input张量的缩小版本
nn.functional.unfold	从批处理输入张量中提取滑动局部块
ravel	返回连续的展平张量
select	在指定维度上按给定索引切片input张量
split	将张量分割为多个块
stack	沿新维度拼接张量序列
t	要求input为≤2维张量并转置第0和第1维度
transpose	返回input张量的转置版本
vsplit	沿垂直方向将二维及以上的input张量按indices_or_sections分割
vstack	垂直（按行）顺序堆叠张量
Tensor.expand	将self张量的单例维度扩展至更大尺寸的新视图
Tensor.expand_as	将当前张量扩展至与other相同尺寸
Tensor.reshape	返回与self数据相同但形状被重新指定的张量
Tensor.reshape_as	返回与other形状相同的当前张量
Tensor.unfold	返回包含self张量在dimension维度上所有size大小切片的新视图
Tensor.view	返回与self数据相同但形状不同的新张量

---

torch.nested

---

简介

---

警告：PyTorch 的嵌套张量 API 目前处于原型阶段，近期将会发生变化。

嵌套张量允许将不规则形状的数据作为单个张量进行存储和操作。这类数据在底层以高效的压缩形式存储，同时对外提供标准的 PyTorch 张量接口以支持各类运算。

嵌套张量的一个典型应用场景是处理不同领域中的变长序列数据，例如长度不一的句子、尺寸各异的图像以及时长不同的音频/视频片段。传统做法是通过填充（padding）将批次内的序列统一为最大长度，在填充后的数据上进行计算，最后通过掩码（masking）去除填充部分。这种方式既低效又容易出错，而嵌套张量正是为解决这些问题而生。

调用嵌套张量运算的 API 与常规 torch.Tensor 完全一致，可以无缝集成到现有模型中，主要区别在于输入数据的构建方式。

由于这是原型功能，当前支持的运算有限但正在逐步扩展。我们欢迎问题反馈、功能请求和代码贡献。更多贡献信息请参阅本说明文件。

---

构造方法

---

注意：PyTorch中存在两种形式的嵌套张量，通过构造时指定的布局进行区分。布局可以是torch.strided或torch.jagged之一。
我们建议尽可能使用torch.jagged布局。虽然目前它仅支持单个不规则维度，但具有更好的算子覆盖范围，正在积极开发中，并且与torch.compile集成良好。本文档遵循此建议，为简洁起见，将采用torch.jagged布局的嵌套张量称为"NJT"。

构造过程很简单，只需将张量列表传递给torch.nested.nested_tensor构造函数即可。采用torch.jagged布局的嵌套张量（即"NJT"）支持单个不规则维度。该构造函数会根据下方数据布局章节描述的布局方式，将输入张量复制到一个连续的内存块中进行打包存储。

---

>>> a, b = torch.arange(3), torch.arange(5) + 3
>>> a tensor([0, 1, 2])
>>> b
tensor([3, 4, 5, 6, 7])
>>> nt = torch.nested.nested_tensor([a, b], layout=torch.jagged)
>>> print([component for component in nt])
[tensor([0, 1, 2]), tensor([3, 4, 5, 6, 7])]

---

列表中的每个张量必须具有相同的维度数，但各张量的形状可以在单一维度上有所不同。如果输入组件的维度不匹配，构造函数将抛出错误。

---

>>> a = torch.randn(50, 128) # 2D tensor
>>> b = torch.randn(2, 50, 128) # 3D tensor
>>> nt = torch.nested.nested_tensor([a, b], layout=torch.jagged)
...
RuntimeError: When constructing a nested tensor, all tensors in list must have the same dim

---

在构建过程中，可以通过常规的关键字参数选择数据类型（dtype）、设备（device）以及是否需要梯度计算。

---

>>> nt = torch.nested.nested_tensor([a, b], layout=torch.jagged, dtype=torch.float32, device="cuda", requires_grad=True)
>>> print([component for component in nt])
[tensor([0., 1., 2.], device='cuda:0', grad_fn=<UnbindBackwardAutogradNestedTensor0>), tensor([3., 4., 5., 6., 7.], device='cuda:0', grad_fn=<UnbindBackwardAutogradNestedTensor0>)]

---

torch.nested.as_nested_tensor 可用于保留传递给构造函数的张量的自动求导历史。当使用此构造函数时，梯度将通过嵌套张量回传到原始组件中。需要注意的是，该构造函数仍会将输入组件复制到一个连续的内存块中。

---

>>> a = torch.randn(12, 512, requires_grad=True)
>>> b = torch.randn(23, 512, requires_grad=True)
>>> nt = torch.nested.as_nested_tensor([a, b], layout=torch.jagged, dtype=torch.float32)
>>> nt.sum().backward()
>>> a.grad
tensor([[1., 1., 1., ..., 1., 1., 1.], [1., 1., 1., ..., 1., 1., 1.], [1., 1., 1., ..., 1., 1., 1.], ...,  [1., 1., 1., ..., 1., 1., 1.], [1., 1., 1., ..., 1., 1., 1.], [1., 1., 1., ..., 1., 1., 1.]])
>>> b.grad
tensor([[1., 1., 1., ..., 1., 1., 1.], [1., 1., 1., ..., 1., 1., 1.], [1., 1., 1., ..., 1., 1., 1.], ...,  [1., 1., 1., ..., 1., 1., 1.], [1., 1., 1., ..., 1., 1., 1.], [1., 1., 1., ..., 1., 1., 1.]])

---

上述函数都会创建连续的NJT（嵌套跳跃张量），即分配一块连续内存来存储底层组件的压缩形式（更多细节请参阅下方的数据布局部分）。

此外，我们还可以在已有带填充的密集张量上创建非连续的NJT视图，从而避免内存分配和复制操作。实现这一功能的工具是torch.nested.narrow()。

---

>>> padded = torch.randn(3, 5, 4)
>>> seq_lens = torch.tensor([3, 2, 5], dtype=torch.int64)
>>> nt = torch.nested.narrow(padded, dim=1, start=0, length=seq_lens, layout=torch.jagged)
>>> nt.shape
torch.Size([3, j1, 4])
>>> nt.is_contiguous()
False

---

请注意，嵌套张量(NJT)作为原始填充密集张量的视图，会引用相同的内存而无需复制/重新分配内存。对于非连续存储的NJT，其操作支持相对有限。如果您遇到功能缺失的情况，随时可以通过调用contiguous()方法将其转换为连续存储的NJT。

---

数据布局与形状

出于效率考虑，嵌套张量通常将其张量组件打包存储在一块连续的内存区域中，并通过额外的元数据来指定批次项的边界。对于torch.jagged布局，连续内存块存储在values组件中，而offsets组件则用于标记不规则维度的批次项边界。

---

---

在需要时可以直接访问底层的NJT组件。

---

>>> a = torch.randn(50, 128) # text 1
>>> b = torch.randn(32, 128) # text 2
>>> nt = torch.nested.nested_tensor([a, b], layout=torch.jagged, dtype=torch.float32)
>>> nt.values().shape  # note the "packing" of the ragged dimension; no padding needed
torch.Size([82, 128])
>>> nt.offsets()
tensor([0, 50, 82])

---

直接通过不规则的values和offsets组件来构建NJT（嵌套张量）也很有用；为此目的提供了torch.nested.nested_tensor_from_jagged()构造函数。

---

>>> values = torch.randn(82, 128)
>>> offsets = torch.tensor([0, 50, 82], dtype=torch.int64)
>>> nt = torch.nested.nested_tensor_from_jagged(values=values, offsets=offsets)

---

一个NJT具有明确的形状，其维度比其组件高1。不规则维度的底层结构由一个符号值表示（如下例中的j1）。

---

>>> a = torch.randn(50, 128)
>>> b = torch.randn(32, 128)
>>> nt = torch.nested.nested_tensor([a, b], layout=torch.jagged, dtype=torch.float32)
>>> nt.dim()
3
>>> nt.shape
torch.Size([2, j1, 128])

---

NJTs必须具有相同的锯齿状结构才能相互兼容。例如，当对两个NJTs执行二元运算时，它们的锯齿结构必须匹配（即形状中必须包含相同的锯齿形状符号）。具体来说，每个符号对应一个精确的offsets张量，因此两个NJTs必须拥有相同的offsets张量才能相互兼容。

---

>>> a = torch.randn(50, 128)
>>> b = torch.randn(32, 128)
>>> nt1 = torch.nested.nested_tensor([a, b], layout=torch.jagged, dtype=torch.float32)
>>> nt2 = torch.nested.nested_tensor([a, b], layout=torch.jagged, dtype=torch.float32)
>>> nt1.offsets() is nt2.offsets()
False
>>> nt3 = nt1 + nt2
RuntimeError: cannot call binary pointwise function add.Tensor with inputs of shapes (2, j2, 128) and (2, j3, 128)

---

在上面的例子中，尽管两个NJT的概念形状相同，但它们并未共享同一个offsets张量的引用，因此它们的形状存在差异，导致彼此不兼容。我们意识到这种行为不够直观，正在努力为嵌套张量的测试版发布放宽这一限制。如需临时解决方案，请参阅本文档的故障排除部分。

除了offsets元数据外，NJT还可以计算并缓存其组件的最小和最大序列长度，这对调用特定内核（例如SDPA）很有帮助。目前尚未提供访问这些数据的公开API，但这一情况将在测试版发布时改变。

---

支持的操作

本节列出了针对嵌套张量的常见操作列表，这些操作可能对您有所帮助。
由于PyTorch包含数千种操作，此列表并不全面。虽然目前已有相当一部分操作支持嵌套张量，但实现全面支持仍是一项艰巨任务。

嵌套张量的理想状态是全面支持所有可用于普通张量的PyTorch操作。为帮助我们实现这一目标，您可以：

• 在此处提交您需要的特定操作需求，以协助我们确定优先级
• 参与贡献！为PyTorch操作添加嵌套张量支持并不困难，具体请参阅下方的贡献指南章节

（注：保留所有代码块、链接格式及专有名词，如"PyTorch"、"nested tensors"等未作翻译）

---

查看嵌套张量的组成元素

unbind() 方法可用于获取嵌套张量各组成元素的视图。

---

>>> import torch
>>> a = torch.randn(2, 3)
>>> b = torch.randn(3, 3)
>>> nt = torch.nested.nested_tensor([a, b], layout=torch.jagged)
>>> nt.unbind()
(tensor([[-0.9916, -0.3363, -0.2799], [-2.3520, -0.5896, -0.4374]]), tensor([[-2.0969, -1.0104, 1.4841], [2.0952, 0.2973, 0.2516], [0.9035, 1.3623, 0.2026]]))
>>> nt.unbind()[0] is not a True
>>> nt.unbind()[0].mul_(3)
tensor([[3.6858, -3.7030, -4.4525], [-2.3481, 2.0236, 0.1975]])
>>> nt.unbind()
(tensor([[-2.9747, -1.0089, -0.8396], [-7.0561, -1.7688, -1.3122]]), tensor([[-2.0969, -1.0104, 1.4841], [2.0952, 0.2973, 0.2516], [0.9035, 1.3623, 0.2026]]))

---

请注意，nt.unbind()[0] 并不是一个副本，而是底层内存的一个切片，它表示嵌套张量的第一个条目或组成部分。

---

填充张量的相互转换

torch.nested.to_padded_tensor() 方法可将非规则嵌套张量(NJT)转换为具有指定填充值的填充密集张量。其中不规则维度会被填充至最大序列长度的尺寸。

---

>>> import torch
>>> a = torch.randn(2, 3)
>>> b = torch.randn(6, 3)
>>> nt = torch.nested.nested_tensor([a, b], layout=torch.jagged)
>>> padded = torch.nested.to_padded_tensor(nt, padding=4.2)
>>> padded
tensor([[[1.6107, 0.5723, 0.3913], [0.0700, -0.4954, 1.8663], [4.2000, 4.2000, 4.2000], [4.2000, 4.2000, 4.2000], [4.2000, 4.2000, 4.2000], [4.2000, 4.2000, 4.2000]], [[-0.0479, -0.7610, -0.3484], [1.1345, 1.0556, 0.3634], [-1.7122, -0.5921, 0.0540], [-0.5506, 0.7608, 2.0606], [1.5658, -1.1934, 0.3041], [0.1483, -1.1284, 0.6957]]])

---

这可以作为绕过NJT支持不足的应急方案，但为了获得最佳内存使用和性能表现，应尽可能避免此类转换，因为更高效的嵌套张量布局不会实际填充空白数据。

反向转换可以通过torch.nested.narrow()实现，该操作会对给定的密集张量应用不规则结构以生成NJT。请注意，默认情况下此操作不会复制底层数据，因此输出的NJT通常是非连续的。如果需要连续的NJT，在此处显式调用contiguous()可能很有帮助。

---

>>> padded = torch.randn(3, 5, 4)
>>> seq_lens = torch.tensor([3, 2, 5], dtype=torch.int64)
>>> nt = torch.nested.narrow(padded, dim=1, length=seq_lens, layout=torch.jagged)
>>> nt.shape
torch.Size([3, j1, 4])
>>> nt = nt.contiguous()
>>> nt.shape
torch.Size([3, j2, 4])

---

形状操作

嵌套张量支持多种形状操作，包括视图操作。

---

>>> a = torch.randn(2, 6)
>>> b = torch.randn(4, 6)
>>> nt = torch.nested.nested_tensor([a, b], layout=torch.jagged)
>>> nt.shape
torch.Size([2, j1, 6])
>>> nt.unsqueeze(-1).shape
torch.Size([2, j1, 6, 1])
>>> nt.unflatten(-1, [2, 3]).shape
torch.Size([2, j1, 2, 3])
>>> torch.cat([nt, nt], dim=2).shape
torch.Size([2, j1, 12])
>>> torch.stack([nt, nt], dim=2).shape
torch.Size([2, j1, 2, 6])
>>> nt.transpose(-1, -2).shape
torch.Size([2, 6, j1])

---

注意力机制

由于变长序列是注意力机制的常见输入，嵌套张量支持两个重要的注意力算子：Scaled Dot Product Attention (SDPA) 和 FlexAttention。

关于嵌套张量与SDPA结合的使用示例，请参阅此处；关于嵌套张量与FlexAttention结合的使用示例，请参阅此处。

---

与 torch.compile 的配合使用

NJTs 专为与 torch.compile() 配合使用以实现最佳性能而设计。我们始终建议在可能的情况下将 NJTs 与 torch.compile() 结合使用。无论是将 NJTs 作为输入传递给已编译的函数/模块，还是直接在函数内部实例化 NJTs，它们都能开箱即用地工作且不会导致计算图中断。

---

注意：如果您的使用场景无法应用 torch.compile()，使用 NJTs 仍可能带来性能和内存优势，但这种优势并非绝对。关键在于确保所操作的张量足够大，以避免 Python 张量子类带来的开销超过性能收益。

---

>>> import torch
>>> a = torch.randn(2, 3)
>>> b = torch.randn(4, 3)
>>> nt = torch.nested.nested_tensor([a, b], layout=torch.jagged)
>>> def f(x): return x.sin() + 1
...
>>> compiled_f = torch.compile(f, fullgraph=True)
>>> output = compiled_f(nt)
>>> output.shape
torch.Size([2, j1, 3])
>>> def g(values, offsets): return torch.nested.nested_tensor_from_jagged(values, offsets) * 2、...
>>> compiled_g = torch.compile(g, fullgraph=True)
>>> output2 = compiled_g(nt.values(), nt.offsets())
>>> output2.shape
torch.Size([2, j1, 3])

---

请注意，NJT 支持

动态形状功能，可避免因不规则结构变化而导致不必要的重新编译。

---

>>> a = torch.randn(2, 3)
>>> b = torch.randn(4, 3)
>>> c = torch.randn(5, 3)
>>> d = torch.randn(6, 3)
>>> nt1 = torch.nested.nested_tensor([a, b], layout=torch.jagged)
>>> nt2 = torch.nested.nested_tensor([c, d], layout=torch.jagged)
>>> def f(x): return x.sin() + 1
...
>>> compiled_f = torch.compile(f, fullgraph=True)
>>> output1 = compiled_f(nt1)
>>> output2 = compiled_f(nt2)  # NB: No recompile needed even though ragged structure differs

---

如果在使用 NJT + torch.compile 时遇到问题或晦涩的错误，请提交 PyTorch issue。目前对 torch.compile 的完整子类支持是一项长期工作，现阶段可能存在一些不完善之处。

---

故障排查

本节列出了使用嵌套张量时可能遇到的常见错误，同时说明了这些错误的原因，并提供了相应的解决建议。

---

未实现的操作

随着嵌套张量操作支持的增加，这类错误已越来越少见。但由于 PyTorch 中有数千种操作，目前仍有可能遇到这种情况。

---

NotImplementedError: aten.view_as_real.default

---

这个错误很直接：我们目前尚未实现对这一特定操作的支持。如果你愿意，可以自行贡献一个实现，或者直接提交请求，让我们在未来的PyTorch版本中添加对该操作的支持。

---

不规则结构不兼容问题

---

RuntimeError: cannot call binary pointwise function add.Tensor with inputs of shapes (2, j2, 128) and (2, j3, 128)

---

当调用一个操作多个 NJT 且这些 NJT 具有不兼容的参差结构的操作时，会出现此错误。目前要求输入的 NJT 必须具有完全相同的 offsets 组成部分，才能拥有相同的符号化参差结构符号（例如 j1）。

针对这种情况，可以通过直接从 values 和 offsets 组件构建 NJT 来解决。当两个 NJT 引用相同的 offsets 组件时，它们将被视为具有相同的参差结构，因此是兼容的。

---

>>> a = torch.randn(50, 128)
>>> b = torch.randn(32, 128)
>>> nt1 = torch.nested.nested_tensor([a, b], layout=torch.jagged, dtype=torch.float32)
>>> nt2 = torch.nested.nested_tensor_from_jagged(values=torch.randn(82, 128), offsets=nt1.offsets())
>>> nt3 = nt1 + nt2
>>> nt3.shape
torch.Size([2, j1, 128])

---

torch.compile 中的数据依赖操作

---

torch._dynamo.exc.Unsupported: data dependent operator: aten._local_scalar_dense.default; to enable, set torch._dynamo.config.capture_scalar_outputs = True

---

当调用在torch.compile内部执行数据相关操作的算子时会出现此错误，这通常发生在需要检查NJT的offsets值以确定输出形状的算子中。例如：

>>> a = torch.randn(50, 128)
>>> b = torch.randn(32, 128)
>>> nt = torch.nested.nested_tensor([a, b], layout=torch.jagged, dtype=torch.float32)
>>> def f(nt): return nt.chunk(2, dim=0)[0]
...
>>> compiled_f = torch.compile(f, fullgraph=True)
>>> output = compiled_f(nt)

---

在这个示例中，对NJT的批次维度调用chunk()方法需要检查NJT的offsets数据，以确定打包不规则维度内的批次项边界。作为一种变通方案，可以设置几个torch.compile标志：

>>> torch._dynamo.config.capture_dynamic_output_shape_ops = True
>>> torch._dynamo.config.capture_scalar_outputs = True

---

如果在设置这些参数后，您仍然遇到与数据相关的算子错误，请向 PyTorch 提交 issue。当前 torch.compile() 的 NJT 支持功能仍在密集开发中，某些方面可能还不完善。

---

贡献指南

如果您想为嵌套张量开发做出贡献，最具影响力的方式之一是为当前尚未支持的PyTorch算子添加嵌套张量支持。该过程通常包含以下几个简单步骤：

1、确定要添加的算子名称，例如aten.view_as_real.default。可以在aten/src/ATen/native/native_functions.yaml中找到该算子的签名定义。
2、在torch/nested/_internal/ops.py中按照现有模式注册算子实现。使用native_functions.yaml中的签名进行模式验证。

实现算子的最常见方法是：将NJT解构为其组成部分，在底层values缓冲区上重新派发算子，并将相关NJT元数据（包括offsets）传播到新的输出NJT。如果算子的输出形状与输入不同，则必须重新计算新的offsets等元数据。

当在批处理维度或非规则维度上应用算子时，以下技巧可以帮助快速实现：

• 对于非批处理操作，基于unbind()的回退方案应该可行
• 对于非规则维度的操作，可考虑转换为适当选择填充值的密集张量（确保填充值不会对输出产生负面影响），执行操作后再转换回NJT。在torch.compile中，这些转换可以被融合以避免具体化填充中间结果。

---

构造与转换函数详细文档

---

torch.nested.nested_tensor(tensor_list, *, dtype=None, layout=None, device=None, requires_grad=False, pin_memory=False)

---

从 tensor_list（一个张量列表）构造一个没有自动梯度历史记录的嵌套张量（也称为“叶张量”，参见自动梯度机制）。

参数

• tensor_list (List[array_like]) – 一个张量列表，或任何可以传递给 torch.tensor 的对象，维度（其中列表的每个元素具有相同的维度）。

关键字参数

• dtype (torch.dtype, 可选) – 返回嵌套张量的期望数据类型。
  默认值：如果为 None，则与列表中左侧第一个张量的 torch.dtype 相同。
• layout ([torch.layout](tensor_attributes.html#torch.layout "torch.layout"), 可选) – 返回嵌套张量的期望布局。
  仅支持 strided 和 jagged 布局。默认值：如果为 None，则为 strided 布局。
• device ([torch.device](tensor_attributes.html#torch.device "torch.device"), 可选) – 返回嵌套张量的期望设备。
  默认值：如果为 None，则与列表中左侧第一个张量的 torch.device 相同。
• requires_grad ([bool], 可选) – 如果为 True，自动梯度将记录对返回嵌套张量的操作。默认值：False。
• pin_memory ([bool], 可选) – 如果设置为 True，返回的嵌套张量将被分配在锁页内存中。仅适用于 CPU 张量。默认值：False。

返回类型 : Tensor

---

示例:

---

>>> a = torch.arange(3, dtype=torch.float, requires_grad=True)
>>> b = torch.arange(5, dtype=torch.float, requires_grad=True)
>>> nt = torch.nested.nested_tensor([a, b], requires_grad=True)
>>> nt.is_leaf
True

---

torch.nested.nested_tensor_from_jagged(values, offsets=None, lengths=None, jagged_dim=None, min_seqlen=None, max_seqlen=None)

---

根据给定的不规则组件构建一个不规则布局的嵌套张量。该不规则布局包含一个必需的值缓冲区，其中不规则维度被打包到单一维度中。

偏移量/长度元数据决定了如何将此维度拆分为批次元素，并且预期与值缓冲区分配在同一设备上。

预期的元数据格式：

• 偏移量：在打包维度内的索引，将其分割为不同大小的批次元素。例如：[0, 2, 3, 6] 表示大小为6的打包不规则维度应概念上分割为长度为[2, 1, 3]的批次元素。注意，为了内核便利性，需要提供起始和结束偏移量（即形状为batch_size + 1）。

• 长度：单个批次元素的长度；形状 == batch_size。例如：[2, 1, 3] 表示大小为6的打包不规则维度应概念上分割为长度为[2, 1, 3]的批次元素。

注意，同时提供偏移量和长度可能很有用。这描述了一个带有"空洞"的嵌套张量，其中偏移量表示每个批次项的起始位置，长度指定元素总数（参见下面的示例）。

返回的不规则布局嵌套张量将是输入值张量的视图。

参数：

• values (torch.Tensor) - 基础缓冲区，形状为(sum_B(), D_1, …, D_N)。不规则维度被打包到单一维度中，使用偏移量/长度元数据来区分批次元素。
• offsets (可选 torch.Tensor) - 形状为B + 1的偏移量，指向不规则维度。
• lengths (可选 torch.Tensor) - 形状为B的批次元素长度。
• jagged_dim (可选 python:int) - 指示值中哪个维度是打包的不规则维度。如果为None，则设置为dim=1（即紧接批次维度后的维度）。默认值：None
• min_seqlen (可选 python:int) - 如果设置，使用指定值作为返回嵌套张量的缓存最小序列长度。这可以避免按需计算此值，可能避免GPU-CPU同步。默认值：None
• max_seqlen (可选 python:int) - 如果设置，使用指定值作为返回嵌套张量的缓存最大序列长度。这可以避免按需计算此值，可能避免GPU-CPU同步。默认值：None

返回类型：Tensor

---

示例：

>>> values = torch.randn(12, 5)
>>> offsets = torch.tensor([0, 3, 5, 6, 10, 12])
>>> nt = nested_tensor_from_jagged(values, offsets)
>>> # 3D shape with the middle dimension jagged
>>> nt.shape
torch.Size([5, j2, 5])
>>> # Length of each item in the batch:
>>> offsets.diff()
tensor([3, 2, 1, 4, 2])>>> values = torch.randn(6, 5)
>>> offsets = torch.tensor([0, 2, 3, 6])
>>> lengths = torch.tensor([1, 1, 2])
>>> # NT with holes
>>> nt = nested_tensor_from_jagged(values, offsets, lengths)
>>> a, b, c = nt.unbind()
>>> # Batch item 1 consists of indices [0, 1)
>>> torch.equal(a, values[0:1, :])
True
>>> # Batch item 2 consists of indices [2, 3)
>>> torch.equal(b, values[2:3, :])
True
>>> # Batch item 3 consists of indices [3, 5)
>>> torch.equal(c, values[3:5, :])
True

---

torch.nested.as_nested_tensor(ts, dtype=None, device=None, layout=None)

---

从张量或张量列表/元组构建保留自动梯度历史记录的嵌套张量。

如果传入的是嵌套张量，除非设备/数据类型/布局不同，否则会直接返回该张量。注意：转换设备/数据类型会导致复制操作，而当前此函数不支持布局转换。

如果传入的是非嵌套张量，将被视为具有一致尺寸的批量成分张量。当传入的设备/数据类型与输入不同，或输入非连续时，将发生复制操作。否则会直接使用输入的存储空间。

如果提供的是张量列表，在构建嵌套张量时总会复制列表中的张量。

参数：

• ts (Tensor 或 *List[Tensor] 或* *Tuple[Tensor]) – 待处理的嵌套张量，或具有相同维度的张量列表/元组

关键字参数：

• dtype (torch.dtype, 可选) – 返回嵌套张量的目标数据类型。默认值：若为None，则与列表中第一个张量的数据类型相同
• device (torch.device, 可选) – 返回嵌套张量的目标设备。默认值：若为None，则与列表中第一个张量的设备相同
• layout (torch.layout, 可选) – 返回嵌套张量的目标布局。仅支持strided和jagged布局。默认值：若为None，则使用strided布局

返回类型：Tensor

---

示例：

>>> a = torch.arange(3, dtype=torch.float, requires_grad=True)
>>> b = torch.arange(5, dtype=torch.float, requires_grad=True)
>>> nt = torch.nested.as_nested_tensor([a, b])
>>> nt.is_leaf
False
>>> fake_grad = torch.nested.nested_tensor([torch.ones_like(a), torch.zeros_like(b)])
>>> nt.backward(fake_grad)
>>> a.grad
tensor([1., 1., 1.])
>>> b.grad
tensor([0., 0., 0., 0., 0.])
>>> c = torch.randn(3, 5, requires_grad=True)
>>> nt2 = torch.nested.as_nested_tensor(c)

---

torch.nested.to_padded_tensor(input, padding, output_size=None, out=None) → Tensor  

---

通过填充input嵌套张量返回一个新的（非嵌套）张量。

前导条目将用嵌套数据填充，而后随条目将被填充。

警告：to_padded_tensor()总是会复制底层数据，因为嵌套张量和非嵌套张量的内存布局不同。

参数

• padding (float) - 用于填充后随条目的填充值。

关键字参数

• output_size (Tuple[int]) - 输出张量的大小。

如果指定，它必须足够大以包含所有嵌套数据；

否则，将通过沿每个维度取每个嵌套子张量的最大尺寸来推断。

• out ( Tensor , optional) - 输出张量。

---

示例：

>>> nt = torch.nested.nested_tensor([torch.randn((2, 5)), torch.randn((3, 4))])
nested_tensor([tensor([[1.6862, -1.1282, 1.1031, 0.0464, -1.3276],  [-1.9967, -1.0054, 1.8972, 0.9174, -1.4995]]), tensor([[-1.8546, -0.7194, -0.2918, -0.1846],  [0.2773, 0.8793, -0.5183, -0.6447],  [1.8009, 1.8468, -0.9832, -1.5272]])])
>>> pt_infer = torch.nested.to_padded_tensor(nt, 0.0)
tensor([[[1.6862, -1.1282, 1.1031, 0.0464, -1.3276], [-1.9967, -1.0054, 1.8972, 0.9174, -1.4995], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000]], [[-1.8546, -0.7194, -0.2918, -0.1846, 0.0000], [0.2773, 0.8793, -0.5183, -0.6447, 0.0000], [1.8009, 1.8468, -0.9832, -1.5272, 0.0000]]])
>>> pt_large = torch.nested.to_padded_tensor(nt, 1.0, (2, 4, 6))
tensor([[[1.6862, -1.1282, 1.1031, 0.0464, -1.3276, 1.0000], [-1.9967, -1.0054, 1.8972, 0.9174, -1.4995, 1.0000], [1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000], [1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000]], [[-1.8546, -0.7194, -0.2918, -0.1846, 1.0000, 1.0000], [0.2773, 0.8793, -0.5183, -0.6447, 1.0000, 1.0000], [1.8009, 1.8468, -0.9832, -1.5272, 1.0000, 1.0000], [1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000]]])
>>> pt_small = torch.nested.to_padded_tensor(nt, 2.0, (2, 2, 2))
RuntimeError: Value in output_size is less than NestedTensor padded size. Truncation is not supported.

---

torch.nested.masked_select(tensor, mask)

---

给定一个跨步张量输入和一个跨步掩码，构建一个嵌套张量，生成的锯齿状布局嵌套张量将保留掩码值为True处的数值。掩码的维度会被保留并通过偏移量表示，这与masked_select()不同，后者会将输出压缩为一维张量。

参数：

tensor ( torch.Tensor )：用于构建锯齿状布局嵌套张量的跨步张量。

mask ( torch.Tensor )：应用于输入张量的跨步掩码张量

---

示例：

>>> tensor = torch.randn(3, 3)
>>> mask = torch.tensor([[False, False, True], [True, False, True], [False, False, True]])
>>> nt = torch.nested.masked_select(tensor, mask)
>>> nt.shape
torch.Size([3, j4])
>>> # Length of each item in the batch:
>>> nt.offsets().diff()
tensor([1, 2, 1])>>> tensor = torch.randn(6, 5)
>>> mask = torch.tensor([False])
>>> nt = torch.nested.masked_select(tensor, mask)
>>> nt.shape
torch.Size([6, j5])
>>> # Length of each item in the batch:
>>> nt.offsets().diff()
tensor([0, 0, 0, 0, 0, 0])

---

返回类型：Tensor

---

torch.nested.narrow(tensor, dim, start, length, layout=torch.strided)

---

从跨步张量tensor构造一个嵌套张量（可能是视图）。其语义类似于torch.Tensor.narrow方法，在指定维度dim上，新嵌套张量仅显示区间[start, start+length)内的元素。由于嵌套表示允许在该维度的每个"行"设置不同的起始点和长度，start和length也可以是形状为tensor.shape[0]的张量。

具体行为会因嵌套张量的布局类型而异：

• 使用跨步布局(strided layout)时，torch.narrow会将收窄后的数据复制到新的连续跨步布局NT中
• 使用锯齿布局(jagged layout)时，narrow()会创建原始跨步张量的非连续视图。这种特殊表示对Transformer模型中的kv缓存非常有用，因为专用SDPA内核可以轻松处理此格式，从而提升性能。

参数说明：

• tensor (torch.Tensor) - 跨步张量。使用锯齿布局时作为嵌套张量的基础数据，使用跨步布局时会被复制
• dim (int) - 应用narrow操作的维度。锯齿布局仅支持dim=1，跨步布局支持所有维度
• start (Union[int, torch.Tensor]) - narrow操作的起始元素
• length (Union[int, torch.Tensor]) - narrow操作选取的元素数量

关键字参数：

• layout (torch.layout, 可选) - 返回嵌套张量的目标布局。仅支持跨步和锯齿布局，默认为None时使用跨步布局

返回类型：Tensor

---

示例：

>>> starts = torch.tensor([0, 1, 2, 3, 4], dtype=torch.int64)
>>> lengths = torch.tensor([3, 2, 2, 1, 5], dtype=torch.int64)
>>> narrow_base = torch.randn(5, 10, 20)
>>> nt_narrowed = torch.nested.narrow(narrow_base, 1, starts, lengths, layout=torch.jagged)
>>> nt_narrowed.is_contiguous()
False

---

torch.Size

torch.Size 是调用 torch.Tensor.size() 返回的结果类型。它描述了原始张量所有维度的大小。作为 tuple 的子类，它支持常见的序列操作，如索引和获取长度。

---

示例：

>>> x = torch.ones(10, 20, 30)
>>> s = x.size()
>>> s
torch.Size([10, 20, 30])
>>> s[1]
20
>>> len(s)
3

---

class torch.Size(iterable=(), /) 

---

count(value, /) 

---

返回该值出现的次数。

---

index(value, start=0, stop=9223372036854775807, /) 

---

返回值的第一个索引。

如果值不存在，则引发 ValueError。

---

numel() → int

---

返回给定尺寸的torch.Tensor所包含的元素数量。

更正式地说，对于一个尺寸为s = torch.Size([10, 10])的张量x = tensor.ones(10, 10)，等式x.numel() == x.size().numel() == s.numel() == 100成立。

---

示例：

>>> x=torch.ones(10, 10)
>>> s=x.size()
>>> s
torch.Size([10, 10])
>>> s.numel()
100
>>> x.numel() == s.numel()
True

---

警告：此函数返回的不是 torch.Size 描述的维度数量，而是具有该尺寸的 torch.Tensor 所包含的元素总数。

---

torch.sparse

---

https://docs.pytorch.org/docs/stable/sparse.html

警告：PyTorch 的稀疏张量 API 目前处于测试阶段，近期可能会发生变化。
我们非常欢迎通过 GitHub issues 提交功能请求、错误报告和一般性建议。

---

稀疏化的适用场景与优势

默认情况下，PyTorch会将torch.Tensor元素以连续方式存储在物理内存中。这种存储方式能高效支持需要快速访问元素的各类数组处理算法实现。

但某些场景下，用户可能选择用大部分元素为零值的张量来表示数据，例如图邻接矩阵、剪枝后的权重或点云数据。我们认识到这些应用的重要性，旨在通过稀疏存储格式为这类用例提供性能优化。

业界已发展出多种稀疏存储格式，如COO、CSR/CSC、半结构化、LIL等。虽然具体布局方式不同，但它们都通过高效表示零值元素来实现数据压缩。我们将未压缩的值称为显式值，以区别于被压缩的隐式值。通过压缩重复的零值，稀疏存储格式能节省CPU和GPU的内存与计算资源。特别是在高稀疏度或高度结构化稀疏场景下，这可能带来显著的性能提升。因此，稀疏存储格式可视为一种性能优化手段。

与其他性能优化技术类似，稀疏存储格式并非总是有利。实际测试中，您可能会发现执行时间不降反增。

如果您通过理论分析预期应获得显著性能提升，但实测结果却出现性能下降，欢迎提交GitHub issue。这将帮助我们优先实现高效内核和更广泛的性能优化。

我们提供了便捷的方式来尝试不同稀疏布局，并支持格式间转换，而不会对特定应用场景预设最优方案。

---

功能概述

我们希望通过为每种布局提供转换例程，能够轻松地从给定的稠密张量构建稀疏张量。

在接下来的示例中，我们将一个默认稠密（跨步）布局的二维张量转换为由COO内存布局支持的二维张量。在这种情况下，仅存储非零元素的值和索引。

---

>>> a = torch.tensor([[0, 2.], [3, 0]])
>>> a.to_sparse()
tensor(indices=tensor([[0, 1], [1, 0]]), values=tensor([2., 3.]), size=(2, 2), nnz=2, layout=torch.sparse_coo)

---

PyTorch 目前支持 COO、CSR、CSC、BSR 和 BSC 稀疏格式。

我们还提供了支持 :ref: 半结构化稀疏 的原型实现。

更多详情请参阅相关文档。

请注意，我们对这些格式进行了轻微泛化。

批处理：GPU 等设备需要批处理才能获得最佳性能，因此我们支持批处理维度。

当前我们提供了一种非常简单的批处理方式，即稀疏格式的每个组件本身都进行批处理。这要求每个批次条目具有相同数量的指定元素。

在这个示例中，我们从 3D 密集张量构建了一个 3D（批处理）CSR 张量。

---

>>> t = torch.tensor([[[1., 0], [2., 3.]], [[4., 0], [5., 6.]]])
>>> t.dim()
3
>>> t.to_sparse_csr()
tensor(crow_indices=tensor([[0, 1, 3], [0, 1, 3]]), col_indices=tensor([[0, 0, 1], [0, 0, 1]]), values=tensor([[1., 2., 3.], [4., 5., 6.]]), size=(2, 2, 2), nnz=3, layout=torch.sparse_csr)

---

稠密维度：另一方面，像图嵌入这样的数据更适合被视为向量的稀疏集合，而非标量。

在这个示例中，我们从一个3D跨步张量创建了一个具有2个稀疏维度和1个稠密维度的3D混合COO张量。如果3D跨步张量中的整行都为零，则不会存储该行。但如果行中有任何非零值，则会完整存储整行。这种方式减少了索引数量，因为我们只需要每行一个索引，而非每个元素一个索引。但同时也增加了值的存储量，因为只有完全为零的行才能被省略，而任何非零元素的存在都会导致整行被存储。

---

>>> t = torch.tensor([[[0., 0], [1., 2.]], [[0., 0], [3., 4.]]])
>>> t.to_sparse(sparse_dim=2)
tensor(indices=tensor([[0, 1], [1, 1]]), values=tensor([[1., 2.], [3., 4.]]), size=(2, 2, 2), nnz=2, layout=torch.sparse_coo)

---

算子概述

从根本上说，采用稀疏存储格式的 Tensor 运算与采用跨步（或其他）存储格式的 Tensor 运算行为一致。存储的特殊性（即数据的物理布局）会影响运算性能，但不应该影响运算语义。

我们正在积极扩展稀疏张量的算子覆盖范围。但目前用户不应期望获得与稠密张量相同级别的支持。具体支持算子列表请参阅我们的算子文档。

---

>>> b = torch.tensor([[0, 0, 1, 2, 3, 0], [4, 5, 0, 6, 0, 0]])
>>> b_s = b.to_sparse_csr()
>>> b_s.cos()
Traceback (most recent call last):File "<stdin>", line 1, in <module>
RuntimeError: unsupported tensor layout: SparseCsr
>>> b_s.sin()
tensor(crow_indices=tensor([0, 3, 6]), col_indices=tensor([2, 3, 4, 0, 1, 3]), values=tensor([0.8415, 0.9093, 0.1411, -0.7568, -0.9589, -0.2794]), size=(2, 6), nnz=6, layout=torch.sparse_csr)

---

如上述示例所示，我们不支持非零保留的一元运算符（如cos）。非零保留一元运算的输出无法像输入那样充分利用稀疏存储格式的优势，可能导致内存使用量灾难性增长。

因此，我们建议用户先显式转换为稠密张量（dense Tensor），然后再执行运算。

---

>>> b_s.to_dense().cos()
tensor([[1.0000, -0.4161], [-0.9900, 1.0000]])

---

我们注意到部分用户希望在诸如余弦（cos）等运算中忽略压缩零值，而非严格保持运算的原始语义。为此，我们可以推荐使用 torch.masked 及其 MaskedTensor，该功能同样由稀疏存储格式和计算内核提供支持。

还需注意的是，目前用户无法自主选择输出布局。例如，将稀疏张量与常规步幅张量相加时，结果会转为步幅张量。部分用户可能更希望保持稀疏布局，因为他们预知运算结果仍会保持足够的稀疏性。

---

>>> a + b.to_sparse()
tensor([[0., 3.], [3., 0.]])

---

我们认识到，能够高效生成不同输出布局的内核访问非常有用。后续操作可能会因接收特定布局而显著受益。我们正在开发一个API来控制结果布局，并意识到这是规划任何给定模型更优执行路径的重要功能。

---

稀疏半结构化张量

---

警告：稀疏半结构化张量目前是原型功能，可能会发生变化。如果发现错误或有任何反馈，欢迎提交问题报告。

半结构化稀疏是一种稀疏数据布局，最初由NVIDIA的Ampere架构引入。它也被称为细粒度结构化稀疏或2:4结构化稀疏。

这种稀疏布局存储每2n个元素中的n个元素，其中n由张量数据类型(dtype)的宽度决定。最常用的dtype是float16，此时n=2，因此称为"2:4结构化稀疏"。

关于半结构化稀疏的更详细说明，请参阅NVIDIA的这篇博客文章。

在PyTorch中，半结构化稀疏通过张量子类实现。通过子类化，我们可以重写__torch_dispatch__，从而在执行矩阵乘法时使用更快的稀疏内核。我们还可以在子类中以压缩形式存储张量，以减少内存开销。

在这种压缩形式中，稀疏张量仅存储指定的元素和一些编码掩码的元数据。

---

注意：半结构化稀疏张量的指定元素和元数据掩码一起存储在一个扁平压缩张量中。它们相互追加形成一个连续的内存块。

压缩张量 = [原始张量的指定元素 | 元数据掩码]

对于大小为(r, c)的原始张量，前m * k // 2个元素是保留的元素，张量的其余部分是元数据。

为了方便用户查看指定元素和掩码，可以使用.indices()和.values()分别访问掩码和指定元素：

• .values()返回指定元素，形成一个大小为(r, c//2)的张量，且与密集矩阵具有相同的dtype
• .indices()返回元数据掩码，形成一个大小为(r, c//2)的张量，元素类型为torch.int16（当dtype是torch.float16或torch.bfloat16时）或torch.int32（当dtype是torch.int8时）

对于2:4稀疏张量，元数据开销很小——每个指定元素只需2比特。

---

注意：需要特别注意的是，torch.float32仅支持1:2稀疏度，因此不遵循上述相同的公式。

下面我们分解计算2:4稀疏张量的压缩比（密集大小/稀疏大小）：

设(r, c) = tensor.shape，e = bitwidth(tensor.dtype)，因此对于torch.float16和torch.bfloat16，e=16；对于torch.int8，e=8。

$$\begin{gathered} M_{dense}=r\times c\times e \\ {M}_{sparse}=M_{specified}+M_{metadata}=r\times \frac{c}{2}\times e+r\times \frac{c}{2}\times 2=\frac{rce}{2}+rc=rce(\frac{1}{2}+\frac{1}{e}) \end{gathered}$$

通过这些计算，我们可以确定原始密集表示和新稀疏表示的总内存占用。

这给出了一个简单的压缩比公式，该公式仅依赖于张量数据类型的位宽：

$$C=\frac{M_{sparse}}{M_{dense}}=\frac{1}{2}+\frac{1}{e}$$

使用这个公式，我们发现对于torch.float16或torch.bfloat16，压缩比为56.25%；对于torch.int8，压缩比为62.5%。

---

构建稀疏半结构化张量

只需使用 torch.to_sparse_semi_structured 函数，即可将密集张量转换为稀疏半结构化张量。

请注意，由于半结构化稀疏性仅支持 NVIDIA GPU 的硬件兼容性，因此我们仅支持 CUDA 张量。

以下是支持半结构化稀疏性的数据类型。注意每种数据类型都有其特定的形状约束和压缩因子。

PyTorch 数据类型	形状约束	压缩因子	稀疏模式
torch.float16	张量必须为 2D，且 (r, c) 必须均为 64 的正整数倍	9/16	2:4
torch.bfloat16	张量必须为 2D，且 (r, c) 必须均为 64 的正整数倍	9/16	2:4
torch.int8	张量必须为 2D，且 (r, c) 必须均为 128 的正整数倍	10/16	2:4

要构建半结构化稀疏张量，首先需要创建一个符合 2:4（或半结构化）稀疏格式的常规密集张量。为此，我们可以平铺一个小的 1x4 条带，生成一个 16x16 的密集 float16 张量。之后，调用 to_sparse_semi_structured 函数对其进行压缩，以加速推理。

---

>>> from torch.sparse import to_sparse_semi_structured
>>> A = torch.Tensor([0, 0, 1, 1]).tile((128, 32)).half().cuda()
tensor([[0., 0., 1.,  ..., 0., 1., 1.],[0., 0., 1.,  ..., 0., 1., 1.],[0., 0., 1.,  ..., 0., 1., 1.],...,[0., 0., 1.,  ..., 0., 1., 1.],[0., 0., 1.,  ..., 0., 1., 1.],[0., 0., 1.,  ..., 0., 1., 1.]], device='cuda:0', dtype=torch.float16)
>>> A_sparse = to_sparse_semi_structured(A)
SparseSemiStructuredTensor(shape=torch.Size([128, 128]), transposed=False, values=tensor([[1., 1., 1.,  ..., 1., 1., 1.],[1., 1., 1.,  ..., 1., 1., 1.],[1., 1., 1.,  ..., 1., 1., 1.],...,[1., 1., 1.,  ..., 1., 1., 1.],[1., 1., 1.,  ..., 1., 1., 1.],[1., 1., 1.,  ..., 1., 1., 1.]], device='cuda:0', dtype=torch.float16), metadata=tensor([[-4370, -4370, -4370,  ..., -4370, -4370, -4370],[-4370, -4370, -4370,  ..., -4370, -4370, -4370],[-4370, -4370, -4370,  ..., -4370, -4370, -4370],...,[-4370, -4370, -4370,  ..., -4370, -4370, -4370],[-4370, -4370, -4370,  ..., -4370, -4370, -4370],[-4370, -4370, -4370,  ..., -4370, -4370, -4370]], device='cuda:0',
dtype=torch.int16))

---

稀疏半结构化张量运算

目前支持对半结构化稀疏张量进行以下运算：

• torch.addmm(bias, dense, sparse.t())
• torch.mm(dense, sparse)
• torch.mm(sparse, dense)
• aten.linear.default(dense, sparse, bias)
• aten.t.default(sparse)
• aten.t.detach(sparse)

要使用这些运算，只需在张量已转换为半结构化稀疏格式（包含0值）后，传入to_sparse_semi_structured(tensor)的输出结果替代原始tensor即可，示例如下：

>>> a = torch.Tensor([0, 0, 1, 1]).tile((64, 16)).half().cuda()
>>> b = torch.rand(64, 64).half().cuda()
>>> c = torch.mm(a, b)
>>> a_sparse = to_sparse_semi_structured(a)
>>> torch.allclose(c, torch.mm(a_sparse, b))
True

---

加速半结构化稀疏的 nn.Linear

只需几行代码，如果权重已经是半结构化稀疏的，就可以加速模型中的线性层：

>>> input = torch.rand(64, 64).half().cuda()
>>> mask = torch.Tensor([0, 0, 1, 1]).tile((64, 16)).cuda().bool()
>>> linear = nn.Linear(64, 64).half().cuda()
>>> linear.weight = nn.Parameter(to_sparse_semi_structured(linear.weight.masked_fill(~mask, 0)))

---

稀疏COO张量

PyTorch实现了所谓的坐标格式(COO格式)，作为实现稀疏张量的存储格式之一。在COO格式中，指定的元素以索引元组和对应值的形式存储。具体来说：

• 指定元素的索引收集在大小为(ndim, nse)、元素类型为torch.int64的indices张量中
• 对应的值收集在大小为(nse,)、元素类型为任意整数或浮点数的values张量中

其中ndim是张量的维度数，nse是指定元素的数量。

---

注意：稀疏COO张量的内存消耗至少为(ndim * 8 + <元素类型字节大小>) * nse字节（加上存储其他张量数据的固定开销）。

而跨步张量的内存消耗至少为product(<张量形状>) * <元素类型字节大小>。

例如，一个10,000×10,000大小、包含100,000个非零32位浮点数的张量，使用COO张量布局时内存消耗至少为(2 * 8 + 4) * 100 000 = 2 000 000字节，而使用默认跨步张量布局时为10 000 * 10 000 * 4 = 400 000 000字节。可见使用COO存储格式可节省200倍内存。

---

构造方式

可以通过向 torch.sparse_coo_tensor() 函数提供索引张量、值张量以及稀疏张量的尺寸（当无法从索引和值张量推断时）来构建一个稀疏COO张量。

假设我们需要定义一个稀疏张量，其中位置(0,2)处值为3，位置(1,0)处值为4，位置(1,2)处值为5。未指定的元素默认采用相同的填充值（默认为零），此时可以这样编写代码：

>>> i = [[0, 1, 1], [2, 0, 2]]
>>> v =  [3, 4, 5]
>>> s = torch.sparse_coo_tensor(i, v, (2, 3))
>>> s
tensor(indices=tensor([[0, 1, 1], [2, 0, 2]]), values=tensor([3, 4, 5]), size=(2, 3), nnz=3, layout=torch.sparse_coo)
>>> s.to_dense()
tensor([[0, 0, 3], [4, 0, 5]])

---

请注意，输入参数 i 并不是一个索引元组列表。如果你想以这种方式编写索引，应在传递给稀疏矩阵构造函数之前先进行转置操作：

>>> i = [[0, 2], [1, 0], [1, 2]]
>>> v =  [3,  4,  5    ]
>>> s = torch.sparse_coo_tensor(list(zip(i)), v, (2, 3))
>>> # Or another equivalent formulation to get s
>>> s = torch.sparse_coo_tensor(torch.tensor(i).t(), v, (2, 3))
>>> torch.sparse_coo_tensor(i.t(), v, torch.Size([2,3])).to_dense()
tensor([[0, 0, 3], [4, 0, 5]])

---

可以仅通过指定尺寸来构造一个空的稀疏COO张量

---

>>> torch.sparse_coo_tensor(size=(2, 3))
tensor(indices=tensor([], size=(2, 0)), values=tensor([], size=(0,)), size=(2, 3), nnz=0, layout=torch.sparse_coo)

---

稀疏混合COO张量

PyTorch实现了从标量值的稀疏张量到（连续）张量值的稀疏张量的扩展。这类张量被称为混合张量。

PyTorch混合COO张量扩展了稀疏COO张量的功能，允许values张量是一个多维张量，因此我们具有：

• 指定元素的索引收集在大小为(sparse_dims, nse)、元素类型为torch.int64的indices张量中；
• 对应的（张量）值收集在大小为(nse, dense_dims)、元素类型为任意整数或浮点数的values张量中。

---

注意：我们使用(M + K)维张量来表示一个N维稀疏混合张量，其中M和K分别是稀疏维度和密集维度的数量，满足M + K == N的关系。

假设我们要创建一个(2 + 1)维的张量，其中位置(0, 2)处的条目为[3, 4]，位置(1, 0)处的条目为[5, 6]，位置(1, 2)处的条目为[7, 8]。我们可以这样表示：

>>> i = [[0, 1, 1], [2, 0, 2]]
>>> v =  [[3, 4], [5, 6], [7, 8]]
>>> s = torch.sparse_coo_tensor(i, v, (2, 3, 2))
>>> s
tensor(indices=tensor([[0, 1, 1], [2, 0, 2]]), values=tensor([[3, 4], [5, 6], [7, 8]]), size=(2, 3, 2), nnz=3, layout=torch.sparse_coo)

---

>>> s.to_dense()
tensor([[[0, 0], [0, 0], [3, 4]], [[5, 6], [0, 0], [7, 8]]])

---

通常来说，如果 s 是一个稀疏 COO 张量，且 M = s.sparse_dim()，K = s.dense_dim()，那么以下不变式成立：

• M + K == len(s.shape) == s.ndim - 张量的维度等于稀疏维度和密集维度之和，
• s.indices().shape == (M, nse) - 稀疏索引被显式存储，
• s.values().shape == (nse,) + s.shape[M : M + K] - 混合张量的值是 K 维张量，
• s.values().layout == torch.strided - 值以跨步张量的形式存储。

注意：密集维度始终位于稀疏维度之后，也就是说，不支持混合稀疏维度和密集维度。

注意：为了确保构造的稀疏张量具有一致的索引、值和大小，可以通过 check_invariants=True 关键字参数在每次张量创建时启用不变式检查，或者全局使用 torch.sparse.check_sparse_tensor_invariants 上下文管理器实例。默认情况下，稀疏张量的不变式检查是禁用的。

---

未合并的稀疏COO张量

PyTorch稀疏COO张量格式允许存在稀疏的未合并张量，其索引中可能包含重复坐标。这种情况下，该索引处的值被解释为所有重复值条目的总和。例如，可以为同一个索引1指定多个值3和4，这将生成一个一维未合并张量：

>>> i = [[1, 1]]
>>> v =  [3, 4]
>>> s=torch.sparse_coo_tensor(i, v, (3,))
>>> s
tensor(indices=tensor([[1, 1]]), values=tensor(  [3, 4]), size=(3,), nnz=2, layout=torch.sparse_coo)

---

合并过程将通过求和运算将多值元素累积为单一值：

>>> s.coalesce()
tensor(indices=tensor([[1]]), values=tensor([7]), size=(3,), nnz=1, layout=torch.sparse_coo)

---

通常来说，torch.Tensor.coalesce() 方法的输出是一个具有以下特性的稀疏张量：

• 指定张量元素的索引是唯一的，且按字典序排序，此时 torch.Tensor.is_coalesced() 会返回 True。

注意：在大多数情况下，你不需要关心稀疏张量是否经过合并(coalesced)，因为大多数操作对于合并或未合并的稀疏张量都能同样工作。

然而，某些操作在未合并张量上可以实现更高效率，而另一些则在合并张量上更高效。

例如，稀疏COO张量的加法实现方式就是简单地拼接索引张量和值张量。

---

>>> a = torch.sparse_coo_tensor([[1, 1]], [5, 6], (2,))
>>> b = torch.sparse_coo_tensor([[0, 0]], [7, 8], (2,))
>>> a + b
tensor(indices=tensor([[0, 0, 1, 1]]), values=tensor([7, 8, 5, 6]), size=(2,), nnz=4, layout=torch.sparse_coo)

---

如果你反复执行可能产生重复条目的操作（例如 torch.Tensor.add()），应该定期合并稀疏张量以防止其变得过大。

另一方面，索引的字典序排列有利于实现涉及大量元素选择操作的算法，例如切片或矩阵乘积。

---

稀疏COO张量操作

让我们来看以下示例：

>>> i = [[0, 1, 1], [2, 0, 2]]
>>> v =  [[3, 4], [5, 6], [7, 8]]
>>> s = torch.sparse_coo_tensor(i, v, (2, 3, 2))

---

如前所述，稀疏COO张量是torch.Tensor的实例。为了将其与其他布局类型的张量实例区分开，可以使用torch.Tensor.is_sparse属性或torch.Tensor.layout属性进行判断：

>>> isinstance(s, torch.Tensor)
True
>>> s.is_sparse
True
>>> s.layout == torch.sparse_coo
True

---

可以通过以下方法分别获取稀疏维度和密集维度的数量：

torch.Tensor.sparse_dim() 和 torch.Tensor.dense_dim()。例如：

>>> s.sparse_dim(), s.dense_dim()
(2, 1)

---

如果 s 是一个稀疏 COO 张量，可以通过 torch.Tensor.indices() 和 torch.Tensor.values() 方法获取其 COO 格式数据。

注意：目前仅当张量实例处于合并状态时，才能获取其 COO 格式数据。

---

>>> s.indices()
RuntimeError: Cannot get indices on an uncoalesced tensor, please call .coalesce() first

---

要获取未合并张量的COO格式数据，请使用 torch.Tensor._values() 和 torch.Tensor._indices()：

>>> s._indices()
tensor([[0, 1, 1], [2, 0, 2]])

---

警告：调用 torch.Tensor._values() 将返回一个分离的张量。

如需跟踪梯度，必须改用 torch.Tensor.coalesce().values()。

构建新的稀疏 COO 张量会产生一个未合并的张量：

>>> s.is_coalesced()
False

---

但可以通过 torch.Tensor.coalesce() 方法构造稀疏 COO 张量的合并副本：

>>> s2 = s.coalesce()
>>> s2.indices()
tensor([[0, 1, 1], [2, 0, 2]])

---

在处理未合并的稀疏COO张量时，必须考虑未合并数据的可加性特性：相同索引的值是求和项，其计算结果对应张量元素的值。例如，稀疏未合并张量的标量乘法可以通过将所有未合并值与标量相乘来实现，因为c*(a + b) == c*a + c*b成立。然而，任何非线性操作（比如平方根）不能直接应用于未合并数据，因为sqrt(a + b) == sqrt(a) + sqrt(b)通常不成立。

稀疏COO张量的切片操作（步长为正）仅支持稠密维度。索引操作则同时支持稀疏维度和稠密维度。

---

>>> s[1]
tensor(indices=tensor([[0, 2]]), values=tensor([[5, 6], [7, 8]]), size=(3, 2), nnz=2, layout=torch.sparse_coo)
>>> s[1, 0, 1]
tensor(6)
>>> s[1, 0, 1:]
tensor([6])

---

在PyTorch中，稀疏张量的填充值通常无法显式指定，一般默认为零。但某些操作可能会以不同方式解释填充值。例如，torch.sparse.softmax()在计算softmax时会假设填充值为负无穷。

---

稀疏压缩张量

稀疏压缩张量代表了一类具有共同特征的稀疏张量：通过对特定维度的索引进行压缩编码，从而实现对稀疏压缩张量线性代数核的特定优化。该编码基于压缩稀疏行(CSR)格式，PyTorch稀疏压缩张量在此基础上扩展了稀疏张量批次支持、允许多维张量值，并以密集块形式存储稀疏张量值。

---

注意：我们使用(B + M + K)维张量来表示N维稀疏压缩混合张量，其中B、M和K分别表示批次维度、稀疏维度和密集维度的数量，满足B + M + K == N关系。稀疏压缩张量的稀疏维度数始终为二，即M == 2。

---

注意：当满足以下不变条件时，我们称索引张量compressed_indices使用了CSR编码：

• compressed_indices是连续步进的32位或64位整数张量
• compressed_indices的形状为(batchsize, compressed_dim_size + 1)，其中compressed_dim_size表示压缩维度数（如行或列）
• compressed_indices[..., 0] == 0，其中...表示批次索引
• compressed_indices[..., compressed_dim_size] == nse，其中nse表示指定元素的数量
• 对于i=1,...,compressed_dim_size，满足0 <= compressed_indices[..., i] - compressed_indices[..., i - 1] <= plain_dim_size，其中plain_dim_size表示正交于压缩维度的普通维度数（如列或行）。

---

为确保构建的稀疏张量具有一致的索引、值和尺寸，可通过check_invariants=True关键字参数在张量创建时启用不变性检查，或全局使用torch.sparse.check_sparse_tensor_invariants上下文管理器实例。默认情况下，稀疏张量不变性检查处于禁用状态。

---

注意：稀疏压缩布局向N维张量的泛化可能导致关于指定元素计数的混淆。当稀疏压缩张量包含批次维度时，指定元素数量将对应每个批次的此类元素数量。当稀疏压缩张量具有密集维度时，所考虑的元素变为K维数组。对于块稀疏压缩布局，被指定的元素是二维块。以三维块稀疏张量为例，设批次维度长度为b，块形状为p, q。若该张量有n个指定元素，则实际表示每个批次有n个指定块。该张量的values形状将为(b, n, p, q)。这种对指定元素数量的解释源于所有稀疏压缩布局都派生自二维矩阵的压缩——批次维度被视为稀疏矩阵的堆叠，密集维度则将元素含义从简单标量值更改为具有自身维度的数组。

---

稀疏CSR张量

相比COO格式，CSR格式的主要优势在于更高效的存储利用，以及更快的计算操作（例如使用MKL和MAGMA后端进行稀疏矩阵-向量乘法）。

在最简单的情况下，(0 + 2 + 0)维的稀疏CSR张量由三个一维张量组成：crow_indices、col_indices和values：

• crow_indices张量包含压缩的行索引。这是一个大小为nrows + 1（行数加1）的一维张量。crow_indices的最后一个元素是已指定元素的数量nse。该张量根据给定行的起始位置，编码values和col_indices中的索引。张量中每个连续数字减去前一个数字，表示该行的元素数量。
• col_indices张量包含每个元素的列索引。这是一个大小为nse的一维张量。
• values张量包含CSR张量元素的值。这是一个大小为nse的一维张量。

---

注意：索引张量crow_indices和col_indices的元素类型应为torch.int64（默认）或torch.int32。如果要使用MKL启用的矩阵操作，请使用torch.int32。这是因为PyTorch默认链接的是MKL LP64，它使用32位整数索引。

在一般情况下，(B + 2 + K)维的稀疏CSR张量由两个(B + 1)维的索引张量crow_indices和col_indices，以及一个(1 + K)维的values张量组成，满足以下条件：

• crow_indices.shape == (batchsize, nrows + 1)
• col_indices.shape == (batchsize, nse)
• values.shape == (nse, densesize)

而稀疏CSR张量的形状为(batchsize, nrows, ncols, densesize)，其中len(batchsize) == B且len(densesize) == K。

---

注意：稀疏CSR张量的批次是相互依赖的：所有批次中已指定元素的数量必须相同。这种人为约束允许高效存储不同CSR批次的索引。

---

注意：稀疏维度和密集维度的数量可以通过torch.Tensor.sparse_dim()和torch.Tensor.dense_dim()方法获取。批次维度可以从张量形状计算得出：batchsize = tensor.shape[:-tensor.sparse_dim() - tensor.dense_dim()]。

---

注意：稀疏CSR张量的内存消耗至少为(nrows * 8 + (8 + <元素类型字节大小> * prod(densesize)) * nse) * prod(batchsize)字节（加上存储其他张量数据的常量开销）。以稀疏COO格式介绍中的注释示例为例，一个10,000 x 10,000的张量，包含100,000个非零32位浮点数，使用CSR张量布局时，内存消耗至少为(10000 * 8 + (8 + 4 * 1) * 100 000) * 1 = 1 280 000字节。请注意，与COO和strided格式相比，使用CSR存储格式分别节省了1.6倍和310倍的内存。

---

CSR张量的构建

稀疏CSR张量可以直接通过使用torch.sparse_csr_tensor()函数来构建。用户需要分别提供行索引、列索引和值张量，其中行索引必须使用CSR压缩编码格式进行指定。size参数是可选的，如果未提供该参数，系统会根据crow_indices和col_indices自动推断张量尺寸。

---

>>> crow_indices = torch.tensor([0, 2, 4])
>>> col_indices = torch.tensor([0, 1, 0, 1])
>>> values = torch.tensor([1, 2, 3, 4])
>>> csr = torch.sparse_csr_tensor(crow_indices, col_indices, values, dtype=torch.float64)
>>> csr
tensor(crow_indices=tensor([0, 2, 4]), col_indices=tensor([0, 1, 0, 1]), values=tensor([1., 2., 3., 4.]), size=(2, 2), nnz=4, dtype=torch.float64)
>>> csr.to_dense()
tensor([[1., 2.], [3., 4.]], dtype=torch.float64)

---

注意：推导出的size中稀疏维度的值是根据crow_indices的大小和col_indices中的最大索引值计算得出的。如果需要列数大于推导出的size，则必须显式指定size参数。

从跨步(strided)或稀疏COO张量构建2-D稀疏CSR张量的最简单方法是使用torch.Tensor.to_sparse_csr()方法。(跨步)张量中的任何零值将被解释为稀疏张量中的缺失值。

---

>>> t = torch.tensor([[[1., 0], [2., 3.]], [[4., 0], [5., 6.]]])
>>> t.dim()
3
>>> t.to_sparse_csr()
tensor(crow_indices=tensor([[0, 1, 3],[0, 1, 3]]),col_indices=tensor([[0, 0, 1],[0, 0, 1]]),values=tensor([[1., 2., 3.],[4., 5., 6.]]), size=(2, 2, 2), nnz=3,layout=torch.sparse_csr)

---

CSR张量运算

稀疏矩阵-向量乘法可以通过tensor.matmul()方法执行。这是目前CSR张量唯一支持的数学运算。

---

>>> vec = torch.randn(4, 1, dtype=torch.float64)
>>> sp.matmul(vec)
tensor([[0.9078], [1.3180], [0.0000]], dtype=torch.float64)

---

稀疏 CSC 张量

稀疏 CSC（压缩稀疏列）张量格式实现了用于存储二维张量的 CSC 格式，并扩展支持批量稀疏 CSC 张量及多维张量值。

---

注意：当转置操作涉及交换稀疏维度时，稀疏 CSC 张量本质上是稀疏 CSR 张量的转置形式。

与稀疏 CSR 张量类似，稀疏 CSC 张量由三个张量组成：ccol_indices、row_indices 和 values：

• ccol_indices 张量包含压缩的列索引。这是一个 (B + 1) 维张量，形状为 (batchsize, ncols + 1)。最后一个元素表示指定元素的数量 nse。该张量根据给定列起始位置编码 values 和 row_indices 中的索引。张量中每个连续数字减去前一个数字的结果表示该列中的元素数量。
• row_indices 张量包含每个元素的行索引。这是一个 (B + 1) 维张量，形状为 (batchsize, nse)。
• values 张量存储 CSC 张量元素的值。这是一个 (1 + K) 维张量，形状为 (nse, densesize)。

---

CSC 张量的构建

稀疏 CSC 张量可以直接通过 torch.sparse_csc_tensor() 函数构建。用户需要分别提供行索引、列索引和值张量，其中列索引必须使用 CSR 压缩编码格式进行指定。size 参数是可选的，如果未提供该参数，系统会从 row_indices 和 ccol_indices 张量中自动推断出张量尺寸。

---

>>> ccol_indices = torch.tensor([0, 2, 4])
>>> row_indices = torch.tensor([0, 1, 0, 1])
>>> values = torch.tensor([1, 2, 3, 4])
>>> csc = torch.sparse_csc_tensor(ccol_indices, row_indices, values, dtype=torch.float64)
>>> csc
tensor(ccol_indices=tensor([0, 2, 4]), row_indices=tensor([0, 1, 0, 1]), values=tensor([1., 2., 3., 4.]), size=(2, 2), nnz=4, dtype=torch.float64, layout=torch.sparse_csc)
>>> csc.to_dense()
tensor([[1., 3.], [2., 4.]], dtype=torch.float64)

---

注意：稀疏 CSC 张量构造函数的参数顺序中，压缩列索引参数排在行索引参数之前。

您可以使用 torch.Tensor.to_sparse_csc() 方法，将任何二维张量构造为 (0 + 2 + 0) 维的稀疏 CSC 张量。在（跨步）张量中的任何零值，都将被解释为稀疏张量中的缺失值。

---

>>> a = torch.tensor([[0, 0, 1, 0], [1, 2, 0, 0], [0, 0, 0, 0]], dtype=torch.float64)
>>> sp = a.to_sparse_csc()
>>> sp
tensor(ccol_indices=tensor([0, 1, 2, 3, 3]), row_indices=tensor([1, 1, 0]), values=tensor([1., 2., 1.]), size=(3, 4), nnz=3, dtype=torch.float64, layout=torch.sparse_csc)

---

稀疏BSR张量

稀疏BSR（块压缩稀疏行）张量格式实现了BSR存储格式，用于存储二维张量，并扩展支持批量稀疏BSR张量及多维张量块组成的值。

稀疏BSR张量由三个张量组成：crow_indices、col_indices和values：

• crow_indices张量包含压缩的行索引。这是一个(B+1)维张量，形状为(batchsize, nrowblocks + 1)。最后一个元素是已指定块的数量nse。该张量根据列块的起始位置，编码values和col_indices中的索引。张量中每个连续数字减去前一个数字，表示该行中的块数量。
• col_indices张量包含每个元素的列块索引。这是一个(B+1)维张量，形状为(batchsize, nse)。
• values张量包含收集到二维块中的稀疏BSR张量元素值。这是一个(1+2+K)维张量，形状为(nse, nrowblocks, ncolblocks, *densesize)。

---

BSR张量的构建

稀疏BSR张量可以直接通过使用torch.sparse_bsr_tensor()函数来构建。用户需要分别提供行块索引、列块索引和值张量，其中行块索引必须使用CSR压缩编码格式进行指定。

size参数是可选的，如果未提供该参数，系统会根据crow_indices和col_indices张量自动推断大小。

---

>>> crow_indices = torch.tensor([0, 2, 4])
>>> col_indices = torch.tensor([0, 1, 0, 1])
>>> values = torch.tensor([1, 2, 3, 4])
>>> csr = torch.sparse_csr_tensor(crow_indices, col_indices, values, dtype=torch.float64)
>>> csr
tensor(crow_indices=tensor([0, 2, 4]),col_indices=tensor([0, 1, 0, 1]),values=tensor([1., 2., 3., 4.]), size=(2, 2), nnz=4,dtype=torch.float64)
>>> csr.to_dense()
tensor([[1., 2.],[3., 4.]], dtype=torch.float64)

---

可以通过 torch.Tensor.to_sparse_bsr() 方法，从任意二维张量构造 (0 + 2 + 0) 维稀疏 BSR 张量。该方法还需要指定值块的大小：

>>> dense = torch.tensor([[0, 1, 2, 3, 4, 5],
...                       [6, 7, 8, 9, 10, 11],
...                       [12, 13, 14, 15, 16, 17],
...                       [18, 19, 20, 21, 22, 23]])
>>> bsr = dense.to_sparse_bsr(blocksize=(2, 3))
>>> bsr
tensor(crow_indices=tensor([0, 2, 4]),col_indices=tensor([0, 1, 0, 1]),values=tensor([[[ 0,  1,  2],[ 6,  7,  8]],[[ 3,  4,  5],[ 9, 10, 11]],[[12, 13, 14],[18, 19, 20]],[[15, 16, 17],[21, 22, 23]]]), size=(4, 6), nnz=4,layout=torch.sparse_bsr)

---

稀疏BSC张量

稀疏BSC（块压缩稀疏列）张量格式实现了BSC存储格式，用于存储二维张量，并扩展支持批量稀疏BSC张量以及多维张量块的值。

一个稀疏BSC张量由三个张量组成：ccol_indices、row_indices和values：

• ccol_indices张量包含压缩的列索引。这是一个(B + 1)维张量，形状为(batchsize, ncolblocks + 1)。最后一个元素是指定块的数量nse。该张量根据给定行块的起始位置编码values和row_indices中的索引。张量中每个连续数字减去前一个数字表示给定列中的块数量。
• row_indices张量包含每个元素的行块索引。这是一个(B + 1)维张量，形状为(batchsize, nse)。
• values张量包含收集到二维块中的稀疏BSC张量元素值。这是一个(1 + 2 + K)维张量，形状为(nse, nrowblocks, ncolblocks, *densesize)。

---

BSC张量的构建

稀疏BSC张量可以直接通过使用torch.sparse_bsc_tensor()函数来构建。用户需要分别提供行块索引、列块索引和值张量，其中列块索引必须使用CSR压缩编码格式进行指定。

size参数是可选的，如果未提供该参数，系统会根据ccol_indices和row_indices张量自动推导出张量尺寸。

---

>>> ccol_indices = torch.tensor([0, 2, 4])
>>> row_indices = torch.tensor([0, 1, 0, 1])
>>> values = torch.tensor([[[0, 1, 2], [6, 7, 8]],
...                        [[3, 4, 5], [9, 10, 11]],
...                        [[12, 13, 14], [18, 19, 20]],
...                        [[15, 16, 17], [21, 22, 23]]])
>>> bsc = torch.sparse_bsc_tensor(ccol_indices, row_indices, values, dtype=torch.float64)
>>> bsc
tensor(ccol_indices=tensor([0, 2, 4]),row_indices=tensor([0, 1, 0, 1]),values=tensor([[[ 0.,  1.,  2.],[ 6.,  7.,  8.]],[[ 3.,  4.,  5.],[ 9., 10., 11.]],[[12., 13., 14.],[18., 19., 20.]],[[15., 16., 17.],[21., 22., 23.]]]), size=(4, 6), nnz=4,dtype=torch.float64, layout=torch.sparse_bsc)

---

稀疏压缩张量处理工具

所有稀疏压缩张量（包括CSR、CSC、BSR和BSC张量）在概念上都非常相似，它们的索引数据被分为两部分：采用CSR编码的压缩索引（compressed indices），以及与压缩索引正交的普通索引（plain indices）。这种设计使得针对这些张量的各种工具可以共享相同的实现逻辑，只需通过张量布局进行参数化配置即可。

---

稀疏压缩张量的构建

可以通过使用 torch.sparse_compressed_tensor() 函数来构建稀疏的 CSR、CSC、BSR 和 BSC 张量。该函数的接口与之前讨论的构造函数 torch.sparse_csr_tensor()、torch.sparse_csc_tensor()、torch.sparse_bsr_tensor() 和 torch.sparse_bsc_tensor() 相同，但需要额外提供一个必需的 layout 参数。以下示例展示了如何通过为 torch.sparse_compressed_tensor() 函数指定相应的布局参数，使用相同输入数据构建 CSR 和 CSC 张量的方法：

>>> compressed_indices = torch.tensor([0, 2, 4])
>>> plain_indices = torch.tensor([0, 1, 0, 1])
>>> values = torch.tensor([1, 2, 3, 4])
>>> csr = torch.sparse_compressed_tensor(compressed_indices, plain_indices, values, layout=torch.sparse_csr)
>>> csr
tensor(crow_indices=tensor([0, 2, 4]),col_indices=tensor([0, 1, 0, 1]),values=tensor([1, 2, 3, 4]), size=(2, 2), nnz=4,layout=torch.sparse_csr)
>>> csc = torch.sparse_compressed_tensor(compressed_indices, plain_indices, values, layout=torch.sparse_csc)
>>> csc
tensor(ccol_indices=tensor([0, 2, 4]),row_indices=tensor([0, 1, 0, 1]),values=tensor([1, 2, 3, 4]), size=(2, 2), nnz=4,layout=torch.sparse_csc)
>>> (csr.transpose(0, 1).to_dense() == csc.to_dense()).all()
tensor(True)

---

支持的操作

---

线性代数运算

下表总结了稀疏矩阵支持的线性代数运算，其中操作数的布局可能有所不同。这里 T[layout] 表示具有给定布局的张量。类似地，M[layout] 表示矩阵（2维 PyTorch 张量），V[layout] 表示向量（1维 PyTorch 张量）。此外，f 表示标量（浮点数或0维 PyTorch 张量），* 表示逐元素乘法，@ 表示矩阵乘法。

PyTorch 运算	支持稀疏梯度？	布局签名
torch.mv()	否	M[sparse_coo] @ V[strided] -V[strided]
torch.mv()	否	M[sparse_csr] @ V[strided] -V[strided]
torch.matmul()	否	M[sparse_coo] @ M[strided] -M[strided]
torch.matmul()	否	M[sparse_csr] @ M[strided] -M[strided]
torch.matmul()	否	M[SparseSemiStructured] @ M[strided] -M[strided]
torch.matmul()	否	M[strided] @ M[SparseSemiStructured] -M[strided]
torch.mm()	否	M[sparse_coo] @ M[strided] -M[strided]
torch.mm()	否	M[SparseSemiStructured] @ M[strided] -M[strided]
torch.mm()	否	M[strided] @ M[SparseSemiStructured] -M[strided]
torch.sparse.mm()	是	M[sparse_coo] @ M[strided] -M[strided]
torch.smm()	否	M[sparse_coo] @ M[strided] -M[sparse_coo]
torch.hspmm()	否	M[sparse_coo] @ M[strided] -M[hybrid sparse_coo]
torch.bmm()	否	T[sparse_coo] @ T[strided] -T[strided]
torch.addmm()	否	f * M[strided] + f * (M[sparse_coo] @ M[strided]) -M[strided]
torch.addmm()	否	f * M[strided] + f * (M[SparseSemiStructured] @ M[strided]) -M[strided]
torch.addmm()	否	f * M[strided] + f * (M[strided] @ M[SparseSemiStructured]) -M[strided]
torch.sparse.addmm()	是	f * M[strided] + f * (M[sparse_coo] @ M[strided]) -M[strided]
torch.sparse.spsolve()	否	SOLVE(M[sparse_csr], V[strided]) -V[strided]
torch.sspaddmm()	否	f * M[sparse_coo] + f * (M[sparse_coo] @ M[strided]) -M[sparse_coo]
torch.lobpcg()	否	GENEIG(M[sparse_coo]) -M[strided], M[strided]
torch.pca_lowrank()	是	PCA(M[sparse_coo]) -M[strided], M[strided], M[strided]
torch.svd_lowrank()	是	SVD(M[sparse_coo]) -M[strided], M[strided], M[strided]

其中“支持稀疏梯度？”列表示 PyTorch 运算是否支持对稀疏矩阵参数的梯度反向传播。除 torch.smm() 外，所有 PyTorch 运算均支持对 strided 矩阵参数的梯度反向传播。

---

注意：目前 PyTorch 不支持布局签名为 M[strided] @ M[sparse_coo] 的矩阵乘法。但应用仍可通过矩阵关系 D @S == (S.t() @ D.t()).t() 计算该运算。

---

张量方法与稀疏性

以下是与稀疏张量相关的Tensor方法：

Tensor.is_sparse	若张量采用稀疏COO存储布局则为True，否则为False
Tensor.is_sparse_csr	若张量采用稀疏CSR存储布局则为True，否则为False
Tensor.dense_dim	返回稀疏张量self中的稠密维度数量
Tensor.sparse_dim	返回稀疏张量self中的稀疏维度数量
Tensor.sparse_mask	通过稀疏张量mask的索引过滤步进张量self的值，返回新的稀疏张量
Tensor.to_sparse	返回张量的稀疏副本
Tensor.to_sparse_coo	将张量转换为坐标格式
Tensor.to_sparse_csr	将张量转换为压缩行存储格式(CSR)
Tensor.to_sparse_csc	将张量转换为压缩列存储格式(CSC)
Tensor.to_sparse_bsr	将张量转换为给定块大小的块稀疏行(BSR)存储格式
Tensor.to_sparse_bsc	将张量转换为给定块大小的块稀疏列(BSC)存储格式
Tensor.to_dense	若self不是步进张量则创建其步进副本，否则返回self
Tensor.values	返回稀疏COO张量的值张量

以下方法专用于稀疏COO张量：

Tensor.coalesce	若self是未合并张量则返回其合并副本
Tensor.sparse_resize_	将self稀疏张量调整为指定尺寸及稀疏/稠密维度数量
Tensor.sparse_resize_and_clear_	从稀疏张量self中移除所有指定元素并调整尺寸
Tensor.is_coalesced	若self是已合并的稀疏COO张量则返回True，否则False
Tensor.indices	返回稀疏COO张量的索引张量

以下方法专用于稀疏CSR张量和稀疏BSR张量：

Tensor.crow_indices	当self是布局为sparse_csr的稀疏CSR张量时，返回包含压缩行索引的张量
Tensor.col_indices	当self是布局为sparse_csr的稀疏CSR张量时，返回包含列索引的张量

以下方法专用于稀疏CSC张量和稀疏BSC张量：

Tensor.row_indices
Tensor.ccol_indices

以下Tensor方法支持稀疏COO张量：

add()
add_()
addmm()
addmm_()
any()
asin()
asin_()
arcsin()
arcsin_()
bmm()
clone()
deg2rad()
deg2rad_()
detach()
detach_()
dim()
div()
div_()
floor_divide()
floor_divide_()
get_device()
index_select()
isnan()
log1p()
log1p_()
mm()
mul()
mul_()
mv()
narrow_copy()
neg()
neg_()
negative()
negative_()
numel()
rad2deg()
rad2deg_()
resize_as_()
size()
pow()
sqrt()
square()
smm()
sspaddmm()
sub()
sub_()
t()
t_()
transpose()
transpose_()
zero_()

---

稀疏张量专用 Torch 函数

sparse_coo_tensor	在给定indices位置构造一个COO(坐标)格式的稀疏张量，并填充指定值。
sparse_csr_tensor	在给定crow_indices和col_indices位置构造一个CSR(压缩稀疏行)格式的稀疏张量，并填充指定值。
sparse_csc_tensor	在给定ccol_indices和row_indices位置构造一个CSC(压缩稀疏列)格式的稀疏张量，并填充指定值。
sparse_bsr_tensor	在给定crow_indices和col_indices位置构造一个BSR(块压缩稀疏行)格式的稀疏张量，并填充指定的二维块数据。
sparse_bsc_tensor	在给定ccol_indices和row_indices位置构造一个BSC(块压缩稀疏列)格式的稀疏张量，并填充指定的二维块数据。
sparse_compressed_tensor	在给定compressed_indices和plain_indices位置构造一个压缩稀疏格式(CSR/CSC/BSR/BSC)的稀疏张量，并填充指定值。
sparse.sum	返回给定稀疏张量每行的元素和。
sparse.addmm	该函数在前向计算中与torch.addmm()功能完全相同，但额外支持稀疏COO矩阵mat1的反向传播。
sparse.sampled_addmm	在input的稀疏模式指定位置，对稠密矩阵mat1和mat2执行矩阵乘法。
sparse.mm	执行稀疏矩阵mat1的矩阵乘法运算。
sspaddmm	将稀疏张量mat1与稠密张量mat2进行矩阵乘法，再将稀疏张量input加到结果上。
hspmm	执行稀疏COO矩阵mat1与跨步矩阵mat2的矩阵乘法。
smm	执行稀疏矩阵input与稠密矩阵mat的矩阵乘法。
sparse.softmax	应用softmax函数。
sparse.spsolve	计算具有唯一解的线性方程组的解。
sparse.log_softmax	应用softmax函数后再进行对数运算。
sparse.spdiags	通过将diagonals行的值沿指定对角线放置，构造一个稀疏的二维张量。

---

其他函数

以下 torch 函数支持稀疏张量：

cat()
dstack()
empty()
empty_like()
hstack()
index_select()
is_complex()
is_floating_point()
is_nonzero()
is_same_size()
is_signed()
is_tensor()
lobpcg()
mm()
native_norm()
pca_lowrank()
select()
stack()
svd_lowrank()
unsqueeze()
vstack()
zeros()
zeros_like()

---

稀疏张量约束检查

sparse.check_sparse_tensor_invariants	用于控制稀疏张量约束检查的工具。

---

梯度检查扩展

sparse.as_sparse_gradcheck	装饰器函数，用于扩展稀疏张量的梯度检查功能。

---

保零一元函数

我们致力于支持所有"保零一元函数"：即那些将零映射为零的单参数函数。

如果您发现我们遗漏了您需要的保零一元函数，欢迎提交功能请求的issue。在创建issue前，请一如既往地先尝试使用搜索功能。

以下运算符目前支持稀疏COO/CSR/CSC/BSR/CSR张量输入：

abs()
asin()
asinh()
atan()
atanh()
ceil()
conj_physical()
floor()
log1p()
neg()
round()
sin()
sinh()
sign()
sgn()
signbit()
tan()
tanh()
trunc()
expm1()
sqrt()
angle()
isinf()
isposinf()
isneginf()
isnan()
erf()
erfinv()

---

torch.Storage

在PyTorch中，常规张量是一个由以下组件定义的多维数组：

• Storage：张量的实际数据，以连续的字节一维数组形式存储
• dtype：张量元素的数据类型，例如torch.float32或torch.int64
• shape：表示张量各维度大小的元组
• Stride：在每个维度中从一个元素移动到下一个元素所需的步长
• Offset：张量数据在存储中的起始位置。对于新创建的张量，该值通常为0

这些组件共同定义了张量的结构和数据，其中Storage保存实际数据，其余部分作为元数据。

---

无类型存储 API

torch.UntypedStorage 是一个连续的、一维的元素数组。其长度等于张量的字节数。该存储作为张量的底层数据容器。

通常，使用常规构造函数（如 zeros()、zeros_like() 或 new_zeros()）在 PyTorch 中创建的张量，其存储与张量本身存在一一对应关系。

然而，一个存储可以被多个张量共享。例如，任何张量的视图（通过 view() 或某些但不是所有类型的索引（如整数和切片）获得）将指向与原始张量相同的底层存储。当序列化和反序列化共享同一存储的张量时，这种关系会被保留，张量继续指向同一存储。有趣的是，反序列化指向单个存储的多个张量可能比反序列化多个独立张量更快。

可以通过 untyped_storage() 方法访问张量的存储。这将返回一个 torch.UntypedStorage 类型的对象。幸运的是，存储有一个唯一的标识符，可通过 torch.UntypedStorage.data_ptr() 方法访问。在常规情况下，具有相同数据存储的两个张量将具有相同的存储 data_ptr。

然而，张量本身可以指向两个独立的存储，一个用于其数据属性，另一个用于其梯度属性。每个存储都需要自己的 data_ptr()。一般来说，不能保证 torch.Tensor.data_ptr() 和 torch.UntypedStorage.data_ptr() 匹配，因此不应假设这一点成立。

无类型存储与构建在其上的张量在一定程度上是独立的。实际上，这意味着具有不同数据类型或形状的张量可以指向同一存储。这也意味着张量的存储可以更改，如下例所示：

>>> t = torch.ones(3)
>>> s0 = t.untyped_storage()
>>> s0001286300128630012863
[torch.storage.UntypedStorage(device=cpu) of size 12]
>>> s1 = s0.clone()
>>> s1.fill_(0)000000000000
[torch.storage.UntypedStorage(device=cpu) of size 12]
>>> # Fill the tensor with a zeroed storage
>>> t.set_(s1, storage_offset=t.storage_offset(), stride=t.stride(), size=t.size())
tensor([0., 0., 0.])

---

警告：请注意，直接修改张量的存储（如本示例所示）并非推荐做法。

此处展示底层操作仅出于教学目的，用于说明张量与其底层存储之间的关系。通常情况下，使用标准torch.Tensor方法（如clone()和fill_()）来实现相同效果会更高效且更安全。

除data_ptr外，无类型存储还具有其他属性，例如：

• filename（当存储指向磁盘文件时）
• device
• is_cuda（用于设备检查）

存储可通过以下方法进行原地或非原地操作：

• copy_
• fill_
• pin_memory

更多信息请参阅下方API参考。请注意，修改存储属于底层API操作，存在风险！

这些API大多在张量层级也有对应实现：如果存在，应优先使用张量层级的对应方法。

---

特殊情况

我们提到过，当张量的 grad 属性不为 None 时，实际上它内部包含两部分数据。在这种情况下，untyped_storage() 会返回 data 属性的存储空间，而梯度部分的存储空间可以通过 tensor.grad.untyped_storage() 获取。

---

>>> t = torch.zeros(3, requires_grad=True)
>>> t.sum().backward()
>>> assert list(t.untyped_storage()) == [0] * 12  # the storage of the tensor is just 0s
>>> assert list(t.grad.untyped_storage()) != [0] * 12  # the storage of the gradient isn't

---

还存在一些特殊情况，张量可能没有典型的存储结构，或者根本没有存储：

• "meta"设备上的张量：这类张量用于形状推断，并不保存实际数据。

• 伪张量(Fake Tensors)：PyTorch编译器使用的另一种内部工具是FakeTensor，其基于相似原理实现。

张量子类或类张量对象也可能表现出非典型行为。总体而言，我们预计大多数使用场景不需要在存储层级进行操作！

---

class torch.UntypedStorage(*args, **kwargs)

---

bfloat16()

---

将此存储转换为 bfloat16 类型。

---

bool()

---

将此存储转换为布尔类型。

---

byte()

---

将此存储转换为字节类型。

---

byteswap(dtype)

---

交换底层数据中的字节顺序。

---

char()

---

将此存储转换为 char 类型。

---

clone()

---

返回此存储的一个副本。

---

complex_double()

---

将此存储转换为复数双精度类型。

---

complex_float()

---

将此存储转换为复数浮点类型。

---

copy_() 

---

cpu()

---

如果该存储不在CPU上，则返回其CPU副本。

---

cuda(device=None, non_blocking=False)

---

返回该对象在CUDA内存中的副本。

如果该对象已在CUDA内存中且位于正确的设备上，则不会执行复制操作，直接返回原对象。

参数

• device ( int ) – 目标GPU的ID。默认为当前设备。
• non_blocking ([bool]) – 如果为True且源数据位于固定内存中，则复制操作将与主机异步执行。否则该参数无效。

返回类型：Union [_StorageBase, TypedStorage]

---

data_ptr() 

---

device:  device 

---

double()

---

将此存储转换为双精度类型。

---

element_size() 

---

property filename: Optional[str ] 

---

返回与此存储关联的文件名。

如果存储位于CPU上，并且是通过from_file()方法创建且shared参数为True时，文件名将是一个字符串。否则该属性为None。

---

fill_() float()

---

将此存储转换为浮点类型。

---

float8_e4m3fn()

---

将此存储转换为 float8_e4m3fn 类型

---

float8_e4m3fnuz()

---

将此存储转换为 float8_e4m3fnuz 类型

---

float8_e5m2()

---

将此存储转换为 float8_e5m2 类型

---

float8_e5m2fnuz()

---

将此存储转换为 float8_e5m2fnuz 类型

---

static from_buffer() 

---

static from_file(filename, shared=False, size=0) → Storage 

---

创建一个基于内存映射文件的CPU存储。

如果shared为True，则所有进程之间共享内存。所有更改都会写入文件。如果shared为False，则存储上的更改不会影响文件。

size表示存储中的元素数量。如果shared为False，则文件必须至少包含size * sizeof(Type)字节（Type是存储类型，对于UnTypedStorage，文件必须至少包含size字节）。如果shared为True，则会在需要时创建文件。

参数

• filename (str) – 要映射的文件名
• shared ([bool]) – 是否共享内存（决定底层mmap(2)调用传递的是MAP_SHARED还是MAP_PRIVATE）
• size ( int ) – 存储中的元素数量

---

get_device()

---

返回类型：int

---

half()

---

将此存储转换为半精度类型。

---

hpu(device=None, non_blocking=False)

---

返回该对象在HPU内存中的副本。

如果该对象已在HPU内存中且位于正确的设备上，则不会执行复制操作，直接返回原对象。

参数

• device ( int ) – 目标HPU设备ID。默认为当前设备。
• non_blocking ([bool]) – 如果为True且源数据位于固定内存中，则复制操作将与主机异步执行。否则该参数无效。

返回类型：Union [_StorageBase, TypedStorage]

---

int()

---

将此存储转换为 int 类型。

---

property is_cuda 

---

property is_hpu 

---

is_pinned(device='cuda')

---

判断CPU存储是否已在设备上固定。

参数

• device (str 或 torch.device) – 用于固定内存的设备（默认值：'cuda'）。
  不建议使用此参数，未来可能被弃用。

返回值

一个布尔变量。

---

is_shared() is_sparse:  bool * = False is_sparse_csr:  bool * = False long()

---

将此存储转换为 long 类型。

---

mps()

---

如果该存储不在 MPS 上，则返回其 MPS 副本。

---

nbytes() new() pin_memory(device='cuda')

---

将CPU存储复制到固定内存中（如果尚未固定）。

参数

• device (str 或 torch.device) – 用于固定内存的设备（默认：'cuda'）。不推荐使用此参数，未来可能会被弃用。

返回值：一个已固定的CPU存储。

---

resizable() resize_() share_memory_(*args, **kwargs)

---

将存储移动到共享内存中。

对于已经在共享内存中的存储和CUDA存储（这些存储无需移动即可跨进程共享），此操作无效。

共享内存中的存储无法调整大小。

请注意，为了避免类似此问题的情况，从多个线程对同一对象调用此函数是线程安全的。

但如果没有适当的同步机制，调用其他任何函数都不是线程安全的。更多详情请参阅多进程最佳实践。

注意：当共享内存中存储的所有引用被删除时，关联的共享内存对象也会被删除。PyTorch有一个特殊的清理过程，确保即使当前进程意外退出，这种情况也会发生。

值得注意 share_memory_() 和 from_file() 与 shared = True 的区别：

1、share_memory_ 使用 shm_open(3) 创建一个POSIX共享内存对象，而 from_file() 使用 open(2) 打开用户传递的文件名。

2、两者都使用 mmap(2) 调用 和 MAP_SHARED 将文件/对象映射到当前虚拟地址空间。

3、share_memory_ 在映射后会调用 shm_unlink(3) 以确保当没有进程打开该对象时，共享内存对象会被释放。torch.from_file(shared=True) 不会取消链接文件。该文件是持久性的，将一直存在，直到用户删除它。

返回

self

---

short()

---

将此存储转换为 short 类型。

---

size()

---

返回类型：int

---

to(*, device, non_blocking=False)

---

tolist()

---

返回包含此存储元素的列表。

---

type(dtype=None, non_blocking=False)

---

返回类型：Union [_StorageBase, TypedStorage]

---

untyped()

---

遗留类型化存储

---

警告：出于历史背景考虑，PyTorch 曾使用类型化存储类，这些类现已弃用，应避免使用。以下内容详细介绍了该 API，以防您遇到它，但强烈不建议使用。未来将移除除 torch.UntypedStorage 之外的所有存储类，并且 torch.UntypedStorage 将在所有情况下使用。

torch.Storage 是与默认数据类型 (torch.get_default_dtype()) 对应的存储类的别名。例如，如果默认数据类型是 torch.float，则 torch.Storage 解析为 torch.FloatStorage。

torch.<type>Storage 和 torch.cuda.<type>Storage 类，如 torch.FloatStorage、torch.IntStorage 等，实际上从未实例化。调用它们的构造函数会创建一个具有适当 torch.dtype 和 torch.device 的 torch.TypedStorage。torch.<type>Storage 类具有 torch.TypedStorage 的所有类方法。

torch.TypedStorage 是一个连续的、一维的特定 torch.dtype 元素数组。它可以接受任何 torch.dtype，并且内部数据将被正确解释。torch.TypedStorage 包含一个 torch.UntypedStorage，后者将数据存储为无类型的字节数组。

每个跨步 torch.Tensor 都包含一个 torch.TypedStorage，用于存储 torch.Tensor 视图中的所有数据。

---

class torch.TypedStorage(*args, wrap_storage=None, dtype=None, device=None, _internal=False)

---

bfloat16()

---

将此存储转换为 bfloat16 类型。

---

bool()

---

将此存储转换为布尔类型。

---

byte()

---

将此存储转换为字节类型。

---

char()

---

将此存储转换为 char 类型。

---

clone()

---

返回此存储的一个副本。

---

complex_double()

---

将此存储转换为复数双精度类型。

---

complex_float()

---

将此存储转换为复数浮点类型。

---

copy_(source, non_blocking=None)

---

cpu()

---

如果该存储不在CPU上，则返回其CPU副本。

---

cuda(device=None, non_blocking=False)

---

返回该对象在CUDA内存中的副本。

如果该对象已在CUDA内存中且位于正确的设备上，则不会执行复制操作，直接返回原对象。

参数

• device (int) - 目标GPU ID。默认为当前设备。
• non_blocking ([bool]) - 如果为True且源数据位于固定内存中，则复制操作将与主机异步执行。否则该参数无效。

返回类型
Self

---

data_ptr()

---

property device double()

---

将此存储转换为双精度类型。

---

dtype: [dtype](tensor_attributes.html#torch.dtype "torch.dtype")

---

element_size()

---

property filename: Optional[str ] 
Returns the file name associated with this storage if the storage was memory mapped from a file. or `None` if the storage was not created by memory mapping a file.fill_(value)

---

float()

---

将此存储转换为浮点类型。

---

float8_e4m3fn()

---

将此存储转换为 float8_e4m3fn 类型

---

float8_e4m3fnuz()

---

将此存储转换为 float8_e4m3fnuz 类型

---

float8_e5m2()

---

将此存储转换为 float8_e5m2 类型

---

float8_e5m2fnuz()

---

将此存储转换为 float8_e5m2fnuz 类型

---

CLASSMETHOD from_buffer(*args, **kwargs)

---

CLASSMETHOD from_file(filename, shared=False, size=0) → Storage

---

创建一个基于内存映射文件的CPU存储。

如果shared为True，则所有进程之间共享该内存。

所有更改都会写入文件。如果shared为False，则存储上的更改不会影响文件。

size表示存储中的元素数量。如果shared为False，则文件必须至少包含size * sizeof(Type)字节（Type是存储的类型）。如果shared为True，则会在需要时创建文件。

参数

• filename (str) – 要映射的文件名
• shared ([bool]) –
  是否共享内存（决定是传递MAP_SHARED还是MAP_PRIVATE给底层的mmap(2)调用）
• size ( int ) – 存储中的元素数量

---

get_device()

---

返回类型：int

---

half()

---

将此存储转换为半精度浮点类型。

---

hpu(device=None, non_blocking=False)

---

返回该对象在HPU内存中的副本。

如果该对象已在HPU内存中且位于正确的设备上，则不会执行复制操作，直接返回原对象。

参数

• device ( int ) - 目标HPU设备ID。默认为当前设备。
• non_blocking ([bool]) - 如果为True且源数据位于固定内存中，则复制操作将与主机异步执行。否则该参数无效。

返回类型：Self

---

int()

---

将此存储转换为 int 类型。

---

property is_cuda 

---

property is_hpu 

---

is_pinned(device='cuda')

---

判断 CPU TypedStorage 是否已在设备上固定。

参数

• device (str 或 torch.device) – 要固定内存的设备（默认：'cuda'）。不建议使用此参数，未来将被弃用。

返回

一个布尔值变量。

---

is_shared()

---

is_sparse:  bool * = False long()

---

将此存储转换为 long 类型。

---

nbytes()

---

pickle_storage_type()

---

pin_memory(device='cuda')

---

将CPU的TypedStorage复制到固定内存中（如果尚未固定）。

参数

• device (str 或 torch.device) – 用于固定内存的设备（默认：'cuda'）。

不建议使用此参数，未来可能会被弃用。

返回值：一个已固定的CPU存储。

---

resizable()

---

resize_(size)

---

share_memory_()

---

请参考 torch.UntypedStorage.share_memory_() 方法文档

---

short()

---

将此存储转换为短整型。

---

size()

---

to(*, device, non_blocking=False)

---

返回该对象在设备内存中的副本。

如果该对象已在目标设备上，则不会执行复制操作，直接返回原对象。

参数

• device ( int ) – 目标设备编号。
• non_blocking ([bool]) – 若为 True 且源数据位于固定内存中，则复制操作将与主机异步执行。否则该参数无效。

返回类型：Self

---

tolist()

---

返回包含此存储元素的列表。

---

type(dtype=None, non_blocking=False)

---

如果未提供 dtype 参数，则返回当前类型；否则将对象转换为指定类型。

若对象已符合目标类型，则不会创建副本，直接返回原对象。

参数说明

• dtype (type 或 *字符串) – 目标类型
• non_blocking ([布尔值]) – 当设为 True 时，若源数据位于固定内存而目标在GPU（或反之），则复制操作会以异步方式执行（相对于主机）。其他情况下该参数无效。
• **kwargs – 为保持兼容性，可用 async 键替代 non_blocking 参数。注意：async 参数已弃用。

返回类型

Union [_StorageBase, TypedStorage, 字符串 ]

---

untyped()

---

返回内部的 torch.UntypedStorage。

---

class torch.DoubleStorage(*args, wrap_storage=None, dtype=None, device=None, _internal=False)

---

dtype:  torch.dtype = torch.float64*

---

class torch.FloatStorage(*args, wrap_storage=None, dtype=None, device=None, _internal=False)

---

dtype:  torch.dtype = torch.float32*

---

class torch.HalfStorage(*args, wrap_storage=None, dtype=None, device=None, _internal=False)

---

dtype:  torch.dtype = torch.float16

---

class torch.LongStorage(*args, wrap_storage=None, dtype=None, device=None, _internal=False)

---

dtype:  torch.dtype = torch.int64*

---

class torch.IntStorage(*args, wrap_storage=None, dtype=None, device=None, _internal=False)

---

dtype:  torch.dtype = torch.int32*

---

class torch.ShortStorage(*args, wrap_storage=None, dtype=None, device=None, _internal=False)

---

dtype:  torch.dtype = torch.int16*

---

class torch.CharStorage(*args, wrap_storage=None, dtype=None, device=None, _internal=False)

---

dtype:  torch.dtype = torch.int8*

---

class torch.ByteStorage(*args, wrap_storage=None, dtype=None, device=None, _internal=False)

---

dtype:  torch.dtype = torch.uint8*

---

class torch.BoolStorage(*args, wrap_storage=None, dtype=None, device=None, _internal=False)

---

dtype:  torch.dtype = torch.bool*

---

class torch.BFloat16Storage(*args, wrap_storage=None, dtype=None, device=None, _internal=False)

---

dtype:  torch.dtype = torch.bfloat16*

---

class torch.ComplexDoubleStorage(*args, wrap_storage=None, dtype=None, device=None, _internal=False)

---

dtype:  torch.dtype = torch.complex128*

---

class torch.ComplexFloatStorage(*args, wrap_storage=None, dtype=None, device=None, _internal=False)

---

dtype:  torch.dtype = torch.complex64*

---

class torch.QUInt8Storage(*args, wrap_storage=None, dtype=None, device=None, _internal=False)

---

dtype:  torch.dtype = torch.quint8*

---

class torch.QInt8Storage(*args, wrap_storage=None, dtype=None, device=None, _internal=False)

---

dtype:  torch.dtype = torch.qint8*

---

class torch.QInt32Storage(*args, wrap_storage=None, dtype=None, device=None, _internal=False)

---

dtype:  torch.dtype = torch.qint32*

---

class torch.QUInt4x2Storage(*args, wrap_storage=None, dtype=None, device=None, _internal=False)

---

dtype:  torch.dtype = torch.quint4x2*

---

class torch.QUInt2x4Storage(*args, wrap_storage=None, dtype=None, device=None, _internal=False)

---

dtype:  torch.dtype = torch.quint2x4*

---

torch.testing

---

torch.testing.assert_close(actual, expected, *, allow_subclasses=True, rtol=None, atol=None, equal_nan=False, check_device=True, check_dtype=True, check_layout=True, check_stride=False, msg=None)

---

断言 actual 和 expected 近似相等。

如果 actual 和 expected 是步进式(strided)、非量化、实数值且有限的张量，当满足以下条件时认为两者近似：

$|\text{actual}-\text{expected}|\le \text{atol}+\text{rtol}\cdot |\text{expected}|$

非有限值（-inf 和 inf）仅在完全相等时才被认为近似。NaN 值仅在 equal_nan 为 True 时被认为彼此相等。

此外，还需满足以下条件才被视为近似：

• 相同的 device（当 check_device 为 True）
• 相同的 dtype（当 check_dtype 为 True）
• 相同的 layout（当 check_layout 为 True）
• 相同的步长(stride)（当 check_stride 为 True）

如果 actual 或 expected 是元张量(meta tensor)，则仅执行属性检查。

对于稀疏张量（COO、CSR、CSC、BSR 或 BSC 布局），会分别检查其步进式成员。索引（COO的indices，CSR/BSR的crow_indices和col_indices，CSC/BSC的ccol_indices和row_indices）始终检查是否相等，而值则根据上述定义检查近似性。

对于量化张量，当具有相同的 qscheme() 且 dequantize() 后的结果符合上述近似定义时，认为两者近似。

actual 和 expected 可以是 Tensor 或任何能通过 torch.as_tensor() 转换为张量的类张量/标量。除Python标量外，输入类型必须直接相关。此外，它们也可以是 Sequence 或 Mapping，此时要求结构匹配且所有元素都符合上述近似定义。

注意：Python标量是类型关系要求的例外，因为它们的 type()（如 int、float、complex）等价于张量的dtype。因此可以检查不同类型的Python标量，但需要设置 check_dtype=False。

参数：

• actual (Any) - 实际输入
• expected (Any) - 预期输入
• allow_subclasses ([bool]) - 若为True（默认），除Python标量外允许直接相关的类型输入；否则要求类型严格相等
• rtol (Optional[float]) - 相对容差。若指定则必须同时指定atol。未指定时根据dtype按下表选择默认值
• atol (Optional[float]) - 绝对容差。若指定则必须同时指定rtol。未指定时根据dtype按下表选择默认值
• equal_nan (Union[[bool],* str]) - 若为True，两个NaN值将被视为相等
• check_device ([bool]) - 若为True（默认），断言对应张量位于相同 device。禁用时会将不同设备的张量移至CPU再比较
• check_dtype ([bool]) - 若为True（默认），断言对应张量具有相同dtype。禁用时会按 torch.promote_types() 提升至共同类型
• check_layout ([bool]) - 若为True（默认），断言对应张量具有相同layout。禁用时会转换为步进式张量再比较
• check_stride ([bool]) - 若为True且对应张量是步进式，断言它们具有相同步长
• msg (Optional[Union[str, Callable[[str],* str]]]) - 比较失败时使用的可选错误信息。也可传入可调用对象，接收生成的消息并返回新消息

抛出异常：

• ValueError - 无法从输入构造torch.Tensor时
• ValueError - 仅指定rtol或atol时
• AssertionError - 对应输入不是Python标量且不直接相关时
• AssertionError - allow_subclasses为False但对应输入不是Python标量且类型不同时
• AssertionError - 输入为 Sequence 但长度不匹配时
• AssertionError - 输入为 Mapping 但键集合不匹配时
• AssertionError - 对应张量 shape 不同时
• AssertionError - check_layout为True但对应张量layout不同时
• AssertionError - 仅一个对应张量被量化时
• AssertionError - 对应量化张量 qscheme() 不同时
• AssertionError - check_device为True但对应张量不在相同 device 时
• AssertionError - check_dtype为True但对应张量dtype不同时
• AssertionError - check_stride为True但对应步进式张量步长不同时
• AssertionError - 对应张量值不满足上述近似定义时

---

下表展示了不同dtype的默认rtol和atol。当dtype不匹配时，取两者容差的最大值。

dtype	rtol	atol
float16	1e-3	1e-5
bfloat16	1.6e-2	1e-5
float32	1.3e-6	1e-5
float64	1e-7	1e-7
complex32	1e-3	1e-5
complex64	1.3e-6	1e-5
complex128	1e-7	1e-7
quint8	1.3e-6	1e-5
quint2x4	1.3e-6	1e-5
quint4x2	1.3e-6	1e-5
qint8	1.3e-6	1e-5
qint32	1.3e-6	1e-5
其他	0.0	0.0

注意：assert_close() 具有严格的默认配置。建议使用 partial() 定制需求。例如若需等值检查，可定义默认对所有dtype使用零容差的assert_equal。

---

>>> import functools
>>> assert_equal = functools.partial(torch.testing.assert_close, rtol=0, atol=0)
>>> assert_equal(1e-9, 1e-10)
Traceback (most recent call last):
...
AssertionError: Scalars are not equal!Expected 1e-10 but got 1e-09、Absolute difference: 9.000000000000001e-10
Relative difference: 9.0

---

Examples

---

>>> # tensor to tensor comparison
>>> expected = torch.tensor([1e0, 1e-1, 1e-2])
>>> actual = torch.acos(torch.cos(expected))
>>> torch.testing.assert_close(actual, expected)

---

>>> # scalar to scalar comparison
>>> import math
>>> expected = math.sqrt(2.0)
>>> actual = 2.0 / math.sqrt(2.0)
>>> torch.testing.assert_close(actual, expected)

---

>>> # numpy array to numpy array comparison
>>> import numpy as np
>>> expected = np.array([1e0, 1e-1, 1e-2])
>>> actual = np.arccos(np.cos(expected))
>>> torch.testing.assert_close(actual, expected)

---

>>> # sequence to sequence comparison
>>> import numpy as np
>>> # The types of the sequences do not have to match. They only have to have the same >>> # length and their elements have to match.
>>> expected = [torch.tensor([1.0]), 2.0, np.array(3.0)]
>>> actual = tuple(expected)
>>> torch.testing.assert_close(actual, expected)

---

>>> # mapping to mapping comparison
>>> from collections import OrderedDict
>>> import numpy as np
>>> foo = torch.tensor(1.0)
>>> bar = 2.0
>>> baz = np.array(3.0)
>>> # The types and a possible ordering of mappings do not have to match. They only
>>> # have to have the same set of keys and their elements have to match.
>>> expected = OrderedDict([("foo", foo), ("bar", bar), ("baz", baz)])
>>> actual = {"baz": baz, "bar": bar, "foo": foo}
>>> torch.testing.assert_close(actual, expected)

---

>>> expected = torch.tensor([1.0, 2.0, 3.0])
>>> actual = expected.clone()
>>> # By default, directly related instances can be compared
>>> torch.testing.assert_close(torch.nn.Parameter(actual), expected)
>>> # This check can be made more strict with allow_subclasses=False
>>> torch.testing.assert_close(
...     torch.nn.Parameter(actual), expected, allow_subclasses=False
... )
Traceback (most recent call last):
...
TypeError: No comparison pair was able to handle inputs of type
<class 'torch.nn.parameter.Parameter'and <class 'torch.Tensor'>.
>>> # If the inputs are not directly related, they are never considered close
>>> torch.testing.assert_close(actual.numpy(), expected)
Traceback (most recent call last):
...
TypeError: No comparison pair was able to handle inputs of type <class 'numpy.ndarray'and <class 'torch.Tensor'>.
>>> # Exceptions to these rules are Python scalars. They can be checked regardless of >># their type if check_dtype=False.
>>> torch.testing.assert_close(1.0, 1, check_dtype=False)

---

>>> # NaN != NaN by default.
>>> expected = torch.tensor(float("Nan"))
>>> actual = expected.clone()
>>> torch.testing.assert_close(actual, expected)
Traceback (most recent call last):
...
AssertionError: Scalars are not close!Expected nan but got nan.
Absolute difference: nan (up to 1e-05 allowed)
Relative difference: nan (up to 1.3e-06 allowed)
>>> torch.testing.assert_close(actual, expected, equal_nan=True)

---

>>> expected = torch.tensor([1.0, 2.0, 3.0])
>>> actual = torch.tensor([1.0, 4.0, 5.0])
>>> # The default error message can be overwritten.
>>> torch.testing.assert_close(actual, expected, msg="Argh, the tensors are not close!")
Traceback (most recent call last):
...
AssertionError: Argh, the tensors are not close!
>>> # If msg is a callable, it can be used to augment the generated message with >># extra information
>>> torch.testing.assert_close(
...     actual, expected, msg=lambda msg: f"Header\n\n{msg}\n\nFooter"
... )
Traceback (most recent call last):
...
AssertionError: HeaderTensor-likes are not close!Mismatched elements: 2 / 3 (66.7%)
Greatest absolute difference: 2.0 at index (1,) (up to 1e-05 allowed)
Greatest relative difference: 1.0 at index (1,) (up to 1.3e-06 allowed)Footer

---

torch.testing.make_tensor(*shape, dtype, device, low=None, high=None, requires_grad=False, noncontiguous=False, exclude_zero=False, memory_format=None)

---

创建一个具有指定shape、device和dtype的张量，其值均匀采样自区间[low, high)。

如果指定的low或high超出了该dtype可表示有限值的范围，则会被分别截断至最低或最高可表示有限值。

若参数为None，则low和high的默认值如下表所示，具体取决于dtype：

dtype	low	high
布尔类型	0	2
无符号整型	0	10
有符号整型	-9	10
浮点类型	-9	9
复数类型	-9	9

---

参数说明

• shape (Tuple[int, …]) - 定义输出张量形状的整数或整数序列
• dtype (torch.dtype) - 返回张量的数据类型
• device (Union[str, torch.device]) - 返回张量的设备位置
• low (Optional[Number]) - 设置区间下限（包含）。若提供数值，会被截断至该dtype的最小可表示有限值。默认为None时根据dtype自动确定（见上表）
• high (Optional[Number]) - 设置区间上限（不包含）。若提供数值，会被截断至该dtype的最大可表示有限值。默认为None时根据dtype自动确定（见上表）

---

自版本2.1起弃用：为浮点或复数类型传递low==high参数的行为已被弃用，将在2.3版本移除，请改用torch.full()

• requires_grad (Optional[bool]) - 是否在返回张量上启用自动求导记录。默认：False
• noncontiguous (Optional[bool]) - 若为True则返回非连续张量。当张量元素少于两个时此参数无效，且与memory_format互斥
• exclude_zero (Optional[bool]) - 若为True则将零值替换为dtype的最小正值：布尔/整型替换为1；浮点型替换为该dtype的最小正规数（来自finfo()的"tiny"值）；复数型替换为实部/虚部均为复数类型最小正规数的复数。默认：False
• memory_format (Optional[torch.memory_format]) - 返回张量的内存格式，与noncontiguous互斥

---

异常抛出

• ValueError - 整型dtype传入了requires_grad=True
• ValueError - 当low >= high时
• ValueError - 当low或high为nan时
• ValueError - 同时传入了noncontiguous和memory_format
• TypeError - 不支持的dtype类型

返回类型：Tensor

---

使用示例

---

>>> from torch.testing import make_tensor
>>> # Creates a float tensor with values in [-1, 1)
>>> make_tensor((3,), device='cpu', dtype=torch.float32, low=-1, high=1)
tensor([0.1205, 0.2282, -0.6380])
>>> # Creates a bool tensor on CUDA
>>> make_tensor((2, 2), device='cuda', dtype=torch.bool)
tensor([[False, False], [False, True]], device='cuda:0')

---

torch.testing.assert_allclose(actual, expected, rtol=None, atol=None, equal_nan=True, msg='')

---

警告：自 1.12 版本起，torch.testing.assert_allclose() 已被弃用，并将在未来版本中移除。

请改用 torch.testing.assert_close()。详细的升级指南可参阅此处。

---

torch.utils

rename_privateuse1_backend	重命名privateuse1后端设备，使其在PyTorch API中作为设备名更方便使用。
generate_methods_for_privateuse1_backend	在重命名privateuse1后端后，自动为自定义后端生成属性和方法。
get_cpp_backtrace	返回包含当前线程C++堆栈跟踪的字符串。
set_module	为Python对象设置模块属性，以便更清晰地打印显示。
swap_tensors	该函数用于交换两个Tensor对象的内容。

---

2025-05-10（六）