当前位置：首页 > news >正文

ArcScroll: 弧形滑动控件

news 来源：原创 2025/8/4 3:46:05

一. 什么是ArcScroll?

ArcScroll是一种基于Scroll控件实现的弧形滑动控件。可以让Scroll内容项沿着一个圆心的轨迹滑动，从而实现内容弧形滑动的效果。如下图：

水平滑动：

垂直滑动：

二. 实现方案

以下，以水平的方向为例，介绍如何实现这种效果

2.1 计算Item的初始位置

前提条件：

（1）以Scroll的左上角为坐标系，每个Item之间的夹角为固定, 值等于a

（2）Scroll的宽度为w, 高度为h

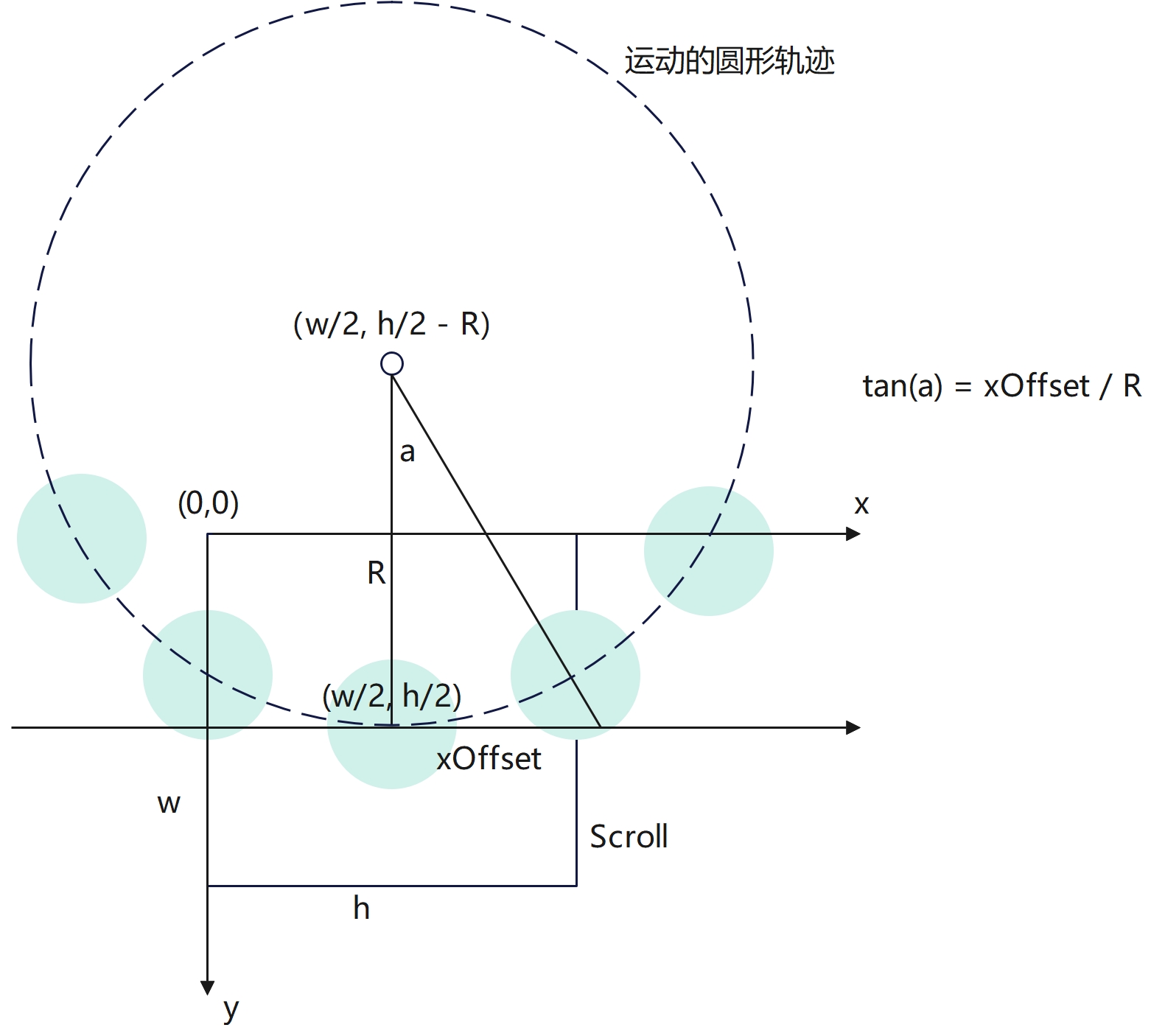
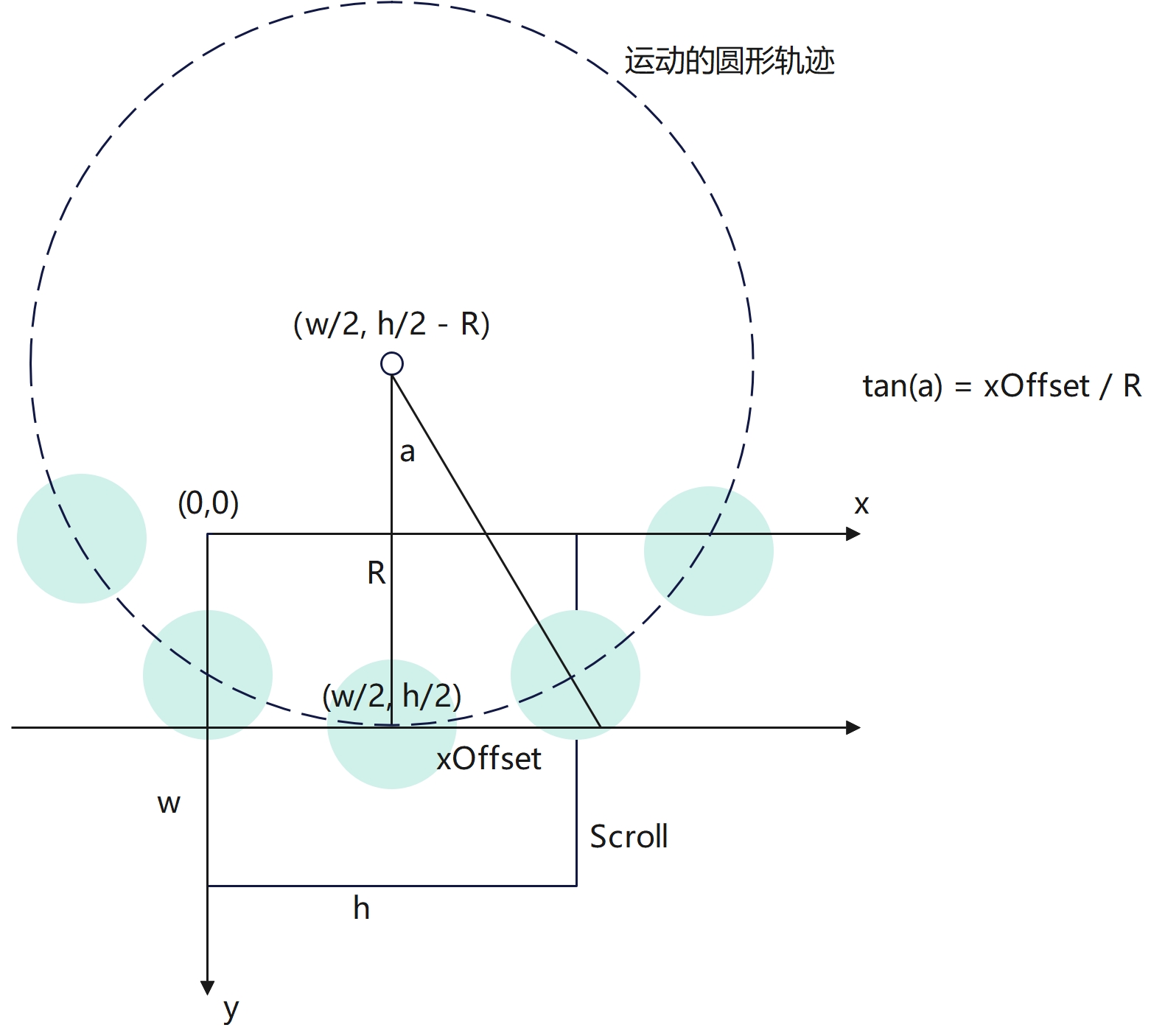
2.1.1 计算Item之间的水平投射距离

大圆半径circleRadius：R

大圆圆心circleCenter坐标：（w/2, h/2 -R）

Scroll中心点screenCenter坐标：(w/2, h/2)

假设两个Item之间的水平投射距离为xOffset，那么根据公式tan(a) = xOffset / R, xOffset = tan(a) * R

代码如下：

 /*** 获取两个Item之间的水平距离* 根据tan公式，计算投射在水平上的距离* @returns*/
private getOffsetOfItem(): number {// 因为ArkTs中tan的参数为弧度，所以这里需要转为弧度const radian = a * Math.PI / 180return Math.tan(radian) * this.arcScrollInfo.circleRadius}

2.1.2 计算Item 在圆上的坐标

已知大圆的圆心坐标(a, b)，圆上最低点坐标(x0, y0)和Item之间的夹角α, 根据公式可计算其他Item的坐标，公式如下：

x=a+(x0-a)cosα-(y0-b)sinα

y=b+(x0-a)sinα+(y0-b)cosα

对应到如上坐标系的值，计算如下：

const radian = -(a * Math.PI / 180);
const x = w/2 + (w/2 - w/2)* Math.cos(radian) - (h/2 - (h/2 - R)) * Math.sin(radian);
const y = (h/2 -R) + (w/2 - w/2) * Math.sin(radian) + (h/2 - (h/2 - R)) * Math.cos(radian);

根据如上公式，则可计算出所有Item的中心点位置

2.2 计算Scroll内容的宽度

Scroll本身的宽度为w，只有超过w, Scroll才能开始滑动，所以要想所有的Item都能够滑入Scroll中，则内容宽度为：

w + （Item的个数 - 1）* xOffset;

  /*** 获取Scroll内容的宽度* @returns*/public getScrollContentWidth(): number {const offsetDis = this.getOffsetOfItem() * (this.modelList.length - 1);let width = this.arcScrollInfo.screenWidth;width += +offsetDis;return width;}

2.3 滑动中Item的位置计算

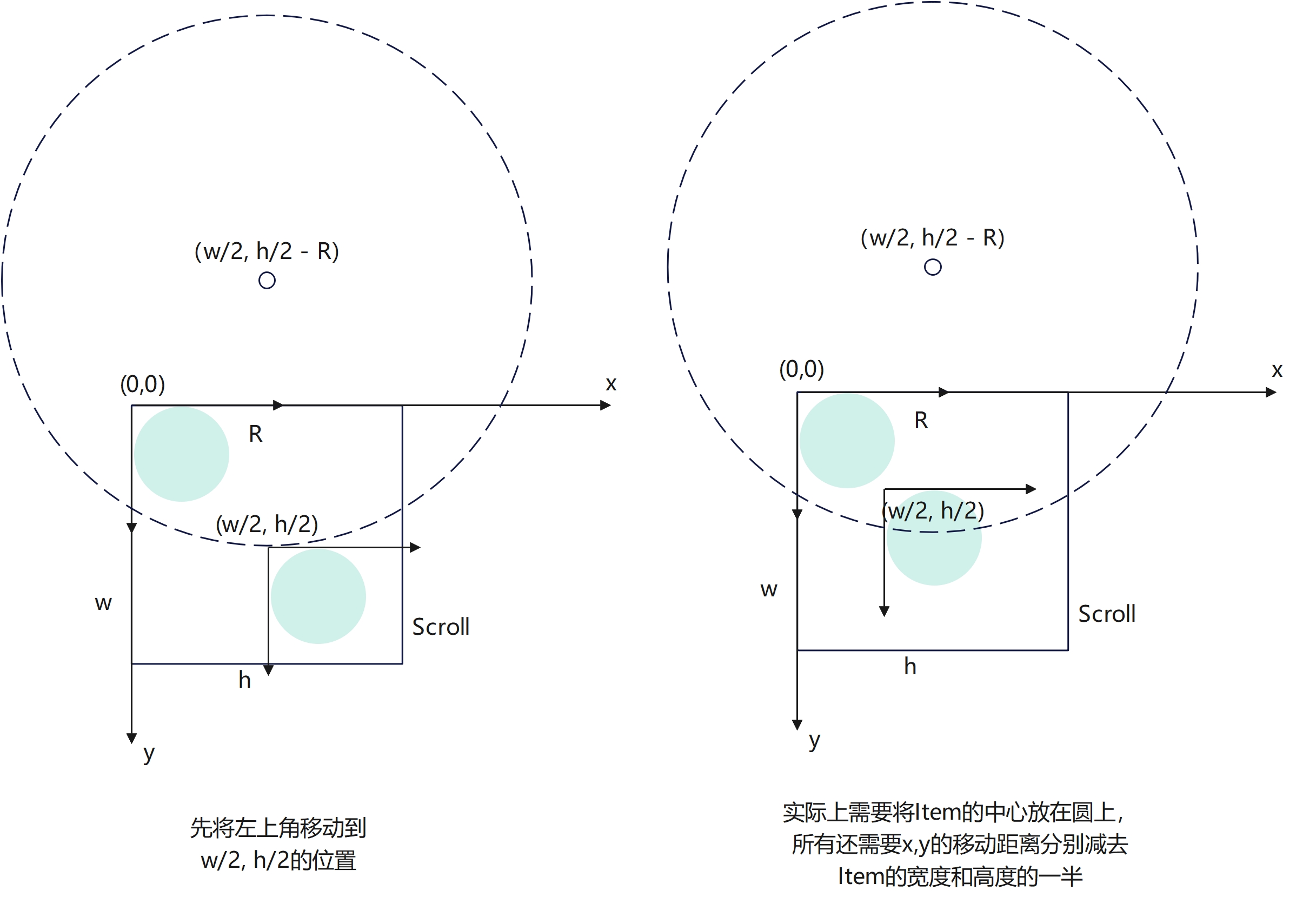
2.3.1 偏移公式

如图所示，所有Item的初始化位置都在Scroll的左上角位置，第一步，将Item从起始点移动到(w/2, h/2)的位置，那么x,y 的translate分别为：

translateX = w/2 - 0, translateY = h/2 - 0

但是移动后，Item的左上角在圆上，中心点并不在圆上，所以，还需要分别减去Item的自身的宽度和高度的一半，最终的计算如下：

translateX = w/2 - 0 - itemWidth/2,

translateY = h/2 - 0 - itemHeight/2

则可以计算出从起始点将Item的中心点移动到(w/2,h/2)的偏移量。那么根据此公式，我们可以计算出圆上任意一点和起始位置的偏移量，假设圆上任意一点为（x0, y0）,那么

translateX = x0 - 0 - itemWidth/2,

translateY = y0 - 0 - itemHeight/2

 /*** 获取当前位置和起始位置的偏移值* @param currentPoint 当前位置* @param startPoint 起始位置* @param item Item项* @returns*/private getOffSet(currentPoint: Point, startPoint: Point, item: ItemBean): Offset {const dx = currentPoint.x - startPoint.x - item.width / 2;const dy = currentPoint.y - startPoint.y - item.height / 2;return { dx: dx, dy: dy }}

注：在ArkTs中，translate的移动，永远是从控件自身的左上角位置开始，移动到需要移动的位置，可参考官方文档：translate

2.3.2 Scroll滑动中Item的位置

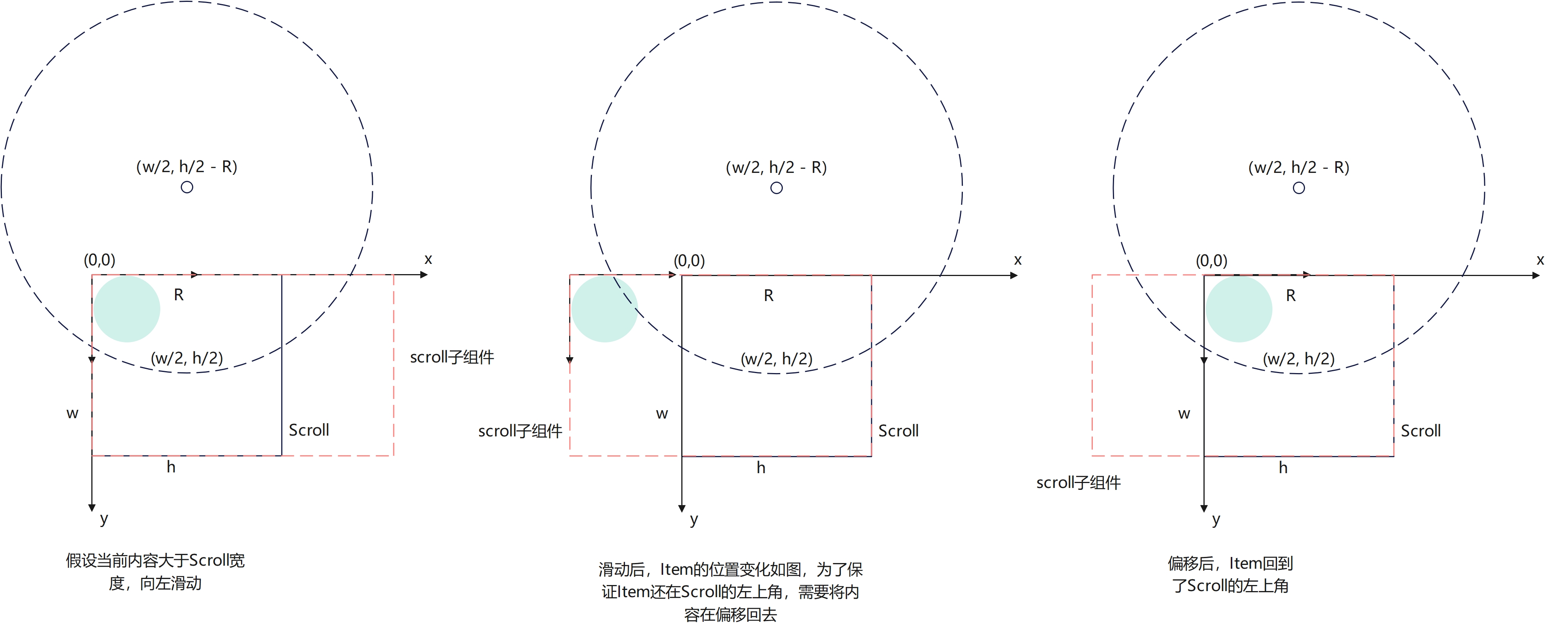
首先，Scroll在左右滑动的过程中，其内从是会跟着偏移的，那么为了保证Item的起始位置(Scroll左上角)不变，需要将Scroll内容滑动过的偏移量，再使用translate偏移回来

@Component
export struct ArcScrollView {@State totalOffset: number = 0build(){Stack(){Scroll(){// Scroll子控件，需要将滑动的距离偏移会拉Stack(){ForEach(...){// Item项}}.translate({ x: this.totalOffset })}.onWillScroll((xOffset: number, yOffset: number, scrollState: ScrollState) => {this.totalOffset += xOffset;}}}
}

其次，根据水平的移动距离，需要计算Item在圆上的位置坐标，然后从起始位置translate到计算后的位置上即可。

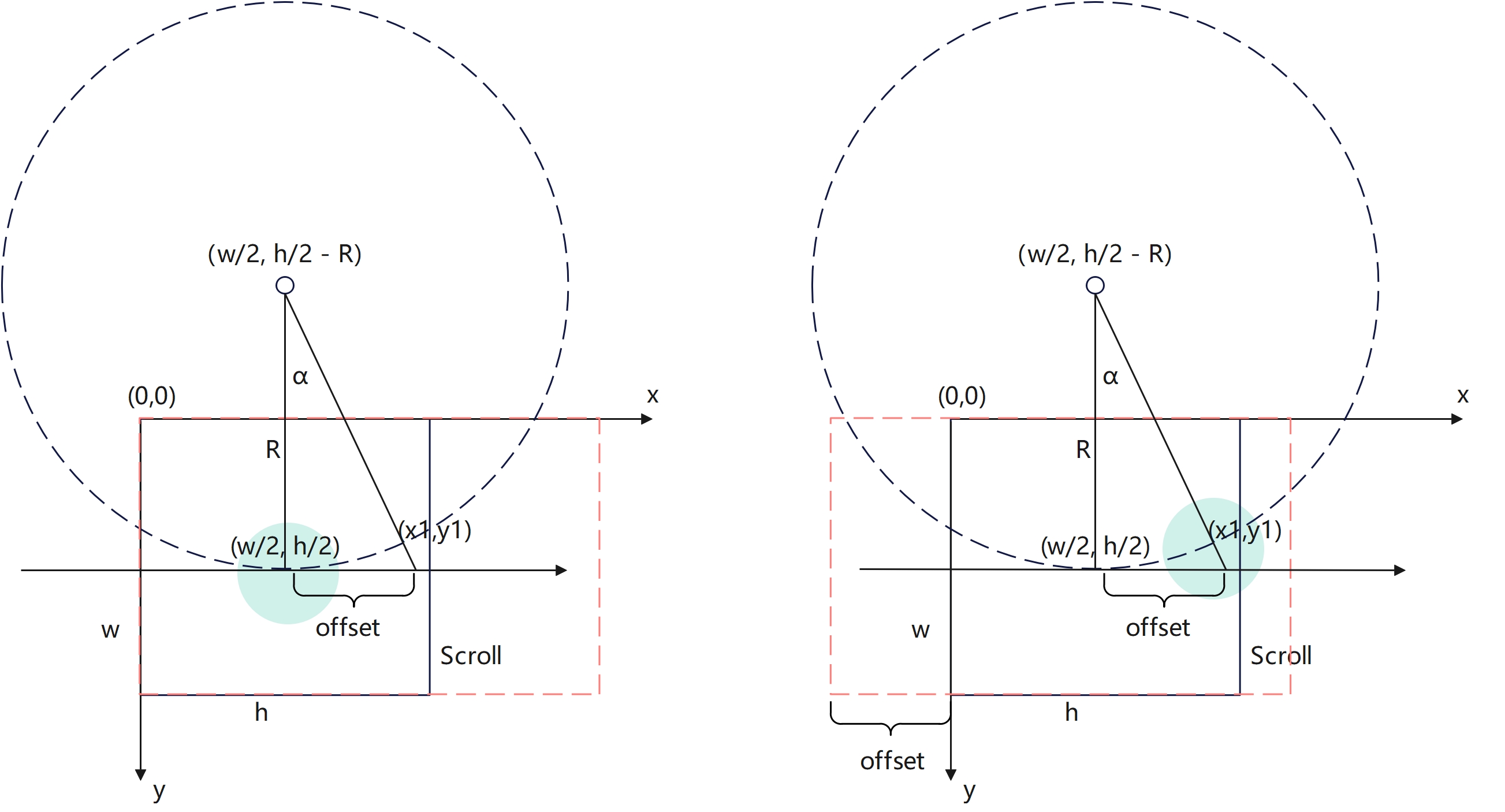
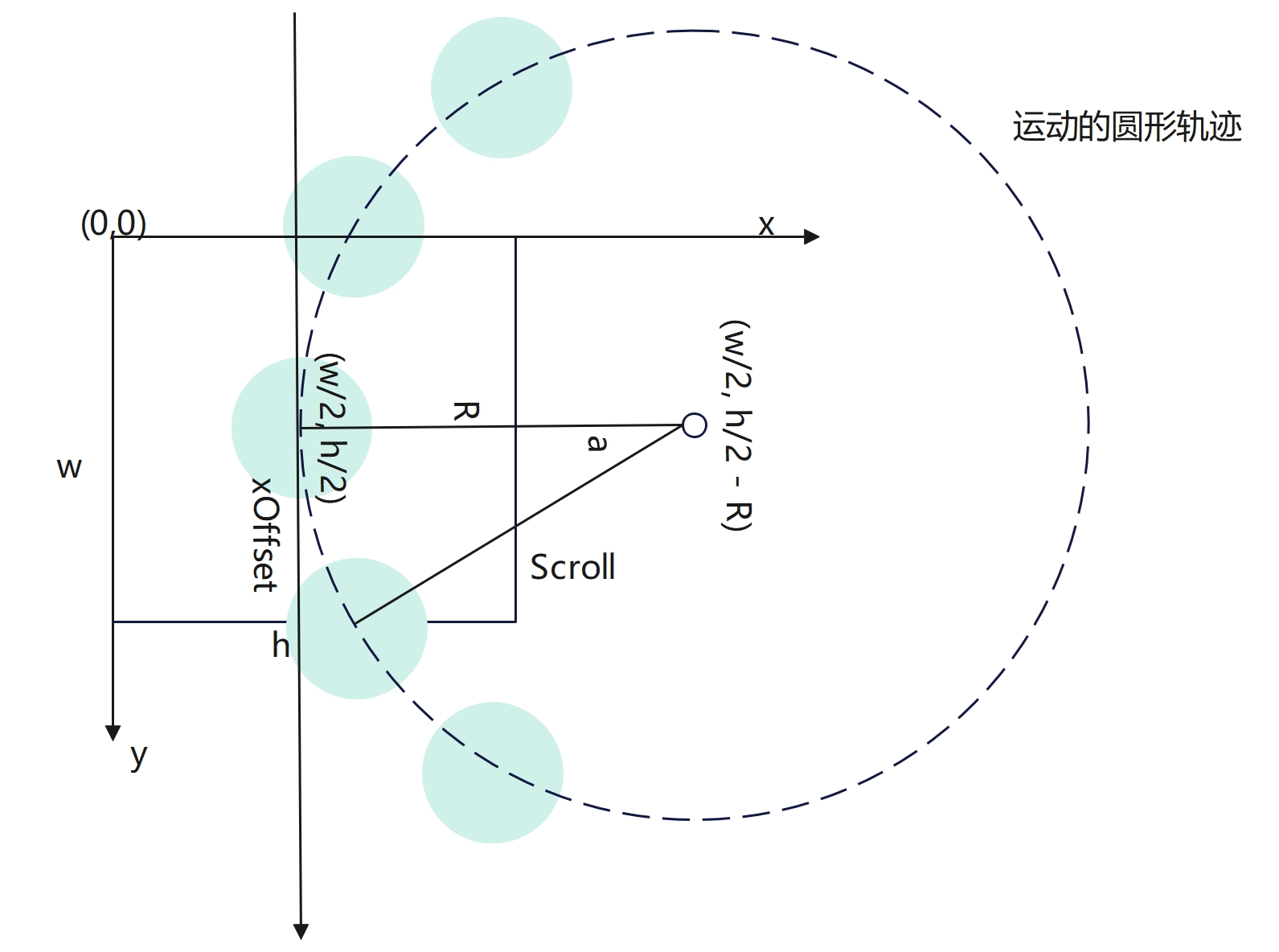
如图，假设Scroll向右滑动了offset的距离，夹角为α，那么需要计算出移动后，Item在圆上的位置(x1, y1)的坐标值。

在2.1.1章节中，我们知道Item之前的夹角为a, 可计算出水平投射距离为xOffset = tan(a) * R, 据此可以计算出Item之间的弧度和水平距离的一个比例，如下：

radio = (a * π / 180) / (tan(a) * R)

根据此比例，可以计算出水平滑动offset后，(x1, y1)和(w/2, h/2)两点之间夹角的弧度值：

radian = offset * radio

根据弧度值radian, 圆上一点的坐标(w/2, h/2), 圆心坐标(w/2, h/2 - R), 可使用2.1.2中的公式，计算出圆上的点(x1, y1)的坐标值。在根据坐标值和起始点，求取Item的偏移量进行移动。

/*** 更新Item的位置* @param offset*/public updateItemPosition(offset: number): void {const radian = offset * this.RADIAN_OFFSET_RADIO;for (let i = 0; i < this.modelList.length; i++) {const item = this.modelList[i];const pos = this.getPointInCircle(radian, item.currentPos);const translate = this.getOffSet(pos, { x: 0, y: 0 }, item);item.translateX = translate.dx as number;item.translateY = translate.dy as number;item.currentPos = pos;}}

以此类推，每次根据Scroll的偏移量计算Item的下一个坐标点，然后偏移，这样就形成了Scroll滑动中，Item沿着圆形路径滑动的效果。

垂直方向的实现方式跟水平一样，把相关x方向移动的距离计算换成y方向的即可，效果如下：

三. ArcScroll支持的能力

3.1 弹簧动画效果

Scroll 设置了手尾的弹簧动画效果，当Scroll滑到开始或结束时，继续往前滑，会有回弹的效果，设置属性如下：

Scroll(){
}
.edgeEffect(EdgeEffect.Spring)

3.2 Scroll限位滑动

为了使Scroll滑动停止时，Item可以显示在Scroll的中心位置，设置了Scroll的限位滑动，如下：

Scroll(){
}
.scrollSnap({snapAlign: ScrollSnapAlign.START,snapPagination: this.arcScrollViewModel?.getSnapPagination()})

限位滑动的距离为Item之间的水平投射距离。

3.3 Scroll属性条件

export class ConditionControl {// 是否显示滑动条public isShowScrollBar?: boolean;// 是否水平滑动public isScrollHorizontal?: boolean;
}

isShowScrollBar: true,显示滚动条，false，不显示

isScrollHorizontal: true: 水平滑动，false：垂直滑动

3.4 ItemView布局

ArcScroll控制Item的移动方式，但是Item自身的布局，则不收ArcScroll控制，所以ArcScroll在Item的参数中提供了传递布局的参数：

// item的布局方法(@Builder方法)public itemView: (item: ItemBean) => void

在初始化ArcScroll时，可以传递每个Item自己的布局方法给ArcScroll,如下：

@Component
struct ItemContainerView {@ObjectLinkitem: ItemBean;@BuilderParamitemView: ($$: ItemBean) => void = this.defaultItemViewBuilder;build() {Stack() {this.itemView(this.item);}.size({ width: this.item.width, height: this.item.height }).translate({ x: this.item.translateX, y: this.item.translateY })}@Builderprivate defaultItemViewBuilder(item: ItemBean): void {}
}@Component
export struct ArcScrollTest {// 将builderItemView传给Itemprivate modelList: ItemBean[] = [new ItemBean(1, px2vp(300), px2vp(300), this.builderItemView),new ItemBean(2, px2vp(300), px2vp(300), this.builderItemView),new ItemBean(3, px2vp(300), px2vp(300), this.builderItemView),new ItemBean(4, px2vp(300), px2vp(300), this.builderItemView),new ItemBean(5, px2vp(300), px2vp(300), this.builderItemView)]private arcScrollInfo: ArcScrollInfo = new ArcScrollInfo();aboutToAppear(): void {this.arcScrollInfo.setConditionControl({ isShowScrollBar: true, isScrollHorizontal: false })}build() {Stack() {ArcScrollView({ modelList: this.modelList, arcScrollInfo: this.arcScrollInfo })}.border({ width: 2, color: Color.Pink })}// Item 的布局方法，可根据自己的实际布局写@Builderprivate builderItemView($$: ItemBean): void {Shape() {Circle().fill(Color.Green).width('100%').height('100%')}.width('100%').height('100%')Text($$.index.toString())}
}

这里需要注意的是，为了使ItemBean中的状态变量能够引起UI刷新，builderItemView中需要按照引入传递参数:

$$: ItemBean

四. 总结

ArcScroll的实现，主要是计算圆形路径上的位置，以及转换水平移动的距离和圆上的角度，计算出移动后Item的位置，然后在根据translate的属性移动，达到弧形移动的效果。

ArcScroll: 弧形滑动控件

一. 什么是ArcScroll? ArcScroll是一种基于Scroll控件实现的弧形滑动控件。可以让Scroll内容项沿着一个圆心的轨迹滑动，从而实现内容弧形滑动的效果。如下图： 水平滑动： 垂直滑动： 二. 实现方案以下，以水平的方向…...

编程日记 2025/8/4 3:46:05

芋道框架账号未登录、租户标识未传递

一. 账号未登陆 {"code": 401,"data": null,"msg": "账号未登录" } 将接口中的 PreAuthorize 注解删除, 使用 PermitAll 注解, 设置 PermitAll 无需认证 Spring Security 中的 YudaoWebSecurityConfigurerAdapter 有详细说明 PostM…...

编程日记 2025/7/31 8:51:23

【计算机视觉】OpenCV项目实战：get_inverse_perspective：基于OpenCV的透视图转化为不同平面

get_inverse_perspective：逆透视变换的算法实现与实战指南一、项目概述与技术背景1.1 核心功能与技术价值1.2 逆透视变换原理1.3 技术指标对比二、环境配置与算法实现2.1 硬件要求2.2 软件部署依赖安装核心代码结构 2.3 校准参数配置三、核心算法优化3.1 矩阵运算…...

编程日记 2025/7/31 8:51:20

Jsoup与HtmlUnit：两大Java爬虫工具对比解析

Jsoup：HTML解析利器定位：专注HTML解析的轻量级库（也就是快，但动态页面无法抓取） 核心能力： DOM树解析与CSS选择器查询 HTML净化与格式化支持元素遍历与属性提取应用场景：静态页面数据抽…...

编程日记 2025/7/31 8:51:14

使用 ANSYS AEDT（单向耦合）进行高功率同轴射频滤波器的热分析

电热模拟当今无线射频设备日益复杂，对大型复杂射频设计的精确高效仿真需求也随之增加。在设计早期识别和预测潜在问题可以节省资源、时间和成本。热量会降低电子设备的性能和可靠性，因此热分析对于确定设备在实际工作条件下是否能达到预期性能至关重要…...

编程日记 2025/8/2 9:19:57

Baklib实战企业内容与中台管理差异解析

企业内容管理中台本质差异企业内容管理系统（CMS）与内容中台的核心差异在于战略定位与技术路径的本质性区隔。传统CMS聚焦于内容存储与审批流程的线性管理，而内容中台则构建起全域数据服务中枢，通过API接口实现跨系统内容资产调用…...

编程日记 2025/7/31 8:51:06

API请求参数有哪些？

通用参数 app_key：应用的唯一标识，用于验证应用身份，调用API时必须提供。 timestamp：请求时间戳，通常为当前时间的毫秒级时间戳，用于防止请求被重放攻击。 format：返回数据的格式，…...

编程日记 2025/7/31 8:51:03

探秘 InSAR：数据处理与形变信息提取全解析

技术点目录 InSAR技术应用现状分析及其发展InSAR原理、技术方法讲解数据处理环境建立与软件熟悉SAR影像数据获取、DEM数据获取InSAR数据前处理技术InSAR地形三维重建DInSAR形变信息提取时序InSAR技术形变速率与形变时间序列信息获取星地InSAR技术监测案例了解更多 ——————…...

编程日记 2025/7/31 11:29:29

Nginx静态资源增加权限验证

Nginx静态资源增加权限验证一、前言二、解决思路2.1、方式一2.2、方式二三、代码3.1、方式一3.1.1、前端代码3.1.2、后端代码3.1.3、Nginx调整3.1.4、注意事项3.2.方式二四、参考资料一、前言在项目开发的过程中，项目初期，及大部分小型项目都是使用共享磁盘进行静态文件的…...

编程日记 2025/7/31 11:29:27

初识MySQL

1. 什么是数据库 2. 什么是MySQL 我们在使用MySQL与Java进行交互时使用的接口为JDBC 3. MySQL安装与SQLyog管理工具附录将会提供相关绿色版软件，不用从官网下载了配置环境变量： 双击打开，新建（根据mysql的根目录写path&#xff…...

编程日记 2025/7/31 11:29:24

计算机网络：深度解析基于链路状态的内部网关协议IS-IS

IS-IS（Intermediate System to Intermediate System）路由协议详解 IS-IS（Intermediate System to Intermediate System）是一种基于链路状态的内部网关协议（IGP），最初由ISO为OSI（开放系统互连）模型设计，后经扩展支持IP路由。它广泛应用于大型运营商网络、数据中心及复…...

编程日记 2025/7/31 11:29:22

python---kafka常规使用

安装依赖在开始之前，需要安装 kafka-python 库。可以通过以下命令安装： pip install kafka-python创建生产者生产者负责将消息发送到 Kafka 主题。以下是一个简单的生产者示例： from kafka import KafkaProducer import json import ti…...

编程日记 2025/8/2 15:32:14

图像泊松融合(convpyr_small版本)

一、背景介绍前面已经讲过泊松融合算法和它的fft快速版本实现了，想看下还有没有更快的版本，继续翻了下论文，找到了更快速的版本：Convolution Pyramids 。找到它的matlab代码跑了下，效果还不错。学习记录，…...

编程日记 2025/7/31 11:29:18

ABP vNext + EF Core 实战性能调优指南

ABP vNext EF Core 实战性能调优指南 🚀 目标本文面向中大型 ABP vNext 项目，围绕查询性能、事务隔离、批量操作、缓存与诊断，系统性地给出优化策略和最佳实践，帮助读者快速定位性能瓶颈并落地改进。 📑 目录 ABP vN…...

编程日记 2025/7/31 2:09:05

Spark，在shell中运行RDD程序

在hdfs中/wcinput中创建一个文件：word2.txt在里面写几个单词启动hdfs集群 [roothadoop100 ~]# myhadoop start [roothadoop100 ~]# cd /opt/module/spark-yarn/bin [roothadoop100 ~]# ./spark-shell 写个11测试一下按住ctrlD退出进入环境：spar…...

编程日记 2025/7/31 11:29:13

【Python 元组】

Python 中的元组（Tuple）是一种不可变的有序数据集合，用于存储多个元素的序列。与列表（List）类似，但元组一旦创建后无法修改，这种特性使其在特定场景下具有独特优势。一、核心特性不可变性&am…...

编程日记 2025/7/31 11:29:10

如何将邮件送达率从60%提升到95%

一、邮件送达率的重要性邮件送达率是邮件营销效果的关键指标。高送达率能增加邮件被打开、阅读和互动的机会；低送达率则可能导致邮件被误判为垃圾邮件，浪费企业资源。二、影响邮件送达率的因素及优化策略 1.发件人信誉建立良好信誉：发…...

编程日记 2025/7/31 11:29:08

【Python】‌Python单元测试框架unittest总结

1. 本期主题：Python单元测试框架unittest详解 unittest是Python内置的单元测试框架，遵循Java JUnit的"测试驱动开发"（TDD）理念，通过继承TestCase类实现测试用例的模块化组织。本文聚焦于独立测试脚本的编写…...

编程日记 2025/8/5 3:43:14

机器人运动控制技术简介

机器人运动控制详解：从基础原理到技术方案一、机器人运动控制本质机器人运动控制是通过算法协调电机、传感器和机械结构，实现精确的位姿（位置姿态）控制。其核心要解决三个问题： 去哪里 - 路径规划&#x…...

编程日记 2025/8/4 4:37:39

在linux系统中，没有网络如何生成流量以使得wireshark能捕获到流量

在没有网络连接的情况下，仍然可以通过生成本地流量来测试Wireshark的捕获功能。以下是一些方法可以在Linux系统中生成本地流量，以便Wireshark可以捕获到这些流量： 1. 使用ping命令 ping命令可以生成ICMP（Internet Control Messa…...

编程日记 2025/7/31 11:29:00

常见图像融合算法(图像泊松融合)

一、背景介绍上一篇已经讲过alpha和金字塔融合基本实现，这里主要是继续对图像常用的泊松融合算法和他的一些性能版本实现的基本讲解。二、原始版本 1、基本原理图像泊松融合也是普遍使用的常规算法，很多小伙伴已经分享过它的基本原理和实现了&#…...

编程日记 2025/8/2 21:28:57

大疆无人机搭载树莓派进行目标旋转检测

环境部署首先是环境创建，创建虚拟环境，名字叫 pengxiang python -m venv pengxiang随后激活环境 source pengxiang/bin/activate接下来便是依赖包安装过程了: pip install onnxruntime #推理框架 pip install fastapi uvicorn[standard] #网络请求…...

编程日记 2025/7/30 18:54:11

tryhackme——Active Directory Basics

文章目录一、Windows Domains二、活动目录AD2.1 Active Directory Users and Computers2.2 安全组和组织单位OU 三、管理AD中的用户3.1 删除额外的OUs和用户3.2 委托四、管理AD中的计算机五、组策略5.1 查看GPO5.2 GPO分发5.3 新建GPO 六、认证方式6.1 Kerberos认证6.2 NetNT…...

编程日记 2025/7/31 11:28:53

Linux基础(关于进程相关命令)

1.查看系统进程 ps -aux 查看所有的系统进程我们一般配合 | grep 使用，比如 ps -aux | grep bin 就是查看所有bin的进程信息 2.查看系统实时进程 top 和Windows的任务管理器的功能类似 3.结束进程 kill -9 PID 根据上面的进程信息可得，每个进程都有一个…...

编程日记 2025/7/31 11:28:50

切比雪夫不等式详解

切比雪夫不等式详解一、引言切比雪夫不等式（Chebyshev’s Inequality）是概率论和统计学中最重要的基本定理之一，由俄国数学家切比雪夫（P. L. Chebyshev，1821-1894）提出。它为我们提供了一个强大工具&am…...

编程日记 2025/8/4 17:21:12

自然语言处理 (NLP) 技术发展：从规则到大型语言模型的演进之路

自然语言处理 (NLP) 技术发展：从规则到大型语言模型的演进之路自然语言处理（NLP）是人工智能领域中一个极具挑战性和活力的分支，其目标是赋予计算机理解、解释和处理人类语言的能力。从早期的基于规则的系统到当前由大型语言模型（LLM）引领的时代，NLP 技术经历了深刻的演…...

编程日记 2025/8/4 4:51:17

CurrentHashMap的整体系统介绍及Java内存模型(JVM)介绍

当我们提到ConurrentHashMap时，先想到的就是HashMap不是线程安全的： 在多个线程共同操作HashMap时，会出现一个数据不一致的问题。 ConcurrentHashMap是HashMap的线程安全版本。它通过在相应的方法上加锁，来保证多线程情况下的…...

编程日记 2025/7/31 11:28:42

手撕红黑树的左旋与右旋

一、为什么需要旋转？ 在红黑树中，插入或删除节点可能会破坏其五条性质，比如高度不平衡或连续红节点。为了恢复红黑性质，我们采用局部旋转来“调整树形结构”，保持平衡。二、旋转本质是“局部变形” 左旋和右旋不会…...

编程日记 2025/7/31 11:28:40

Java——反射

目录 5 反射 5 反射类信息：方法、变量、构造器、继承和实现的类或接口。反射：反射是 Java 中一项强大的特性，它赋予了程序在运行时动态获取类的信息，并能够调用类的方法、访问类的字段以及操作构造函数等的能力。通过反射&#…...

编程日记 2025/7/31 11:21:42

一文了解Python中的requests库：网络交互的基础

目录 1. 前言 2. requests库的基本概念 3. requests库的适应场景 4. requests库的基本使用 4.1 安装requests 4.2 发送第一个请求 4.3 常见HTTP请求方法 4.4 响应对象的属性 4.5 发送带参数的请求 4.6 处理请求和响应 5. 高级功能 5.1 文件上传 5.2 会话对象 5.3…...

编程日记 2025/7/31 11:28:34

基于大模型预测的足月胎膜早破行阴道分娩全流程研究报告

目录一、引言 1.1 研究背景与意义 1.2 研究目的与方法 1.3 研究创新点二、胎膜早破（足月）行阴道分娩概述 2.1 胎膜早破定义与分类 2.2 足月胎膜早破行阴道分娩的现状与挑战 2.3 大模型预测引入的必要性三、大模型预测原理与技术 3.1 大模型介绍 3.2 数据收集与…...

编程日记 2025/7/31 11:28:32

ISP流程介绍(Raw格式阶段)

一、ISP之DPC DPC(Defective Pixel Correction)也就是坏点矫正，在sensor接收光信号，并做光电转换之后。这一步设计的意义在于：摄像头sensor的感光元件通常很多会存在一些工艺缺陷缺陷，让图像上某些像素无法正常收集到需要的光信号…...

编程日记 2025/7/31 11:28:29

Codeforces Round 1023 (Div. 2)

Dashboard - Codeforces Round 1023 (Div. 2) - Codeforces 一个构造问题，我把最大的数放在一个数组，其余数放在另一个数组，就能保证gcd不同来看代码： #include <bits/stdc.h> using namespace std;int main() {int t;ci…...

编程日记 2025/8/5 1:57:57

按位宽提取十六进制值

需求：给出一个十六进制值，要求提取high和low位之间的值。比如16ha0f0，这是一个16bit宽的十六进制数0xa0f0，提取[15:12]范围内的值。 def extract_bits(value, high, low):"""从 value 中提取 [high:low] 位的值:p…...

编程日记 2025/7/31 11:28:24

Android设备序列号获取方式全解析

Android设备序列号获取方式全解析前言在Android开发中，获取设备序列号（SN）是设备管理类应用常见的需求。但不同厂商设备获取方式存在差异，且Android系统版本升级也带来了API变化。本文将系统梳理7种主流序列号获取方式&#x…...

编程日记 2025/7/31 13:36:03

Spring框架（1）

Spring框架是Java企业级开发中最受欢迎的框架之一，它通过简化开发流程、降低耦合度，让开发者能够更专注于业务逻辑的实现。本文将带你了解Spring框架的核心概念和基本用法。一、Spring框架简介 Spring是一个轻量级的开源Java开发框架，由Ro…...

编程日记 2025/7/31 11:28:21

软件安全（二）优化shellcode

我们在上一节课中所写的shellcode，其中使用到的相关的API是通过写入其内存地址来实现调用。这种方法具有局限性，如切换其他的操作系统API的内存地址就会发生变化，从而无法正常调用。所谓的shellcode不过是在目标程序中加一个区段使得程序可…...

编程日记 2025/7/31 11:28:18

前端使用腾讯地图api实现定位功能

1.配置key 申请地址： https://lbs.qq.com/dev/console/key/manage 2.在项目中引入jssdk <script type"text/javascript" src"https://apis.map.qq.com/tools/geolocation/min?keykey&referermyapp"></script>使用 const g…...

编程日记 2025/7/31 11:28:16

单片机-STM32部分：10、串口UART

飞书文档https://x509p6c8to.feishu.cn/wiki/W7ZGwKJCeiGjqmkvTpJcjT2HnNf 串口说明电平标准是数据1和数据0的表达方式，是传输线缆中人为规定的电压与数据的对应关系，串口常用的电平标准有如下三种： TTL电平：3.3V或5V表示1&am…...

编程日记 2025/7/31 11:28:13

STM32外设-串口UART

STM32外设-串口UART 一，串口简介二，串口基础概念1，什么是同步和异步/UART与USART对比2，串行与并行3，波特率 (Baud Rate)4，数据帧 (Data Frame)5，TX 和 RX 三，硬件连接1，u…...

编程日记 2025/7/31 8:19:42

《工业计算机硬件技术支持手册》适用于哪些人群？

《工业计算机硬件技术支持手册》于2024年出版，主要讲当前正在应用的最新计算硬件技术。包括计算机各种功能接口、扩展总线、各种国际通行的板型规格等等。书中引用的数据，全部来自国际行业技术规范，书中还融入了作者几十年的工作经验和操作技…...

编程日记 2025/7/31 11:28:09

element-ui时间线样式修改

element-ui时间线样式修改前两天公司给了一个需求要求如下图所示需求是时间在步骤条左边,看了element-ui的文档发现并没有参数可以设置时间在步骤条的左边那没办法只能自己想一想办法了首先想到的是用样式直接改变活不多说直接搞第一步选中时间这个元素发现了这个类…...

编程日记 2025/7/31 11:28:05

动态规划之背包问题：组合优化中的经典NP挑战

背包问题概念： 背包问题是一种经典的组合优化的NP问题，在计算机科学、运筹学等领域有着广泛的应用。问题可以简单的描述为： 假设有一个容量为C的背包和n个物品，每个物品i都有重量w[i]和价值v[i]。目标是选择一些物品放入背包&…...

编程日记 2025/8/2 3:28:57

JavaScript 基础

JS概念 JS基础概念 JS是一种运行在客户端(浏览器)的编程语言, 实现人机交换结果作用: 网页特效表单验证数据交互服务端编程(node.js) JS的组成 ECMAScript—javaScript语言基础Web APIs—(DOM: 页面文档对象模型)(BOM: 浏览器对象模型) JS书写位置内部: 写到< /body…...

编程日记 2025/7/31 11:27:53