正态分布和幂律分布
1. 背景与引入
-
正态分布
- 历史来源:18世纪由高斯(Gauss)在研究测量误差时提出,后被广泛应用于自然现象和社会科学的数据建模。
- 重要性:被称为“钟形曲线”,是统计学中最核心的分布之一,支撑中心极限定理,解释为何大量独立随机变量的均值趋于稳定。
- 实际问题:人的身高、考试成绩、工厂零件尺寸等数据为何大多集中在平均值附近?如何用数学描述这种“中间多、两头少”的规律?
- 学习目标:掌握正态分布的核心特征(对称性、集中趋势),学会用均值和方差描述数据,并理解其在机器学习中数据预处理(如标准化)和假设检验中的作用。
-
幂律分布
- 历史来源:19世纪帕累托(Pareto)研究财富分布时发现“二八法则”,后被推广到网络科学、地震强度、城市人口等领域。
- 重要性:描述“长尾现象”和极端事件的重要性,挑战传统统计学对平均值的依赖,在复杂系统分析中不可或缺。
- 实际问题:为何互联网流量集中在少数网站?为何社交媒体上少数用户拥有巨量粉丝?如何量化这类“富者愈富”的现象?
- 学习目标:理解幂律分布的标度不变性(无特征尺度),识别数据中的“长尾”形态,并掌握其在推荐系统、风险建模等场景的应用逻辑。
共同铺垫:
通过对比身高(正态)与财富(幂律)的差异,引出两种分布对现实建模的本质区别——前者强调均值代表性,后者强调极端值主导性,为后续数学性质和算法设计埋下伏笔。
2. 核心概念与定义
正态分布(Normal Distribution)
-
正式定义:
若随机变量 X X X的概率密度函数为
f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 ( − ∞ < x < ∞ ) , f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}} \quad (-\infty < x < \infty), f(x)=2πσ1e−2σ2(x−μ)2(−∞<x<∞),
则称 X X X服从参数为 μ \mu μ(均值)和 σ 2 \sigma^2 σ2(方差)的正态分布,记作 X ∼ N ( μ , σ 2 ) X \sim \mathcal{N}(\mu, \sigma^2) X∼N(μ,σ2)。 -
核心思想:
数据围绕中心值(均值)对称分布,越靠近中心的值出现概率越高,极端值极少。
类比:
想象一个沙漏——沙子在中间最集中,两端逐渐减少;或人群身高分布,大多数人接近平均身高,极高或极矮的人很少。 -
几何直观:
- 钟形曲线:对称的单峰曲线,均值处最高,两侧对称衰减。
- 参数意义:
- 均值 μ \mu μ决定曲线的中心位置(如男性平均身高 175cm)。
- 标准差 σ \sigma σ决定曲线的“胖瘦”(如学生考试成绩标准差大,曲线矮胖;标准差小,曲线尖瘦)。
幂律分布(Power Law Distribution)
-
正式定义:
若随机变量 X X X的概率密度函数满足
f ( x ) = C x − α ( x ≥ x min , α > 1 ) , f(x) = Cx^{-\alpha} \quad (x \ge x_{\min}, \alpha > 1), f(x)=Cx−α(x≥xmin,α>1),
其中 C C C为归一化常数,则称 X X X服从幂律分布,参数 α \alpha α为幂律指数。 -
核心思想:
小概率事件的累积效应显著,极端值可能出现且影响巨大,数据呈现“长尾”特征。
类比:
社交网络中,少数“网红”拥有上亿粉丝(极端值),而大多数人只有几十个好友(平凡值),但所有平凡值的总和仍不可忽视。 -
几何直观:
- 长尾曲线:横轴表示取值(如财富),纵轴表示概率,曲线在右侧拖出极长的尾部(如极少数人占据社会大部分财富)。
- 双对数图特征:在双对数坐标系中,幂律分布表现为一条直线,斜率与 α \alpha α相关(如斜率越陡,尾部越薄)。
关键对比铺垫:
- 正态分布的钟形曲线“收尾快”(极端值概率趋近于 0),幂律分布的长尾“收尾慢”(极端值仍有可观概率)。
- 正态分布的均值和方差有限,幂律分布当 α ≤ 3 \alpha \leq 3 α≤3时方差无穷大,极端事件主导统计性质。
3. 拆解与解读
正态分布(Normal Distribution)
-
公式拆解:
f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}} f(x)=2πσ1e−2σ2(x−μ)2
分解为三部分:- 系数项: 1 2 π σ \frac{1}{\sqrt{2\pi}\sigma} 2πσ1—— 归一化常数,确保概率密度积分总和为1。
- 指数项: e − ( x − μ ) 2 2 σ 2 e^{-\frac{(x-\mu)^2}{2\sigma^2}} e−2σ2(x−μ)2—— 决定曲线形状的核心部分。
- 参数: μ \mu μ(均值)、 σ \sigma σ(标准差)。
-
逐项解读:
(1) 系数项:- 类比:类似“调整音量”——无论曲线形状如何,必须保证总面积(概率总和)为1。
- 数学意义: 2 π \sqrt{2\pi} 2π是高斯积分的结果( ∫ − ∞ ∞ e − x 2 d x = π \int_{-\infty}^\infty e^{-x^2} dx = \sqrt{\pi} ∫−∞∞e−x2dx=π),乘以 σ \sigma σ后反映分布的宽窄。
(2) 指数项:
- 结构: − ( x − μ ) 2 2 σ 2 -\frac{(x-\mu)^2}{2\sigma^2} −2σ2(x−μ)2是一个“惩罚项”,当 x x x远离均值 μ \mu μ时,指数快速衰减。
- 生活化解释:
- ( x − μ ) 2 (x-\mu)^2 (x−μ)2:像“距离中心的平方代价”——离中心越远,代价越大。- 分母 2 σ 2 2\sigma^2 2σ2:类似“调节放大镜倍数”—— σ \sigma σ越大,衰减越慢(曲线越胖)。
- 几何意义:形成钟形曲线的对称下降趋势。
(3) 参数 μ \mu μ与 σ \sigma σ:
- μ \mu μ:控制“中心位置”(如男性平均身高175cm vs 女性162cm)。
- σ \sigma σ:控制“分散程度”(如考试难度低时成绩 σ \sigma σ小,难度高时 σ \sigma σ大)。 -
推导逻辑:
从中心极限定理出发:独立同分布的随机变量之和趋向正态分布(即使原分布非正态)。
例如:抛100次硬币的正面次数服从近似正态分布,均值50,标准差5。
幂律分布(Power Law Distribution)
-
公式拆解:
f ( x ) = C x − α ( x ≥ x min ) f(x) = Cx^{-\alpha} \quad (x \ge x_{\min}) f(x)=Cx−α(x≥xmin)
分解为三部分:- 归一化常数 C C C:确保概率密度积分总和为1。
- 幂律核 x − α x^{-\alpha} x−α:决定长尾特性的核心。
- 参数: α \alpha α(幂律指数)、 x min x_{\min} xmin(最小取值阈值)。
-
逐项解读:
(1) 幂律核 x − α x^{-\alpha} x−α:- 结构:反比例函数的推广,指数 α \alpha α决定衰减速率。
- 生活化解释:
- α = 2 \alpha=2 α=2:若 x x x翻倍,概率密度降至原来的 1 / 4 1/4 1/4(如收入翻倍,人数减少到1/4)。
- α \alpha α越小,尾部越“重”(极端值越多)。 - 几何意义:在双对数坐标系中, log f ( x ) = log C − α log x \log f(x) = \log C - \alpha \log x logf(x)=logC−αlogx为直线,斜率 − α -\alpha −α。
(2) 归一化常数 C C C:
- 推导:通过积分 ∫ x min ∞ C x − α d x = 1 \int_{x_{\min}}^\infty Cx^{-\alpha} dx = 1 ∫xmin∞Cx−αdx=1解得:
KaTeX parse error: Expected 'EOF', got '}' at position 49: …-(\alpha - 1)}}}̲
类比:类似“按比例缩放蛋糕”——无论 α \alpha α如何变化,总概率必须为1。
(3) 参数 α \alpha α与 x min x_{\min} xmin:
- α \alpha α:决定分布形态——
- α > 3 \alpha > 3 α>3:方差有限(尾部较薄)。
- 1 < α ≤ 3 1 < \alpha \leq 3 1<α≤3:方差无限(极端事件主导)。
- x min x_{\min} xmin:过滤“平凡值”,仅关注显著事件(如研究地震强度时忽略小震)。 -
长尾效应推导:
计算累积概率 P ( X ≥ x ) P(X \geq x) P(X≥x):
P ( X ≥ x ) = ∫ x ∞ C x − α d x ∝ x − ( α − 1 ) P(X \geq x) = \int_x^\infty Cx^{-\alpha} dx \propto x^{-(\alpha - 1)} P(X≥x)=∫x∞Cx−αdx∝x−(α−1)
例如:若 α = 2 \alpha=2 α=2,收入超过100万的概率是10万的 1 / 10 1/10 1/10,但极端值仍存在(如亿万富翁)。
关键对比总结
- 形状差异:
- 正态分布:钟形(快速衰减,极端值稀有)。
- 幂律分布:长尾(缓慢衰减,极端值显著)。
- 参数作用:
- 正态分布: μ \mu μ决定中心, σ \sigma σ决定胖瘦。
- 幂律分布: α \alpha α决定尾部厚度, x min x_{\min} xmin设定起点。
- 现实意义:
- 正态分布:适用于独立随机过程(如身高、测量误差)。
- 幂律分布:适用于复杂系统(如社交网络、金融市场)。
4. 几何意义与图形化展示
正态分布(Normal Distribution)
几何意义
- 钟形曲线:对称分布,峰值位于均值 μ \mu μ,标准差 μ ± σ \mu \pm \sigma μ±σ包含约68%的数据。
- 参数影响:
- μ \mu μ决定中心位置(平移曲线)。
- σ \sigma σ决定曲线胖瘦( σ \sigma σ越大,曲线越宽)。 - 极端值稀有性: μ ± 3 σ \mu \pm 3\sigma μ±3σ以外区域概率极低(约0.3%)。
代码实现
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm# 参数设定
mu, sigma = 0, 1 # 均值和标准差
x = np.linspace(-5, 5, 1000)# 计算概率密度
y = norm.pdf(x, mu, sigma)# 绘图
plt.figure(figsize=(8, 5))
plt.plot(x, y, label=f"μ={mu}, σ={sigma}", color='blue')
plt.fill_between(x, y, where=(x >= mu - sigma) & (x <= mu + sigma), color='blue', alpha=0.2, label=r"±1σ (68%)")
plt.fill_between(x, y, where=(x >= mu - 2*sigma) & (x <= mu + 2*sigma), color='green', alpha=0.1, label=r"±2σ (95%)")
plt.title("Figure-1: 正态分布的几何意义")
plt.xlabel("x")
plt.ylabel("概率密度")
plt.legend()
plt.grid(True)
plt.show()

图形解读
- Figure-1:
- 曲线对称性:左右两侧严格对称。
- 阴影区域:标注 μ ± σ \mu \pm \sigma μ±σ和 μ ± 2 σ \mu \pm 2\sigma μ±2σ的概率覆盖范围。
- 极端值区域: x > 3 x > 3 x>3或 x < − 3 x < -3 x<−3的概率密度接近零。
幂律分布(Power Law Distribution)
几何意义
- 长尾特性:小概率事件占比显著,无明确边界(如少数人拥有巨量财富)。
- 标度不变性:双对数坐标下为直线, log f ( x ) = − α log x + 常数 \log f(x) = -\alpha \log x + \text{常数} logf(x)=−αlogx+常数。
- 极端值主导: α \alpha α较小时,尾部贡献主要概率质量。
代码实现
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import powerlaw# 参数设定
alpha = 2.5
x_min = 1
x = np.linspace(x_min, 100, 1000)# 计算概率密度
y = powerlaw.pdf(x, alpha, scale=x_min)# 绘图(普通坐标)
plt.figure(figsize=(8, 5))
plt.plot(x, y, label=f"α={alpha}", color='red')
plt.fill_between(x, y, where=(x >= 50), color='red', alpha=0.1, label=r"x ≥ 50 的长尾区域")
plt.title("Figure-2: 幂律分布在普通坐标下的长尾")
plt.xlabel("x")
plt.ylabel("概率密度")
plt.legend()
plt.grid(True)
plt.show()# 双对数坐标验证标度不变性
plt.figure(figsize=(8, 5))
plt.loglog(x, y, label=f"α={alpha}", color='red')
plt.title("Figure-3: 幂律分布的双对数坐标验证")
plt.xlabel("log(x)")
plt.ylabel("log(f(x))")
plt.legend()
plt.grid(True)
plt.show()

图形解读
- Figure-2:
- 曲线陡峭下降,但右侧阴影区域(长尾)仍占显著面积。
- 小 x x x值概率密度高,大 x x x值概率密度衰减缓慢。
- Figure-3:
- 双对数坐标下为直线,斜率 − α -\alpha −α,验证标度不变性。
- 直线截距反映归一化常数 C C C。
关键对比总结
| 特性 | 正态分布 | 幂律分布 |
|---|---|---|
| 坐标系 | 普通坐标下钟形曲线 | 普通坐标下陡峭,双对数坐标下为直线 |
| 极端值 | 稀有( μ ± 3 σ \mu \pm 3\sigma μ±3σ外概率≈0.3%) | 常见(长尾区域概率不可忽略) |
| 参数作用 | μ \mu μ决定中心, σ \sigma σ决定宽度 | α \alpha α决定尾部厚度, x min x_{\min} xmin设定起点 |
| 现实意义 | 自然现象(身高、温度) | 社会与复杂系统(财富、网络流量) |
通过图形对比,可直观理解正态分布适用于独立随机过程,而幂律分布揭示复杂系统中“富者愈富”和极端事件的重要性。
5. 常见形式与变换
正态分布(Normal Distribution)
常见形式与等价变换
-
标准正态分布(Standard Normal Distribution)
- 定义: μ = 0 , σ = 1 \mu = 0, \sigma = 1 μ=0,σ=1,记为 Z ∼ N ( 0 , 1 ) Z \sim \mathcal{N}(0, 1) Z∼N(0,1)。
- 用途:简化计算(如查标准正态表),数据标准化(Z-score)。
- 变换逻辑:任意正态分布 X ∼ N ( μ , σ 2 ) X \sim \mathcal{N}(\mu, \sigma^2) X∼N(μ,σ2)可通过 Z = X − μ σ Z = \frac{X - \mu}{\sigma} Z=σX−μ转换。
-
多维正态分布(Multivariate Normal Distribution)
- 定义:
f ( x ) = 1 ( 2 π ) d / 2 ∣ Σ ∣ 1 / 2 e − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) f(\mathbf{x}) = \frac{1}{(2\pi)^{d/2} |\Sigma|^{1/2}} e^{-\frac{1}{2} (\mathbf{x} - \boldsymbol{\mu})^T \Sigma^{-1} (\mathbf{x} - \boldsymbol{\mu})} f(x)=(2π)d/2∣Σ∣1/21e−21(x−μ)TΣ−1(x−μ)
其中 μ \boldsymbol{\mu} μ为均值向量, Σ \Sigma Σ为协方差矩阵。 - 用途:多变量建模(如金融资产收益率、图像特征向量)。
- 变换逻辑:单变量正态分布的高维推广,协方差矩阵捕捉变量间相关性。
- 定义:
-
截断正态分布(Truncated Normal Distribution)
- 定义:限制在区间 [ a , b ] [a, b] [a,b]内的正态分布。
- 用途:有界数据(如考试分数、物理量测量范围)。
- 变换逻辑:原分布乘以归一化因子 1 Φ ( b ) − Φ ( a ) \frac{1}{\Phi(b) - \Phi(a)} Φ(b)−Φ(a)1,其中 Φ \Phi Φ为累积分布函数。
代码实现与图形对比
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm, multivariate_normal# 标准正态分布 vs 截断正态分布
x = np.linspace(-5, 5, 1000)
y_std = norm.pdf(x, 0, 1)
y_trunc = norm.pdf(x, 0, 1) / (norm.cdf(2) - norm.cdf(-2)) # 截断范围[-2, 2]plt.figure(figsize=(8, 4))
plt.plot(x, y_std, label="标准正态分布", color='blue')
plt.plot(x, y_trunc, label="截断正态分布 [-2, 2]", color='orange', linestyle='--')
plt.title("Figure-1: 标准与截断正态分布对比")
plt.legend()
plt.grid(True)
plt.show()# 多维正态分布(二维示例)
mean = [0, 0]
cov = [[1, 0.5], [0.5, 1]] # 协方差矩阵
x, y = np.mgrid[-3:3:.05, -3:3:.05]
pos = np.dstack((x, y))
rv = multivariate_normal(mean, cov)
z = rv.pdf(pos)plt.figure(figsize=(6, 5))
plt.contourf(x, y, z, cmap='viridis', levels=20)
plt.colorbar(label='概率密度')
plt.title("Figure-2: 二维正态分布等高线图")
plt.xlabel("X1")
plt.ylabel("X2")
plt.show()


图形解读
- Figure-1:
- 标准正态分布曲线对称且全域存在概率密度。
- 截断分布在 [ − 2 , 2 ] [-2, 2] [−2,2]外概率为零,内部密度被拉高(归一化)。
- Figure-2:
- 等高线椭圆反映变量间正相关(协方差 0.5),轴对齐时协方差为零。
幂律分布(Power Law Distribution)
常见形式与等价变换
-
离散 vs 连续幂律分布
- 离散形式:如 Zipf 定律(词频排名 f ( r ) ∝ r − α f(r) \propto r^{-\alpha} f(r)∝r−α)。
- 连续形式:如帕累托分布( f ( x ) = C x − α f(x) = Cx^{-\alpha} f(x)=Cx−α)。
- 联系:离散形式是连续形式的采样版本,常用于计数数据(如网页访问次数)。
-
累积分布函数(CCDF)形式
- 定义:
P ( X ≥ x ) = ∫ x ∞ f ( x ′ ) d x ′ ∝ x − ( α − 1 ) P(X \geq x) = \int_x^\infty f(x') dx' \propto x^{-(\alpha - 1)} P(X≥x)=∫x∞f(x′)dx′∝x−(α−1) - 用途:实证分析中更易观察长尾特性(如财富分布)。
- 变换逻辑:概率密度函数积分后斜率从 − α -\alpha −α变为 − ( α − 1 ) -(\alpha - 1) −(α−1)。
- 定义:
-
广义幂律分布(Exponential Cutoff)
- 定义:
f ( x ) = C x − α e − λ x f(x) = Cx^{-\alpha} e^{-\lambda x} f(x)=Cx−αe−λx - 用途:有限系统中截断极端值(如地震强度上限)。
- 变换逻辑:指数项 e − λ x e^{-\lambda x} e−λx在大 x x x时抑制增长。
- 定义:
代码实现与图形对比
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import powerlaw# 离散 vs 连续幂律分布(连续帕累托)
x_cont = np.linspace(1, 100, 1000)
y_cont = powerlaw.pdf(x_cont, a=2.5, scale=1)x_disc = np.arange(1, 101)
y_disc = x_disc**-2.5
y_disc /= y_disc.sum() # 归一化plt.figure(figsize=(8, 4))
plt.plot(x_cont, y_cont, label="连续幂律(帕累托)", color='blue')
plt.stem(x_disc, y_disc, linefmt='r--', markerfmt='ro', basefmt='none', label="离散幂律(Zipf)", use_line_collection=True)
plt.title("Figure-3: 离散与连续幂律分布对比")
plt.xscale('log')
plt.yscale('log')
plt.legend()
plt.grid(True)
plt.show()# CCDF vs PDF 对比
y_ccdf = 1 - powerlaw.cdf(x_cont, a=2.5, scale=1)plt.figure(figsize=(8, 4))
plt.plot(x_cont, y_cont, label="PDF", color='blue')
plt.plot(x_cont, y_ccdf, label="CCDF", color='green', linestyle='--')
plt.title("Figure-4: 幂律分布的PDF与CCDF对比")
plt.xscale('log')
plt.yscale('log')
plt.legend()
plt.grid(True)
plt.show()


图形解读
- Figure-3:
- 连续曲线平滑,离散点呈阶梯状(符合计数数据特性)。
- 双对数坐标下均为直线,但离散形式因归一化略有偏移。
- Figure-4:
- PDF 斜率 − 2.5 -2.5 −2.5,CCDF 斜率 − 1.5 -1.5 −1.5,验证积分关系。
- CCDF 在尾部更陡峭,凸显极端事件概率衰减速度。
关键对比总结
| 形式 | 正态分布 | 幂律分布 |
|---|---|---|
| 标准形式 | N ( μ , σ 2 ) \mathcal{N}(\mu, \sigma^2) N(μ,σ2) | f ( x ) = C x − α f(x) = Cx^{-\alpha} f(x)=Cx−α |
| 变换核心 | 平移( μ \mu μ)、缩放( σ \sigma σ) | 指数调整( α \alpha α)、截断( x min x_{\min} xmin) |
| 图形特性 | 钟形曲线,双侧快速衰减 | 长尾,双对数坐标下为直线 |
| 适用场景 | 独立随机过程(如身高、误差) | 复杂系统(如网络、金融) |
通过形式变换,可灵活应对不同数据特性(如多维性、离散性、有限性),同时保持分布的核心规律(正态的集中性、幂律的长尾性)。
6. 实际应用场景
正态分布(Normal Distribution)
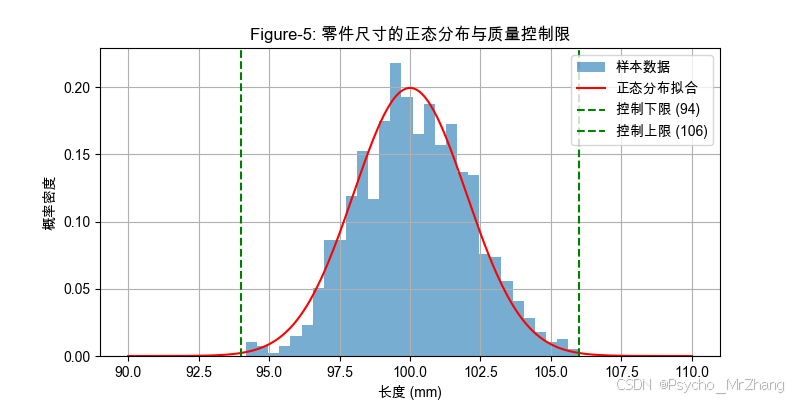
应用场景 1:工业质量控制(零件尺寸检测)
-
问题描述:工厂生产某零件,设计长度为 100mm,标准差 2mm。如何设定合格范围(如 95% 置信区间)并检测异常批次?
-
解决步骤:
- 数据采集:测量一批次零件长度。
- 假设检验:验证数据是否符合正态分布(如 Q-Q 图)。
- 计算控制限:
下限 = μ − 3 σ = 100 − 6 = 94 , 上限 = μ + 3 σ = 106 \text{下限} = \mu - 3\sigma = 100 - 6 = 94, \quad \text{上限} = \mu + 3\sigma = 106 下限=μ−3σ=100−6=94,上限=μ+3σ=106 - 异常检测:若零件长度超出 [94, 106],判定为不合格。
- 动态监控:绘制控制图(Control Chart),实时追踪生产稳定性。
-
代码实现:
import matplotlib.pyplot as plt import numpy as np from scipy.stats import norm# 模拟数据 mu, sigma = 100, 2 data = np.random.normal(mu, sigma, 1000) x = np.linspace(90, 110, 1000) y = norm.pdf(x, mu, sigma)# 绘图:直方图 + 控制限 plt.figure(figsize=(8, 4)) plt.hist(data, bins=30, density=True, alpha=0.6, label="样本数据") plt.plot(x, y, 'r-', label="正态分布拟合") plt.axvline(mu - 3*sigma, color='g', linestyle='--', label="控制下限 (94)") plt.axvline(mu + 3*sigma, color='g', linestyle='--', label="控制上限 (106)") plt.title("Figure-5: 零件尺寸的正态分布与质量控制限") plt.xlabel("长度 (mm)") plt.ylabel("概率密度") plt.legend() plt.grid(True) plt.show()
应用场景 2:金融风险评估(VaR 计算)
- 问题描述:估算某股票组合未来一天的 95% 置信水平下的最大亏损(Value at Risk, VaR)。
- 解决步骤:
- 数据准备:收集历史收益率数据。
- 参数估计:计算均值 μ \mu μ和标准差 σ \sigma σ。
- VaR 计算:
VaR 95 % = μ − z 0.95 ⋅ σ ( z 0.95 = 1.645 ) \text{VaR}_{95\%} = \mu - z_{0.95} \cdot \sigma \quad (z_{0.95} = 1.645) VaR95%=μ−z0.95⋅σ(z0.95=1.645) - 结果解读:置信水平下最大预期亏损。
- 注意事项:实际金融数据常存在“肥尾”,需结合历史模拟法或蒙特卡洛方法修正。
幂律分布(Power Law Distribution)
应用场景 1:社交媒体影响力分析
-
问题描述:识别社交平台上的关键意见领袖(KOL),并量化长尾效应。
-
解决步骤:
- 数据采集:统计用户粉丝数或转发量。
- 分布拟合:用幂律模型 P ( x ) ∝ x − α P(x) \propto x^{-\alpha} P(x)∝x−α拟合数据。
- 参数估计:通过极大似然法估算 α \alpha α。
- KOL 判定:设定阈值 x min x_{\min} xmin,筛选头部高影响力用户。
- 长尾价值:计算长尾部分(如尾部 80% 用户)的总影响力占比。
-
代码实现:
import matplotlib.pyplot as plt import numpy as np from scipy.stats import powerlaw# 模拟数据(粉丝数) alpha = 2.2 x_min = 100 data = powerlaw.rvs(alpha, scale=x_min, size=10000) data = np.sort(data)[::-1] # 按降序排列# 双对数坐标绘图 plt.figure(figsize=(8, 4)) plt.loglog(data, np.arange(1, len(data)+1)/len(data), 'b.', label="用户粉丝排名") plt.title("Figure-6: 社交媒体粉丝数的幂律分布(双对数坐标)") plt.xlabel("粉丝数 (log)") plt.ylabel("累积概率 (log)") plt.grid(True) plt.legend() plt.show()

应用场景 2:推荐系统中的长尾商品优化
- 问题描述:电商平台如何平衡热门商品(头部)与冷门商品(长尾)的推荐策略?
- 解决步骤:
- 数据建模:分析商品销量分布,验证幂律特性(如 α ≈ 1.5 \alpha \approx 1.5 α≈1.5)。
- 策略制定:
- 头部商品:采用协同过滤强化推荐。
- 长尾商品:基于内容特征或多样性算法提升曝光。
- 效果评估:通过 A/B 测试比较不同策略的 GMV(总成交额)提升。
- 关键价值:长尾商品总销量占比可能超过头部(如亚马逊图书销售),需针对性优化。
关键对比总结
| 场景 | 正态分布应用 | 幂律分布应用 |
|---|---|---|
| 核心逻辑 | 集中趋势 + 对称性 | 长尾效应 + 标度不变性 |
| 典型问题 | 质量控制、风险评估 | 社交影响力分析、推荐系统优化 |
| 参数作用 | μ \mu μ决定中心, σ \sigma σ决定阈值 | α \alpha α决定头部集中度, x min x_{\min} xmin过滤噪声 |
| 图形特征 | 钟形曲线 + 控制限 | 双对数直线 + 长尾占比计算 |
通过实际案例可见:
- 正态分布适用于独立随机过程驱动的稳定系统(如工业生产、金融风险)。
- 幂律分布揭示复杂系统中“强者恒强”与“长尾价值”的共存规律(如社交网络、电商生态)。
7. Python 代码实现
正态分布(Normal Distribution)
代码 1:生成正态分布数据并绘制概率密度曲线
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm# 参数设置
mu, sigma = 0, 1 # 均值和标准差
sample_size = 1000 # 样本量# 生成数据
data = np.random.normal(mu, sigma, sample_size)# 概率密度计算
x = np.linspace(-5, 5, 1000)
pdf = norm.pdf(x, mu, sigma)# 绘图
plt.figure(figsize=(8, 4))
plt.hist(data, bins=30, density=True, alpha=0.6, label="样本直方图")
plt.plot(x, pdf, 'r-', label="理论PDF")
plt.title("Figure-1: 正态分布概率密度曲线")
plt.xlabel("x")
plt.ylabel("概率密度")
plt.legend()
plt.grid(True)
plt.show()
作用:
- 输入:均值
mu、标准差sigma、样本量sample_size。 - 输出:生成的样本数据及理论概率密度曲线。
- 关键点:直方图显示样本分布,红色曲线为理论密度。
代码 2:参数估计与假设检验
from scipy.stats import norm, kstest# 参数估计
estimated_mu, estimated_sigma = norm.fit(data)
print(f"估计均值: {estimated_mu:.2f}, 估计标准差: {estimated_sigma:.2f}")# Kolmogorov-Smirnov 检验
ks_stat, p_value = kstest(data, 'norm', args=(mu, sigma))
print(f"K-S检验p值: {p_value:.4f}")
作用:
- 输入:样本数据
data。 - 输出:估计的均值和标准差,以及K-S检验的p值(判断是否符合正态分布)。
- 关键点:p值 > 0.05 表示无法拒绝正态分布假设。
幂律分布(Power Law Distribution)
代码 3:生成幂律分布数据并绘制双对数曲线
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import powerlaw# 参数设置
alpha = 2.5 # 幂律指数
x_min = 1 # 最小值阈值
sample_size = 1000 # 样本量# 生成数据
data = powerlaw.rvs(alpha, scale=x_min, size=sample_size)# 排序与累积概率计算
sorted_data = np.sort(data)[::-1] # 降序排列
ccdf = np.arange(1, len(sorted_data)+1) / len(sorted_data)# 双对数坐标绘图
plt.figure(figsize=(8, 4))
plt.loglog(sorted_data, ccdf, 'b.', label="CCDF")
plt.title("Figure-2: 幂律分布的双对数坐标验证")
plt.xlabel("x (log)")
plt.ylabel("P(X ≥ x) (log)")
plt.grid(True)
plt.legend()
plt.show()
作用:
- 输入:幂律指数
alpha、最小值x_min、样本量sample_size。 - 输出:生成的样本数据及其累积分布函数(CCDF)在双对数坐标下的直线。
- 关键点:直线斜率反映幂律指数
alpha。
代码 4:参数估计与拟合优度检验
from scipy.stats import powerlaw# 参数估计
params = powerlaw.fit(data, floc=0) # 固定位置参数为0
estimated_alpha, loc, scale = params
print(f"估计幂律指数: {estimated_alpha:.2f}")# 拟合优度检验(通过视觉判断直线性)
作用:
- 输入:样本数据
data。 - 输出:估计的幂律指数
alpha。 - 关键点:
powerlaw.fit返回参数(alpha, loc, scale),需固定loc=0以避免偏移。
关键对比总结
| 功能 | 正态分布代码 | 幂律分布代码 |
|---|---|---|
| 数据生成 | np.random.normal(mu, sigma, size) | powerlaw.rvs(alpha, scale=x_min, size) |
| 参数估计 | norm.fit(data) | powerlaw.fit(data, floc=0) |
| 可视化重点 | 钟形曲线与直方图对比 | 双对数坐标下的直线性验证 |
| 检验方法 | K-S检验(正态性) | 直观判断直线性(幂律性) |
通过代码可直接验证理论分布特性,并应用于实际数据分析(如金融风险评估、社交网络分析)。
8. 总结与拓展
核心知识点总结
正态分布(Normal Distribution)
- 核心特征:
- 对称钟形曲线,由均值 μ \mu μ和标准差 σ \sigma σ完全定义。
- 中心极限定理支撑其在独立随机变量中的普适性。
- 关键性质:
- μ ± σ \mu \pm \sigma μ±σ覆盖约68%数据, μ ± 3 σ \mu \pm 3\sigma μ±3σ外为稀有事件。- 适用于稳定系统(如工业质量控制、金融风险评估)。
幂律分布(Power Law Distribution)
- 核心特征:
- 长尾特性,无特征尺度(标度不变性),由指数 α \alpha α决定尾部厚度。
- 极端值主导现象(如“二八法则”、社交网络影响力)。
- 关键性质:
- 双对数坐标下为直线,斜率 − α -\alpha −α。
- 方差可能无限(当 α ≤ 3 \alpha \leq 3 α≤3时)。
- 适用于复杂系统(如推荐系统、城市人口建模)。
关键对比
| 特性 | 正态分布 | 幂律分布 |
|---|---|---|
| 数据形态 | 集中对称,尾部快速衰减 | 长尾,极端值显著 |
| 参数作用 | μ \mu μ定中心, σ \sigma σ定胖瘦 | α \alpha α定尾部厚度, x min x_{\min} xmin过滤噪声 |
| 适用场景 | 独立随机过程(如身高、误差) | 复杂系统(如网络、金融) |
进一步学习方向
-
广义分布与混合模型
- 正态分布延伸:
- 多元正态分布(协方差矩阵分析)、t分布(小样本统计)、混合高斯模型(聚类分析)。
- 幂律分布延伸:
- 稳定分布(α-Stable Distribution,含正态分布为特例)、分形理论(自相似性)。
- 正态分布延伸:
-
复杂系统建模
- 网络科学:无标度网络(Barabási-Albert 模型)的幂律度分布。
- 金融工程:极值理论(EVT)量化尾部风险,替代正态假设下的风险价值(VaR)。
- 机器学习:
- 数据预处理:正态化(Box-Cox变换) vs 长尾修正(对数变换)。
- 异常检测:基于正态分布的3σ准则 vs 基于幂律的尾部阈值筛选。
-
深度学习与分布假设
- 正态分布的应用:
- 变分自编码器(VAE)的隐空间正态化约束。
- 批归一化(BatchNorm)依赖数据近似正态分布。
- 幂律分布的挑战:
- 长尾标签问题(如推荐系统的冷启动)。
- 图神经网络(GNN)中节点度分布的幂律特性处理。
- 正态分布的应用:
开放性思考问题
-
正态分布的局限性
- 若数据真实分布严重偏离正态(如存在多峰性或强偏态),传统基于均值和方差的方法会失效吗?如何改进?
-
幂律分布的生成机制
- “富者愈富”是幂律分布的唯一成因吗?是否存在其他动态过程(如优先连接、自组织临界)导致长尾现象?
-
现实世界的混合分布
- 许多数据可能同时包含正态和幂律特性(如用户活跃度:中间集中,头部超活跃)。如何设计混合模型更精准建模?
-
分布假设对算法的影响
- 在强化学习中,策略梯度方法假设动作空间服从正态分布,这对探索长尾策略空间有何限制?
通过系统掌握正态分布与幂律分布的数学本质、应用场景及代码实现,可为后续深入研究概率建模、复杂系统分析及高级机器学习算法奠定坚实基础。
9. 练习与反馈
练习题
基础题(概念与计算)
-
正态分布参数意义
- 设某公司员工年薪服从正态分布 N ( 60 , 1 0 2 ) \mathcal{N}(60, 10^2) N(60,102)(单位:万元)。
- (a)计算年薪在 50-70 万元之间的概率。
- (b)若标准差变为 5,概率如何变化?
- 设某公司员工年薪服从正态分布 N ( 60 , 1 0 2 ) \mathcal{N}(60, 10^2) N(60,102)(单位:万元)。
-
幂律分布的标度不变性
- 已知某网站访问量服从幂律分布 f ( x ) = C x − α f(x) = Cx^{-\alpha} f(x)=Cx−α,其中 α = 2 \alpha=2 α=2。
- (a)若将 x x x扩大 10 倍,概率密度 f ( x ) f(x) f(x)如何变化?
- (b)在双对数坐标下,曲线斜率是多少?
- 已知某网站访问量服从幂律分布 f ( x ) = C x − α f(x) = Cx^{-\alpha} f(x)=Cx−α,其中 α = 2 \alpha=2 α=2。
-
图形识别
- 给出以下两组数据(图略),判断哪组符合正态分布,哪组符合幂律分布,并说明理由。
- 数据A:直方图呈钟形,尾部快速衰减。
- 数据B:双对数坐标下近似直线,右侧长尾显著。
- 给出以下两组数据(图略),判断哪组符合正态分布,哪组符合幂律分布,并说明理由。
提高题(应用与推导)
-
参数估计与假设检验
- 使用 Python 对以下数据进行正态分布拟合:
import numpy as np data = np.random.normal(loc=5, scale=2, size=1000)- (a)估计均值和标准差。
- (b)通过 K-S 检验判断是否符合正态分布(显著性水平 α=0.05)。
- 使用 Python 对以下数据进行正态分布拟合:
-
幂律分布的长尾效应
- 某电商平台商品销量数据如下(数据已排序):
sales = [1000, 800, 600, 500, 400, 300, 200, 100, 50, 10]- (a)绘制双对数坐标图,判断是否符合幂律分布。
- (b)估算幂律指数 α \alpha α(提示:对数据进行线性回归)。
- 某电商平台商品销量数据如下(数据已排序):
-
代码实现与验证
- 编写 Python 代码,生成 1000 个幂律分布样本( α = 2.5 , x min = 1 \alpha=2.5, x_{\min}=1 α=2.5,xmin=1),并验证其 CCDF 在双对数坐标下的直线性。
挑战题(综合与创新)
-
混合分布建模
- 现实数据中可能同时包含正态分布和幂律分布成分(如用户活跃度:中间集中,头部超活跃)。
- (a)设计一个混合模型:正态分布(占 80%)与幂律分布(占 20%)。
- (b)生成合成数据并可视化其直方图。
- (c)尝试用拟合方法分离两种成分。
- 现实数据中可能同时包含正态分布和幂律分布成分(如用户活跃度:中间集中,头部超活跃)。
-
金融风险评估的局限性
- 金融资产收益率常被假设为正态分布,但实际数据存在“肥尾”现象。
- (a)用幂律分布替代正态分布,重新计算 VaR(95% 置信水平)。
- (b)比较两种方法在极端风险预测上的差异。
- 金融资产收益率常被假设为正态分布,但实际数据存在“肥尾”现象。
-
社交网络影响力优化
- 某社交平台用户粉丝数服从幂律分布( α = 2.0 \alpha=2.0 α=2.0)。
- (a)若要求前 1% 用户贡献 50% 的总粉丝量,是否符合当前分布?
- (b)提出一种策略调整 α \alpha α,使得长尾用户(后 90%)的总粉丝量占比提升至 30%。
- 某社交平台用户粉丝数服从幂律分布( α = 2.0 \alpha=2.0 α=2.0)。
答案与提示
基础题
-
正态分布参数意义
- (a)概率 ≈ 68%( μ ± σ \mu \pm \sigma μ±σ覆盖范围)。
- (b)概率增加至约 95%( μ ± 2 σ \mu \pm 2\sigma μ±2σ)。
-
幂律分布的标度不变性
- (a) f ( 10 x ) = C ( 10 x ) − 2 = C x − 2 / 100 f(10x) = C(10x)^{-2} = Cx^{-2}/100 f(10x)=C(10x)−2=Cx−2/100,即概率密度降至原来的 1/100。
- (b)斜率为 − α = − 2 -\alpha = -2 −α=−2。
-
图形识别
- 数据A:正态分布(钟形曲线)。
- 数据B:幂律分布(双对数直线 + 长尾)。
提高题
-
参数估计与假设检验
- (a)估计均值 ≈ 5,标准差 ≈ 2。
- (b)K-S 检验 p 值 > 0.05,接受正态分布假设。
- 代码参考:
from scipy.stats import norm, kstest mu_est, sigma_est = norm.fit(data) ks_stat, p_value = kstest(data, 'norm', args=(mu_est, sigma_est))
-
幂律分布的长尾效应
- (a)双对数图近似直线,符合幂律分布。
- (b)对 log f ( x ) = − α log x + 常数 \log f(x) = -\alpha \log x + \text{常数} logf(x)=−αlogx+常数做线性回归,斜率即 α \alpha α。
-
代码实现与验证
- 代码参考:
from scipy.stats import powerlaw import matplotlib.pyplot as plt data = powerlaw.rvs(2.5, scale=1, size=1000) sorted_data = np.sort(data)[::-1] ccdf = np.arange(1, len(sorted_data)+1)/len(sorted_data) plt.loglog(sorted_data, ccdf, 'b.') plt.show()
- 代码参考:
挑战题
-
混合分布建模
- 提示:
- (a)使用
np.random.normal和powerlaw.rvs生成混合数据。 - (b)直方图呈现中间峰 + 右侧长尾。
- (c)尝试用最大似然法拟合混合参数。
- (a)使用
- 提示:
-
金融风险评估的局限性
- 提示:
- (a)幂律 VaR 计算需积分求分位点: P ( X ≥ x ) = 0.05 P(X \geq x) = 0.05 P(X≥x)=0.05。
- (b)幂律 VaR 远大于正态分布结果(极端风险更高)。
- 提示:
-
社交网络影响力优化
- 提示:
- (a)当前头部 1% 用户贡献 ∝ ∫ x 99 % ∞ x ⋅ x − 2 d x ∝ 1 / x 99 % \propto \int_{x_{99\%}}^\infty x \cdot x^{-2} dx \propto 1/x_{99\%} ∝∫x99%∞x⋅x−2dx∝1/x99%,需计算具体比例。
- (b)增大 α \alpha α(如 α = 2.5 \alpha=2.5 α=2.5)可减少头部集中度。
- 提示:
反馈与答疑
- 常见疑问解答:
- Q1:如何判断数据是正态分布还是幂律分布?
A:正态分布直方图对称且尾部快速衰减;幂律分布双对数坐标下为直线。 - Q2:为何幂律分布的方差可能无限?
A:当 α ≤ 3 \alpha \leq 3 α≤3时,积分 ∫ x 2 f ( x ) d x \int x^2 f(x) dx ∫x2f(x)dx发散,导致方差不存在。 - Q3:如何处理数据中的混合分布?
A:可使用高斯混合模型(GMM)或贝叶斯方法分离成分,或通过分段拟合。
- Q1:如何判断数据是正态分布还是幂律分布?
相关文章:

正态分布和幂律分布
1. 背景与引入 正态分布 历史来源:18世纪由高斯(Gauss)在研究测量误差时提出,后被广泛应用于自然现象和社会科学的数据建模。重要性:被称为“钟形曲线”,是统计学中最核心的分布之一,支撑中心极…...

网络安全赛题解析
扫描之后发现目标靶机 上开启了 ftp ssh http mysql等服务 第一题 第一题需要获取文件 首先尝试 ftp 匿名用户 从这里可以发现 hint.txt 文件的大小为 127b 或 127bytes 提交127b 第二题 通过hint.txt 文件可以发现目标主机 上有用户 Jay 密码为五位字符串 其中三位不知道 利…...

Android单例模式知识总结
六种核心实现方式对比 1. 饿汉式单例(Eager Initialization) 原理:利用类加载时静态变量初始化的特性,天然线程安全。 代码: public class EagerSingleton {private static final EagerSingleton INSTANCE new Eag…...

何不乘东风?利用mcp实现小红书自动发布
1.准备环境 conda create -n mcpo python3.11 conda activate mcpo pip install mcpo pip install uvnpx puppeteer/browsers install chromedriver134.0.6998.166pip install xhs-mcp-server 2.进行登陆 env phoneYOUR_PHONE_NUMBER json_pathPATH_TO_STORE_YOUR_COOKIES u…...

DeepSeek多尺度数据:无监督与原则性诊断方案全解析
DeepSeek 多尺度数据诊断方案的重要性 在当今的 IT 领域,数据如同石油,是驱动各类智能应用发展的核心资源。随着技术的飞速发展,数据的规模和复杂性呈爆炸式增长,多尺度数据处理成为了众多领域面临的关键挑战。以计算机视觉为例,在目标检测任务中,小目标可能只有几个像素…...

【开源】Python打造高效剪贴板历史管理器:实现跨平台生产力工具
📋【开源】Python打造高效剪贴板历史管理器:实现跨平台生产力工具 🌈 个人主页:创客白泽 - CSDN博客 🔥 系列专栏:🐍《Python开源项目实战》 💡 热爱不止于代码,热情源自…...

Day 14 训练
Day 14 训练 SHAP(SHapley Additive exPlanations)1.创建解释器2.将特征贡献可视化第一部分:绘制SHAP特征重要性条形图第二部分:绘制SHAP特征重要性蜂巢图 SHAP(SHapley Additive exPlanations) 旨在解释复…...

V型球阀材质性能深度解析:专攻颗粒、料浆与高腐蚀介质的工业利器-耀圣
V型球阀材质性能深度解析:专攻颗粒、料浆与高腐蚀介质的工业利器 在工业流体控制领域,V型球阀凭借其独特的V型切口设计与多元化材质适配能力,成为含颗粒、纤维、料浆及强腐蚀性介质的“终极克星”。本文从材质性能与驱动适配性两大维度切入&…...

缓存套餐-01.Spring Cache入门案例
一.导入案例代码 application.yml server:port: 8888 spring:datasource:druid:driver-class-name: com.mysql.cj.jdbc.Driverurl: jdbc:mysql://localhost:3306/spring_cache_demo?serverTimezoneAsia/Shanghai&useUnicodetrue&characterEncodingutf-8&zeroDat…...

2025年APP安全攻防指南:抵御DDoS与CC攻击的实战策略
2025年,随着AI技术与物联网设备的深度渗透,DDoS与CC攻击的复杂性和破坏性显著升级。攻击者通过伪造用户行为、劫持智能设备、利用协议漏洞等手段,对APP发起精准打击,导致服务瘫痪、用户流失甚至数据泄露。面对这一挑战,…...

力扣:多数元素
题目 给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。 你可以假设数组是非空的,并且给定的数组总是存在多数元素。 示例 示例 1: 输入:nums [3,2,3] 输出ÿ…...

2025年小程序DDoS与CC攻击防御全指南:构建智能安全生态
2025年,小程序已成为企业数字化转型的核心载体,但随之而来的DDoS与CC攻击也愈发复杂化、智能化。攻击者利用AI伪造用户行为、劫持物联网设备发起T级流量冲击,甚至通过漏洞窃取敏感数据。如何在高并发业务场景下保障小程序的稳定与安全&#x…...
)
【Python】PDF文件处理(PyPDF2、borb、fitz)
Python提供了多种方法和库用于处理PDF文件,这些工具可以帮助开发者实现诸如读取、写入、合并、拆分以及压缩等功能。以下是几个常用的Python PDF操作库及其基本用法(PyPDF2、borb、fitz)。 1. PyPDF2 PyPDF2 是一个功能强大的库࿰…...

Web 架构之前后端分离
文章目录 思维导图一、引言二、前后端分离的概念代码示例(简单的前后端分离交互)后端(使用 Python Flask 框架)前端(使用 JavaScript 和 jQuery) 三、前后端分离的优势3.1 提高开发效率3.2 代码可维护性增强…...

Pycharm安装后打开提示:此应用无法在你的电脑上运行,若要找到合适于你的电脑的版本,请咨询发布者
问题描述 今天下载安装好社区版的pycharm之后双击运行出现提示:此应用无法在你的电脑上运行,若要找到合适于你的电脑的版本,请咨询发布者。 首先我们需要查看Windows如何查看系统是ARM64还是X64架构 在 cmd 命令窗中输入 systeminfo 即可&a…...

正则表达式实战指南:原理、口诀与高频场景案例
正则表达式实战指南:原理、口诀与高频场景案例 正则表达式(Regular Expression)是程序员处理文本的瑞士军刀,被广泛应用于数据验证、日志分析、爬虫开发等领域。本文将从原理讲解、口诀速查到高频实战案例,带你系统掌…...

Spark缓存--persist方法
1. 功能本质 persist:这是一个通用的持久化方法,能够指定多种不同的存储级别。存储级别决定了数据的存储位置(如内存、磁盘)以及存储形式(如是否序列化)。 2. 存储级别指定 persist:可以通过传入…...

【LeetCode 热题 100】二叉树 系列
📁 104. 二叉树的最大深度 深度就是树的高度,即只要左右子树其中有一个不为空,就继续往下递归,知道节点为空,向上返回。 int maxDepth(TreeNode* root) {if(root nullptr)return 0;return max(maxDepth(root->lef…...

CTF之常见的文件头和文件尾
1、图片 JPEG 文件头:FF D8 FF 文件尾:FF D9TGA 未压缩的前4字节 00 00 02 00 RLE压缩的前5字节 00 00 10 00 00PNG 文件头:89 50 4E 47 0D 0A 1A 0A 文件尾:AE 42 60 82GIF 文件头:47 49 46 38 39(37) 61 文件尾&…...
)
软件设计师教程——第一章 计算机系统知识(上)
前言 在竞争激烈的就业市场中,证书是大学生求职的重要加分项。中级软件设计师证书专业性强、认可度高,是计算机相关专业学生考证的热门选择,既能检验专业知识,又有助于职业发展。本教程将聚焦核心重点,以点带面构建知…...
 集群配置指南(超简单,脱离 ZooKeeper 集群)还包含了简化测试指令的脚本!!!)
KRaft (Kafka 4.0) 集群配置指南(超简单,脱离 ZooKeeper 集群)还包含了简化测试指令的脚本!!!
docker-compose方式部署kafka集群 Kafka 4.0 引入了 KRaft 模式(Kafka Raft Metadata Mode),它使 Kafka 集群不再依赖 ZooKeeper 进行元数据管理。KRaft 模式简化了 Kafka 部署和管理,不需要额外配置 ZooKeeper 服务,…...

安全月演讲比赛活动讲话稿
同志们:在公司上下万众一心创建“无违章企业”的大形势下,由公司工会、团委举办的“安全与我”演讲比赛,经过紧张激烈的预赛,今天进行正式决赛。 从预赛的38名选手中脱颖而出的10名选手,今天将再次登台献技,…...

实时操作系统:航空电子系统的安全基石还是创新枷锁?
引言:航空电子系统的进化论 在航空电子技术的漫长发展历程中,飞行器控制系统实现从机械仪表到数字计算机的跨越,这一进步具有深远意义。现代战机以超过 2 马赫的速度突破音障,无人机群在复杂电磁环境下完成自主编队,这…...

windows 部署 Kafka3.x KRaft 模式 不依赖 ZooKeeper
1.下载 https://archive.apache.org/dist/kafka/3.9.0/kafka_2.12-3.9.0.tgz2.配置使用 KRaft 模式 2.1 修改 Kafka 的配置文件 cd D:\data\bigdata\kafka_2.12-3.9.0\config\kraft 修改 server.properties # 设置 Kafka 数据日志存储目录 log.dirsD:\\data\\bigdata\\kaf…...
-(一))
SEMI E40-0200 STANDARD FOR PROCESSING MANAGEMENT(加工管理标准)-(一)
1 目的 物料(例如晶圆)加工在设备中的自动化管理与控制是实现工厂自动化的关键要素。本标准针对半导体制造环境中与设备内部物料处理相关的通信需求进行了规范。本标准规定了在加工单元接收到的指定材料所应适用的加工方法(例如Etch腔室需要Run哪支Recipe)。它阐述了物料加工的…...

Web 架构之高可用基础
文章目录 引言一、无状态服务设计(Session 托管至 Redis 集群)1. 概念与原理2. 代码示例(Python Flask 应用)3. 常见问题及解决办法 二、数据库读写分离(MySQL 主从 ProxySQL 流量分发)1. 概念与原理2. 配…...
)
巧用python之--模仿PLC(PLC模拟器)
工作中用到了VM(VisionMaster4.3)有时候需要和PLC打交道,但是PLC毕竟是别人的,不方便修改别人的程序,这时候需要一个灵活的PLC模拟器是多么好呀! 先说背景: PLC型号 汇川Easy521: Modbus TCP 192.168.1.10:502 在汇川Easy521中Modbus保持寄存器D寄存器 ,在modbus协议中 0-4区…...

Nginx +Nginx-http-flv-module 推流拉流
这两天为了利用云服务器实现 Nginx 进行OBS Rtmp推流,Flv拉流时发生了诸多情况,记录实现过程。 环境 OS:阿里云CentOS 7.9 64位Nginx:nginx-1.28.0Nginx-http-flv-module:nginx-http-flv-module-1.2.12 安装Nginx编…...

DRF+Vue项目线上部署:腾讯云+Centos7.6
1.服务器选购和配置 1.1.服务器选购 1.2.防火墙/安全组配置 80是HTTP的端口,443是HTTPS的端口,22是远程连接的端口,3306是mysql的端口。 1.3.远程连接软件(tabby)配置 下载:https://github.com/Eugeny/ta…...
拉流至电脑,实现直播)
大疆无人机(全系列,包括mini)拉流至电脑,实现直播
参考视频 【保姆级教程】大疆无人机rtmp推流直播教程_哔哩哔哩_bilibili VLC使用教程: VLC工具使用指南-CSDN博客 目录 实现效果: 电脑端 编辑 编辑 无人机端 VLC拉流 分析 实现效果: (实验机型:大疆mini4kRC-N2遥控器、大…...

Spring普通配置类 vs 自动配置类-笔记
1.简要版 Configuration和Bean,既可以用于普通配置类,也可以用于自动配置类。二者的区别和联系是什么呢? 区别: Configuration和Bean是Spring框架本身的注解,用于定义配置类和生成Bean。而自动配置通常是Spring Boo…...

解决Ceph 14.2.22 Nautilus版本监视器慢操作问题的实践指南
解决Ceph Nautilus版本监视器慢操作问题的实践指南 问题背景问题现象问题分析1. 确认监视器状态2. 检查慢操作详情3. 深入分析操作状态 问题原因解决方案立即解决方法 总结 在生产环境中执行任何操作前,请确保已备份重要数据,并在测试环境中验证解决方案…...

Go使用Gin写一个对MySQL的增删改查服务
首先用SQL创建一个包含id、name属性的users表 create table users (id int auto_incrementprimary key,name varchar(255) null );查询所有用户信息: func queryData(db *sql.DB, w http.ResponseWriter) {rows, err : db.Query("SELECT * FROM users"…...

数字孪生医疗:构建患者特异性数字孪生体路径探析
引言 数字孪生技术正逐渐成为医疗健康领域的一场革命性力量,它通过创建人体器官和系统的数字复制品,为疾病预测、诊断和个性化治疗开辟了前所未有的可能性。在心血管疾病领域,数字孪生技术的应用尤为引人注目,特别是对于扩张型心肌病(Dilated Cardiomyopathy,DCM)这一常…...

rust程序静态编译的两种方法总结
1. 概述 经过我的探索,总结了两种rust程序静态编译的方法,理论上两种方法都适用于windows、mac os和linux(mac os未验证),实测方法一性能比方法二好,现总结如下,希望能够帮到你. 2.方法一 2.1 添加配置文件 在项目的同级文件夹下新…...

threejs 添加css3d标签 vue3
如图所示,给收费站标注标签。步骤如下: 一、引入 import {CSS3DRenderer,CSS3DObject, } from "three/examples/jsm/renderers/CSS3DRenderer"; 二、 //一、申明css3渲染器 const label3DRenderer ref()//二、创建css3d渲染器--将渲染器加…...

【git】git fsmonitor
git fsmonitor 是 Git 提供的一个特性,用于提高 Git 的性能,尤其是在处理文件状态检查(git status)时。它通过文件系统监控服务(如 Windows 上的 FileSystemWatcher 或 Linux 上的 inotify)来跟踪文件系统的…...

开源照片管理系统PhotoPrism的容器化部署与远程管理配置
文章目录 前言1.关于PhotoPrism2.本地部署PhotoPrism3.PhotoPrism简单使用4. 安装内网穿透5.配置PhotoPrism公网地址6. 配置固定公网地址 前言 你是不是用手机拍照片的时候无所谓拍了多少张,但在整理的时候却要占用超多时间?别怕,今天给大家…...

macOS Python 环境配置指南
1. 检查现有 Python 环境 python3 --version # 检查 Python 3 版本 pip3 --version # 检查 pip 版本 2. 安装 pyenv(Python 版本管理工具) # 使用 Homebrew 安装 pyenvbrew install pyenv# 配置 pyenv 环境变量(添加到 ~/.zshrc&#…...

如何阅读、学习 Git 核心源代码 ?
学习 Git 核心源代码是一个深入理解版本控制系统底层原理的绝佳方式。以下是分阶段的系统性建议,结合了实践经验和学习路径设计: 一、前置知识储备 C语言进阶 重点掌握指针操作(尤其是二级指针和函数指针)结构体嵌套与内存对齐…...

学习黑客 MAC 地址深入了解
在江湖之中,每位少侠既有“门派”加身,也需持有“令牌”通行。MAC地址便是我被师门铁订在骨血里的“先天武功心法”,铸于出厂之时,终身不变,只有破阵高手才能暗度陈仓才能改写;而IP地址则是我行走江湖的“后…...

长事务:数据库中的“隐形炸弹“——金仓数据库运维避坑指南
引言:凌晨三点的告警 "张工!生产库又告警了!"凌晨三点的电话铃声总是格外刺耳。运维团队发现数据库频繁进入单用户模式,排查发现某核心表的年龄值(Age)已突破20亿大关。经过一夜奋战,…...

WTK6900C-48L:离线语音芯片重构玩具DNA,从“按键操控”到“声控陪伴”的交互跃迁
一:开发背景 随着消费升级和AI技术进步,传统玩具的机械式互动已难以满足市场需求。语音控制芯片的引入使玩具实现了从被动玩耍到智能交互的跨越式发展。通过集成高性价比的语音识别芯片,现代智能玩具不仅能精准响应儿童指令,还能实…...
)
一文读懂Python之requests模块(36)
一、requests模块简介 requests模块是python中原生的一款基于网络请求的模块,功能强大,简单便捷且高效 ,该模块可以模拟浏览器发送请求,主要包括指定url、发起请求、获取响应数据和持久化存储,包括 GET、POST、PUT、…...

Java 异常
Java 异常的体系结构 java.lang.Throwable ├── Error(严重错误,程序无法处理) │ ├── OutOfMemoryError │ ├── StackOverflowError │ └── ... └── Exception(程序可以处理的异常)├── Check…...

智能外呼机器人的核心优势
随着人工智能技术的快速发展,智能外呼机器人已成为企业降本增效的重要工具。其通过整合语音识别(ASR)、自然语言处理(NLP)、语音合成(TTS)等技术,不仅替代了大量重复性人工劳动&…...

n8n - 开放灵活的智能自动化工作流平台
n8n - 开放灵活的智能自动化工作流平台 在当今数字化转型的大潮中,自动化已成为众多企业提升效率、优化流程的关键手段。而在众多自动化工具中,n8n以其开放灵活且强大的功能脱颖而出,成为技术团队的可靠选择。今天,我们将深入了解n8n这个开源自动化工作流平台,探索其广泛…...
)
window 显示驱动开发-处理内存段(二)
KMD 不需要在其内存段中指定 GPU 可用的所有视频内存资源。 但是,KMD 必须指定 VidMm 在系统上运行的所有进程中管理的所有内存资源。 例如: 实现固定函数管道的顶点着色器微代码可以驻留在 GPU 地址空间中,但在 VidMm 管理的内存之外&#x…...

RSS 2025|斯坦福提出「统一视频行动模型UVA」:实现机器人高精度动作推理
导读 在机器人领域,让机器人像人类一样理解视觉信息并做出精准行动,一直是科研人员努力的方向。今天,我们要探讨的统一视频行动模型(Unified Video Action Model,UVA),就像给机器人装上了一个“…...

代码随想录算法训练营第60期第三十天打卡
大家好,今天我们要走进一个全新的章节,这一章叫做贪心算法,前面我们讲的是回溯算法,那究竟什么是贪心算法呢?我们一起走进今天的内容。 第一部分贪心的理论基础 其实大家看这个名字估计也会有一定了解,贪心…...
