二叉树的遍历与构造

唉，好想回家，我想回家跟馒头酱玩，想老爸老妈。如果上天再给我一次选择的机会，我会选择当一只小动物，或者当棵大树也好，或者我希望自己不要有那么多多余的情绪，不要太被别人影响，开心点，想睡就睡，想玩就玩，不要为难自己。老爸每次都和我说累了就回家，但越是这样我就越希望自己变得更强大一点。希望明天是个好天气。

目录

一、遍历

1 前序遍历

（1）递归

（2）非递归（先右后左哈）

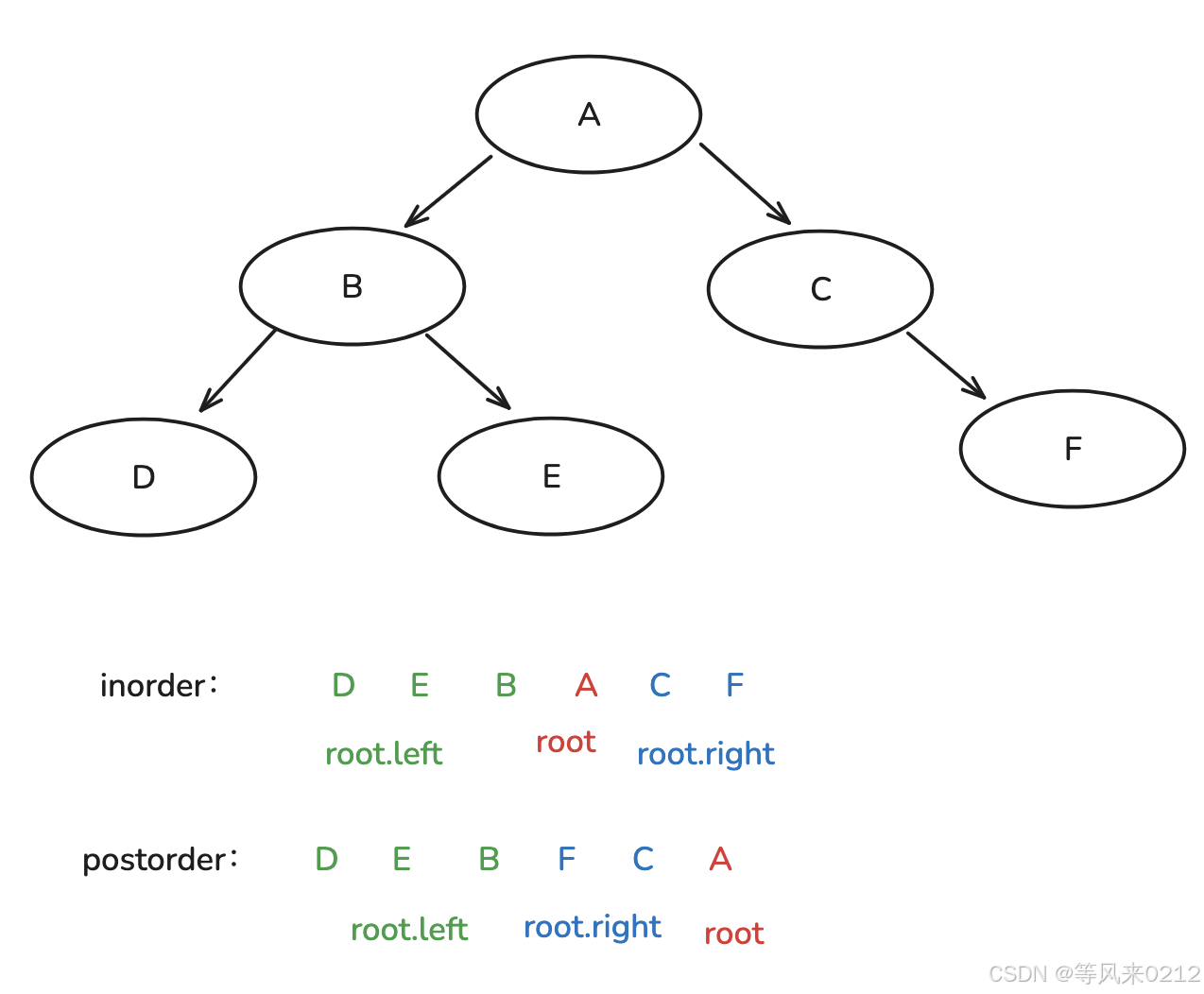
2 中序遍历

（1）递归

（2）非递归

3 后序遍历

（1）递归

（2）非递归（中右左，反转列表后变成左右中）

4 层序遍历

（1）bfs（借助队列）

（2）dfs

二、构造

1 构建最大二叉树

2 由 前 中 构造

3 由 前 后 构造

4 由 中 后 构造

---

一、遍历

1 前序遍历

（1）递归

   private static void preorderHelper(TreeNode node, List<Integer> result) {if (node == null) return;result.add(node.val);preorderHelper(node.left, result);preorderHelper(node.right, result);}

（2）非递归（先右后左哈）

// 前序遍历 - 非递归public static List<Integer> preorderTraversalIterative(TreeNode root) {List<Integer> result = new ArrayList<>();if (root == null) return result;Stack<TreeNode> stack = new Stack<>();stack.push(root);while (!stack.isEmpty()) {TreeNode node = stack.pop();result.add(node.val);if (node.right != null) stack.push(node.right);if (node.left != null) stack.push(node.left);}return result;}

2 中序遍历

（1）递归

 private static void inorderHelper(TreeNode node, List<Integer> result) {if (node == null) return;inorderHelper(node.left, result);result.add(node.val);inorderHelper(node.right, result);}

（2）非递归

核心思路是先将当前节点及其所有左子节点依次入栈，直到左子节点为空，接着从栈中弹出节点进行访问，然后将当前节点更新为弹出节点的右子节点，继续重复上述操作。

// 中序遍历 - 非递归public static List<Integer> inorderTraversalIterative(TreeNode root) {List<Integer> result = new ArrayList<>();Stack<TreeNode> stack = new Stack<>();TreeNode current = root;while (current != null || !stack.isEmpty()) {while (current != null) {stack.push(current);current = current.left;}current = stack.pop();result.add(current.val);current = current.right;}return result;}

3 后序遍历

（1）递归

private static void postorderHelper(TreeNode node, List<Integer> result) {if (node == null) return;postorderHelper(node.left, result);postorderHelper(node.right, result);result.add(node.val);}

（2）非递归（中右左，反转列表后变成左右中）

 // 后序遍历 - 非递归public static List<Integer> postorderTraversalIterative(TreeNode root) {List<Integer> result = new ArrayList<>();if (root == null) return result;Stack<TreeNode> stack = new Stack<>();stack.push(root);while (!stack.isEmpty()) {TreeNode node = stack.pop();result.add(node.val);if (node.left != null) stack.add(node.left);if (node.right != null) stack.add(node.right);}Collections.reverse(result);return result;}

4 层序遍历

（1）bfs（借助队列）

 // 层序遍历 - BFS（借助队列）public static List<List<Integer>> levelOrderTraversalBFS(TreeNode root) {List<List<Integer>> result = new ArrayList<>();if (root == null) return result;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {int levelSize = queue.size();List<Integer> level = new ArrayList<>();for (int i = 0; i < levelSize; i++) {TreeNode node = queue.poll();level.add(node.val);if (node.left != null) queue.offer(node.left);if (node.right != null) queue.offer(node.right);}result.add(level);}return result;}

（2）dfs

 // 层序遍历 - DFSpublic static List<List<Integer>> levelOrderTraversalDFS(TreeNode root) {List<List<Integer>> result = new ArrayList<>();dfs(root, 0, result);return result;}private static void dfs(TreeNode node, int level, List<List<Integer>> result) {if (node == null) return;if (level >= result.size()) {result.add(new ArrayList<>());}result.get(level).add(node.val);dfs(node.left, level + 1, result);dfs(node.right, level + 1, result);}

二、构造

1 构建最大二叉树

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。
递归地在最大值 左边 的 子数组前缀上 构建左子树。
递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树

输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：

[3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
[3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
空数组，无子节点。
[2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
空数组，无子节点。
只有一个元素，所以子节点是一个值为 1 的节点。
[0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
只有一个元素，所以子节点是一个值为 0 的节点。
空数组，无子节点。

解法&思路

首先要解决的是找到每次递归传入数组的最大值做为根节点
该最大值下标左边的元素递归构造为左子树，右边的元素递归构造为右子树

// 定义二叉树节点类
class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val = val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}
}class Solution {public TreeNode constructMaximumBinaryTree(int[] nums) {return build(nums, 0, nums.length);}private TreeNode build(int[] nums, int start, int end) {// 如果数组为空，返回 nullif (start == end) {return null;}// 找到最大值和最大值的索引int maxIndex = start;for (int i = start + 1; i < end; i++) {if (nums[i] > nums[maxIndex]) {maxIndex = i;}}// 用最大值创建根节点TreeNode rootNode = new TreeNode(nums[maxIndex]);// 最大值左侧为左子树rootNode.left = build(nums, start, maxIndex);// 最大值右侧为右子树rootNode.right = build(nums, maxIndex + 1, end);return rootNode;}
}

2 由 前 中 构造

// 定义二叉树节点类
class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val = val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}
}class Solution {public TreeNode buildTree(int[] preorder, int[] inorder) {return build(preorder, inorder, 0, 0, inorder.length - 1);}private TreeNode build(int[] preorder, int[] inorder, int preStart, int inStart, int inEnd) {// 如果中序遍历的起始下标大于结束下标，说明当前子树为空if (inStart > inEnd) {return null;}// 从前序遍历中找到根节点int rootVal = preorder[preStart];TreeNode rootNode = new TreeNode(rootVal);// 在中序遍历中找到根节点的位置int rootIndex = -1;for (int i = inStart; i <= inEnd; i++) {if (inorder[i] == rootVal) {rootIndex = i;break;}}// 计算左子树的大小int leftSize = rootIndex - inStart;// 递归构造左子树// 左子树的前序遍历范围：preStart + 1 到 preStart + leftSize// 左子树的中序遍历范围：inStart 到 rootIndex - 1rootNode.left = build(preorder, inorder, preStart + 1, inStart, rootIndex - 1);// 递归构造右子树// 右子树的前序遍历范围：preStart + leftSize + 1 到 preStart + leftSize + 右子树大小// 右子树的中序遍历范围：rootIndex + 1 到 inEndrootNode.right = build(preorder, inorder, preStart + leftSize + 1, rootIndex + 1, inEnd);return rootNode;}
}

至于为什么只需要中序遍历的终点，而不需要前序遍历的终点？因为在我们的思路中其实可以发现只需要前序遍历的起点确认根节点的值，并不需要终点值。我们可以随便选择一个遍历的终点值用来确认边界值，即这部分代码。

if(inStart > inEnd){return null
}

3 由 前 后 构造

// 定义二叉树节点类
class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val = val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}
}class Solution {public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {return build(preorder, 0, preorder.length - 1, postorder, 0, postorder.length - 1);}private TreeNode build(int[] preorder, int preStart, int preEnd, int[] postorder, int postStart, int postEnd) {// 如果前序遍历的起始下标大于结束下标，说明当前子树为空if (preStart > preEnd) {return null;}// 当前子树只有一个节点时，直接返回该节点if (preStart == preEnd) {return new TreeNode(preorder[preStart]);}// 找到根节点int rootVal = preorder[preStart];TreeNode root = new TreeNode(rootVal);// 找到左子树起点在后序遍历中的位置int leftStartIndex = -1;for (int i = postStart; i <= postEnd; i++) {if (postorder[i] == preorder[preStart + 1]) {leftStartIndex = i;break;}}// 计算左子树的长度int size = leftStartIndex - postStart + 1;// 递归构造左子树// 左子树的前序范围：preStart + 1 到 preStart + size// 左子树的后序范围：postStart 到 leftStartIndexroot.left = build(preorder, preStart + 1, preStart + size, postorder, postStart, leftStartIndex);// 递归构造右子树// 右子树的前序范围：preStart + size + 1 到 preEnd// 右子树的后序范围：leftStartIndex + 1 到 postEnd - 1root.right = build(preorder, preStart + size + 1, preEnd, postorder, leftStartIndex + 1, postEnd - 1);return root;}
}

4 由 中 后 构造

// 定义二叉树节点类
class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val = val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}
}class Solution {public TreeNode buildTree(int[] inorder, int[] postorder) {return build(inorder, 0, inorder.length - 1, postorder, 0, postorder.length - 1);}private TreeNode build(int[] inorder, int inStart, int inEnd, int[] postorder, int postStart, int postEnd) {// 如果中序遍历的起始下标大于结束下标，说明当前子树为空if (inStart > inEnd) {return null;}// 后序遍历的最后一个节点是根节点int rootVal = postorder[postEnd];TreeNode rootNode = new TreeNode(rootVal);// 找到根节点在中序遍历中的位置int rootIndex = -1;for (int i = inStart; i <= inEnd; i++) {if (inorder[i] == rootVal) {rootIndex = i;break;}}// 计算左子树的大小int leftSize = rootIndex - inStart;// 递归构造左子树// 左子树的中序范围：inStart 到 rootIndex - 1// 左子树的后序范围：postStart 到 postStart + leftSize - 1rootNode.left = build(inorder, inStart, rootIndex - 1, postorder, postStart, postStart + leftSize - 1);// 递归构造右子树// 右子树的中序范围：rootIndex + 1 到 inEnd// 右子树的后序范围：postStart + leftSize 到 postEnd - 1rootNode.right = build(inorder, rootIndex + 1, inEnd, postorder, postStart + leftSize, postEnd - 1);return rootNode;}
}