当前位置：首页 > news >正文

【漫话机器学习系列】240.真正类率（True Positive Rate，TPR）

news 来源：原创 2025/8/24 8:21:32

理解真正类率（True Positive Rate，TPR）：公式、意义与应用

在机器学习与深度学习模型评估中，"真正类率"（True Positive Rate，简称TPR）是一个非常重要的指标。TPR反映了分类器对正样本识别能力的强弱，也常常被称为召回率（Recall）或灵敏度（Sensitivity）。

今天我们通过一张非常直观的图片，来深入理解TPR的定义、公式推导、实际应用场景，并探讨其与其他评估指标的关系。

什么是真正类率（TPR）？

真正类率（TPR） 衡量的是模型对实际为正的样本识别正确的比例。
直观地讲，它回答了这样一个问题：

在所有真实为正的样本中，有多少被正确地识别出来了？

如果一个模型能够将所有正样本都正确分类为正，那么它的TPR就是100%。

TPR的数学公式

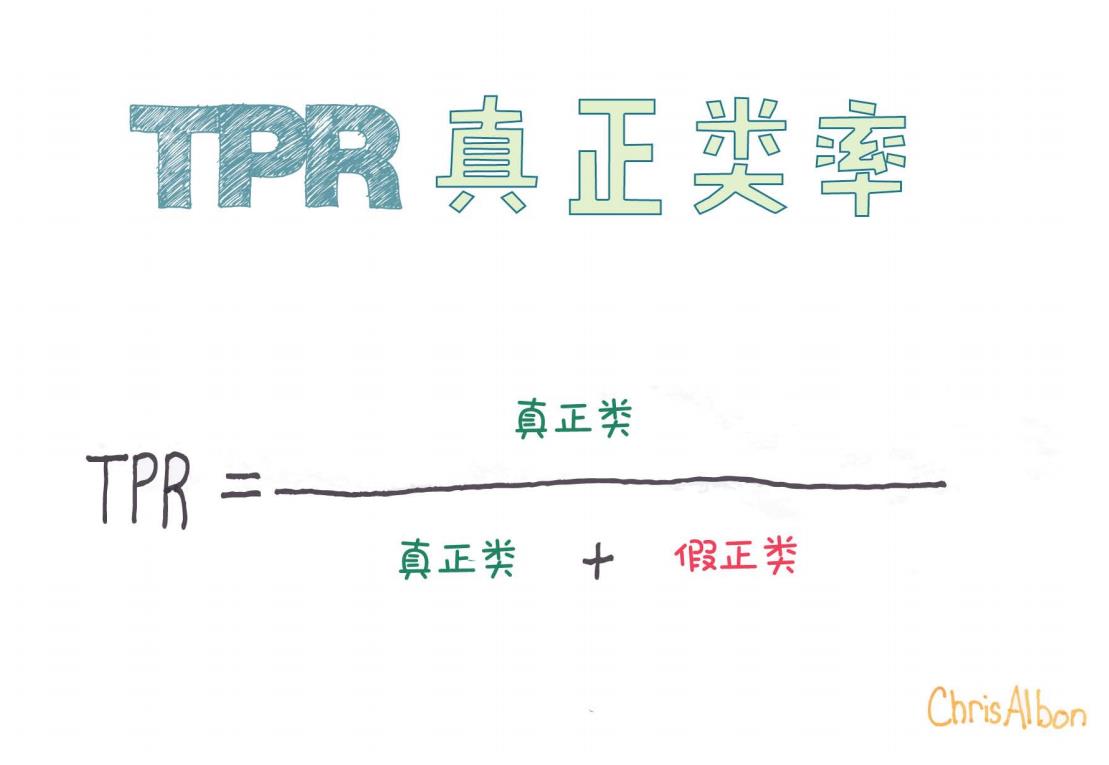
根据上面提供的图片，TPR的公式可以写成：

TPR=真正类真正类+假负类\text{TPR} = \frac{\text{真正类}}{\text{真正类} + \text{假负类}}

但是，图片里公式写成了另一种变形，稍有误导。让我们来细致地拆解一下：

真正类（True Positive，TP）：模型正确预测为正的样本数量。
假负类（False Negative，FN）：实际为正但被错误预测为负的样本数量。

因此标准的TPR公式应该是：

图片中提到的“假正类”其实是False Positive（FP），应该注意区分。

如果按照图片的公式（真正类 / (真正类 + 假正类)），其实描述的是**精准率（Precision）**而不是TPR。
所以，总结：真正类率（TPR）= 真正类 / (真正类 + 假负类)。

✅ 正确的TPR公式是基于假负类而不是假正类！

为什么TPR很重要？

在某些应用场景中，漏掉真正的正样本是非常严重的错误。例如：

疾病检测：将一个患病患者预测为健康（假负类）可能导致严重后果。
欺诈检测：漏掉一个真实欺诈行为（假负类）可能带来经济损失。
安全检查：漏检危险品可能导致安全事故。

因此，在这些场景中，我们希望TPR尽可能高，确保真正的正样本都能被识别出来。

举个例子

假设我们做了一个癌症检测模型，检测了100个病人，真实情况如下：

30个病人确实患有癌症（正样本）。
70个病人没有癌症（负样本）。

模型的预测结果：

成功检测出25个患癌者（True Positive = 25）。
漏掉5个患癌者，误判为健康（False Negative = 5）。

那么TPR就是：

$\text{TPR} = \frac{25}{25+5} = \frac{25}{30} \approx 0.8333$

即，模型的真正类率是83.33%，意味着83.33%的癌症患者被成功检测出来了。

TPR与其他指标的关系

在模型评估中，TPR通常不会单独使用，而是和其他指标一起分析，比如：

指标	公式	含义
精准率(Precision)	$\frac{TP}{TP+FP}$	预测为正的样本中，正确的比例
召回率(Recall/TPR)	$\frac{TP}{TP+FN}$	实际为正的样本中，预测正确的比例
F1分数(F1 Score)	$2 \times \frac{Precision \times Recall}{Precision + Recall}$	综合考虑精准率和召回率

通常在精度（Precision）和召回率（Recall）之间存在权衡：

提高召回率，可能会降低精准率；
提高精准率，可能会降低召回率。

因此，实际应用中要根据业务需求选择最合适的指标。

总结

TPR（True Positive Rate）也叫召回率（Recall）或灵敏度（Sensitivity）。
正确公式是：TPR = 真正类 / (真正类 + 假负类)。
TPR用于衡量模型正确识别正样本的能力。
在医疗、金融安全等领域，TPR至关重要。

希望通过这篇文章，你对TPR有了更系统深入的理解！

附录：错误提示

⚠️ 图片中使用了“假正类（False Positive）”来计算TPR，这在严谨的定义中是错误的。
正确的TPR公式应该涉及假负类（False Negative）。

大家在学习过程中，务必注意区分**假正类（FP）和假负类（FN）**的不同概念哦！

如果你觉得这篇文章对你有帮助，欢迎点赞收藏！如果有疑问或者想继续了解其他评估指标（比如ROC曲线、AUC指标等），可以在评论区告诉我～

【漫话机器学习系列】240.真正类率（True Positive Rate，TPR）

理解真正类率（True Positive Rate，TPR）：公式、意义与应用在机器学习与深度学习模型评估中，"真正类率"（True Positive Rate，简称TPR）是一个非常重要的指标。TPR反映了分类…...

编程日记 2025/8/24 8:21:32

ThreadLocal源码深度剖析：内存管理与哈希机制

ThreadLocal是Java并发编程中的重要工具，它为每个线程提供独立的变量存储空间，实现了线程之间的数据隔离。本文将从源码实现角度，深入分析ThreadLocal的内部机制，特别是强弱引用关系、内存泄漏问题、ThreadLocalMap的扩容机制以及…...

编程日记 2025/8/23 2:30:28

Softmax回归与单层感知机对比

(1) 输出形式 Softmax回归输出是一个概率分布，通过Softmax函数将线性得分转换为概率： 其中 KK 是类别数，模型同时计算所有类别的概率。单层感知机输出是二分类的硬决策（如0/1或1）： 无概率解释&#x…...

编程日记 2025/8/24 8:21:31

数字社会学家唐兴通谈数字行动主义网络行动主义与标签行动主义，理解它才算抓住AI社会学与网络社会学关键所在

让我们继续探讨一个在数字时代至关重要的概念——数字行动主义（Digital Activism）、网络行动主义（Cyberactivism）以及标签行动主义（Hashtag Activism）。我将尽力从一个数字社会学家的角度，抽丝剥…...

编程日记 2025/8/24 1:56:54

PandasAI：对话式数据分析新时代

PandasAI：对话式数据分析新时代引言项目概述分析基本信息核心功能详解1. 自然语言查询处理2. 数据可视化生成3. 多数据源集成分析4. 安全沙箱执行5. 云平台协作功能安装和使用教程1.环境要求2.安装步骤3.基本使用方法4.切换其他LLM 应用场景和实际价值1.适用业务…...

编程日记 2025/8/24 8:19:14

全球化电商平台AWS云架构设计

业务需求： 支撑全球三大区域（北美/欧洲/亚洲）用户访问，延迟<100ms处理每秒50,000订单的峰值流量混合云架构整合本地ERP系统全年可用性99.99%满足GDPR和PCI DSS合规要求以下是一个体现AWS专家能力的全球化电商平台架构设计方…...

编程日记 2025/8/24 8:18:03

Linux 怎么使用局域网内电脑的网络访问外部

一次性 export http_proxy"http://192.168.0.188:7890" export https_proxy"http://192.168.0.188:7890"一直生效写入 ~/.bashrc（或 ~/.bash_profile） nano ~/.bashrc加入这一行： export http_proxy"http://19…...

编程日记 2025/8/24 8:16:09

Python-numpy中ndarray对象创建，数据类型，基本属性

numpy库 numpy中的数据结构ndarrayndarray中的dtypendarray中的dtype的指定方式创建ndarray及指定dtype从列表创建ndarray使用 np.empty(), np.zeros(), np.ones() 和 np.full() 创建特定值的数组使用 np.arange() 创建等差数列数组使用 np.linspace() 创建等差数组使用np.logs…...

编程日记 2025/8/24 8:19:55

Python从入门到高手8.2节-元组的常用操作符

目录 8.2.1 元组的常用操作符 8.2.2 []操作符: 索引访问元组 8.2.3 [:]操作符：元组的切片 8.2.4 操作符：元组的加法 8.2.5 *操作符：元组的乘法 8.2.6 元组的关系运算 8.2.7 in操作符：查找元素 8.2.8 五一她玩了个狗吃…...

编程日记 2025/8/21 11:45:29

Python内置函数

Python作为一门简洁强大的编程语言，提供了丰富的内置函数（Built-in Functions），这些函数无需导入任何模块即可直接使用。本文将介绍Python中最常用、最重要的内置函数，帮助初学者快速掌握这些强大的工具。官方地址&a…...

编程日记 2025/8/21 11:45:27

一款基于 .NET 开源的多功能的 B 站视频下载工具

前言哔哩哔哩（B站）是一个知名的视频学习平台，作为程序员而言这是一个非常值得推荐的网站。今天大姚给大家推荐一款基于 .NET 开源的多功能的 B 站视频下载工具：downkyi。项目介绍 downkyi（哔哩下载姬）…...

编程日记 2025/8/21 12:46:00

【PostgreSQL数据分析实战：从数据清洗到可视化全流程】5.2 数据分组与透视（CUBE/ROLLUP/GROUPING SETS）

👉 点击关注不迷路 👉 点击关注不迷路 👉 点击关注不迷路文章大纲 5.2 数据分组与透视：CUBE/ROLLUP/GROUPING SETS深度解析5.2.1 数据准备与分析目标数据集与表结构分析目标 5.2.2 ROLLUP：层级化分组汇总功能与语法示…...

编程日记 2025/8/24 8:19:56

20、数据可视化：魔镜报表——React 19 图表集成

一、魔镜的预言本质 "数据可视化是霍格沃茨的预言水晶球，将混沌的数据星尘转化为可解读的命运轨迹！" 魔法部占卜司官员挥舞魔杖，Echarts与Three.js的图表矩阵在空中交织成动态星图。 ——基于《国际魔法联合会》第9号可视化协议&a…...

编程日记 2025/8/24 8:19:14

笔记本电脑升级计划（2017———2025）

ThinkPad T470 (2017) vs ThinkBook 16 (2025) 完整性能对比报告一、核心硬件性能对比 1. CPU性能对比（i5-7200U vs Ultra9-285H） 参数i5-7200U (2017)Ultra9-285H (2025)提升百分比核心架构2核4线程 (Skylake)16核16线程 (6P8E2LPE)700%核心数制程工…...

编程日记 2025/8/21 12:45:55

Flutter——数据库Drift开发详细教程(四)

目录参考正文表达式1.比较2.布尔代数3.算术BigIn 4.空值检查6.日期和时间7.IN和NOT IN8.聚合函数（例如 count 和 sum）8.1比较8.2算术8.4计数8.5group_concat8.9窗口函数 9.数学函数和正则表达式10.子查询10.1 标量子查询10.2 isInQuery10.3 存在10.4完整…...

编程日记 2025/8/20 22:25:22

android-ndk开发(6): 查看反汇编

android-ndk开发(6): 查看反汇编 2025/05/05 1. 概要 android-ndk 是基于 clang 的工具链， clang 则保持了和 gcc 的高度兼容。在 Linux 开发机上， GCC 套件里的 objdump 提供了反汇编的功能。实际上 android-ndk 也提供了一份 objdump，…...

编程日记 2025/8/24 8:19:13

浅析AI大模型为何需要向量数据库？【入门基础】

文章目录引言：大模型时代的存储挑战一、向量数据库：大模型的"海马体"1.1 什么是向量数据库？1.2 为什么大模型离不开向量数据库？(1) 嵌入(Embedding)的本质(2) 突破上下文窗口限制二、相似性度量：欧氏距离与…...

编程日记 2025/8/24 8:20:27

Java面试：微服务与大数据场景下的技术挑战

面试对话场景第一轮：基础知识考察面试官：谢先生，您能简单介绍一下Java SE 8的新特性吗？ 谢飞机：当然，Java SE 8引入了Lambda表达式、Stream API和新的日期时间API，大大简化了代码编写。面…...

编程日记 2025/8/21 12:45:51

[前端]异步请求的竞态问题

竞态条件简介遇到的问题切换标签请求数据，但又快速切换标签请求数据，展示的是前一个标签的数据， 需要在切换标签时添加取消请求的机制，使用AbortController来取消正在进行的请求。当用户快速切换标签时，取消之前的请…...

编程日记 2025/8/20 14:21:56

【PDF拆分+提取内容改名】批量拆分PDF提取拆分后的每个PDF物流面单数据改名或导出表格，基于WPF的PDF物流面单批量处理方案

应用场景物流行业每天需要处理大量包含物流面单的PDF文件，这些文件通常包含运单号、收发货人信息、货物详情等重要数据。传统手动处理方式效率低下且容易出错。本方案通过WPF实现一个自动化工具，能够：批量拆分多页PDF为单页文件提取每页面单中的关键信息（如运单号、收件人…...

编程日记 2025/8/21 12:45:47

adb无线调试步骤

环境： macOS； 换成 linux 或 windows 也支持的小米15 Pro； 换成其他 android 手机也支持的电脑和手机接入相同Wifi在电脑上，确保安装了 adb 对于 Android 开发者， 一般是是通过 Android Studio 安装对于 ndk 开发者…...

编程日记 2025/8/24 8:20:24

RocketMQ与Kafka的区别

文章目录相同之处不同之处存储形式性能对比传输系统调用存储可靠性单机支持的队列数延时消息消息重复消息过滤消息失败重试死信队列 DLQ回溯消息分布式事务服务发现开发语言友好性开源社区活跃度商业支持成熟度总结Kafka 和 RocketMQ 怎么选？ 本文参考&#xff1a…...

编程日记 2025/8/24 8:20:23

剥开 MP4 的千层 “数字洋葱”：从外到内拆解通用媒体容器的核心

在当今数字化时代，MP4 格式随处可见，无论是在线视频、手机拍摄的短片，还是从各种渠道获取的音频视频文件，MP4 都占据着主流地位。它就像一个万能的 “数字媒体集装箱”，高效地整合和传输着各种视听内容。接下来&#x…...

编程日记 2025/8/24 8:19:56

设计模式(结构型)-组合模式

定义组合模式的定义为：将对象组合成树形结构以表示 “部分 - 整体” 的层次结构，并且使得用户对单个对象和组合对象的使用具有一致性。其最关键的实现要点在于，简单对象和复合对象必须实现相同的接口，这一特性正是组合模式能够对…...

编程日记 2025/8/24 8:21:31

使用 IDEA + Maven 搭建传统 Spring MVC + Thymeleaf 项目的详细步骤

使用 IDEA Maven 搭建传统 Spring MVC Thymeleaf 项目环境准备步骤 1：创建 Maven 项目步骤 2：添加依赖（pom.xml）步骤 3：配置 web.xml步骤 4：Spring 配置类（Java Config）步骤 5&am…...

编程日记 2025/8/23 22:01:23

「Mac畅玩AIGC与多模态19」开发篇15 - 判断节点与工具节点联动示例

一、概述本篇在引入工具节点的基础上，进一步结合判断节点（条件分支），实现根据用户输入内容动态控制是否调用外部接口。通过构建“用户是否需要天气信息”的条件逻辑，开发人员将掌握如何在 Dify 工作流中通过条件判断…...

编程日记 2025/8/21 12:45:35

docker 外部能访问外网，内部不行(代理问题)

如果宿主机访问外网依赖代理（比如 http_proxy 环境变量），容器默认不会继承。需要显式传入代理： docker run -e http_proxy... -e https_proxy... ...在 docker-compose 中配置 HTTP/HTTPS 代理 version: 3 services:app:image: …...

编程日记 2025/8/21 12:45:33

模糊控制理论（含仿真）

本文讲解模糊控制理论、设计步骤以及案例。 1. 模糊控制原理： 模糊控制（Fuzzy Control）是一种基于模糊逻辑推理的人类经验规则实现的控制方法，适用于对系统模型不精确或难以建立精确数学模型的复杂系统。它利用“如果…那么…”&…...

编程日记 2025/8/22 11:59:42

《 C++ 点滴漫谈：三十六》lambda表达式

一、引言在 C98 和 C03 时代，尽管 C 拥有强大的泛型编程能力和丰富的面向对象特性，但在表达局部逻辑、回调行为或一次性函数处理时，程序员却常常需要冗长的代码来定义函数对象（functor），或者使用函数指针…...

编程日记 2025/8/23 23:12:52

【C/C++】函数模板

🎯 C 学习笔记：函数模板（Function Template） 本文是面向 C 初学者的函数模板学习笔记，内容包括基本概念、定义与使用、实例化过程、注意事项等，附带示例代码，便于理解与复现。 📌 一…...

编程日记 2025/8/21 12:45:29

电赛经验分享——模块篇

1、前言打算在这一个专栏中，分享一些本科控制题电赛期间的经验，和大家共同探讨，也希望能帮助刚刚参加电赛的同学，了解一些基本的知识。一些见解和看法可能不同或有错误，欢迎批评指正。在本文中，主要介绍笔…...

编程日记 2025/8/21 12:45:27

LeetCode 热题 100 70. 爬楼梯

LeetCode 热题 100 | 70. 爬楼梯大家好，今天我们来解决一道经典的动态规划入门题——爬楼梯。这道题在LeetCode上被标记为简单难度，要求我们计算爬到第n阶楼梯的不同方法数，每次可以爬1或2个台阶。下面我将详细讲解解题思路，并附…...

编程日记 2025/8/21 12:45:25

浔川AI测试版内测报告

浔川AI测试版内测报告一、引言本次对浔川AI测试版进行内测，旨在全面评估其功能表现与性能状况，为后续的优化升级及正式上线提供有力依据。二、测试环境 1. 硬件环境：[Windows 10】 2. 软件环境：操作系统为【核桃编程]&#xff…...

编程日记 2025/8/22 22:08:44

Leetcode刷题记录31——旋转图像

题源：https://leetcode.cn/problems/rotate-image/description/?envTypestudy-plan-v2&envIdtop-100-liked 题目描述： 思路一： 💡 解题思路：分两步完成旋转虽然“直接旋转”看起来有点抽象，但我们…...

编程日记 2025/8/21 12:45:21

攻防世界-php伪协议和文件包含

fileinclude 可以看到正常回显里面显示lan参数有cookie值表示为language 然后进行一个判断，如果参数不是等于英语，就加上.php，那我们就可以在前面进行注入一个参数，即flag， payload：COOKIE:languageflag …...

编程日记 2025/8/22 23:00:51

[C++] 小游戏决战苍穹

大家好，各位看到这个标题，斗破苍穹什么时候改叫决战苍穹了？其实，因为版权等一系列问题，斗破苍穹正式改名为决战苍穹，这个版本主要更新内容为解决了皇冠竞技场太过影响游戏平衡，并且提高了一些装…...

编程日记 2025/8/22 20:12:31

项目成本管理_挣得进度ES

在项目成本管理的新实践中， 通过挣值管理(EVM) 的扩展，引入挣得进度ES 这一概念， ES是EVM理论和实践的延伸，挣得进度理论用ES和实际时间(AT) 替代了传统EVM所使用的进度偏差测量指标SV(挣值—计划价值)。使用这种替代方法计算…...

编程日记 2025/8/22 3:06:42

矩阵快速幂快速求解递推公式

文章目录习题790.多米诺和托米诺平铺对于一个给定的递推公式，例如dp[i] dp[i-1] * a dp[i-2] * b,那么常用的做法，肯定是使用o(n)的时间复杂度进行线性求解，但是如果 n 10 18 n{10}^{18} n1018，那么肯定超时的，这…...

编程日记 2025/8/23 13:09:00

驱动开发硬核特训 · Day 28（上篇）：pinctrl 子系统详解与实战分析

📅 日期：2025-05-05 📚 技术平台：嵌入式Jerry（B站） 一、引言在嵌入式系统中，SoC 芯片的引脚通常具有多种功能，如 GPIO、UART、I2C、SPI 等。为了在不同的应用场景中灵活配置引脚功…...

编程日记 2025/8/21 12:45:11

20250505下载VLC for Android

20250505下载VLC for Android 2025/5/5 14:35 缘起：做Rockchip的RK3566的Android13下的跨网段PING。酷芯的图传网段和 softAP/以太网RJ45共享网段之间互相PING通。图传的原厂/供应商说可以使用ffmpeg进行rtsp流的转发。后来确认VLC for Android版本只有接受流&a…...

编程日记 2025/8/21 12:45:09

Jetpack Compose 响应式布局实战：BoxWithConstraints 完全指南

深入理解 Jetpack Compose 中的 BoxWithConstraints 前言在构建现代 Android 应用时，响应式设计已成为必不可少的要求。Jetpack Compose 作为 Android 的现代 UI 工具包，提供了 BoxWithConstraints 这一强大组件，帮助我们轻松创建能够适应…...

编程日记 2025/8/23 2:30:34

ZYNQ笔记（十七）：IP核封装与接口定义

版本：Vivado2020.2（Vitis） 任务：将“HDMI彩条显示实验”（正点原子 ZYNQ FPGA 开发视频）中所实现的 RGB2DVI 模块封装成一个 IP 核。目录一、介绍 （1）IP核 （2&#x…...

编程日记 2025/8/23 4:04:37

学习笔记msp430f5529lp

注：本文仅用于个人学习使用，记录笔记。学习视频msp430f5529库函数入门教程 00.序言_哔哩哔哩_bilibili 向大佬致敬理工男小帅-CSDN博客 CCS环境快捷键使用代码注释：Ctrl/ 提示/补全: CtrlShiftC 放大:Ctrl 缩小:Ctrl- 切换选择模式&…...

编程日记 2025/8/21 12:45:03

人工智能应用：从技术突破到生态重构的演进之路

一、人工智能的发展历程：从符号主义到通用智能探索人工智能（AI）的发展始于20世纪中叶，其历程可划分为四个关键阶段： 符号主义与早期探索（1950s-1970s） 以逻辑推理和专家系统为核心&…...

编程日记 2025/8/23 1:06:08

【ZYNQ Linux移植】4-内核移植

文章目录 0 写在前面1 内核源码的文件结构2 Linux内核移植2.1 移植配置文件2.2 移植设备树2.3 创建脚本进行编译2.4 备份相关文件 3 测试4 总结5 参考资料 0 写在前面这是一个系列博客，详细介绍如何在 ZYNQ 与 ZYNQ MP 平台上如何移植 Linux 系统。目前网络上的大部…...

编程日记 2025/8/23 5:48:46

代码随想录算法训练营第三十二天

LeetCode/卡码网题目: 518. 零钱兑换 II377. 组合总和 Ⅳ790. 多米诺和托米诺平铺(每日一题)57. 爬楼梯（第八期模拟笔试） 其他: 今日总结往期打卡背包问题特点: 滚动数组背包遍历顺序完全背包从小到大,即基于当前物品更新过的继续更新01背包从大到…...

编程日记 2025/8/21 12:44:57

java CompletableFuture 异步编程工具用法1

1、测试异步调用： static void testCompletableFuture1() throws ExecutionException, InterruptedException {// 1、无返回值的异步任务。异步线程执行RunnableCompletableFuture.runAsync(() -> System.out.println("only you"));// 2、有返回值的异…...

编程日记 2025/8/21 12:44:55

Spring Boot 集成 Solr 的详细步骤及示例

环境准备安装 Solr ：从 Solr 官网（Welcome to Apache Solr - Apache Solr）下载并安装最新版本，然后通过命令 bin/solr start 启动 Solr 服务，使用 bin/solr create -c mycore 创建一个新的 Solr 核心。安装 JDK &am…...

编程日记 2025/8/21 11:42:59