当前位置：首页 > news >正文

计算方法实验六数值积分

news 来源：原创 2025/7/12 21:59:43

【实验性质】综合性实验。

【实验目的】理解插值型积分法；掌握复化积分法算法。

【实验内容】

1对，用复化梯形积分和变步长梯形积分求值（截断误差不超过）。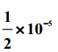

【理论基础】

积分在工程中有重要的应用，数值积分的基本思想是用被积函在区间上的一些点处的值的线性组合作为积分的近似值：

实际应用中 f x( )是未知的，一般用 f x( ) 的次数不超过n的插值多项式来代替（插值型求积方法）：

【实验过程】

1.用复化梯形积分求解，给出代码，并用表格记载求解过程〔区间数n=30、50、70、100、150〕。

程序代码：

头文件：

#ifndef DEFINITEINTEGRAL_H

#define DEFINITEINTEGRAL_H

#include<math.h>

class definiteintegral

{

public:

definiteintegral();

double T_Integral(double a ,double b,double(*f)(double));

double S_Integral(double a ,double b,double(*f)(double));

double C_Integral(double a ,double b,double(*f)(double));

double Tn_Integral(double a ,double b,double(*f)(double),int n);

double Sn_Integral(double a ,double b,double(*f)(double),int n);

double Cn_Integral(double a ,double b,double(*f)(double),int n);

double V_T_Integral(double a, double b, double(*f)(double),double e);

};

#endif // DEFINITEINTEGRAL_H

主函数：

//实验六

#include <iostream>

#include <windows.h>

#include "colvector.h"

#include "matrix.h"

#include <windows.h>

#include "linearequations.h"

#include "interpolationpolynomial.h"

#include "definiteintegral.h"

double f1(double x){

return x*x*x-sin(x)-4*x-1;

}

double f2(double x){

return 3*x*x-cos(x)-4;

}

double f3(double x){

double result =sin(x)+4*x-1;

if(result>0){

return pow(result,1.0/3);

}else{

return -pow(fabs(result),1.0/3);

}

using namespace std;

double f4(double x)

{

return 1/(1+x*x);

}

int main()

{

SetConsoleOutputCP(CP_UTF8);

double a=0,b=1.0;

definiteintegral obj;

cout<<"梯形积分:\t\t"<<obj.T_Integral(a,b,f4)<<endl;

cout<<"Simpson积分:\t\t"<<obj.S_Integral(a,b,f4)<<endl;

cout<<"Cotess积分:\t\t"<<obj.C_Integral(a,b,f4)<<endl;

cout<<endl;

cout<<"复化梯形积分:\t\t"<<obj.Tn_Integral(a,b,f4,150)<<endl;

cout<<"复化Simpson积分:\t"<<obj.Sn_Integral(a,b,f4,30)<<endl;

cout<<"复化Cotes积分:\t\t"<<obj.Cn_Integral(a,b,f4,30)<<endl;

cout<<endl;

cout<<"交步长梯形积分:\t\t"<<obj.V_T_Integral(a,b,f4,0.00001)<<endl;

return 0;

}

代码块：

#include "definiteintegral.h"

definiteintegral::definiteintegral(){}

double definiteintegral::T_Integral(double a,double b,double(*f)(double)){

    return (b-a)/2.0*(f(a)+f(b));

double definiteintegral::S_Integral(double a,double b,double(*f)(double)){

    return (b-a)/6.0*(f(a)+4*f((a+b)/2)+f(b));

double definiteintegral::C_Integral(double a,double b,double(*f)(double)){

    double h=(b-a)/4.0;

    return (b-a)/90*(7*f(a)+32*f(a+h)+12*f(a+2*h)+32*f(a+3*h)+7*f(b));

double definiteintegral::Tn_Integral(double a,double b,double(*f)(double),int n){

    double h=(b-a)/n;

    double result =0;

    double sum=0;

    for(int i=1;i<=n-1;i++){

            sum +=f(a+i*h);

    result =h/2.0*(f(a)+2*sum+f(b));

    return result;

double definiteintegral::Sn_Integral(double a,double b,double(*f)(double),int n){

    double h=(b-a)/n;

    double result =0;

    double sum1=0,sum2=0;

    for(int i=1;i<=n;i++){

            sum1 +=f(a+(i-1)*h+h/2);

    for(int i=1;i<=n-1;i++){

            sum2 +=f(a+i*h);

    result =h/6.0*(f(a)+4*sum1+2*sum2+f(b));

    return result;

double definiteintegral::Cn_Integral(double a,double b,double(*f)(double),int n){

    double h=(b-a)/n;

    double result =0;

    double sum1=0,sum2=0,sum3=0,sum4=0;

    for(int i=1;i<=n;i++){

            sum1 +=f(a+(i-1)*h+h/4);

    for(int i=1;i<=n;i++){

            sum2 +=f(a+(i-1)*h+h/2);

    for(int i=1;i<=n;i++){

            sum3 +=f(a+(i-1)*h+3*h/4);

    for(int i=1;i<=n-1;i++){

            sum4 +=f(a+i*h);

    result =h/90.0*(7*f(a)+32*sum1+12*sum2+32*sum3+14*sum4+7*f(b));

    return result;

double definiteintegral::V_T_Integral(double a, double b, double(*f)(double),double e){

    double h=(b-a);

    double T1=h/2.0*(f(a)+f(b));

    double T2=T1/2.0+h/2.0*f(a+h/2.0);

    double error=fabs(T2-T1);

    while(error>=e){

        T1=T2;

        h=h/2;

        double x=a+h/2;

        double sum=0;

        while(x<b){

            sum+=f(x);

            x+=h;

        T2=T1/2.0+h/2.0*sum;

        error=fabs(T2-T1);

    return T2;

表格：

n=30	n=50	n=70	n=100	n=150
0.785352	0.785381	0.785390	0.785394	0.785396

2.用变步长梯形积分求解，给出代码，并用表格记载求解过程。

代码块：

double definiteintegral::V_T_Integral(double a, double b, double(*f)(double),double e){

    double h=(b-a);

    double T1=h/2.0*(f(a)+f(b));

    double T2=T1/2.0+h/2.0*f(a+h/2.0);

    double error=fabs(T2-T1);

    while(error>=e){

        T1=T2;

        h=h/2;

        double x=a+h/2;

        double sum=0;

        while(x<b){

            sum+=f(x);

            x+=h;

        T2=T1/2.0+h/2.0*sum;

        error=fabs(T2-T1);

    return T2;

表格：

3.比较复化积分与变步长积分，分析实验出现的问题，总结解决办法。

复化积分是将一个区间分成若干子区间，然后在每个子区间上应用数值积分方法。它的优点是简单易实现，计算结果比较稳定。但是，如果子区间的数量不够多，或者函数在某些子区间上变化较大，可能会导致计算结果的误差较大。为了解决这个问题，可以增加子区间的数量，或者使用自适应方法，根据函数的变化情况来调整子区间的数量。

变步长积分是根据函数的变化情况，调整积分步长来提高计算精度。它的优点是能够更好地适应函数的变化情况，减小误差。但是，如果调整步长的策略不合理，可能会导致计算时间过长。为了解决这个问题，可以采用适当的步长调整策略，如自适应选取步长或者根据函数的一阶或二阶导数来调整步长。

【实验心得】

在本次实验中，我们学习了三种数值积分的方法，包括差值积分法、复化积分法和复化梯形公式。通过这些实验，我对数值积分的原理和计算方法有了更深入的了解。

在差值积分法中，我们使用了牛顿-科特斯公式对函数进行了差值，然后通过对差值多项式进行求和来计算积分。这种方法的优点是计算简单，适用于低次多项式的积分，但对于高次多项式的积分误差较大。

复化积分法是将计算区间分成若干小区间，然后对每个小区间应用数值积分方法。我们采用了复化梯形公式，其原理是通过将每个小区间近似为梯形来计算积分。这种方法误差较差值积分法要小，但计算较复杂。

综合考虑精度和计算复杂度，我们可以选择合适的数值积分方法。如果函数是低次多项式，可以使用差值积分法进行计算。对于复杂函数，可以采用复化积分法进行分区间计算。通过这些实验，我掌握了数值积分的基本原理和计算方法，并且了解了不同方法的优缺点，这对于解决实际问题具有重要的参考价值。

得分_____________

评阅日期_____________

教师签名_____________

相关文章：