当前位置：首页 > news >正文

计算机图形学：（二）MVP变换示例

news 来源：原创 2025/5/15 23:35:30

前言

当在阅读计算机图形学系列的书籍时，会发现大部分图书每章内容都如出一辙。从个人实际体会来讲，虽然能理解书中大部分的知识，但到了实际使用时却有点抓耳挠腮。因此，在写了计算机图形学：（一）基础后，觉得应该从一些实例入手去更好地理解那些知识点。

在网上翻找资料时，找到博主charlee44写的一些文章，很受启发，该篇便在其WebGL或OpenGL关于模型视图投影变换的设置技巧-CSDN博客的基础上进行整理补充。

准备工作

先绘制一个立方体，为了更快地理解一些概念，这里不把参数复杂化。

// WebGl的三维坐标系统（笛卡尔坐标系），水平方向是X轴，垂直方向是Y轴，垂直于屏幕的是Z轴
var minX = -2;
var maxX = 2;
var minY = -2;
var maxY = 2;
var minZ = -1;
var maxZ = 1;// 顶点坐标和颜色
var verticesColors = new Float32Array([maxX, maxY, maxZ, 1.0, 0.0, 0.0,  // v0 红minX, maxY, maxZ, 1.0, 0.0, 0.0,  // v1 红minX, minY, maxZ, 1.0, 0.0, 0.0,  // v2 红maxX, minY, maxZ, 1.0, 0.0, 0.0,  // v3 红maxX, minY, minZ, 0.0, 1.0, 0.0,  // v4 绿maxX, maxY, minZ, 0.0, 1.0, 0.0,  // v5 绿minX, maxY, minZ, 0.0, 1.0, 0.0,  // v6 绿minX, minY, minZ, 0.0, 1.0, 0.0   // v7 绿
]);

当前该立方体的中心点正好在（0, 0, 0）处。

var cx = (minX + maxX) / 2.0;
var cy = (minY + maxY) / 2.0;
var cz = (minZ + maxZ) / 2.0;

示例一：初始化

现在假设我们站在Z轴的一个点上（如（0, 0, 2000））去看向该立方体。那么我们看到的立方体是怎样的呢？

通过一些视图变换矩阵我们可以计算一下结果：

// 模型矩阵
// 注：这里不对模型进行任何的旋转，它的位置即中心点的位置
var modelMatrix = new Matrix4();
modelMatrix.rotate(0.0, 1.0, 0.0, 0.0); // 绕x轴旋转 (angle, x, y, z)
modelMatrix.rotate(0.0, 0.0, 1.0, 0.0); // 绕y轴旋转 (angle, x, y, z)
modelMatrix.translate(cx, cy, cz);// 视图矩阵
var viewMatrix = new Matrix4();
// 注：这里我们从(0, 0, 2000)点看向(cx, cy, cz)点（也是立方体的中心点）
viewMatrix.lookAt(0, 0, 2000, cx, cy, cz, 0, 1, 0); // (eye, center, up)// 投影矩阵
var projMatrix = new Matrix4();
var fovy = 60 * Math.PI / 180.0; // 注：这里随便设置一个常见的垂直视场角
var aspect = canvas.width / canvas.height; // 获取成像平面的比例
projMatrix.setPerspective(fovy, aspect, 10, 3000); // (fovv, aspect, near, far)// 模型视图投影矩阵
var mvpMatrix = new Matrix4();
mvpMatrix.set(projMatrix).multiply(viewMatrix).multiply(modelMatrix);

在这种状态下我们看到的结果是：

同理我们可以从不同的相机位置去观察结果：

左：（0, 0, -2000）中：（0, 2000, 2000）右：（200, 2000, 2000）

视场角决定了摄像机所能看到的范围，角度越大，可视范围就越广，看到的东西就越多，但是屏幕上远处的物体也会越小。不同的垂直视场角大小：

示例二：绕点旋转

观察以下两幅动图：

左：旋转摄像机，让摄像机绕着原点顺时针旋转；
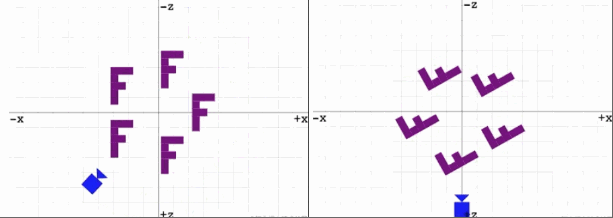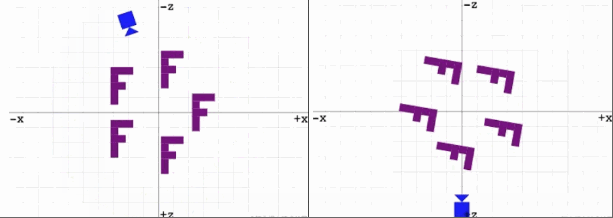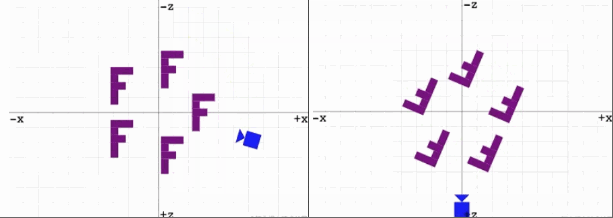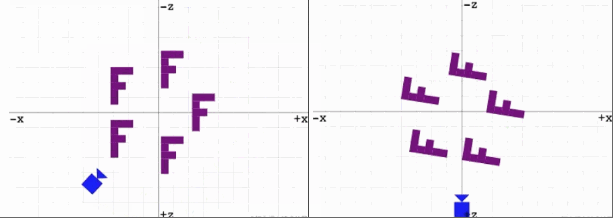
右：旋转场景中的物体，让所有物体绕着原点逆时针。

事实上，无论是摄像机绕原点顺时针旋转还是场景中的物体绕原点逆时针旋转，我们以摄像机的视角来看的话，你会发现这两种方式看到的图像是一样的。但是，移动摄像机比起整体移动场景来说更加的高效且更加的符号人类的生活常识。毕竟我们在生活中想要观察不同的物体时我们会去改变我们观察的位置和角度，而不会去移动物体本身，况且有的东西也根本无法移动 [链接]。

在博文《WebGL或OpenGL关于模型视图投影变换的设置技巧》中使用的是第二种方式（即旋转物体，修改了立方体的模型矩阵），所以这里我们考虑一下第一种方式的实现（即修改相机的视图矩阵）。

① 以固定角度旋转相机

先从简单的入手，我们先考虑让相机以一个固定的旋转度数（如45°）绕立方体中心旋转：

var eyeHight = 2000.0;
var cameraPos = new Vector3([0, 0, eyeHight]); // 相机初始位置const angle = Math.PI / 4; // 例如，旋转45度
var rotateMatrix = new Matrix4();
rotateMatrix.rotate(angle, 0.0, 1.0, 0.0); // 绕Y轴旋转
cameraPos = rotateMatrix.multiplyVector3(cameraPos); // 得到相机旋转后的新坐标

修改视图矩阵，传入相机的新位置（即eye）：

var viewMatrix = new Matrix4();
viewMatrix.lookAt(cameraPos.elements[0], cameraPos.elements[1], cameraPos.elements[2], cx, cy, cz, 0, 1, 0); // eye, center, up

运行结果：

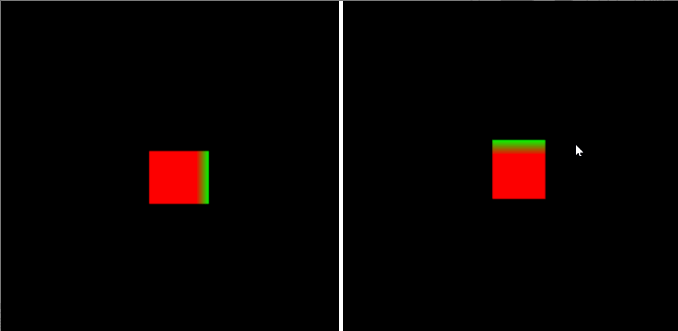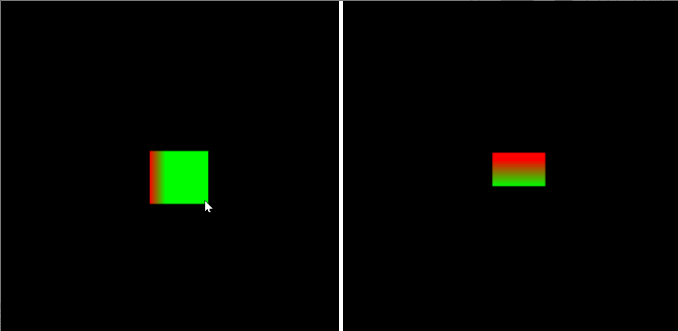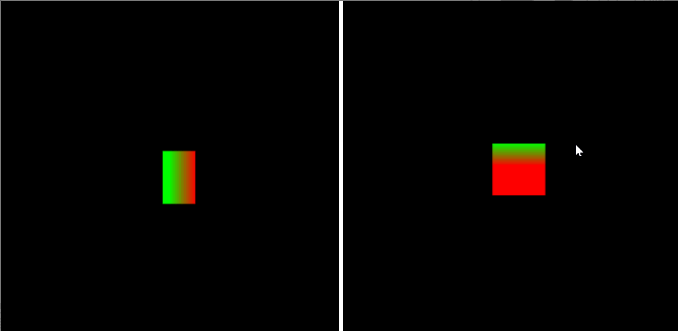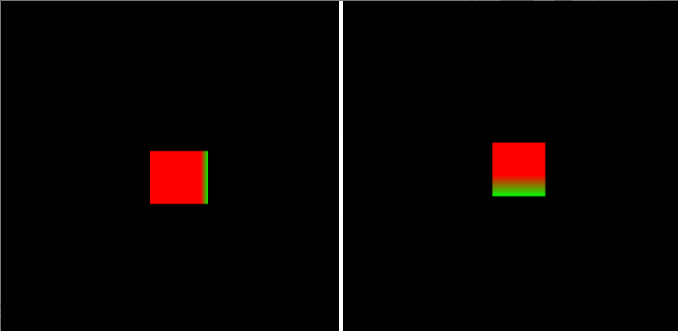
② 鼠标拖拽旋转相机

当在屏幕上按下左键拖拽鼠标时，会形成一个xy偏移量，我们可以根据这个偏移量来计算相机的旋转矩阵。（注：偏移量的大小根据设计的不同会使得鼠标拖动操作的“丝滑度”不同，太小显得拖拽困难，太大立方体轻轻一拖拽就飞速转动

注：关于鼠标句柄handle的逻辑事件处理这里就不进行说明了，不是本文的重点，可以自己看代码理解 [链接]。

var factor = 100 / canvas.height; // The rotation ratio
var dx = factor * (x - lastX);
var dy = factor * (y - lastY);
// 这里把旋转量限制在[-90°, 90°]
currentAngle[0] = Math.max(Math.min(currentAngle[0] + dy, 90.0), -90.0);
currentAngle[1] = Math.max(Math.min(currentAngle[1] + dx, 90.0), -90.0);

根据计算出的角度去更新相机旋转后的坐标：

var rotateMatrix = new Matrix4();
rotateMatrix.rotate(-currentAngle[0], 1.0, 0.0, 0.0); // (angle, x, y, z)
rotateMatrix.rotate(-currentAngle[1], 0.0, 1.0, 0.0); 
cameraPos = rotateMatrix.multiplyVector3(cameraPos);
// 旋转完成后重置currentAngle，否则立方体会一直旋转下去
currentAngle[0] = 0.0;
currentAngle[1] = 0.0;

前言

准备工作

示例一：初始化

示例二：绕点旋转

① 以固定角度旋转相机

② 鼠标拖拽旋转相机

相关文章：