当前位置：首页 > news >正文

大连理工大学选修课——机器学习笔记（6）：决策树

news 来源：原创 2025/5/18 4:00:49

决策树

决策树概述

决策树——非参数机器学习方法

参数方法：

参数估计是定义在整个空间的模型

所有训练数据参与估算

所有的检验输入都用相同的模型和参数

非参数方法：

非参数估计采用局部模型

输入空间被分裂为一系列可以用距离度量的局部空间
每个输入只使用邻近区域由训练样本计算得到的局部模型

决策树特点

采用分治策略
- 简洁高效可并行
- 递归
输入空间被描述为一种树形结构
- 层次递归
- 内部结点：决策节点
- 叶子结点：决策结果，可做分类，也可做回归分析

决策树方法简介

→每个结点的决策函数都是定义在d维空间的判别式

将空间有效地分为较小区域
子结点对父结点确定的区域进一步分裂
每个结点的决策函数是一个简单函数
- 不同的函数确定不同的判别式形状和区域形状

→可以快速确定输入的区域

对于二值分类，每次决策可以排除一半的实例
如果是 $k$ 个类别，可在 $log_2k$ 次决策后找到答案

→可解释性好

可写成容易理解的决策规则

构建决策树

决策树的构建方法

→只采用一个输入维

处理离散变量
- 根据属性值的多少确定分支数量
- 如果是连续数值，则离散化处理
处理连续变量
- 根据数值确定阈值： $f_m(x):x_j>w_{m0}$
- 将空间一分为二

→构造一棵决策树

$L_m=\{x|x_j>w_{m0}\}\\ R_m=\{x|x_j\leq w_{m0}\}\\ 两个区域相互正交，叶子节点定义输入空间的矩形$

→单变量决策树：每次分裂只用一个特征

根据训练样本构造的决策树，称为树归纳。
给定的训练集可以构造很多的编码树，要找到最优树：
- 节点数量
- 决策函数复杂度
- NP完全问题
→通常采用贪心算法

单变量决策树的构建问题

→多特征样本在构建时的特征变量选择

不同的变量分裂结果不同
离散/连续变量分裂也存在差别

→何时分裂会得到最终结果？

没有特征变量时，分裂自然终止
如果还存在可用的特征变量，是否继续分裂？

→建立决策树过程中的评价方法

熵和定义基于熵的评价指标
基尼系数
分类误差

ID3算法

输入输出

输入:

训练数据集 $D$ ，包含若干样本,每个样本有 $d$ 个特征和一个类别标签。
特征集 $A=\{ A_1,A_2,\cdots,A_d \}$ 。
目标属性（类别标签） $C$ 。

输出：一棵决策树。

算法步骤：

检查终止条件

满足以下任意条件，停止分裂，返回叶子结点：
1. 所有样本属于同一类。
2. 无剩余特征可用。
3. 样本集为空（极少发生）。
选择最优分裂特征

对剩余特征逐个计算信息增益，选择增益最大的特征作为当前结点的分裂特征：
1. 计算数据集的熵
  
  $Entropy(D)=-\sum_{k=1}^Kp_k\ log_2\ p_k$
2. 计算特征 $A_i$ 的信息增益
  
  $IG(D,A_i)=Entropy(D)-\sum_{v\in Values(A_i)}\frac{|D_v|}{|D|}Entropy(D_v)$
  
  $Values(A_i)$ ：特征 $A_i$ 的所有可能取值。
  
  $D_v$ ： $D$ 中 $A_i=v$ 的子集。
3. 选择信息增益最大的特征

$A_{best}=arg\ maxIG(D,A_i)$

按特征值分裂数据集

根据 $A_{best}$ 的取值，将 $D$ 划分为若干子集 $D_v$ ，每个子集对应一个分支。

ID3算法存在的问题
- 只能处理离散属性
- 更多值属性偏向问题：当一个属性具有大量可能值时，ID3算法倾向于选择该属性进行分裂，即使它可能不是最有信息量的属性。如：ID号可能会被优先选择，因为它的可能值很多。

C4.5算法

改进：
- 连续属性的离散化
- 解决多值属性的偏向
  - 信息增益计算的标准化
    
    引入增益率，通过特征的固有信息对信息增益进行归一化：
    
    $I_R(D,A)=\frac{I(A,D)}{H_A(D)}\\ （H_A(D)=-\sum_{i=1}^n\frac{|D_i|}{D}log_2\frac{|D_i|}{D}）$
    
    $I_R(D,A)$ ：增益率。
    
    $H_A(D)$ :固有信息，衡量特征 $A_i$ 的取值分布的均匀性。
    
    其中n为特征 A 的类别数， Di为特征 A的第i个取值对应的样本个数，|D| 为样本个数。

CART算法

特点
- 使用基尼系数选择分裂用的最优特征
- 建立的决策树是二叉树
基尼系数的计算

假设有K个类别，第k个类别的概率为pk , 则基尼系数的表达式为：

对于二值分类：

对于样本D，如果根据特征A的某个值a，把D分成D1和D2两部分，则在特征A的条件下，D的基尼系数表达式：

对于个给定的样本D，假设有K个类别，第k个类别的数量|Ck|为，则样本D的基尼系数表达式为：
连续属性的离散化处理
处理思路与C4.5一样，衡量的标准是基尼系数，连续属性还会参与后续的结点分裂
二叉树的实现
找到基尼系数最小的二分结果
例如{A2}和{A1, A3}，建立二叉树
后续还有机会对结点{A1, A3}按照特征A进行分裂
算法描述
算法输入是训练集D，基尼系数的阈值，样本数量的阈值输出是决策树T

对于当前结点的数据集为D，如果样本个数小于阈值或者没有特征，则返回决策子树，当前结点停止递归；
计算样本集D的基尼系数，如果基尼系数小于阈值，则返回决策树子树，当前结点停止递归；
计算当前结点现有的各个特征的各个特征值对数据集D的基尼系数；
在计算出来的各个特征的各个取值对数据集D的基尼系数中，选择基尼系数最小的特征A和对应的取值a。根据这个最优特征和最优值，把数据集分裂成两部分D1和D2，同时建立当前结点的左右结点，左结点的数据集为D1，右结点的数据集为D2；
对左右的子结点递归的调用1-4步，生成决策树。

特殊处理

CART的叶子结点的不纯性不一定降到最低：叶子结点中的样本可能会属于多个类
在用CART树做预测时，选择训练样本所占比例最大的类别作为预测结果
或者在构建决策树时，将叶子结点的类别标签选择为比例最大的训练样本类别
建立回归树
- ID3和C4.5只建立分类树
  这一点限制了两个算法的使用范围
- CART的长处除了计算量小以外，还有该算法既可以做分类又可以做回归
- CART的回归树和分类树大同小异
  回归的输出是连续的
  设置为到达该结点所有样本实例输出的均值
  分裂属性选择的衡量标准是分类误差
均方误差度量
定义二值化的指示函数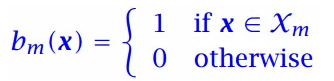

结点m的预测输出：

结点m的误差：
分裂的操作
如果结点m的误差太大，不能接受（根据预设的阈值判断），需要对结点进行分裂
在众多选的分裂结果中选择诸分支误差和最小的，每次递归的分裂都是得到二分的结果
对于结点m的分支 j：

分裂后的总误差：
误差阈值
- 调节模型复杂程度的超参数
- 图片为误差阈值降低后树的变化
  
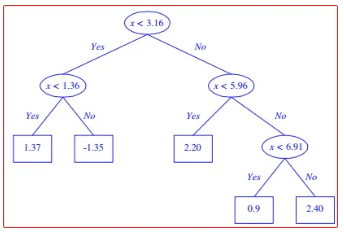
  过拟合

过拟合问题：不要期望把结点的不纯性降到最低，小于某个阈值即可

剪枝

先剪枝

到达一个结点的实例数小于训练集的某个百分比（设个阈值，例如5%），然后就停止该结点的进一步分裂。速度快，但效果不是很理想。

后剪枝

先让树完全增长至零训练误差或者结点不纯性降到最低，然后剪掉导致过拟合的子树。
后剪枝是全局搜索，效果更好，但会很慢。

几种量化结点纯度的指标对比

在这里插入图片描述

                          基尼系数是熵的一个很好的近似

熵与信息增益

熵的概念

——熵度量了事物的不确定性

越不确定的事物，熵越大
随机事件X的熵定义：

$H(X)=-\sum_{i=1}^np_ilogp_i$
联合熵：

$H（X,Y)=-\sum p(x_i,y_i)logp(x_i,y_i)$

条件熵

$H(X|Y)=-\sum p(x_i,y_i)logp(x_i|y_i)=\sum p(y_j)H(X|y_j)$

信息增益

信息增益也称为互信息
定义如下：

$I (X, Y) = H (X) - H (X ∣ Y)$

在这里插入图片描述

计算实例：

在这里插入图片描述

树结点度量指标

→度量结点的不纯性

用熵描述结点m的不纯性

$I_m=H(C)=-\sum_{i=1}^Kp_m^ilogp_m^i$

$p_m^i$ 表示第 $i$ 类样本所占比例

如果结点不需要分裂（到达结点m的所有实例只属于一个类别C，没有不确定性），则不纯性 $I_m=0$ ，即 $H (C) - 0$ 。
子结点不纯性的计算

假设父节点 $m$ 的离散属性有n个取值，即有n个输出
- 连续属性有两个输出 $(n = 2)$ ，有如下统计：
$\sum_{j=1}^nN_{mj}=N_m$

$N_{mj}$ 个实例中有 $N_{mj}^i$ 个属于类 $C_i$

$\sum_{i=1}^K N_{mj}^i = N_{mj}\qquad \sum_{i=1}^n N_{mj}^i=N_m^i$

$\hat p(C_i|x,m,j)=p_{ml}^i=\frac{N_{mj}^i}{N_{mj}}$

n个子结点的总不纯度为：

分裂选用的特征

每次分裂需要选择特定的属性进行
- 选择的策略：
  - 能使不纯度下降最大的属性：
    
    $I_m-I_m^{AH}$
  - 能使信息增益最大的属性
    
    两个随机变量之间的统计依赖性或信息共享程度
    
    衡量已知一个变量的信息后，另一个变量的不确定性减少的程度
  $I(X_m, C_{mj})=H(X_m)-H(X_m|C_{mj})$

连续属性的处理

通常，构建决策树时只考虑使用离散属性
而连续属性需要转换成只有两个取值的离散属性
可以选择使用所可能取值的平均值/均值作为阈值。

决策树C4.5算法的处理

设样本的连续属性有m个不同取值，将所有取值排序，取所有相邻的两个值，计算他们的均值，从而得到 $m - 1$ 个均值，将它们作为候选阈值。测试用每个阈值分裂二值结果的互信息，选择能带来最大互信息的均值作为最后的阈值进行二值分裂。

使用决策树

决策树的每一条从根到叶子的路径：对应的条件的合取（AND）。
对于分类树，可能有过个叶子被标记为相同的类：多个路径对应的条件用析取（OR）。
各个路径可以用IF-THEN规则表示

几种经典模型的对比

| 算法 | 支持
模型 | 树结构 | 特征选择 | 连续值
处理 | 缺失值
处理 | 剪枝 |
| — | — | — | — | — | — | — |
| ID3 | 分类 | 多叉树 | 信息增益 | 不支持 | 不支持 | 不支持 |
| C4.5 | 分类 | 多叉树 | 信息增益比 | 支持 | 支持 | 支持 |
| CART | 分类，
回归 | 二叉树 | 基尼系数，
均方差 | 支持 | 支持 | 支持 |

决策树模型评价

优点

1）简单直观，生成的决策树很直观

2）基本不需要预处理，不需要提前归一化

3）相比于神经网络之类的黑盒分类模型，决策树在逻辑上
可以得到很好的解释

4）可以交叉验证的剪枝来选择模型，从而提高泛化能力

5）对于异常点的容错能力好，健壮性高。

缺点

决策树算法非常容易过拟合，导致泛化能力不强

通常把决策树用作基准模型（baseline）
或作为集成学习的弱学习模型

决策树会因为样本发生一点点的改动，就会导致树
结构的剧烈改变
寻找最优的决策树是一个NP难的问题，我们一般是
通过启发式方法，容易陷入局部最优。

总结

每个类可能存在对各分支对应的多个解释和描述
- 这些不同的解释可能会在空间中不相交
不必考虑各个区域（特征子空间）上的分布信息
- 直接对分离类实例的判别式进行编码
属于基于判别式的（discriminant-based）方法
更多地应用于分类

决策树

决策树概述

决策树——非参数机器学习方法

决策树特点

决策树方法简介

构建决策树

决策树的构建方法

单变量决策树的构建问题

ID3算法

输入输出

C4.5算法

CART算法

剪枝

几种量化结点纯度的指标对比

熵与信息增益

熵的概念

信息增益

计算实例：

树结点度量指标

分裂选用的特征

连续属性的处理

决策树C4.5算法的处理

使用决策树

几种经典模型的对比

决策树模型评价

总结

相关文章：