当前位置：首页 > news >正文

C++ AVL树的实现

news 来源：原创 2025/6/16 6:22:03

在上一篇博客我们学习了二叉搜索树的实现，现在我们开始手动实现AVL树。

二叉搜索树-CSDN博客

1.AVL树的概念

AVL树是最先发明的⾃平衡⼆叉查找树，AVL是⼀颗空树，或者具备下列性质的⼆叉搜索树：它的左右⼦树都是AVL树，且左右⼦树的⾼度差的绝对值不超过1。AVL树是⼀颗⾼度平衡搜索⼆叉树，通过控制⾼度差去控制平衡。

AVL树实现这⾥我们引⼊⼀个平衡因⼦(balance factor)的概念，每个结点都有⼀个平衡因⼦，任何结点的平衡因⼦等于右⼦树的⾼度减去左⼦树的⾼度，也就是说任何结点的平衡因⼦等于0/1/-1，AVL树并不是必须要平衡因⼦，但是有了平衡因⼦可以更⽅便我们去进⾏观察和控制树是否平衡，就像⼀个⻛向标⼀样。

AVL树整体结点数量和分布和完全⼆叉树类似，⾼度可以控制在logN ，那么增删查改的效率也可以控制在 O(logN )，相⽐⼆叉搜索树有了本质的提升。

这里我们展示了一棵树的平衡因子（右子树的高度-左子树的高度）

当平衡因子变成2之后说明该树已经不平衡了，我们AVL树的目的就是不仅要让该树是二叉搜索树，还要平衡。

2、AVL树的实现

2.1AVL树的结构

结合我们二叉搜索树的部分，这里我们节点的结构需要使用KV结构再加上一个parent的节点（方便寻找父节点，这里方便之后旋转的操作和理解），再加上一个平衡因子。

#pragma oncetemplate<class K,class V>
struct AVLTreeNode
{typedef AVLTreeNode Node;pair<K, V> _kv;Node<K, V>* _left;Node<K, V>* _right;Node<K, V>* _parent;int _bf;AVLTreeNode(const pair<K,V>& kv):_kv(kv),_left(nullptr), _right(nullptr), _parent(nullptr), _bf(0){}
};template<class K,class V>
class AVLTree
{typedef AVLTreeNode Node;
public:private:Node<K,V>* _root=nullptr;
};

2.2AVL树的插入

2.2.1插入的大概流程

1.首先因为AVL树要满足二叉搜索树，所以我们可以按照二叉搜索树那部分先来写。

2.新增节点后根据不同的情况更新平衡因子。

3.根据平衡因子做旋转调整。

2.2.2平衡因子的更新

更新原则：
• 平衡因⼦ = 右⼦树⾼度-左⼦树⾼度
• 只有⼦树⾼度变化才会影响当前结点平衡因⼦。
• 插⼊结点，会增加⾼度，所以新增结点在parent的右⼦树，parent的平衡因⼦++，新增结点在parent的左⼦树，parent平衡因⼦--
• parent所在⼦树的⾼度是否变化决定了是否会继续往上更新

更新停⽌条件：有三种情况

• 更新后parent的平衡因⼦等于0，更新中parent的平衡因⼦变化为-1->0 或者 1->0，说明更新前parent⼦树⼀边⾼⼀边低，新增的结点插⼊在低的那边，插⼊后parent所在的⼦树⾼度不变，不会影响parent的⽗亲结点的平衡因⼦，更新结束。

• 更新后parent的平衡因⼦等于1 或 -1，更新前更新中parent的平衡因⼦变化为0->1 或者 0->-1，说明更新前parent⼦树两边⼀样⾼，新增的插⼊结点后，parent所在的⼦树⼀边⾼⼀边低，parent所在的⼦树符合平衡要求，但是⾼度增加了1，会影响parent的⽗亲结点的平衡因⼦，所以要继续向上更新。

• 更新后parent的平衡因⼦等于2 或 -2，更新前更新中parent的平衡因⼦变化为1->2 或者 -1->-2，说明更新前parent⼦树⼀边⾼⼀边低，新增的插⼊结点在⾼的那边，parent所在的⼦树⾼的那边更⾼了，破坏了平衡，parent所在的⼦树不符合平衡要求，需要旋转处理，旋转的⽬标有两个：1、把parent⼦树旋转平衡。2、降低parent⼦树的⾼度，恢复到插⼊结点以前的⾼度。所以旋转后也不需要继续往上更新，插⼊结束。

• 不断更新，更新到根，跟的平衡因⼦是1或-1也停⽌了。

2.2.3插入和更新平衡因子的实现

	bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent=nullptr;Node* cur = _root;while (cur){parent = cur;if (cur->_kv.first > kv.first){cur = cur->_left;}else if (cur->_kv.first < kv.first){cur = cur->_right;}else{return false;}}cur=new Node(kv);if (kv.first > parent->_kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//更新平衡因子while(parent){if (cur==parent->_right)parent->_bf++;else {parent->_bf--;}if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else if (parent->_bf == 0){break;}else{//旋转}}}

2.3 旋转

2.3.1 旋转的原则

1. 保持搜索树的规则

2. 让旋转的树从不满⾜变平衡，其次降低旋转树的⾼度

旋转总共分为四种，左单旋/右单旋/左右双旋/右左双旋。

2.3.2 右单旋

• 本图1展⽰的是10为根的树，有a/b/c抽象为三棵⾼度为h的⼦树(h>=0)，a/b/c均符合AVL树的要

求。10可能是整棵树的根，也可能是⼀个整棵树中局部的⼦树的根。这⾥a/b/c是⾼度为h的⼦树，

是⼀种概括抽象表⽰，他代表了所有右单旋的场景，实际右单旋形态有很多种，具体图2/图3/图4/

图5进⾏了详细描述。

• 在a⼦树中插⼊⼀个新结点，导致a⼦树的⾼度从h变成h+1，不断向上更新平衡因⼦，导致10的平

衡因⼦从-1变成-2，10为根的树左右⾼度差超过1，违反平衡规则。10为根的树左边太⾼了，需要

往右边旋转，控制两棵树的平衡。

• 旋转核⼼步骤，因为5 < b⼦树的值 < 10，将b变成10的左⼦树，10变成5的右⼦树，5变成这棵树新的根，符合搜索树的规则，控制了平衡，同时这棵的⾼度恢复到了插⼊之前的h+2，符合旋转原

则。如果插⼊之前10整棵树的⼀个局部⼦树，旋转后不会再影响上⼀层，插⼊结束了。

void RotateR(Node* parent)
{Node* parentL = parent->_left;Node* parentLR = parentL->_right;Node* parentPa = parent->_parent;if (parentPa){if (parent == parentPa->_left)parentPa->_left = parentL;elseparentPa->_right = parentL;}if(parentLR)parentLR->_parent = parent;parent->_parent = parentL;parent->_left = parentLR;parentL->_right = parent;parentL->_parent = parentPa;//更新平衡因子parent->_bf = 0;parentL->_bf = 0;
}

2.3.3 左单旋

与右单旋同理，不过是换了一个方向。

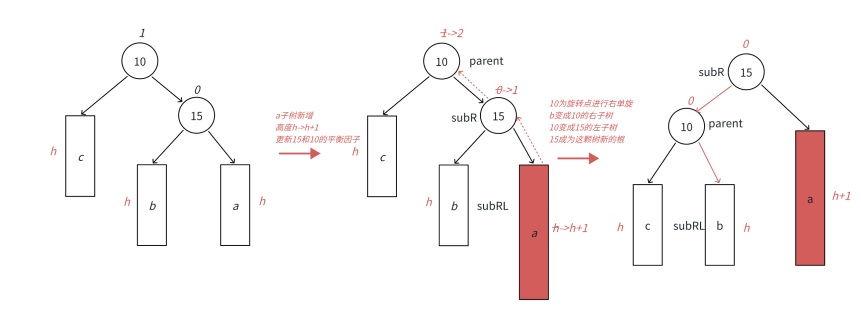
• 本图6展⽰的是10为根的树，有a/b/c抽象为三棵⾼度为h的⼦树(h>=0)，a/b/c均符合AVL树的要
求。10可能是整棵树的根，也可能是⼀个整棵树中局部的⼦树的根。这⾥a/b/c是⾼度为h的⼦树，
是⼀种概括抽象表⽰，他代表了所有右单旋的场景，实际右单旋形态有很多种，具体跟上⾯左旋类
似。

• 在a⼦树中插⼊⼀个新结点，导致a⼦树的⾼度从h变成h+1，不断向上更新平衡因⼦，导致10的平
衡因⼦从1变成2，10为根的树左右⾼度差超过1，违反平衡规则。10为根的树右边太⾼了，需要往
左边旋转，控制两棵树的平衡。

• 旋转核⼼步骤，因为10 < b⼦树的值 < 15，将b变成10的右⼦树，10变成15的左⼦树，15变成这棵树新的根，符合搜索树的规则，控制了平衡，同时这棵的⾼度恢复到了插⼊之前的h+2，符合旋转原则。如果插⼊之前10整棵树的⼀个局部⼦树，旋转后不会再影响上⼀层，插⼊结束了。

void RotateL(Node* parent)
{Node* parentR = parent->_right;Node* parentRL = parentR->_left;Node* parentPa = parent->_parent;if (parentPa){if (parent == parentPa->_left)parentPa->_left = parentR;elseparentPa->_right = parentR;}if(parentRL)parentRL->_parent = parent;parent->_parent = parentR;parent->_right = parentRL;parentR->_parent = parentPa;parentR->_left = parent;//更新平衡因子parent->_bf = 0;parentR->_bf = 0;}

2.3.3 左右双旋

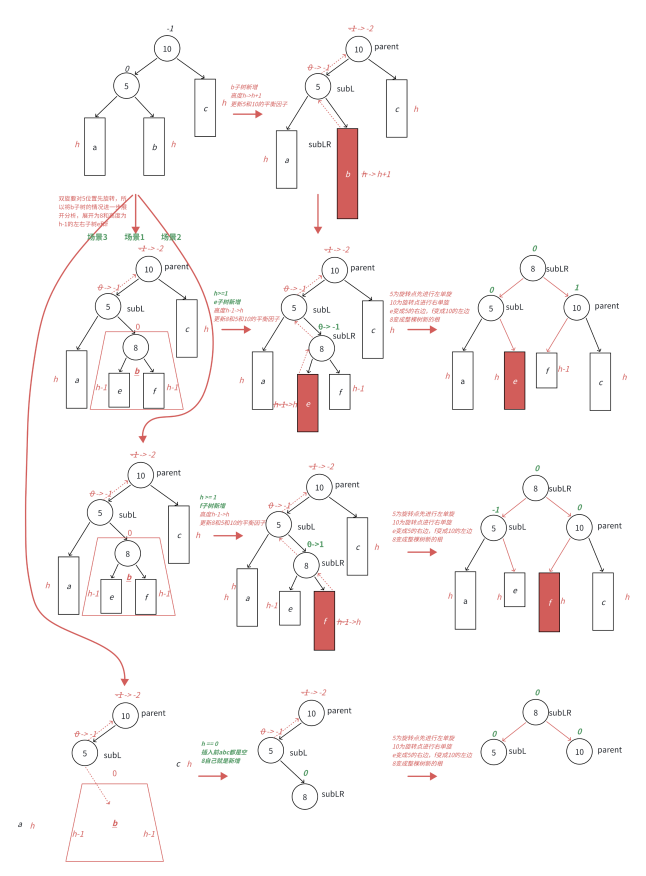
还是拿出抽象图。左单旋和右单旋是针对图中a增加，c增加的话其实并不影响，那么如果是b增加的场景呢，这是一个右单旋或者左单旋就不够看了。

通过图可以看到，左边⾼时，如果插⼊位置不是在a⼦树，⽽是插⼊在b⼦树，b⼦树⾼度从h变成h+1，引发旋转，右单旋⽆法解决问题，右单旋后，我们的树依旧不平衡。右单旋解决的纯粹的左边⾼，但是插⼊在b⼦树中，10为跟的⼦树不再是单纯的左边⾼，对于10是左边⾼，但是对于5是右边⾼，需要⽤两次旋转才能解决，以5为旋转点进⾏⼀个左单旋，以10为旋转点进⾏⼀个右单旋，这棵树这棵树就平衡了。

• 图分别为左右双旋中h==0和h==1具体场景分析，下⾯我们将a/b/c⼦树抽象为⾼度h的AVL
⼦树进⾏分析，另外我们需要把b⼦树的细节进⼀步展开为8和左⼦树⾼度为h-1的e和f⼦树，因为
我们要对b的⽗亲5为旋转点进⾏左单旋，左单旋需要动b树中的左⼦树。b⼦树中新增结点的位置
不同，平衡因⼦更新的细节也不同，通过观察8的平衡因⼦不同，这⾥我们要分三个场景讨论。
• 场景1：h >= 1时，新增结点插⼊在e⼦树，e⼦树⾼度从h-1并为h并不断更新8->5->10平衡因⼦，引发旋转，其中8的平衡因⼦为-1，旋转后8和5平衡因⼦为0，10平衡因⼦为1。
• 场景2：h >= 1时，新增结点插⼊在f⼦树，f⼦树⾼度从h-1变为h并不断更新8->5->10平衡因⼦，引发旋转，其中8的平衡因⼦为1，旋转后8和10平衡因⼦为0，5平衡因⼦为-1。
• 场景3：h == 0时，a/b/c都是空树，b⾃⼰就是⼀个新增结点，不断更新5->10平衡因⼦，引发旋
转，其中8的平衡因⼦为0，旋转后8和10和5平衡因⼦均为0。

void RotateLR(Node* parent)
{int bf = parent->_left->_right->_bf;Node* parentL = parent->_left;Node* parentLR = parentL->_right;RotateL(parent->_left);RotateR(parent);//更新平衡因子if (bf == 1){parentL->_bf = -1;parent->_bf = 0;parentLR->_bf = 0;}else if (bf == -1){parentL->_bf = 0;parent->_bf = 1;parentLR->_bf = 0;}else if (bf == 0){parentL->_bf = 0;parent->_bf = 0;parentLR->_bf = 0;}else{assert(1);}
}

2.3.4 右左双旋

• 跟左右双旋类似，下⾯我们将a/b/c⼦树抽象为⾼度h的AVL⼦树进⾏分析，另外我们需要把b⼦树的细节进⼀步展开为12和左⼦树⾼度为h-1的e和f⼦树，因为我们要对b的⽗亲15为旋转点进⾏右单
旋，右单旋需要动b树中的右⼦树。b⼦树中新增结点的位置不同，平衡因⼦更新的细节也不同，通
过观察12的平衡因⼦不同，这⾥我们要分三个场景讨论。

• 场景1：h >= 1时，新增结点插⼊在e⼦树，e⼦树⾼度从h-1变为h并不断更新12->15->10平衡因
⼦，引发旋转，其中12的平衡因⼦为-1，旋转后10和12平衡因⼦为0，15平衡因⼦为1。
• 场景2：h >= 1时，新增结点插⼊在f⼦树，f⼦树⾼度从h-1变为h并不断更新12->15->10平衡因⼦，
引发旋转，其中12的平衡因⼦为1，旋转后15和12平衡因⼦为0，10平衡因⼦为-1。
比特就业课
• 场景3：h == 0时，a/b/c都是空树，b⾃⼰就是⼀个新增结点，不断更新15->10平衡因⼦，引发旋
转，其中12的平衡因⼦为0，旋转后10和12和15平衡因⼦均为0。

void RotateR(Node* parent)
{Node* parentL = parent->_left;Node* parentLR = parentL->_right;Node* parentPa = parent->_parent;if (parentPa){if (parent == parentPa->_left)parentPa->_left = parentL;elseparentPa->_right = parentL;}if(parentLR)parentLR->_parent = parent;parent->_parent = parentL;parent->_left = parentLR;parentL->_right = parent;parentL->_parent = parentPa;//更新平衡因子parent->_bf = 0;parentL->_bf = 0;
}

2.4 AVL树的查找

那⼆叉搜索树逻辑实现即可，搜索效率为 O(logN)

Node* Find(const K& key)
{Node * cur=_root;while (cur){if (cur->_kv.first > key){cur = cur->_left;}else if (cur->_kv.first < key){cur = cur->_right;}else{return cur;}}return nullptr;
}

2.5 AVL树插入的检测

我们实现的AVL树是否合格，我们通过检查左右⼦树⾼度差的的程序进⾏反向验证，同时检查⼀下结点的平衡因⼦更新是否出现了问题。

结合检测所需要的代码，全部代码如下：

#include<iostream>
#include<set>
#include<map>
#include <utility>
using namespace std;
#include<assert.h>
#include<vector>template<class K,class V>
struct AVLTreeNode
{pair<K,V> _kv;AVLTreeNode<K,V>* _left;AVLTreeNode<K,V>* _right;AVLTreeNode<K,V>* _parent;int _bf;AVLTreeNode(const pair<K,V>& kv):_kv(kv),_left(nullptr), _right(nullptr), _parent(nullptr), _bf(0){}
};template<class K,class V>
class AVLTree
{typedef AVLTreeNode<K,V> Node;
public:void InOrder(){_InOrder(_root);}void _InOrder(const Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << ' ';_InOrder(root->_right);}bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent=nullptr;Node* cur = _root;while (cur){parent = cur;if (cur->_kv.first > kv.first){cur = cur->_left;}else if (cur->_kv.first < kv.first){cur = cur->_right;}else{return false;}}cur=new Node(kv);if (kv.first > parent->_kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//更新平衡因子while(parent){if (cur==parent->_right)parent->_bf++;else {parent->_bf--;}if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else if (parent->_bf == 0){break;}else{//旋转if (parent->_bf == -2 && parent->_left->_bf == -1){//右单旋RotateR(parent);}else if (parent->_bf == 2 && parent->_right->_bf==1){//左单旋RotateL(parent);}else if (parent->_bf == -2 && parent->_left->_bf == 1){//左右双旋RotateLR(parent);}else if (parent->_bf == 2 && parent->_right->_bf == -1){//右左双旋RotateRL(parent);}else{assert(1);}return true;}}return true;}void RotateRL(Node* parent){int bf = parent->_right->_left->_bf;Node* parentR = parent->_right;Node* parentRL = parentR->_left;RotateR(parent->_right);RotateL(parent);//更新平衡因子if (bf == 1){parent->_bf = -1;parentR->_bf = 0;parentRL = 0;}else if (bf == -1){parent->_bf = 0;parentR->_bf = 1;parentRL = 0;}else if (bf == 0){parent->_bf = 0;parentR->_bf = 0;parentRL = 0;}else{assert(1);}}void RotateLR(Node* parent){int bf = parent->_left->_right->_bf;Node* parentL = parent->_left;Node* parentLR = parentL->_right;RotateL(parent->_left);RotateR(parent);//更新平衡因子if (bf == 1){parentL->_bf = -1;parent->_bf = 0;parentLR->_bf = 0;}else if (bf == -1){parentL->_bf = 0;parent->_bf = 1;parentLR->_bf = 0;}else if (bf == 0){parentL->_bf = 0;parent->_bf = 0;parentLR->_bf = 0;}else{assert(1);}}void RotateR(Node* parent){Node* parentL = parent->_left;Node* parentLR = parentL->_right;Node* parentPa = parent->_parent;if (parentPa){if (parent == parentPa->_left)parentPa->_left = parentL;elseparentPa->_right = parentL;}if(parentLR)parentLR->_parent = parent;parent->_parent = parentL;parent->_left = parentLR;parentL->_right = parent;parentL->_parent = parentPa;//更新平衡因子parent->_bf = 0;parentL->_bf = 0;}void RotateL(Node* parent){Node* parentR = parent->_right;Node* parentRL = parentR->_left;Node* parentPa = parent->_parent;if (parentPa){if (parent == parentPa->_left)parentPa->_left = parentR;elseparentPa->_right = parentR;}if(parentRL)parentRL->_parent = parent;parent->_parent = parentR;parent->_right = parentRL;parentR->_parent = parentPa;parentR->_left = parent;//更新平衡因子parent->_bf = 0;parentR->_bf = 0;}Node* Find(const K& key){Node * cur=_root;while (cur){if (cur->_kv.first > key){cur = cur->_left;}else if (cur->_kv.first < key){cur = cur->_right;}else{return cur;}}return nullptr;}int Height(Node* root){return _Height(_root);}int _Height(Node* root){if (root == nullptr)return 0;int heightleft = _Height(root->_left);int heightright = _Height(root->_right);return heightleft > heightright ? heightleft + 1 : heightright + 1;}bool IsBalanceTree(){return _IsBalanceTree(_root);}bool _IsBalanceTree(Node* root){if (root == nullptr)return true;int heightleft = _Height(root->_left);int heightright = _Height(root->_right);int diff = heightright - heightleft;if (abs(diff) >= 2){cout << "高度差异常" << endl;return false;}if (root->_bf != diff){cout << "平衡因子异常" << endl;return false;}return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);}
private:Node* _root=nullptr;
};void TestAVLTree1()
{AVLTree<int, int> t;// 常规的测试?例//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };// 特殊的带有双旋场景的测试?例int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };for (auto e : a){t.Insert({ e, e });}t.InOrder();cout << t.IsBalanceTree() << endl;
}void TestAVLTree2()
{const int N = 100000;vector<int> v;v.reserve(N);srand(time(0));for (size_t i = 0; i < N; i++){v.push_back(rand()+ i);}size_t begin2 = clock();AVLTree<int, int> t;for (auto e : v){t.Insert(make_pair(e, e));}size_t end2 = clock();size_t begin1 = clock();//确定在的值for (auto e : v){t.Find(e);}//随机值/*for (size_t i = 0; i < N; i++){t.Find((rand() + i));}*/size_t end1 = clock();cout << "Find:" << end1 - begin1 << endl;
}int main()
{TestAVLTree1();TestAVLTree2();return 0;
}

2.6 AVL树的删除

学习AVL树我们的主要目的是学会旋转的逻辑，删除与插入的逻辑其实差不了很多，有兴趣的小伙伴可以自行编写，或者看以下博客：

AVL树图解（插入与删除）_avl树的删除-CSDN博客