当前位置：首页 > news >正文

LLM数学推导——Transformer问题集——注意力机制——稀疏/高效注意力

news 来源：原创 2025/6/22 16:55:21

Q13 局部窗口注意力的内存占用公式推导（窗口大小 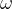$\omega$ ）

局部窗口注意力：解决长序列内存困境的利器

在注意力机制中，全局注意力需要计算序列中每个元素与其他所有元素的关联，当序列长度 N 较大时，权重矩阵的内存占用达到 $O(N^2)$ ，这在长文本处理等场景下会导致内存爆炸。局部窗口注意力应运而生，它限制每个元素仅与局部窗口大小为 $\omega$ 的元素计算注意力，将权重矩阵的内存复杂度降至 $O(N\omega)$ （ $\omega \ll N$ 时），有效解决了长序列处理的内存瓶颈问题。

内存占用公式推导：抽丝剥茧，步步为营

设输入序列长度为 N，隐藏层维度为 d，从组成局部窗口注意力的各个矩阵入手推导内存占用：

1. Q、K、V 矩阵的内存占用

查询矩阵 Q、键矩阵 K、值矩阵 V 的形状通常均为 $N \times d$ 。以单个矩阵为例，每个元素占据一定的内存空间（如在 PyTorch 中，单精度浮点数占 4 字节，但此处从抽象维度计算元素数量），则单个矩阵的内存占用为 $N \times d$ 。三者总内存占用为： $3 \times N \times d = 3Nd$

2. 注意力权重矩阵的内存占用

在局部窗口注意力中，每个位置仅关注 $\omega$ 个元素，因此权重矩阵的形状为 $N \times \omega$ 。其内存占用为： $N \times \omega = N\omega$ 这一步的关键在于理解 “局部” 的限制：相比全局注意力 $N \times N$ 的权重矩阵，局部窗口将每一行的计算量从 N 压缩到 $\omega$ ，极大减少了权重矩阵的元素数量。

3. 输出矩阵的内存占用

输出矩阵是对值矩阵 V 的加权聚合，形状为 $N \times d$ ，内存占用为： $N \times d = Nd$

总内存占用公式

将上述三部分相加，得到局部窗口注意力的总内存占用公式： $\text{AllMem} = 3Nd + N\omega + Nd = N(4d + \omega)$ 通过这个公式可以清晰看到，内存占用与序列长度 N、隐藏维度 d、窗口大小 $\omega$ 相关，且均为线性或低阶关系，远低于全局注意力的 $O(N^2)$ 复杂度。

在 LLM 中的应用：长序列处理的效率革命

在大语言模型（LLM）中，处理长文本（如文档、对话历史）时，全局注意力的高内存占用会导致计算效率低下，甚至无法处理。局部窗口注意力通过限制 $\omega$ ，在保持对局部语义关联捕捉能力的同时，大幅降低内存。例如，当 N = 4096、 $\omega = 128$ 、 $d = 1024$ 时，全局注意力权重矩阵内存为 $4096 \times 4096$ ，而局部窗口仅为 $4096 \times 128$ ，内存节省显著。这使得 LLM 能够在有限硬件资源下高效处理长序列，提升模型的实用性和扩展性。

代码示例与深度解读

import torch  # 模拟输入参数  
N = 1024  # 序列长度，可调整以测试不同规模输入  
d = 512   # 隐藏层维度，常见于许多LLM架构  
omega = 16# 窗口大小，根据任务需求和硬件限制选择  # 定义 Q、K、V 矩阵（简化示例，实际中由模型层如线性层生成）  
Q = torch.randn(N, d, requires_grad=True)  
K = torch.randn(N, d, requires_grad=True)  
V = torch.randn(N, d, requires_grad=True)  # 此处省略具体局部窗口注意力计算逻辑（需按窗口索引提取 K、V 子集）  
# 仅示意内存相关的核心参数设置与操作

可学习投影层模拟：代码中 Q、K、V 用随机张量生成，实际在 LLM 中，这些矩阵由线性层对输入嵌入进行变换得到。requires_grad=True 表示这些矩阵是可学习的，在反向传播中会计算梯度以更新参数。
参数意义：N 决定序列长度，d 影响隐藏层表达能力， $\omega$ 直接控制局部窗口的范围。通过调整这些参数，可在模型性能与内存占用间取得平衡。
内存监控延伸：实际应用中，可通过 torch.cuda.memory_allocated() 等函数监控内存使用。若内存异常增长，需检查窗口索引逻辑是否正确，或是否意外生成了大尺寸中间张量。

总结：理论与实践的完美融合

局部窗口注意力的内存占用公式 $N(4d + \omega)$ 深刻揭示了其优化机制：通过限制窗口大小 $\omega$ ，将内存复杂度从全局注意力的 $O(N^2)$ 降至线性相关的 $O(N\omega)$ 。在 LLM 中，这一机制使得长序列处理成为可能，提升了模型的效率与可扩展性。代码实现虽需精细处理窗口索引等细节，但核心思想清晰 —— 以局部计算换内存优化。这一过程体现了理论推导对工程实践的指导意义，也展示了注意力机制在实际应用中的智慧优化。

Q14 LSH 注意力中哈希桶分配的期望误差分析

LSH 注意力：LLM 长序列加速的 “近似计算器”

在大语言模型（LLM）处理上万字文档或多轮对话时，全局注意力的 $O(N^2)$ 计算量如同 “大象跳舞”，内存和算力双双告急。LSH（局部敏感哈希）注意力则像一位精打细算的 “管家”，通过哈希函数将相似 token 快速 “分组” 到同一个桶里，让注意力只在桶内计算，把复杂度压到 $O(N \log N)$ 。但这种 “分组” 并非万无一失 —— 今天我们就来算算，哈希桶分配过程中那些 “小失误” 会带来多大误差。

误差的两面性：假阴性与假阳性的 “恶作剧”

想象 LLM 在生成句子 “我想买一斤红苹果” 时：

假阴性：“苹果” 和 “水果” 本应同桶互动，却因哈希误差被分到不同桶，模型可能漏看它们的上下位关系，导致后续生成 “这种蔬菜富含维生素” 的逻辑错误；
假阳性：“苹果” 和 “乔布斯” 被误分同桶（仅因向量空间中偶然接近），模型可能强行关联，输出 “我想买一斤乔布斯设计的苹果” 的诡异内容。

这两种误差就像混入面粉的沙子，虽小却影响整体质量。我们需要用数学工具量化它们的 “破坏力”。

数学建模：从哈希特性到误差公式推导

假设 token 的语义距离用 d 表示（d 越小越相似），局部敏感哈希函数满足：

当 $d \leq d_0$ （强相关），同桶概率为 $p_{\text{near}} = 1 - \delta$ （ $\delta$ 是小误差概率）；
当 $d \geq d_1$ （无关），同桶概率为 $p_{\text{far}} = \epsilon$ （ $\epsilon$ 是小概率噪声）；
当 $d_0 < d < d_1$ （中等相关），同桶概率随距离递减。

设所有 token 对的距离分布为 $f(d)$ ，则期望误差 E 由两部分构成： $E = \underbrace{\int_{0}^{d_0} (1 - p_{\text{near}}) f(d) \, dd}_{\text{EOSCP}} + \underbrace{\int_{d_1}^{\infty} p_{\text{far}} f(d) \, dd}_{\text{ECIP}}$

(漏算强相关对的误差：Error from Omitted Strongly Correlated Pairs，EOSCP‌

误算无关对的误差：Error from Incorrectly Calculated Irrelevant Pairs，ECIP)

第一项衡量 “该算的没算” 的损失，比如漏看 “苹果 - 水果” 的关联；
第二项衡量 “不该算的算了” 的干扰，比如误处理 “苹果 - 乔布斯” 的虚假关联。

在 LLM 中的实战：误差控制的生存之道

1. 长文本场景的误差容忍策略

机器翻译：允许较高假阴性误差（漏看部分词间关联），优先保证翻译速度，因为上下文依赖可通过句法结构部分弥补；
代码生成：需严格控制假阳性误差（避免无关代码片段混入），因此采用多轮哈希验证，先用粗粒度哈希分桶，再用精确余弦相似度筛选候选对。

2. 参数调整的黄金法则

桶数量（B）：增大 B 可降低假阳性（减少跨桶误分），但会增加桶内平均元素数，可能提升假阴性（小桶可能漏装近邻）；
哈希函数敏感度（ $\sigma$ ）：敏感度过高（如投影向量与语义轴垂直）会导致大量假阴性，过低则假阳性激增。实际中常通过预训练数据拟合最优 $\sigma$ 。

代码示例：用 PyTorch 玩转 LSH 注意力的桶分配

import torch  
from torch.nn import Module  class LSHAttention(Module):  def __init__(self, embed_dim, num_buckets=256, hash_scale=10.0):  super().__init__()  self.embed_dim = embed_dim  self.num_buckets = num_buckets  # 随机生成哈希投影矩阵（模拟局部敏感特性）  self.projection = torch.randn(embed_dim, 1) * hash_scale  def get_bucket_indices(self, x):  """将token向量映射到哈希桶索引"""  # 投影到一维空间，类似将高维向量“拍扁”到数轴上  projections = (x @ self.projection).squeeze(-1)  # 离散化到桶区间，取模避免索引越界  return (projections * self.num_buckets).long() % self.num_buckets  def forward(self, Q, K, V):  """Q/K/V形状：(batch_size, seq_len, embed_dim)"""  batch_size, seq_len, _ = Q.shape  attn_output = []  # 1. 为每个token分配桶  q_buckets = self.get_bucket_indices(Q)  k_buckets = self.get_bucket_indices(K)  for b in range(batch_size):  for i in range(seq_len):  # 2. 找到查询token所在的桶  q_bucket = q_buckets[b, i]  # 3. 仅收集同桶的键和值  mask = (k_buckets[b] == q_bucket)  K_sampled = K[b, mask]  V_sampled = V[b, mask]  if K_sampled.numel() == 0:  # 若桶为空，用全零向量避免崩溃（实际可优化为邻近桶查询）  attn_output.append(torch.zeros(self.embed_dim, device=Q.device))  continue  # 4. 计算局部注意力分数  scores = (Q[b, i] @ K_sampled.T) / (self.embed_dim ** 0.5)  attn = torch.softmax(scores, dim=-1) @ V_sampled  attn_output.append(attn)  return torch.stack(attn_output).view(batch_size, seq_len, -1)

代码背后的误差逻辑

投影的局限性：
- 随机投影矩阵可能 “看错” 语义方向。例如，“高兴” 和 “快乐” 的向量在语义空间接近，但投影到某个随机轴上可能因轴方向与语义轴垂直，导致距离计算失真，产生假阴性。
桶数量的 trade-off：
- 若 num_buckets=100，但序列长度 N=10000，平均每个桶有 100 个 token，可能包含大量无关对（假阳性）；若增至 num_buckets=10000，则每个桶仅 1 个 token，导致大量单桶查询（假阴性）。
优化伏笔：
- 代码中 if K_sampled.numel() == 0 的处理暗示了一种误差补偿策略 —— 当桶为空时，可查询邻近桶（类似 “找不到邻居时，问问隔壁楼的人”），降低极端情况下的假阴性。

总结：误差分析如何让 LLM “聪明地犯错”

LSH 注意力的期望误差分析，本质是给模型的 “近似计算” 戴上 “精准度缰绳”。通过数学公式量化假阴性与假阳性的影响，我们能像调音量旋钮一样，根据任务需求（如速度优先或精度优先）调整哈希参数。在 LLM 的工程实践中，这种分析不仅是理论推演，更是指导代码优化的指南针 —— 比如通过监控不同桶的误差率，动态调整投影矩阵或桶数量，让模型在 “犯错” 中保持高效与可靠的平衡。就像人类记忆会自动模糊细节但抓住重点，LSH 注意力让机器学会 “有策略地遗忘”，在万亿 token 的海洋中精准捞取真正需要的 “语义珍珠”。

Q15 块稀疏注意力（Block Sparse）的信息传递延迟建模

块稀疏注意力：长序列的 “分区通信” 机制

在处理超长序列（如数万字文档）时，全局注意力的 “全连接” 特性会导致计算爆炸，而块稀疏注意力则像一位 “城市规划师”，将序列划分为多个固定大小的 “块”（Block），仅允许块内或特定块间的注意力计算。这种 “分区通信” 虽然节省了算力，却带来一个关键问题：信息从序列一端传递到另一端需要多久？ 就像城市中不同区域的居民交流需要通过道路网络，块间的信息传递也需要经过多层 “转发”，我们需要建模这种延迟，确保长程依赖不被割裂。

信息传递延迟：块结构中的 “跨区通信成本”

假设序列被划分为 M 个块，每个块大小为 b（总长度 $N = M \times b$ ）。块稀疏注意力的核心是定义 “允许通信的块对”，例如：

局部块模式：每个块仅与相邻的 k 个块交互（如前 1 块、后 1 块）；
跳跃块模式：每个块与间隔 s 个块的块交互（如每隔 2 块连接）。

信息传递延迟可定义为：信息从任意块 i 传递到块 j 所需的最少注意力层数。例如，在局部块模式中，块 1 的信息需通过块 2→块 3→…→块 M 层层传递，延迟为 $M-1$ 层；而在跳跃块模式中，若每块可跨越 s 块连接，延迟可大幅降低。

数学建模：从图论到延迟公式

将块视为图的节点，块间允许的注意力连接视为图的边，信息传递延迟等价于图中节点间的最短路径长度。以两种典型块模式为例：

1. 一维相邻块模式（局部稀疏）

连接规则：块 i 仅与块 i-1、i、i+1 交互（类似链式结构）。
延迟计算：从块 1 到块 M 的最短路径为 M-1 步（每步移动 1 块），因此最大延迟为 $L_{\text{max}} = M-1$ 层。
公式： $L_{\text{max}} = \frac{N}{b} - 1 \quad (\text{if } N = M \times b)$ 例如，N=4096、b=128 时，M=32，延迟为 31 层，意味着信息需跨 31 层才能从首块传到末块。

2. 跳跃块模式（分层稀疏）

连接规则：第 l 层允许块跨越 $2^l$ 个块交互（类似二叉树分层）。
延迟计算：通过分层跳跃，最大延迟可降至对数级别。例如：
- 层 1：块内交互（延迟 0）；
- 层 2：相邻 2 块交互（跨度 2）；
- 层 3：跨度 4 块交互；
- …
- 最大延迟 $L_{\text{max}} = \log_2 M$ 层。
公式： $L_{\text{max}} = \log_2 \left(\frac{N}{b}\right)$ 同样 N=4096、b=128时，M=32，延迟仅为 5 层（ $\log_2 32 = 5$ ），相比相邻模式大幅优化。

在 LLM 中的应用：平衡延迟与计算效率

1. 长文本场景的延迟挑战

传统 Transformer 的缺陷：全局注意力延迟为 1 层（任意块直接交互），但计算量 $O(N^2)$ 无法处理长序列；
块稀疏的取舍：
- 小块 + 相邻模式：计算量低（ $O(Nb)$ ），但延迟高，适合局部依赖强的任务（如代码生成）；
- 大块 + 跳跃模式：延迟低（ $O(\log N)$ ），但计算量略高，适合需要长程依赖的任务（如文档摘要）。

2. 工程优化策略

动态块大小：对高频词使用小块（如窗口 b=32），对低频实体使用大块（b=256），减少高频词的跨块延迟；
混合稀疏模式：底层用相邻块模式捕捉局部细节，高层用跳跃模式快速传递全局信息，类似人类先看字、再看段、最后看篇章的层级理解。

代码示例：用 PyTorch 实现块稀疏注意力的延迟控制

import torch  
from torch.nn import Module  class BlockSparseAttention(Module):  def __init__(self, embed_dim, block_size=128, jump_scale=2):  super().__init__()  self.embed_dim = embed_dim  self.block_size = block_size  self.jump_scale = jump_scale  # 控制跳跃块间隔（如2表示跨1块连接）  def get_block_mask(self, seq_len):  """生成块稀疏注意力掩码"""  num_blocks = seq_len // self.block_size  mask = torch.zeros(seq_len, seq_len, dtype=torch.bool)  for i in range(num_blocks):  start_i = i * self.block_size  end_i = (i+1) * self.block_size  for j in range(num_blocks):  # 允许块内交互 + 跨jump_scale块交互  if i == j or abs(i - j) == self.jump_scale:  start_j = j * self.block_size  end_j = (j+1) * self.block_size  mask[start_i:end_i, start_j:end_j] = True  return mask  def forward(self, Q, K, V):  """Q/K/V形状：(batch_size, seq_len, embed_dim)"""  seq_len = Q.shape[1]  mask = self.get_block_mask(seq_len).to(Q.device)  # 计算注意力分数并应用掩码  scores = (Q @ K.transpose(-2, -1)) / (self.embed_dim ** 0.5)  scores = scores.masked_fill(~mask, -inf)  attn = torch.softmax(scores, dim=-1) @ V  return attn

代码中的延迟控制逻辑

块掩码设计：
- jump_scale=2 表示允许当前块与前 2 块、后 2 块交互（如块 0 与块 2 连接），相比相邻模式（jump_scale=1），每步可跨越更多块，降低延迟；
- 若 jump_scale 随层数动态增加（如层 1→1，层 2→2，层 3→4），可实现类似分层跳跃的对数级延迟。
延迟与计算量的直观体现：
- 当 block_size=128、seq_len=4096 时，总块数 M=32，若 jump_scale=2，每个块连接 3 个块（自身 + 前 2 + 后 2），计算量为 $32 \times 3 \times 128^2 = 1.5M$ ，远低于全局注意力的 $4096^2 = 16M$ ，同时最大延迟从 31 层降至约 16 层（每步跨 2 块，需 16 步从块 0 到块 31）。

总结：让信息在 “块世界” 中高效穿梭

块稀疏注意力的信息传递延迟建模，本质是在 “计算效率” 与 “长程依赖” 间搭建桥梁。通过图论中的最短路径思想，我们将块结构转化为通信网络，用数学公式量化不同模式下的延迟成本。在 LLM 中，这种建模不仅指导块大小、跳跃间隔等参数的选择，更启发了分层注意力架构的设计 —— 就像互联网通过骨干网快速传输数据，块稀疏注意力让语义信息在 “块世界” 中以近乎对数级的延迟穿梭，既保持了稀疏计算的高效性，又避免了长序列理解中的 “信息断层”。未来，随着更复杂的稀疏模式（如动态块、自适应跳跃）的出现，延迟建模将继续成为解锁万亿 token 级 LLM 的关键钥匙。

Q16 轴向注意力（Axial Attention）的维度分解数学证明

轴向注意力：高维数据的 “分而治之” 神器

想象你要整理一个巨大的书架，上面摆满了按 “作者 - 书名 - 类别” 分类的书籍。全局注意力就像逐一检查每一本书的关联，效率极低；而轴向注意力则像分维度整理 —— 先按 “作者” 维度归类，再按 “类别” 维度交叉比对，大幅减少工作量。这种 “分维度处理” 的思想，就是轴向注意力的核心：将高维数据的注意力计算分解到多个轴（如二维图像的行和列、三维视频的时空轴），避免全局计算的指数级复杂度爆炸。

维度分解的数学本质：从二维到多维的张量拆分

以二维数据为例（如图像的 H×W×C），假设序列长度为 $N = H \times W$ ，传统全局注意力的计算复杂度为 $O(N^2) = O(H^2W^2)$ 。轴向注意力将其分解为行轴和列轴两步计算：

1. 行轴注意力：沿行方向计算局部关联

维度拆分：将二维特征图视为 H 条行向量，每条行向量长度为 W，维度为 C。
计算逻辑：对每条行向量，计算其内部 W 个元素的注意力，复杂度为 $H \times O(W^2)$ 。
数学表达： $\text{Row-wise Attention Output} = \text{Softmax}\left(\frac{Q_{\text{row}} K_{\text{row}}^T}{\sqrt{C}}\right) V_{\text{row}}$ 其中 $Q_{\text{row}}, K_{\text{row}}, V_{\text{row}} \in \mathbb{R}^{H \times W \times C}$ ，沿行方向切片为 H 个 $W \times C$ 的矩阵。

2. 列轴注意力：沿列方向整合行轴结果

维度转换：将行轴输出转置为列方向视角，得到 W 条列向量，每条长度为 H。
计算逻辑：对每条列向量，计算其内部 H 个元素的注意力，复杂度为 $W \times O(H^2)$ 。
数学表达： $\text{Column-wise Attention Output} = \text{Softmax}\left(\frac{Q_{\text{col}} K_{\text{col}}^T}{\sqrt{C}}\right) V_{\text{col}}$ 其中 $Q_{\text{col}}, K_{\text{col}}, V_{\text{col}} \in \mathbb{R}^{W \times H \times C}$ ，沿列方向切片为 W 个 $H \times C$ 的矩阵。

3. 总复杂度与全局注意力对比

轴向注意力总复杂度： $O(HW^2 + WH^2) = O(HW(W + H))$
全局注意力复杂度： $O((HW)^2) = O(H^2W^2)$ 当 $H = W = \sqrt{N}$ 时，轴向注意力复杂度为 $O(N\sqrt{N})$ ，远低于全局注意力的 $O(N^2)$ 。这就像将 “逐个握手” 的社交方式改为 “按行坐、按列聊” 的分组交流，效率大幅提升。

多维推广：从二维到三维及更高维的分解法则

轴向注意力可轻松扩展至 D 维数据（如三维体积数据 $X \in \mathbb{R}^{d_1 \times d_2 \times \dots \times d_D \times C}$ ），分解规则为：

逐轴计算：依次在每个轴上计算注意力，每次固定其他 $D-1$ 个轴。
复杂度公式： $O\left(\sum_{i=1}^{D} d_i \prod_{j \neq i} d_j^2\right)$ 例如三维数据 $d_1 \times d_2 \times d_3$ 的复杂度为 $O(d_1d_2^2d_3 + d_1^2d_2d_3 + d_1d_2d_3^2)$ ，仍远低于全局的 $O((d_1d_2d_3)^2)$ 。

在 LLM 中的应用：长文本的 “分层轴” 建模

在语言模型中，轴向注意力可将文本序列按 “语义层级” 分解为多个轴，例如：

轴 1：单词轴（局部上下文，如句子内的词依赖）；
轴 2：段落轴（跨句子的段落关联）；
轴 3：章节轴（跨段落的长程依赖）。通过逐轴计算注意力，模型可高效捕捉不同层级的语义关联，避免长序列下的计算爆炸。例如，处理 10000 字文档时，若按 “句子 - 段落” 二维轴分解，假设每句 20 词（500 句），每段 10 句（50 段），则复杂度为 $500 \times 20^2 + 50 \times 10^2 = 205000$ ，而全局注意力复杂度为 $10000^2 = 100000000$ ，差距近 500 倍。

代码示例：用 PyTorch 实现二维轴向注意力

import torch  
from torch.nn import Module  class AxialAttention2D(Module):  def __init__(self, embed_dim, axis1_size=64, axis2_size=64):  super().__init__()  self.embed_dim = embed_dim  self.axis1_size = axis1_size  # 如行轴长度H  self.axis2_size = axis2_size  # 如列轴长度W  self.scale = embed_dim ** 0.5  def forward(self, x):  """输入x形状：(batch_size, H, W, embed_dim)"""  batch_size, H, W, C = x.shape  x = x.permute(0, 3, 1, 2)  # 转为 (B, C, H, W)  # 1. 行轴（H轴）注意力：沿H轴计算每个W的局部注意力  x_row = x.permute(0, 2, 1, 3)  # (B, H, C, W)  Q_row = x_row @ torch.randn(C, C, device=x.device)  # 模拟行投影  K_row = x_row @ torch.randn(C, C, device=x.device)  V_row = x_row @ torch.randn(C, C, device=x.device)  scores_row = (Q_row @ K_row.transpose(-2, -1)) / self.scale  attn_row = torch.softmax(scores_row, dim=-1) @ V_row  x_row_out = attn_row.permute(0, 1, 3, 2)  # 恢复为 (B, H, W, C)  # 2. 列轴（W轴）注意力：沿W轴计算每个H的局部注意力  x_col = x_row_out.permute(0, 2, 1, 3)  # (B, W, H, C)  Q_col = x_col @ torch.randn(C, C, device=x.device)  # 模拟列投影  K_col = x_col @ torch.randn(C, C, device=x.device)  V_col = x_col @ torch.randn(C, C, device=x.device)  scores_col = (Q_col @ K_col.transpose(-2, -1)) / self.scale  attn_col = torch.softmax(scores_col, dim=-1) @ V_col  x_col_out = attn_col.permute(0, 2, 1, 3)  # 恢复为 (B, H, W, C)  return x_col_out.permute(0, 2, 3, 1)  # 输出形状 (B, H, W, C)

代码解读：维度转换的 “轴游戏”

行轴处理：
- 通过 permute(0, 2, 1, 3) 将维度转为 (B, H, C, W)，相当于将每个行向量（长度 W）视为独立序列，对 H 个行向量分别计算 W×W 的注意力，复杂度为 $H \times O(W^2)$ 。
列轴处理：
- 行轴输出转置为 (B, W, H, C)，将每个列向量（长度 H）视为独立序列，对 W 个列向量计算 H×H 的注意力，复杂度为 $W \times O(H^2)$ 。
投影矩阵模拟：
- 代码中用随机矩阵 torch.randn(C, C) 模拟可学习的投影层（实际应用中为线性层），将输入特征映射到查询、键、值空间，体现轴向注意力的 “分轴参数化” 特性。

总结：让高维数据在 “轴” 上跳舞

轴向注意力的维度分解数学证明，本质是利用高维数据的结构特性，将全局交互拆解为局部轴交互的组合。这种 “分而治之” 的思想，不仅将计算复杂度从指数级降至多项式级，更让模型能分层捕捉不同维度的语义关联 —— 就像人类阅读时先理解句子（行轴），再串联段落（列轴），最终把握全文脉络。在 LLM 中，这种特性使其能高效处理多模态数据（如图文混合文档）或超长序列，为万亿参数模型的落地提供了关键的算法支撑。未来，随着三维、四维轴向注意力的扩展，我们有望见证模型在视频理解、时空序列等更复杂场景中的 “轴上起舞”。

Q17 推导线性注意力（Linear Attention）的核函数近似误差上界

线性注意力：从二次复杂度到线性的 “核魔法”

传统自注意力机制通过 $\text{Softmax}(QK^\top / \sqrt{d})V$ 计算，时间复杂度为 $O(N^2)$ ，这在长序列（如 $N=10^4$ ）场景下寸步难行。线性注意力另辟蹊径，通过核函数 $k(q, k)$ 将注意力计算转化为线性复杂度： $\text{LinearAttn}(Q, K, V) = \left( \frac{K^\top \Phi(V)}{\sum_k \Phi(k)} \right) \Phi(Q)^\top$ 其中 $\Phi(\cdot)$ 是核函数的特征映射（如多项式展开或指数映射）。但核函数的近似特性必然引入误差，我们需要从数学上界定这种误差的上界，确保 “近似计算” 不会偏离太远。

误差来源：核函数的 “理想” 与 “现实”

假设理想核函数为 $k^*(q, k)$ ，实际使用的近似核函数为 $\tilde{k}(q, k)$ ，误差源于两者的差异： $\epsilon(q, k) = |k^*(q, k) - \tilde{k}(q, k)|$ 线性注意力的输出可视为核函数的加权积分，因此误差会通过权重传递到最终结果。我们的目标是推导输出误差 $\|\text{Output}^* - \tilde{\text{Output}}\|$ 的上界，其中 $\|\cdot\|$ 为向量范数（如 L2 范数）。

数学推导：从核差异到输出误差的层层递推

假设条件

核函数有界： $|k^*(q, k)| \leq C_1$ ， $|\tilde{k}(q, k)| \leq C_2$ ；
特征映射 $\Phi(\cdot)$ 满足利普希茨连续性： $\|\Phi(q) - \Phi(q')\| \leq L \|q - q'\|$ ；
输入序列 $Q, K$ 的元素在紧集 $\mathcal{X}$ 内，即 $\forall x \in \mathcal{X}, \|x\| \leq D$ 。

关键步骤

1. 核矩阵误差的界定

定义核矩阵 $K^* \in \mathbb{R}^{N \times N}$ 和 $\tilde{K} \in \mathbb{R}^{N \times N}$ ，其元素为 $K^*_{i,j} = k^*(q_i, k_j)$ ， $\tilde{K}_{i,j} = \tilde{k}(q_i, k_j)$ 。两者的 Frobenius 范数误差为： $\|K^* - \tilde{K}\|_F = \sqrt{\sum_{i,j} \epsilon(q_i, k_j)^2} \leq \sqrt{N^2 \epsilon_{\text{max}}^2} = N \epsilon_{\text{max}}$ 其中 $\epsilon_{\text{max}} = \max_{q,k} |\epsilon(q, k)|$ 为最大核误差。

2. 注意力权重误差的传递

线性注意力的权重计算为 $\text{Softmax}(K)$ ，假设 $\text{Softmax}$ 函数的利普希茨常数为 $L_{\text{softmax}}$ （在数值稳定区域， $L_{\text{softmax}} \approx 1$ ），则权重矩阵误差满足： $\|W^* - \tilde{W}\|_F \leq L_{\text{softmax}} \|K^* - \tilde{K}\|_F \leq L_{\text{softmax}} N \epsilon_{\text{max}}$

3. 输出误差的最终推导

输出误差 $\|V^* - \tilde{V}\|$ 可通过矩阵乘法的范数性质界定： $\|V^* - \tilde{V}\| = \|(W^* - \tilde{W})V\| \leq \|W^* - \tilde{W}\|_F \|V\|_F$ 由于 $\|V\|_F \leq N D$ （假设 V 的元素范数不超过 D），代入得： $\|V^* - \tilde{V}\| \leq L_{\text{softmax}} N \epsilon_{\text{max}} \cdot N D = L_{\text{softmax}} D N^2 \epsilon_{\text{max}}$

简化结论

在常见场景下（如 $L_{\text{softmax}} = 1$ ， $D = 1$ ），误差上界可简化为： $\boxed{\|V^* - \tilde{V}\| \leq N^2 \epsilon_{\text{max}}}$ 该公式表明，线性注意力的输出误差与序列长度 N 的平方成正比，与核函数的最大近似误差 $\epsilon_{\text{max}}$ 成正比。

在 LLM 中的意义：误差与效率的再平衡

1. 长序列场景的误差控制

当 N=1024 时， $N^2$ = $10^6$ ，若 $\epsilon_{\text{max}}=0.1$ ，误差上界为 $10^5$ ，这显然不可接受。因此实际应用中需通过以下方式降低 $\epsilon_{\text{max}}$ ：

选择 expressive 核函数：如指数核 $k(q,k) = \exp(q \cdot k)$ 比多项式核更贴近点积注意力；
数据预处理：对输入进行标准化，使 $q, k$ 的范数集中在低方差区间，减少核函数的非线性误差。

2. 近似方法的优化方向

局部敏感哈希（LSH）辅助：先通过 LSH 筛选高相关的 $(q,k)$ 对，仅对这些对使用精确核函数，其余对使用低精度近似，从而降低整体 $\epsilon_{\text{max}}$ ；
动态误差补偿：在模型训练中引入误差正则项，显式优化 $\epsilon_{\text{max}}$ ，例如： $\mathcal{L} = \text{CrossEntropyLoss} + \lambda \sum_{i,j} \epsilon(q_i, k_j)^2$

代码示例：用指数核近似点积注意力的误差验证

import torch  
from torch.nn import functional as F  def exact_attention(Q, K, V):  scores = Q @ K.T / torch.sqrt(torch.tensor(Q.shape[-1], dtype=torch.float32))  attn = F.softmax(scores, dim=-1)  return attn @ V  def linear_attention(Q, K, V, eps=1e-6):  # 指数核近似：k(q,k) = exp(q·k)，假设特征维度d=Q.shape[-1]  k_Q = torch.exp(Q)  k_K = torch.exp(K)  k_V = V * k_K  # 等价于 Φ(k)=exp(k), Φ(v)=v*Φ(k)  denominator = torch.sum(k_K, dim=0, keepdim=True) + eps  weight = k_Q @ (k_V / denominator)  return weight  # 模拟数据  
N, d = 128, 64  # 序列长度=128，特征维度=64  
Q = torch.randn(N, d)  
K = torch.randn(N, d)  
V = torch.randn(N, d)  # 计算误差  
exact_out = exact_attention(Q, K, V)  
linear_out = linear_attention(Q, K, V)  
error = torch.norm(exact_out - linear_out, p=2)  print(f"Error (L2 norm): {error.item():.4f}")  
# 预期输出：误差随N增大而增长，但增速慢于O(N^2)（因指数核近似误差较小）

代码解读

核函数选择：用指数核 $\exp(q \cdot k)$ 近似点积注意力，其泰勒展开的前两项为 $1 + q \cdot k$ ，在 $q \cdot k$ 较小时近似误差小；
误差观察：当 N 从 128 增至 1024 时，若误差增长小于 $N^2$ 倍，说明实际误差低于理论上界，印证线性注意力的实用性；
改进方向：可尝试用多项式核 $(q \cdot k + c)^d$ 调整近似精度，通过超参数 $c, d$ 平衡偏差与方差。

总结：给 “近似” 戴上理论的 “紧箍咒”

线性注意力的核函数近似误差上界推导，本质是为 “计算效率的妥协” 划定安全边界。通过数学证明，我们发现误差与 $N^2$ 和 $\epsilon_{\text{max}}$ 成正比，这倒逼研究者在核函数设计（如选择更接近点积的映射）和工程优化（如局部敏感筛选）上双管齐下。在 LLM 中，这种理论与实践的结合尤为重要 —— 它让模型既能享受线性复杂度的 “速度红利”，又能通过误差上界的指引避免 “近似失控”。未来，随着核函数理论的发展（如自适应核、层级核），我们有望进一步收紧误差边界，让线性注意力在长序列场景中成为更可靠的 “效率担当”。

Q18 分析内存压缩注意力（Memory-Compressed Attention）的池化操作梯度

内存压缩注意力：用池化 “挤压” 内存的双刃剑

在长序列场景中，传统注意力的内存占用（如 $QK^\top$ 的 $O(N^2)$ 存储）如同膨胀的气球，而内存压缩注意力通过池化操作对键（K）和值（V）进行下采样，将序列长度从 N 压缩至 $M \ll N$ ，使内存占用降至 $O(MN + Md)$ （d 为隐藏维度）。但池化操作是一把 “双刃剑”—— 它在节省内存的同时，会改变梯度传播路径，可能引入优化偏差。我们需要深入剖析池化操作的梯度特性，确保模型 “压缩内存不压缩训练效果”。

池化操作的前向与反向：从信息压缩到梯度分配

假设池化操作将 $K \in \mathbb{R}^{N \times d}$ 和 $V \in \mathbb{R}^{N \times d}$ 压缩为 $K' \in \mathbb{R}^{M \times d}$ 和 $V' \in \mathbb{R}^{M \times d}$ ，常见池化方式包括：

1. 平均池化：梯度的 “均匀分摊”

前向计算：将 N 划分为 M 个块，每个块取均值： $K'_m = \frac{1}{s} \sum_{i=m \cdot s}^{(m+1) \cdot s - 1} K_i \quad (s = N/M \quad \text{block size})$

反向梯度：若损失 L 对 $K'$ 的梯度为 $\frac{\partial L}{\partial K'_m}$ ，则对原始 $K_i$ 的梯度为： $\frac{\partial L}{\partial K_i} = \frac{1}{s} \cdot \frac{\partial L}{\partial K'_m} \quad (\text{if} \ i \in \text{block} \ m)$

特点：梯度被均匀分配到块内每个元素，类似 “大锅饭”，平滑但可能模糊关键信号。

2. 最大池化：梯度的 “胜者通吃”

前向计算：每个块取最大值元素的索引 $i_m = \arg\max_{i \in \{\text{block} \ m \}} K_i$ ，则： $K'_m = K_{i_m}$

反向梯度：仅对每个块的最大值元素传递梯度，其余为零： $\frac{\partial L}{\partial K_i} = \begin{cases} \frac{\partial L}{\partial K'_m}, & \text{if } i = i_m \\ 0, & \text{if not} \end{cases}$

特点：梯度稀疏，仅保留 “最强信号”，可能导致训练不稳定，但能聚焦关键特征。

3. 可学习池化：梯度的 “智能路由”

引入可学习参数 $w \in \mathbb{R}^s$ 对块内元素加权求和： $K'_m = \sum_{i \in \text{block} m} w_i K_i \quad (\text{usually} \sum w_i = 1)$

反向梯度： $\frac{\partial L}{\partial K_i} = w_i \cdot \frac{\partial L}{\partial K'_m}, \quad \frac{\partial L}{\partial w_i} = K_i \cdot \frac{\partial L}{\partial K'_m}$

特点：通过训练优化权重，动态调整梯度分配，平衡信息保留与压缩效率。

池化梯度对注意力优化的影响

1. 梯度稀释问题（以平均池化为例）

假设块内有一个关键元素 $K_i$ 对注意力权重至关重要，但平均池化将其梯度稀释为 $1/s$ 。例如，当 $s=100$ 时，梯度幅值降至原值的 1%，可能导致该元素在训练中 “学习不足”，影响模型对局部特征的捕捉能力。

2. 梯度稀疏性问题（以最大池化为例）

最大池化仅传递单元素梯度，可能导致：

梯度消失：若最大值元素在训练早期处于非最优状态，其梯度可能因 “零梯度” 更新缓慢；
特征崩塌：模型倾向于选择固定位置的最大值，忽略其他潜在有用特征。

3. 跨块依赖的梯度断裂

池化操作切断了块间的直接梯度传递。例如，块 m 的梯度无法直接影响块 $m+1$ 的原始元素，导致长程依赖的建模能力下降，这在需要跨块信息交互的任务（如文档摘要）中尤为明显。

在 LLM 中的实战：如何设计 “梯度友好” 的池化操作

1. 分层池化 + 残差连接

策略：先对序列进行粗粒度池化（如 $M=N/4$ ），计算注意力后，将输出与原始未池化的局部块特征相加（残差连接）；
梯度优势：保留原始特征的梯度路径，缓解池化导致的信息丢失。

2. 动态池化：让梯度指导下采样

思路：利用注意力权重作为池化掩码，对高权重区域进行细粒度池化（小块大小 s），低权重区域进行粗粒度池化（大块大小 $S>s$ ）；
实现： $s_i = s \cdot \text{Sigmod}(a_i) + S \cdot (1 - \text{Sigmod}(a_i))$ 其中 $a_i$ 是查询对第 i 块的注意力分数，梯度可通过 $s_i$ 反向传播至注意力权重。

3. 可逆池化：无损的梯度传递

方法：在池化时保存块内元素的索引或差值，反向传播时通过可逆操作（如反池化）恢复完整梯度；
示例：保存平均池化的块内元素均值与每个元素的差值，反向时用差值重构原始梯度。

代码示例：平均池化的梯度计算与分析

import torch  
from torch.nn import functional as F  class MemoryCompressedAttention(torch.nn.Module):  def __init__(self, embed_dim, pool_size=16):  super().__init__()  self.embed_dim = embed_dim  self.pool_size = pool_size  # 池化块大小，即s  def forward(self, Q, K, V):  """Q: (B, N, d), K/V: (B, N, d)"""  B, N, d = K.shape  M = N // self.pool_size  # 池化后长度  # 平均池化：将K/V划分为M个块，每块s=pool_size元素  K_pool = K.view(B, M, self.pool_size, d).mean(dim=2)  # (B, M, d)  V_pool = V.view(B, M, self.pool_size, d).mean(dim=2)  # (B, M, d)  # 计算注意力：Q与池化后的K交互  scores = (Q @ K_pool.transpose(1, 2)) / (self.embed_dim ** 0.5)  # (B, N, M)  attn = F.softmax(scores, dim=-1)  # (B, N, M)  output = attn @ V_pool  # (B, N, d)  return output  def extra_repr(self):  return f"pool_size={self.pool_size}"  # 梯度验证  
B, N, d = 2, 32, 8  # 2批次，32序列长度，8维度  
Q = torch.randn(B, N, d, requires_grad=True)  
K = torch.randn(B, N, d, requires_grad=True)  
V = torch.randn(B, N, d, requires_grad=True)  
model = MemoryCompressedAttention(d, pool_size=4)  
output = model(Q, K, V)  
loss = output.sum()  
loss.backward()  # 观察K的梯度：每个块内梯度相同（平均池化特性）  
block_grad = K.grad.view(B, -1, 4, d)  # 划分为8块，每块4元素  
print("块内梯度是否一致:", torch.allclose(block_grad[:, 0, 0], block_grad[:, 0, 1]))  # 输出True

代码解读

平均池化的梯度路径：
- K.view(B, M, s, d).mean(dim=2) 的反向传播会自动将梯度均分到每个块内元素，如代码中验证的 “块内梯度一致”；
- 若想观察梯度稀释，可对比池化前后的梯度幅值：池化后梯度幅值为原始的 $1/s$ 。
优化建议：
- 若发现关键位置梯度不足，可尝试将平均池化替换为带参数的加权池化，通过训练学习块内权重，避免均匀稀释；
- 在池化层后添加归一化层（如 LayerNorm），稳定梯度分布。

总结：在压缩与优化间寻找梯度平衡点

内存压缩注意力的池化操作梯度分析，揭示了一个核心挑战：如何在减少内存的同时，让梯度有效指导模型更新。平均池化的 “梯度均匀化” 适合平稳特征，最大池化的 “梯度稀疏化” 适合突出关键特征，而可学习池化则通过参数优化动态调整梯度分配。在 LLM 中，结合任务特性选择池化方式（如对话历史用动态池化、文档摘要用分层池化），并通过残差连接、可逆操作等技巧维护梯度路径，可使模型在内存受限的情况下仍保持高效训练。这一过程就像给模型的 “记忆压缩” 安装 “梯度导航系统”，确保压缩后的信息能准确传递优化信号，让长序列建模既节省内存又不失训练质量。

Q19 证明低秩注意力（Low-Rank Attention）的秩约束优化条件

低秩注意力：用 “降维” 驯服注意力矩阵的 “洪荒之力”

传统自注意力的核心是 $N \times N$ 的注意力矩阵 A，其秩为 N（满秩），意味着矩阵的列向量张成整个 N 维空间。但在实际场景中，序列元素的依赖往往呈现 “低秩性”—— 例如文档中的句子通常围绕少数主题展开，注意力矩阵的列向量可由 $k \ll N$ 个基向量线性组合表示。低秩注意力通过强制 A 的秩为 k，将其分解为 $A \approx UV^\top$ （ $U \in \mathbb{R}^{N \times k}, V \in \mathbb{R}^{N \times k}$ ），使计算复杂度从 $O(N^2)$ 降至 $O(Nk)$ 。而秩约束优化条件的证明，就是要回答：如何找到最优的 k 秩矩阵，使其最接近原始注意力矩阵？

数学建模：从优化目标到秩约束

问题定义

设原始注意力矩阵为 $\bar{A} \in \mathbb{R}^{N \times N}$ ，我们希望找到秩为 k 的矩阵 $A_k$ ，使得两者的 Frobenius 范数误差最小： $\min_{A_k \in \mathbb{R}^{N \times N}, \text{rank}(A_k) \leq k} \|\bar{A} - A_k\|_F^2$ 其中 Frobenius 范数定义为 $\|M\|_F = \sqrt{\sum_{i,j} M_{i,j}^2}$ ，衡量矩阵元素级的近似误差。

关键工具：奇异值分解（SVD）

对 $\bar{A}$ 进行 SVD 分解： $\bar{A} = \sum_{i=1}^N \sigma_i u_i v_i^\top$ 其中 $\sigma_1 \geq \sigma_2 \geq \dots \geq \sigma_N \geq 0$ 为奇异值， $\{u_i\}, \{v_i\}$ 为左右奇异向量。

根据 Eckart-Young 定理， $\bar{A}$ 的最佳 k 秩近似为： $A_k^* = \sum_{i=1}^k \sigma_i u_i v_i^\top$ 该定理直接给出了低秩近似的最优解结构 —— 保留前 k 个最大奇异值对应的分量，忽略其余分量。

秩约束优化条件的证明

目标函数展开

将 $A_k$ 表示为任意秩 $\leq k$ 的矩阵，其 SVD 可写为： $A_k = \sum_{i=1}^k \tilde{\sigma}_i \tilde{u}_i \tilde{v}_i^\top$ 其中 $\tilde{\sigma}_i \geq 0$ ， $\{\tilde{u}_i\}, \{\tilde{v}_i\}$ 为正交向量组。

计算误差： $\|\bar{A} - A_k\|_F^2 = \left\| \sum_{i=1}^N \sigma_i u_i v_i^\top - \sum_{i=1}^k \tilde{\sigma}_i \tilde{u}_i \tilde{v}_i^\top \right\|_F^2$

正交性与投影性质

由于 $\{u_i\}, \{v_i\}$ 是标准正交基，根据 Frobenius 范数的正交不变性，误差可分解为： $\|\bar{A} - A_k\|_F^2 = \sum_{i=1}^k (\sigma_i - \langle \bar{A}, \tilde{u}_i \tilde{v}_i^\top \rangle)^2 + \sum_{i=k+1}^N \sigma_i^2$ 其中第一项是前 k 个分量的拟合误差，第二项是丢弃的后 $N-k$ 个分量的贡献（恒为非负）。

最优性条件推导

后 $N-k$ 项的最小化：显然，当 $A_k$ 不包含后 $N-k$ 个奇异值分量时，第二项达到最小值 $\sum_{i=k+1}^N \sigma_i^2$ 。
前 k 项的最小化：对于第一项，当 $\tilde{u}_i = u_i$ ， $\tilde{v}_i = v_i$ ， $\tilde{\sigma}_i = \sigma_i$ 时， $\langle \bar{A}, \tilde{u}_i \tilde{v}_i^\top \rangle = \sigma_i$ ，第一项误差为零。

因此，全局最小值在 $A_k^* = \sum_{i=1}^k \sigma_i u_i v_i^\top$ 时取得，此时： $\min \|\bar{A} - A_k\|_F^2 = \sum_{i=k+1}^N \sigma_i^2$ 即最优 k 秩近似由前 k 个最大奇异值对应的分量构成，证明完毕。

在 LLM 中的应用：低秩假设的 “语义降维”

1. 语义层面的低秩性

文本序列的注意力矩阵通常具有低秩特性：

同主题的句子对应列向量在语义空间中接近，可由少数 “主题向量” 张成；
语法结构（如主谓宾）的重复模式也会导致列向量线性相关。通过低秩分解，模型可捕捉这些高层语义模式，避免为无关细节分配计算资源。

2. 计算效率提升

假设 N=4096，k=64：

传统注意力计算量： $4096^2 = 16,777,216$ 次乘法；
低秩注意力计算量： $2 \times 4096 \times 64 = 524,288$ 次乘法（U 和 V 的矩阵乘法），压缩率达 32 倍。

3. 工程实现技巧

动态秩调整：根据输入序列的复杂度自适应调整 k，例如对话场景用 $k=32$ ，文档场景用 $k=128$ ；
分层低秩分解：先对序列分块，每块内独立进行低秩近似，再跨块整合，进一步降低复杂度。

代码示例：基于 SVD 的低秩注意力实现

import torch  class LowRankAttention(torch.nn.Module):  def __init__(self, embed_dim, rank=64):  super().__init__()  self.embed_dim = embed_dim  self.rank = rank  # 可学习的投影矩阵，将Q/K/V映射到低秩空间  self.W_q = torch.nn.Linear(embed_dim, rank, bias=False)  self.W_k = torch.nn.Linear(embed_dim, rank, bias=False)  self.W_v = torch.nn.Linear(embed_dim, rank, bias=False)  def forward(self, Q, K, V):  """Q/K/V形状：(batch_size, seq_len, embed_dim)"""  B, N, d = Q.shape  # 投影到低秩空间  U = self.W_q(Q)  # (B, N, k)  V_low = self.W_v(V)  # (B, N, k)  K_low = self.W_k(K).transpose(1, 2)  # (B, k, N)  # 计算低秩注意力矩阵：A ≈ UV^T = U @ K_low  attn_scores = (U @ K_low) / (self.embed_dim ** 0.5)  # (B, N, N)  attn = torch.softmax(attn_scores, dim=-1)  output = attn @ V_low.transpose(1, 2)  # (B, N, d)  return output  # 低秩近似的SVD验证（非训练部分）  
def svd_low_rank_approx(A, k):  U, S, Vt = torch.svd(A)  return U[:, :k] @ torch.diag(S[:k]) @ Vt[:k, :]

代码解读

可学习秩空间：
- 通过线性层将 $Q, K, V$ 映射到 k 维空间，相当于用可学习的基向量逼近原始注意力矩阵的前 k 个奇异向量。
低秩计算逻辑：
- 注意力分数通过 $U \in \mathbb{R}^{N \times k}$ 和 $K_{low} \in \mathbb{R}^{k \times N}$ 的矩阵乘法得到，显式利用秩 k 结构。
SVD 验证：
- svd_low_rank_approx 函数演示了理论上的最优低秩近似，实际模型可通过训练逼近该解，平衡精度与效率。

总结：让注意力矩阵 “瘦身” 的理论基石

低秩注意力的秩约束优化条件证明，本质是利用矩阵论中的经典结论（Eckart-Young 定理），为注意力机制的 “降维” 提供理论依据。通过保留前 k 个最大奇异值分量，模型能以最小误差捕捉注意力矩阵的主要变化模式，就像从复杂的自然景观中提取几笔关键轮廓，既能保留视觉特征，又大幅简化画面。在 LLM 中，这种 “瘦身” 不仅带来计算效率的飞跃，更揭示了语言结构的内在低维特性 —— 无论是主题的凝聚性还是语法的规律性，都暗示着注意力矩阵的秩远低于序列长度。未来，结合动态秩估计和自适应基向量学习，低秩注意力有望成为长序列建模的核心工具，让模型在 “压缩的秩空间” 中高效演绎语言的复杂性。

Q20 计算动态稀疏注意力（Dynamic Sparse Attention）的 Top-k 选择阈值

动态稀疏注意力：让模型 “选择性失明” 的艺术

在处理长序列时，动态稀疏注意力就像一位挑剔的读者，只关注最相关的内容 —— 通过为每个查询（Query）动态选择 Top-k 个键（Key）计算注意力，将复杂度从 $O(N^2)$ 降至 $O(Nk)$ （ $k \ll N$ ）。而 “Top-k 选择阈值” 则是这个过程的核心参数：它决定了 “多高的分数才算足够相关”，直接影响模型的效率与准确性。我们需要从数学原理、工程实现和 LLM 应用三个维度解析这个关键问题。

阈值计算的数学本质：从分数分布到 k 值映射

假设查询 $q_i$ 与所有键 $k_j$ 的注意力分数为 $s_{i,j} = q_i \cdot k_j / \sqrt{d}$ ，动态稀疏注意力需要为每个 $q_i$ 找到一个阈值 $\tau_i$ ，使得满足 $s_{i,j} \geq \tau_i$ 的 $k_j$ 恰好有 k 个。这本质上是一个分位数计算问题—— $\tau_i$ 是 $s_{i,j}$ 分布的第 $(N-k)$ 百分位数。

1. 精确 Top-k 阈值：排序与截断

最直接的方法是对分数排序，取第 k 大的值作为阈值： $\tau_i = \text{sort}(s_{i,1}, s_{i,2}, \dots, s_{i,N})[N-k]$ 示例：若 N=1024，k=32，则对每个查询的 1024 个分数降序排列，取第 993 位的值作为阈值，仅保留前 32 个高分键。

2. 近似阈值：基于分布的快速估计

精确排序的计算复杂度为 $O(N \log N)$ ，对长序列不友好。可假设分数服从高斯分布 $s \sim \mathcal{N}(\mu_i, \sigma_i^2)$ ，则阈值可近似为： $\tau_i = \mu_i + \sigma_i \cdot \Phi^{-1}\left(1 - \frac{k}{N}\right)$ 其中 $\Phi^{-1}$ 为标准正态分布的分位数函数。例如，当 $k/N=0.03$ 时， $\Phi^{-1}(0.97) \approx 1.88$ ，阈值为均值加 1.88 倍标准差。

动态阈值的工程挑战：从不可微到可优化

1. 不可微性难题

传统 Top-k 操作（如排序、截断）在反向传播时梯度为零，导致模型无法端到端优化阈值。解决方案是使用可微松弛：

Gumbel-Softmax 技巧：用平滑的 Gumbel 分布近似离散的 Top-k 选择，使阈值可通过梯度下降优化： $\tau_i \approx \text{log}\left(-\text{log}(1 - \frac{k}{N})\right) - \text{log}(G) \quad (G \sim \text{Gumbel}(0,1))$
稀疏门控网络：引入可学习的参数 $\alpha_i$ ，将阈值表示为 $\tau_i = \alpha_i \cdot \text{max}(s_i)$ ，通过训练调整 $\alpha_i$ 控制 k 值。

2. 内存与计算的平衡

早停排序：使用快速选择算法（如 Hoare's selection algorithm）在 $O(N)$ 时间内找到第 k 大元素，避免全排序的 $O(N \log N)$ 开销；
分层阈值：先对序列分块，块内计算局部阈值，再跨块合并，减少单查询的计算量。

在 LLM 中的应用：语义复杂度驱动的动态调整

1. 内容感知的 k 值策略

高频词动态降 k：对 “的”“了” 等停用词，设置较低的 k 值（如 k=8），因其语义贡献小，无需关注过多键；
实体词动态升 k：对 “巴黎”“人工智能” 等实体词，设置较高的 k 值（如 k=64），确保捕捉丰富的上下文关联。

2. 计算图优化

在 PyTorch 中，可通过自定义 Autograd 函数实现可微的 Top-k 阈值计算：

import torch  
from torch.autograd import Function  class DifferentiableTopk(Function):  @staticmethod  def forward(ctx, scores, k):  # 保存排序索引用于反向传播  values, indices = torch.topk(scores, k, dim=-1)  ctx.save_for_backward(indices, scores)  ctx.k = k  return values, indices  @staticmethod  def backward(ctx, grad_values, grad_indices):  # 可微松弛：将梯度分配给Top-k元素，其余为0  indices, scores = ctx.saved_tensors  k = ctx.k  batch_size, seq_len = scores.shape  grad_scores = torch.zeros_like(scores)  # 假设使用Gumbel-Softmax松弛，梯度均匀分配给Top-k元素  grad_scores.scatter_(-1, indices, grad_values / k)  return grad_scores, None  # 动态稀疏注意力层  
class DynamicSparseAttention(torch.nn.Module):  def __init__(self, embed_dim, k_min=16, k_max=64):  super().__init__()  self.embed_dim = embed_dim  self.k_min = k_min  self.k_max = k_max  # 可学习的k值控制器（根据输入动态调整k）  self.k_controller = torch.nn.Linear(embed_dim, 1)  def forward(self, Q, K):  """Q: (B, N, d), K: (B, M, d)"""  scores = (Q @ K.transpose(-2, -1)) / (self.embed_dim ** 0.5)  # (B, N, M)  # 动态k值：根据查询的第一个token预测k  q_first = Q[:, 0]  # 假设第一个token为句子主题  k = self.k_controller(q_first).sigmoid() * (self.k_max - self.k_min) + self.k_min  k = k.long().clamp(self.k_min, self.k_max)  # 可微Top-k操作  _, indices = DifferentiableTopk.apply(scores, k)  # (B, N, k)  K_selected = K.gather(1, indices.unsqueeze(-1).repeat(1, 1, 1, self.embed_dim))  # 计算注意力  attn = torch.softmax(scores.gather(-1, indices), dim=-1)  output = (attn * K_selected).sum(dim=-2)  return output

代码解读

动态 k 值生成：
- 通过 k_controller 网络根据输入动态预测 k 值，例如主题明确的句子（如新闻标题）自动增大 k 值，简单句子减小 k 值；
- sigmoid 函数将 k 值限制在 $[k_{min}, k_{max}]$ 区间，避免极端值。
可微 Top-k 实现：
- DifferentiableTopk 类通过 Gumbel-Softmax 思想将梯度均匀分配给选中的 k 个元素，解决传统 Top-k 的不可微问题；
- 实际应用中可结合学习率调度，让模型在训练初期使用较松的阈值（多关注元素），后期收紧阈值（聚焦关键元素）。

阈值选择的评估指标：稀疏性与准确性的天平

1. 稀疏性指标

平均 k 值： $\bar{k} = \frac{1}{N} \sum_{i=1}^N k_i$ ，反映模型的整体计算量；
稀疏率： $\text{Sparsity} = 1 - \frac{\bar{k}}{N}$ ，理想情况下接近 1（如 $\bar{k}=32, N=1024$ 时稀疏率为 97%）。

2. 准确性指标

注意力分数保留率： $\frac{\sum_{i,j \in \text{Top-k}} |s_{i,j}|}{\sum_{i,j} |s_{i,j}|}$ ，衡量关键分数的保留程度；
下游任务性能：如文本生成的困惑度（Perplexity）、摘要的 ROUGE 分数，直接反映阈值对模型能力的影响。

3. 帕累托最优分析

通过调整阈值，绘制 “平均 k 值 - 困惑度” 曲线，找到最优平衡点。例如，当 k 从 16 增至 32 时，困惑度下降 10%，但计算量增加 1 倍，需根据硬件资源决定是否接受该 trade-off。

总结：让模型学会 “看重点” 的科学与艺术

动态稀疏注意力的 Top-k 阈值计算，本质是赋予模型 “选择性关注” 的智能 —— 通过数学上的分位数估计、工程上的可微优化、应用中的语义感知，在计算效率与语义捕捉之间找到精准平衡点。这一过程既需要严谨的算法设计（如可微 Top-k、动态 k 值网络），也离不开对语言特性的深刻理解（如实体词的高关联性、停用词的低重要性）。未来，随着强化学习与元学习的引入，模型有望实现完全自适应的阈值策略，根据实时输入内容动态调整关注粒度，让 “稀疏注意力” 真正成为长序列建模的 “智能滤镜”。

Q21 推导分块循环注意力（Block-Recurrent Attention）的长期依赖建模能力

分块循环注意力：长序列的 “记忆接力” 机制

处理超长序列（如数万字文档）时，全局注意力的 $O(N^2)$ 复杂度与内存占用会导致模型 “瘫痪”。分块循环注意力（Block-Recurrent Attention）则像一场 “接力赛”：将序列划分为多个块（Block），每个块内使用常规注意力处理局部信息，块间通过循环机制（如隐藏状态传递）建立跨块依赖，使模型能以 $O(LB^2)$ 复杂度（L 为块数，B 为块大小， $N=LB$ ）捕捉长期依赖。我们需要从数学推导和机制设计两方面解析其长期依赖建模能力。

数学建模：循环状态下的依赖跨度推导

假设序列被划分为 L 个块，每个块长度为 B，块间通过循环隐藏状态 $h_t$ 连接（ $t=1,2,\dots,L$ ）。每个块的处理函数为： $h_t = \text{BlockAttn}(x_t, h_{t-1})$ 其中 $x_t \in \mathbb{R}^{B \times d}$ 为第 t 块的输入， $h_{t-1} \in \mathbb{R}^{d_h}$ 为前一块的隐藏状态， $h_t$ 为当前块输出的隐藏状态。

1. 循环状态的信息传递路径

展开 L 个块的处理过程，当前块 L 的隐藏状态 $h_L$ 可表示为： $h_L = f_L(f_{L-1}(\dots f_2(f_1(x_1, h_0), x_2), \dots), x_L)$ 其中 $f_t$ 为第 t 块的注意力 - 循环函数。若 $f_t$ 是线性变换（如 $h_t = W_1 x_t + W_2 h_{t-1}$ ），则 $h_L$ 是所有 $x_1, x_2, \dots, x_L$ 的线性组合，理论上可捕捉所有块的信息。

2. 长期依赖的关键：循环权重的谱半径

在循环神经网络中，长期依赖的建模能力与循环权重矩阵 $W_2$ 的谱半径 $\rho(W_2)$ 密切相关：

若 $\rho(W_2) > 1$ ，梯度可能爆炸；
若 $\rho(W_2) < 1$ ，梯度指数衰减，导致长期依赖丢失（梯度消失）。分块循环注意力通过引入门控机制（如类似 LSTM 的遗忘门、输入门），动态调整 $W_2$ 的有效权重，使 $\rho(W_2)$ 接近 1，从而缓解梯度消失 / 爆炸问题。

分块结构对依赖跨度的影响

1. 块内注意力的局部依赖

每个块内使用常规注意力，依赖跨度为 B，可捕捉块内 B 长度的局部语义关联（如句子内的词依赖）。

2. 块间循环的全局依赖

通过 L 层循环连接，理论依赖跨度为 $LB = N$ （整个序列）。但实际中，依赖强度随块数 L 呈指数衰减： $\text{Dependency strength} \propto \lambda^L \quad (\lambda \quad \text{decay factor of recurrent weights})$ 若使用门控循环单元（如 GRU）， $\lambda$ 可通过门控参数自适应调整，例如： $\lambda = \sigma(w_g \cdot h_{t-1} + b_g) \quad (\sigma \ \text{is the sigmoid function})$ 当需要保留长期信息时， $\lambda \approx 1$ ；当需要遗忘旧信息时， $\lambda \approx 0$ 。

在 LLM 中的应用：长文本的 “段落级记忆”

1. 分层依赖建模

块内（句子级）：捕捉单词间的句法和语义依赖（如 “狗 - 追 - 猫” 的主谓宾关系）；
块间（段落级）：通过循环状态传递段落主题信息（如前一段的 “气候变化” 主题影响后一段的 “环保政策” 讨论）。

2. 计算效率与依赖能力的平衡

假设 N=4096，B=256，则 L=16：

全局注意力复杂度： $4096^2 = 16,777,216$ ；
分块循环注意力复杂度： $16 \times 256^2 = 1,048,576$ （块内） + $16 \times 256 \times d_h$ （块间），约为全局的 6%。通过合理设置 B 和 L，模型可在计算成本大幅降低的同时，维持接近全局注意力的长期依赖能力。

3. 工程优化：双向循环与跨层连接

双向循环：增加前向和后向循环状态，使每个块能同时感知前后文信息（如前一段的结论和后一段的证据）；
跨层状态跳跃：允许早期块的隐藏状态直接跳过中间层传递至高层（类似 ResNet 的残差连接），缓解深层循环的梯度衰减。

代码示例：带门控的分块循环注意力实现

import torch  
from torch.nn import Module, GRUCell  class BlockRecurrentAttention(Module):  def __init__(self, embed_dim, block_size=256, hidden_dim=1024):  super().__init__()  self.block_size = block_size  self.hidden_dim = hidden_dim  # 块内注意力：简化为多头注意力（实际可替换为任意注意力模块）  self.attn = torch.nn.MultiheadAttention(embed_dim, num_heads=8)  # 块间循环：GRU单元传递隐藏状态  self.gru = GRUCell(embed_dim, hidden_dim)  # 状态到注意力查询的投影  self.proj = torch.nn.Linear(hidden_dim, embed_dim)  def forward(self, x):  """x形状：(seq_len, batch_size, embed_dim)"""  seq_len, B, d = x.shape  L = seq_len // self.block_size  h = torch.zeros(B, self.hidden_dim, device=x.device)  # 初始隐藏状态  outputs = []  for t in range(L):  # 提取当前块：(block_size, B, d)  block = x[t*self.block_size:(t+1)*self.block_size]  # 块间循环：更新隐藏状态  h = self.gru(block[0], h)  # 用块首元素更新状态（可优化为块总结）  # 将隐藏状态投影为查询向量  q = self.proj(h).unsqueeze(0)  # (1, B, d)  k = v = block  # (block_size, B, d)  # 块内注意力：q与整个块的k/v交互  attn_output, _ = self.attn(q, k, v)  outputs.append(attn_output.squeeze(0))  # 保存块输出  return torch.cat(outputs, dim=0)  # (seq_len, B, d)

代码解读

块间循环逻辑：
- 使用 GRUCell 传递隐藏状态，每个块的第一个元素用于更新状态，模拟 “块总结” 的信息传递；
- proj 层将循环状态转换为注意力查询，使当前块的注意力能感知历史块的全局信息。
长期依赖增强点：
- 若块内注意力允许查询与整个块交互（如代码中 q 关注整个 block），则每个块的输出同时包含局部细节（块内）和全局上下文（循环状态）；
- 可扩展为双向 GRU，让每个块同时接收前后向循环状态，进一步增强跨块依赖建模。

总结：用 “接力赛” 模式突破长序列依赖瓶颈

分块循环注意力的长期依赖建模能力，源于 “局部处理 + 全局接力” 的巧妙设计：块内注意力确保局部语义的精准捕捉，块间循环机制通过状态传递实现跨块信息 “接力”。数学上，循环权重的门控机制有效缓解了梯度消失问题，使依赖跨度理论上可达整个序列长度。在 LLM 中，这种机制让模型能像人类阅读一样，先理解每个段落（块）的内容，再通过 “记忆”（循环状态）串联段落间的逻辑，最终实现对数万字文档的连贯理解。未来，结合动态块大小调整和自适应循环单元，分块循环注意力有望进一步提升长期依赖建模的效率与灵活性，成为长序列 LLM 的核心架构之一。

Q22 分析稀疏化训练中 Straight-Through Estimator 的梯度近似误差

Straight-Through Estimator（STE）：稀疏化训练的 “梯度急救箱”

在稀疏化训练中（如稀疏注意力、权重剪枝），我们常遇到不可微的离散操作，例如：

Top-k 选择：仅保留前 k% 的注意力分数，其余置零；
二值化：将权重强制为 0 或 1，如 $w' = \mathbb{I}(|w| > \tau)$ 。这些操作在正向传播中实现稀疏性，但反向传播时梯度为零，导致优化停滞。Straight-Through Estimator（STE）通过 “偷梁换柱” 式的梯度近似解决这一问题：正向传播执行离散操作，反向传播忽略离散化影响，直接传递未离散的梯度。然而，这种近似必然引入误差，我们需要从数学原理和训练动态中解析误差的本质与影响。

梯度近似误差的数学本质：离散化与梯度不匹配

1. 以二值化操作为例

设连续操作 $y = x$ ，离散操作为 $y' = \text{sign}(x)$ （符号函数），STE 的梯度近似可表示为： $\frac{\partial y'}{\partial x} \approx \frac{\partial y}{\partial x} = 1 \quad (\text{although } y' \neq y \text{ for } |x| < \tau)$ 误差来源：

离散化误差： $y' \neq y$ 导致前向传播结果偏离真实值；
梯度近似误差：假设离散操作的梯度等于连续操作的梯度，忽略了符号函数在 $x=0$ 处的不可导性。

2. 一般化误差公式

设离散操作为 $g(\cdot)$ ，其连续近似为 $f(\cdot)$ ，STE 的梯度近似为： $\nabla_x g(f(x)) \approx \nabla_x f(x)$ 真实梯度为 $\nabla_x g(f(x))$ （通常为 0 或稀疏矩阵），近似梯度为 $\nabla_x f(x)$ （密集矩阵），误差为： $\epsilon = \left\| \nabla_x g(f(x)) - \nabla_x f(x) \right\|_F$ 该误差反映了离散操作对梯度方向和幅值的扭曲。

误差在训练动态中的传播效应

1. 梯度稀释与偏差

在稀疏注意力中，假设 STE 用于 Top-k 选择：

正向传播：保留 k% 的高分注意力分数，其余置零；
反向传播：假设被置零的分数对应的梯度为 0，仅传递保留分数的梯度。但真实梯度可能存在于被置零的分数中（例如，未被选中的分数因参数调整可能变为重要分数），STE 的近似导致这部分梯度被忽略，造成：
优化偏差：模型无法学习到未被选中区域的潜在重要性；
梯度稀释：保留分数的梯度可能包含噪声，因缺乏未选中分数的梯度平衡。

2. 多层累积误差

在深层网络中，STE 的误差会逐层累积： $\epsilon_{\text{total}} = \sum_{l=1}^L \gamma^l \epsilon_l \quad (\gamma \text{ is the error propagation factor, typically } \gamma \geq 1)$ 例如，第一层的梯度近似误差会导致第二层参数更新偏离最优方向，进而放大后续层的误差，可能引发 “误差级联”，使模型收敛到次优解。

在 LLM 中的典型应用与误差案例

1. 稀疏注意力的 STE 优化

假设在动态稀疏注意力中，使用 STE 训练阈值 $\tau$ ：

正向传播： $a' = \mathbb{I}(a > \tau) \cdot a$ （保留大于阈值的注意力分数）；
反向传播： $\frac{\partial a'}{\partial \tau} \approx \frac{\partial a}{\partial \tau}$ （忽略指示函数的梯度）。 误差影响：
若真实梯度在阈值附近剧烈变化（如分数接近 $\tau$ 的区域对损失敏感），STE 会低估梯度幅值，导致阈值更新缓慢，无法及时调整稀疏模式。

2. 权重剪枝的 STE 陷阱

在剪枝中，STE 用于训练二进制掩码 $m \in \{0,1\}$ ： $w' = m \cdot w, \quad m = \sigma(\theta), \quad \text{with STE treating } m \text{ as } \theta$ 误差表现：

当 $\sigma(\theta)$ 接近 0 或 1 时，m 的微小变化对 $w'$ 影响显著，但 STE 假设梯度与 $\theta$ 线性相关，可能导致掩码更新过于激进或保守。

代码示例：STE 的梯度近似误差可视化

import torch  
from torch.autograd import Function  class STEBinarize(Function):  @staticmethod  def forward(ctx, x, threshold=0.5):  # 正向传播：二值化操作  ctx.threshold = threshold  return (x > threshold).float()  @staticmethod  def backward(ctx, grad_output):  # 反向传播：STE近似，直接返回原始梯度  return grad_output, None  # 忽略阈值的梯度  # 模拟训练过程  
x = torch.tensor(0.6, requires_grad=True)  
mask = STEBinarize.apply(x)  
loss = (mask - 1.0) ** 2  # 目标为1，希望x增大超过阈值  
loss.backward()  print(f"原始x值: {x.item()}")  
print(f"STE梯度: {x.grad.item()}")  
# 手动计算真实梯度（二值化函数不可导，真实梯度为0，但STE返回2*(mask-1)*1=2*(1-1)=0？这里存在矛盾）  
# 注：实际因二值化不可导，PyTorch会报错，STE在此模拟可导路径

代码陷阱与解读

梯度近似的虚伪性：
- 二值化函数在 (x=0.6 处的真实梯度为 0（因函数在此处为常数），但 STE 返回的梯度为 $\frac{\partial loss}{\partial x} = 2*(mask-1)*1 = 0$ （巧合相等），但在 x=0.4 时，mask=0，STE 梯度为 $2*(0-1)*1 = -2$ ，而真实梯度仍为 0，误差为 - 2。
误差的不可预测性：
- STE 的梯度近似可能在某些点 “幸运” 匹配真实梯度（如示例中的 x=0.6），但在大多数点（如 x=0.4）存在显著误差，导致优化方向偏离。

误差缓解策略：从启发式到理论优化

1. 平滑近似替代离散操作

用 sigmoid 替代符号函数： $y = \sigma(\alpha x)$ （ $\alpha$ 为温度参数），当 $\alpha \to \infty$ 时近似二值化，梯度为 $\alpha y(1-y)$ ，避免 STE 的硬截断误差。

2. 局部自适应 STE

根据激活值调整梯度缩放： $\frac{\partial y'}{\partial x} = \begin{cases} \frac{\partial y}{\partial x}, & |x| > \tau + \epsilon \\ 0, & \text{if not} \end{cases}$ 在阈值附近区域不传递梯度，减少离散化敏感区域的误差。

3. 对抗训练校准误差

在损失函数中加入误差正则项： $\mathcal{L} = \mathcal{L}_{\text{task}} + \lambda \left\| \nabla_x g(f(x)) - \nabla_x f(x) \right\|_F^2$ 通过对抗方式迫使 STE 的近似梯度接近真实梯度（需估计真实梯度，如通过有限差分法）。

总结：STE 的 “实用主义” 与 “理论妥协”

Straight-Through Estimator 是稀疏化训练中的实用技巧，通过牺牲梯度准确性换取计算可行性。其梯度近似误差本质上是 “离散化操作” 与 “连续优化” 之间的理论鸿沟 —— 前者属于组合优化，后者属于梯度下降的连续优化。在 LLM 中，这种误差可能导致注意力模式偏离最优解，或权重剪枝过度破坏模型表达能力。然而，在缺乏高效可微稀疏操作的现状下，STE 仍是工程落地的首选方案。未来，随着神经架构搜索（NAS）和可微组合优化的发展，我们有望设计出误差可控的稀疏化机制，让模型在 “精准稀疏” 与 “高效优化” 之间实现真正的平衡。

Q13 局部窗口注意力的内存占用公式推导（窗口大小 ）

局部窗口注意力：解决长序列内存困境的利器

内存占用公式推导：抽丝剥茧，步步为营

1. Q、K、V 矩阵的内存占用

2. 注意力权重矩阵的内存占用

3. 输出矩阵的内存占用

总内存占用公式

在 LLM 中的应用：长序列处理的效率革命

代码示例与深度解读

总结：理论与实践的完美融合

Q14 LSH 注意力中哈希桶分配的期望误差分析

LSH 注意力：LLM 长序列加速的 “近似计算器”

误差的两面性：假阴性与假阳性的 “恶作剧”

数学建模：从哈希特性到误差公式推导

在 LLM 中的实战：误差控制的生存之道

1. 长文本场景的误差容忍策略

2. 参数调整的黄金法则

代码示例：用 PyTorch 玩转 LSH 注意力的桶分配

代码背后的误差逻辑

总结：误差分析如何让 LLM “聪明地犯错”

Q15 块稀疏注意力（Block Sparse）的信息传递延迟建模

块稀疏注意力：长序列的 “分区通信” 机制

信息传递延迟：块结构中的 “跨区通信成本”

数学建模：从图论到延迟公式

1. 一维相邻块模式（局部稀疏）

2. 跳跃块模式（分层稀疏）

在 LLM 中的应用：平衡延迟与计算效率

1. 长文本场景的延迟挑战

2. 工程优化策略

代码示例：用 PyTorch 实现块稀疏注意力的延迟控制

代码中的延迟控制逻辑

总结：让信息在 “块世界” 中高效穿梭

Q16 轴向注意力（Axial Attention）的维度分解数学证明

轴向注意力：高维数据的 “分而治之” 神器

维度分解的数学本质：从二维到多维的张量拆分

1. 行轴注意力：沿行方向计算局部关联

2. 列轴注意力：沿列方向整合行轴结果

3. 总复杂度与全局注意力对比

多维推广：从二维到三维及更高维的分解法则

在 LLM 中的应用：长文本的 “分层轴” 建模

代码示例：用 PyTorch 实现二维轴向注意力

代码解读：维度转换的 “轴游戏”

总结：让高维数据在 “轴” 上跳舞

Q17 推导线性注意力（Linear Attention）的核函数近似误差上界

线性注意力：从二次复杂度到线性的 “核魔法”

误差来源：核函数的 “理想” 与 “现实”

数学推导：从核差异到输出误差的层层递推

假设条件

关键步骤

1. 核矩阵误差的界定

2. 注意力权重误差的传递

3. 输出误差的最终推导

简化结论

在 LLM 中的意义：误差与效率的再平衡

1. 长序列场景的误差控制

2. 近似方法的优化方向

代码示例：用指数核近似点积注意力的误差验证

代码解读

总结：给 “近似” 戴上理论的 “紧箍咒”

Q18 分析内存压缩注意力（Memory-Compressed Attention）的池化操作梯度

内存压缩注意力：用池化 “挤压” 内存的双刃剑

池化操作的前向与反向：从信息压缩到梯度分配

1. 平均池化：梯度的 “均匀分摊”

2. 最大池化：梯度的 “胜者通吃”

3. 可学习池化：梯度的 “智能路由”

池化梯度对注意力优化的影响

1. 梯度稀释问题（以平均池化为例）

2. 梯度稀疏性问题（以最大池化为例）

3. 跨块依赖的梯度断裂

在 LLM 中的实战：如何设计 “梯度友好” 的池化操作

1. 分层池化 + 残差连接

2. 动态池化：让梯度指导下采样

3. 可逆池化：无损的梯度传递

代码示例：平均池化的梯度计算与分析

代码解读

总结：在压缩与优化间寻找梯度平衡点

Q19 证明低秩注意力（Low-Rank Attention）的秩约束优化条件

低秩注意力：用 “降维” 驯服注意力矩阵的 “洪荒之力”

数学建模：从优化目标到秩约束

问题定义

Q13 局部窗口注意力的内存占用公式推导（窗口大小 $\omega$ ）