当前位置：首页 > news >正文

理解欧拉公式

news 来源：原创 2025/7/3 14:04:50

1. 欧拉公式中的符号

欧拉公式
$e^{ix}=\cos x+i\sin x$
当 $=\pi$ 时
$e^{i\:\pi}+1=0 //欧拉恒等式$
- $e$ :自然对数的底
- $i$ :虚数， $i^2 = -1$
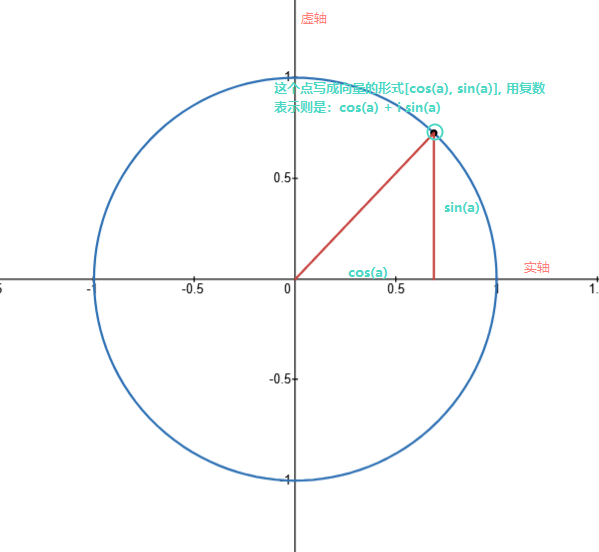
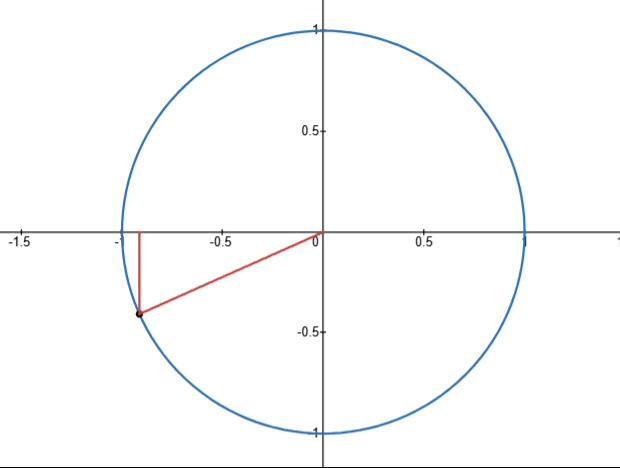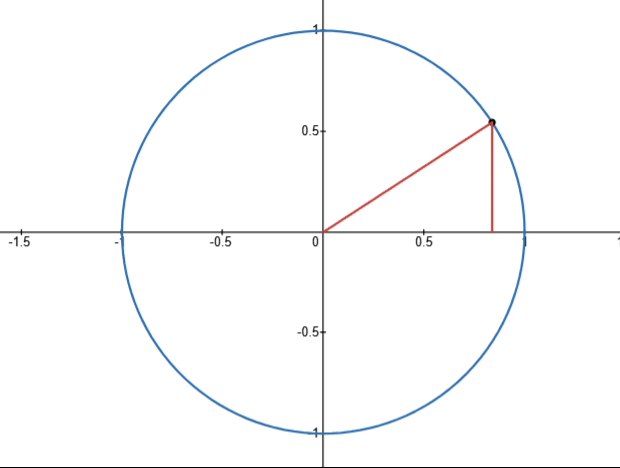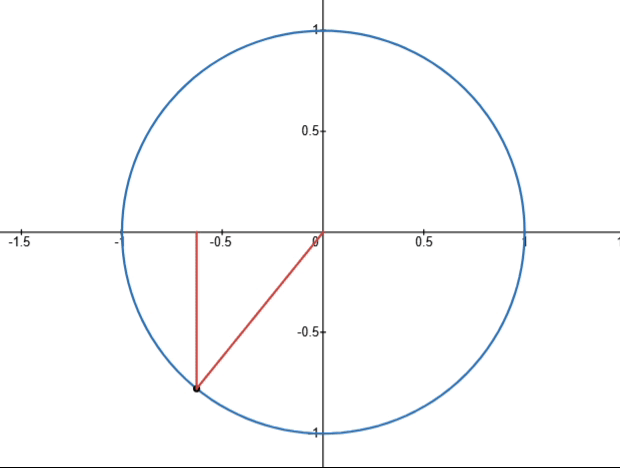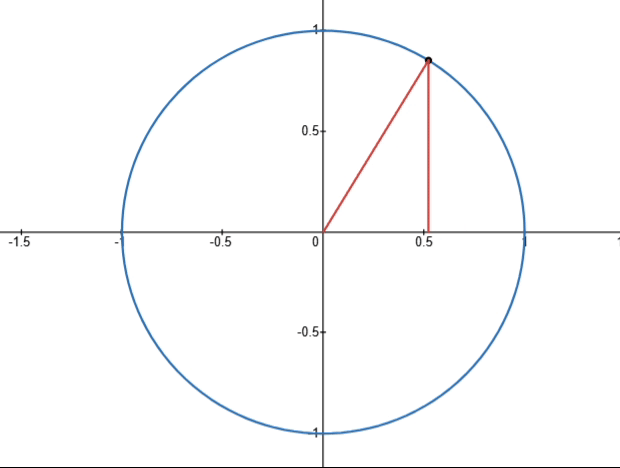
- $\cos x+i\sin x$ :复数， $\cos x$ 为实部， $\sin x$ 为虚部，实部和虚部对应复平面的一个点，在复平面中如下图所示(所有的点都落在一个单位圆上)：

2. 理解欧拉公式的左右两边为什么是相等的

2.1 自然对数的底 $e$ 是什么

$e$ 表示 $n$ 趋近于无穷大时 $(1+\frac1n)^n$ 的极限，约等于 $2.718281828459045$
$e=\lim_{n\to\infty}\left(1+\frac1n\right)^n$
记住一点：无论对 $e^x$ 求几阶导，结果都为 $e^x$ ,它的变化率是等于它本身的，它变化率的变化率也本身，变化率的变化率的变化率也等于它本身。。。。。。。可以无限套娃下去

2.2 $e^{ix}$ 为什么等于 $\cos x+i\sin x$

方法是对左右两边分别进行泰勒展开，关于泰勒展开可以参考我的另外一篇文章《泰勒多项式》
对 $e^{ix}$ 在 $0$ 点处进行泰勒展开：
$泰勒公式\\ P_n(x)=f(a)+f'(a)(x-a)+ f''(a)\frac {(x-a)^2}{2!} + ... + f^{(n)}(a)\frac{(x-a)^n}{n!}\\ ------------\\ 在零点处展开的公式（麦克劳林公式）\\ P_n(x)=f(0)+f'(0)(x)+ f''(0)\frac {(x)^2}{2!} + ... + f^{(n)}(0)\frac{(x)^n}{n!}\\ ------------\\ 将e^{ix}带入麦克劳林公式\\ e^x = e^0+(e^0)'(ix)+(e^0)''\frac {(ix)^2}{2!} + ... + (e^0)^{(n)}\frac{(ix)^n}{n!}\\ ------------\\ e^0的导数 = e^0 = 1\\ e^{ix} = 1 + ix + \frac {(ix)^2}{2!} + \frac {(ix)^3}{3!} ... + \frac{(ix)^n}{n!}\\ ------------\\ e^{ix}=\sum_{n=0}^\infty\frac{(ix)^n}{n!} //注：0! = 1\\ ------------\\ 因为 i^2 = -1, 所以在n为偶数的时候，i是可以消掉的，所以，上述公式也可以写成实部和虚部两部分\\ e^{ix}=\sum_{n=0}^\infty\frac{(ix)^{2n}}{(2n)!}+\sum_{n=0}^\infty\frac{(ix)^{2n+1}}{(2n+1)!}\\ --\\ e^{ix}=\sum_{n=0}^\infty(-1)^n\frac{x^{2n}}{(2n)!}+i\sum_{n=0}^\infty(-1)^n\frac{x^{2n+1}}{(2n+1)!}$
对 $\cos x+i\sin x$ 进行泰勒展开
- 对 $\cos x$ 进行泰勒展开，过程不过多赘述了，直接写结果
  $\cos x = \cos(x)=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots.\\\cos x = \sum_{n=0}^\infty\left(-1\right)^n\frac{x^{2n}}{(2n)!}$
- 对 $\sin x$ 进行泰勒展开，过程不过多赘述了，直接写结果
  $\sin(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots.\\ \sin(x) = \sum_{n=0}^\infty\left(-1\right)^n\frac{x^{2n+1}}{(2n+1)!}$
- $\cos x+i\sin x$ 的泰勒展开为
  $\cos x+i\sin x = \sum_{n=0}^\infty(-1)^n\frac{x^{2n}}{(2n)!}+i\sum_{n=0}^\infty(-1)^n\frac{x^{2n+1}}{(2n+1)!}$
总结：
如下图所示 $e^{ix}=\cos x+i\sin x$ 的泰勒展开是完全一样的，所以等式两边是等价的

3. $e^{i\:\pi}+1=0$ 又为什么成立

3.1 分析

$e^{i\:\pi}$ 中的 $\pi$ 代表的是什么？直接说答案 - 角度，准确的说是 $180^0$ ，这是弧度值的表示方法
使用弧度制如何表示一个角度呢？其实很简单，就是弧长 / 半径 $\theta\left(\text{弧度}\right)=\frac{\text{弧长}s}{\text{半径}r}$
半圆的弧长是 $\:\pi r$ ，所以 $180^0 = \frac{\:\pi r}{r} = \:\pi$
常见角度与弧度对照表：

角度（度）	弧度（rad）
0°	0
30°	$\frac{\pi}{6}$
45°	$\frac{\pi}{4}$
60°	$\frac{\pi}{3}$
90°	$\frac{\pi}{2}$
180°	$\pi$

3.2 结论

因为 $\pi = 180^o$ ,所以
$e^{i\:\pi} = \cos {180^o}+i\sin {180^o}\\ e^{i\:\pi} = -1 + i*0\\ e^{i\:\pi} = -1\\ ----------------------------------------------\\ e^{i\:\pi}+1=0$

理解欧拉公式

1. 欧拉公式中的符号欧拉公式 e i x cos ⁡ x i sin ⁡ x e^{ix}\cos xi\sin x eixcosxisinx当 x π x \pi xπ时 e i π 1 0 / / 欧拉恒等式 e^{i\:\pi}10 //欧拉恒等式 eiπ10//欧拉恒等式 e e e:自然对数的底 i i i:虚数， i 2 − 1 i^2 -1 i2−1 cos…...

编程日记 2025/7/3 14:04:50

7.9 Python+Click实战：5步打造高效的GitHub监控CLI工具

Python+Click实战：5步打造高效的GitHub监控CLI工具 GitHub Sentinel Agent 命令行界面开发实战关键词：CLI 开发实践、Click 框架、API 集成、命令行参数解析、错误处理机制 1. 命令行界面技术选型与架构设计 GitHub Sentinel 采用 Click + Requests 技术栈构建 CLI 工具，…...

编程日记 2025/6/29 9:20:28

leetcode28. 找出字符串中第一个匹配项的下标_简单KMP

28. 找出字符串中第一个匹配项的下标 - 力扣（LeetCode） 模仿：algorithm-journey/src/class100/Code01_KMP.java at main algorithmzuo/algorithm-journey GitHub #include <stdio.h> #include <stdlib.h> #include <strin…...

编程日记 2025/6/29 9:20:20

代码随想录算法训练营第二十六天

LeetCode题目: 452. 用最少数量的箭引爆气球435. 无重叠区间763. 划分字母区间2799. 统计完全子数组的数目(每日一题) 其他: 今日总结往期打卡 452. 用最少数量的箭引爆气球跳转: 452. 用最少数量的箭引爆气球学习: 代码随想录公开讲解问题: 有一些球形气球贴在一堵用 X…...

编程日记 2025/6/29 9:20:21

精益数据分析（20/126）：解析经典数据分析框架，助力创业增长

精益数据分析（20/126）：解析经典数据分析框架，助力创业增长在创业和数据分析的学习道路上，每一次深入探索都可能为我们带来新的启发。今天，依旧带着和大家共同进步的想法，我们一起深入研读《精…...

编程日记 2025/6/29 12:29:13

基于Django的权限管理平台

目录单元一：项目准备任务一：创建项目 1.1配置 DRF 模型任务二：设置CSRF令牌 2.1创建app包 2.2检查浏览器Cookies权限 2.3获取cookies 单元二：用户平台任务一：用户数据模型搭建 1.1创建user模块 1.2生成…...

编程日记 2025/6/29 9:22:52

深度解析 LangChain、ReAct、ReROO 架构及其在 AI Agent 中的应用

一、LangChain 架构：模块化智能代理的核心框架 1. 架构特性与设计原理 LangChain 是构建智能代理的模块化框架，其核心通过 Chains（任务链）、Agents（代理）、Memory（记忆） 和 Tools&a…...

编程日记 2025/6/29 11:27:15

数据库day-07

一、实验名称和性质子查询验证设计二、实验目的 1．掌握子查询的嵌套查询； 2.掌握集合操作 3．了解EXISTS嵌套查询方法； 三、实验的软硬件环境要求硬件环境要求： PC机(单机) 使用的软件名称、版本号以及模块…...

编程日记 2025/6/29 11:12:32

使用Tauri 2.3.1+Leptos 0.7.8开发桌面小程序汇总

近期断断续续学习了Rust编程，使用Tauri 2.3.1Leptos 0.7.8开发了一个自用的桌面小程序。Win10操作系统，使用VS Code及rust analyzer插件搭建的开发环境，后期开始使用Roo Code绑定DeepSeek API 辅助编程，对我这个初学者编程帮助很大…...

编程日记 2025/6/29 11:05:51

计算机视觉——速度与精度的完美结合的实时目标检测算法RF-DETR详解

概述目标检测已经取得了长足的发展，尤其是随着基于 Transformer 的模型的兴起。RF-DETR，由 Roboflow 开发，就是这样一种模型，它兼顾了速度和精度。使用 Roboflow 的工具可以让整个过程变得更加轻松。他们的平台涵盖了从上传和标…...

编程日记 2025/6/29 10:14:37

JS 应用算法逆向三重断点调试调用堆栈BP 插件发包安全结合

# 前置知识 1 、作用域：（本地 & 全局） 简单来说就是运行后相关的数据值 2 、调用堆栈：（由下到上） 简单来说就是代码的执行逻辑顺序 3 、常见分析调试： - 代码全局搜索 - 文件流程断点…...

编程日记 2025/6/29 19:35:03

从零开始在Win上添加一块QEMU开发板（四）实现简单USART

文章目录一、前言背景二、QEMU的字符设备模拟三、USART的发送1. USART发送的QEMU字符设备模拟2. MMIO设计3. 中断连接4. 复位三、代码验证1. 输出到serial控制台2. 输出到文件一、前言背景 QEMU是一款开源的模拟器及虚拟机管理器。而QEMU内置支持了一些开发板，我…...

编程日记 2025/6/29 10:37:21

目标检测篇---faster R-CNN

目标检测系列文章第一章 R-CNN 第二篇 Fast R-CNN 目录目标检测系列文章📄 论文标题🧠 论文逻辑梳理1. 引言部分梳理 (动机与思想) 📝 三句话总结🔍 方法逻辑梳理🚀 关键创新点🔗 方法流程图关键疑问解答…...

编程日记 2025/6/29 11:57:22

【计算机视觉】CV实战项目- 深度解析FaceAI：一款全能的人脸检测与图像处理工具库

深度解析FaceAI：一款全能的人脸检测与图像处理工具库项目概述核心功能与技术实现1. 人脸检测与识别2. 数字化妆与轮廓标识3. 性别与表情识别4. 高级图像处理实战指南：项目运行与开发环境配置典型应用示例常见问题与解决方案学术背景与相关研究项目扩展…...

编程日记 2025/6/29 10:22:04

Linux下编译opencv-4.10.0（静态链接库和动态链接库）

1. 安装依赖在编译之前，确保系统中安装了必要的依赖工具和库。运行以下命令安装： sudo apt update sudo apt-get install build-essential sudo apt-get install cmake git libgtk2.0-dev pkg-config sudo apt-get install libavcodec-dev libavforma…...

编程日记 2025/6/29 12:15:34

OpenBMC：BmcWeb login创建session

OpenBMC：BmcWeb login认证-CSDN博客完成用户的认证后，还需要为该用户创建session，从而为后续的rest api访问铺平道路 inline void handleLogin(const crow::Request& req,const std::shared_ptr<bmcweb::AsyncResp>& asyncResp) {...auto session =persisten…...

编程日记 2025/6/29 11:01:33

Java高频面试之并发编程-07

hello啊，各位观众姥爷们！！！本baby今天来报道了！哈哈哈哈哈嗝🐶 面试官：线程之间有哪些通信方式？ 在 Java 多线程编程中，线程间通信（Inter-Thread Communica…...

编程日记 2025/6/29 9:20:27

四、Python编程基础04

这里写目录标题一、集合[了解]二、函数1. 函数定义与调用2. 函数返回值三、模块和包1. 登录案例2.登录案例优化3. 随机数案例四、异常五、web自动化测试1、selenium介绍2、环境搭建具体安装步骤请看 3、入门案例3.1 自动化测试步骤3.2 案例一、集合[了解] 1, 集合 set, 表…...

编程日记 2025/6/29 10:49:18

专家系统的一般结构解析——基于《人工智能原理与方法》的深度拓展

不同的专家系统，其功能与结构都不尽相同，但一般都包括人机接口、推理机、知识库及其管理系统、数据库及其管理系统、知识获取机构、解释机构这六个部分，如下图所示。一、人机接口（Human-Computer Interface, HCI）（一）基本思想与定义 1. 核心思想：双向交互的桥梁人…...

编程日记 2025/6/29 9:20:34

手搓雷达图（MATLAB）

看下别人做出来什么效果话不多说，咱们直接开始 %% 可修改 labels {用户等级, 发帖数, 发帖频率, 点度中心度, 中介中心度, 帖子类型计分, 被列为提案数}; cluster_centers [0.8, 4.5, 3.2, 4.0, 3.8, 4.5, 4.2; % 核心用户0.2, 0.5, 0.3, 0.2, 0.1, 0.0, 0.0;…...

编程日记 2025/6/29 9:20:23

FastMCP与FastAPI：构建自定义MCP服务器

FastMCP与FastAPI：构建自定义MCP服务器模型上下文协议(Model Context Protocol, MCP)是一种让AI模型与外部工具和服务交互的标准。本文将介绍FastMCP和FastAPI，并通过实例展示如何创建自定义MCP服务器。 MCP基础概念 MCP允许语言模型: 访问外部工具…...

编程日记 2025/6/29 9:22:48

基于 springboot+vue+elementui 的办公自动化系统设计(

基于 springbootvueelementui 的办公自动化系统设计(前端代码在oa文件夹里) 系统主要功能： 1、统一的信息发布平台：公告栏，公司活动，项目进度，公司周报 2、统一的文件管理平台：收文管理、发文管理。文件查询…...

编程日记 2025/6/29 12:16:55

Java发展史及版本详细说明

Java发展史及版本详细说明 1. Java 1.0（1996年1月23日） 核心功能： 首个正式版本，支持面向对象编程、垃圾回收、网络编程。包含基础类库（java.lang、java.io、java.awt）。支持Applet（浏览器嵌入…...

编程日记 2025/6/29 9:20:46

高企复审奖补！2025年合肥市高新技术企业重新认定奖励补贴政策及申报条件

一、合肥市高新技术企业重新认定奖励补贴政策 （一）高新区高新技术企业重新认定复审补贴奖励重新认定为国家高新技术企业的给予5万元一次性奖励。 （二）经开区高新技术企业重新认定复审补贴奖励对重新认定的企业，给…...

编程日记 2025/6/29 9:20:32

elementui日历显示红点及根据日程范围判断是否有红点

生成指定日期范围内的所有日期 generateDateRange(startStr, endStr) {const dates []; 日期列表const start new Date(startStr); 日程开始日期const end new Date(endStr); 日程结束日期end.setHours(23, 59, 59, 999); 结束的那一天设置为23点59分59秒// 生成日期范围内…...

编程日记 2025/6/29 11:01:47

第六章 QT基础：5、QT的UDP网络编程

在 Qt 中，QUdpSocket 类用于实现基于 UDP 协议的网络通信。UDP（用户数据报协议）是一种无连接的协议，与 TCP 不同，它不需要建立连接，因此它的传输速度较快，但也不保证数据的可靠传输。 1. Qt UDP…...

编程日记 2025/6/29 12:21:36

JAVA设计模式——（五）享元模式（Flyweight Pattern）

JAVA设计模式——（五）享元模式（Flyweight Pattern） 概念理解实现创建内部状态定义享元工厂测试适用性概念使共享对象可以有效的支持大量的细粒度对象。主要采用池技术实现。理解享元模式主要解决大量对象的共享&#xff0…...

编程日记 2025/6/29 9:20:36

电竞俱乐部护航点单小程序，和平地铁俱乐部点单系统，三角洲护航小程序，暗区突围俱乐部小程序

电竞俱乐部护航点单小程序开发，和平地铁俱乐部点单系统，三角洲护航小程序，暗区突围俱乐部小程序开发端口包含： 超管后台， 老板端，打手端，商家端，客服端，管事端&#x…...

编程日记 2025/6/29 11:34:32

mybatis log convert使用

1. idea 搜索插件 mybatis log convert. 安装后重启idea 启动程序. 日志打印后选中输出的内容右键。这里随意选中一段日志做演示必须要在console中复制才能使用这个日志解析 2. 还有一种用法。没找到...

编程日记 2025/6/29 9:20:31

[U-Net]DA-TRANSUNET

论文题目：DA-TRANSUNET: INTEGRATING SPATIAL AND CHANNEL DUAL ATTENTION WITH TRANSFORMER U-NET FOR MEDICAL IMAGE SEGMENTATION ∗ 中文题目：DA-TRANSUNET：结合空间和通道双注意力与Transformer U-NET的医学图像分割算法 0摘要精确的医学图像分割对疾病定量和治疗评…...

编程日记 2025/6/29 9:20:39

AI大模型从0到1记录学习数据结构和算法 day20

4.3 分治算法 4.3.1 概述分治算法的基本思想为：将原问题递归的分解为若干个（通常是两个以上）规模较小、相互独立且性质相同的子问题，直到子问题足够简单，简单到可以直接求解。然后再返回结果，逐个解决上层…...

编程日记 2025/6/29 12:19:13

面阵相机中M12镜头和远心镜头的区别及性能优势

以下是关于面阵相机中M12镜头和远心镜头的区别及性能优势的详细分析，结合知识库内容整理如下： 一、M12镜头与远心镜头的核心区别 1. 设计原理与光学特性特性M12镜头远心镜头光学设计标准镜头设计，无特殊光学校正，依赖传统光路。…...

编程日记 2025/6/29 9:20:24

[创业之路-385]：企业法务 - 初创公司如何做好商业秘密的管理

一、商业秘密的定义与价值定义： 商业秘密是企业的核心资产，包括技术信息（如算法、配方）和经营信息（如客户名单、定价策略），具有非公开性、商业价值、保密性三大特征。价值： 初创公…...

编程日记 2025/6/29 11:49:12

Qt5.15.2+OpenCV4.9.0开发环境搭建详细图文教程（OpenCV使用Qt自带MinGW编译的全过程，包教包会）

【系列专栏】：博主结合工作实践输出的，解决实际问题的专栏，朋友们看过来！《项目案例分享》《极客DIY开源分享》《嵌入式通用开发实战》《C++语言开发基础总结》《从0到1学习嵌入式Linux开发》《QT开发实战》《Android开发实战》《实用硬件方案设计》《结构建模设…...

编程日记 2025/6/29 9:22:34

怎么实现RAG检索相似文档排序：similarities

怎么实现RAG检索相似文档排序：similarities top_5_indices = similarities.argsort()[-5:][::-1] 这行代码的作用是从一组相似度得分中获取相似度最高的5个元素的索引。 similarities：这是一个包含了某个问题与所有文档之间余弦相似度得分的一维数组（假设 similarities 是通…...

编程日记 2025/6/29 10:15:58

NLP高频面试题（五十三）——深度学习正则化详解

一、动因篇为什么要正则化？深度神经网络通常包含数以万计甚至数以亿计的参数，模型容量极大，极易在有限的训练数据上“记住”噪声与异常样本，从而出现过拟合（overfitting）现象。过拟合导致模型在训练集上表现优异，但在测试集或真实场景中泛化能力大幅下降。正则化（r…...

编程日记 2025/6/29 12:01:01

2.idea查看某个类的方法名称和实现

2.idea查看某个类的方法名称和实现 ctrl鼠标左键单击类名点击侧边栏Structure可看到方法名称的统计，这样直观...

编程日记 2025/6/29 9:20:40

FeignClient用法笔记

1. FeignClient简介在微服务架构中总需要各个服务相互调用，各个服务又是以接口方式暴露，所以需要Http远程调用；为了简化调用，Spring Cloud OpenFeign 库提供了org.springframework.cloud.openfeign.FeignClient 注解&#xff1a…...

编程日记 2025/6/29 9:22:59

【Redis】 Redis中常见的数据类型（二）

文章目录前言一、 List 列表1. List 列表简介2.命令3. 阻塞版本命令4. 内部编码5. 使用场景二、Set 集合1. Set简单介绍2. 普通命令3 . 集合间操作4. 内部编码5. 使用场景三、Zset 有序集合1.Zset 有序集合简介2. 普通命令3. 集合间操作4. 内部编码5. 使用场景结语前言在…...

编程日记 2025/6/29 9:20:30

电力作业安全工器具全解析：分类、配置与检查要点

在电力行业，每一次作业都面临潜在危险，安全工器具是保障作业人员生命安全的关键。今天，金能电力带大家深入了解电力作业中常见的安全工器具，以及它们的检查与使用要点。电力作业中安全工器具种类繁多。绝缘安全工器具因直接关联带…...

编程日记 2025/6/29 9:22:23

PowerBI-使用参数动态修改数据源路径

PowerBI-使用参数动态修改数据源路径在PowerQuery中可以使用参数，通过参数我们可以将多个文件路径相同的字符串进行替换。以一个案例分享下过程： 第一步，导入一个含有多个sheet表的EXCEL工作薄，点击转换数据，如图…...

编程日记 2025/6/29 11:54:02

Temperature

模型中Temperature参数的详细解释 Temperature 是生成模型（如GPT、LLaMA等）中用于控制输出多样性和随机性的关键超参数。它通过调整模型预测概率分布的平滑程度，直接影响生成文本的创造性与稳定性。模型中Temperature参数的详细解…...

编程日记 2025/6/29 9:20:25

C++ 日志系统实战第二步：不定参数函数解析

全是通俗易懂的讲解，如果你本节之前的知识都掌握清楚，那就速速来看我的项目笔记吧~ 相关技术知识补充不定参宏函数在 C 语言中，不定参宏函数是一种强大的工具，它允许宏接受可变数量的参数，类似于不定参函数&#…...

编程日记 2025/6/29 9:22:26

【高并发】 MySQL锁优化策略

在数据库高并发场景中，行锁、表锁和高并发处理是密切相关的概念，它们共同影响着系统的并发性能和数据一致性。以下是三者的详细解释及高并发处理的策略： 1. 行锁（Row-Level Locking） 行锁是数据库中最小的锁粒度&…...

编程日记 2025/6/29 12:25:03

C语言——填充矩阵

C语言——填充矩阵一、问题描述二、格式要求1.输入形式2.输出形式3.样例三、实验代码一、问题描述编程实现自动填充nn矩阵元素数值，填充规则为：从第一行最后一列矩阵元素开始按逆时针方向螺旋式填充数值1，2，…，nn…...

编程日记 2025/6/29 12:28:22

CSS3 基础（背景-文本效果）

二、背景效果属性功能示例值说明background设置背景颜色或渐变background: linear-gradient(45deg, #4CAF50, #FF5722);设置背景颜色、图片或渐变效果。background-size调整背景图片大小background-size: cover;设置背景图片的显示大小，如 cover 或 contain。back…...

编程日记 2025/6/29 10:55:09

点云配准算法之NDT算法原理详解

一、算法概述 NDT（Normal Distributions Transform）最初用于2D激光雷达地图构建（Biber & Straer, 2003），后扩展为3D点云配准。它将点云数据空间划分为网格单元（Voxel），在每个体…...

编程日记 2025/6/29 10:22:26

springboot在eclipse里面运行 run as 是Java Application还是 Maven

在 Eclipse 里运行 Spring Boot 项目时，既可以选择以“Java Application”方式运行，也可以通过 Maven 命令来运行，下面为你详细介绍这两种方式及适用场景。以“Java Application”方式运行操作步骤在项目中找到带有 SpringBootApplicat…...

编程日记 2025/6/29 12:08:07