PaddlePaddle线性回归详解：从模型定义到加载，掌握深度学习基础

目录

• 前言
• 一、paddlepaddle框架的线性回归
• 1.1 paddlepaddle模型的定义方式
• 1.1.1 使用序列的方式 nn.Sequential 组网
• 1.1.2 使用类的方式 class nn.Layer组网
• 1.2 数据加载 
• 1.3 paddlepaddle模型的保存
• 1.3.1 基础API保存
• 1.3.2 高级API模型的保存
• 1.3.2.1 训练fit进行保存
• 1.3.2.2 利用paddle.Model类进行保存
• 1.4 paddlepaddle模型的加载 
• 1.4.1 基础API模型的加载
• 1.4.2 高级API加载
• 1.5 paddlepaddle模型网络结构的查看 
• 1.5.1 summary
• 1.5.2 netron
• 1.5.3 visualdl
• 二、曲线拟合
• 1.1案例引入
• 1.2 散点输入
• 1.3 前向计算
• 1.4 Sigmoid函数引入
• 1.5 激活函数的引入
• 1.6 参数初始化
• 1.7 损失函数
• 1.8 开始迭代
• 1.9反向传播
• 1.10 梯度下降显示
•  1.11 曲线拟合代码
• 三、激活函数
• 3.1 激活函数及其导数算法理论讲解
• 3.2 激活函数的作用？
• 3.3 激活函数的概念
• 3.4 Sigmoid
• 总结

---

前言

书接上文

PyTorch与TensorFlow模型全方位解析：保存、加载与结构可视化-CSDN博客文章浏览阅读479次，点赞6次，收藏17次。本文深入探讨了PyTorch和TensorFlow中模型管理的关键方面，包括模型的保存与加载以及网络结构的可视化。涵盖了PyTorch中模型和参数的保存与加载，以及使用多种工具进行模型结构分析。同时，详细介绍了TensorFlow中模型的定义方式、保存方法、加载流程以及模型结构的可视化技术，旨在帮助读者全面掌握两大深度学习框架的模型管理技巧。https://blog.csdn.net/qq_58364361/article/details/147382076?spm=1011.2415.3001.10575&sharefrom=mp_manage_link

---

一、paddlepaddle框架的线性回归

从以下5个方面对深度学习框架paddlepaddle框架的线性回归进行介绍
1.paddlepaddle模型的定义
2.paddlepaddle模型的保存
3.paddlepaddle模型的加载
4.paddlepaddle模型网络结构的查看
5.paddlepaddle框架线性回归的代码实现
上面这5方面的内容，让大家，掌握并理解paddlepaddle框架实现线性回归的过程。
1.paddlepaddle 官网 ：https://www.paddlepaddle.org.cn/
安装
pip install paddlepaddle==2.6.2 -i https://mirror.baidu.com/pypi/simple

---

1.1 paddlepaddle模型的定义方式

主要针对基础API

1.1.1 使用序列的方式 nn.Sequential 组网

model=nn.Sequential(nn.Linear(1,1))

#导入库
import numpy as np
import paddle
import paddle.nn as nn
#设置随机数种子 ,保证结果可复现
seed=1
paddle.seed(seed)# 1.散点输入 定义输入数据
data = [[-0.5, 7.7], [1.8, 98.5], [0.9, 57.8], [0.4, 39.2], [-1.4, -15.7], [-1.4, -37.3], [-1.8, -49.1], [1.5, 75.6], [0.4, 34.0], [0.8, 62.3]]
#转化为数组
data=np.array(data)
# 提取x 和y
x_data=data[:,0]
y_data=data[:,1]
#转成张量 转成paddlepaddle张量
x_train=paddle.to_tensor(x_data,dtype=paddle.float32)
y_train=paddle.to_tensor(y_data,dtype=paddle.float32)
# 2. 定义前向模型
# model=paddle.nn.Linear(1,1)#主要针对基础API
#方式1 使用序列的方式 nn.Sequential 组网
model=nn.Sequential(nn.Linear(1,1))# 3.定义损失函数和优化器
#3.1损失函数
criterion=paddle.nn.MSELoss()
#3.2 优化器
optimizer=paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())
# 4.开始迭代
epochs=500
for epoch in range(1,epochs+1):#前向传播#unsqueeze()扩展一维y_prd=model(x_train.unsqueeze(1))loss=criterion(y_prd.squeeze(1),y_train)#清除之前计算的梯度optimizer.clear_grad()#自动计算梯度loss.backward()#更新参数optimizer.step()# 5.显示频率的设置if epoch % 10==0 or epoch==1:#可以使用float(loss)或者 loss.numpy()会报警告print(f"epoch:{epoch},loss:{float(loss)}")

---

1.1.2 使用类的方式 class nn.Layer组网

#导入库
import numpy as np
import paddle
import paddle.nn as nn
#设置随机数种子 ,保证结果可复现
seed=1
paddle.seed(seed)# 1.散点输入 定义输入数据
data = [[-0.5, 7.7], [1.8, 98.5], [0.9, 57.8], [0.4, 39.2], [-1.4, -15.7], [-1.4, -37.3], [-1.8, -49.1], [1.5, 75.6], [0.4, 34.0], [0.8, 62.3]]
#转化为数组
data=np.array(data)
# 提取x 和y
x_data=data[:,0]
y_data=data[:,1]
#转成张量 转成paddlepaddle张量
x_train=paddle.to_tensor(x_data,dtype=paddle.float32)
y_train=paddle.to_tensor(y_data,dtype=paddle.float32)
#主要针对基础API
#方式 2 单独定义 使用类的方式 class nn.Layer组网
class LinearModel(nn.Layer):def __init__(self):super(LinearModel,self).__init__()self.linear=nn.Linear(1,1)def forward(self,x):x=self.linear(x)return x
# #定义模型的对象
model=LinearModel()# 3.定义损失函数和优化器
#3.1损失函数
criterion=paddle.nn.MSELoss()
#3.2 优化器
optimizer=paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())
# 4.开始迭代
epochs=500
for epoch in range(1,epochs+1):#前向传播#unsqueeze()扩展一维y_prd=model(x_train.unsqueeze(1))loss=criterion(y_prd.squeeze(1),y_train)#清除之前计算的梯度optimizer.clear_grad()#自动计算梯度loss.backward()#更新参数optimizer.step()# 5.显示频率的设置if epoch % 10==0 or epoch==1:#可以使用float(loss)或者 loss.numpy()会报警告print(f"epoch:{epoch},loss:{float(loss)}")

---

1.2 数据加载 

#1.先来看数据加载
#2.模型构建高层API#导入库
import numpy as np
import paddle
import paddle.nn as nn
from paddle.io import DataLoader,TensorDataset
#设置随机数种子 ,保证结果可复现
seed=1
paddle.seed(seed)# 1.散点输入 定义输入数据
data = [[-0.5, 7.7], [1.8, 98.5], [0.9, 57.8], [0.4, 39.2], [-1.4, -15.7], [-1.4, -37.3], [-1.8, -49.1], [1.5, 75.6], [0.4, 34.0], [0.8, 62.3]]
#转化为数组
data=np.array(data)
# 提取x 和y
x_data=data[:,0]
y_data=data[:,1]
#转成张量 转成paddlepaddle张量
x_train=paddle.to_tensor(x_data,dtype=paddle.float32)
y_train=paddle.to_tensor(y_data,dtype=paddle.float32)
#TensorDataset是接收一个值，不是接收两个值,使用列表
dataset=TensorDataset([x_train.unsqueeze(1),y_train.unsqueeze(1)])
#创建Dataloader对象
dataloader=DataLoader(dataset,batch_size=10,shuffle=True)
# 2. 定义前向模型
#方式2 单独定义 使用类的方式 class nn.Layer组网
class LinearModel(nn.Layer):def __init__(self):super(LinearModel,self).__init__()self.linear=nn.Linear(1,1)def forward(self,x):x=self.linear(x)return x
#定义模型的对象
model=LinearModel()# 3.使用高层api进行封装
# step1 使用paddle.Model(xxx)进行封装
model=paddle.Model(model)
#step2 使用prepare
model.prepare(optimizer=paddle.optimizer.SGD(learning_rate=0.01,parameters=model.parameters()),loss=nn.MSELoss(),metrics=paddle.metric.Accuracy())
#step3启动训练
#需要用到数据，训练轮次 是否显示日志过程
model.fit(dataloader,epochs=500,verbose=1)

---

1.3 paddlepaddle模型的保存

1.3.1 基础API保存

按照字典的形式保存

paddle.save(model.state_dict(),'./基础API/model.pdparams')

#导入库
import numpy as np
import paddle
import paddle.nn as nn
#设置随机数种子 ,保证结果可复现
seed=1
paddle.seed(seed)# 1.散点输入 定义输入数据
data = [[-0.5, 7.7], [1.8, 98.5], [0.9, 57.8], [0.4, 39.2], [-1.4, -15.7], [-1.4, -37.3], [-1.8, -49.1], [1.5, 75.6], [0.4, 34.0], [0.8, 62.3]]
#转化为数组
data=np.array(data)
# 提取x 和y
x_data=data[:,0]
y_data=data[:,1]
#转成张量 转成paddlepaddle张量
x_train=paddle.to_tensor(x_data,dtype=paddle.float32)
y_train=paddle.to_tensor(y_data,dtype=paddle.float32)
# 2. 定义前向模型
# model=paddle.nn.Linear(1,1)#主要针对基础API
#方式1 使用序列的方式 nn.Sequential 组网
# model=nn.Sequential(nn.Linear(1,1))#方式2 单独定义 使用类的方式 class nn.Layer组网
class LinearModel(nn.Layer):def __init__(self):super(LinearModel,self).__init__()self.linear=nn.Linear(1,1)def forward(self,x):x=self.linear(x)return x
#定义模型的对象
model=LinearModel()# 3.定义损失函数和优化器
#3.1损失函数
criterion=paddle.nn.MSELoss()
#3.2 优化器
optimizer=paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())
# 4.开始迭代
epochs=500
final_checkpoint={}
for epoch in range(1,epochs+1):#前向传播#unsqueeze()扩展一维y_prd=model(x_train.unsqueeze(1))loss=criterion(y_prd.squeeze(1),y_train)#清除之前计算的梯度optimizer.clear_grad()#自动计算梯度loss.backward()#更新参数optimizer.step()# 5.显示频率的设置if epoch % 10==0 or epoch==1:#可以使用float(loss)或者 loss.numpy()会报警告print(f"epoch:{epoch},loss:{float(loss)}")#添加检查点程序if epoch==epochs:#把迭代次数写入final_checkpoint['epoch']=epoch#把训练损失写入final_checkpoint['loss']=loss#基础API模型的保存
paddle.save(model.state_dict(),'./基础API/model.pdparams')
#保存检查点checkpoint信息 是序列化的文件
paddle.save(final_checkpoint, "./基础API/final_checkpoint.pkl")

---

1.3.2 高级API模型的保存

1.3.2.1 训练fit进行保存

model.fit(dataloader,epochs=500,verbose=1,save_dir='./高层API1',save_freq=10)

#1.先来看数据加载
#2.模型构建高层API#导入库
import numpy as np
import paddle
import paddle.nn as nn
from paddle.io import DataLoader,TensorDataset
#设置随机数种子 ,保证结果可复现
seed=1
paddle.seed(seed)# 1.散点输入 定义输入数据
data = [[-0.5, 7.7], [1.8, 98.5], [0.9, 57.8], [0.4, 39.2], [-1.4, -15.7], [-1.4, -37.3], [-1.8, -49.1], [1.5, 75.6], [0.4, 34.0], [0.8, 62.3]]
#转化为数组
data=np.array(data)
# 提取x 和y
x_data=data[:,0]
y_data=data[:,1]
#转成张量 转成paddlepaddle张量
x_train=paddle.to_tensor(x_data,dtype=paddle.float32)
y_train=paddle.to_tensor(y_data,dtype=paddle.float32)
#TensorDataset是接收一个值，不是接收两个值,使用列表
dataset=TensorDataset([x_train.unsqueeze(1),y_train.unsqueeze(1)])
#创建Dataloader对象
dataloader=DataLoader(dataset,batch_size=10,shuffle=True)
# 2. 定义前向模型
#方式2 单独定义 使用类的方式 class nn.Layer组网
class LinearModel(nn.Layer):def __init__(self):super(LinearModel,self).__init__()self.linear=nn.Linear(1,1)def forward(self,x):x=self.linear(x)return x
#定义模型的对象
model=LinearModel()# 3.使用高层api进行封装
# step1 使用paddle.Model(xxx)进行封装
model=paddle.Model(model)
#step2 使用prepare
model.prepare(optimizer=paddle.optimizer.SGD(learning_rate=0.01,parameters=model.parameters()),loss=nn.MSELoss(),metrics=paddle.metric.Accuracy())
#step3启动训练
#需要用到数据，训练轮次 是否显示日志过程
# model.fit(dataloader,epochs=500,verbose=1)#高级API模型的保存
#保存第一种方式,训练fit进行保存
model.fit(dataloader,epochs=500,verbose=1,save_dir='./高层API1',save_freq=10)

---

1.3.2.2 利用paddle.Model类进行保存

注意 这边的model.save和基础API中的model.save不一样，基础API是自己申请出来的对象

# 这里是paddle.Model 大类

model.save('./高层API2/model') #save for train 动态图

# 静态图(可以c++调用)

model.save('./高层API2/infer_model',False) #save for inference 静态图(可以c++调用)

#1.先来看数据加载
#2.模型构建高层API#导入库
import numpy as np
import paddle
import paddle.nn as nn
from paddle.io import DataLoader,TensorDataset
#设置随机数种子 ,保证结果可复现
seed=1
paddle.seed(seed)# 1.散点输入 定义输入数据
data = [[-0.5, 7.7], [1.8, 98.5], [0.9, 57.8], [0.4, 39.2], [-1.4, -15.7], [-1.4, -37.3], [-1.8, -49.1], [1.5, 75.6], [0.4, 34.0], [0.8, 62.3]]
#转化为数组
data=np.array(data)
# 提取x 和y
x_data=data[:,0]
y_data=data[:,1]
#转成张量 转成paddlepaddle张量
x_train=paddle.to_tensor(x_data,dtype=paddle.float32)
y_train=paddle.to_tensor(y_data,dtype=paddle.float32)
#TensorDataset是接收一个值，不是接收两个值,使用列表
dataset=TensorDataset([x_train.unsqueeze(1),y_train.unsqueeze(1)])
#创建Dataloader对象
dataloader=DataLoader(dataset,batch_size=10,shuffle=True)
# 2. 定义前向模型
#方式2 单独定义 使用类的方式 class nn.Layer组网
class LinearModel(nn.Layer):def __init__(self):super(LinearModel,self).__init__()self.linear=nn.Linear(1,1)def forward(self,x):x=self.linear(x)return x
#定义模型的对象
model=LinearModel()# 3.使用高层api进行封装
# step1 使用paddle.Model(xxx)进行封装
model=paddle.Model(model)
#step2 使用prepare
model.prepare(optimizer=paddle.optimizer.SGD(learning_rate=0.01,parameters=model.parameters()),loss=nn.MSELoss(),metrics=paddle.metric.Accuracy())
#step3启动训练
#需要用到数据，训练轮次 是否显示日志过程
# model.fit(dataloader,epochs=500,verbose=1)#高级API模型的保存
#保存第一种方式,训练fit进行保存
model.fit(dataloader,epochs=500,verbose=1)#保存方式2 利用paddle.Model类进行保存
#注意 这边的model.save和基础API中的model.save不一样，基础API是自己申请出来的对象
# 这里是paddle.Model 大类
model.save('./hig_API2/model') #save for train 动态图
# 静态图(可以c++调用)
model.save('./hig_API2/infer_model',False) #save for inference 静态图(可以c++调用)

---

1.4 paddlepaddle模型的加载 

1.4.1 基础API模型的加载

model_state_dict=paddle.load('./基础API/model.pdparams')

模型和参数联系起来

model.set_state_dict(model_state_dict)

#导入库
import numpy as np
import paddle
import paddle.nn as nn
#设置随机数种子 ,保证结果可复现
from paddle.io import DataLoader,TensorDataset
seed=1
paddle.seed(seed)# 1.散点输入 定义输入数据
data = [[-0.5, 7.7], [1.8, 98.5], [0.9, 57.8], [0.4, 39.2], [-1.4, -15.7], [-1.4, -37.3], [-1.8, -49.1], [1.5, 75.6], [0.4, 34.0], [0.8, 62.3]]
#转化为数组
data=np.array(data)
# 提取x 和y
x_data=data[:,0]
y_data=data[:,1]
#转成张量 转成paddlepaddle张量
x_train=paddle.to_tensor(x_data,dtype=paddle.float32)
y_train=paddle.to_tensor(y_data,dtype=paddle.float32)
# 2. 定义前向模型
# model=paddle.nn.Linear(1,1)#主要针对基础API
#方式1 使用序列的方式 nn.Sequential 组网
# model=nn.Sequential(nn.Linear(1,1))#方式2 单独定义 使用类的方式 class nn.Layer组网
class LinearModel(nn.Layer):def __init__(self):super(LinearModel,self).__init__()self.linear=nn.Linear(1,1)def forward(self,x):x=self.linear(x)return x
#定义模型的对象
model=LinearModel()# 3.定义损失函数和优化器
#3.1损失函数
criterion=paddle.nn.MSELoss()
#3.2 优化器
optimizer=paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())
#基础API模型的加载
model_state_dict=paddle.load('./基础API/model.pdparams')
# optimizer_state_dict=paddle.load('./基础API/optimizer.pdopt')
# final_checkpoint_state_dict=paddle.load('./基础API/final_checkpoint.pkl')
# print(final_checkpoint_state_dict)#模型和参数联系起来
model.set_state_dict(model_state_dict)#训练 评估 和推理
# 模型验证模式
model.eval()
#使用TensorDateset 和DateLoader封装
dataloader_test=DataLoader(TensorDataset([paddle.to_tensor([1.5],dtype=paddle.float32)]),batch_size=1)#迭代
for x_test in dataloader_test:predict=model(x_test[0])print(predict)

---

1.4.2 高级API加载

import paddle
# 3.使用高层api进行封装
# step1 使用paddle.Model(xxx)进行封装
model=paddle.Model(model)
#高级API模型的加载
model.load("./高层API1/final")

#1.先来看数据加载
#2.模型构建高层API#导入库
import numpy as np
import paddle
import paddle.nn as nn
from paddle.io import DataLoader,TensorDataset
#设置随机数种子 ,保证结果可复现
seed=1
paddle.seed(seed)# 1.散点输入 定义输入数据
data = [[-0.5, 7.7], [1.8, 98.5], [0.9, 57.8], [0.4, 39.2], [-1.4, -15.7], [-1.4, -37.3], [-1.8, -49.1], [1.5, 75.6], [0.4, 34.0], [0.8, 62.3]]
#转化为数组
data=np.array(data)
# 提取x 和y
x_data=data[:,0]
y_data=data[:,1]
#转成张量 转成paddlepaddle张量
x_train=paddle.to_tensor(x_data,dtype=paddle.float32)
y_train=paddle.to_tensor(y_data,dtype=paddle.float32)
#TensorDataset是接收一个值，不是接收两个值,使用列表
dataset=TensorDataset([x_train.unsqueeze(1),y_train.unsqueeze(1)])
#创建Dataloader对象
dataloader=DataLoader(dataset,batch_size=10,shuffle=True)
# 2. 定义前向模型
#方式2 单独定义 使用类的方式 class nn.Layer组网
class LinearModel(nn.Layer):def __init__(self):super(LinearModel,self).__init__()self.linear=nn.Linear(1,1)def forward(self,x):x=self.linear(x)return x
#定义模型的对象
model=LinearModel()# 3.使用高层api进行封装
# step1 使用paddle.Model(xxx)进行封装
model=paddle.Model(model)
#step2 使用prepare
model.prepare(optimizer=paddle.optimizer.SGD(learning_rate=0.01,parameters=model.parameters()),loss=nn.MSELoss(),metrics=paddle.metric.Accuracy())#高级API模型的加载
model.load("./高层API1/final")
#验证
dataset=TensorDataset([paddle.to_tensor([1.5],dtype=paddle.float32),paddle.to_tensor([82],dtype=paddle.float32)])
datalaoder_eval=DataLoader(dataset)
eval_pre=model.evaluate(datalaoder_eval,verbose=1)
print(eval_pre)#预测
dataset=TensorDataset([paddle.to_tensor([1.5],dtype=paddle.float32)])
datalaoder_eval=DataLoader(dataset)
pre_result=model.predict(datalaoder_eval,verbose=1)
print(pre_result)

---

1.5 paddlepaddle模型网络结构的查看 

1.5.1 summary

paddle.summary(model,(1,))

---

1.5.2 netron

netron pycharm 终端下输入 pip install netron

下载好后，在终端下输入 netron，在浏览器上输入 http://localhost:8080 即可

---

1.5.3 visualdl

安装网络查看库pip install visualdl==2.5.3

看文档查看结构网络(切记运行的程序不能有中文路径)

https://www.paddlepaddle.org.cn/documentation/docs/zh/guides/advanced/visualdl_usage_cn.html

这是使用visualdl写入

from visualdl import LogWriter

logwriter=LogWriter(logdir='logs')

这是使用visualdl查看

查看方式 需要写上host 和port 不然不成功

visualdl --logdir ./logs --model ./logs/model.pdmodel --host 0.0.0.0 --port 8040

---

二、曲线拟合

从以下2个方面对曲线拟合进行介绍

1.曲线拟合算法理论讲解

2.编程实例与步骤

上面这2方面的内容，让大家，掌握并理解曲线拟合算法。

---

1.1案例引入

蝌蚪变青蛙

在某池塘中，有某类蝌蚪，它们随着天数的增加，开始慢慢需要觅食，在需要觅食之前，都是从卵黄带来的营养维持生命。

于是采集了7只蝌蚪是否需要觅食的数据：

横坐标的单位是天数；

纵坐标是否需要觅食，0是不需要觅食，1是需要觅食。

如右图所示 x轴表示天数，y轴表示是否需要觅食。

---

1.2 散点输入

本实验中，采集了天数与是否觅食的的关系数据，x轴表示天数，y轴表示是否觅食，0表示不需要觅食，1表示需要觅食，从图上看有3只蝌蚪是不需要觅食的，3天以下的不需要觅食。有4只需要觅食，大于3天的需要觅食。

并且将它们绘制在一个二维坐标中，其分布如下图所示：

坐标分别为[0.8, 0]，[1.1, 0] ，[1.7, 0] ，[3.2, 1] ，[3.7, 1] ，[4.0, 1] ，[4.2, 1]。

---

1.3 前向计算

我们的目的是拟合这些散点，通过前向计算，我们通过修改w和b只能部分点落在线上，从实验看直线无法拟合这些点。

直线无法拟合那应该怎么办呢？

对于直线无法拟合这些点，是不是需要将直线变成曲线来拟合这些散点，在没有引入直线变曲线之前，使用直线是无法拟合这些点的。

这个σ是一个激活函数。

如果σ是阶跃函数，

那么这个阶跃函数的缺点是什么？

不连续性：在x=2.5处不连续；

不可导性：在x=2.5处不存在导数；

怎么解决阶跃函数导数不存在的问题呢？

是不是得找一个函数它要处处可微，是连续的，在各个地方都可导的，是不是就能很好的拟合当前曲线了。

---

1.4 Sigmoid函数引入

sigmoid拟合数据点效果图

下面引入Sigmoid函数，当然是是前人慢慢发现的这个函数

Sigmoid的函数，其函数公式为：

其函数图像如下所示：

的值域处于（0，1）之间，两边无限接近于0和1。但永远不等于0和1。定义域是负无穷到正无穷。

在线性回归中，直线的方程是

，带入Sigmoid激活函数中，得到：

---

1.5 激活函数的引入

在该实验中，将直线转换成曲线，可以在直线

加入一个新的函数

，这个 是一个激活函数，在上面实验中使用的激活函数是Sigmoid函数，当然还有其他激活函数，后面的课程会讲。

激活函数是神经网络中一种重要的非线性函数，其作用在于引入非线性特性，使得神经网络能够学习和表示更加复杂的数据模式和关系。激活函数通常在每个神经元的输出上应用，将输入信号转换为输出信号。

以下是激活函数的主要作用：

1. 引入非线性特性：如果在神经网络中只使用线性变换，例如线性加权和求和，那么整个网络的组合效果将仍然是线性的。激活函数的非线性特性能够在每个神经元上引入非线性转换，从而让神经网络能够学习和表示更加复杂的函数和数据模式。
2. 提高模型的表达能力：激活函数的引入增加了神经网络的表达能力，使得网络可以逼近任何复杂的函数，这种特性称为“普遍逼近定理”（Universal Approximation Theorem）。
3. 稀疏性和稳定性：一些激活函数(如Relu)具有稀疏性和稳定性的特点，可以缓解梯度消失和梯度爆炸的问题，从而有助于训练更深的神经网络。

梯度消失简单解释：w新=w旧-学习率*梯度 (梯度为0 w新一直等于w旧，引起w不更新就是梯度消失)

梯度爆炸简单解释：w新=w旧-学习率*梯度 (梯度非常大 ，只要大于1，因为模型会有很多层，链式求导法则需要连乘，就会导致梯度爆炸。)

综上所述，激活函数在神经网络中扮演着非常重要的角色，它们的引入使得神经网络具备非线性表达能力，从而能够处理和解决更加复杂的任务。

---

1.6 参数初始化

在之前的前向计算中，可以通过改变自己修改w和b来拟合这条曲线，但是在很多实际场景中，并没办法做到直接求出最优的w，b值，所以需要先随机定一个w和b，然后让梯度下降去拟合这些点。

在“参数初始化”组件中，可以初始化w和b的值以及学习率的值。

---

1.7 损失函数

根据公式：

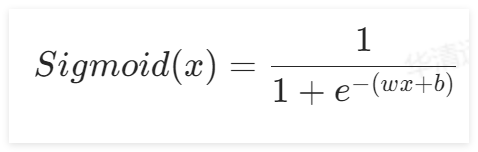
入均方差损失函数中，于是损失函数就成了：

---

1.8 开始迭代

定义好损失函数后，选择好迭代次数，然后就可以进行反向传播了。

---

1.9反向传播

在上面得到了损失函数的表达式，本实验中使用梯度下降的方式去降低损失函数值，于是需要对损失函数进行求导：

将其拆分成复合函数，得到：

对复合函数求导，可得：

该过程对应了本实验中的“反向传播”组件，其内容如下所示：

---

1.10 梯度下降显示

为了更好的观察到迭代过程中的参数变化和损失函数的变化，提供了“显示频率组件”，其内容如下图所示：

通过设置显示频率，可以实时反馈当前的参数值和损失值，在“梯度下降显示”组件中可以查看，其组件内容如下图所示：

在该图像中，1.46对应的是w的值，-3.27对应的是b的值，0.03是损失值，这三个值都是根据显示频率实时反馈回来的。

左边的图像是根据当前的w和b的值所绘制的曲线，右边的图像是绘制的损失值的变化。

---

 1.11 曲线拟合代码

import numpy as np  # 导入 numpy 库，用于数值计算
import matplotlib.pyplot as plt  # 导入 matplotlib.pyplot 库，用于绘图# 原始数据，第一列是 x，第二列是 y（标签）
data = np.array([[0.8, 0], [1.1, 0], [1.7, 0], [3.2, 1], [3.7, 1], [4.0, 1], [4.2, 1]])data = np.array(data)  # 转换为 numpy 数组 (虽然这里重复了，但保留了原始代码)x_data = data[:, 0]  # 获取所有行的第一列 (x 值)
y_data = data[:, 1]  # 获取所有行的第二列 (y 值，也就是标签)# 定义 sigmoid 函数
def sigmoid(x):return 1 / (1 + np.exp(-x))  # sigmoid 函数的公式w = 0  # 初始化权重 w
b = 0  # 初始化偏置 b
l = 0.05  # 学习率 learning rate
epochs = 1000  # 迭代次数
fig, (ax1, ax2) = plt.subplots(2, 1)  # 创建一个包含两个子图的 figure，垂直排列
epoch_list = []  # 用于存储 epoch 的列表，用于绘制损失曲线
loss_list = []  # 用于存储 loss 的列表，用于绘制损失曲线# 迭代训练
for i in range(1, epochs + 1):z = w * x_data + b  # 计算线性模型的输出a = sigmoid(z)  # 将线性输出通过 sigmoid 函数，得到预测值loss = np.mean((y_data - a) ** 2)  # 计算均方误差损失epoch_list.append(i)  # 将当前 epoch 添加到 epoch_listloss_list.append(loss)  # 将当前 loss 添加到 loss_list# 反向传播，计算梯度deda = -2 * (y_data - a)  # loss 对 a 的导数dadz = a * (1 - a)  # sigmoid 函数的导数dzdw = x_data  # z 对 w 的导数dzdb = 1  # z 对 b 的导数dw = np.mean(deda * dadz * dzdw)  # 计算 w 的梯度db = np.mean(deda * dadz * dzdb)  # 计算 b 的梯度# 更新权重和偏置w = w - l * dw  # 更新 wb = b - l * db  # 更新 b# 每 50 个 epoch 或第一个 epoch，打印 loss 并更新图表if i % 50 == 0 or i == 1:print(f"epoch:{i},loss:{loss}")  # 打印 epoch 和 loss# 画图显示x_min = x_data.min()  # x 最小值x_max = x_data.max()  # x 最大值# 按照等间隔从x_min到x_max之间的数据x_values = np.linspace(x_min, x_max, int(x_max - x_min) * 10)  # 在 x_min 和 x_max 之间创建一系列均匀间隔的值y_values = sigmoid(w * x_values + b)  # 计算 sigmoid 函数的值# 画第一个图ax1.clear()  # 清除 ax1ax1.scatter(x_data, y_data, color='b')  # 画散点图# 画曲线ax1.plot(x_values, y_values, c='r')  # 画 sigmoid 曲线ax1.set_title(f"Curve Regression: w={round(w, 3)}, b={round(b, 3)}")  # 设置 ax1 的标题# 画 ax2ax2.clear()  # 清除 ax2ax2.plot(epoch_list, loss_list, color='g')  # 画损失曲线ax2.set_xlabel("Epoch")  # 设置 x 轴标签ax2.set_ylabel("Loss")  # 设置 y 轴标签ax2.set_title(f"Loss Curve")  # 设置 ax2 的标题plt.pause(1)  # 暂停 1 秒，以便显示图表

---

三、激活函数

从以下3个方面对激活函数及其导数进行介绍
1.激活函数及其导数算法理论讲解
2.编程实例与步骤
3.实验现象
上面这3方面的内容，让大家，掌握并理解激活函数及其导数算法。

---

3.1 激活函数及其导数算法理论讲解

24年刚出版的<<激活函数的三十年：神经网络 400 个激活函数的综合调查>>

《Three Decades of Activations: A Comprehensive Survey of 400 Activation Functions for Neural Networks》

包括常用的激活函数和不常用的，400种，大家如果感兴趣可以看看。

文件分享https://share.weiyun.com/3t76DytU

---

3.2 激活函数的作用？

激活函数的作用就是在神经网络中经过线性计算后，进行的非线性化。

下面讲解Sigmoid，tanh、Relu，Leaky Relu、Prelu、Softmax、ELU七种激活函数。

---

3.3 激活函数的概念

激活函数给神经元引入了非线性因素，让神经网络可以任意逼近任何非线性函数，

通俗理解为把线性函数转换为非线性函数

---

3.4 Sigmoid

Sigmoid的函数公式为：

函数图像如下图所示：

该函数处于（0，1）之间，两边无限接近于0和1，但永远不等于0和1。

sigmoid函数的导数公式为：

导数图像为：

Sigmoid特点总结：

Sigmoid 函数的输出范围被限制在 0 到 1 之间，这使得它适用于需要将输出解释为概率或者介于 0 和 1 之间的任何其他值的场景。
Sigmoid 函数的两端，导数的值非常接近于零，这会导致在反向传播过程中梯度消失的问题，特别是在深层神经网络中。

Sigmoid激活函数有着如下几种缺点：

梯度消失：Sigmoid函数趋近0和1的时候变化率会变得平坦，从导数图像可以看出，当x值趋向两侧时，其导数趋近于0，在反向传播时，使得神经网络在更新参数时几乎无法学习到低层的(不明显的)特征，从而导致训练变得困难。 w新=w旧-lr*梯度

不以零为中心：Sigmoid函数的输出范围是0到1之间，它的输出不是以零为中心的，会导致其参数只能同时向同一个方向更新，当有两个参数需要朝相反的方向更新时，该激活函数会使模型的收敛速度大大的降低

计算成本高：Sigmoid激活函数引入了exp()函数，导致其计算成本相对较高，尤其在大规模的深度神经网络中，可能会导致训练速度变慢。

不是稀疏激活：Sigmoid函数的输出范围是连续的，并且不会将输入变为稀疏的激活状态。在某些情况下，稀疏激活可以提高模型的泛化能力和学习效率。

不以零中心有什么问题？举例讲解：

此时，模型为了收敛，w0、w1…改变的方向是统一的，或正或负。所以如果你的最优值是需要w0增加，w1减少，那么不得不向逆风前行的风助力帆船一样，走 Z 字形逼近最优解。如下图所示

模型参数走绿色箭头能够最快收敛，但由于输入值的符号总是为正，所以模型参数可能走类似红色折线的箭头。如此一来，使用 Sigmoid 函数作为激活函数的神经网络，收敛速度就会慢上不少了。

---

总结

        本文详细介绍了PaddlePaddle框架下线性回归的实现，从模型定义到加载，再到网络结构查看，提供了全面的指导。同时，文章还讲解了曲线拟合的原理，并重点介绍了Sigmoid等激活函数及其导数，强调了激活函数在神经网络中的重要作用。通过本文的学习，读者可以不仅掌握PaddlePaddle的基本使用，还能深入理解线性回归、曲线拟合以及激活函数等核心概念，为后续的深度学习研究打下坚实的基础。