热门算法面试题第19天|Leetcode39. 组合总和40.组合总和II131.分割回文串
39. 组合总和
力扣题目链接(opens new window)
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
- 所有数字(包括 target)都是正整数。
- 解集不能包含重复的组合。
示例 1:
- 输入:candidates = [2,3,6,7], target = 7,
- 所求解集为: [ [7], [2,2,3] ]
示例 2:
- 输入:candidates = [2,3,5], target = 8,
- 所求解集为: [ [2,2,2,2], [2,3,3], [3,5] ]
思路:
在我们之前做过的组合总和中,取法都是不能重复的,现在给出的数组元素可以重复
本题搜索的过程抽象成树形结构如下:

注意图中叶子节点的返回条件,因为本题没有组合数量要求,仅仅是总和的限制,所以递归没有层数的限制,只要选取的元素总和超过target,就返回!
确定递归函数及其参数
这里依然是定义两个全局变量,二维数组result存放结果集,数组path存放符合条件的结果。(这两个变量可以作为函数参数传入)
首先是题目中给出的参数,集合candidates, 和目标值target。
此外我还定义了int型的sum变量来统计单一结果path里的总和,其实这个sum也可以不用,用target做相应的减法就可以了,最后如何target==0就说明找到符合的结果了,但为了代码逻辑清晰,我依然用了sum。
本题还需要startIndex来控制for循环的起始位置,对于组合问题,什么时候需要startIndex呢?
如果是一个集合来求组合的话,就需要startIndex
如果是多个集合取组合,各个集合之间相互不影响,那么就不用startIndex
代码如下:
// 存储所有符合条件的组合private List<List<Integer>> result = new ArrayList<>();// 当前路径(当前组合)private List<Integer> path = new ArrayList<>();// 回溯算法核心private void backtracking(int[] candidates, int target, int sum, int startIndex) {递归终止条件:

终止情况就两种,要么sum==target,要么sum>target
// 当前和超过目标值,直接返回if (sum > target) {return;}// 找到符合条件的组合if (sum == target) {result.add(new ArrayList<>(path)); // 注意创建新列表return;}
sum等于result直接add,大于return吊
确定单层递归逻辑
单层for循环依然是从startIndex开始,搜索candidates集合。
// 从startIndex开始遍历候选数字for (int i = startIndex; i < candidates.length; i++) {sum += candidates[i]; // 尝试选择当前数字path.add(candidates[i]);backtracking(candidates, target, sum, i); // 关键点:允许重复使用同一数字sum -= candidates[i]; // 撤销选择path.remove(path.size() - 1); // 移除最后添加的数字}}但与之前也有不同,我们在循环里面的递归的时候不用更新startindex
因为可以无限制重复选取
我们来看完整代码
import java.util.ArrayList;
import java.util.List;class Solution {// 存储所有符合条件的组合private List<List<Integer>> result = new ArrayList<>();// 当前路径(当前组合)private List<Integer> path = new ArrayList<>();// 回溯算法核心private void backtracking(int[] candidates, int target, int sum, int startIndex) {// 当前和超过目标值,直接返回if (sum > target) {return;}// 找到符合条件的组合if (sum == target) {result.add(new ArrayList<>(path)); // 注意创建新列表return;}// 从startIndex开始遍历候选数字for (int i = startIndex; i < candidates.length; i++) {sum += candidates[i]; // 尝试选择当前数字path.add(candidates[i]);backtracking(candidates, target, sum, i); // 关键点:允许重复使用同一数字sum -= candidates[i]; // 撤销选择path.remove(path.size() - 1); // 移除最后添加的数字}}// 主方法public List<List<Integer>> combinationSum(int[] candidates, int target) {result.clear(); // 清空结果集path.clear(); // 清空当前路径backtracking(candidates, target, 0, 0); // 从和为0,索引0开始回溯return result;}
}
剪枝优化
在这个树形结构中:

以及上面的版本一的代码大家可以看到,对于sum已经大于target的情况,其实是依然进入了下一层递归,只是下一层递归结束判断的时候,会判断sum > target的话就返回。
其实如果已经知道下一层的sum会大于target,就没有必要进入下一层递归了。
那么可以在for循环的搜索范围上做做文章了。
对总集合排序之后,如果下一层的sum(就是本层的 sum + candidates[i])已经大于target,就可以结束本轮for循环的遍历。
如图:

最终代码
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;class Solution {private List<List<Integer>> result = new ArrayList<>();private List<Integer> path = new ArrayList<>();private void backtracking(int[] candidates, int target, int sum, int startIndex) {if (sum == target) {result.add(new ArrayList<>(path));return;}// 剪枝优化:sum + candidates[i] <= targetfor (int i = startIndex; i < candidates.length && sum + candidates[i] <= target; i++) {sum += candidates[i];path.add(candidates[i]);backtracking(candidates, target, sum, i); // 允许重复使用sum -= candidates[i];path.remove(path.size() - 1);}}public List<List<Integer>> combinationSum(int[] candidates, int target) {result.clear();path.clear();Arrays.sort(candidates); // 关键:排序后才能剪枝backtracking(candidates, target, 0, 0);return result;}
}
40.组合总和II
力扣题目链接(opens new window)
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
说明: 所有数字(包括目标数)都是正整数。解集不能包含重复的组合。
- 示例 1:
- 输入: candidates = [10,1,2,7,6,1,5], target = 8,
- 所求解集为:
[[1, 7],[1, 2, 5],[2, 6],[1, 1, 6]
]
- 示例 2:
- 输入: candidates = [2,5,2,1,2], target = 5,
- 所求解集为:
[[1,2,2],[5]
]思路:
这道题目和39.组合总和 (opens new window)如下区别:
本题candidates 中的每个数字在每个组合中只能使用一次。
本题数组candidates的元素是有重复的,而39.组合总和 (opens new window)是无重复元素的数组candidates
最后本题和39.组合总和 (opens new window)要求一样,解集不能包含重复的组合。
本题的难点在于区别2中:集合(数组candidates)有重复元素,但还不能有重复的组合。
那么问题来了,我们是要同一树层上使用过,还是同一树枝上使用过呢?
回看一下题目,元素在同一个组合内是可以重复的,怎么重复都没事,但两个组合不能相同。
所以我们要去重的是同一树层上的“使用过”,同一树枝上的都是一个组合里的元素,不用去重。
为了理解去重我们来举一个例子,candidates = [1, 1, 2], target = 3,(方便起见candidates已经排序了)
强调一下,树层去重的话,需要对数组排序!
选择过程树形结构如图所示:

确定递归函数及其参数
与上一题的套路相同,此题还需要加一个bool型数组used,用来记录同一树枝上的元素是否使用过。
这个集合去重的重任就是used来完成的。
private List<List<Integer>> result = new ArrayList<>();private List<Integer> path = new ArrayList<>();private void backtracking(int[] candidates, int target, int sum, int startIndex, boolean[] used) {确定终止条件:
和上一题相同
if (sum > target) { // 这个条件其实可以省略return;
}
if (sum == target) {result.push_back(path);return;
}确定单层递归逻辑
for (int i = startIndex; i < candidates.length && sum + candidates[i] <= target; i++) {// 去重逻辑:当前元素和前一个相同,且前一个未被使用if (i > 0 && candidates[i] == candidates[i - 1] && !used[i - 1]) {continue;}sum += candidates[i];path.add(candidates[i]);used[i] = true;backtracking(candidates, target, sum, i + 1, used); // i+1 表示每个数字只能用一次used[i] = false;sum -= candidates[i];path.remove(path.size() - 1);}前面我们提到:要去重的是“同一树层上的使用过”,如何判断同一树层上元素(相同的元素)是否使用过了呢。
如果candidates[i] == candidates[i - 1] 并且 used[i - 1] == false,就说明:前一个树枝,使用了candidates[i - 1],也就是说同一树层使用过candidates[i - 1]。
不然会重复,比如第一个树枝的取1取我,和第二个树枝取1取2重复
此时for循环里就应该做continue的操作。
这块比较抽象,如图:

我在图中将used的变化用橘黄色标注上,可以看出在candidates[i] == candidates[i - 1]相同的情况下:
- used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
- used[i - 1] == false,说明同一树层candidates[i - 1]使用过
为什么 used[i - 1] == false 就是同一树层呢,因为同一树层,used[i - 1] == false 才能表示,当前取的 candidates[i] 是从 candidates[i - 1] 回溯而来的。
而 used[i - 1] == true,说明是进入下一层递归,去下一个数,所以是树枝上,如图所示:

剪枝优化总体和之前相同
我们来看完整的代码
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;class Solution {private List<List<Integer>> result = new ArrayList<>();private List<Integer> path = new ArrayList<>();private void backtracking(int[] candidates, int target, int sum, int startIndex, boolean[] used) {if (sum == target) {result.add(new ArrayList<>(path));return;}for (int i = startIndex; i < candidates.length && sum + candidates[i] <= target; i++) {// 去重逻辑:当前元素和前一个相同,且前一个未被使用if (i > 0 && candidates[i] == candidates[i - 1] && !used[i - 1]) {continue;}sum += candidates[i];path.add(candidates[i]);used[i] = true;backtracking(candidates, target, sum, i + 1, used); // i+1 表示每个数字只能用一次used[i] = false;sum -= candidates[i];path.remove(path.size() - 1);}}public List<List<Integer>> combinationSum2(int[] candidates, int target) {result.clear();path.clear();Arrays.sort(candidates); // 必须先排序boolean[] used = new boolean[candidates.length];backtracking(candidates, target, 0, 0, used);return result;}
}
131.分割回文串
力扣题目链接(opens new window)
给定一个字符串 s,将 s 分割成一些子串,使每个子串都是回文串。
返回 s 所有可能的分割方案。
示例: 输入: "aab" 输出: [ ["aa","b"], ["a","a","b"] ]
思路:
其实切割问题类似组合问题。
例如对于字符串abcdef:
- 组合问题:选取一个a之后,在bcdef中再去选取第二个,选取b之后在cdef中再选取第三个.....。
- 切割问题:切割一个a之后,在bcdef中再去切割第二段,切割b之后在cdef中再切割第三段.....。
感受出来了不?
所以切割问题,也可以抽象为一棵树形结构,如图:
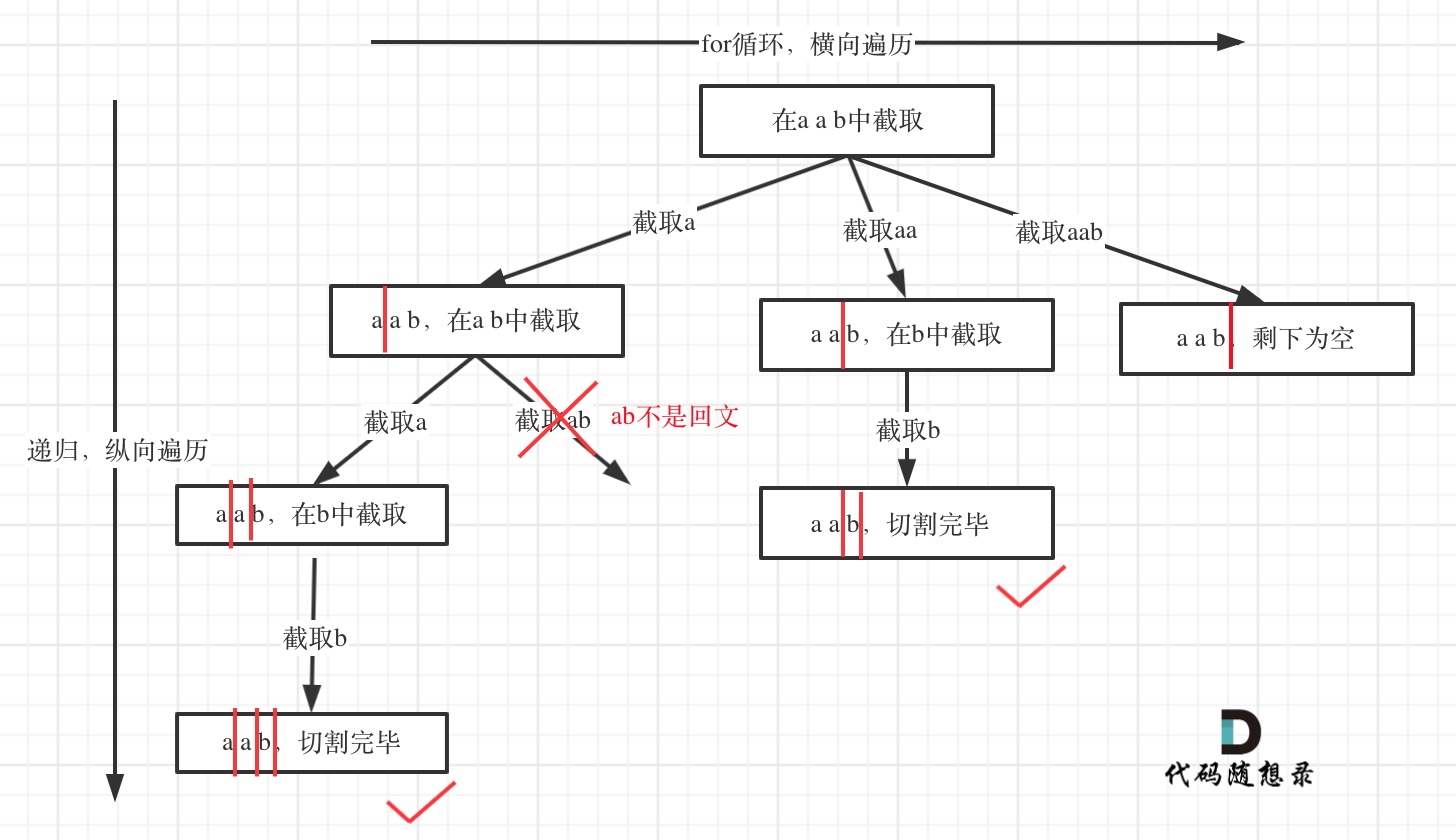
递归用来纵向遍历,for循环用来横向遍历,切割线(就是图中的红线)切割到字符串的结尾位置,说明找到了一个切割方法。
此时可以发现,切割问题的回溯搜索的过程和组合问题的回溯搜索的过程是差不多的。
确定递归函数及其参数
全局变量数组path存放切割后回文的子串,二维数组result存放结果集。 (这两个参数可以放到函数参数里)
本题递归函数参数还需要startIndex,因为切割过的地方,不能重复切割,和组合问题也是保持一致的。
private List<List<String>> result = new ArrayList<>();private List<String> path = new ArrayList<>();private void backtracking(String s, int startIndex) {确定递归终止条件

从树形结构的图中可以看出:切割线切到了字符串最后面,说明找到了一种切割方法,此时就是本层递归的终止条件。
在处理组合问题的时候,递归参数需要传入startIndex,表示下一轮递归遍历的起始位置,这个startIndex就是切割线。
// 如果起始位置已经大于等于字符串长度,说明找到一组分割方案if (startIndex >= s.length()) {result.add(new ArrayList<>(path));return;}确定单层递归逻辑
在for (int i = startIndex; i < s.size(); i++)循环中,我们 定义了起始位置startIndex,那么 [startIndex, i] 就是要截取的子串。
首先判断这个子串是不是回文,如果是回文,就加入在vector<string> path中,path用来记录切割过的回文子串。
代码如下:
for (int i = startIndex; i < s.length(); i++) {// 如果是回文子串if (isPalindrome(s, startIndex, i)) {// 获取当前回文子串String str = s.substring(startIndex, i + 1);path.add(str);// 递归处理剩余部分backtracking(s, i + 1);// 回溯path.remove(path.size() - 1);}// 不是回文则跳过}
判断回文子串
就是之前的双指针,从前后选两个指针,然后分别遍历就行
// 判断是否是回文串private boolean isPalindrome(String s, int start, int end) {for (int i = start, j = end; i < j; i++, j--) {if (s.charAt(i) != s.charAt(j)) {return false;}}return true;}完整代码
import java.util.ArrayList;
import java.util.List;class Solution {private List<List<String>> result = new ArrayList<>();private List<String> path = new ArrayList<>();private void backtracking(String s, int startIndex) {// 如果起始位置已经大于等于字符串长度,说明找到一组分割方案if (startIndex >= s.length()) {result.add(new ArrayList<>(path));return;}for (int i = startIndex; i < s.length(); i++) {// 如果是回文子串if (isPalindrome(s, startIndex, i)) {// 获取当前回文子串String str = s.substring(startIndex, i + 1);path.add(str);// 递归处理剩余部分backtracking(s, i + 1);// 回溯path.remove(path.size() - 1);}// 不是回文则跳过}}// 判断是否是回文串private boolean isPalindrome(String s, int start, int end) {for (int i = start, j = end; i < j; i++, j--) {if (s.charAt(i) != s.charAt(j)) {return false;}}return true;}public List<List<String>> partition(String s) {result.clear();path.clear();backtracking(s, 0);return result;}
}
相关文章:

热门算法面试题第19天|Leetcode39. 组合总和40.组合总和II131.分割回文串
39. 组合总和 力扣题目链接(opens new window) 给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。 candidates 中的数字可以无限制重复被选取。 说明: 所有数字(包括 ta…...

IDEA连接达梦数据库
1. 参考在IDEA中连接达梦数据库:详细配置指南_idea连接达梦数据库-CSDN博客 . jdbc:dm://127.0.0.1:5236?schemaSALES...

React Router V7使用详解
1,安装 React Router是React生态系统中最流行的路由解决方案,它允许开发者在单页应用的不同页面之间进行切换,而不需要重新加载整个页面,React Router与React框架深度集成,使得开发者在单页面应用中进行页面切换时变得轻而易举。 作为官方推荐的路由解决方案,React Rou…...
详解)
国际数据加密算法(IDEA)详解
以下是修正后的准确版本,已解决原文中的术语、符号及技术细节问题: 国际数据加密算法(IDEA) IDEA是一种分组加密算法,由Xuejia Lai(来学嘉)和James Massey于1990年设计。IDEA使用128位密钥对64位明文分组进行加密,经过8轮迭代运算后生成64位密文分组。其安全性基于…...

2025年4月19日-米哈游春招笔试题-第三题
📌 点击直达笔试专栏 👉《大厂笔试突围》 💻 春秋招笔试突围在线OJ 👉 笔试突围OJ 03. 魔法网格变换术 问题描述 在魔法学院,卢小姐正在研究一种特殊的魔法网格变换术。这种魔法作用于一个 n n n...

基于STM32串口通信
基于STM32串口通信 一、串口简介 串口,也称为串行接口或串行通信接口(通常指COM接口),是一种采用串行通信方式的扩展接口。它实现了数据一位一位地顺序传送,具有通信线路简单、成本低但传送速度慢的特点。 只要一对传…...

即梦AI与可灵AI视频生成功能对比分分析
一、核心功能与特点对比 维度可灵AI(快手旗下)即梦AI(字节跳动旗下)视频生成能力✅ 支持最长3分钟视频生成(通过续写功能)✅ 1080p分辨率、30fps帧率✅ 物理模拟(流体运动、重力效果࿰…...

【任务调度】Quartz入门
Quartz 入门 代码仓库地址: GitHub:chenmeng-test-demos/demo8-task at master cmty256/chenmeng-test-demosGitee:demo8-task chenmeng/chenmeng-test-demos - 码云 - 开源中国 基本介绍 Quartz 是一个开源的作业调度框架,它完…...
)
【网络编程】从零开始彻底了解网络编程(二)
本篇博客给大家带来的是网络编程的知识点,. 🐎文章专栏: JavaEE初阶 🚀若有问题 评论区见 ❤ 欢迎大家点赞 评论 收藏 分享 如果你不知道分享给谁,那就分享给薯条. 你们的支持是我不断创作的动力 . 王子,公主请阅🚀 要开心要快乐顺便进步 1. …...

常见浏览器 WebDriver 驱动下载
以下是常见浏览器 WebDriver 驱动的下载地址及注意事项,综合多个可靠来源整理而成: 一、Chrome 浏览器(ChromeDriver) 官方下载地址 http://chromedriver.storage.googleapis.com/index.html • • 版本匹配:需与 Chro…...

【每日八股】复习计算机网络 Day3:TCP 协议的其他相关问题
文章目录 昨日内容复习TCP 的四次挥手?TCP 为什么要四次挥手?在客户端处于 FIN_WAIT_2 状态时,如果此时收到了乱序的来自服务端的 FIN 报文,客户端会如何处理?何时进入 TIME_WAIT 状态?TCP 四次挥手丢了怎么…...
预测及治疗方案制定中的应用研究)
大模型在胆管结石(无胆管炎或胆囊炎)预测及治疗方案制定中的应用研究
目录 一、引言 1.1 研究背景与意义 1.2 研究目的 1.3 国内外研究现状 二、胆管结石相关理论基础 2.1 胆管结石概述 2.2 临床表现与诊断方法 2.3 传统治疗方法 三、大模型技术原理与应用优势 3.1 大模型基本原理 3.2 在医疗领域的应用潜力 3.3 用于胆管结石预测的可…...

LeetCode第159题_至多包含两个不同字符的最长子串
LeetCode 第159题:至多包含两个不同字符的最长子串 题目描述 给定一个字符串 s,找出 至多 包含两个不同字符的最长子串 t,并返回该子串的长度。 难度 中等 题目链接 点击在LeetCode中查看题目 示例 示例 1: 输入: s &qu…...

PG CTE 递归 SQL 翻译为 达梦版本
文章目录 PG SQLDM SQL总结 PG SQL with recursive result as (select res_id,phy_res_code,res_name from tbl_res where parent_res_id (select res_id from tbl_res where phy_res_code org96000#20211203155858) and res_type_id 1 union all select t1.res_id, t1.p…...

JavaScript 位掩码常量教程
JavaScript 位掩码常量教程 位掩码(Bitmask)是一种高效使用内存的技术,在JavaScript中可以用来存储和操作多个布尔值标志。下面我将为您介绍位掩码的基本概念、应用场景以及实践示例。 什么是位掩码常量? 位掩码利用二进制位&a…...

Linux守护进程
一、相关概念 QQ邮箱关于三种协议的解释:SMTP/IMAP服务 1.SMTP协议 SMTP(Simple Mail Transfer Protocol,简单邮件传输协议)是一种用于发送电子邮件的互联网标准。它在TCP/IP协议族中,通常使用25端口进行通…...

Python多进程并发编程:深入理解Lock与Semaphore的实战应用与避坑指南
引言 在多进程并发编程中,资源竞争问题如同“隐形炸弹”,稍有不慎就会导致数据不一致或程序崩溃。无论是银行转账的余额错误,还是火车票超卖,其根源都在于共享资源的无序访问。如何安全高效地管理这些资源?Python中的锁…...

mysql的5.7版本与8.0版本的差异与兼容性
MySQL 5.7 和 8.0 是两个重要的版本,它们在性能、功能、安全性等方面都有显著的改进,同时也存在一些兼容性问题。以下是具体的改进点和兼容性问题: 一、MySQL 8.0 的改进点 性能提升 优化器改进:MySQL 8.0 对查询优化器进行了重大…...

【Rust 精进之路之第4篇-数据基石·上】标量类型:整数、浮点数、布尔与字符的精妙之处
系列: Rust 精进之路:构建可靠、高效软件的底层逻辑 作者: 码觉客 发布日期: 2025-04-20 引言:构成万物的“原子”——标量类型 在上一篇文章【变量观】中,我们深入探讨了 Rust 如何通过 let、mut、const、static 和 Shadowing 来管理变量绑定,并理解了其背后对安全性…...

LangChain4j模型参数配置全解析:释放大语言模型的真正潜力
LangChain4j模型参数配置全解析:释放大语言模型的真正潜力 前言 在大语言模型应用开发中,参数配置是连接算法理论与工程实践的关键桥梁。合理的参数设置能让模型输出更精准、响应更高效,而错误的配置可能导致成本激增或业务逻辑失效。本文将…...

【深度学习入门_NLP自然语言处理】序章
本部分开始深度学习第二大部分NLP章节学习,找了好多资料,终于明确NLP的学习目标了,介于工作之余学习综合考量,还是决定以视频学习为主后期自主实践为主吧。 分享一个总图,其实在定位的时候很迷茫,单各章节…...
——4.1基本算术运算的实现)
计算机组成原理笔记(十六)——4.1基本算术运算的实现
计算机中最基本的算术运算是加法运算,加、减、乘、除运算最终都可以归结为加法运算。 4.1.1加法器 一、加法器的基本单元 加法器的核心单元是 全加器(Full Adder, FA),而所有加法器都由 半加器(Half Adder, HA&…...

AI日报 - 2025年04月21日
🌟 今日概览(60秒速览) ▎🤖 AGI突破 | O3模型性能引热议,Rich Sutton提出「体验时代」新范式,自递归AI构建仍存挑战。 新模型如O3展示高IQ,但AGI定义与实现路径讨论加剧,强调自主生成数据与体验学习。 ▎&…...

基于Python的推荐算法的电影推荐系统的设计
标题:基于Python的推荐算法的电影推荐系统的设计与实现 内容:1.摘要 本文围绕基于Python的推荐算法的电影推荐系统展开研究。背景在于随着电影数量的急剧增加,用户在海量电影中找到符合自身喜好的影片变得困难。目的是设计并实现一个高效准确的电影推荐系统&#x…...

【perf】perf工具的使用生成火焰图
文章目录 1. What is perf?2. perf使用2.1 perf的子工具集2.2 常用指令perf list指令格式参数perf中事件分类使用示例 perf stat指令格式参数 perf top指令格式参数交互式界面操作使用示例 perf record指令格式参数使用示例 perf report指令格式参数交互式界面操作使用示例 pe…...

Sentinel源码—6.熔断降级和数据统计的实现一
大纲 1.DegradeSlot实现熔断降级的原理与源码 2.Sentinel数据指标统计的滑动窗口算法 1.DegradeSlot实现熔断降级的原理与源码 (1)熔断降级规则DegradeRule的配置Demo (2)注册熔断降级监听器和加载熔断降级规则 (3)DegradeSlot根据熔断降级规则对请求进行验证 (1)熔断降级…...

C语言自增自减题目
一、题目引入 二、运行结果 三、题目分析 这一题中 i的初始值是2 所以执行case2中的命令i-- 表达式的值此时是2 i--完了之后i最后的值是1 由于是switch没有break 就会往下贯穿 直到遇到break为止 case3里面 i 表达式的值是2 i完了之后i的值也是2 综上所述 i的值最终的值是…...

paddleocr出现: [WinError 127] 找不到指定的程序解决办法
paddleocr是一个由百度开发开源的OCR(光学字符识别)工具库。它支持多种语言的文本识别,包括中文、英文、日文等,并具备高效的文本检测和识别能力。paddleocr基于PaddlePaddle深度学习框架开发,提供了丰富的预处理、模型…...

c++STL——list的使用和模拟实现
文章目录 list的使用和模拟实现使用部分list的结构声名默认成员函数initializer_list容量和访问操作修改操作其他接口list的迭代器迭代器的种类 list的模拟实现明确基本结构预处理函数迭代器部分(重点)思路进一步考虑最终代码operator->的重载总结 begin和end访问接口修改操…...

交换机端口安全
端口安全 端口安全(PortSecurity)通过将接口学习到的动态MAC地址转换为安全MAC地址(包括安全动态MAC、安全静态MAC和Sticky MAC),阻止非法用户通过本接口和交换机通信,从而增强设备的安全性。 1、安全mac地址分类 安全动态MAC地址…...

【Oracle专栏】Oracle中的虚拟列
Oracle相关文档,希望互相学习,共同进步 风123456789~-CSDN博客 1.背景 在EXP方式导出时,发现 出现如下提示 EXP-00107: virtual column 不支持,因此采用expdp方式导出。于是本文针对oracle虚拟列进行简单介绍。 2. 相…...

shell 正则表达式与文本处理器
目录 前言 一、正则表达式 (一)定义与用途 (二)基础正则表达式 (三)基础正则表达式元字符 (四)扩展正则表达式 二、文本处理器:Shell 编程的得力助手 ࿰…...
:定时器中断)
ZYNQ笔记(九):定时器中断
版本:Vivado2020.2(Vitis) 任务:使用定时器 (私有定时器) 中断 实现 LED(PS端) 定时1s亮灭翻转 目录 一、介绍 二、硬件设计 三、软件设计 四、效果 一、介绍 Zynq系列是Xilinx(现为AMD)推出的集成了AR…...

idea中运行groovy程序报错
我的项目是使用的 gradle 构建的。 在 idea 中运行Groovy的面向对象程序报错如下: Execution failed for task :Person.main(). > Process command G:/Program Files/jdk-17/jdk-17.0.12/bin/java.exe finished with non-zero exit value 1* Try: Run with --s…...
:联合嵌入预测架构(JEPAs)详解)
具身智能零碎知识点(四):联合嵌入预测架构(JEPAs)详解
联合嵌入预测架构(JEPAs)详解 联合嵌入预测架构(JEPAs)详解一、核心思想二、技术原理1. 核心组件2. 训练目标 三、与传统方法的对比四、具体实例例1:视频预测(如Meta的I-JEPA)例2:多…...

linux 搭建 dvwa 渗透测试环境
linux 安装 dvwa 1、分为4个部分,搭建dvwa渗透测试环境2、安装centos 7.63、安装apache http server4、安装mysql5、安装php6、运行dvwa 1、分为4个部分,搭建dvwa渗透测试环境 本文基于centos 7.6 搭建 dvwa 渗透测试环境 安装一个linux系统安装apache…...
(双缓冲区异步任务处理器(AsyncLooper)设计))
C++项目 —— 基于多设计模式下的同步异步日志系统(4)(双缓冲区异步任务处理器(AsyncLooper)设计)
C项目 —— 基于多设计模式下的同步&异步日志系统(4)(双缓冲区异步任务处理器(AsyncLooper)设计) 异步线程什么是异步线程?C 异步线程简单例子代码解释程序输出关键点总结扩展:使…...

【Linux学习笔记】Linux的环境变量和命令行参数
【Linux学习笔记】Linux的环境变量和命令行参数 🔥个人主页:大白的编程日记 🔥专栏:Linux学习笔记 文章目录 【Linux学习笔记】Linux的环境变量和命令行参数前言一.环境变量1.1基本概念1.2常见环境变量1.3和环境变量相关的命令1…...

排序算法-快速排序
描述: 基准值选择:选取数组的最后一个元素 arr[high] 作为基准值 p。初始化索引:i 初始化为 low - 1,其作用是指向比基准值小的最后一个元素的索引。遍历数组:借助 for 循环从 low 到 high - 1 遍历数组。若当前元素 …...

软考高级系统架构设计师-第16章 数学与经济管理
【本章学习建议】 根据考试大纲,本章主要考查系统架构设计师单选题,预计考2分左右。主要是运筹学的计算问题,范围广、难度大,超纲题较多,不用深究。 16.1 线性规划 线性规划是研究在有限的资源条件下,如果…...

爱在冰川-慢就是快
【游资大佬の搞钱心法🔥|小白逆袭必看冰川语录真实案例‼️】 💡刚扒完爱在冰川的万字访谈 发现游资搞钱真的靠"反人性思维" 总结6条狠人法则真实案例 建议收藏反复背诵👇 1️⃣【周期为王】💫 "行情…...

Mac-VScode-C++环境配置
mac上自带了clang所以不是必须下载Homebrew 下面是配置文件(注释记得删一下) package.json {"name": "git-base","displayName": "%displayName%","description": "%description%",&quo…...
)
【JAVA EE初阶】多线程(1)
这样的代码,虽然也能打印hello thread,但是没有创建新的线程,而是直接在main方法所在的主线程中执行了run的逻辑 start方法,是调用系统api,真正在操作系统内部创建一个线程。这个新的线程会以run作为入口方法ÿ…...

PHP伪协议读取文件
借鉴php伪协议实现命令执行,任意文件读取_ctf php文件读取-CSDN博客 总结 在ctf中常用的有data:// , php://input , php://filter ,file:// php://input ,data://用来执行命令 1.php://input 的用法 http://127.0.0.1/include.php?filephp://input [P…...

动态调整映射关系的一致性哈希负载均衡算法详解
一、核心原理与设计要点 双重映射结构 一致性哈希负载均衡通过 哈希环 和 槽动态分配 实现双重映射关系: • 哈希环构建:将节点(物理或虚拟)和数据键(Key)通过哈希函数(如MD5、CRC32)…...
和依赖注入(DI))
控制反转(IOC)和依赖注入(DI)
Target Retention Documented 元注解 Component 将类交给IOC容器管理,成为IOC容器中的bean Autowired 注入运行时所需要依赖的对象 因为Mabatis DAO层注解Reponsitory 基本不用了,现在Mapper层Mapper注解,这里的Mapper层相当于原来的DAO层…...

【每日八股】复习 MySQL Day1:事务
文章目录 复习 MySQL Day1:事务MySQL 事务的四大特性?并发事务会出现什么问题?MySQL 事务的隔离级别?不同事务隔离级别下会发生什么问题?MVCC 的实现原理?核心数据结构版本链构建示例可见性判断算法MVCC 可…...

【数据结构和算法】1. 数据结构和算法简介、二分搜索
本文根据 数据结构和算法入门 视频记录 文章目录 1. 数据结构和算法简介1.1 什么是数据结构?什么是算法?1.2 数据结构和算法之间的关系1.3 “数据结构和算法”有那么重要吗? 2. 二分搜索(Binary Search)2.1 算法概念2…...
算了和周日一块写了 4月20日日记)
4月19日记(补)算了和周日一块写了 4月20日日记
周六啊 昨天晚上又玩的太嗨了。睡觉的时候有点晚了,眼睛疼就没写日记。现在补上 实际上现在是20号晚上八点半了。理论上来说应该写今天的日记。 周六上午打比赛啦,和研究生,输了,我是替补没上场。没关系再练一练明天就可以变强…...

面试常用基础算法
目录 快速排序归并排序堆排序 n n n皇后问题最大和子数组爬楼梯中心扩展法求最长回文子序列分割回文串动态规划求最长回文子序列最长回文子串单调栈双指针算法修改 分割回文串滑动窗口栈 快速排序 #include <iostream> #include <algorithm>using namespace std;…...
