当前位置：首页 > news >正文

算法训练之动态规划（一）

news 来源：原创 2025/9/18 2:25:59

♥♥♥~~~~~~欢迎光临知星小度博客空间~~~~~~♥♥♥

♥♥♥零星地变得优秀~也能拼凑出星河~♥♥♥

♥♥♥我们一起努力成为更好的自己~♥♥♥

♥♥♥如果这一篇博客对你有帮助~别忘了点赞分享哦~♥♥♥

♥♥♥如果有什么问题可以评论区留言或者私信我哦~♥♥♥
✨✨✨✨✨✨ 个人主页✨✨✨✨✨✨

在前面，我们练习了很多不同类型的题目，这一篇博客，我们来看看算法中比较重要的知识点——动态规划~准备好了吗~我们发车啦~🚗🚗🚗🚗🚗🚗

前置知识

第N个泰波那契数

使用最小花费爬楼梯

状态表示方法一

状态表示方法二

解码方法

常规解法

优化解法

前置知识

在正式开始动态规划的题目练习之前，我们来看看动态规划的一般步骤~

一般步骤：

1、创建一个dp表，进行状态表示（状态表示就是dp表里面的值dp[i]有什么含义）

怎么得到状态表示呢？——一般是经验+题目要求

2、状态转移方程

dp[i]等于什么，怎么推导出dp[i]

3、初始化（保证填表的时候不越界）

4、填表顺序

正确的填表顺序是为了填写当前的状态所需要的状态是已经得到了的~

5、返回结果

根据题目要求和状态表示返回最终的结果~

仅仅是说可能有点抽象，接下来我们会结合具体的题目来进行了解这些一般步骤~接下来我们根据这些步骤来看看下面的这些题目~

第N个泰波那契数

这个题目一看与我们前面写过的斐波那契数有点类似，不过这里是前面三个数的和构成了当前的数~

接下来，我们根据步骤一步步来分析：

1、状态表示

结合这里的题目要求+经验：我们这里的状态表示dp[i]可以是当前位置的泰波那契数

2、状态转移方程

这个题目很容易分析出当前位置dp[i]也就是前面三数之和：
dp[i] = dp[i-1]+dp[i-2]+dp[i-3]

3、初始化

我们可以看到，状态转移方程里面有dp[i-1],dp[i-2],dp[i-3],当i=1的时候显然会出现越界的情况，所以我们需要进行初始化

根据题目可以得到：
dp[0]=0,dp[1]=1,dp[2]=1

4、填表顺序

我们这里的逻辑是从前面依次推出后面的，所以填表顺序是从前向后

5、返回结果

dp表的第i个位置就是第i个泰波那契数，直接返回dp[n]就是我们的结果

这里还需要添加一步就是处理边界情况

题目给出的n的范围是0~37，当n=0，1，2的时候会出现越界，直接返回就好了~

接下来，我们来进行代码实现：

class Solution 
{
public:int tribonacci(int n) {//1、创建dp表vector<int> dp(n+1);//处理边界情况if(n==0) return 0;if(n==1||n==2) return 1;//2、初始化——避免越界dp[0]=0,dp[1]=1,dp[2]=1;//3、根据状态转移方程填表for(int i=3;i<=n;i++){dp[i]=dp[i-1]+dp[i-2]+dp[i-3];}//4、返回结果return dp[n];}
};

可以看到分析完成之后，这里的代码还是比较简单的~

算法复杂度：

时间复杂度是O（N），空间复杂度O（N）

那么有没有什么办法让空间复杂度变为O（1）呢？答案是有的，因为我们只需要得到第N个泰波那契数，那么我们只需要三个变量来模拟这个相加的过程就可以了~

优化：

class Solution 
{
public:int tribonacci(int n) {//同样需要处理边界情况if(n==0) return 0;if(n==1||n==2) return 1;//创建三个变量模拟相加过程int a=0,b=1,c=1;int d=0;//最终结果int count=n-2;//需要相加次数while(count--){d=a+b+c;//新得到的数//更新前面三个数a=b;b=c;c=d;}//返回结果return d;}
};

这个方法我们也把它叫做滚动数组~可以极大地优化空间复杂度~

使用最小花费爬楼梯

我们同样可以一步步来分析：

注意点：根据示例我们可以知道楼顶不是最后一个下标的位置，而是最后一个下标后面的那一个位置~

状态表示方法一

1、状态表示

结合这里的题目要求+经验：我们这里的状态表示dp[i]是到该台阶的最小花费是多少（也就是以i位置为结尾的最小花费）

2、状态转移方程

       我们以离【i】位置最近的状态分析状态转移方程

1、到达该台阶，可能是从第【i-1】位置花费cost【i-1】走一步到达的

2、到达该台阶，可能是从第【i-2】位置花费cost【i-2】走两步到达的

        因为是最小花费，所以应该是两种情况中花费最少的那一个，状态转移方程也就是：

        dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])

3、初始化

我们可以看到，状态转移方程里面有dp[i-1],dp[i-2],当i=0、1的时候显然会出现越界的情况，所以我们需要进行初始化

根据题目（可以从下标为0或者为1的位置开始爬楼梯，所以到可以得到到达下标为0或者为1的位置是不需要花钱的），所以初始化：
dp[0]=0,dp[1]=0

4、填表顺序

我们这里的逻辑是从前面依次推出后面的，所以填表顺序是从前向后

5、返回结果

楼顶是最后一个下标后面的那一个位置~直接返回dp[n]就是我们的结果

这里不需要添加处理边界情况了，题目给出长度的范围是2~1000，直接返回就好了~

代码实现：

class Solution 
{
public:int minCostClimbingStairs(vector<int>& cost) {//1、创建dp表int n=cost.size();//楼顶是最后一个下标后面的那一个位置vector<int> dp(n+1,0);//里面的值全部初始化为0//2、初始化 dp[0],dp[1]已经在前面初始化为0了//3、根据状态转移方程填表for(int i=2;i<=n;i++){dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}//4、返回结果return dp[n];}
};

这是第一种状态表示方式——以【i】位置为结尾，到达【i】位置的最小花费~接下来我们来看看第二种状态表示方法~

状态表示方法二

1、状态表示

前面的状态表示是以【i】位置为结尾，到达【i】位置的最小花费~我们这里的状态表示dp[i]是以i位置为起点到达楼顶的最小花费

2、状态转移方程

       我们以离【i】位置最近的状态分析状态转移方程，同样有两种情况

1、从【i】位置开始花费cost【i】走一步到达第【i+1】位置再加上以第【i+1】位置为起点到达楼顶的最小花费~

2、从【i】位置开始花费cost【i】走两步到达第【i+2】位置再加上以第【i+2】位置为起点到达楼顶的最小花费~

        因为是最小花费，所以应该是两种情况中花费最少的那一个，状态转移方程也就是：

        dp[i]=min(dp[i+1]+cost[i],dp[i+2]+cost[i])

3、初始化

我们可以看到，状态转移方程里面有dp[i+1],dp[i+2],当i=n-1,n的时候显然会出现越界的情况，所以我们需要进行初始化

根据题目i=n-1的时候往上走一步花费cost[i-1]就可以了，i=n的时候已经在楼顶不需要花钱了，所以初始化：
dp[n-1]=cost[i-1],dp[n]=0

4、填表顺序

我们这里的逻辑是从后面依次推出前面的，所以填表顺序是从后向前

5、返回结果

起点位置可能是1，也可能是0，返回dp[0]和dp[1]的较小值就是我们的结果

代码实现：

class Solution 
{
public:int minCostClimbingStairs(vector<int>& cost) {//1、创建dp表int n=cost.size();vector<int> dp(n+1);//2、初始化dp[n-1]=cost[n-1];dp[n]=0;//3、根据状态转移方程填表for(int i=n-2;i>=0;i--){dp[i]=min(dp[i+1]+cost[i],dp[i+2]+cost[i]);}//4、返回结果return min(dp[0],dp[1]);}
};

当然，这里的dp表大小也可以创建为n个大小，只是初始化以及填表的实现需要注意一下范围~

解码方法

接下来，我们来分析一道有点难度的题目~

常规解法

        首先分析一下题目，题目给出了解码方式，现在我们需要又数字转换为编码，A~Z的字符依次对应的是1~26，这就说明0是没有办法解码的，同时前置0，比如06也是没有办法进行解码的~

        所以解码可以分为以下两种情况：

       1、单独一个字符解码

       2、与附近的字符组合进行解码，只能再结合一位

接下来，我们就按照以前的思路来进行一步步的分析：

1、状态表示

结合这里的题目要求+经验：我们这里的状态表示为dp[i]是以【i】位置为结尾，一共有多少种解码方式

2、状态转移方程

       我们以离【i】位置最近的状态分析状态转移方程，我们可以分为单独解码和组合解码两种方式来进行讨论：

1、以【i】位置为结尾，如果【i】位置可以进行单独解码，那么就说明【i】位置的解码方式种数也就需要加上【i-1】位置解码种数~否则不能成功解码（比如为0），这说明前面解码是有问题的，那么就不需要加~

2、以【i】位置为结尾，如果【i】位置与【i-1】位置可以进行组合解码，那么就说明【i】位置的解码方式种数也就需要加上【i-2】位置解码种数~否则不能成功解码（比如为06），这说明前面解码是有问题的，那么就不需要加~

       根据分析也就可以得到状态转移方程也就是：

                        dp[i]=dp[i-1]+dp[i-2]

是否加dp[i-1]或者dp[i-2]需要先进行判断~

3、初始化

        我们可以看到，状态转移方程里面有dp[i-1],dp[i-2],当i=0、1的时候显然会出现越界的情况，所以我们需要进行初始化

        根据题目当i=0的时候，目前只有一个字符，如果可以单独解码的话，那么dp[0]=1,否则为0，也就是dp[0]有0或者1这两种情况；

        当i=1的时候，如果可以1位置可以单独解码的话，那么dp[1]+=dp[0],如果还可以组合解码的话，那么dp[1]+=1，也就是dp[1]有0或者1或者2这三种情况

        这里涉及到判断就不给出具体结论，我们在代码中会进行实现~

4、填表顺序

我们这里的逻辑是从前面依次推出后面的，所以填表顺序是从前向后

5、返回结果

根据状态表示和题目要求，直接返回dp[n-1]就是我们的结果

这里需要我们处理边界情况，当长度为1的时候，dp[1]是越界的，我们直接返回dp[0]的结果就可以了

代码实现：

class Solution
{
public:int numDecodings(string s){//1、创建dp表int n = s.size();vector<int> dp(n, 0);//最开始就初始化为0//2、判断进行初始化//dp[0]if (s[0] != '0') dp[0] = 1;//不为0就说明可以单独解码//  处理边界情况if (n == 1) return dp[0];//dp[1]if (s[1] != '0') dp[1] += dp[0];//可以单独解码，也就可以加上dp[0]解码数//判断是否可以组合解码int t = (s[0] - '0') * 10 + (s[1] - '0');if (t >= 10 && t <= 26)//判断两位数是否有效dp[1] += 1;//3、根据状态转移方程填表for (int i = 2; i < n; i++){//先判断//1、是否可以单独解码if (s[i] != '0') dp[i] += dp[i - 1];//2、是否可以组合解码int tt = (s[i - 1] - '0') * 10 + (s[i] - '0');if (tt >= 10 && tt <= 26){dp[i] += dp[i - 2];}}//4、返回结果return dp[n - 1];}
};

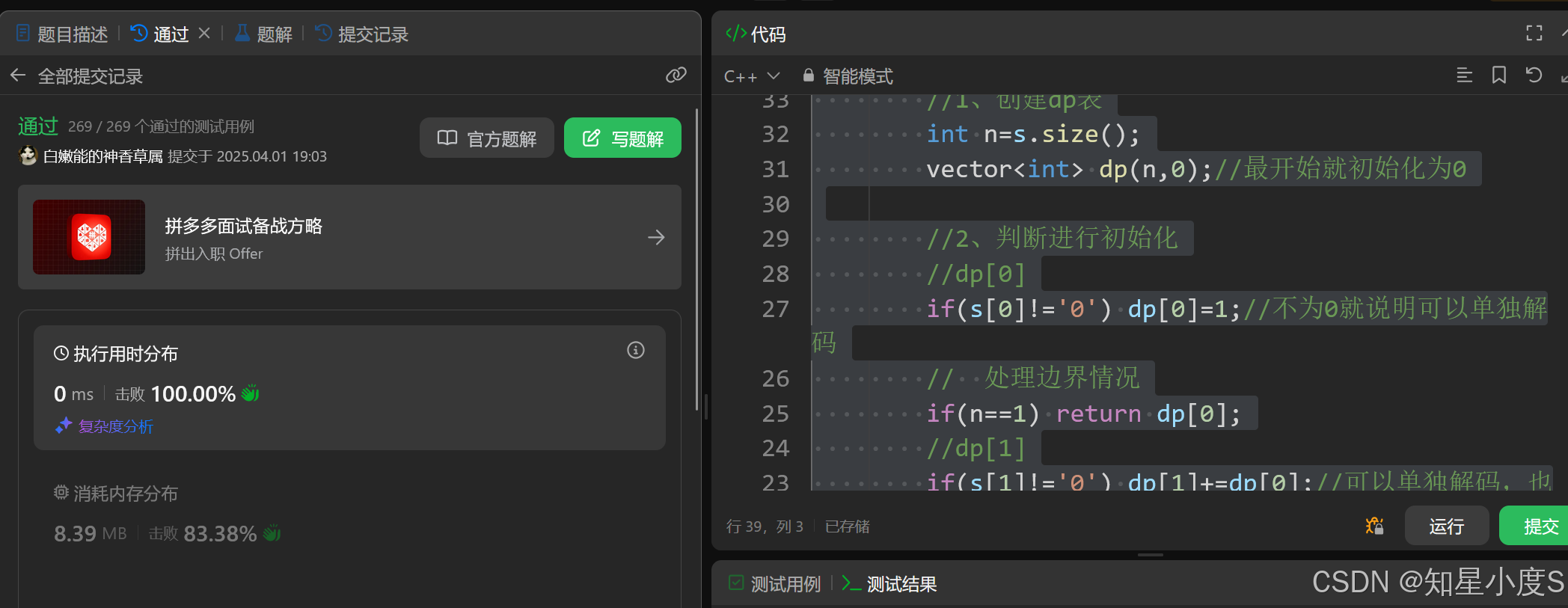
顺利通过~

优化解法

事实上，这一段代码还可以进行优化，我们可以发现初始化和循环内部的代码事实上是高度类似的，我们可不可以把初始化的代码也写进循环里面呢？答案是可以的，我们只需要多开辟一个空间就可以了~不过这个方法有两个注意点~

1、多开的那一个空间表示什么？

这里我们多开一个空间是想把初始化的代码写入循环中，避免越界的情况出现，我们初始化最开始是处理dp[0]和dp[1],那么我们优化一下就让dp1[i]的数据放入dp2[i+1]的位置，这样dp2[2]+=dp2[1]和dp2[2]+=dp2[0]（也就是处理最开始两个字符）就不会出现越界情况，那么我们多开的空间显然就是dp2[0],那么dp2[0]的值应该是多少呢？

使用dp2[0]是在dp2[2]+=dp2[0]的时候，如果最开始两个字符可以组合，说明解码总数就得+1，所以我们的dp2[0]=1

2、下标的映射关系

因为多开了一个空间，所以dp表第【i】个位置事实上是字符串s第【i-1】位置的解码总数~所以应该返回dp2[n]了

代码实现：

class Solution
{
public:int numDecodings(string s){//优化——多开一个空间int n = s.size();vector<int> dp(n + 1, 0);dp[0] = 1;if (s[0] != '0') dp[1] += 1;for (int i = 2; i <= n; i++){//是否可以单独解码if (s[i - 1] != '0') dp[i] += dp[i - 1];//是否可以组合解码int tt = (s[i - 2] - '0') * 10 + (s[i - 1] - '0');if (tt >= 10 && tt <= 26) dp[i] += dp[i - 2];}return dp[n];}
};

可以发现这样处理，把我们的处理边界情况和初始化的代码极大地简化了，但是使用时候需要注意前面的两个注意点，避免出错~

♥♥♥本篇博客内容结束，期待与各位优秀程序员交流，有什么问题请私信♥♥♥

♥♥♥如果这一篇博客对你有帮助~别忘了点赞分享哦~♥♥♥

✨✨✨✨✨✨个人主页✨✨✨✨✨✨

算法训练之动态规划（一）

♥♥♥~~~~~~欢迎光临知星小度博客空间~~~~~~♥♥♥ ♥♥♥零星地变得优秀~也能拼凑出星河~♥♥♥ ♥♥♥我们一起努力成为更好的自己~♥♥♥ ♥♥♥如果这一篇博客对你有帮助~别忘了点赞分享哦~♥♥♥ ♥♥♥如果有什么问题可以评论区留言或者私信我哦~♥♥♥ ✨✨✨✨✨✨ 个…...

编程日记 2025/9/18 2:25:59

dubbo配置中心

配置中心简介配置中心（config-center）在dubbo中可承担两类职责： 外部化配置：启动配置的集中式存储。流量治理规则存储。 Dubbo动态配置中心定义了两个不同层次的隔离选项，分别是namespace和group。 namespace&a…...

编程日记 2025/9/9 10:50:50

移动端六大语言速记：第11部分 - 内存管理

移动端六大语言速记：第11部分 - 内存管理本文将对比Java、Kotlin、Flutter(Dart)、Python、ArkTS和Swift这六种移动端开发语言在内存管理方面的特性，帮助开发者理解和掌握各语言的内存管理机制。 11. 内存管理 11.1 垃圾回收机制对比各语言垃圾回收…...

编程日记 2025/9/10 18:16:39

对象的创建方式有哪些?在虚拟机中具体的创建过程是怎样的？

在Java中，对象的创建方式及其在虚拟机中的具体过程如下： 一、对象的创建方式使用 new 关键字最常见的对象创建方式，直接调用类的构造方法。 MyClass obj new MyClass();反射（Reflection） 通过 Class 或 Constructor…...

编程日记 2025/9/14 3:17:02

openwrt软路由配置3

1.启用sftp文件连接使用ssh连接openwrt时，我发现无法打开sftp windows进行上传和下载文件，提示 sftp channel closed by server: stderr:ash /usr/libexec/sftp-server:not found 原因是系统刚刚装好后，没有安装openssh-sftp-server包 opk…...

编程日记 2025/9/5 15:51:35

C语言for循环嵌套if相关题目

一、题目引入以下代码程序运行结果是多少? 二、思路解析进入一个for循环 a<100 进入第一个if b1不大于20为假进入第二个if b4 a这时a自增为2 当b4时,满足第二个if条件 1.b4,a2 当b7时,满足第二个if条件 2.bb37,a3 当b10时,满足第二个if条件 …...

编程日记 2025/9/16 5:50:39

Redis与Mysql双写一致性如何保证？

我们在面试的时候redis与mysql双写一致性是一个常考的问题，今天我们就一起探讨一下吧所谓的一致性就是数据的一致性，在分布式系统中，可以理解为多个节点中数据的值是一致的。强一致性： 这种一致性级别是最符合用户直觉的&…...

编程日记 2025/9/15 7:28:23

STM32 CRC校验与芯片ID应用全解析：从原理到实践 | 零基础入门STM32第九十七步

主题内容教学目的/扩展视频CRC与芯片ID原理实现CRC校验和读取芯片ID为单片机应用提供数据验证和身份识别的功能。师从洋桃电子，杜洋老师 📑文章目录一、CRC校验功能解析1.1 CRC基本原理1.2 核心功能对比二、CRC校验应用实战2.1 典型应用场景2.2 程序实…...

编程日记 2025/9/12 1:15:02

《微服务与事件驱动架构》读书分享

《微服务与事件驱动架构》读书分享 Building Event-Driver Microservices 英文原版由 OReilly Media, Inc. 出版，2020 作者：[加] 亚当 • 贝勒马尔译者：温正东作者简介： 这本书由亚当贝勒马尔（Adam Bellemare…...

编程日记 2025/8/17 21:45:46

⼤模型（LLMs）基础

⼤模型（LLMs）基础⽬前主流的开源模型体系有哪些？prefix Decoder 和 causal Decoder 和 Encoder-Decoder 区别是什么？⼤模型LLM的训练⽬标是什么？涌现能⼒是啥原因？为何现在的⼤模型⼤部分是Decoder o…...

编程日记 2025/9/16 22:31:13

IDEA ：物联网ThingsBoard-gateway配置，运行Python版本，连接thingsboard，接入 MQTT 设备

准备阶段（教程只针对本地操作，未涉及虚拟机环境） Thingsboard源码编译并运行没有操作过的小伙伴，可以看我上一篇文章物联网ThingsBoard源码本地编译篇，超详细教程，小白看过来！_thingsboard…...

编程日记 2025/9/16 8:09:28

面向大模型的开发框架LangChain

这篇文章会带给你如何使用 LangChain：一套在大模型能力上封装的工具框架如何用几行代码实现一个复杂的 AI 应用面向大模型的流程开发的过程抽象文章目录这篇文章会带给你写在前面LangChain 的核心组件文档（以 Python 版为例）模型 I/O 封装…...

编程日记 2025/9/12 0:48:35

每日算法：洛谷U535992 J-C 小梦的宝石收集（双指针、二分）

题目描述小梦有 n 颗能量宝石，其中第 i 颗的能量为 ai，但这些能量宝石十分不稳定，随时有可能发生崩坏，导致他们全部消失！ 小梦想要留住宝石们，不希望他们发生崩坏，同时他发现：如…...

编程日记 2025/9/16 15:52:57

写给新人的深度学习扫盲贴：ReLu和梯度

一、ReLU（Rectified Linear Unit，修正线性单元） 梯度是深度学习中最常用的激活函数之一，因其简单、高效且能有效缓解梯度消失问题而被广泛使用。 1. 数学定义函数表达式： $$ \text{ReLU}(x) \max(0, x) \begin{…...

编程日记 2025/9/10 22:56:11

Spring 框架的核心基础：IoC 和 AOP

一、IoC（Inversion of Control，控制反转） 定义： IoC（Inversion of Control，控制反转），就是把对象创建和依赖关系的管理交给 Spring 容器，而不是由程序员手动去创建对象…...

编程日记 2025/9/9 3:40:07

JavaScript逆向工程实战：如何精准定位加密参数生成位置

前言：一个令人困惑的调试案例最近在进行某网站的JavaScript逆向分析时，我遇到了一个有趣的现象：当我尝试定位一个名为m的加密参数（值为MTIwMTE3NDQxODk1NTY1NjkA这样的Base64字符串）时，调试器却带我来到了…...

编程日记 2025/9/9 4:12:02

SSM智能停车场管理系统

🍅点赞收藏关注 → 添加文档最下方联系方式咨询本源代码、数据库🍅 本人在Java毕业设计领域有多年的经验，陆续会更新更多优质的Java实战项目希望你能有所收获，少走一些弯路。🍅关注我不迷路🍅 项目视频 SS…...

编程日记 2025/8/30 6:58:06

[定位器]晶艺LA1823,4.5V~100V, 3.5A,替换MP9487,MP9486A,启烨科技

Features  4.5V to 100V Wide Input Range  3.5A Typical Peak Current Limit  Integrated 500mΩ low resistance high side power MOS.  Constant On Time Control with Constant Switching Frequency.  180μA Low Quiescent Current  150kHz/240kHz/420kHz Swi…...

编程日记 2025/9/8 0:09:50

天元证券｜A股大反攻！北证50涨超10%！芯片股大爆发

今日，A股全线走强。科技成长股领涨，北证50指数飙升逾10%，科创50也大涨超4%，深证成指、上证指数午后也稳步拉升涨逾1%。值得注意的是，上证50指数临近收盘集合竞价的时候直线拉升。近4600只个股上涨，成交稳步…...

编程日记 2025/9/13 11:56:40

利用python从零实现Byte Pair Encoding(BPE)：NLP 中的“变形金刚”

BPE：NLP 界的“变形金刚”，从零开始的奇幻之旅在自然语言处理（NLP）的世界里，有一个古老而神秘的传说，讲述着一种强大的魔法——Byte Pair Encoding（BPE）。它能够将普通的文本“变形…...

编程日记 2025/9/9 3:11:45

OpenBMC：BmcWeb 处理http请求6 调用路由处理函数

OpenBMC：BmcWeb 处理http请求5 检查权限-CSDN博客检查完权限后，调用了rule.handle(*req, asyncResp, params); template <typename... Args> class TaggedRule :public BaseRule,public RuleParameterTraits<TaggedRule<Args...>> {void handle(const Req…...

编程日记 2025/9/17 23:37:36

售货机管理系统：智慧零售时代的运营新引擎

一、引言在快节奏的都市生活中，自动售货机已成为便捷消费的重要场景。然而，传统售货机依赖人工补货、手工对账，常面临库存失衡、设备故障发现滞后、数据孤岛等痛点。如何突破效率瓶颈？本文将深入剖析榕壹云售货机管理系统的项目背景、客户定位、技术与核心功能、系统优势…...

编程日记 2025/9/12 6:00:23

Python基础全解析：从输入输出到字符编码的深度探索

一、Python程序交互的基石：Print函数详解 1.1 基础输出功能 # 输出数字 print(20.5) # 输出浮点数：20.5 print(0b0010) # 输出二进制数：10# 输出字符串 print(Hello World!) # 经典输出示例# 表达式计算 print(4 4 * (2-1)…...

编程日记 2025/9/16 1:58:31

Python第八章02：数据可视化Pyecharts包无法使用

PS:本节纯属个人在学习过程中遇到问题、解决问题的经验分享，对学习进度没影响，没有遇到该问题的小伙伴可跳过。首先，在学习数据图形化过程中，通过命令提示符安装了Pyecharts包，在命令提示符中验证安装成功。在PyChar…...

编程日记 2025/9/11 8:15:49

【人工智能】如何通过精准提示工程实现完美的珠宝首饰展示

AI艺术创作指南：如何通过精准提示工程实现完美的珠宝首饰展示引言：认知边界的突破在AI艺术创作的漫长探索中，许多创作者面临着相似的困扰：当他们看到别人能够通过算法编织出如同文艺复兴时期细腻油画般的奢华珠宝展示图&#…...

编程日记 2025/9/17 14:07:33

Redis学习总结（持续更新）

Redis 目前在学习redis，遇到的一些问题会放在这里，加深自己的印象。 1. Redis缓存相较于传统Session存储的特点 Session的存储方式： 通常，传统的Session是存储在应用服务器的内存中，比如Tomcat的Session管理器。用户…...

编程日记 2025/9/16 4:22:37

RabbitMQ从入门到实战-3(高可靠性)

文章目录发送者可靠性发送者重连发送者确认（一般不会开启）指定returncallback和confrimfallbacktips MQ可靠性数据持久化LazyQueue（默认模式且不可更改） 消费者的可靠性消费者确认机制消费者失败重试业务幂等性唯一消息id业务判断…...

编程日记 2025/9/12 20:17:23

RTK 实时动态定位概述

01 引言 RTK（实时动态定位，Real-Time Kinematic）是一种高精度的卫星导航定位技术，通过差分校正方法，将GNSS（全球导航卫星系统）的定位精度从米级提升至厘米级（通常1-3厘米），广泛应用于测绘、无人机、自动驾驶、精准农业等领域。 02 概述 1. RTK的基本原理 RTK的核…...

编程日记 2025/8/29 16:25:15

Conda 环境离线迁移实战：解决生产环境网络限制的高效方案20250409

Conda 环境离线迁移实战：解决生产环境网络限制的高效方案在生产环境无法联网的前提下，如何高效、安全地部署 Python 虚拟环境，是许多企业在实际运维中必须面对的问题。特别是当前常见的开发环境基于 Miniconda，生产环境使用 Ana…...

编程日记 2025/9/17 15:23:40

dify使用知识库

注意要用向量模型导入文件选择向量模型要下载好后，才可以导入模型， 这个模型没法在ollama中run 聊天工具添加知识库效果...

编程日记 2025/8/17 21:45:43

HTTP：一.概述

http是干嘛的？超文本传输协议（英语：HyperText Transfer Protocol，缩写：HTTP）是一种用于分布式、协作式和超媒体信息系统的应用层协议。HTTP是万维网的数据通信的基础。设计HTTP最初的目的是为了提供一种发布和接收HTML页面的方法。通过HTTP或者HTTPS协议请求的资源由统…...

编程日记 2025/9/15 15:09:38

Appium工作原理及环境的搭建（1）

1、Appium的介绍： 一、什么是Appium Desktop？ Appium Desktop是Appium项目的桌面版GUI工具，提供了一个友好的界面，用于启动Appium服务器、查看设备日志、与设备交互、调试自动化脚本等。相比于命令行工具，Appium Des…...

编程日记 2025/9/16 1:58:23

Interactron: Embodied Adaptive Object Detection(训练时进行更新参数) 还没看懂

Interactron: Embodied Adaptive Object Detection 创新点这些方法通常存在两个主要的共同假设。第一，模型在固定的训练集上进行训练，并在预先录制的测试集上进行评估。第二，模型在训练阶段结束后保持冻结状态，即训练完成后不再…...

编程日记 2025/9/16 1:58:27

【Pandas】pandas DataFrame copy

Pandas2.2 DataFrame Conversion 方法描述DataFrame.astype(dtype[, copy, errors])用于将 DataFrame 中的数据转换为指定的数据类型DataFrame.convert_dtypes([infer_objects, …])用于将 DataFrame 中的数据类型转换为更合适的类型DataFrame.infer_objects([copy])用于尝试…...

编程日记 2025/9/10 14:51:25

Redis基础指令(Windows)

1.cmd命令行启动redis 直接cmd打开整个文件 1.1.启动server 输入指令： redis-server.exe redis.windows.conf 会进入serve端 1.2.启动客户端 ！！重新打开一个cmd，方法和上面一样！！ 之后输入 redis-…...

编程日记 2025/9/15 1:38:41

MV-DLS600P激光振镜立体相机（MV-DLS600P）重要参数解析

功能特性采用激光振镜技术，亚毫米级图像采集精度高能效激光模块配合精准曝光同步，性能更稳定支持多帧融合，无惧金属工件表面反光干扰支持RGB、深度图同步对齐输出，便于二次开发配备窄带滤光片，抗干扰能力更强&…...

编程日记 2025/9/12 3:28:15

C语言【输出字符串中的大写字母】

题目输出字符串中的大写字母思路（注意事项） 纯代码 #include<stdio.h> #include<string.h>int main(){char str[20], ans[20];fgets(str, sizeof(str), stdin);str[strcspn(str, "\n")] \0;for (int i 0, j 0; i < strl…...

编程日记 2025/9/13 20:40:44

UniApp基于xe-upload实现文件上传组件

xe-upload地址：文件选择、文件上传组件（图片，视频，文件等） - DCloud 插件市场致敬开发者！！！ 感觉好用的话，给xe-upload的作者一个好评背景：开发中经常会有…...

编程日记 2025/9/9 13:32:51

deque容器

1.定义也叫双端数组，可以对头部进行插入和删除。 2.与vector区别 3.内部工作原理他是把整个地址划分成多块小地址（缓冲区），然后有一个中控区去记录这些地址，然后访问的时候先通过中控区然后再转到相应的缓冲区&am…...

编程日记 2025/9/11 13:23:07

git 总结遇到的问题

git Push 报错 Push failed send-pack: unexpected disconnect while reading sideband packet Total 2269 (delta 418), reused 0 (delta 0), pack-reused 0 the remote end hung up unexpectedly 解决方案：增加 Git 的缓冲区，有时由于数据量大或网络…...

编程日记 2025/8/17 23:51:41

python基础语法11-文件读写

在 Python 中，文件操作是日常编程中的常见任务之一。Python 提供了简单且强大的工具来读取和写入文件。通过使用内置的 open() 函数、read()、readline()、write() 等方法，我们可以轻松实现对文件的操作。此外，Python 的 with 语句可以帮助我…...

编程日记 2025/9/8 15:19:58

Webstorm 使用搜不到node_modules下的JS内容 TS项目按Ctrl无法跳转到函数实现

将node_modules标记为不排除，此时要把内存改大，不然webstorm中途建立索引时，会因为内存不足，导致索引中途停止，造成后续搜索不出来更改使用内存设置内存调为4096 若出现搜不出来js内容时，请直接重启下该项…...

编程日记 2025/9/12 8:07:12

转行嵌入式，需要自学多久？

作为一个本硕都学机械，却阴差阳错进入嵌入式行业的老兵，这个问题我能聊一整天。十几年前我还在工厂车间穿着工装和机床打交道，偶然接触到单片机后就一发不可收拾。转行这条路我走得异常艰辛，踩过的坑比写过的代码还多。去年我终…...

编程日记 2025/9/15 1:38:37

BLE 协议栈事件驱动机制详解

在 BlueNRG-LP 等 BLE 系统中，事件驱动是控制状态转移、数据交互和外设协作的基础。本文将深入讲解 BLE 协议栈中事件的来源、分发流程、处理结构与实际工程实践策略，帮助你构建稳定、可维护的 BLE 系统。 📦 一、BLE 事件的来源分类 BLE 协议栈中的事件严格来自协议栈本身…...

编程日记 2025/9/16 1:31:52

AI开发学习路线（闯关升级版）

以下是一份轻松版AI开发学习路线，用「闯关升级」的方式帮你从零开始变身AI开发者，每个阶段都配有有趣的任务和实用资源，保证不枯燥、可落地！👇 目录 🔰 新手村：打基础（1-2个月&…...

编程日记 2025/9/13 21:01:32

突破，未观测地区罕见极端降雨的估计

文章中文总结（重点为方法细节） 一、研究背景与目的在无测站或短观测记录地区，传统极值理论（如GEV）难以估计稀有极端降雨事件；本文提出一种新的区域化极值估计方法：区域化 Metastatistical Ex…...

编程日记 2025/9/14 22:54:25

zk源码—4.会话的实现原理一

大纲 1.创建会话 (1)客户端的会话状态 (2)服务端的会话创建 (3)会话ID的初始化实现 (4)设置的会话超时时间没生效的原因 2.分桶策略和会话管理 (1)分桶策略和过期队列 (2)会话激活 (3)会话超时检查 (4)会话清理 1.创建会话 (1)客户端的会话状态 (2)服务端的会话创建…...

编程日记 2025/9/4 1:23:45