当前位置：首页 > news >正文

第15周：注意力汇聚：Nadaraya-Watson 核回归

news 来源：原创 2025/9/6 15:19:18

注意力汇聚：Nadaraya-Watson 核回归

Nadaraya-Watson 核回归是一个经典的注意力机制模型，它展示了如何通过注意力权重来对输入数据进行加权平均。以下是该内容的核心总结：

关键概念

注意力机制框架：由查询（自主提示）、键（非自主提示）和值（感官输入）组成，通过查询和键的交互形成注意力权重，然后加权聚合值。
Nadaraya-Watson核回归：
- 非参数形式： $\color{red}f(x) = ∑(softmax(-(x - x_i)²/2) * y_i)$
- 参数形式：引入可学习参数 $w$ ， $\color{red}f(x) = ∑(softmax(-((x - x_i)w)²/2) * y_i)$
核函数：使用高斯核来衡量查询和键之间的相似度。

主要特点

非参数模型：
- 直接基于训练数据进行预测
- 具有一致性（随着数据量增加会收敛到最优解）
- 预测结果平滑
参数模型：
- 引入可学习参数w
- 可以调整注意力权重的分布
- 预测结果可能不如非参数模型平滑
注意力权重可视化：展示了查询与键之间的关系，距离越近权重越高。

实现要点

使用批量矩阵乘法高效计算小批量数据的注意力权重
通过softmax计算归一化的注意力权重
训练时使用平方损失和随机梯度下降

应用意义

Nadaraya-Watson核回归提供了一个简单但完整的例子，展示了注意力机制如何通过加权平均的方式选择性地聚焦于相关的输入数据。这种注意力汇聚的思想是现代注意力机制的基础，后续发展出了更复杂的注意力评分函数和模型结构。

这个模型清楚地演示了注意力机制的核心思想：根据查询与键的相似度来决定对相应值的关注程度，从而实现对输入数据的有选择性的聚合。

Nadaraya-Watson 核回归示例

以下为完整的代码示例Nadaraya-Watson核回归的实现和应用，包括非参数和带参数两种形式。

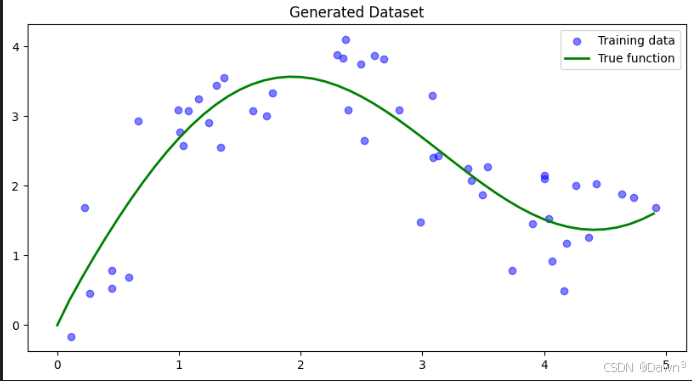
1. 生成数据集

首先我们生成一个非线性数据集，加入一些噪声：

import numpy as np
import matplotlib.pyplot as plt# 生成训练数据
n_train = 50
x_train = np.sort(np.random.rand(n_train) * 5)
def f(x):return 2 * np.sin(x) + x**0.8y_train = f(x_train) + np.random.normal(0.0, 0.5, n_train)  # 添加噪声# 生成测试数据
x_test = np.arange(0, 5, 0.1)
y_true = f(x_test)  # 真实函数值# 绘制数据
plt.figure(figsize=(10, 5))
plt.scatter(x_train, y_train, label='Training data', color='blue', alpha=0.5)
plt.plot(x_test, y_true, label='True function', color='green', linewidth=2)
plt.legend()
plt.title('Generated Dataset')
plt.show()

在这里插入图片描述

2. 非参数Nadaraya-Watson核回归实现

def nadaraya_watson(x_query, x_keys, y_values, bandwidth=1.0):"""非参数Nadaraya-Watson核回归:param x_query: 查询点:param x_keys: 训练数据键:param y_values: 训练数据值:param bandwidth: 核带宽:return: 预测值"""predictions = []for x in x_query:# 计算高斯核权重weights = np.exp(-0.5 * ((x - x_keys) / bandwidth)**2)# 归一化权重weights /= np.sum(weights)# 加权平均prediction = np.sum(weights * y_values)predictions.append(prediction)return np.array(predictions)# 使用不同带宽进行预测
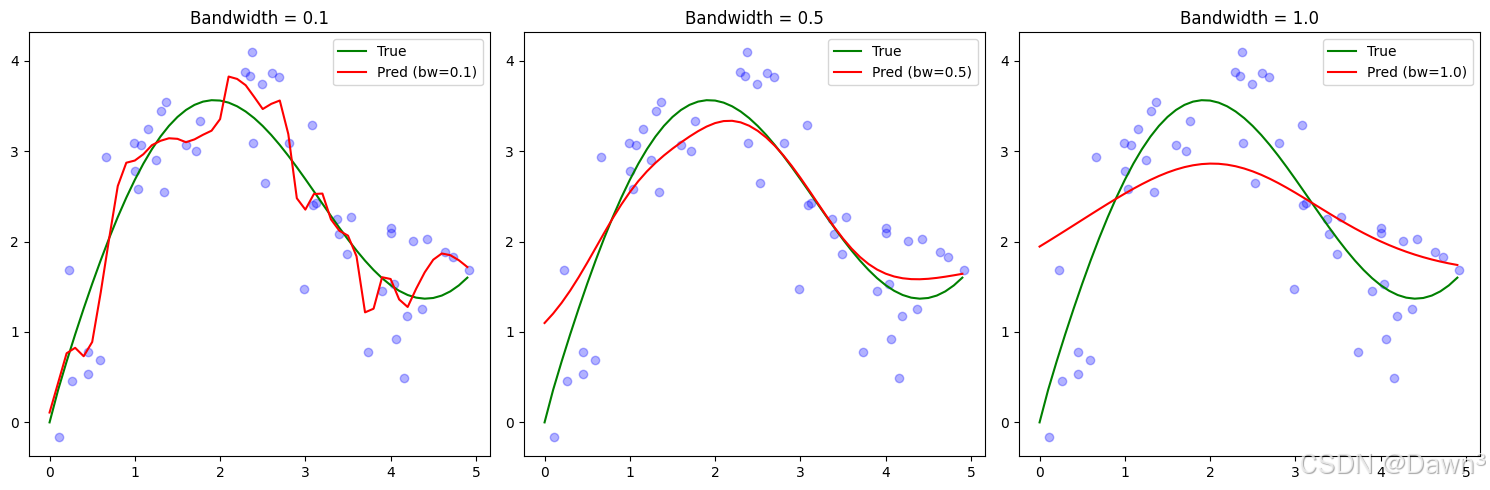
bandwidths = [0.1, 0.5, 1.0]
plt.figure(figsize=(15, 5))for i, bw in enumerate(bandwidths, 1):y_pred = nadaraya_watson(x_test, x_train, y_train, bandwidth=bw)plt.subplot(1, 3, i)plt.scatter(x_train, y_train, color='blue', alpha=0.3)plt.plot(x_test, y_true, label='True', color='green')plt.plot(x_test, y_pred, label=f'Pred (bw={bw})', color='red')plt.legend()plt.title(f'Bandwidth = {bw}')plt.tight_layout()
plt.show()

在这里插入图片描述

3. 带参数Nadaraya-Watson核回归实现

class ParametricNWKernelRegression:def __init__(self, learning_rate=0.1, n_epochs=100):self.w = None  # 可学习参数self.lr = learning_rateself.epochs = n_epochsdef fit(self, x_train, y_train):# 初始化参数self.w = np.random.randn(1)# 训练过程losses = []for epoch in range(self.epochs):# 前向传播weights = np.exp(-0.5 * (self.w * (x_train[:, None] - x_train[None, :]))**2)weights /= np.sum(weights, axis=1, keepdims=True)y_pred = np.sum(weights * y_train[None, :], axis=1)# 计算损失loss = np.mean((y_pred - y_train)**2)losses.append(loss)# 反向传播# (这里简化了梯度计算，实际实现可能需要更精确的梯度)grad = np.random.randn(1) * 0.1  # 简化的梯度self.w -= self.lr * gradif epoch % 10 == 0:print(f'Epoch {epoch}, Loss: {loss:.4f}')return lossesdef predict(self, x_query, x_keys, y_values):weights = np.exp(-0.5 * (self.w * (x_query[:, None] - x_keys[None, :]))**2)weights /= np.sum(weights, axis=1, keepdims=True)return np.sum(weights * y_values[None, :], axis=1)# 训练带参数模型
model = ParametricNWKernelRegression(learning_rate=0.1, n_epochs=100)
losses = model.fit(x_train, y_train)# 预测并绘制结果
y_pred_param = model.predict(x_test, x_train, y_train)plt.figure(figsize=(10, 5))
plt.scatter(x_train, y_train, color='blue', alpha=0.3, label='Training data')
plt.plot(x_test, y_true, label='True function', color='green')
plt.plot(x_test, y_pred_param, label='Parametric NW', color='red')
plt.legend()
plt.title('Parametric Nadaraya-Watson Regression')
plt.show()# 绘制训练损失
plt.figure(figsize=(10, 4))
plt.plot(losses)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Training Loss')
plt.show()

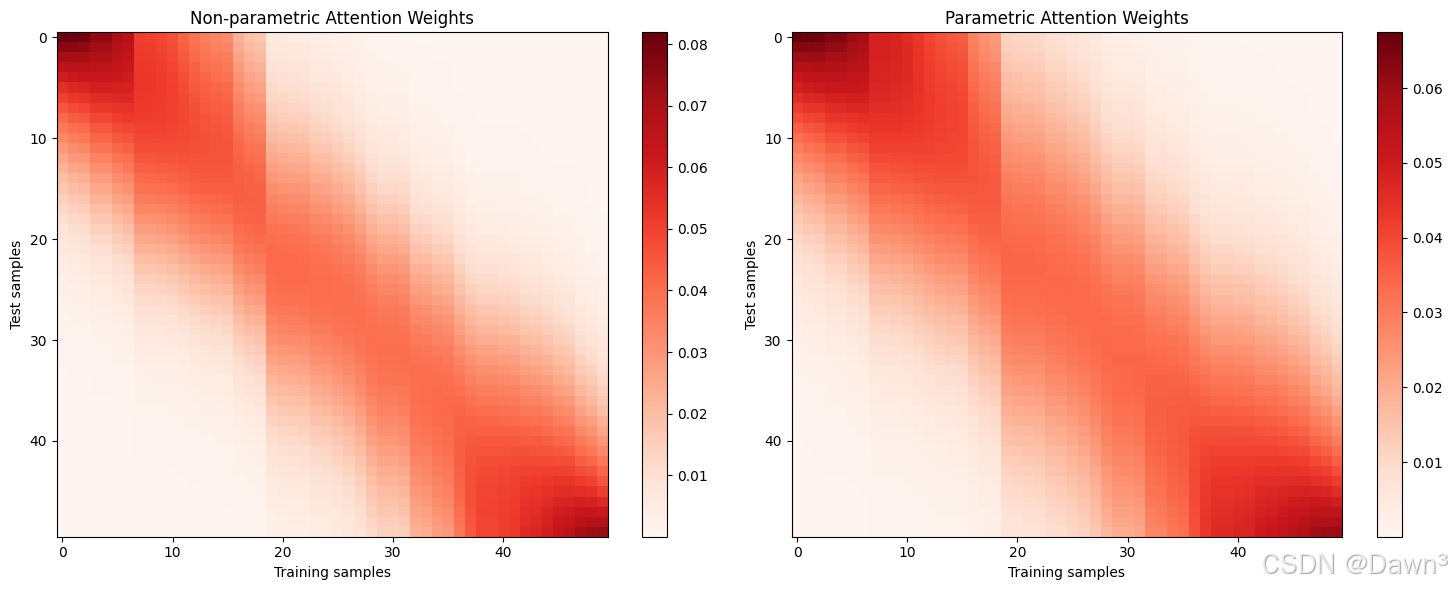
在这里插入图片描述

4. 注意力权重可视化

# 计算注意力权重
def compute_attention(x_query, x_keys, w=1.0):weights = np.exp(-0.5 * (w * (x_query[:, None] - x_keys[None, :]))**2)weights /= np.sum(weights, axis=1, keepdims=True)return weights# 非参数模型注意力权重
attn_nonparam = compute_attention(x_test, x_train)# 带参数模型注意力权重
attn_param = compute_attention(x_test, x_train, w=model.w)# 可视化
plt.figure(figsize=(15, 6))
plt.subplot(1, 2, 1)
plt.imshow(attn_nonparam, cmap='Reds', aspect='auto')
plt.colorbar()
plt.title('Non-parametric Attention Weights')
plt.xlabel('Training samples')
plt.ylabel('Test samples')plt.subplot(1, 2, 2)
plt.imshow(attn_param, cmap='Reds', aspect='auto')
plt.colorbar()
plt.title('Parametric Attention Weights')
plt.xlabel('Training samples')
plt.ylabel('Test samples')plt.tight_layout()
plt.show()

在这里插入图片描述

注意

带宽影响：在非参数模型中，带宽参数控制着平滑程度：
- 小带宽(0.1)导致过拟合，预测曲线波动大
- 大带宽(1.0)导致欠拟合，预测曲线过于平滑
- 中等带宽(0.5)通常效果最好
参数模型：通过学习参数w，模型可以自动调整注意力权重的分布：
- 通常比固定带宽的非参数模型更灵活
- 但需要足够的训练数据来学习合适的参数
注意力模式：从注意力权重图中可以看到：
- 查询点附近的键会获得更高的注意力权重
- 参数模型通常会学习到更集中的注意力分布

第15周：注意力汇聚：Nadaraya-Watson 核回归

注意力汇聚：Nadaraya-Watson 核回归 Nadaraya-Watson 核回归是一个经典的注意力机制模型，它展示了如何通过注意力权重来对输入数据进行加权平均。以下是该内容的核心总结： 关键概念注意力机制框架：由查询（自主提示…...

编程日记 2025/9/6 15:19:18

批量图片文本识别重命名，批量ocr识别图片重命名，基于WPF和腾讯OCR云部署实，现批量对图片局部提取文字后重命名的操作详细步骤

1. 项目背景在日常工作中，我们经常需要处理大量图片文件，这些图片可能包含重要的文字信息。为了提高工作效率，我们需要一种自动化的方式，从图片中提取文字，并根据提取的文字对图片进行重命名。本项目基于 WPF 框架开发桌面应用程序，结合腾讯 OCR…...

编程日记 2025/9/4 22:44:45

26考研——排序（8）

408答疑文章目录一、排序的基本概念二、插入排序三、交换排序四、选择排序五、归并排序、基数排序和计数排序六、排序的代码实操七、各种内部排序算法的比较及应用八、外部排序九、参考资料鲍鱼科技课件26王道考研书十、总结基本排序算法希尔排序快速排序、堆排序和归并排序…...

编程日记 2025/9/5 7:02:59

KUKA机器人导入设备说明文件

KUKA机器人在应用中需要进行通讯配置，通讯前需要导入设备说明文件，比如常用的倍福设备说明文件。在Workvisual软件上通过以下步骤即可导入设备说明文件。一、打开Workvisual软件，在选项卡【File】下找到【Import/Export】输入/输出并点击打…...

编程日记 2025/8/31 5:17:52

ssl.SSLCertVerificationError报错解决方案

这个错误 ssl.SSLCertVerificationError: [SSL: CERTIFICATE_VERIFY_FAILED] certificate verify failed: unable to get local issuer certificate 指出 Python 在尝试建立安全的 HTTPS 连接时，无法验证远程服务器（在此案例中是 GitHub 或 Hugging Face…...

编程日记 2025/9/6 13:37:09

drawio导出流程图为白色背景png图片

draw.io 操作路径： 1.纯白背景图片（一般导出流程图就这种纯白背景，看自己需求什么都不勾选导出效果图 2.田字格白背景只勾选网格导出效果图 3.方块背景只勾选背景导出效果图 4.大方块背景都勾选导出效果图...

编程日记 2025/8/17 22:42:28

【Linux】——手撕线程池、简易线程池

前言在现代计算机编程领域，随着多核处理器和分布式系统的广泛应用，并发编程变得越来越重要。而线程作为实现并发的基本手段之一，其重要性不言而喻。然而，在实际的应用开发中，如何高效地管理和调度线程，以充…...

编程日记 2025/9/2 7:39:43

使用mcp自定义编写mcp tool，使用 conda 启动，在cline中配置使用

自定义 mcp tool 例子 ## /langchain_learn/mcp学习/base_mcp_tool_study2.py # 导入必要模块 import os from typing import Optional from mcp.server.fastmcp import FastMCP# 初始化 MCP 服务器实例，指定服务器名称和版本 mcp_server FastMCP(name"DemoS…...

编程日记 2025/9/5 9:57:12

OpenEuler/CentOS一键部署OpenGauss数据库教程（脚本+视频）

📌OpenEuler/CentOS一键安装OpenGauss数据库教程为什么需要OpenGauss一键安装脚本？ 手动部署OpenGauss数据库时，环境适配、依赖冲突等问题常让开发者头疼。尤其对新人而言，官方文档的配置步骤可能耗时数小时甚至引发未知报错。 …...

编程日记 2025/8/19 11:20:18

python如何快速删除文件夹中的大量文件

在 Python 中，删除文件夹中的大量小图片文件可以通过使用 os 模块或 shutil 模块来实现。以下是一个示例代码，展示了如何快速删除指定文件夹中的所有文件。如果你只需要删除小图片文件，可以添加额外的逻辑来检查文件大小。以下是一个示例代…...

编程日记 2025/9/6 1:29:05

【mongodb】MongoDB的应用场景

目录 1.说明2.内容管理系统（CMS）2.1 场景描述2.2 MongoDB优势2.3 示例 3.实时分析与大数据3.1 场景描述3.2 MongoDB优势3.3 示例 4.移动应用后端4.1 场景描述4.2 MongoDB优势4.3 示例 5.游戏开发5.1 场景描述5.2 MongoDB优势5.3 示例 6.电子商务平台6.1 …...

编程日记 2025/9/5 12:22:52

使用 Swift 实现 LRU 缓存淘汰策略

📌 实现思路一、核心目标我们要实现一个缓存类： 支持通过 get(key) 获取缓存的值；支持通过 put(key, value) 写入缓存；缓存容量有限，当超过容量时要淘汰最久未使用的元素。二、为什么用「哈希表双向链表」功…...

编程日记 2025/9/3 4:43:02

【面试篇】Dubbo

基础概念问题：请简要介绍一下 Dubbo 是什么，它的主要用途是什么？答案：Dubbo 是阿里巴巴开源的高性能、轻量级的分布式服务框架，它致力于提供高性能和透明化的 RPC 远程服务调用方案，以及 SOA 服务治理方案…...

编程日记 2025/9/4 0:04:15

01-STM32（介绍、工具准备、新建工程）p1-4

文章目录工具准备和介绍硬件设备stm32简介和arm简介stm32简介STM32命名规则STM32选型STM32F103C8T6最小系统板引脚定义STM32启动配置STM32最小系统电路ARM简介软件安装注册器件支持包安装ST-LINK驱动安装USB转串口驱动新建工程创建stm32工程STM32工程编译和下载型号分类及缩…...

编程日记 2025/9/3 10:53:02

关于termux运行pc交叉编译的aarch64 elf的问题

在Linux系统上交叉编译Nim程序到Android Termux环境需要特殊处理，以下是详细的解决方案： 问题根源分析 ABI不兼容 Android使用bionic libc而非标准glibc，直接编译的Linux ARM二进制无法直接运行动态链接错误默认编译会链…...

编程日记 2025/9/2 4:27:44

Ansible Playbook 进阶探秘：Handlers、变量、循环及条件判断全解析

192.168.60.100ansible.com192.168.60.110 client-1.com 192.168.60.120client-2.com192.168.60.130client-1.com 一、Handlers 介绍：在发生改变时执行的操作(类似puppet通知机制) 示例： 当apache的配置文件发生改变时，apache服务才会重启…...

编程日记 2025/9/3 5:14:45

解决GraalVM Native Maven Plugin错误：JAVA_HOME未指向GraalVM Distribution

目录问题描述解决方案为什么需要这样配置？ 问题描述在你的项目中，如果你遇到了以下错误信息： [ERROR] Failed to execute goal org.graalvm.buildtools:native-maven-plugin:0.10.5:test (native-test) on project DIctSystemInJavaUsing…...

编程日记 2025/8/31 18:03:28

006贪心——算法备赛

跨步问题跳跃游戏|| 问题描述给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。每个元素 nums[i] 表示从索引 i 向后跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i j] 处: 0 < j < nums[i]i j &…...

编程日记 2025/9/4 8:58:37

Hyperlane：高性能 Rust HTTP 服务器框架评测

Hyperlane：高性能 Rust HTTP 服务器框架评测在当今快速发展的互联网时代，选择一个高效、可靠的 HTTP 服务器框架对于开发者来说至关重要。最近，我在评估各种服务器框架性能时，发现了一个名为 Hyperlane 的 Rust HTTP 服务器库&a…...

编程日记 2025/9/4 4:32:19

解锁多元养生密码，开启活力生活

在车水马龙、节奏飞快的现代社会，亚健康像阴霾一样，笼罩着不少人的生活。不少上班族长期久坐，肩颈酸痛；有的人作息混乱，皮肤状态差。想要驱散这些健康阴霾，拥抱活力生活，不妨解锁下面这些多元养…...

编程日记 2025/9/5 18:58:04

如何安全地访问AWS

如何安全地访问AWS 推荐超级课程：本地离线DeepSeek AI方案部署实战教程【完全版】Docker快速入门到精通Kubernetes入门到大师通关课AWS云服务快速入门实战目录如何安全地访问AWS当可以使用AWS Organizations & IAM Identity Center时理想的访问方式补充：什么是IAM IIC…...

编程日记 2025/9/1 21:06:45

机器视觉工程师的专业精度决定职业高度，而专注密度决定成长速度。低质量的合群，不如高质量独处

在机器视觉行业，真正的技术突破往往诞生于深度思考与有效碰撞的辩证统一。建议采用「70%高质量独处30%精准社交」的钻石结构，构建可验证的技术能力护城河。记住：你的专业精度决定职业高度，而专注密度决定成长速度。作为机器视觉工…...

编程日记 2025/9/6 0:28:33

Linux的 `sysctl` 命令笔记250404

Linux的 sysctl 命令笔记250404 sysctl 是 Linux 系统中用于动态查看和修改内核运行时参数的核心工具。它通过 /proc/sys/ 目录的虚拟文件系统接口，允许用户在不重启系统的前提下调整内核行为，涵盖网络、内存、文件系统等关键功能。 📜 核…...

编程日记 2025/9/1 20:53:23

prism WPF 导航

导航和浏览器的后退前进是一样的功能项目结构 App.xaml.cs using Prism.Ioc; using Prism.Modularity; using Prism.Unity; using PrismWpfApp.ViewModels; using PrismWpfApp.Views; using System; using System.Collections.Generic; using System.Configuration; using S…...

编程日记 2025/8/30 0:58:47

Pytorch实现线性分类

目录 1.导包 2.加载数据 3.获取X与Y数据 4.将X，Y数据转化成tensor张量, tensor张量必须是二维数据 5.用封装的API实现线性分类 5.1导包 5.2建模-神经网络（二分类问题） 5.3定义损失函数 5.4定义优化器 5.5定义训练过程 5.6 计算正确…...

编程日记 2025/9/3 15:26:16

使用人工智能大模型kimi，如何免费高效制作PPT？

今天我们学习人工智能大模型kimi，如何免费协助我们做班会PPT。免费手把手讲解视频，请访问 https://edu.csdn.net/learn/40402/666417 第一步使用谷歌浏览器，搜索Kimi，看到Kimi智能助手，点击，在Kimi对话框…...

编程日记 2025/9/2 22:24:11

YOLO学习笔记｜基于YOLO与光流融合的车牌识别方法研究（附Matlab代码）

🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓 基于YOLO与光流融合的车牌识别方法研究 🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓 摘要针对动态场景下车牌识别易受运动模糊影响的问题，提出结合YOLO目标检测与Lucas-Kanade…...

编程日记 2025/9/4 19:25:43

leetcode 数组总结篇

基础理论数组：下标时从 0 开始的，地址是连续的，不能删除，只能覆盖；数组的实现：vector动态数组常用操作头文件 #include <iostream> #include <vector> #include <cstdint> // IN…...

编程日记 2025/9/2 19:15:28

CCF GESP C++编程四级认证真题 2025年3月

C 四级 2025 年 03 月题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 答案 A B B D D C D D B B B B A A C 1 单选题（每题 2 分，共 30 分） 第 1 题关于下述代码，说法错误的是（ ）。 int multiply(int x, int …...

编程日记 2025/9/5 7:39:41

元宇宙浪潮下，前端开发如何“乘风破浪”？

一、元宇宙对前端开发的新要求元宇宙的兴起，为前端开发领域带来了全新的挑战与机遇。元宇宙作为一个高度集成、多维互动的虚拟世界，要求前端开发不仅具备传统网页开发的能力，还需要掌握虚拟现实（VR）、增强现实&#…...

编程日记 2025/9/6 13:37:07

室内指路机器人是否支持环境监测功能？

并非所有室内指路机器人都具备环境监测功能。那些支持环境监测的室内指路机器人，往往在设计上进行了针对性的优化，搭载了一系列先进且实用的传感器。温湿度传感器犹如一位敏锐的 “温度湿度侦探”，时刻精准地监测室内温度与湿度，为…...

编程日记 2025/9/5 22:24:00

redis的数据类型（1）

https://redis.io/docs/latest/develop/data-types/strings/ 社区版支持： String，字符串 Hash，key-value格式 List，根据插入顺序排序 Set，集合 Sorted set，有排序 Stream， Bitmap， …...

编程日记 2025/9/5 17:37:50

模运算核心性质与算法应用：从数学原理到编程实践

目录 🚀前言🌟数学性质：模运算的理论基石💯基本定义：余数的本质💯四则运算规则：保持同余性的关键 🦜编程实践：模运算的工程化技巧💯避免数值溢出：…...

编程日记 2025/9/1 11:39:17

使用 Messenger 跨进程通讯

在Android中使用Messenger进行跨进程通信（IPC）的步骤如下： 1. 服务端（Service）实现 1.1 创建Service并绑定Messenger public class MessengerService extends Service {private static final String TAG "Mess…...

编程日记 2025/9/3 23:35:43

css炫酷的3D水波纹文字效果实现详解

炫酷的3D水波纹文字效果实现详解这里写目录标题炫酷的3D水波纹文字效果实现详解项目概述技术栈核心实现1. 基础布局2. 渐变背景3. 文字效果实现3.1 基础样式3.2 文字漂浮动画 4. 水波纹效果4.1 模糊效果4.2 水波动画 5. 交互效果技术要点项目难点与解决方案总结项目概述在…...

编程日记 2025/9/4 21:50:33

C++类的特殊成员函数：构造、拷贝构造与析构函数详解

目录编辑一、构造函数二、拷贝构造函数三、析构函数在C 编程中，类的特殊成员函数扮演着至关重要的角色，它们负责对象的创建、复制以及销毁过程。本文将深入探讨构造函数、拷贝构造函数和析构函数的概念、特性及应用场景，并结合代…...

编程日记 2025/9/5 1:02:43

ffmpeg常见命令3

文章目录 1. **文字水印（Text Watermark）**示例命令：更多选项： 2. **图片水印（Image Watermark）**示例命令：更多选项： 3. **画中画（Picture-in-Picture, PIP）…...

编程日记 2025/9/4 10:12:22

C# 中创建统一 API 接口实现方案

在 C# 中创建统一 API 接口需要从架构设计、技术选型和代码实现等多个层面进行规划。以下是详细的实现方案和完整示例代码： 一、技术选型与架构设计框架选择 ASP.NET Core (6.0)RESTful API 规范核心组件统一响应格式：标准化 JSON 响应结构全局异常处…...

编程日记 2025/9/1 15:40:53

考研单词笔记 2025.04.04

accord n一致，符合，协议，条约v与…一致符合，给予，赠予 align v使一致，使对齐 alike a相同的，相似的ad相同地，相似地，同等地 analogous a类似的，相似的 co…...

编程日记 2025/9/4 9:01:55

leetcode 代码随想录数组-区间和

题目给定一个整数数组 Array，请计算该数组在每个指定区间内元素的总和。输入： 第一行输入：为整数数组 Array 的长度 n，接下来 n 行，每行一个整数，表示数组的元素。随后的输入为需要计算总和的区间&…...

编程日记 2025/9/5 4:21:18

Linux学习笔记7：关于i.MX6ULL主频与时钟配置原理详解

以下是关于正点原子B站课程中 i.MX6ULL主频和时钟配置实验的博客内容框架与详细解析，结合实验原理、配置流程及关键代码实现，适合嵌入式开发者参考学习： 一、实验背景 i.MX6ULL默认启动时由内部BootROM将主频设置为396MHz，但其…...

编程日记 2025/9/3 7:37:29

第三期：深入理解 Spring Web MVC [特殊字符]（数据传参+ 特殊字符处理 + 编码问题解析）

✨前言：传参和状态管理，看似简单其实门道不少在 Web 开发中，前端和后端最核心的交流方式就是“传参”，而“传参”除了涉及如何写代码获取参数，还藏着很多开发者容易忽略的细节： 为什么 URL 带了中文&…...

编程日记 2025/9/3 0:29:01

洛谷题单3-P1075 [NOIP 2012 普及组] 质因数分解-python-流程图重构

题目描述已知正整数 n n n 是两个不同的质数的乘积，试求出两者中较大的那个质数。输入格式输入一个正整数 n n n。输出格式输出一个正整数 p p p，即较大的那个质数。输入输出样例输入 21输出 7说明/提示 1 ≤ n ≤ 2 1 0 9 1 \le n\…...

编程日记 2025/9/6 5:17:39

Vue组件化开发深度解析：Element UI与Ant Design Vue对比实践

一、Vue组件化开发的核心优势 1.1 组件化架构的天然优势 Vue的组件系统是其最核心的特性之一，采用单文件组件（.vue）形式，将HTML、CSS和JavaScript组合在同一个文件中，形成高内聚、低耦合的代码单元。这种设计显著提升…...

编程日记 2025/9/3 22:50:41

ctfshow VIP题目限免 robots后台泄露

根据题目提示是 robots后台泄露，所以我们试着访问它的后台文件 robots.txt 访问之后发现了有一个/flagishere.txt 目录文件。接着拼接访问它发现了 flag...

编程日记 2025/8/27 19:42:54

突破传统认知：聚类算法的底层逻辑与高阶应用全景解析

一、维度革命：重新定义聚类分析的认知边界在人工智能的浩瀚星空中，聚类算法犹如一组精密的星际导航仪，帮助我们在无序的数据宇宙中发现隐藏的秩序。这项起源于人类本能分类需求的技术，经历了从简单分组到智能识别的蜕变&#xf…...

编程日记 2025/8/28 21:22:42

获取ssh密钥

git bash GitHub官网: Redirecting… ssh-keygen -t rsa -C “git账号” 出现id_rsa.pub 登录github添加将id_rsa.pub中内容复制点击SSH and GPG keys 点击New SSH key 起个名字将id_rsa.pub中内容复制到这里报错： ssh: connect to host github.com port 2…...

编程日记 2025/9/4 13:56:37

MINIQMT学习课程Day7

在上一篇，我们安装好xtquant，qmt以及python后，这一章，我们学习如何使用xtquant 本章学习，如何获取账号的资金使用状况。首先，打开qmt，输入账号密码，选择独立交易。进入交易界面&…...

编程日记 2025/9/2 17:49:42

`accept_ra` 和 `autoconf` 和 `forwarding` 的关系笔记250404

accept_ra 和 autoconf 和 forwarding 的关系笔记250404 在 Linux 的 IPv6 网络配置中，accept_ra、autoconf 和 forwarding 是三个密切相关的核心参数，它们的组合直接影响设备在网络中的角色（主机或路由器）和地址配置行为。以下是…...

编程日记 2025/9/1 9:49:00

leetcode数组-二分查找

题目题目链接：https://leetcode.cn/problems/binary-search/ 文章讲解：https://programmercarl.com/0704.%E4%BA%8C%E5%88%86%E6%9F%A5%E6%89%BE.html 视频讲解：https://www.bilibili.com/video/BV1fA4y1o715 给定一个 n 个元素有序的&…...

编程日记 2025/9/6 4:06:46

注意力汇聚：Nadaraya-Watson 核回归

关键概念

主要特点

实现要点

应用意义

Nadaraya-Watson 核回归示例

1. 生成数据集

2. 非参数Nadaraya-Watson核回归实现

3. 带参数Nadaraya-Watson核回归实现

4. 注意力权重可视化

注意

相关文章：