当前位置：首页 > news >正文

【CVPR2024】基于小波的傅里叶信息交互与频率扩散调整的水下图像恢复

news 来源：原创 2025/9/11 6:05:17

论文信息

题目： Wavelet-based Fourier Information Interaction with Frequency Diffusion Adjustment for Underwater Image Restoration
基于小波的傅里叶信息交互与频率扩散调整的水下图像恢复
源码:https://github.com/ChenzhaoNju/WF-Diff

论文创新点

基于频域信息的探索与利用：论文首次深入探索了水下图像在频域中的特性，特别是通过傅里叶变换和小波变换，发现水下图像的退化信息主要包含在幅度分量中，尤其是低频子图像的幅度分量。
WFI2-net网络设计：论文提出了一种新颖的Wavelet-based Fourier信息交互网络（WFI2-net），该网络通过结合Transformer和傅里叶先验信息，分别增强图像的高频和低频分量。特别是设计了宽Transformer块（WTB）和空间-频率融合块（SFFB），有效提升了图像的质量。
频率残差扩散调整模块（FRDAM）：论文提出了一个创新的频率残差扩散调整模块（FRDAM），该模块通过在小波空间中使用两个扩散模型，分别学习高频和低频信息的残差分布，进一步细化图像的细节和纹理。
跨频率调节器（CFC）：论文设计了一个跨频率调节器（CFC），用于实现高频和低频信息之间的交互。通过CFC，高频和低频特征能够相互增强，从而提升整体图像的表示能力。

摘要

水下图像通常受到复杂且多样化的退化影响，这不可避免地影响了水下视觉任务的效果。然而，大多数方法主要在图像的原始像素空间中进行操作，限制了对水下图像频率特性的探索，导致深度模型在生成高质量图像时的表示能力未能得到充分利用。本文提出了一种新颖的水下图像增强（UIE）框架，名为WF-Diff，旨在充分利用频域信息和扩散模型的特性。WF-Diff由两个可分离的网络组成：基于小波的傅里叶信息交互网络（WFI2-net）和频率残差扩散调整模块（FR-DAM）。通过对频域信息的全面探索，WFI2-net旨在在小波空间中对频率信息进行初步增强。作者提出的FR-DAM可以进一步细化初始增强图像的高频和低频信息，可以视为一个即插即用的通用模块，用于调整水下图像的细节。通过上述技术，作者的算法在真实世界的水下图像数据集上展示了最先进的性能，并在视觉质量上具有竞争力。’

关键字

水下图像增强
频域信息
扩散模型
小波变换
傅里叶变换

3.方法

3.1整体框架

给定一幅水下图像作为输入，作者的目标是学习一个网络来生成消除输入图像颜色偏差并增强图像细节的输出。WF-Diff旨在充分利用频域信息的特性和扩散模型的强大能力。具体来说，WF-Diff由两个可分离的网络组成：基于小波的傅里叶信息交互网络（WFI2-net）和频率残差扩散调整模块（FRDAM）。作者首先使用离散小波变换（DWT）将输入图像转换到小波空间，获得一个低频系数和三个高频系数。WFI2-net致力于实现频率信息的初步增强。作者充分整合了Transformer和傅里叶先验信息的特性，并设计了宽Transformer块（WTB）和空间-频率融合块（SFFB）来分别增强高频和低频内容。FRDAM由低频扩散分支（LDFB）和高频扩散分支（HDFB）组成，旨在进一步调整初始增强图像的高频和低频信息。需要注意的是，作者提出的FRDAM使用两个扩散模型分别学习真实图像和初始增强结果之间的高频和低频信息的残差分布。此外，作者提出的跨频率调节器（CFC）旨在实现高频和低频信息之间的跨频率交互。
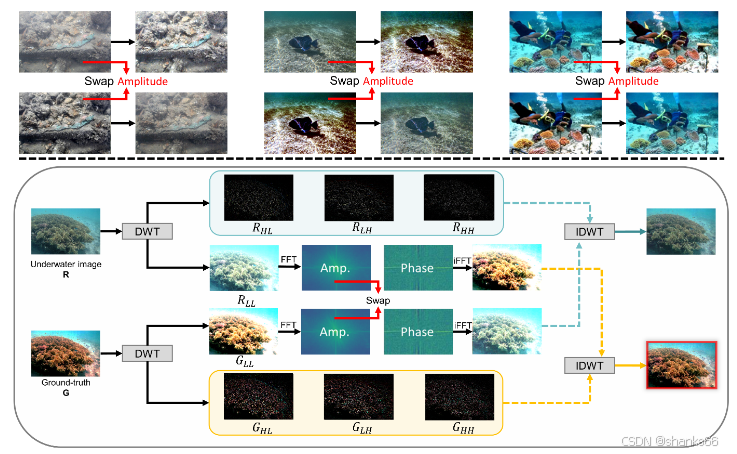
在这里插入图片描述

3.2 离散小波和傅里叶变换

离散小波变换（DWT）已广泛应用于低级视觉任务。我们首先使用DWT将输入分解为多个频率子带，以便我们可以分别实现低频信息的颜色校正和高频信息的细节增强。给定一幅水下图像输入(I \in \mathbb{R}^{H ×W ×c})，我们使用带有Haar小波的DWT对输入进行分解。Haar小波由低通滤波器(L)和高通滤波器(H)组成，如下所示：
$L=\frac{1}{\sqrt{2}}[1,1]^{T}, H=\frac{1}{\sqrt{2}}[1,-1]^{T}$

我们可以获得四个子带，可表示为：
$I_{LL},\left\{I_{LH}, I_{HL}, I_{HH}\right\}=DWT(I)$
其中(I_{LL},{I_{LH}, I_{HL}, I_{HH}} \in \mathbb{R}^{\frac{H}{2} ×\frac{W}{2} ×c})分别表示输入的低频分量以及垂直、水平和对角方向的高频分量。更具体地说，低频分量包含输入图像的内容和颜色信息，而其他三个高频系数包含全局结构和纹理的细节信息。子带被下采样到输入分辨率的一半，但由于DWT的双正交性，不会导致信息丢失。对于低频分量(I_{LL})，我们将在傅里叶空间中探索其特性。

然后，我们介绍傅里叶变换的操作。给定一幅图像(x \in \mathbb{R}^{H ×W ×1})，其形状为(H ×W)，将(x)转换到傅里叶空间(X)的傅里叶变换(\mathcal{F})可以表示为：
$\mathcal{F}(x)(u, v)=X(u, v)=\frac{1}{\sqrt{H W}} \sum_{h=0}^{H-1} \sum_{w=0}^{W-1} x(h, w) e^{-j 2 \pi\left(\frac{h}{H} u+\frac{w}{W} v\right)}$
其中(h)，(w)是空间空间中的坐标，(u)，(v)是傅里叶空间中的坐标。( $\mathcal{F}^{-1}$ )表示( $\mathcal{F}$ )的逆变换。傅里叶空间中的复分量(X(u, v))可以由幅度分量( $\mathcal{A}(X(u, v))$ )和相位分量( $\mathcal{P}(X(u, v))$ )表示如下：
$\begin{aligned} &\mathcal{A}(X(u, v))=\sqrt{R^{2}(X(u, v))+I^{2}(X(u, v))}\\ &\mathcal{P}(X(u, v))=\arctan \left[\frac{I(X(u, v))}{R(X(u, v))}\right] \end{aligned}$
其中(R(x))和(I(x))分别表示(X(u, v))的实部和虚部。请注意，傅里叶操作可以在特征图的每个通道中单独计算。
在这里插入图片描述

在这里插入图片描述

从图表中我们得出结论，水下图像的颜色退化信息主要包含在低频子带的幅度分量中，而纹理和细节退化信息主要包含在高频子带中。

3.3 频率初步增强

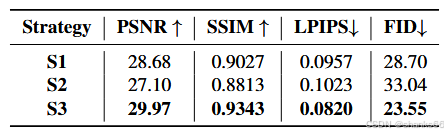
基于上述分析，在频率初步增强阶段，我们设计了一个简单但有效的WFI2-net，采用并行编码器 - 解码器（类似U - Net）的格式，分别恢复低频信息的幅度分量和高频分量。
在这里插入图片描述

我们还利用跳跃连接来连接编码器和解码器中相同级别的特征。对于高频分支，我们利用Transformer建模全局信息的优势来增强高频系数。我们使用多尺度信息设计了宽Transformer块（WTB），旨在建模长程依赖关系。我们的低频分支旨在恢复傅里叶空间中的幅度分量。为了获得丰富的频率和空间信息，我们设计了空间 - 频率融合块（SFFB）。

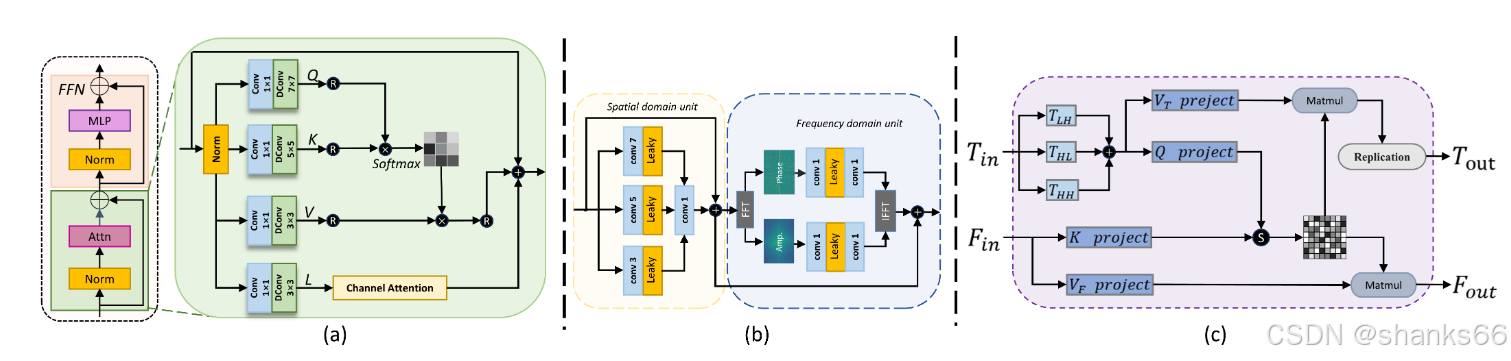
3.3.1 宽Transformer块

WTB如图3（a）所示。给定(I_{LH})，(I_{HL})，(I_{HH} \in \mathbb{R}^{\frac{H}{2} ×\frac{W}{2} ×c})，WTB首先通过卷积投影获得它们的嵌入特征(T_{in } \in \mathbb{R}^{3 ×\frac{H}{2} ×\frac{W}{2} ×C})。具体来说，WTB由一个注意力（Atten）模块和一个前馈网络（FFN）模块组成，其计算可以在WTB中表示为：
$\hat{T}_{i}=SA(Q, K, V)+CA(L)+T_{i-1}$
$L=Split\left(W_{d}W_{p}\left(Norm\left(T_{i-1}\right)\right)\right)$
$T_{i}=FFN\left(Norm\left(\hat{T}_{i}\right)\right)+\hat{T}_{i}$
其中(SA)和(CA)分别指自注意力和通道注意力。Norm指归一化。(T_{i-1})表示当前WTB的输入嵌入。(W_{d})和(W_{p})分别表示1×1逐点卷积和多尺度内核深度卷积；(Split)指分割操作。(L)旨在关注局部信息。

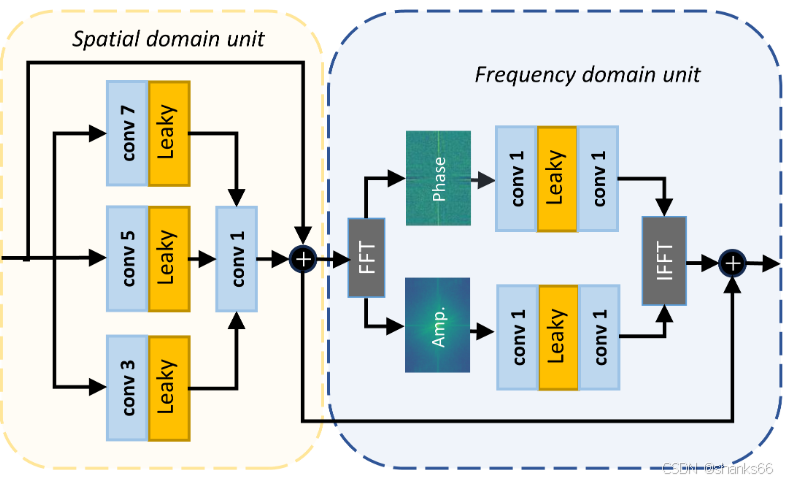
3.3.2 空间 - 频率融合块

我们在图3（b）中展示了SFFB的结构，它有一个空间域单元（SDU）和一个频率域单元（FDU）用于双域表示的交互。在空间域单元中，我们采用多尺度卷积核以扩大有限的空间感受野。在获得空间嵌入(F_{S})后，我们首先利用FFT获得幅度(A(F_{s}))和相位(P(F_{s}))分量。然后，将(A(F_{s}))和(P(F_{s}))输入到两层1×1卷积中，得到(A’(F_{s}))和(P’(F_{s}))。最后，我们使用IFFT算法将(A’(F_{s}))和(P’(F_{s}))映射到图像空间，得到频率嵌入(F_{f})。空间域和频率域的融合嵌入可以表示为：
$F_{sf}=F_{s}+F_{f}$

3.3.3 损失函数

我们将低频分支的输出表示为(I_{LL}‘)，高频分支的输出表示为(I_{LH}’)，(I_{HL}‘)和(I_{HH}’)。真实图像（G）可以通过DWT分解为(G_{LL})，(G_{LH})，(G_{HL})，(G_{HH})。高频损失可以表示为：
$\mathcal{L}_{h}=\left\| I_{(i)}'-G_{(i)}\right\| _{2}$
其中(i \in{LH, HL, HH})。对于低频信息，我们仅约束幅度分量。因此，低频损失可以表示为：
$\mathcal{L}_{a}=\left\| \mathcal{A}\left(I_{LL}'\right)-\mathcal{A}\left(G_{LL}\right)\right\| _{1}$
其中(\mathcal{A}())指傅里叶变换中的幅度分量。最后，我们进一步使用Wasserstein GAN中的对抗损失作为重建损失(L_{rec})。

3.4 跨频率调节器

CFC的详细结构如图3（c）所示。CFC旨在实现跨频率交互。我们将 $T_{in}$ 和 $F_{in}$ 表示为CFC的输入特征，分别代表高频和低频嵌入。

对于高频嵌入特征 $T_{in} \in \mathbb{R}^{3 ×\frac{H}{2} ×\frac{W}{2} ×C}$ ，我们可以通过拆分操作得到 $T_{LH}$ 、 $T_{HL}$ 、 $T_{HH} \in \mathbb{R}^{\frac{H}{2} ×\frac{W}{2} ×c}$ 。

通过将这些提取的系数相加，我们得到聚合的高频嵌入。我们在CFC中使用不同的线性投影来构建Q和K：
$Q = Conv_{1×1}(T_{LH} + T_{HL} + T_{HH})$
$K = Conv_{1×1}(F_{in})$

类似地，可以得到高频嵌入的 $V_T$ 和低频嵌入的 $V_F$ ：
$V_T = Conv_{1×1}(T_{LH} + T_{HL} + T_{HH})$
$V_F = Conv_{1×1}(F_{in})$

然后，输出特征图 $T_{out}$ 和 $F_{out}$ 可以通过以下公式获得：
$T_{out} = R(Softmax(\frac{QK^T}{\sqrt{d_k}})V_T)$
$F_{out} = Softmax(\frac{QK^T}{\sqrt{d_k}})V_F$
其中 $R$ 表示复制操作， $\sqrt{d_k}$ 是矩阵 $Q$ 的列数。

我们优化网络估计的噪声与LDFB中实际添加的噪声 $\epsilon^{(l)}$ 之间的目标函数。因此，扩散损失过程为：
$L_{dm}(\theta) = \left\| \epsilon^{(l)} - \epsilon_{\theta}(\sqrt{\overline{\alpha}_{t}} x_{0} + \sqrt{1 - \overline{\alpha}_{t}} \epsilon^{(l)}, x_{c}^{(l)}, t) \right\|$

一般来说，频率扩散调整过程是对初始增强的高频和低频分量进行细化。整个扩散过程可以表示为：
$\hat{I}_{(i)} = \mathcal{F}_{HDFB}(\epsilon_{s}^{(h)}, I_{(i)'}), i \in \{LH, HL, HH\}$
$\hat{I}_{LL} = \mathcal{F}_{LDFB}(\epsilon_{s}^{(l)}, I_{LL}')$
其中 $\epsilon_{s}^{(h)} \in \mathbb{R}^{3 ×\frac{H}{2} ×\frac{W}{2} ×3}$ 和 $\epsilon_{s}^{(l)} \in \mathbb{R}^{\frac{H}{2} ×\frac{W}{2} ×3}$ 是高斯噪声。

3.5 频率扩散调整

FRDAM旨在利用扩散模型强大的表示能力进一步调整高频和低频信息。一般来说，FRDAM可以分为两个分支，即低频扩散分支（LDFB）和高频扩散分支（HDFB）。我们采用DDPM中提出的扩散过程为每个分支构建高频和低频信息的残差分布，这可以描述为正向扩散过程和反向扩散过程。

3.5.1 正向扩散过程

正向扩散过程可以看作是一个马尔可夫链，逐步向数据中添加高斯噪声。给定初始增强的频率分量 $I_{i}'$ 及其真实值 $G_{i}$ ， $\in \{LL, LH, HL, HH\}$ ，我们计算它们的残差分布 $x_{0} = G_{i} - I_{i}'$ ，然后根据时间步引入高斯噪声，如下所示：
$q(x_{t} | x_{t - 1}) = \mathcal{N}(x_{t}; \sqrt{1 - \beta_{t}} x_{t - 1}, \beta_{t} I)$
其中 $\beta_{t}$ 是一个控制噪声方差的变量。引入 $\alpha_{t} = 1 - \beta_{t}$ ，这个过程可以描述为：
$x_{t} = \sqrt{\alpha_{t}} x_{t - 1} + \sqrt{1 - \alpha_{t}} \epsilon_{t - 1}, \epsilon_{t - 1} \sim \mathcal{N}(0, \mathcal{Z})$

随着高斯分布的合并，我们可以得到：
$q(x_{t} | x_{0}) = \mathcal{N}(x_{t}; \sqrt{\alpha_{t}} x_{0}, (1 - \overline{\alpha}_{t}) I)$

3.5.2 反向扩散过程

反向扩散过程旨在从高斯噪声中恢复残差分布。反向扩散可以表示为：
$p_{\theta}(x_{t - 1} | x_{t}, x_{c}^{(l)}) = \mathcal{N}(x_{t - 1}; \mu_{\theta}(x_{t}, x_{c}^{(l)}, t), \sigma_{t}^{2} \mathcal{Z})$
这里我们以LDFB为例， $x_{c}^{(l)}$ 指的是条件图像 $I_{LL}'$ 。 $\mu_{\theta}(x_{t}, x_{c}^{(l)}, t)$ 和 $\sigma_{t}^{2}$ 分别是步骤 $t$ 估计的均值和方差。在LDFB和HDFB中，我们遵循文献[33]的设置，它们可以表示为：
$\mu_{\theta}(x_{t}, x_{c}^{(l)}, t) = \frac{1}{\sqrt{\alpha}_{t}}(x_{t} - \frac{\beta_{t}}{(1 - \overline{\alpha}_{t})} \epsilon_{\theta}(x_{t}, x_{c}^{(l)}, t))$
$\sigma_{t}^{2} = \frac{1 - \overline{\alpha}_{t - 1}}{1 - \overline{\alpha}_{t}} \beta_{t}$
其中 $\epsilon_{\theta}(x_{t}, x_{c}^{(l)}, t)$ 是由U - net估计的值。

最终，经过细化的频率分量通过扩散生成的残差分布与初始增强的频率分量相加得到。然后，我们使用IDWT获得最终生成的图像：
$I_{final} = IDWT(I_{(i)}' + \hat{I}_{(i)}, I_{LL}' + \hat{I}_{LL}), i \in \{LH, HL, HH\}$

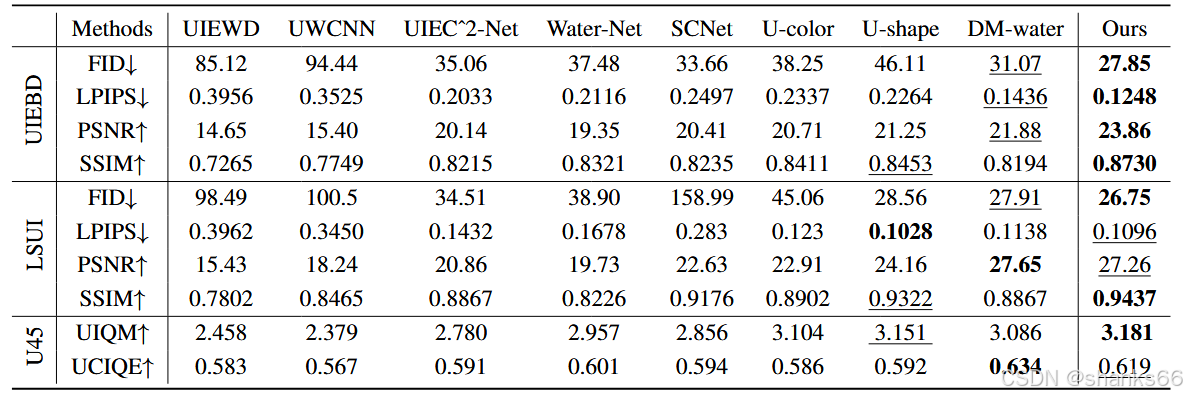
4.实验