【C++篇】哈希表
目录
一,哈希概念
1.1,直接定址法
1.2,哈希冲突
1.3,负载因子
二,哈希函数
2.1,除法散列法 /除留余数法
2.2,乘法散列法
2.3,全域散列法
三,处理哈希冲突
3.1,开放定址法
线性探测
二次探测
双重探测
3.2,开放定址法代码实现
哈希表扩容问题
key不能取模的问题
完整代码实现
3.3,链地址法
哈希表扩容问题
链地址法代码实现
小结:
一,哈希概念
哈希(hash)又称散列,是一种组织数据的方式。从译名看,有散乱排列的意思。本质就是通过哈希函数把关键字key和存储位置建立一个映射关系,查找时通过这个哈希函数计算出key存储的位置,实现快速查找。
说白了,hash函数就是根据key计算出应该存储地址的位置,而哈希表是基于hash函数建立的一种查找表。
1.1,直接定址法
当关键字的范围比较集中时,直接定址法就是非常简单高效的方法。比如一组关键字的值在[0,99]之间,那么我们开一个100大小的数组,每个关键字的值直接就是存储位置的下标。再比如一组数据a~z的字符,我们可以开一个大小为26的数组,每个关键字的acsll值减去 a的ascll值,就是对应的存储位置下标。也就是说直接定址法是用关键字计算出一个绝对位置或相对位置。
本题链接:387. 字符串中的第一个唯一字符 - 力扣(LeetCode)

class Solution {
public:
int firstUniqChar(string s) {
int hash[26]={0};
//统计次数
for(auto& ch:s)
{
hash[ch-'a']++;
}
for(int i=0;i<s.size();i++)
{
if(hash[s[i]-'a']==1)
return i;
}
return -1;
}
};
1.2,哈希冲突
不同的key值产生相同的地址,即H(key1)=H(key2)。这种问题叫做哈希冲突或哈希碰撞。
1.3,负载因子
假设哈希表已经存储N个值,哈希表的大小为M,那么负载因子=N/M。负载因子越大,代表哈希冲突的概率越高,空间利用率越高;负载因子越小,代表哈希冲突的概率越低,空间利用率越低。
二,哈希函数
两个不同的key值可能 会映射到同一个位置,这个问题叫做哈希冲突。理想情况是找一个哈希函数避免冲突,但是实际场景中,冲突不可避免,所以我们尽可能设计出好的哈希函数,来减少哈希冲突。
哈希函数的设计可能有很多讲究,比如要考虑均匀性、确定性、高效性等等。不同的应用场景可能需要不同的哈希函数。比如,非加密的哈希函数可能更注重速度,而加密的哈希函数则需要更高的安全性,防止被逆向或者找到碰撞。
2.1,除法散列法 /除留余数法
- 除法散列法也叫除留余数法,假设哈希表的大小为M,那么通过key除以M的余数作为映射的下标。也就是哈希函数为H(key)=key%M。
- 当使用 除法散列法时,应避免M的大小为某些值,比如2的幂,10的幂等。如果是2的x次方,那么key%2^x相当于保留key的二进制前x位。那么前x位二进制相同的key值,计算出的哈希值都是一样的,就会加剧哈希冲突。原因:key%2^x,相当于key&(2^x-1),其中 2^x-1的二进制表示中前x均为1,其余为均为0,所以最后按位与的结果取决于key的前x位。【见下图】

- 当使用除法散列 法时,建议M取不太接近2的整数次幂的一个质数(素数)
2.2,乘法散列法
- 乘法散列法对哈希表的大小M没有要求,它的大思路第一步:用关键字key乘上A(0<A<1),并抽取出key*A的小数部分。第二步:再用M乘以key*A的小数部分,再向下取整。
- H(key)=floor(M*((A*key)%1.0)),其中floor表示对表达式进行向下取整。0<A<1,这里最重要的时A的值该如何设定。Knuth认为设为黄金分割点比较好
2.3,全域散列法
- 如果存在一个对手,他针对我们的哈希函数,特意构造出一个发生严重冲突的数据集。比如,让所有关键字落入同一个位置,这种情况是可以存在的。只要哈希函数公开且时确定的,就可以实现次攻击。解决此方法就是给哈希函数增加随机性,攻击者就无法找出确定的导致冲突 加剧的数据。这种方法叫做全域散列。
- H[a][b](key)=((a*key+b)%P)%M。P选择一个足够大的质数,a可以任意选[1,P-1]之间的一个整数,b可以选[0,P-1]之间的任意整数,这些函数就构成了一个P*(P-1)组全域散列函数组。假设P=17,M=6,a=3,b=4,则H[3][4](8)=((3*8+4)&17)%6=5。
- 需要注意的是,每次初始化哈希表时,随机选取全域散列函数组中的一个散列(哈希)函数使用,后序增删查改都固定使用这个散列函数。否则每次哈希都是随机选一个散列函数,那么插入是一个散列函数,查找又是另一个散列函数,就会导致查找不到插入的key值。
总结:实践中,哈希表一般是选择除法散列法作为哈希函数。当然哈希表无论选择什么哈希函数,都无法避免哈希冲突,那么插入数据时,如何解决哈希冲突呢?主要有两种方法,开放定址法和链地址法。
三,处理哈希冲突
3.1,开放定址法
开放定址法中,所有元素都放到哈希表里。当一个关键字key用哈希函数计算出的位置冲突了,则按照某种规则找到一个没有存储数据的位置存储。这里的规则有三种:线性探测,二次探测,双重探测。
线性探测
- 从发生冲突的位置开始,依次向后进行 线性探测,直到寻找到一个没有存储数据的位置为止,如果走到哈希表尾,则回绕到哈希表头 的位置。
- H(key)=key%M=hash0,其中hash0代表映射的位置,如果该位置没有数据,则将key填入 。如果hash0位置已经存在数据,也就是hash0位置冲突了,则线性探测公式为:Hc(key)=(hash0+i)%M=hashi,i=0,1,2,3...,M-1。其中hashi就是经过线性探测找到没有存储数据的位置,再将key填入。
下面演示{19,30,5,36,13,20,21,12} 等映射到M=11的表中.

- 线性探测问题,假设hash0位置连续冲突,hash0,hash1,hash2已经存储数据了,后序映射到hash0,hash1,hash2的值都会 争夺hash3位置,这种现象叫做群集/堆积。下面的二次探测可以解决这个问题。
二次探测
- 从发生冲突的位置,依次左右按二次方跳跃式探测,直到寻找到下一个没有存储数据的位置为止。如果 往右走到哈希表尾,则回绕到哈希表头的位置;如果往左走到哈希表头,则会绕道哈希表尾的位置。
- H(key)=key%M=hash0,hash0位置冲突了,则二次探测公式为,Hc(key)=(hash0+/-i*i)%M,i=1,2,3..,M/=hashi.
- 二次探测结果hashi可能为负数,当hashi<0时,hashi+=M。
下面演示{19,30,52,63,11,22}映射到M=11的表中

双重探测
- 第⼀个哈希函数计算出的值发生冲突,使用第二个哈希函数计算出⼀个跟key相关的偏移量值,不断往后探测,直到寻找到下一个没有存储数据的位置为止。
- H(key)=key%M=hash0,hash0位置冲突了,则双重探测公式为:Hc(key)=(hash0+i*H2(key))%M=hashi,i=1,2,3,...,M
3.2,开放定址法代码实现
开放定址法在时间中不如下面的连地址法,所以我们选择简单的线性探测实现即可。
结构:
//当前位置的状态
//存在 空 已删除
enum State
{EXIT,EMPTY,DELETE
};template <class k,class v>
struct HashData
{pair<k, v> _kv;State _state = EMPTY;
};template <class k,class v>
class HashTable
{
private:vector<Hashdata<k, v>> _tables; //哈希表size_t n = 0; //表中存储数据的个数
};要注意的是这⾥需要给每个存储值的位置加⼀个状态标识,否则删除⼀些值以后,会影响后⾯冲突的值的查找。如下图,我们删除30,会导致查找20失败,当我们给每个位置加⼀个状态标识{EXIST,EMPTY,DELETE},删除30就可以不用删除值,而是把状态改为DELETE,那么查找20时遇到EMPTY才停,就可以找到20。

哈希表扩容问题
这里我们哈希表负载因子控制在0.7,当负载因子到0.7以后我们就需要扩容了,我们如果还是按照2倍扩 容,但是同时我们要保持哈希表大小是一个质数,第一个是质数,2倍后就不是质数了。所以我们可以按照sgi版本的哈希表使用的方法。,给了⼀个近似2倍的质数表,每次去质数表获取扩容后的大小。
inline unsigned long __stl_next_prime(unsigned long n)
{
static const int __stl_num_primes = 28;
static const unsigned long __stl_prime_list[__stl_num_primes] =
{
53, 97, 193, 389, 769,
1543, 3079, 6151, 12289, 24593,
49157, 98317, 196613, 393241, 786433,
1572869, 3145739, 6291469, 12582917, 25165843,
50331653, 100663319, 201326611, 402653189, 805306457,
1610612741, 3221225473, 4294967291
};
const unsigned long* first = __stl_prime_list;
const unsigned long* last = __stl_prime_list + __stl_num_primes;
const unsigned long* pos = lower_bound(first, last, n);
return pos == last ? *(last - 1) : *pos;
}
在需要扩容时,调用__stl_next_prime(n),在__stl_prime_list数组中查找第一个大于等于n的数组并返回。
key不能取模的问题
当key是string/Date等类型时,key不能取模,那么我们需要给HashTable增加⼀个仿函数,这个仿函 数⽀持把key转换成⼀个可以取模的整形,如果key可以转换为整形并且不容易冲突,那么这个仿函数就用默认参数即可,如果这个Key不能转换为整形我们就需要自己实现⼀个仿函数传给这个参数,实 现这个仿函数的要求就是尽量key的每个值都参与到计算中,让不同的key转换出的整形值不同。string做哈希表的key值很常见,我们可以考虑把string特化一下。
template <class k>
class HashFunc
{
size_t operator()(const k& key)
{
return (size_t)key;
}
};
//特化
template<>
struct HashFunc<string>
{
// 字符串转换成整形,可以把字符ascii码相加即可
// 但是直接相加的话,类似"abcd"和"bcad"这样的字符串计算出是相同的
// 这⾥我们使⽤BKDR哈希的思路,用上次的计算结果去乘以⼀个质数,这个质数⼀般去31, 131等效果会比较好
size_t operator()(const string& s)
{
size_t hash = 0;
for (auto ch : s)
{
hash += ch;
hash *= 131;
}
return hash;
}
};
完整代码实现
//当前位置的状态
//存在 空 已删除
enum State
{EXIT,EMPTY,DELETE
};template <class k,class v>
struct HashData
{pair<k, v> _kv;State _state = EMPTY;
};template <class k>
class HashFunc
{size_t operator()(const k& key){return (size_t)key;}
};
//特化
template<>
struct HashFunc<string>
{// 字符串转换成整形,可以把字符ascii码相加即可// 但是直接相加的话,类似"abcd"和"bcad"这样的字符串计算出是相同的// 这⾥我们使⽤BKDR哈希的思路,⽤上次的计算结果去乘以⼀个质数,这个质数⼀般去31, 131等效果会比较好size_t operator()(const string& s){size_t hash = 0;for (auto ch : s){hash += ch;hash *= 131;}return hash;}
};template<class k, class v, class Hash = HashFunc<k>>
class HashTable
{
public:HashTable():_tables(__stl_next_prime(0)), _n(0){}inline unsigned long __stl_next_prime(unsigned long n){static const int __stl_num_primes = 28;static const unsigned long __stl_prime_list[__stl_num_primes] ={53, 97, 193, 389, 769,1543, 3079, 6151, 12289, 24593,49157, 98317, 196613, 393241, 786433,1572869, 3145739, 6291469, 12582917, 25165843,50331653, 100663319, 201326611, 402653189, 805306457,1610612741, 3221225473, 4294967291};const unsigned long* first = __stl_prime_list;const unsigned long* last = __stl_prime_list + __stl_num_primes;const unsigned long* pos = lower_bound(first, last, n);return pos == last ? *(last - 1) : *pos;}bool insert(const pair<k, v>& kv){Hash hash;//负载因子>=0.7 扩容if (_n * 10 / _tables.size() >= 7){//创建一个新表HashTable<k, v, Hash> newht;//扩容newht._tables.resize(__stl_next_prime(_tables.size() + 1));//旧表数据映射到新表for (auto& data : _tables){if (data._state == EXIST)newht.insert(data._kv);}//_tables=newht._tables;_tables.swap(newht._tables);}size_t hash0 = hash(kv.first) % _tables.size();size_t hashi = hash0;int i = 1;while (_tables[hashi]._state == EXIST){//线性探测hashi = (hash0 + i) % _tables.size();//防止越界i++;}_tables[hashi]._kv = kv;_tables[hashi]._state = EXIST;_n++;return true;}HashData<k, v>* find(const k& key){Hash hash;size_t hash0 = hash(key) % _tables.size();size_t hashi = hash0;int i = 1;while (_tables[hashi]._state != EMPTY){if (_tables[hashi]._kv.first == key && _tables[hashi]._state == EXIST){return &_tables[hashi];}//线性探测hashi = (hash0 + i) % _tables.size();//防止越界i++;}return nullptr;}bool erase(const k& key){HashData<k, v>* ret = find(key);if (ret){ret->_state = DELETE;return true;}else{return false;}}
private:vector<HashData<k, v>> _tables;size_t _n;
};
3.3,链地址法
开放定址法中所有的元素都放到哈希表里,链地址法中所有的数据不再直接存储在哈希表中。哈希表 中存储一个指针,没有数据映射这个位置时,这个指针为空,有多个数据映射到这个位置时,我们把这些冲突的数据链接成⼀个链表,挂在哈希表这个位置下面,链地址法也叫做拉链法或者哈希桶。
下面演示{19,30,5,36,13,20,21,12,24,96} 等这一组值映射到M=11的表中
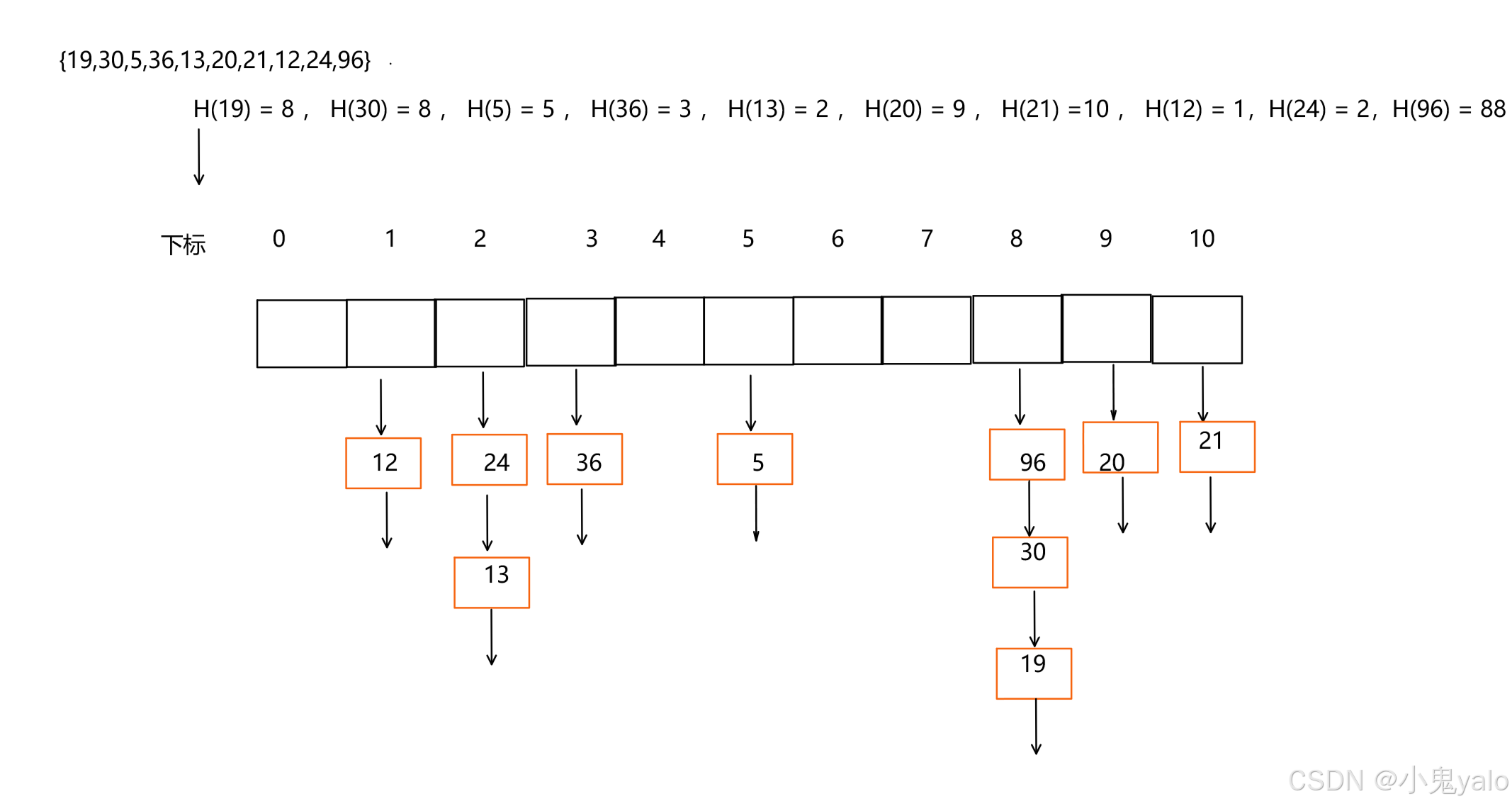
哈希表扩容问题
开放定址法负载因子必须小于1,链地址法的负载因子就没有限制了,可以大于1。负载因子越大,哈 希冲突的概率越高,空间利用率越高;负载因子越小,哈希冲突的概率越低,空间利用率越低;STL中的unordered_map和unordered_set最大复杂因子进本控制在1,大于1就开始扩容。
链地址法代码实现
//链地址法
//哈希桶
template<class k, class v>
struct HashNode
{pair<k, v> _kv;HashNode<k, v>* _next;HashNode(const pair<k, v>& kv):_kv(kv), _next(nullptr){}
};
template<class k, class v>
class Hash_bucket
{
public:typedef HashNode<k, v> Node;Hash_bucket():_tables(__stl_next_prime(0)), _n(0){}~Hash_bucket(){for (int i = 0; i < _tables.size(); i++){Node* cur = _tables[i];while (cur){Node* next = cur->_next;delete cur;cur = next;}_tables[i] = nullptr;}}inline unsigned long __stl_next_prime(unsigned long n){static const int __stl_num_primes = 28;static const unsigned long __stl_prime_list[__stl_num_primes] ={53, 97, 193, 389, 769,1543, 3079, 6151, 12289, 24593,49157, 98317, 196613, 393241, 786433,1572869, 3145739, 6291469, 12582917, 25165843,50331653, 100663319, 201326611, 402653189, 805306457,1610612741, 3221225473, 4294967291};const unsigned long* first = __stl_prime_list;const unsigned long* last = __stl_prime_list + __stl_num_primes;const unsigned long* pos = lower_bound(first, last, n);return pos == last ? *(last - 1) : *pos;}bool insert(const pair<k, v>& kv){//防止键值冗余if (find(kv.first))return false;//负载因子>=1时,扩容if (_n / _tables.size() >= 1){//创建新表vector<Node*> newtables(__stl_next_prime(_tables.size() + 1));for (int i = 0; i < _tables.size(); i++){Node* cur = _tables[i];//直接将旧表中的节点插入到新表中 所映射的位置while (cur){Node* next = cur->_next;//直接插入到新表size_t hashi = cur->_kv.first % newtables.size();cur->_next = newtables[hashi];newtables[hashi] = cur;cur = next;}}_tables.swap(newtables);}size_t hashi = kv.first % _tables.size();Node* newnode = new Node(kv);//头插到新表newnode->_next = _tables[hashi];_tables[hashi] = newnode;++_n;return true;}Node* find(const k& key){size_t hashi = key % _tables.size();Node* cur = _tables[hashi];while (cur){if (cur->_kv.first == key)return cur;cur = cur->_next;}return nullptr;}bool erase(const k& key){size_t hashi = key % _tables.size();Node* cur = _tables[hashi];Node* prev = nullptr;while (cur){if (cur->_kv.first == key){if (prev == nullptr){_tables[hashi] = cur->_next;}else{prev->_next = cur->_next;}delete cur;--_n;return true;}else{prev = cur;cur = cur->_next;}}return false;}private:vector<Node*> _tables;size_t _n;
};
小结:
哈希表这种数据结构,是利用哈希函数来快速定位数据的位置,然后存储到数组中的相应位置。
这样在查找的时候,时间复杂度可以接近O(1),非常高效。不过如果多个键被哈希到同一个位置,就会发生冲突,这时候需要解决冲突的方法,比如链地址法或者开放寻址法。
那哈希表的实现原理大概是怎样的呢?当插入一个键值对时,首先用哈希函数计算键的哈希值,然后根据哈希值找到对应的数组下标,如果该位置已经有元素了,就用链表或者其他方式处理冲突,然后存储进去。查找的时候同样计算哈希值,找到位置后,如果该位置有多个元素,需要遍历链表进行查找。好的哈希函数应该尽量均匀分布,减少冲突,这样哈希表的效率才会高。
相关文章:

【C++篇】哈希表
目录 一,哈希概念 1.1,直接定址法 1.2,哈希冲突 1.3,负载因子 二,哈希函数 2.1,除法散列法 /除留余数法 2.2,乘法散列法 2.3,全域散列法 三,处理哈希冲突 3.1&…...

Nginx开发01:基础配置
一、下载和启动 1.下载、使用命令行启动:Web开发:web服务器-Nginx的基础介绍(含AI文稿)_nginx作为web服务器,可以承担哪些基本任务-CSDN博客 注意:我配置的端口是81 2.测试连接是否正常 访问Welcome to nginx! 如果…...

mysqldump+-binlog增量备份
注意:二进制文件删除必须使用help purge 不可用rm -f 会崩 一、概念 增量备份:仅备份上次备份以后变化的数据 差异备份:仅备份上次完全备份以后变化的数据 完全备份:顾名思义,将数据完全备份 其中,…...

hive:数据导入,数据导出,加载数据到Hive,复制表结构
hive不建议用insert,因为Hive是建立在Hadoop之上的数据仓库工具,主要用于批处理和大数据分析,而不是为OLTP(在线事务处理)操作设计的。INSERT操作会非常慢 数据导入 命令行界面:建一个文件 查询数据>>复制>>粘贴到新…...

【工欲善其事】利用 DeepSeek 实现复杂 Git 操作:从原项目剥离出子版本树并同步到新的代码库中
文章目录 利用 DeepSeek 实现复杂 Git 操作1 背景介绍2 需求描述3 思路分析4 实现过程4.1 第一次需求确认4.2 第二次需求确认4.3 第三次需求确认4.4 V3 模型:中间结果的处理4.5 方案验证,首战告捷 5 总结复盘 利用 DeepSeek 实现复杂 Git 操作 1 背景介绍…...

mac 手工安装OpenSSL 3.4.0
如果你希望继续安装 openssl-3.4.0 而不是降级到 3.1.1,可以尝试以下解决方案。根据你提供的错误信息,问题可能出在测试阶段(make test),我们可以尝试跳过测试或修复测试失败的原因。 --- ### **解决方案:…...

构建一个数据分析Agent:提升分析效率的实践
在上一篇文章中,我们讨论了如何构建一个智能客服Agent。今天,我想分享另一个实际项目:如何构建一个数据分析Agent。这个项目源于我们一个金融客户的真实需求 - 提升数据分析效率,加快决策速度。 从分析师的痛点说起 记得和分析师团队交流时的场景: 小张ÿ…...

【SRC排名】安全应急响应中心SRC上榜记录
2023年 新氧第三 https://security.soyoung.com/top 合合第四 https://security.intsig.com/index.php?m&chall&aindex 2024年 好未来第一 https://src.100tal.com/index.php?m&chall&aindex(官网是总榜,年榜只有海报)…...

截止到2025年2月1日,Linux的Wayland还有哪些问题是需要解决的?
截至2025年2月1日,Wayland需要解决的核心问题可按权重从高到低排序如下: 1. 屏幕共享与远程桌面的完整支持(权重:★★★★★) 问题:企业场景(如 腾讯会议)、开发者远程调试依赖稳定的屏幕共享功能。当前Wayland依赖PipeWire和XWayland,存在权限管理复杂、多显示器选择…...

TCP编程
1.socket函数 int socket(int domain, int type, int protocol); 头文件:include<sys/types.h>,include<sys/socket.h> 参数 int domain AF_INET: IPv4 Internet protocols AF_INET6: IPv6 Internet protocols AF_UNIX, AF_LOCAL : Local…...
)
Java泛型深度解析(JDK23)
第一章 泛型革命 1.1 类型安全的进化史 前泛型时代的类型转换隐患 代码的血泪史(Java 1.4版示例): List rawList new ArrayList(); rawList.add("Java"); rawList.add(Integer.valueOf(42)); // 编译通过// 灾难在运行时爆发…...

【JavaEE进阶】图书管理系统 - 壹
目录 🌲序言 🌴前端代码的引入 🎋约定前后端交互接口 🚩接口定义 🍃后端服务器代码实现 🚩登录接口 🚩图书列表接口 🎄前端代码实现 🚩登录页面 🚩…...
)
搜索旋转排序数组(二分查找)
测试链接:https://leetcode.cn/problems/search-in-rotated-sorted-array/https://leetcode.cn/problems/search-in-rotated-sorted-array/https://leetcode.cn/problems/search-in-rotated-sorted-array/ 问题描述 假设我们有一个旋转排序的数组,这个…...

STM32 TIM定时器配置
TIM简介 TIM(Timer)定时器 定时器可以对输入的时钟进行计数,并在计数值达到设定值时触发中断 16位计数器、预分频器、自动重装寄存器的时基单元,在72MHz计数时钟下可以实现最大59.65s的定时 不仅具备基本的定时中断功能ÿ…...

AI开发之 ——Anaconda 介绍
Anaconda 是什么? 在这里插入图片描述 一句话:Anaconda 是Python 库和环境便捷管理的平台。 Anaconda 是数据科学和 AI 领域的工具,通过集成常用库和工具,简化了环境管理和包安装,特别适合初学者和需要快速上手的开…...
:从均方误差到绝对误差的完美过渡)
Uber损失(Huber Loss):从均方误差到绝对误差的完美过渡
前言 在机器学习的世界里,损失函数就像是你在迷宫中的导航系统,它决定了你到底能否顺利找到出口,而出口的大小就代表着模型的表现。而在这么多的“导航系统”中,Huber损失(你可以叫它“Uber损失”,我觉得这名字挺有意思的,能不能打车到一个更好的模型呢?)凭借其独特的…...

【Arxiv 大模型最新进展】TOOLGEN:探索Agent工具调用新范式
【Arxiv 大模型最新进展】TOOLGEN:探索Agent工具调用新范式 文章目录 【Arxiv 大模型最新进展】TOOLGEN:探索Agent工具调用新范式研究框图方法详解 作者:Renxi Wang, Xudong Han 等 单位:LibrAI, Mohamed bin Zayed University o…...

41【文件名的编码规则】
我们在学习的过程中,写出数据或读取数据时需要考虑编码类型 火山采用:UTF-16 易语言采用:GBK php采用:UTF-8 那么我们写出的文件名应该是何种编码的?比如火山程序向本地写出一个“测试.txt”,理论上这个“测…...

Linux命令入门
Linux命令入门 ls命令 ls命令的作用是列出目录下的内容,语法细节如下: 1s[-a -l -h] [Linux路径] -a -l -h是可选的选项 Linux路径是此命令可选的参数 当不使用选项和参数,直接使用ls命令本体,表示:以平铺形式,列出当前工作目录下的内容 ls命令的选项 -a -a选项&a…...
)
如何用函数去计算x年x月x日是(C#)
如何用函数去计算x年x月x日是? 由于现在人工智能的普及,我们往往会用计算机去算,或者去记录事情 1.计算某一年某一个月有多少天 2.计算某年某月某日是周几 using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threadin…...

29.Word:公司本财年的年度报告【13】
目录 NO1.2.3.4 NO5.6.7 NO8.9.10 NO1.2.3.4 另存为F12:考生文件夹:Word.docx选中绿色标记的标题文本→样式对话框→单击右键→点击样式对话框→单击右键→修改→所有脚本→颜色/字体/名称→边框:0.5磅、黑色、单线条:点…...

Flutter常用Widget小部件
小部件Widget是一个类,按照继承方式,分为无状态的StatelessWidget和有状态的StatefulWidget。 这里先创建一个简单的无状态的Text小部件。 Text文本Widget 文件:lib/app/app.dart。 import package:flutter/material.dart;class App exte…...

高可用 Keepalived 服务部署流程
一、配置文件 vim /etc/keepalived/keepalived.confGLOBAL CONFIGURATION --- 全局配置部分VRRPD CONFIGURATION --- VRRP协议配置部分LVS CONFIGURATION --- LVS服务管理配置部分[rootlb01 ~]# cat /etc/keepalived/keepalived.…...

网站结构优化:加速搜索引擎收录的关键
本文来自:百万收录网 原文链接:https://www.baiwanshoulu.com/9.html 网站结构优化对于加速搜索引擎收录至关重要。以下是一些关键策略,旨在通过优化网站结构来提高搜索引擎的抓取效率和收录速度: 一、合理规划网站架构 采用扁…...

【深度学习】softmax回归的从零开始实现
softmax回归的从零开始实现 (就像我们从零开始实现线性回归一样,)我们认为softmax回归也是重要的基础,因此(应该知道实现softmax回归的细节)。 本节我们将使用Fashion-MNIST数据集,并设置数据迭代器的批量大小为256。 import torch from IP…...

AMS仿真方法
1. 准备好verilog文件。并且准备一份.vc文件,将所有的verilog file的路径全部写在里面。 2. 将verilog顶层导入到virtuoso中: 注意.v只要引入顶层即可。不需要全部引入。实际上顶层里面只要包含端口即可,即便是空的也没事。 引入时会报warni…...

多模态论文笔记——ViViT
大家好,这里是好评笔记,公主号:Goodnote,专栏文章私信限时Free。本文详细解读多模态论文《ViViT: A Video Vision Transformer》,2021由google 提出用于视频处理的视觉 Transformer 模型,在视频多模态领域有…...

Flink2支持提交StreamGraph到Flink集群
最近研究Flink源码的时候,发现Flink已经支持提交StreamGraph到集群了,替换掉了原来的提交JobGraph。 新增ExecutionPlan接口,将JobGraph和StreamGraph作为实现。 Flink集群Dispatcher也进行了修改,从JobGraph改成了接口Executio…...

机器学习优化算法:从梯度下降到Adam及其变种
机器学习优化算法:从梯度下降到Adam及其变种 引言 最近deepseek的爆火已然说明,在机器学习领域,优化算法是模型训练的核心驱动力。无论是简单的线性回归还是复杂的深度神经网络,优化算法的选择直接影响模型的收敛速度、泛化性能…...

2024具身智能模型汇总:从训练数据、动作预测、训练方法到Robotics VLM、VLA
前言 本文一开始是属于此文《GRAPE——RLAIF微调VLA模型:通过偏好对齐提升机器人策略的泛化能力》的前言内容之一(该文发布于23年12月底),但考虑到其重要性,加之那么大一张表格 看下来 阅读体验较差,故抽出取来独立成文且拆分之 …...

基于Spring Security 6的OAuth2 系列之七 - 授权服务器--自定义数据库客户端信息
之所以想写这一系列,是因为之前工作过程中使用Spring Security OAuth2搭建了网关和授权服务器,但当时基于spring-boot 2.3.x,其默认的Spring Security是5.3.x。之后新项目升级到了spring-boot 3.3.0,结果一看Spring Security也升级…...

当WebGIS遇到智慧文旅-以长沙市不绕路旅游攻略为例
目录 前言 一、旅游数据组织 1、旅游景点信息 2、路线时间推荐 二、WebGIS可视化实现 1、态势标绘实现 2、相关位置展示 三、成果展示 1、第一天旅游路线 2、第二天旅游路线 3、第三天旅游路线 4、交通、订票、住宿指南 四、总结 前言 随着信息技术的飞速发展&…...

浅析CDN安全策略防范
CDN(内容分发网络)信息安全策略是保障内容分发网络在提供高效服务的同时,确保数据传输安全、防止恶意攻击和保护用户隐私的重要手段。以下从多个方面详细介绍CDN的信息安全策略: 1. 数据加密 数据加密是CDN信息安全策略的核心之…...
)
Python安居客二手小区数据爬取(2025年)
目录 2025年安居客二手小区数据爬取观察目标网页观察详情页数据准备工作:安装装备就像打游戏代码详解:每行代码都是你的小兵完整代码大放送爬取结果 2025年安居客二手小区数据爬取 这段时间需要爬取安居客二手小区数据,看了一下相关教程基本…...

Python爬虫获取custom-1688自定义API操作接口
一、引言 在电子商务领域,1688作为国内领先的B2B平台,提供了丰富的API接口,允许开发者获取商品信息、店铺信息等。其中,custom接口允许开发者进行自定义操作,获取特定的数据。本文将详细介绍如何使用Python调用1688的…...

CAPL与外部接口
CAPL与外部接口 目录 CAPL与外部接口1. 引言2. CAPL与C/C++交互2.1 CAPL与C/C++交互简介2.2 CAPL与C/C++交互实现3. CAPL与Python交互3.1 CAPL与Python交互简介3.2 CAPL与Python交互实现4. CAPL与MATLAB交互4.1 CAPL与MATLAB交互简介4.2 CAPL与MATLAB交互实现5. 案例说明5.1 案…...

解析与使用 Apache HttpClient 进行网络请求和数据抓取
目录 1. 什么是 HttpClient? 2. 基本使用 3. 使用 HttpClient 爬取腾讯天气的数据 4. 爬取拉勾招聘网站的职位信息 5. 总结 前言 Apache HttpClient 是 Apache 提供的一个用于处理 HTTP 请求和响应的工具类库。它提供了一种便捷、功能强大的方式来发送 HTTP 请…...

【go语言】结构体
一、type 关键字的用法 在 go 语言中,type 关键字用于定义新的类型,他可以用来定义基础类型、结构体类型、接口类型、函数类型等。通过 type 关键字,我们可以为现有类型创建新的类型别名或者自定义新的类型。 1.1 类型别名 使用 type 可以为…...

Kotlin 委托详解
Kotlin 委托详解 引言 Kotlin 作为一种现代化的编程语言,在 Android 开发等领域得到了广泛的应用。在 Kotlin 中,委托(Delegation)是一种强大的特性,它可以让我们以更简洁的方式实现代码的复用和扩展。本文将详细解析…...

用QT做一个网络调试助手
文章目录 前言一、TCP网络调试助手介绍1. 项目概述2. 开发流程3. TCP服务器的关键流程4. TCP客户端的关键流程 二、实现UI界面1. 服务器界面2. 客户端界面 三、实现代码框架1. 服务器代码1.1 初始化服务器地址1.2 开始监听1.3 与客户端连接1.4 接收客户端信息1.5 判断客户端状态…...

Qt 5.14.2 学习记录 —— 이십이 QSS
文章目录 1、概念2、基本语法3、给控件应用QSS设置4、选择器1、子控件选择器2、伪类选择器 5、样式属性box model 6、实例7、登录界面 1、概念 参考了CSS,都是对界面的样式进行设置,不过功能不如CSS强大。 可通过QSS设置样式,也可通过C代码…...

HTML 符号详解
HTML 符号详解 引言 HTML(超文本标记语言)符号是HTML文档中用来表示特殊字符的标记。这些符号在日常网页设计和开发中扮演着重要角色,特别是在需要显示版权、商标、货币符号等特殊字符时。本文将详细介绍HTML符号的用法、类型以及如何在HTML文档中插入这些符号。 HTML符号…...

第十二章 I 开头的术语
文章目录 第十二章 I 开头的术语以 I 开头的术语被识别 (identified by)识别关系 (identifying relationship)身份 (identity)idkey隐式全局引用 (implicit global reference)隐含命名空间 (implied namespace)包含文件 (include file)传入锁 (incoming lock) 索引 (index)索引…...
)
用XAMPP安装PHP环境(Window系统)
视频教程 BV1jA411v791 进入XAMPP官网 Download XAMPP 找到最新版本,64位的下载,一路安装,语言只有英语德语两个(不会德语) 安装好以后启动软件,点Apache,MySql,start 在C:\xampp\…...

02.01 生产者消费者
请使用条件变量实现2生产者2消费者模型,注意1个生产者在生产的时候,另外一个生产者不能生产。 1>程序代码 #include <stdio.h> #include <string.h> #include <unistd.h> #include <stdlib.h> #include <sys/types.h>…...

区块链项目孵化与包装设计:从概念到市场的全流程指南
区块链技术的快速发展催生了大量创新项目,但如何将一个区块链项目从概念孵化成市场认可的产品,是许多团队面临的挑战。本文将从孵化策略、包装设计和市场落地三个维度,为你解析区块链项目成功的关键步骤。 一、区块链项目孵化的核心要素 明确…...

Redis|前言
文章目录 什么是 Redis?Redis 主流功能与应用 什么是 Redis? Redis,Remote Dictionary Server(远程字典服务器)。Redis 是完全开源的,使用 ANSIC 语言编写,遵守 BSD 协议,是一个高性…...

电脑优化大师-解决电脑卡顿问题
我们常常会遇到电脑运行缓慢、网速卡顿的情况,但又不知道是哪个程序在占用过多资源。这时候,一款能够实时监控网络和系统状态的工具就显得尤为重要了。今天,就来给大家介绍一款小巧实用的监控工具「TrafficMonitor」。 「TrafficMonitor 」是…...

Linux篇——权限
在生活中我们知道,一个人能够从事的工作或任务,不是取决于你是谁,而是取决于你的身份是什么,就比如同一个人,如果他是校长,那就可以说放假就放假,如果是学生,就没有这个决定的权力。…...
:Nadam Optimize)
Python 梯度下降法(六):Nadam Optimize
文章目录 Python 梯度下降法(六):Nadam Optimize一、数学原理1.1 介绍1.2 符号定义1.3 实现流程 二、代码实现2.1 函数代码2.2 总代码 三、优缺点3.1 优点3.2 缺点 四、相关链接 Python 梯度下降法(六):Nad…...
