
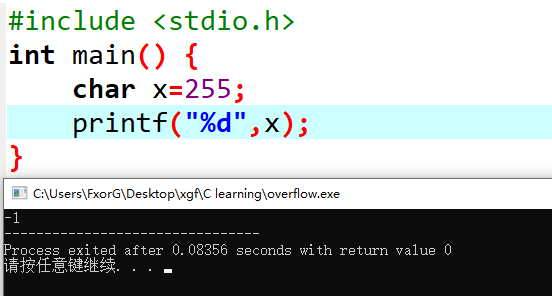
这个 negative(i) 表示的就是 (-i) 这个数(其中 i>=0),在二进制下的编码。
这个编码满足 \(i+negative(i)=2^k\),可是由于我们二进制下只有 \(k\) 位,最高位是 \(2^{k-1}\),所以那个 \(1\) 会被丢掉,所以加起来结果为 \(0\)。
那如何确定一个数被存储为多少,因为前面那些它都会被舍弃,我们可以在 \(\mod 256\) 下找对应编号,以及编号对应的值,比如 \(- 1 \mod 256=255\),所以我们找到编号为 255 的值是 -1,而 -1 的编号就是 255,也就是我们变量里可以看成存的是编号,实际的值我们要去找对应。
对于我们赋值为 255,最后却输出了 -1,这种东西就叫 溢出(overflow)
负数&补码
好的,我们来详细讲解一下这张图片所传达的核心概念——计算机中负数的表示方法,也就是补码(Complement)。
这张图是一个非常直观的教学材料,它系统地解释了为什么以及如何用补码来表示负数。
核心思想:什么是“补”?
图片左侧首先解释了“补”的概念:
a + b = 常数,则称a是b的补,b是a的补。
这就像我们日常生活中:
- 在十进制里,7 是 3 关于10的补数,因为 7 + 3 = 10。
- 在时钟上,11点 也可以看作是 -1点 关于12的补数,因为 11 + 1 = 12。
计算机借鉴了这个聪明的思想,但它的世界是二进制的,所以这个“常数”是 2 的 k 次方(k是二进制数的位数)。
二进制的补:补码的定义
图片给出了二进制补码的计算公式:
Negative(i) = 2^k - i
- k: 代表数据的位数。例如,一个字节(byte)由8个比特(bit)组成,所以 k = 8。
- i: 我们想要表示的正数。
- Negative(i): 我们要求得的负数 -i 的二进制表示(即补码)。
举个例子(k=8):
我们想求十进制数 5 的负数表示。
Negative(5) = 2^8 - 5 = 256 - 5 = 251
所以,十进制数 251 所对应的二进制码,就代表了 -5。
这也解释了图片中的另一个要点:
负数 + 对应的正数 = 256
(5 + 251 = 256)
深入理解:字节(Byte)的例子
图片以 8 位的字节(Byte)为例进行了说明,这是理解补码最经典的场景。
-
取值范围:一个字节可以表示 2^8 = 256 个不同的值。
- 正数:
0到127(共128个) - 负数:
-1到-128(共128个) - 没有 +0 和 -0:这是补码设计的精妙之处,它完美地解决了“零”有两种表示的问题。
- 正数:
-
符号位 (Sign Bit):
- 图片指出:“负数第一位是1正数是0,所以它称为符号位”。
- 在8位二进制中,最高位(最左边的那一位)就是符号位。
- 0 开头的数字是正数或零。(例如:
0xxxxxxx) - 1 开头的数字是负数。(例如:
1xxxxxxx)
- 0 开头的数字是正数或零。(例如:
- 这让我们能非常快速地判断一个数是正还是负。
-
-1 的特殊性:
- 图片提到 “-1即是从第k位借位减一,一定是全111...111”。
- 根据公式:
Negative(1) = 256 - 1 = 255 - 255 的二进制表示正是
1111 1111。 - 你可以把它想象成 “向高位借1”(也就是256),然后减去1,结果自然是255(即8个1)。这在数学上和电路设计上都非常方便。
解读右侧的对照表
右侧的表格是以上所有理论的具体实践。它清晰地展示了:
- 绿色部分(上半部分):正数。从
0(二进制0000 0000) 开始,向上递增到127(二进制0111 1111)。注意,所有正数的符号位都是 0。 - 红色部分(下半部分):负数(补码形式)。从
-1(二进制1111 1111) 开始,向下递减(数值变小)到-128(二进制1000 0000)。注意,所有负数的符号位都是 1。 - 黑色箭头:指示了二进制码本身的数值(如果把它当作无符号数来看)是从上到下递增的。
0000 0000(0) 最小,1111 1111(255) 最大。- 这带来了一个巨大的好处:计算机的CPU不需要为有符号数设计专门的加法器!
- 例如,计算
5 + (-3):5的补码是0000 0101-3的补码是1111 1101(因为 256 - 3 = 253,253的二进制是1111 1101)- 直接把两个二进制码相加:
0000 0101 + 1111 1101 = 1 0000 0010 - 由于byte只有8位,最高位的1被舍弃,剩下
0000 0010,这正是十进制2的补码!结果完全正确。
总结
这张图片精炼地介绍了计算机表示负数的核心方法——补码。
- 目的:为了解决计算机中负数的存储和计算问题。
- 原理:利用“补数”的概念,用正数编码来表示对应的负数。
负数的补码 = 模 - 正数的值。 - 特点:
- 有符号位,最高位为1代表负数。
- 0有唯一的表示(全0)。
- 表示范围不对称(例如byte是 -128 ~ +127)。
- 优势:可以将减法运算转换为加法运算,极大简化了CPU内部硬件电路的设计。这是补码方案成为业界标准的最主要原因。
希望这个讲解能帮助你彻底理解这张图的内容!
原码&反码&补码
好的,我们来系统地梳理一下 原码、反码、补码 这三种表示方法,它们都是为了解决同一个核心问题:如何在计算机中用二进制表示有符号整数(正数、负数和零)?
计算机的CPU只有加法器,没有减法器。为了让它能计算 5 - 3,我们需要想办法把 -3 表示出来,并且让 5 + (-3) 能得到正确的结果 2。这三种编码就是历史上出现的不同解决方案。
1. 原码 (Sign-Magnitude)
- 核心思想:最直观的想法
- 用最高位表示符号:
0代表正数,1代表负数。 - 剩下的位表示这个数的绝对值(大小)。
- 用最高位表示符号:
- 例子 (8位):
+5:0000 0101(符号位0 + 5的二进制)-5:1000 0101(符号位1 + 5的二进制)+0:0000 0000-0:1000 0000(问题来了!)
- 优点:
- 非常直观,人类最容易理解。
- 致命缺点:
- 存在两个零 (
+0和-0): 这不仅浪费了一个编码组合,还会在比较和运算时带来麻烦(计算机需要额外判断0 == -0为真)。 - 加减运算复杂: CPU不能直接用加法器进行运算。
- 例如计算
5 + (-3):- 原码:
0000 0101+1000 0011=1000 1000(即-8),这显然是错误的!
- 原码:
- 进行加减法时,CPU需要先判断符号位:
- 如果符号相同,做加法,结果符号不变。
- 如果符号不同,要用绝对值大的数减去绝对值小的数,结果的符号取绝对值大的数的符号。
- 这需要额外的逻辑电路,效率低下。
- 例如计算
- 存在两个零 (
总结: 原码虽然直观,但存在 ±0 问题和复杂的运算逻辑,不适合计算机硬件实现。
2. 反码 (Ones' Complement)
- 核心思想:尝试解决运算问题
- 正数的反码 = 其原码。
- 负数的反码 = 其原码的符号位不变,其他位按位取反(
0变1,1变0)。
- 例子 (8位):
+5:0000 0101(和原码一样)-5:- 原码:
1000 0101 - 符号位不变:
1 - 其他位取反:
111 1010 - 反码:
1111 1010
- 原码:
+0:0000 0000-0:- 原码:
1000 0000 - 反码:
1111 1111(问题依然存在!)
- 原码:
- 优点(相比原码):
- 进行加法运算时,如果最高位有进位,需要把这个进位加回到结果的最低位(称为“循环进位”或“回绕”)。这样,加法器可以统一处理正负数相加(至少在部分情况下)。
- 例如计算
5 + (-3):5的反码:0000 0101-3的反码:1111 1100(3是0000 0011,取反1111 1100)- 相加:
0000 0101 + 1111 1100 = 1 0000 0001(产生进位) - 把进位
1加回最低位:0000 0001 + 1 = 0000 0010(即2,正确!)
- 例如计算
- 进行加法运算时,如果最高位有进位,需要把这个进位加回到结果的最低位(称为“循环进位”或“回绕”)。这样,加法器可以统一处理正负数相加(至少在部分情况下)。
- 缺点:
- 仍然存在两个零 (
+0和-0):0000 0000和1111 1111。 - 循环进位增加硬件复杂度: 每次加法都需要判断是否有进位并处理,降低了效率。
- 表示范围不对称: 对于8位,范围是
-127 (1111 1111)到+127 (0111 1111),缺少了-128。
- 仍然存在两个零 (
总结: 反码解决了原码的部分运算问题(加法可以统一处理),但 ±0 问题和循环进位依然存在,效率不够理想。
3. 补码 (Two's Complement) - 现代计算机的标准!
- 核心思想:完美解决
±0和运算问题- 正数的补码 = 其原码。
- 负数的补码 = 其反码 + 1。
- 或者更本质地: 负数的补码 =
2^k - |X|(k是位数)。对于8位,2^8 = 256,所以-5的补码是256 - 5 = 251(1111 1011)。
- 例子 (8位):
+5:0000 0101(和原码、反码一样)-5:- 原码:
1000 0101 - 反码:
1111 1010 - 反码 + 1:
1111 1010 + 1 = 1111 1011(1111 1011) - (或
256 - 5 = 251->1111 1011)
- 原码:
+0:0000 0000-0: 不存在!- 计算
-0的补码:- 原码:
1000 0000 - 反码:
1111 1111 - 反码 + 1:
1111 1111 + 1 = 1 0000 0000(9位)。舍弃最高位进位,剩下0000 0000。结果和+0相同!
- 原码:
- 计算
- 额外收获:
1000 0000这个原本可能表示-0的编码,被赋予了新的意义:-128。- 因为
1000 0000作为无符号数是128,根据补码定义128 - 256 = -128。
- 因为
- 优点:
- 唯一的零 (
0):0000 0000。解决了±0的歧义和浪费。 - 运算最简单: 加法器可以直接用于加法和减法! 不需要判断符号位,不需要循环进位。
- 计算
5 + (-3):5的补码:0000 0101-3的补码:1111 1101(3是0000 0011,取反1111 1100,加11111 1101)- 相加:
0000 0101 + 1111 1101 = 1 0000 0010(产生进位) - 舍弃最高位进位,剩下
0000 0010(即2,正确!)
- 计算
3 - 5等价于3 + (-5):3的补码:0000 0011-5的补码:1111 1011- 相加:
0000 0011 + 1111 1011 = 1111 1110 - 结果
1111 1110是补码。最高位是1,说明是负数。求其数值:- 方法1:
1111 1110作为无符号数是254,254 - 256 = -2。 - 方法2: 对
1111 1110取反(得0000 0001)再加1(得0000 0010,即2),所以原值是-2。正确!
- 方法1:
- 计算
- 表示范围更合理 (不对称但连续): 对于8位,范围是
-128 (1000 0000)到+127 (0111 1111)。比反码多表示了一个数 (-128)。
- 唯一的零 (
总结: 补码完美解决了 ±0 问题,并使得加法和减法运算可以用同一个加法器电路完成,极大地简化了CPU的设计,提高了效率。这就是为什么现代计算机全部使用补码来表示整数。
总结对比表 (以8位为例)
| 特性 | 原码 (Sign-Magnitude) | 反码 (Ones' Complement) | 补码 (Two's Complement) ✅ |
|---|---|---|---|
| 正数表示 | 符号位0 + 绝对值 | 同原码 | 同原码 |
| 负数表示 | 符号位1 + 绝对值 | 符号位不变,其他位取反 | 反码 + 1 (或 `2^k - |
| +0 | 0000 0000 |
0000 0000 |
0000 0000 |
| -0 | 1000 0000 (存在问题) |
1111 1111 (存在问题) |
不存在! (0000 0000) |
| 最小数 | 1111 1111 = -127 |
1000 0000 = -127¹ |
1000 0000 = -128 |
| 最大数 | 0111 1111 = +127 |
0111 1111 = +127 |
0111 1111 = +127 |
| 零的个数 | 2 (+0, -0) |
2 (+0, -0) |
1 (0) |
| 加减运算 | 复杂,需判断符号和绝对值 | 较复杂,需处理循环进位 | 简单!直接相加,舍弃进位 |
| 硬件实现 | 复杂,效率低 | 较复杂,效率较低 | 简单,效率高 |
| 现代应用 | 基本不用 | 基本不用 | 唯一标准 |
¹ 反码的 1000 0000 通常表示 -127,1111 1111 表示 -0。严格来说最小数是 -127。
一句话记住:
- 原码: 直观但有
±0,运算麻烦。 - 反码: 改进运算但有
±0,要循环进位。 - 补码: 消灭
-0,统一加减法,硬件最爱!👍
理解补码是理解计算机如何做整数运算的基础。希望这个详细的解释能帮你理清思路!











































)


)



